前方交会法

浅述电站建设中极坐标放样法与前方交会法一、前言在核电建设过程中，为了使各建筑物中的设备、预埋件及管道等位置在施工过程中始终处于准确的受控状态，施工放样尤为重要。

施工放样的方法很多，如极坐标法、前方交会法、距离交会法等等。

测量技术人员必须兼顾效率、成本及精度要求而采用不同的放样方法，本文结合工程实践，就核电站建设常用的极坐标法放样及前方交会法放样法进行探讨。

二、极坐标法放样1、原理极坐标法放样是利用数学中的极坐标原理，以两个控制点的连线作为极轴，以其中一点作为极点建立极坐标系，根据放样点与控制点的坐标，计算出放样点到极点的距离（极距S）及放样点与极点连线方向和极轴间的夹角（极角）。

极距S、极角即为放样数据。

2、作业步骤（1）如上图，在C点架设全站仪，对中整平，后视B点（2）测设角度，（3）在CA方向上测设距离S（4）标定点位A。

3、精度分析：从上述步骤分析，其主要误差来源包括：架设仪器的对中误差、测角误差、测距误差和标定误差。

这里假定控制点的误差对下一级网影响较小，可忽略不计。

（1）对中误差，一般的光学对点器，其对点精度在0.5mm左右，若利用强制观测墩或者采用徕卡天底仪（NL）对点，我们常将其忽略不计。

（2）测角误差对放样点位的影响为。

（3）测距误差在工程建设中一般用全站仪来测设距离，距离测设的精度主要取决于（不考虑地球曲度，大气折光的影响）仪器的测距所能达到的精度和仪器的对中、反射镜对中杆铅直误差三个方面。

①测距仪的测距精度测距仪本身的测距精度，是指各种仪器所标称的精度指标，常用A+B*s表示。

例如：徕卡TCA2003全站仪，其测距精度为±（1mm+1ppm×s）.其中1mm为该测距仪的固定误差，1 ppm.·s为比例误差。

当D=100 m 时，所引起的测距误差设为，则有：= ± 1mm+1×10¬¬¬¬¬¬¬¬¬¬¬¬¬ ×100000= ± 1.1mm②对中杆倾斜引起的距离误差对中杆的铅直是以圆气泡居中为标准的，实际工作中，人持对中杆进行放样，要使对中杆铅直是非常困难的，因为圆气泡总有偏差。

前方交会实验报告1. 实验目的本实验的目的是通过前方交会方法测量两个点之间的距离和方位角，以及计算出测量误差，并分析误差来源。

2. 实验原理前方交会是一种基本的测量方法，用于确定两点之间的距离和方位角。

根据测量的原理，通过测量基线上A、B两个测站到待测点C的角度，再测量出A、B两个测站之间的方位角，即可计算出C点的坐标。

前方交会方法包括以下几个步骤：1.安装测量仪器：在点A和点B上，分别设置测站，安装全站仪或其他测量仪器。

2.观测角度：从点A观测点C的水平角和垂直角，从点B观测点C的水平角和垂直角。

3.计算方位角：根据测量仪器的读数和设定的测量参数，计算出A、B两个测站之间的方位角。

4.计算距离：根据测量仪器的读数和设定的测量参数，分别计算出A、B两个测站到点C的距离。

5.计算C点坐标：根据前面步骤得到的测量数据和计算结果，通过三角测量原理，计算出点C的坐标。

6.分析误差来源：根据实际测量和计算结果，分析误差的来源，并对测量结果进行评估和修正。

3. 实验步骤1.在实验区域内分别设置测站A和测站B，并确保两个测站之间有明显的目标点C供观测。

2.使用全站仪或其他测量仪器，分别观测点A和点B 到目标点C的水平角和垂直角，并记录测量数据。

3.根据测量数据，计算出测站A和测站B之间的方位角。

4.根据测量数据和方位角，计算出测站A到目标点C的距离，以及测站B到目标点C的距离。

5.使用三角测量原理，计算出目标点C的坐标。

6.分析误差的来源，评估测量结果的准确性，并进行相应的修正。

4. 实验数据和计算结果以下是实验中测量得到的数据和计算出的结果：•测站A到目标点C的水平角：30°•测站A到目标点C的垂直角：60°•测站B到目标点C的水平角：50°•测站B到目标点C的垂直角：40°•测站A和测站B之间的方位角：100°•测站A到目标点C的距离：50米•测站B到目标点C的距离：60米•目标点C的坐标：(100, 200)根据以上数据和计算结果，可以得出点C的坐标为(100, 200)。

一、交会法概述
是一种经常采用的加密控制点的方法。

常用的几种方法有：前方交会、是一种经常采用的加密控制点的方法。

常用的几种方法有：前方交会、侧方交会、侧方交会、侧方交会、后方后方交会。

1.前方交会
如果已知A 、B 两点的坐标，为了计算未知点P 的坐标，只要观测∠A 和∠B 即可。

这种测定未知点P 的平面坐标的方法称为前方交会。

2.侧方交会
若观测∠A 和∠P 或∠B 和∠P ，同样可以测定未知点P 的平面坐标，这种方法称为侧方交会。

3.后方交会
若在未知点P 上瞄准A 、B 、C 三个已知点，测得∠α和∠β，也可确定
未知点P的平面坐标，这种方法称为后方交会。

二、前方交会法加密控制点
已知条件A、B两点坐标分别为(x A,y B)、(x B,y B)，求p点的坐标。

待求数据p点的坐标(X p,Y p) 观测数据
为确定P点的位置，经纬仪分别安置A、B两点，用测回法观测∠A、∠B 坐标计算
根据A、B两点的坐标和∠A、∠B，P点坐标为
Welcome To
Download
欢迎您的下载，资料仅供参考！。

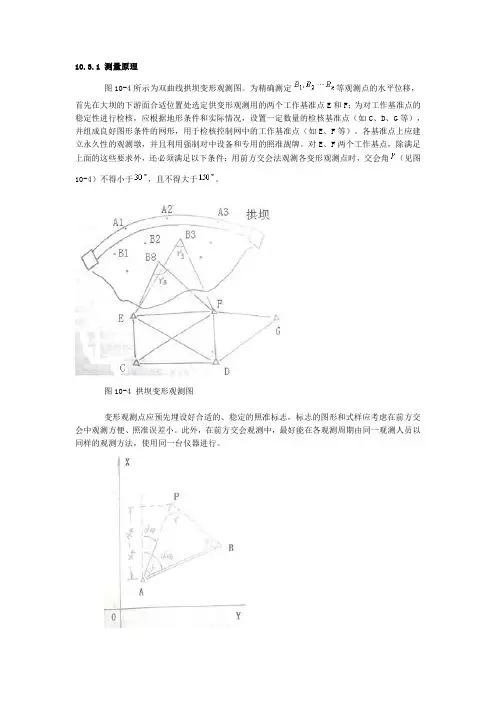
10.3.1 测量原理图10-4所示为双曲线拱坝变形观测图。

为精确测定等观测点的水平位移，首先在大坝的下游面合适位置处选定供变形观测用的两个工作基准点E和F；为对工作基准点的稳定性进行检核，应根据地形条件和实际情况，设置一定数量的检核基准点（如C、D、G等），并组成良好图形条件的网形，用于检核控制网中的工作基准点（如E、F等）。

各基准点上应建立永久性的观测墩，并且利用强制对中设备和专用的照准觇牌。

对E、F两个工作基点，除满足上面的这些要求外，还必须满足以下条件：用前方交会法观测各变形观测点时，交会角（见图10-4）不得小于，且不得大于。

图10-4 拱坝变形观测图变形观测点应预先埋设好合适的、稳定的照准标志，标志的图形和式样应考虑在前方交会中观测方便、照准误差小。

此外，在前方交会观测中，最好能在各观测周期由同一观测人员以同样的观测方法，使用同一台仪器进行。

图10-5 角度前方交会法测量原理利用前方交会法测量水平位移的原理如下：如图10-5所示，A、B两点为工作基准点，P为变形观测点，假设测得两水平夹角为，则由A、B两点的坐标值和水平角观测值、可求得P点的坐标。

从图10-5可见：（10-3a）（10-3b）其中可由A、B两点的坐标值通过“坐标反算”求得，经过对（10-3）式的整理可得：（10-4a）（10-4b）第一次观测时，假设测得两水平夹角为和，由（10-4）式求得P点坐标值为，第二次观测时，假设测得的水平夹角为和，则P点坐标值变为，那么在此两期变形观测期间，P点的位移可按下式解算：，，P点的位移方向为：。

10.3.2 前方交会法的种类前方交会法有三种：测角前方交会法、测边前方交会法、边角前方交会法。

其观测值和观测仪器见表10-5。

表10-5 前方交会法的种类种类测角交会法测边交会法边角交会法观测值,D1,D2,,D1,D2观测仪器精密经纬仪光电测距仪精密全站仪10.3.3 测角前方交会法误差分析下面以测角前方交会法为例来说明前方交会法测定观测点水平位移的误差来源。

角度前方交会法原理角度前方交会法是一种基本的测量方法，主要用于确定某一点的位置，特别是在野外测量和工程建设中。

该方法利用三角形相似性原理，将测量和计算过程分解为若干个简单的步骤，从而得到准确的测量结果。

本文将对角度前方交会法的原理、步骤和应用进行详细讲解。

角度前方交会法的原理角度前方交会法是基于三角形相似性原理的建立的。

三角形相似性原理指的是两个三角形的对应角度相等，对应边成比例关系。

在以下的图形中，三角形 ABC 和 DEF 相似，因为∠ABC =∠DEF，∠ACB =∠DFE和∠BAC =∠EDF。

与BC、AC、DC、EF、DF和DE相似的边成比例，即，BC/EF = AC/DF = DC/DE利用三角形相似性原理，可以得到角度前方交会法的基本原理：在已知两个点的位置和与这些点的连线所成夹角的情况下，可以测量出另外一个点的位置。

角度前方交会法的步骤角度前方交会法的测量可以分为以下步骤：第一步：在地面上确定两点的位置，并测量两点之间的距离。

这些点可以是明显的位置、桩点、或者标志物。

必须确认这些点的位置是精确的，以确保后续步骤的准确性。

第二步：测量这两点之间的夹角（或者方位角）。

这可以通过使用方位仪或者经纬仪测量得出。

如果使用经纬仪，则需要确定两点之间的经度和纬度，并计算方位角。

第三步：在第一点位置处测量与第一条线相交的第二条线的夹角（或者方位角），并测量与第二点位置的连线所成的夹角（或者方位角）。

记住将仪器调整到正确的方向上，确保夹角或者方位角的准确性。

第四步：从两个已知点的位置向前方测量出第三条线。

可以使用三角板或者望远镜或者其他测量仪器来测量这条线。

第五步：将第三条线的长度和与前两条线相交的夹角输入计算器。

计算器将使用三角形相似性原理来计算出第三条线相对于第一个点的位置。

确定了第三条线的位置之后，就可以测量和计算与该点相交的其他线。

角度前方交会法的应用角度前方交会法主要应用于建筑、土木工程和地理学中。

前方交会法.水平位移监测实验要求
1、实验仪器：全站仪1台；反射棱镜2把；脚架3个；铁钉和铁锤。

2、实验场地：五教操场。

3、各组任意选取2个点A、B作为工作基点，在A、B点前方选择一点P作为水平位移观测点，模拟第一次水平位移观测，AP、BP交会成的角度应在60°~ 120°之间。

4、在A点架设全站仪，指定A点坐标为(1000，1000)。

在B点、P点分别架设棱镜，均要求对中整平。

利用全站仪观测得到AP、AB之间的水平夹角α。

5、在B点架设全站仪，测出B点坐标为(x B，y B)。

在A点、P点分别架设棱镜，均要求对中整平。

利用全站仪观测得到BA、BP之间的水平夹角β。

6、在P点附近选择一点P1，模拟P点发生水平位移后的位置。

模拟第二次水平位移观测
7、在B点架设全站仪。

在A点、P1点分别架设棱镜，均要求对中整平。

利用全站仪观测得到BA、BP1之间的水平夹角β1。

8、在A点架设全站仪。

在B点、P1点分别架设棱镜，均要求对中整平。

利用全站仪观测得到AP1、AB之间的水平夹角α1。

9、将A、B点坐标，α、β、α1、β1分别填入表格中，根据前方交会法原理和计算方法，进行内业计算，得到P和P1点坐标值，计算两点的坐标差值，得到P点的水平位移偏移量。

10
模拟第一次水平位移观测计算成果表
模拟第二次水平位移观测计算成果表
y。

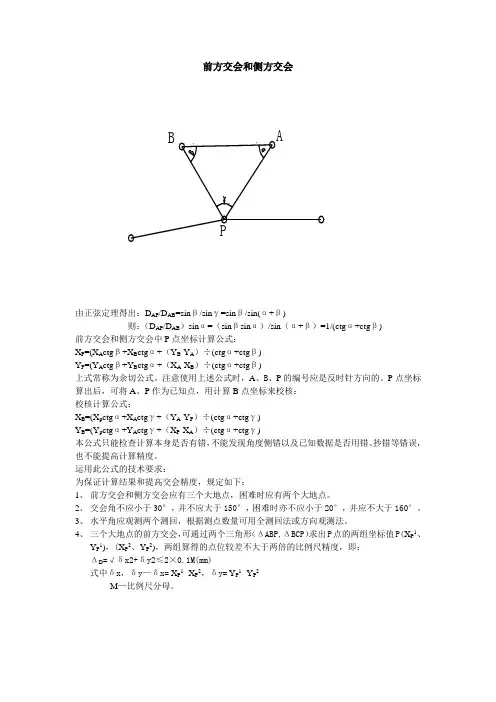
前方交会和侧方交会由正弦定理得出：D AP/D AB=sinβ/sinγ=sinβ/sin(α+β)则：（D AP/D AB）sinα=（sinβsinα）/sin（α+β）=1/(ctgα+ctgβ)前方交会和侧方交会中P点坐标计算公式：X P=(X A ctgβ+X B ctgα+（Y B-Y A）÷(ctgα+ctgβ)Y P=(Y A ctgβ+Y B ctgα+（X A-X B）÷(ctgα+ctgβ)上式常称为余切公式。

注意使用上述公式时，A、B、P的编号应是反时针方向的。

P点坐标算出后，可将A、P作为已知点，用计算B点坐标来校核：校核计算公式：X B=(X p ctgα+X A ctgγ+（Y A-Y P）÷(ctgα+ctgγ)Y B=(Y p ctgα+Y A ctgγ+（X P-X A）÷(ctgα+ctgγ)本公式只能检查计算本身是否有错，不能发现角度侧错以及已知数据是否用错、抄错等错误，也不能提高计算精度。

运用此公式的技术要求：为保证计算结果和提高交会精度，规定如下：1、前方交会和侧方交会应有三个大地点，困难时应有两个大地点。

2、交会角不应小于30°，并不应大于150°，困难时亦不应小于20°，并应不大于160°。

3、水平角应观测两个测回，根据测点数量可用全测回法或方向观测法。

4、三个大地点的前方交会，可通过两个三角形（ΔABP,ΔBCP）求出P点的两组坐标值P(X P1、Y P1)，(X P2、Y P2)，两组算得的点位较差不大于两倍的比例尺精度，即：ΔD=√δx2+δy2≤2×0.1M(mm)式中δx，δy—δx= X P1- X P2，δy= Y P1 -Y P2M—比例尺分母。

后方交会B如图所示，A、B、C是已知三角点，P点是导线点，将仪器安置在P点上，观测P至A、B、C各个方向之间的水平夹角α、β，然后根据已知三角点的坐标，可解算P点坐标。

极坐标法：在平面内取一个定点O，叫极点，引一条射线Ox，叫做极轴，再选定一个长度单位和角度的正方向(通常取逆时针方向)。

对于平面内任何一点M，用ρ表示线段OM的长度，θ表示从Ox到OM的角度，ρ叫做点M的极径，θ叫做点M的极角，有序数对(ρ,θ)就叫点M的极坐标，这样建立的坐标系叫做极坐标系。

角度前方交会法："前方交会"是指北针的一种使用方法：指北针除能指示方位外，并可测量方位角兼可在现地测定水平距离及斜角度；在地图上测量直距离及弯曲距离及绘图时可描绘方向线；并以「前方交会法」判定目的地在地图上的位置；以「后方交会法」判定本人在地图上的位置。

用途非常广泛。

●指北针的类型：指北针大致可分为透镜罗盘仪、表壳式指北针、透明底板型指北针。

透明底板型指北针广为一般户外活动人士、远征队或探险家所爱用，东海山社无论登山、溯溪活动也皆使用透明底板型指北针，所以仅介绍此类指北针。

●透明底板型指北针的构造：1. 放大透镜是为了便於地图之阅读2. 分度盘前方的底板上标示有一红色指向箭头，代表进行线方向及度数指示线。

3. 整个分度盘可自由旋转，以便调整校正。

4. 表盘底面有数条红色平行线及中央的平行箭头，会随分度盘旋转，是测定方向线。

5. 分划刻度由0° ~ 360°，每小格代表2°。

6. 指北针两端以红白两色分别表示北与南的指向。

方向线交会法：根据建筑方格网对边上两对对应已知点，用经纬仪或细线交会测设所求点的定点方法。

直角坐标法：直角坐标法是根据直角坐标原理，利用纵横坐标之差，测设点的平面位置. 直角坐标法适用于施工控制网为建筑方格网或建筑基线的形式，且量距方便的建筑施工场地。

距离交会法：从两个控制点或已测绘好的地物点测量至某一待测定地物点的距离,然后在图上根据这两段按比例尺缩小后的距离的交点绘出该地物点，这种方法称为距离交会法。

测量坐标与施工坐标的关系：建筑总平面图中坐标的主要作用是标定平面图内各建筑物之间的相对位置及与平面图外其它建筑物或参照物的相对位置关系。

前方交会法什么是前方交会法前方交会法是一种用于确定两个航空器在空中相对位置的方法。

在飞行中，飞行员需要准确判断其他航空器与自己的相对位置，以确保航空器的安全。

前方交会法就是一种常用的方法，通过观察目标航空器在飞行中的水平位置和垂直位置变化，确定其与自己的相对位置和相对速度。

前方交会法的原理前方交会法的原理基于几何关系以及飞行物体在空中的运动规律。

在空中，我们可以将飞行器的运动轨迹看作一条直线。

当两个飞行器相对静止时，它们的运动轨迹是平行的。

当两个飞行器发生交会时，它们的运动轨迹会有交点。

通过观察两个飞行器的相对位置的变化，可以判断它们是否在交会的轨迹上。

具体的判断方法有两种：1.水平分离法：观察飞行器在水平方向上的位置变化，如果两个飞行器的水平位置不断接近，那么它们就有可能在交会轨迹上。

2.垂直分离法：观察飞行器在垂直方向上的位置变化，如果两个飞行器的垂直位置不断接近或者相互远离，那么它们就有可能在交会轨迹上。

如何使用前方交会法确定相对位置使用前方交会法来确定两个飞行器的相对位置需要以下步骤：1.观察目标飞行器在水平方向上的位置变化，如果它与自己的距离逐渐缩小，说明它在自己前方。

2.观察目标飞行器在垂直方向上的位置变化，如果它在自己的上方，则可以判断它在前方上方。

3.观察目标飞行器在垂直方向上的位置变化，如果它在自己的下方，则可以判断它在前方下方。

4.根据观察到的水平位置和垂直位置变化，可以综合判断目标飞行器与自己的相对位置和相对速度。

在使用前方交会法进行判断时，需要考虑飞行器的飞行速度和方向，以及观察的时间间隔。

如果时间间隔过长，可能会导致判断不准确。

注意事项在使用前方交会法进行判断时，需要注意以下事项：1.观察目标飞行器的运动轨迹时，尽量选择距离自己较远的飞行器。

距离较近的飞行器由于运动速度较快，可能会造成观察不准确。

2.观察目标飞行器的位置变化时，要注意自己的飞行姿态和方向的变化。

自己的飞行姿态和方向的变化可能会对观察到的位置变化造成影响。

前方交会法原理
嘿，朋友们！今天咱来聊聊前方交会法。

这前方交会法啊，就像是一个神奇的魔法工具，能帮咱解决好多测量上的难题呢！
你想想看，要是咱面前有个大大的目标，就像一个神秘的宝藏，咱得知道它的确切位置，那咋整呢？这时候前方交会法就派上用场啦！它就像个聪明的导航，能指引咱找到那个宝藏的所在。

比如说，咱在这儿设两个观测点，就像两只眼睛一样，从不同的角度去盯着那个目标。

然后通过测量角度啊什么的，就能计算出目标的位置啦！这多有意思啊，就好像我们是侦探，通过一点点线索去揭开谜底。

你说这是不是很神奇？就好像我们在玩一个解谜游戏，一点点地拼凑出答案。

而且这前方交会法可实用了，在好多地方都能派上大用场呢！比如说建房子的时候，要确定房子的位置；或者是修路的时候，得知道路该往哪儿修。

它就像一个默默工作的小能手，不声不响地就把重要的事情给搞定了。

咱再想想，要是没有这前方交会法，那可咋办呀？那好多事情不就变得一团糟啦？就好像没有指南针的航海，那不得迷失方向呀！所以说呀，这前方交会法可真是太重要啦！
它虽然看起来挺简单的，不就是测测角度嘛，但这里面的学问可大着呢！要是不小心测错了一点，那结果可能就差之千里啦！这就好像做饭一样，调料放多一点少一点，味道可就完全不一样喽！
咱在使用前方交会法的时候，可得仔细认真，不能马虎。

就像对待自己最宝贝的东西一样，小心翼翼地去操作。

而且还得有耐心，不能着急，得一步一步慢慢来。

总之呢，前方交会法就是这么个神奇又实用的东西，咱可得好好利用它，让它为我们的生活和工作带来便利。

它就像我们的好帮手，默默地在那里为我们服务。

所以啊，大家可别小瞧了它哟！这就是我对前方交会法的理解，你们觉得呢？。

三角高程测量方法与误差控制指南三角高程测量是地理测量中常用的一种方法，通过测量目标地点与测量点的角度差异，计算出目标地点的高程。

在地理测绘、土地规划、建筑设计等领域中，三角高程测量具有重要的应用价值。

本文将介绍三角高程测量的主要方法及误差控制指南。

1. 三角高程测量方法1.1 前方交会法前方交会法是三角高程测量中最为常用的方法之一。

它基于测量点、目标点和参考点之间的角度关系，通过测量角度来计算高程。

在实际操作中，先选择合适的参考点，测量测量点和目标点与参考点之间的角度，再结合已知的基线长度，利用三角公式求解目标点的高程。

此方法简便易行，适用于小范围的测量。

1.2 三点测高法三点测高法是一种高精度的三角高程测量方法，适用于大范围的测量。

它利用多个参考点和观测点之间的角度关系，通过多次观测求解目标点的高程。

在实际操作中，需要选择至少三个参考点，利用三角公式计算出目标点与不同参考点之间的高程差，再取平均值作为目标点的高程。

此方法具有较高的精度，但操作复杂，适用于需要高精度测量的场合。

2. 误差控制指南2.1 观测误差控制观测误差是三角高程测量中最主要的误差来源之一。

为了保证测量结果的准确性，需要采取一系列措施来控制观测误差。

首先，应选择合适的观测仪器和设备，确保其精度符合要求。

其次，应避免在不稳定的气象条件下进行观测，如大风、降雨等天气。

此外，还应加强对观测仪器的维护与管理，保证其正常运行。

2.2 控制网设计控制网的设计对三角高程测量的精度和可靠性具有重要影响。

在设计控制网时，应根据实际测量的要求和场地条件进行合理布局。

首先，需要选择合适的观测点和参考点，保证其分布均匀、密度适宜。

其次，需要考虑地形和地貌对控制点的影响，尽量选择平坦、高程变化不大的位置作为控制点。

此外，还应合理确定控制网的形状和大小，以满足不同测量目的的需求。

2.3 数据处理与分析数据处理与分析是三角高程测量中不可或缺的环节。

在进行数据处理时，应注意对观测数据的筛查与校正，将异常值和误差数据予以排除。

前方交会测量方法
前方交会呢，简单说就是在两个已知点上设站，然后分别观测未知点的角度，从而确定这个未知点的位置。

这就像是两个人站在不同的地方，一起看着一个神秘的点，然后通过他们看这个点的角度来找到这个点在哪。

想象一下，有A和B这两个已知点，就像两个好朋友站在固定的位置。

我们在这两个点上架设测量仪器，然后瞄准那个未知的点C。

这个时候，仪器会告诉我们从A 点看C点的角度，以及从B点看C点的角度。

那怎么根据这些角度算出C点的位置呢？这里面可是有小窍门的。

我们可以利用三角形的一些原理。

从A、B两点到C点就构成了三角形呀。

根据角度和已知的A、B 两点的坐标，就可以通过一些数学公式来计算C点坐标啦。

在实际操作的时候，可一定要保证测量角度的准确性哦。

要是角度测错了一点，那算出来的C点位置可就差得远啦。

就像你要找宝藏，方向错了一点点，可能就挖不到啦。

而且哦，在选择A、B这两个已知点的时候也有讲究。

这两个点的位置最好能让测量的角度比较合适，不能太刁钻，不然仪器测量起来可能会不太方便，误差也可能会变大。

在野外进行前方交会测量的时候，环境也可能会捣乱。

比如说风太大啦，可能会让仪器晃悠，影响测量的精度。

这时候测量员就得像守护宝贝一样，稳住仪器，确保测量顺利进行。

软基处理过程中边桩位移观测的两种常用方法刘学军(中交第一航务工程勘察设计院，天津300222 )摘要：介绍软基处理过程中边桩位移观测的两种常用方法的操作及其各自的特点和实际操作时应注意的一些事项关键词：边桩位移；边坡轴线；工作基点；前方交会；极坐标中图分类号：U 652. 63 文献标识码：B 文章编号：100429592(2005)0120056 202软基处理边桩位移观测是监测项目中的一种其主要目的是监测软基处理过程中地基土的表层水平位移，以保证边坡的稳定。

边坡位移观测的方法多种多样，比较常用的两种方法是前方交会法和极坐标法。

1 前方交会法前方交会法主要是角度交会，使用的仪器为经纬仪。

观测图形如图1所示,边桩设置在边坡脚，般情况下1组边桩设置2 4个。

在已知工作基点上设置仪器，观测夹角A B根据两己知工作基点间的距离b及观测数据，计算出所测边桩的坐标值。

图1前方交会法示意第1次交会后，计算出边桩A的坐标，作为初始观测值：x 1 = b sin B sin (A+ H ?sin X(1)y1 = bsin B co s( A+ H ?sin X式中：x 1、y 1为边桩A坐标初始值；b为工作基点1和2之间的距离；A、B为观测角度值；X为计算值；A+ B + X = 180; H为两工作基点方位角与边坡轴线方位角的差值。

第2次交会后，计算出边桩A的即时坐标：(2)y 2= b sin B co s( A+ H ?sin X两次观测后即可计算出边桩A的坐标差：d x = A d A- B d B(3)d y = C d A- D d B收稿日期:20042)12162式中：A = F sin B sin ( B- H?sin X;2B = F sin A sin ( A+ H?sin X;2C = - F sin B co s( B- H ?sin X;2D = F sin A co s( A+ H ?sin X;F = b?® 0= 206 265";d A A- A; d B= B- B。

前方交会投影系数法例题摘要：1.前方交会投影系数法简介2.例题介绍3.例题解答过程4.总结正文：一、前方交会投影系数法简介前方交会投影系数法是一种测量和计算工程中点、线、面等空间几何图形的方法。

该方法主要通过投影系数的计算，将空间几何图形投影到平面上，从而实现测量和计算的目的。

前方交会投影系数法的应用领域广泛，如土木工程、建筑工程、机械制造等。

二、例题介绍本例题为一个简单的前方交会投影系数法应用题，题目如下：已知空间几何体ABCD，其中A(0, 0, 0)，B(2, 0, 0)，C(2, 2, 0)，D(0, 2,0)。

现要求在平面xoy 上投影该几何体，并求出投影后的图形。

三、例题解答过程1.计算各点在前方交会投影面上的投影系数以点A 为例，其在平面xoy 上的投影为A"，由于A 在z 轴上，所以A"的坐标为(0, 0, 0)。

根据前方交会投影系数的计算公式，可得A 在平面xoy 上的投影系数为：K_A = (0 - 2) / (0 - 2) = -1同理，可计算出其他点在平面xoy 上的投影系数：K_B = (0 - 2) / (0 - 2) = -1K_C = (2 - 2) / (2 - 0) = 0K_D = (0 - 2) / (0 - 2) = -12.计算各点在平面xoy 上的投影根据投影系数和原点坐标，可以计算出各点在平面xoy 上的投影：A" = A * K_A = (0, 0, 0)B" = B * K_B = (0, 0, 0)C" = C * K_C = (2, 2, 0)D" = D * K_D = (0, -2, 0)3.连接投影后的点，得到投影后的图形将投影后的点A"、B"、C"、D"连接起来，得到投影后的四边形ABCD"。

四、总结本例题通过前方交会投影系数法，计算出了空间几何体在平面xoy 上的投影，并得到了投影后的图形。

经纬仪前方交会法的原理
经纬仪前方交会法是一种测量方法，用于确定一个点的坐标，其原理基于三角
测量和测量仪器的使用。

该方法需要使用经纬仪和测距仪来测量目标点与两个已知点的夹角和距离。

首先，在地面上选取两个已知坐标的点，分别记作A和B，并将其坐标记录下来。

然后，将经纬仪朝向目标点，并根据测量仪器上的角度刻度，测量出目标点与
A点和B点之间的角度，分别记作α和β。

接下来，在地图上将A点和B点相连，并在连接线上按照已知距离的比例将
线段AB延伸出来，以确定目标点C的近似位置。

然后，根据已知距离和测得的角度，使用正弦定理计算出目标点与A点和B点之间的距离AC和BC。

最后，通过测距仪测量目标点与A点和B点之间的实际距离，将其与计算得
出的距离进行比较，进行精确校正，得出目标点的准确坐标。

经纬仪前方交会法的原理基于三角形的几何原理和测量仪器的使用。

通过测量
角度和距离，结合地图上已知的点坐标，可以计算出目标点的坐标。

这种方法在土地测量、地图制作和导航定位中得到广泛应用，能够快速准确地确定目标点的位置。

前方交会法1.前方交会法定义自两已知坐标之三角点上，观测一欲测点之水平角，以推算其坐标位置，称之前方交会法。

图-1，前方交会法。

图-2，前方交会点。

图-1 前方交会法图-2 前方交会点2.前方交会点此种补点（前方交会点），通常为无法设置仪器之测点，如塔尖、避雷针、烟囱等等。

3.前方交会法适用场合：A.具两已知三角点。

B.三点（两已知点及欲测点）间可以通视。

C.两已知点可以架设仪器，但欲测点不方便架设仪器。

D.有数个欲测点待测定时。

图-3，为数个欲测点图-3 数个欲测点4.前方交会法施作步骤：A.经纬仪分别整置于A、B 两三角点上。

B.照准P 点，分别测得α、β两水平角。

C.以计算方法，求P 点坐标。

图-4，为量测角度。

图-4 量测角度5.已知、量测、计算之数据：A.已知：xA、yA、xB、yB。

B.量测：α、β。

C.计算：xP、yP。

图-5，为前方交会法相关角度位置图-5 前方交会法相关角度位置6.限制：α、β、γ三内角均必须介于30°～120°之间。

图-6 ，为角度限制。

图-6 为角度限制7.计算法前方交会法计算方法有三种：A.三角形法; B.角度法; C.方位角法8.三角形法19()()3891802890--++=---= βφφαφφABBP AB AP ()()()()()689cos sin cos 589sin cos sin 48922222---=-==---=-==---+-=∆+∆= ABAB AB AB AB AB A B AB A B A B y y AB ABy y x x AB ABx x y y x x AB y x AB φθφφθφ()()789sin sin sin sin sin sin --+===βαβγβγβAB AB AP ABAP γβαABP AB AB y y y -=∆ABNB.求方位角ψAP 、ψBP ：C.求各邊邊長：①AB 邊長：有三種方法可求得②AP 邊長：()[](βαβαγγβα+=+-==++sin 180sin sin 180γβαsin sin sin AB AP BP ==20()()1289cos 1189sin --+=--+= BPB P BP B P BP y y BP x x φφ()()889sin sin sin sin sin sin --+===βααγαγαAB AB BP ABBP ()()1089cos 989sin --+=--+= APA P AP A P AP y y AP x x φφAPAP l φcos A Py yPBy y BPy y l y BP x x l x yy y x x x BP BP BP B P BP BP B P B P -=∆==-=∆=-=∆+=∆+=φφφφcos cos sin sin ③BP 邊長：D.求P 座標x P 、y P ：①由A 點求P 點②由B 點求P 點9.角度法A.由上法直接代入：將(9-8-2)式與(9-8-7)式代入(9-8-9)式中，可得：yy y x x x A P A P ∆+=∆+=APy y l y AP x x l x AP AP AP AP AP AP -=∆=-=∆=φφcos sin21()()()1389sin sin sin sin ---++=+= αφβαβφAB A APA P AB x AP x x ()αφαφαφsin cos cos sin sin AB AB AB -=-()()()1489cos sin sin cos ---++=+= αφβαβφAB A APA P AB y AP y y ()αααφsin cos sin ABy y AB x x AB A B AB ---=-()()()()()1589sin sin sin sin sin cos --+--+-+= βαβαβαβαA B A B A P y y x x x x ()()()()()1789cot cot cot sin cos sin 1689tan tan tan sin cos sin 1cot cot 1tan tan sin cos sin cos cos sin sin cos sin --+=+--+=++=+=+=+ αβαβαβαββαβαβααββαβαβαβαβαβα或將(9-8-2)式與(9-8-7)式代入(9-8-9)式中，可得：B.化簡x P ：由和差化積公式：將(9-8-5)式與(9-8-6)式代入，可得：再之代入(9-8-13)式中，可得：由和差化積公式：化簡下式，可得：()βαβαβαcos cos cos sin sin +=+22()2289cot cot cot cot --++-+=βααβBA B A P x x y y y ()()()()ABPB PA APBA BP A B A P APA B A P y y y y y y x x φφφφφφφcos sin cos sin tan ---+=-+=()()()()2089tan tan tan tan tan tan tan tan tan tan tan tan tan --+--+=+--+-+= βαβαβαβαβαβαβA B B A P A B A B A P y y x x x y y x x x x ()()()()()1989cot cot sin sin sin 1889tan tan tan tan sin sin sin tan 1tan 1sin sin sin cos cos sin sin sin sin --+=+--+=++=+=+ βαβαβαβαβαβαβααββαβαβαβαβα或()()()2189cot cot cot cot cot cot 1cot cot cot --+-++=+--+-+= βααββαβααBA B A P A B A B A P y y x x x y y x x x x 同理，化簡下式，可得：將(9-8-16)式與(9-8-18)式代入(9-8-15)式中，可得：或將(9-8-17)式與(9-8-19)式代入(9-8-15)式中，可得：C.化簡y P ：（推演過程省略）D.角度法所得公式(9-18-21)式與(9-18-22)式，適於計算機使用，唯應注意：左A ，右B ；左α，右β。