专题二 作图题

专题二光路作图制卷人：打自企；成别使；而都那。

审核人：众闪壹；春壹阑；各厅……日期：2022年二月八日。

1、完成以下光路图1题图2、完成以下光路图2题图3、完成以下各图的光路图3题图4、根据光的反射定律完成图中的光路图：4题图5、完成图中各光路图．5题图6、完成以下光路图，并标出反射角和入射角的读数6题图7、完成以下光路并标出反射角的度数．7题图 8题图8、完成图中光经镜面两次反射的光路图．9、完成下面各图中光反射的光路图．9题图10、〔2021•〕如图，一束光从空气斜射入水中，请你完成光路图．10题图〔1〕〔2〕11题图〔1〕 1题图〔2〕 11、请完成以下光路图〔3〕画出平面镜中的虚像〔4〕完成光线经过玻璃砖的光路图11题图〔3〕 11题图〔4〕12、在图中的虚线框内填上适当的光学器件，完成光路图．12题图13、在图中的方框内填入适宜的光学元件，并完成光路图13题图14、〔1〕完成以下光路并标出反射角的度数〔图a〕．〔2〕作出物体AB在平面镜中所成的像〔图b〕．〔3〕作出点N在平面镜中像的位置，并完成OM的光路〔图c〕．14题图15、如下图，由点光源S发出的光，经平面镜MN反射后，其中一条反射光线经过B点，完成光路图．15题图 16题图16、画出AB在平面镜中的像17、〔4〕太阳光线与程度面成30度的角，假设用平面镜将太阳光反射后，要照到竖直的深井里，镜面与程度面成多大的角度？请在图中画出其光路图，并标出该角度17题图 18题图18在右图的方框中放置一平面镜，光线通过平面镜后的方向变化如图中所示，试画出平面镜并完成光路图．19、如下图两条光线是由同一点光源发出经平面镜反射后形成的，请完成光路图，并确定光源S的位置． 19题图 20题图20、如图，A、B是由同一发光点S发出的反射光线，试完成光路图并确定S的位置．21、如下图，S是水中鱼所在的位置，S’是人眼在A点处看到的鱼的位置，请你完成光路图．21题图 22题图22、光从空气斜射入水中，画出光路图．23、一条与程度地面成60°角的入射光线如图，假设使它的反射光线与地面平行，应该怎样放置平面反射镜？完成以下图中的光路图23题图 24题图24、根据平面镜成像特点画出图中物体在平面镜中的像25、〔2021•〕图中，两条光线是由同一点光源S发出经平面镜反射后形成的，请完成光路图，并确定光源S的位置．25题图 26题图26、如下图，位于B处的眼睛沿BO方向观察到水中有一个发光小球，根据图中给出发光小球和观察到的发光小球像的位置，完成光路图．27、〔1〕完成图1光路并标出反射角的度数．〔2〕画出图2中从A点出发，经平面镜反射后经过B的光线．27题图 28题图28、如下图，从S点发出的一条光线，经平面镜MN反射后，其反射光线恰好通过P点．请你作出这条入射光线并完成光路图．29、在水池的一角有一块平面镜，现有一束光线从水中射向平面镜，如图，请完成光路图，并标出反射角〔用“α〞表示〕和折射角〔用“β〞表示〕29题图 30题图30、〔2021•〕如下图，AB、CD是某一点光源S发出的二条入射光线，请画出它们的反射光线，标出点光源的位置，并完成光路图31、如下图，平面镜前有一点光源S，S发出的一束光线被平面镜反射后经过A点，请作出该光线的光路图．31题图 32题图32、根据光的镜面反射规律，画出光线在潜望镜中的光路图．33、如下图，是某同学在做光由空气射向水中的折射实验时画的一幅草图，他把水面画成实线，法线画成虚线，入射光线与折射光线是现场描的，但没有及时标出箭头，并且图的方向放乱了，请你在图中帮他完成光路图，并标明哪局部是空气，哪局部是水？33题图 34题图34、图中是一个深井，为了使阳光能竖直照到井底请画出平面镜的位置图．〔保存作图过程〕35、如下图，S′为点光源S在平面镜MN中的像，SA为点光源S发出的一条光线，请画出平面镜MN，并完成光线SA的光路．35题图36将一平面镜斜放在装有水的水槽中，有一束光线垂直射向水面，如下图，请画出这束光线在水中行进最后射出水面的光路图．36题图37题图37如下图，S为发光点，由S发出的光经水面反射后通过P点，请你在图中画出入射光线、反射光线以及折射光线的大致方向38、小明站在游泳池边A处，看到路灯B在池水中的像与他看到的池中一条鱼在C点重合，用光学作图法确定路灯B的位置和鱼的大致位置．38题图39题图39位于B处的眼睛沿BO方向观察到水中有一个发光小球，根据图中给出发光小球和观察到的发光小球像的位置，完成光路图．40如下图的两架敌机，一架是实际飞机，一架是从潜水艇上观察到的该飞机的像，请用光的作图法确定哪架是实际飞机．40题图41题图42题图41、如下图，是一只手表在平面镜中的像，那么，这只手表所示的实际时间是是〔〕A、1点40分B、7点零5分C、10点25分D、4点55分42、如下图，平面镜上方有一竖直挡板P，AB和CD是挡板左侧的发光点S经过平面镜反射后的两条反射光线，请在图上作出发光点S．〔要求留下作图痕迹43题图 44题图43、如下图，物体AB在平面镜MN中所成的像为A′B′，请你利用平面镜成像的特点确定平面镜MN的位置．44、如下图，在平面镜前有A、B两光点，人站在镜什么位置观察A、B两点恰好重叠．用作图方法，求出人眼所在位置．制卷人：打自企；成别使；而都那。

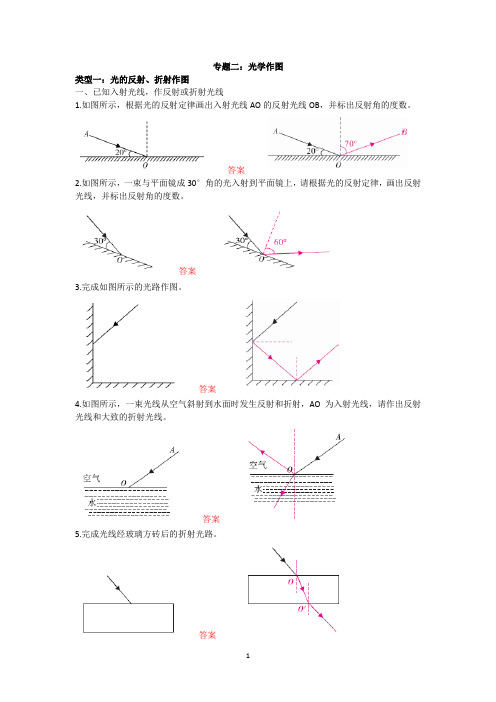
专题二：光学作图类型一：光的反射、折射作图一、已知入射光线，作反射或折射光线1.如图所示，根据光的反射定律画出入射光线AO的反射光线OB，并标出反射角的度数。

答案2.如图所示，一束与平面镜成30°角的光入射到平面镜上，请根据光的反射定律，画出反射光线，并标出反射角的度数。

答案3.完成如图所示的光路作图。

答案4.如图所示，一束光线从空气斜射到水面时发生反射和折射，AO为入射光线，请作出反射光线和大致的折射光线。

答案5.完成光线经玻璃方砖后的折射光路。

答案6.如图所示，光线垂直射入水面，水里有个平面镜，请完成此光路图。

答案二、已知反射或折射光线，作入射光线7.完成如图所示的光路图，并标出入射角的大小。

答案8.如图所示，一束光线在空气和水两种介质的界面上同时发生反射和折射，图中已标出反射光线，请画出折射光线的大致方向和入射光线。

答案9.（2019·深圳）一束光线从空气射入玻璃时，界面MN上的反射光线如图所示，请画出对应的入射光线和大致的折射光线。

答案三、已知入射光线和反射光线，确定镜面位置10.根据光的反射定律确定图中平面镜的位置。

答案11.如图所示，护林员利用一块平面镜使此时的太阳光水平射向山洞中P点，请你通过作图标出平面镜的位置，并标出反射角的度数。

答案类型二：平面镜成像作图12.如图所示，作出物体AB在平面镜中所成的像A′B′。

答案13.如图所示，A′B′是物体AB在平面镜中所成的像，根据平面镜成像的特点在图中画出平面镜。

答案14.（2019·娄底）如图所示，S′为发光点S在平面镜MN中所成的像，请在图中画出发光点S的位置，并画出一条由S点发出，经平面镜反射后通过P点的光线。

答案15.如图所示为发光点S所发出的两条光线经平面镜反射后的光线，请作出发光点S及其像S′的位置。

（保留作图痕迹）答案16.如图所示是平面镜前一个发光点S和它的两条光线，请在图中作出发光点S在平面镜中的像，并作出这两条光线的反射光线。

专题技巧二家庭电路作图题强化训练一、作图题1．（2019·河南西峡·九年级期中）请将图中的“声控开关”、“光控开关”、灯泡正确连入电路，要求只有在夜间且有声音时灯泡才亮的楼道灯自动控制电路，同时安装一个不受开关控制的三孔插座。

2．（2020·山东·烟台芝罘中学九年级月考）小明家新买了一个冰箱，请你帮他通过插座连到家庭线路上。

3．（2019·云南·昆明市官渡区第一中学九年级月考）如图所示的插座和电灯（带开关）是组成家庭电路的常用器件，请你用笔画线代替导线将它们分别正确的接入电路中。

4．（2020·广西·玉林市民族中学九年级月考）连接家庭电路中的灯泡和插座。

5．（2021·全国·九年级单元测试）如图，用笔画线代替导线，将各元件正确接入电路，其中开关只控制电灯。

6．（2021·辽宁鞍山·中考真题）如图所示，两灯泡的额定电压均为220V。

当开关闭合后，两灯泡都正常发光，且插座不受开关控制，请将电路连接完整。

7．（2019·广东·深圳外国语学校九年级期末）居民楼的楼道里，夜间楼道灯一直亮着会造成浪费。

科研人员用“光敏”材料制成“光控开关”，它能在天黑时自动闭合，天亮时自动断开；利用“声敏”材料制成“声控开关”。

它能在有人走动发出声音时闭合，无人走动时自动断开。

请将图中的“光控开关”、“声控开关”、灯泡用笔画线代替导线正确连入电路，设计出只有在夜间且有声音时灯才亮的楼道灯自动控制电路。

8．（宁夏·银川唐徕回民中学三模）如图所示的元件正确连入电路中家庭电路。

要求：开关控制灯泡、三孔插座带保险丝。

9．（2020·黑龙江林甸·九年级期末）家庭电路应特别注意安全用电，在图中请用笔画线代替导线，将图中的电灯、开关和配有保险丝的插座接入家庭电路中．所连接的电路应符合安全用电的原则。

专题02 尺规作图与最短路径几何中，用（无刻度）的直尺和圆规作图为尺规作图.一. 五种基本作图1. 作一条线段等于已知线段2. 作一个角等于已知角3. 作已知角的平分线（理论依据：SSS）4. 过一点（直线上或外）作已知直线的垂线5. 作已知线段的垂直平分线二. 尺规综合作图1. 已知三边作三角形2. 已知两边及夹角作三角形3. 已知两角及夹边作三角形三. 最短路径1. 单动点（P为直线l上一动点，P A+PB最小）2. 双动点（B、C为直线OM，ON上的动点，△ABC周长最小）其中，∠O=90°－12∠BAC. △ABC周长为A’A’’的长.3. 造桥选址【典例解析】【例1-1】（2020·庆云县月考）某地有两条相交叉的公路，计划修建一个饭馆：希望饭馆点P既在MN这条公路上，又到直线OA、OB的距离相等．你能确定饭馆应该建在什么位置吗？（保留作图痕迹）【答案】见解析.【解析】解：如图所示：点P的位置就是饭馆的位置．【例1-2】（2019·舞钢市月考）小安的一张地图上有A，B，C3三个城市，地图上的C城市被墨污染了（如图），但知道∠BAC=∠α，∠ABC=∠β，你能用尺规作图帮他在下图中确定C城市的具体位置吗？（不作法，保留作图痕迹）【答案】见解析.【解析】根据作一个角等于已知角的方法分别以AB为边，作∠BAC=∠α，∠ABC=∠β，两个角的边的交点处就是C的位置．点C为所求的点.【变式1-1】（2020·丽水市莲都区教研室期末）下列尺规作图分别表示：①作一个角的平分线；②作一个角等于已知角；③作一条线段的垂直平分线．其中作法正确的是（）A ．①②B ．①③C ．②③D ．①②③【答案】A 【解析】解：①作一个角的平分线的作法正确；②作一个角等于已知角的方法正确；③作一条线段的垂直平分线，缺少另一个交点，故作法错误；故答案为：A ．【变式1-2】（2019·河北南宫期末）下面是黑板上出示的尺规作图题，需要回答横线上符号代表的内容：如图，已知AOB ∠，求作：DEF ∠，使DEF AOB ∠=∠．作法：（1）以为圆心，任意长为半径画弧，分别交OA 、OB 于点P 、Q ；（2）作射线EG ，并以点E 为圆心，长为半径画弧交EG 于点D ； （3）以点D 为圆心，长为半径画弧交（2）步中所画弧于点F ； （4）作，DEF ∠即为所求作的角．A ．表示点E B ．表示PQ C ．表示OQ D ．表示射线EF【答案】D【解析】作法：（1）以点O 为圆心，任意长为半径画弧，分别交OA 、OB 于点P 、Q ；（2）作射线EG ，并以点E 为圆心，OP 为半径画弧交EG 于点D ；（3）以点D 为圆心，PQ 长为半径画弧交（2）步中所画弧于点F ；（4）作射线EF ，∠DEF 即为所求作的角．故答案为D ．【变式1-3】（2020·山东青岛期中）如图，AB 是某条河上的一座桥，现要在河的下游点C 处再建一座与AB 平行的桥CD ，请用直尺和圆规画出CD 的方向．【答案】见解析【解析】解：如图，线段CD 即为所求．【变式1-4】（2020·广州月考）用直尺和圆规作一个角等于已知角，如图，能得出A O B AOB ∠∠='''的依据是（ ）A ．S ．S ．SB ．S ．A ．SC ．A ．S ．AD ．A ．A ．S【答案】A 【解析】解：由作图知OC =O ’C ’，OD =O ′D '，CD =C ′D '，∴△OCD ≌△O ′C ′D ′，∴∠A ′O ′B ′=∠AOB ，判断依据为SSS ，故答案为：A ．【例2-1】（2020·曲阜月考）如图，在△ABC 中，∠C =90°，按以下步骤作图：①以点A 为圆心、适当长为半径作圆弧，分别交边AC 、AB 于点M 、N ；②分别以点M 和点N 为圆心、大于12MN 的长为半径作圆弧，在∠BAC 内，两弧交于点P ；③作射线AP 交边BC 于点D ，若CD =4，AB =15，则△ABD 的面积是（ ）A ．15B ．30C ．45D ．60【答案】B 【解析】解：过D 作DE ⊥AB 于E ， AP 平分∠CAB ．∵AP 平分∠CAB ，∠C =90°，DE ⊥AB ，∴DE =DC =4，∴△ABD 的面积=12×AB ×DE =30 故答案为B ．【例2-2】（2020·广东广州月考）如图，△ABC 中，90C ∠=︒，AC =BC ．（1）用直尺和圆规作BAC ∠的平分线交BC 于点D （保留作图痕迹）（2）过点D 画△ABD 的边AB 上的高DE ，交线段AB 于点E ，若△BDE 的周长是5cm ，求AB 的长．【答案】见解析.【解析】解：（1）如图，AD 即为所作；（2）∵AD 平分∠BAC ，∠C =90°，DE ⊥AB ，∴CD=DE，在Rt△ACD和Rt△AED中，AD AD CD DE=⎧⎨=⎩，∴Rt△ACD≌Rt△AED（HL），∴AE=AC，∵AC=BC，∴BC=AE，∵△BDE的周长=BE+BD+DE=BE+BD+CD=BE+BC=BE+AE=AB，∴AB=5cm．【变式2-1】（2020·山东博山二模）已知∠AOB＝60°，以O为圆心，以任意长为半径作弧，交OA，OB于点M，N，分别以点M，N为圆心，以大于12MN的长度为半径作弧，两弧在∠AOB内交于点P，以OP为边作∠POC＝15°，则∠BOC的度数为（）A．15°B．45°C．15°或30°D．15°或45°【答案】D【解析】解：（1）以O为圆心，以任意长为半径作弧，交OA，OB于点M，N，分别以点M，N为圆心，以大于12MN的长度为半径作弧，两弧在∠AOB内交于点P，则OP为∠AOB的平分线，∴∠AOP=∠AOB=30°（2）两弧在∠AOB内交于点P，以OP为边作∠POC＝15°，则∠BOC＝15°或45°，故答案为：D．【变式2-2】（2020·广东）如图，在锐角△ABC中，AB＝2cm，AC＝3cm．（1）尺规作图：作BC边的垂直平分线分别交AC，BC于点D、E（保留作图痕迹，不要求写作法）；（2）在（1）的条件下，连结BD，求△ABD的周长．【答案】见解析.【解析】解：（1）如图，DE为所作；（2）∵DE垂直平分BC，∴DB=DC，∴△ABD的周长=AB+BD+AD=AB+CD+AD=AB+AC=2+3=5（cm）．【变式2-3】（2020·山东省陵城区月考）如图，在△ABC中，∠C=90°，∠B=20°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于P，连接AP并延长交BC于点D，则∠ADB=________．【答案】125°【解析】解：由题意可得：AD平分∠CAB，∵∠C=90°，∠B=20°，∴∠CAB=70°，∴∠CAD=∠BAD=35°，∴∠ADB=180°﹣20°﹣35°=125°．故答案为125°．【变式2-4】（2020·长春月考）如图，依据尺规作图的痕迹，计算=α∠（ ）A ．56︒B ．68︒C ．22︒D ．34︒【答案】A 【解析】解：如图所示，AE 平分∠DAC ，EF ⊥AC ，∵∠ACB =68°，∴∠DAC =68°，∵AE 平分∠DAC ，∴∠DAE =∠EAC =34°，∵EF ⊥AC ，∴∠AEF ==α∠90°-34°=56°．故答案为A .【例3】（2020·禹城市期末）如图，等边ABC 中，D 为BC 边中点，CP 是BC 的延长线．按下列要求作图并回答问题：（要求：尺规作图，不写作法，保留作图痕迹）（1）作ACP ∠的平分线CF ；（2）作60ADE ∠=︒，且DE 交CF 于点E ；（3）在（1），（2）的条件下，可判断AD 与DE 的数量关系是__________；请说明理由．【答案】见解析.【解析】解：（1）（2）尺规作图，如下图；（3）AD =DE ，连接AE ，∵等边△ABC 中，D 为BC 边中点，∴BD =CD ，∠ADB =∠ADC =90°，∵∠B =∠ADE =60°，∴∠BAD =∠EDC =30°，∵∠ACP =120°，CE 为∠ACP 的平分线，∴∠ACE =∠ECP =60°，∴∠DEC =30°，∴CE =CD =BD ，∴△ABD ≌△ACE ，∴AE =AD ，又∵∠ADE =60°，∴△ADE 是等边三角形，∴AD =DE .【变式3-1】（2020·福建学业考试）如图，ABC ∆为一钝角三角形，且90BAC ∠>︒∆和等腰Rt EAC（要求：尺规作图，不写作法，保留作（1）分别以AB，AC为底向外作等腰Rt DAB图痕迹）⊥并证明．（2）已知P为BC上一动点，通过尺规作图的方式找出一点P，连接PD，PE，使得PD PE【答案】见解析.【解析】解：（1）如图所示；（2）如图所示，作线段BC的垂直平分线交BC于点P，则P点为所求．证明：延长DP使PF=PD，连接FC，EF∵P为BC中点，∴PB=PC又∵PD=PF，∠DPB=∠CPF∴△BDP≌△CFP∠AD =BD =CF ，∠PBD =∠PCF∴BD ∥CF∵AE =CE延长DG ，FC 交于点G∵BD ∥CF∴∠FGD =90°又∠AEC =90°∴∠EAG =∠ECG∴∠DAE =∠ECF又AE =CE ，AD =CF∴△AED ≌△CEF∴EF =ED∵P 为DF 中点∴DP ⊥PD【变式3-2】（2020·南京师范大学附属中学月考）如图，在ABC 中，90C ∠=︒，30B ∠=︒，以A 为圆心，任意长为半径画弧分别交AB 、AC 于点M 和N ，再分别以M 、N 为圆心，大于MN 的长为半径画弧，两弧交于点P ，射线AP 交BC 于点D ，则下列说法中：①AD 是BAC ∠的平分线；②60ADC ∠=︒；③点D 在AB 的垂直平分线上；④:1:3DAC ABC S S =．其中正确的个数是（ ）A ．1B ．2C ．3D ．4【答案】D 【解析】解：①连接NP ，PM ，易证∠ANP∠∠AMP则∠CAD=∠BAD，故AD是∠BAC的平分线，故∠正确；②∵∠C=90°，∠B=30°∠∠CAB=60°∠AD是∠BAC的平分线∠∠BAD=∠CAD=30°∠∠ADC=∠BAD+∠B=60°，故∠正确；③∵∠BAD=∠CAD=30°∠∠BAD=∠B∠AD=BD，即D在AB的垂直平分线上，故∠正确；④∵在Rt△ACD中，∠CAD=30°∴AD=2CD∴BC=BD+CD=1.5AD，S△DAC=12AC·CD=14AC·AD∴S△ABC=12AC·BC=12AC·32AD=34AC·AD∴S△DAC：S△ABC=1：3，故④正确故答案为：D．【例4-1】（2020·长沙月考）在∠ABC中，∠A=50°，点O为∠ABC内一点，过点O分别作AC，AB的垂线，垂足分别为M，N，点P为AM上一动点，点Q为AN上一动点，连接OP，OQ，PQ，当∠OPQ的周长最小时，∠POQ的度数为______度．【答案】80°【解析】解：作点O关于AC的对称点O’，作点O关于AB的对称点O’’，连结O’O’’，易知当O ’，P ，Q ，O ’’四点共线时，△OPQ 周长最小，最小值为O ’O ’’的长此时，∠A =90°－12∠POQ ∴∠POQ =180°－2∠A =80°；故答案为：80°.【例4-2】（2020·重庆期末）如图，在Rt ABC 中，90C ∠=︒，30A ∠=︒，6AB =，BD 是ABC 的角平分线，点P ，点N 分别是BD ，AC 边上的动点，点M 在BC 上，且1BM=，则PM PN +的最小值为___________．【答案】52． 【解析】解：作点M 关于BD 的对称点M ’，连接PM ’，则PM =PM ’，BM =BM ’=1，易知，当N ，P ，M ’共线时，且M ’N ⊥AC 时，PN +PM ’的最小值为线段M ’N 的长由∠A =30°，知M ’N =12AM ’=52， 故答案为：52.【变式4-1】（2020·江苏无锡二模）如图，一面镜子斜固定在地面OB 上，且60AOB ∠=︒点P 为距离地面OB 为8cm 的一个光源，光线射出经过镜面D 处反射到地面E 点，当光线经过的路径长最短为10cm 时，PD 的长为___________．【答案】4【解析】解：作点P 关于AO 的对称点P ’，当P ’E ⊥OB 时，光线经过的路径长最短，∠P ’E =10，过P 作PF ⊥P ’D 于F ，则P ’F =2，又∠AOB =60°∴∠ODE =30°，∴∠P ’DA =∠PDA =30°，∠P ’DP =60°，PD =P ’D∴△PP ’D 为等边三角形，∴P ’F =DF =2，PD =P ’D =4故答案为：4.【变式4-2】（2020·宜兴市月考）如图，P 为AOB ∠内一定点，M ，N 分别是射线,OA OB 上的点，当PMN周长最小时，80MPN ∠=︒，则AOB ∠=_________．【答案】50°【解析】解：作P 关于OA ，OB 的对称点P 1、P 2，连接OP 1，OP 2，P 1P 2．则当M ，N ，P 1、P 2共线时，△PMN 的周长最小．易知，∠AOB =90°－12∠MPN =50°. 故答案为：50°.【习题专练】1. （2020·南京月考）有三条两两相交的公路，要建一个加油站，使它到三条公路的距离相等，那么加油站可建的地点有_________________个．【答案】4【解析】解：如图所示作出角的平分线包括外角的角平分线，共有4个交点，所以由三条两两相交的公路，要建一个加油站，使它到三条公路的距离相等，则加油站需满足在角平分线的交点上，故可建的地点有4个． 故答案为4．2.（2020·江阴市月考）在正方形网格中，ABC △的位置如图所示，且顶点在格点上，在ABC △内部有E 、F 、G 、H 四个格点，到ABC △三个顶点距离相等的点是（ ）A．点E B．点F C．点G D．点H 【答案】B【解析】解：∠到∠ABC三个顶点距离相等，∠该点是三角形三边垂直平分线的交点，根据网格作AC、BC的垂直平分线，可得交点为F，故答案为：B．3.（2020·洛阳市二模）如图，在ABC中，AB＝4，AC＝9，BC＝11，分别以点A，B为圆心，大于12 AB的长为半径画弧，两弧相交于点D，E，作直线DE，交BC于点M；分别以点A，C为圆心，大于12AC的长为半径画弧，两弧相交于点P、Q，作直线PQ，交BC于点N；连接AM、AN．则MAN的周长为（）A．9B．10C．11D．13【答案】C【解析】解：由作图可知，DE垂直平分线段AB，PQ垂直平分线段AC，∠MA＝MB，NA＝NC，∠∠AMN的周长＝AM+MN+AN＝BM+MN+NC＝BC＝11．故答案为：C ．4.（2020·河南一模）如图，在平行四边形ABCD 中，6AB =，8AD =，120BAD ∠=︒，分别以点A ，B 为圆心，以大于12AB 的长为半径画弧，两弧相交于点P 、Q ，作直线PQ ，交AB 于点E ，交BC 于点F ，则CF 的长为_______．【答案】2.【解析】解：由题意可得，AB ⊥OP ，AE =BE =3∵BC =AD =8，∠B =60°∴∠BFE =30°，∠BEF =90°∴BF =2BE =6∴CF =8-6=2故答案为：2.5．（2020·宜兴市月考）如图，在∠ABC 中，AB ＞AC ．按以下步骤作图：分别以点B 和点C 为圆心，大于BC 一半的长为半径作圆弧，两弧相交于点M 和点N ；作直线MN 交AB 于点D ；连结CD ．若AB =6，AC =4，则∠ACD 的周长为 ．【答案】10．【解析】解：易知直线MN 是线段BC 的垂直平分线，∴BD =CD ，∴BD +AD =CD +AD =AB ，∵AB =6，AC =4，∴△ADC 的周长=（CD +AD ）+AC =AB +AC =6+4=10．故答案为10．6.（2020·商城县第二中学月考）如图，已知∠AOB（1）尺规作图：作出∠AOB的角平分线OP，补充完整作图步骤，（保留作图痕迹）①____________________________分别交OA、OB于F，E两点；②____________________________，两条圆弧交于点P；③____________________________即为所求．（2）过点F作FD∥OB交OP于点D，FM⊥OD，垂足为M，求证：△FMO≌△FMD．【答案】见解析.【解析】解：(1)如下图所示：①以O点为圆心，任意长为半径作圆弧分别交OA、OB于F，E两点；②分别以E、F为圆心，大于二分之一EF长为半径作两段圆弧两条圆弧交于点P；③作射线OP，则射线OP即为所求．故答案为：以O点为圆心，任意长为半径作圆弧；分别以E、F为圆心，大于二分之一EF长为半径作两段圆弧；作射线OP，则射线OP；(2)根据题意，作出如下图所示：由(1)知，OP是∠AOB的角平分线，∴∠2=∠3，又FD∥OB，∴∠1=∠3，∴∠1=∠2，∴△FMO≌△FMD．7．（2019·广东阳山期中）用圆规、直尺作图，不写作法，但要保留作图痕迹．如图，王师傅开车在一条公路上经过点B和点C处两次拐弯后继续前行，且前行方向和原来的方向AB相同．已知第一次的拐角为∠ABC，请借助圆规和直尺作出第二次拐弯后的拐角∠BCD．【答案】见解析．【解析】解：由题意得：AB∥CD，∴∠BCD=∠ABC则∠BCD即为所求作．8．（2020·陕西清涧期末）如图，直线AB与BC相交于点B，D是直线BC上一点，请用尺规求作一点E，DE AB，且点E到B，D两点的距离相等．（保留作图痕迹，不写作法）使直线//【答案】见解析【解析】解：如图，点E即为所求．9．（2020·北京月考）下面是小星同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程：已知：如图，直线l和直线l外一点A求作：直线AP，使得AP∠l作法：如图∠在直线l上任取一点B（AB与l不垂直），以点A为圆心，AB为半径作圆，与直线l交于点C．∠连接AC，AB，延长BA到点D；∠作∠DAC的平分线AP．所以直线AP就是所求作的直线根据小星同学设计的尺规作图过程，（1）使用直尺和圆规，补全图形（保留作图痕迹）（2）完成下面的证明证明：∠AB＝AC，∠∠ABC＝∠ACB（填推理的依据）∠∠DAC是∠ABC的外角，∠∠DAC ＝∠ABC +∠ACB （填推理的依据）∠∠DAC ＝2∠ABC∠AP 平分∠DAC ，∠∠DAC ＝2∠DAP∠∠DAP ＝∠ABC∠AP ∠l （填推理的依据）【答案】见解析．【解析】解：（1）如图所示，直线AP 即为所求．（2）证明：∠AB ＝AC ，∠∠ABC ＝∠ACB （等边对等角），∠∠DAC 是∠ABC 的外角，∠∠DAC ＝∠ABC +∠ACB （三角形外角性质），∠∠DAC ＝2∠ABC ，∠AP 平分∠DAC ，∠∠DAC ＝2∠DAP ，∠∠DAP ＝∠ABC ，∠AP ∠l （同位角相等，两直线平行），故答案为（等边对等角），（三角形外角性质），（同位角相等，两直线平行）．10．（2020·辽宁昌图期末）已知三角形的两角及夹边，求作这个三角形（保留痕迹，不写作法） 已知：,αβ∠∠ ， 线段c ，求作ABC ∆，使,,A B AB c αβ∠=∠∠=∠=【答案】见解析．【解析】解：∠ABC为所求作11．（2020·北京期末）尺规作图之旅下面是一副纯手绘的画作，其中用到的主要工具就是直尺和圆规，在数学中，我们也能通过尺规作图创造出许多带有美感的图形．尺规作图起源于古希腊的数学课题，只允许使用圆规和直尺，来解决平面几何作图问题．（作图原理）在两年的数学学习里中，我们认识了尺规作图，并学会用尺规作图完成一些作图问题，请仔细思考回顾，判断以下操作能否通过尺规作图实现，可以实现的画√，不能实现的画×．（1）过一点作一条直线．()（2）过两点作一条直线．()（3）画一条长为3㎝的线段．()（4）以一点为圆心，给定线段长为半径作圆．()（回顾思考）还记得我们用尺规作图完成的第一个问题吗？那就是“作一条线段等于已知线段”，接着，我们学习了使用尺规作图作线段的垂直平分线，作角平分线，过直线外一点作垂线……而这些尺规作图的背后都与我们学习的数学原理密切相关，下面是用尺规作一个角等于已知角的方法及说理，请补全过程． 已知：∠AOB ．求作：A O B '''∠使A O B AOB '''∠=∠作法：（1）如图，以O 为圆心，任意长为半径画弧，分别交OA ，OB 于点C ，D ；（2）画一条射线O A ''，以点O '为圆心，OC 长为半径画弧，交O A ''于点C '；（3）以点C '为圆心，____________________；（4）过点D 画射线O B ''，则A O B AOB '''∠=∠．说理：由作法得已知：,,OC O C OD O D CD C D ''''''===求证：A O B AOB '''∠=∠证明：OC O C OD O D CD C D ''''=⎧⎪=⎨⎪=''⎩OCD O C D '''∴∆≅∆( )所以A O B AOB '''∠=∠( )（小试牛刀）请按照上面的范例，完成尺规作图并说理：过直线外一点作已知直线的平行线． 已知：直线l 与直线外一点A ．求作：过点A 的直线l '，使得//l l '．（创新应用）现实生活中许多图案设计都蕴含着数学原理，下面是一个常见商标的设计示意图．假设你拥有一家书店，请利用你手中的刻度尺和圆规，为你的书店设计一个图案．要求保留作图痕迹，并写出你的设计意图．【答案】见解析．【解析】解：[作图原理]：（1）过一点作一条直线．可以求作；（2）过两点作一条直线．可以求作；（3）画一条长为3cm的线段．不可以求作；（4）以一点为圆心，给定线段长为半径作圆．可以求作；故答案为：√，√，×，√；[回顾思考]：作法：（1）如图，以O为圆心，任意长为半径画弧，分别交OA，OB于点C，D；（2）画一条射线O′A′，以点O'为圆心，OC长为半径画弧，交O’A’于点C’；（3）以点C′为圆心，以C′为圆心，CD长为半径画弧与第二步中所画的弧交于点D′；（4）过点D′画射线O′B′，则∠A′O′B′＝∠AOB．说理：由作法得已知：OC＝O′C′，OD＝O′D′，CD＝C′D′，求证：∠A′O′B′＝∠AOB．证明：在∠OCD 和∠O ′C ′D ′中, OC O C OD O D CD C D ''''⎧⎪'⎪'⎨⎩＝＝＝，∠∠OCD ∠∠O ′C ′D ′（SSS ），∠∠A ′O ′B ′＝∠AOB （全等三角形的对应角相等），故答案为：以C ′为圆心，CD 长为半径画弧与第二步中所画的弧交于点D ′，SSS ，全等三角形的对应角相等；[小试牛刀]：如图，直线l ′即为所求（方法不唯一），；[创新应用]：如图所示（答案不唯一）.．12．（2020·山东安丘月考）如图所示，在平面直角坐标系xOy 中，ABC 的顶点坐标分别是()2,3A -，()1,1B m -，()1,2C -，点B 关于x 轴的对称点P 的坐标为()3,2n --．（1）求m ，n 的值；（2）画出ABC ，并求出它的面积；（3）画出与ABC 关于y 轴成轴对称的图形111A B C △，并写出111A B C △各个顶点的坐标． （4）在y 轴上找一点Q ，使QA QB +最小（不写作法，保留作图痕迹）【答案】见解析．【解析】解:（1）B 、P 两点关于x 轴对称，∠1321m n -=-⎧⎨-=-⎩，解得：21m n =-⎧⎨=⎩． （2）()1111125435212222ABC S =⨯+⨯-⨯⨯-⨯⨯=△． （3）如图， ()12,3A ，()13,1B ，()1,2C --．（4）连结A 1B 交y 轴于点Q ，则Q 为求．13.（2020·宜兴市月考）现有三个村庄A ，B ，C ，位置如图所示，线段AB ，BC ，AC 分别是连通两个村庄之间的公路．现要修一个水站P ，使水站不仅到村庄A ，C 的距离相等，并且到公路AB ，AC 的距离也相等，请在图中作出水站P 的位置．（要求：尺规作图，不写作法，保留作图痕迹．）【答案】见解析【解析】解：如图所示：14.（2020·滨州渤海中学月考）尺规作图：如图，某地有两个工厂M、N和两条相交又的公路a，b现计划修建一座物资仓库，希望仓库到两个工厂的距离相等，到两条公路的距离也相等．你能确定仓库应该建在什么位置吗？在所给的图形中画出你的设计方案．(保留作图痕迹)．【答案】见解析.【解析】解：如图所示：点P、P′即为所求．15.（2020·南京师范大学附属中学树人学校月考）如图，已知ABC（AC AB BC），请用无刻度的直尺和圆规，完成下列作图（不写作法，保留作图痕迹）；∠=∠；（1）如图1，在AB边上寻找一点M，使AMC ACB+=．（2）如图2，在BC边上寻找一点N，使得NA NB BC【答案】（1）见解析；（2）见解析【解析】解：（1）；（2）．16.如图，在ABC 中，AB AC =，AB 的垂直平分线交AB 于N ，交AC 于M ． （1）若70B ∠=︒，则NMA ∠的度数是 ；（2）连接MB ，若8AB cm =，MBC △的周长是14cm ．∠求BC 的长；∠在直线MN 上是否存在点P ，使由P ，B ，C 构成的PBC 的周长值最小？若存在，标出点P 的位置并求PBC 的周长最小值；若不存在，说明理由．【答案】见解析.【解析】解：（1）∠AB ＝AC ，∠∠B ＝∠C ＝70°，∠∠A ＝180°－70°－70°＝40°∠MN 垂直平分AB 交AB 于N∠MN ∠AB , ∠ANM ＝90°，在∠AMN 中，∠NMA ＝180°－90°－40°＝50°；（2）∠如图所示，连接MB ，∠MN 垂直平分AB 交于AB 于N∠AM ＝BM ，∠∠MBC 的周长＝BM ＋BC ＋CM ＝AM ＋BC ＋CM ＝BC ＋AC ＝14cm又∠AB＝AC＝8cm，∠BC＝14 cm－8 cm＝6cm；∠如图所示，∠MN垂直平分AB，∠点A、B关于直线MN对称，AC与MN交于点M，因此点P与点M重合；∠∠MBC的周长就是∠PBC周长的最小值，∠∠PBC周长的最小值＝∠MBC的周长＝14 cm．。

尺规作图类型一尺规作图命题角度❶尺规作图及判定(2019·慈溪模拟)如图，点P是∠ABC的BC边上一点，作以点P为圆心，且与AB边相切的圆，下列四种作法中错误的是( )【分析】利用基本作图，根据线段的垂直平分线和切线的判定方法可对A，B，C 进行判断；利用圆周角定理和切线的判定可对D进行判断．【自主解答】1．(2019·柯桥区模拟)如图，锐角△ABC中，BC＞AB＞AC，求作一点P，使得∠BPC与∠A互补，甲、乙两人作法分别如下：甲：以B为圆心，AB长为半径画弧交AC于点P，则P即为所求；乙：作BC的垂直平分线和∠BAC的平分线，两线交于点P，则P即为所求．对于甲、乙两人的作法，下列叙述正确的是( )A．两人皆正确B．甲正确，乙错误C．甲错误，乙正确D．两人皆错误2．(2019·南浔区一模)小明在学了尺规作图后，通过“三弧法”作了一个△ACD，其作法步骤是：①作线段AB，分别以A，B为圆心，AB长为半径画弧，两弧的交点为C；②以B 为圆心，AB长为半径画弧交AB的延长线于点D；③连结AC，BC，CD.下列说法不正确的是( )A ．∠A＝60°B ．△ACD 是直角三角形C ．BC ＝32CD D ．点B 是△ACD 的外心命题角度❷ 尺规作图及计算(2019·龙湾区二模)如图，在△ABC 中，∠ACB＝90°，∠B＝28°.分别以点A ，B 为圆心大于12AB 的长为半径画弧，两弧交于点D 和E ，直线DE 交AB 于点F ，连结CF ，则∠AFC 的度数为( )A．62° B．60° C．58° D．56°【分析】利用基本作图得到DE垂直平分AB，则点F为AB的中点，再利用直角三角形斜边上的中线性质得到FC＝FB，然后根据等腰三角形的性质和三角形外角和计算∠AFC的度数．【自主解答】3．(2019·临海一模)如图，在△ABC 中，∠C＝90°，∠B＝15°，AC ＝1，分别以点A ，B 为圆心，大于12AB 的长为半径画弧，两弧相交于点M ，N ，作直线MN交BC 于点D ，连结AD ，则AD 的长为( )A ．1.5 B. 3 C ．2 D. 54．(2019·滦南一模)如图，圆上有两点A ，B ，连结AB ，分别以A ，B 为圆心，AB 的长为半径画弧，两弧相交于点C ，D ，CD 交AB 于点E ，交AB ︵于点F.若EF ＝1，AB ＝6，则该圆的半径长是( )A ．4B ．5C ．6D ．10 类型二 网格作图命题角度❶ 网格作图与点的求法(2019·鹿城区三模)已知网格的小正方形的边长均为1，格点三角形ABC 如图所示，请仅使用无刻度的直尺，且不能用直尺中的直角，画出满足条件的图形(保留作图痕迹)． (1)在图甲AB 边上取点D ，使得△BCD 的面积是△ABC 的13；(2)在图乙中，画出△ABC 所在外接圆的圆心位置．【分析】(1)利用平行线等分线段定理，把线段AB 三等分即可． (2)作出线段AB ，AC 的垂直平分线，两条垂直平分线的交点O 即为所求． 【自主解答】5．(2019·改编题)在直角坐标系中，我们把横、纵坐标都为整数的点称为整点，如图，已知点A(0，1)，B(2，0)，若△PAB的面积等于△OAB的面积，则符合条件的整点P共有______个．6．(2019·黄岩区二模)如图是一个由1×1的正方形点阵组成的点阵图，请用无刻度的直尺按要求作图．(1)如图1，点A，B是点阵中的两个点，请作出线段AB的两个三等分点．(保留作图痕迹)(2)如图2，点A，B是点阵中的两个点，请作出线段AB的两个三等分点．(保留作图痕迹)命题角度❷网格作图与线的求法(2019·北仑区模拟)只用直尺(无刻度)完成下列作图：(1)如图1，过正方形ABCD的顶点A作一条直线平分这个正方形的面积；(2)如图2，不过正方形EFGH的顶点作直线l平分这个正方形的面积；(3)如图3，五个边长相等的正方形组成了一个“L型”图形，作直线m平分这个“L型”图形的面积．【分析】(1)作正方形对角线所在的直线即为所求．(2)过正方形的中心作直线即可．(3)利用分割，补形，调整的策略解决问题即可．【自主解答】7．(2019·温州模拟)如图，在10×10的正方形网格中，△ABC的三个顶点都在网格上，请按要求完成下列作图，①仅用无刻度直尺；②保留作图痕迹．(1)在图甲中画出△ABC的BC边上的中线AD；(2)在图乙中画出△ABC的一条角平分线BE.命题角度❸网格作图与三角形、四边形的求法(2019·温州三模)如图，点A，B在7×5的正方形网格的格点上，按以下要求作出不同的格点三角形．(1)在图甲中，作出以AB为斜边的直角△ABC；(2)在图乙中，作出面积最大的等腰△ABD.【分析】(1)作出直角边长5，25的直角三角形即为所求；(2)作出AB的垂直平分线即可求解．【自主解答】8．(2019·泰顺模拟)在直角坐标系中，我们把横、纵坐标都为整数的点叫整点，顶点都是整点的三角形称为整点三角形，如图，已知整点A(0，1)，B(4，0)，请在所在的网格区域(含边界)画出符合要求的整点三角形．(1)在图1中画一个直角三角形ABC，井计算△ABC的面积；(2)在图2中画一个△ABC，使点C的横纵坐标相等，且△ABC的面积等于3. 9．(2019·义乌模拟)如图，由6个形状、大小完全相同的小矩形组成大矩形网格，小矩形的顶点称为这个矩形网格的格点，由格点构成的四边形称为格点四边形，请按要求作图(标出所画图形的顶点字母)． (1)在图1中画出一个格点正方形；(2)在图2中画出一个一般的格点平行四边形(非菱形、矩形)．参考答案【专题类型突破】 类型一【例1】 A ．由作法得PD 垂直平分AB ，则AB 与⊙P 相切于P ，所以A 选项的作法正确；B ．由作法得PD 垂直平分AB ，则AB 与⊙P 相切于P ，所以B 选项的作法正确；C ．由作法得PB 的垂直平分线与BC 相交于E ，则⊙P 的半径为12PB ，当∠B＝30°时，P 点到AB 的距离等于⊙P 的半径，所以C 选项的作法错误；D ．由作法得PB 的垂直平分线与BC 相交于E ，⊙E 与⊙P 相交于D ，则∠BDP＝90°，则PD⊥BD，AB为⊙O的切线，所以D选项的作法正确．故选C.跟踪训练1．A 2.C【例2】由作法得DE垂直平分AB，∴点F为AB的中点．∵∠ACB＝90°，∴FB＝FA＝FC，∴∠FCB＝∠B＝28°，∴∠AFC＝∠B＋∠FCB＝28°＋28°＝56°.故选D.跟踪训练3．C 4.B类型二【例3】 (1)如图甲，点D即为所求．(2)如图乙，点O即为所求．跟踪训练。