载流导体产生磁场
- 格式:ppt
- 大小:1.34 MB
- 文档页数:30

载流导体的磁场磁场是物理学中一种重要的概念,它是由电荷运动所产生的。
而载流导体就是指电流通过的导体,当电流通过导体时,会产生磁场。
本文将从载流导体的特性、磁场的产生和磁场的应用等方面进行探讨。
一、载流导体的特性载流导体是指电流通过的导体,可以是直线导线、螺线管等。
在导体中,电流的流动是由电荷的迁移所引起的。
导体中的电荷载流会产生磁场,磁场的强弱与导体中的电流有关。
二、磁场的产生1. 法拉第定律法拉第定律是描述电流通过导体时产生磁场的基本规律。
根据法拉第定律,电流通过载流导体时,会在其周围产生一个闭合的磁力线圈。
磁力线的方向可以用拇指右手法则来确定,即将右手握住导线,大拇指指向电流的方向,其他四指所指的方向就是磁力线圈的方向。
2. 磁场的强度载流导体所产生的磁场强度与导线形状、电流大小等参数有关。
当电流通过一段直线导线时,磁场的强度与导线到导线距离的平方成反比,与电流的大小成正比。
当电流通过螺线管等环形导线时,磁场的强度与导线的圈数及电流大小有关。
三、磁场的应用1. 电动机电动机是利用磁场与电流作用产生转动力的装置。
电动机中,通过电流通入导体产生磁场,然后与外部磁场相互作用,产生力矩使电机转动。
电动机的工作原理基于洛伦兹力和电流在磁场中的相互作用。
2. 电磁铁电磁铁是通过电流激励磁铁产生磁场的一种设备。
电磁铁是由一段载流导线绕制而成,通电时产生磁场,使铁芯具有吸力。
电磁铁的应用广泛,如电磁吸盘、电磁制动器等。
3. 传感器磁场的强度可以通过传感器进行检测和测量。
例如,利用霍尔元件可以测量磁场的强度和方向。
传感器在工业控制、导航、测量等领域有着广泛的应用。
4. 磁共振成像磁共振成像是一种利用强大的磁场和无线电波产生图像的医学技术。
人体组织中的原子核受到磁场的激励后会发出信号,通过接收和分析这些信号可以产生高分辨率的图像,用于诊断和研究。
总结:载流导体通过电流产生磁场是物理学中的基本现象,载流导体的磁场强度与电流的大小、导线的形状等参数有关。



教学目标:掌握短路电流热效应和电动力效应的实用计算。
重点:短路电流的效应实用计算方法。
难点:短路电流的效应计算公式。
一、短路电流电动力效应1.电动力:载流导体在相邻载流导体产生的磁场中所受的电磁力。
当电力系统中发生三相短路后,导体流过冲击短路电流时必然会在导体之间产生最大的电动力。
2.电动力的危害:引起载流导体变形、绝缘子损坏,甚至于会造成新的短路故障。
3.两平行导体间最大的电动力载流导体之间电动力的大小,取决于通过导体电流的数值、导体的几何尺寸、形状以及各相安装的相对位置等多种因素。
(N)式中:i1 、i2—通过两根平行导体的电流瞬时最大值,A;L—平行导体长度,(m);ɑ—导体轴线间距离,(m);K f—形状系数。
形状系数K f:表明实际通过导体的电流并非全部集中在导体的轴线位置时,电流分布对电动力的影响。
实际工程中,三相母线采用圆截面导体时,当两相导体之间的距离足够大,形状系数K f取为1;对于矩形导体而言,当两导体之间的净距大于矩形母线的周长时,形状系数K f可取为1。
电动力的方向:两个载流导体中的电流方向相同时,其电动力为相互吸引;两个载流导体中的电流方向相反时,其电动力为相互排斥。
4.两相短路时平行导体间的最大电动力发生两相短路时,平行导体之间的最大电动力F(2)(N):(N)式中:—两相短路冲击电流,(A)。
5.三相短路时平行导体之间的最大电动力发生三相短路时,每相导体所承受的电动力等于该相导体与其它两相之间电动力的矢量和。
三相导体水平布置时,由于各相导体所通过的电流不同,所以边缘相与中间相所承受的电动力也不相同。
边缘相U相与中间相V相导体所承受的最大电动力、分别为:(N)(N)式中:—三相冲击短路电流,(A)。
发生三相短路后,母线为三相水平布置时中间相导体所承受的电动力最大。
计算三相短路时的最大电动力时,应按中间相导体所承受的电动力计算。
6.短路电流电动力效验当系统中同一处发生三相或两相短路时,短路处三相冲击短路电流与两相冲击短路电流之比为。




磁场对载流导体的作用讲授课23 空调01/021、掌握磁场对载流导体的作用重点:磁场对载流导体的作用难点:磁场对载流导体的作用措施:以图示和公式的推导说明《电工基础教学参考书》习题册P27-28§3-4 磁场对载流导体的作用一、磁场对载流直导体的作用:1、大小:通电直导体周围存在磁场(电流的磁效应),它就成了一个磁体,把这个磁体放到另一个磁场中,也会受到磁力的作用,这就是“电磁生力”。
电磁力:指通电导体在磁场中受到的作用力。
电磁力的大小:F=BILsinα式中:F——通电导体受到的电磁力。
牛(N)B——磁感应强度。
特斯拉(T)I——导体中的电流强度。
安培(A)L——导体在磁场的长度。
米(m)α——电流方向与磁感应线的夹角。
当α=90°时,F=BILsinα最大,F=BIL当α=0°时,F=BILsinα最小,等于02、方向通电导体在磁场内的受力方向,可用左手定则判断:平伸左手,使拇指垂直其余四指,手心正对磁场的方向,四指指向表示电流的方向,拇指的指向就是通电导体的受力方向。
3、相距较近且相互平等的通电直导体之间的关系:由于每根载流导线的周围都产生磁场,所以每根导线都处在另一根导线产生的磁场中,即两根导线都受到电磁力的作用。
结论:通过同方向电流的平行导线是互相吸引的,通过反方向电流的平行导线是互相排斥的。
如:输电线上为什么要相距一定距离就安装一个绝缘支柱?4、讲解P59 例3-1二、磁场对通电矩形线圈的作用。
1、线圈平面与磁感应线平行:ab和cd与磁力线垂直将受到磁场的作用力F1和F2,而且F1=F2,根据左手定则,F1和F2的方向相反。
受到作用力的两个边叫做有效边。
两有效边所受到力大小相等,方向相反。
构成一对力偶。
此时的转矩为:M=F1L2=BIL1L2=BIS当线圈平面与磁力线的夹角为α时:M=BIScosα当线圈由N匝线构成时:M=NBIScosα当α=0°时,M=NBIScosα最大,M=NBIS 当α=90°时,线圈平面与磁感应线垂直:M=NBIScosα最小,等于02、讲解P60 例3-2。

磁场对载流导体的作用磁场是物质与电磁场相互作用的一种现象,它对载流导体的作用十分重要。
当电流通过载流导体时,会产生磁场,而磁场的存在又会影响导体本身以及周围环境。
本文将就磁场对载流导体的作用进行探讨。
一、洛伦兹力的作用当电流通过载流导体时,磁场对导体中自由电子的运动方向施加一个垂直于电流方向和磁场方向的洛伦兹力。
根据右手定则,电子将偏转到与电流方向和磁场方向垂直的方向,形成电子漂流。
而洛伦兹力也是电动力计和霍尔效应的基础。
在实际应用中,这个力对于电磁铁、电动机、变压器等设备的正常运行起着至关重要的作用。
例如,电动机的旋转就是通过利用导体在磁场中受力而产生的机械运动来实现的。
二、磁感应强度的作用磁感应强度是磁场的物理量,用符号B表示。
磁感应强度的大小决定了磁场的强弱程度。
当电流通过载流导体时,根据安培定则,磁感应强度的大小与电流强度成正比,与载流导体的长度成反比。
磁感应强度的作用表现在许多方面。
首先,它影响载流导体周围的磁场分布。
其次,磁场的方向与磁感应强度方向一致,可以用来确定磁场的方向。
此外,磁感应强度也是磁场中一些重要物理量的计算基础,例如磁通量。
三、感应电动势的作用根据法拉第电磁感应定律,当载流导体与磁场相对运动或磁场发生变化时,导体中会产生感应电动势。
这个现象广泛应用于发电机、变压器等设备中。
感应电动势的大小与磁感应强度的变化速率以及导体的几何形状有关。
感应电动势的作用可见于各种电器设备中。
例如,发电机通过导体与磁场的相对运动产生感应电动势,将机械能转化为电能。
而变压器则通过磁场的变化来调整电压大小,实现电能的传输和变换。
四、磁化效应的作用载流导体在磁场中也会发生磁化效应。
当磁场的强度足够大时,导体内的电子受到力的作用而形成自旋磁矩,导致导体整体呈现磁性。
这种现象被称为磁化。
磁化效应的作用在于为实际应用中的电磁设备提供了基础。
例如,磁化效应可用于制造磁铁,用于吸附物体、辅助定位等。
另外,它也是电磁感应定律中感应电动势产生的原理之一。

无限长载流圆柱导体内外磁场的分布载流圆柱导体内外磁场的分布是电磁学中的一个重要问题。
在这篇文章中,我们将以此为主题,详细讨论这个问题,并一步一步解答。
一、导体内外磁场的形成原理载流圆柱导体内外磁场的形成原理可以通过安培环路定理来解释。
根据安培环路定理,磁场的总磁通量等于该环路上所有电流元的磁通量之和。
对于一段长度为L的导线,其磁通量可以表示为:Φ= B ×A ,其中,B表示磁感应强度,A表示过该面积的磁场线的数量。
由于导线内部存在电流,通过安培环路定理可知,导体内外磁场的形成原理是由导体内部的电流元和其它电流元产生的。
导体内外的磁场由导体内部电流元的磁场叠加而成,并随着距离导体表面的距离不断减小。
二、导体内磁场的分布在讨论导体内磁场的分布之前,我们首先需要确定正交坐标系。
在本文中,我们选择柱坐标系。
在柱坐标系中,磁场的分布可以表示为B = (B_r, B_θ, B_z)。
其中,B_r表示径向磁场分量,B_θ表示角向磁场分量,B_z表示轴向磁场分量。
为了计算导体内磁场的分布,我们可以应用安培定理。
根据安培定理,电流周围的磁场线是以电流元为轴线的圆周。
根据对称性,我们可以得出导体内电流元的磁场与其它电流元在磁场线中的贡献是一样的。
这意味着在任意一个彼此距离相等的电流元上,它们对磁场的贡献相等。
所以,在导体内部的圆柱体积元上,径向磁场分量B_r = 0。
同理,角向磁场分量B_θ= 0。
因此,在导体内部,只存在轴向磁场分量B_z。
它的大小可以通过安培环路定理计算。
假设导体内流过的电流为I,半径为R,那么在径向表面上环路定理可以表示为:B_z ×2πrL = μ_0I,其中,r是径向表面到轴线的距离,L是导体的长度,μ_0是真空中的磁导率。
由此可以得到导体内的轴向磁场分量为:B_z = (μ_0I)/(2πrL)。
在导体外,磁场的计算较为复杂。
但有一种常用的简化方法是采用比例法和对称性法。
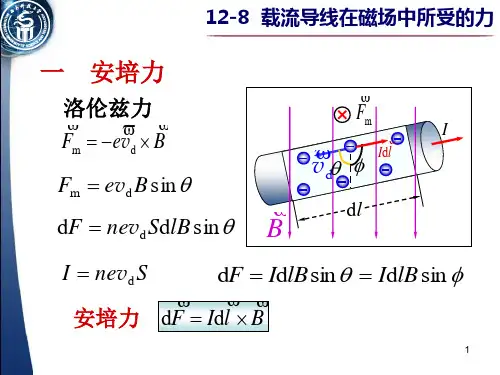
磁场对载流导体的作用我们知道运动电荷在磁场中要受到磁场力给予的作用力,即洛仑兹力。
电流是由电荷的定向运动产生的,因此磁场中的载流导体内的每一定向运动的电荷,都要受到洛仑兹力。
由于这些电荷(例如金属导体中的自由电子)受到导体的约束,而将这个力传递给导体,表现为载流导体受到的一个磁场力,通常称为安培力,下面我们从运动电荷所受到的洛仑兹力导出安培力公式。
如图1表示一个固定不动的电流元,其电流强度为I ,横截面为dS ,长为dl 。
设在电流元范围内有相同的磁感应强度B 。
则金属载流导体内每一定向运动的电子所受到的洛仑兹力为B ev f ⨯-=,v 为电子定向漂移速度,与电流密度矢量j 方向相反(nev j =,n 为导体单位体积的自由电子数)。
电流元内作定向运动的自由电子数ndSdl N =,因而电流元内作定向运动的电子所受到的合力为B dSdlj B nev dSdl B ev N dF ⨯=⨯-=⨯-=)()(在电流元的条件下,我们用dl 来表示其中电流密度的方向,并注意到电流强度dS j I ⋅=,于是上式表示为:B Idl dF ⨯=。
(1)式(1)式为电流元Idl 内定向运动的电子所受到的合磁场力。
如前所述,这个力被传递给载流体,表现为电流元这个载流导体所受到的磁场力。
通常称(1)式为安培力公式。
(1)式由运动电荷在磁场中受到的磁场力B ev f ⨯-=推导而得。
但在历史上(1)式首先是由实验得出的,因此不少作者将(1)式作为基本实验定律,从(1)式导出B ev f ⨯-=,并用(1)式给磁感应强度B 下定义。
由(1)式原则上可以求得任意形状的电流在磁场中所受到的合力,即求积分⎰⨯=l B Idl F 0,l 为在磁场中的导线长度。
下面我们来探讨一下金属载流导体(例如金,铜,铝,银等)中,定向运动的电子所受到的洛仑兹力是怎样成为载流导体的安培力的。
如图2所示,因为载流导体中每一个定向运动的电子,都要受到一个洛仑兹力B ev f ⨯-=,方向沿z 轴正方向。
载流导体在磁场中一定受到磁场力的作用吗
载流导体在磁场中不一定受到磁场力的作用。
只有载流导体与磁场存在一定夹角时才有磁场力,如果导体和磁场的夹角为0或180度,则没有磁场力磁场力包括磁场对运动电荷作用的洛仑兹力和磁场对电流作用的安培力磁场力现象中涉及3个物理量的方向:磁场方向、电荷运动方向、洛仑兹力方向磁场方向、电流方向、安培力方向。
磁场
磁场,物理概念,是指传递实物间磁力作用的场。
磁场是由运动着的微小粒子构成的,在现有条件下看不见、摸不着。
磁场具有粒子的辐射特性。
磁体周围存在磁场,磁体间的相互作用就是以磁场作为媒介的,所以两磁体不用在物理层面接触就能发生作用。
由于磁体的磁性来源于电流,电流是电荷的运动,因而概括地说,磁场是相对于观测点运动的电荷的运动的电场的强度与速度,带来的观测点处电荷所受力
的变化的表现。
用现代物理的观点来考察,物质中能够形成电荷的终极成分只有电子(带单位负电荷)和质子(带单位正电荷)。
因此负电荷就是带有过剩电子的带电物体,正电荷就是带有过剩质子的带电物体。
运动电荷产生磁场的真正场源是运动电子或运动质子所产生的磁场。
例如电流所产生的磁场就是在导线中运动的电子所产生的磁场。