当前位置：文档之家 › 数字信号处理课后答案第6章(高西全丁美玉第三版)

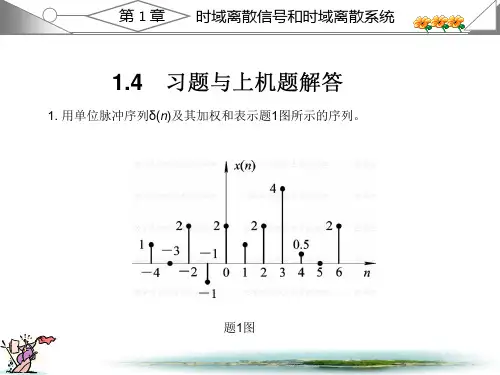
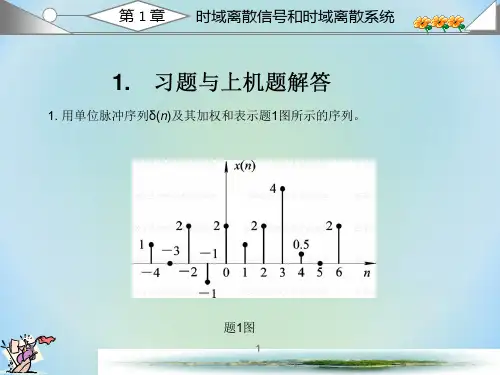
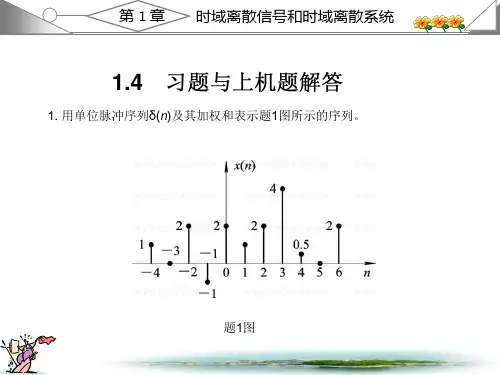
数字信号处理课后答案第6章(高西全丁美玉第三版)

  • 格式：ppt
  • 大小：1004.50 KB
  • 文档页数：96

下载文档原格式

  / 96

合集下载

数字信号处理课后习题答案 第六章习题与答案

数字信号处理课后习题答案 第六章习题与答案

1．用冲激响应不变法将以下 )(s H a 变换为 )(z H ，抽样周期为T。

为任意正整数 ,)()( )2()()( )1(022n s s As H b a s a s s H na a -=+++=分析：①冲激响应不变法满足)()()(nT h t h n h a nT t a ===，T 为抽样间隔。

这种变换法必须)(s H a 先用部分分式展开。

②第（2）小题要复习拉普拉斯变换公式1!][+=n n S n t L ,n a n t s a S S As H t u n t Ae t h )()()()!1()(010-=⇔-=-，可求出)()()(kT Th t Th k h a kT t a ===，又dz z dX zk kx )()(-⇔，则可递推求解。

解: (1)22111()()2a s a H s s a b s a jb s a jb ⎡⎤+==+⎢⎥+++++-⎣⎦[])( 21)()()(t u e e t h tjb a t jb a a --+-+=由冲激响应不变法可得：[]()()()() ()2a jb nTa jb nT a T h n Th nT ee u n -+--==+ 11011() () 211n aT jbT aT jbT n T H z h n z e e z e e z ∞------=⎡⎤==+⎢⎥--⎣⎦∑2211cos 21cos 1 ------+--⋅=ze bT z e bTz e T aT aT aT(2) 先引用拉氏变换的结论[]1!+=n n sn t L可得： na s s As H )()(0-=)()!1()(10t u n t Ae t h n t s a -=-则)()!1()()()(10k u n kT Ae T Tk Th k h n kT s a -⋅==-dzz dX zk kx azk u a ZZk )()( , 11)( 1-−→←-−→←-且按)11()()!1( )()!1( )()(111111000--∞=---∞=----=-==∑∑ze dz d z n AT e z k n T TA z k h z H T s n n k kT s n n k k可得⎪⎪⎩⎪⎪⎨⎧=-=-=•••---,3,2)1(1,1)(111000n z e z e AT n z e AT z H n T s T S n T s ，可以递推求得：2. 已知模拟二阶巴特沃思低通滤波器的归一化系统函数为：2'4142136.111)(ss s H a ++=而3dB 截止频率为50Hz 的模拟滤波器，需将归一化的)('s H a 中的s 变量用502⨯πs来代替424'108696044.928830.444108696044.9)100()(⨯++⨯==s s s H s H a a π 设系统抽样频率为Hz f s 500=，要求从这一低通模拟滤波器设计一个低通数字滤波器，采用阶跃响应不变法。

数字信号处理第三版课后答案丁玉美

数字信号处理第三版课后答案丁玉美
（5） 系统是因果系统， 因为系统的输出不取决于x(n) 的未来值。 如果|x(n)|≤M, 则|y(n)|=|ex(n)|≤e|x(n)|≤eM， 因此系统
7． 设线性时不变系统的单位脉冲响应h(n)和输入序列 x(n)如题7图所示， 要求画出y(n)输出的波形。
解： 解法（一）采用列表法。
y(n)=x(n)*h(n)= x(m)h(n－m) m
有以下三种情况， 分别求出输出y(n)。
（1） h(n)=R4(n), x(n)=R5(n) （2） h(n)=2R4(n), x(n)=δ(n)－δ(n－2) （3） h(n)=0.5nu(n), xn=R5(n)
解： （1） y(n)=x(n)*h(n)=
R4(m)R5(n－m)
m
先确定求和域。 由R4(m)和R5(n－m)确定y（n）对于m的 非零区间如下:
（5）y(n)=x2(n)
（6）y(n)=x(n2)
n
（7）y(n)= x(m) m0
（8）y(n)=x(n)sin(ωn)
解： （1） 令输入为
输出为
x(n－n0)
y′(n)=x(n－n0)+2x(n－n0－1)+3x(n－n0－2) y(n－n0)=x(n－n0)+2x(n—n0—1)+3(n－n0－2)
由于
x(n)=－δ(n+2)+δ(n－1)+2δ(n－3) 1
h(n)=2δ(n)+δ(n－1)+ δ2(n－2)
x(n)*δ(n)=x(n)
x(n)*Aδ(n－k)=Ax(n－k)
故
第 1 章 时域离散信号和时域离散系统
y(n)=x(n)*h(n)
=x(n)*［2δ(n)+δ(n－1)+ δ1(n－2) 2

数字信号处理西安电子高西全丁美玉第三版课后习题答案全1-7章

数字信号处理西安电子高西全丁美玉第三版课后习题答案全1-7章
=y′(n)
第 1 章 时域离散信号和时域离散系统
故该系统是非时变系统。 因为 y(n)=T［ax1(n)+bx2(n) =ax1(n)+bx2(n)+2［ax1(n－1)+bx2(n－1)］ +3［ax1(n－2)+bx2(n－2)］ T［ax1(n)］=ax1(n)+2ax1(n－1)+3ax1(n－2) T［bx2(n)］=bx2(n)+2bx2(n－1)+3bx2(n－2)
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器， 延时器是线性非时变系统， 下面证明。 令输入为
输出为
x(n－n1)
y′(n)=x(n－n1－n0) y(n－n1)=x(n－n1－n0)=y′(n) 故延时器是非时变系统。 由于
T［ax1(n)+bx2(n)］=ax1(n－n0)+bx2(n－n0) =aT［x1(n)］+bT［x2(n)］
=aT［x1(n)］+mbT0 ［x2(n)］
故系统是线性系统。
n
m0
第 1 章 时域离散信号和时域离散系统
（8） y(n)=x(n) sin(ωn)
令输入为
输出为
x(n－n0)
y′(n)=x(n－n0) sin(ωn) y(n－n0)=x(n－n0) sin［ω(n－n0)］≠y′(n) 故系统不是非时变系统。 由于
(5) 画x3(n)时， 先画x(－n)的波形(即将x(n)的波形以纵轴为中心翻转180°)， 然后再右移2位， x3(n)波形如题2解图（四）所示。
第 1 章 时域离散信号和时域离散系统
题2解图（一）
第 1 章 时域离散信号和时域离散系统

数字信号处理高西全课后答案ppt

数字信号处理高西全课后答案ppt
线性时不变系统是数字信号处理中最基础的系统，具有线性、时不变和因果性等重要特性。
详细描述
线性时不变系统是指系统的输入和输出之间存在线性关系，并且系统的特性不随时间变化而变化。这种系统的行为可以用线性常系数微分方程来描述，同时它的输出不依赖于输入的时间函数，只依赖于输入的初始状态。
线性时不变系统
VS
频域分析可以揭示信号的频率成分和频率域中的每个成分与原始信号之间的关系。通过在频域中对信号进行分析和处理，可以实现信号的滤波、去噪、压缩和恢复等功能。
频域分析在信号处理、图像处理、通信系统等领域得到广泛应用。例如，在图像处理中，频域分析可以用于图像滤波、边缘检测等任务；在通信系统中，频域分析可用于调制解调、频谱分析等。
详细描述
04
第四章 傅里叶变换与频域分析
傅里叶变换的定义
傅里叶变换是一种将时间域信号转换到频域的方法，通过将信号分解成一系列不同频率的正弦和余弦函数的线性组合。
傅里叶变换的性质
傅里叶变换具有一些重要性质，包括线性、对称性、可逆性、Parseval等式等。这变换的定义与性质
离散时间信号
定义
如果信号仅在离散时间点上有定义，则该信号称为离散时间信号。
例子
数字音频、图像数据等。
数学表示方法
通常使用序列形式来表示，例如y[n] = sin(n)。
01
03
02
连续时间信号的数学表示方法
离散时间信号的数学表示方法
其他表示方法
信号的数学表示方法
03
第三章 系统分析基础
总结词
快速傅里叶变换（FFT）算法的基本思想
根据算法实现方式的不同，可以分为按时间抽取（DIT）和按频率抽取（DFT）两种FFT算法。

数字信号处理第三版 教材第六章习题解答

数字信号处理第三版 教材第六章习题解答

6.2 教材第六章习题解答1. 设计一个巴特沃斯低通滤波器，要求通带截止频率6p f kHz =，通带最大衰减3p a dB =，阻带截止频率12s f kHz =，阻带最小衰减3s a dB =。

求出滤波器归一化传输函数()a H p 以及实际的()a H s 。

解：（1）求阶数N 。

lg lg sp spk N λ=-0.10.30.1 2.51011010.0562101101p s asp a k --==≈--332121022610s sp p πλπΩ⨯⨯===Ω⨯⨯将sp k 和sp λ值代入N 的计算公式得lg 0.05624.15lg 2N =-=所以取N=5（实际应用中，根据具体要求，也可能取N=4，指标稍微差一点，但阶数低一阶，使系统实现电路得到简化。

） （2）求归一化系统函数()a H p ，由阶数N=5直接查表得到5阶巴特沃斯归一化低通滤波器系统函数()a H p 为54321() 3.2361 5.2361 5.2361 3.23611a H p p p p p p =+++++或 221()(0.6181)( 1.6181)(1)a H p p p p p p =+++++ 当然，也可以按（6.12）式计算出极点:121()22,0,1,2,3,4k j Nk p ek π++==按（6.11）式写出()a H p 表达式41()()a k k H p p p ==-代入k p 值并进行分母展开得到与查表相同的结果。

（3）去归一化（即LP-LP 频率变换），由归一化系统函数()a H p 得到实际滤波器系统函数()a H s 。

由于本题中3p a dB =，即32610/c p rad s πΩ=Ω=⨯⨯，因此()()a a cH s H p s p ==Ω5542332453.2361 5.2361 5.2361 3.2361c c c cc cs s ss s Ω=+Ω+Ω+Ω+Ω+Ω对分母因式形式，则有()()a a cH s H p s p ==Ω52222(0.6180)( 1.6180)()c c c c cc s s s s s Ω=+Ω-Ω+Ω-Ω+Ω如上结果中，c Ω的值未代入相乘，这样使读者能清楚地看到去归一化后，3dB 截止频率对归一化系统函数的改变作用。

数字信号处理课后答案+第6章(高西全丁美玉第三版)

数字信号处理课后答案+第6章(高西全丁美玉第三版)
式中 Ωc=2πfc=2π×20×103=4π×104 rad/s
4. 已知模拟滤波器的系统函数Ha(s)如下： (1)
H a (s) =
s+a ( s + a) 2 + b 2
(2)
b H a (s) = (s + a)2 + b 2
式中a、 b为常数， 设Ha(s)因果稳定， 试采用脉冲响应不变 法将其转换成数字滤波器H(z)。
7.2687 ×10 16 H a (s ) = 2 ( s − 2 Re[ s1 ]s + | s1 |2 )( s 2 − 2 Re[ s2 ]s + | s2 |2 ) = 7.2687 ×1016 ( s 2 + 1.6731 ×10 4 s + 4.7791 ×10 8)( s 2 +4.0394 × 4 s +4.7790 × 8 10 10 )
1⎞ ⎛ 3 ⎞ ⎟ +⎜ ⎜ 2 ⎟ ⎟ 2⎠ ⎝ ⎠
Ak 1/ 2 1/ 2 H ( z) = ∑ = + s k T −1 ( − a + jb )T −1 1− e z 1− e z 1 − e ( −a − jb )T z −1 k =1
按照题目要求， 上面的H(z)表达式就可作为该题的答案。 但在工程实际中， 一般用无复数乘法器的二阶基本节结构 来实现。 由于两个极点共轭对称， 所以将H(z)的两项通分 并化简整理， 可得
1 G( p) = 2 ( p + 0.618 p + 1)( p2 + 1.618 p + 1)( p + 1)
当然， 也可以先按教材（6.2.13）式计算出极点：
pk = e

数字信号处理高西全课后答案

数字信号处理高西全课后答案
第 1 章 时域离散信号和时域离散系统
1.4
1. 用单位脉冲序列δ(n)及其加权和表示题1图所示的序列。
题1图
第 1 章 时域离散信号和时域离散系统
解：
x(n)=δ(n+4)+2δ(n+2)－δ(n+1)+2δ(n)+δ(n－1)
+2δ(n－2)+4δ(n－3)+0.5δ(n－4)+2δ(n－6)
第 1 章 时域离散信号和时域离散系统
解法（二） 采用解析法。 按照题7图写出x(n)和h(n)的表达式分别为
x(n)=－δ(n+2)+δ(n－1)+2δ(n－3)
h(n)=2δ(n)+δ(n－1)+ δ(n－2)
由于
x(n)*δ(n)=x(n)
1
x(n)*Aδ(n－k)=Ax(n－k)
2
故
第 1 章 时域离散信号和时域离散系统
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器， 延时器是线性非时变系统， 下面证明。 令输入为
输出为
x(n－n1)
y′(n)=x(n－n1－n0) y(n－n1)=x(n－n1－n0)=y′(n) 故延时器是非时变系统。 由于
T［ax1(n)+bx2(n)］=ax1(n－n0)+bx2(n－n0) =aT［x1(n)］+bT［x2(n)］
还和x(n)的将来值有关。
第 1 章 时域离散信号和时域离散系统
（4）假设n0>0， 系统是因果系统， 因为n时刻输出只和n时刻以后的输入 有关。 如果|x(n)|≤M, 则|y(n)|≤M，
（5） 系统是因果系统， 因为系统的输出不取决于x(n)的未来值。 如果

数字信号处理-西安电子科技大学出版(_高西全丁美玉)第三版_课后习题答案(全)

数字信号处理-西安电子科技大学出版(_高西全丁美玉)第三版_课后习题答案(全)

A
18
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器， 延时器是线性非时变系统， 下面证明。 令输入为
输出为
x(n－n1)
y′(n)=x(n－n1－n0) y(n－n1)=x(n－n1－n0)=y′(n) 故延时器是非时变系统。 由于
T［ax1(n)+bx2(n)］=ax1(n－n0)+bx2(n－n0) =aT［x1(n)］+bT［x2(n)］
5． 设系统分别用下面的差分方程描述， x(n)与y(n)分别表示系统输入和输 出， 判断系统是否是线性非时变的。
（1）y(n)=x(n)+2x(n－1)+3x(n－2) （2）y(n)=2x(n)+3 （3）y(n)=x(n－n0) n0 （4）y(n)=x(－n)
A
15
第 1 章 时域离散信号和时域离散系统
解：（1） x(－n)的波形如题4 (2) 将x(n)与x(－n)的波形对应相加， 再除以2， 得到xe(n)。 毫无疑问， 这是 一个偶对称序列。 xe(n)的波形如题4解图（二）所示。 (3) 画出xo(n)的波形如题4解图（三）所示。
A
11
第 1 章 时域离散信号和时域离散系统
题4解图（一）
题2解图（三）
A
7
第 1 章 时域离散信号和时域离散系统
题2解图（四）
A
8
第 1 章 时域离散信号和时域离散系统
3． 判断下面的序列是否是周期的; 若是周期的， 确定其周期。
(1) x(n)Acos3πn A是常数
7 8
(2)
j(1n )
x(n) e 8
解： （1） 因为ω= 列， 周期T=14

《数字信号处理》第三版课后答案(完整版)

《数字信号处理》第三版课后答案(完整版)
1.计算以下诸序列的N点DFT,在变换区间 内,序列定义为
（2） ；
（4） ；
（6） ；
（8） ；
（10） 。
解：
（2）
（4）
（6）
（8）解法1直接计算
解法2由DFT的共轭对称性求解
因为
所以
即
结果与解法1所得结果相同。此题验证了共轭对称性。
（10）解法1
上式直接计算较难，可根据循环移位性质来求解X(k)。
画出级联型结构如题3解图（b）所示。
4.图中画出了四个系统，试用各子系统的单位脉冲响应分别表示各总系统的单位脉冲响应，并求其总系统函数。图d
解：
(d)
5.写出图中流图的系统函数及差分方程。图d
解：
(d)
6.写出图中流图的系统函数。图f
解：
(f)
8．已知FIR滤波器的单位脉冲响应为 ，试用频率采样结构实现该滤波器。设采样点数N=5，要求画出频率采样网络结构，写出滤波器参数的计算公式。
总结以上x(n)是实、偶函数时，对应的傅里叶变换 是实、偶函数。
（2）x(n)是实、奇函数。
上面已推出，由于x(n)是实序列， 具有共轭对称性质，即
由于x(n)是奇函数，上式中 是奇函数，那么
因此
这说明 是纯虚数，且是w的奇函数。
10.若序列 是实因果序列，其傅里叶变换的实部如下式:
求序列 及其傅里叶变换 。
因为
所以
将x(n)的表达式代入上式，得到
8.设线性时不变系统的单位取样响应 和输入 分别有以下三种情况，分别求出输出 。
（1） ；
（2） ；
（3） 。
解：
（1）
先确定求和域，由 和 确定对于m的非零区间如下：

数字信号处理课后答案第6章(高西全丁美玉第三版)

数字信号处理课后答案第6章(高西全丁美玉第三版)

Ha
(s)

(s2

2
7.2687 1016 Re[s1]s | s1 |2 )(s2 2
Re[s2
]s
|
s2
|2 )
7.2687 1016
(s2 1.6731104 s 4.7791108 )(s2 4.0394104 s 4.7790108 )
也可得到分母多项式形式， 请读者自己计算。 3． 设计一个巴特沃斯高通滤波器， 要求其通带截止频率
解: （1） 确定滤波器技术指标。 αp=0.2 dB, Ωp=2πfp=6π×103 rad/s αs=50 dB, Ωs=2πfs=24π×103 rad/s
λp=1,
s
Hale Waihona Puke s p4(4) 求阶数N和ε。
N arch k 1
arch s
k 1
100.1as 1 100.1ap 1 1456.65
sa (1) Ha (s) (s a)2 b2
Ha(s)的极点为 s1=－a+jb, s2=－a－jb
将Ha(s)部分分式展开（用待定系数法）：
Ha (s)

sa (s a)2 b2

A1 s s1

A2 s s2
A1(s s2 ) A2 (s s1) (s a)2 b2
H (z)

2
Ak
k 1 1 es k T z 1

1

1/ 2 e(a jb)T
z
1

1

1/ 2 e(a jb)T
z
1
按照题目要求， 上面的H(z)表达式就可作为该题的答案。 但在工程实际中， 一般用无复数乘法器的二阶基本节结构 来实现。 由于两个极点共轭对称， 所以将H(z)的两项通分 并化简整理， 可得

数字信号处理第三版课后答案丁玉美

数字信号处理第三版课后答案丁玉美
7 8
(2)
j( 1n )
x(n) e 8
3
解： （1） 因为ω= 7 π, 所以 数， 因此是周期序列， 周期T=14
2 π 14 , 这是有理 3
（2） 因为ω=
1 8
, 所以
2π
=16π, 这是无理数， 因
此是非周期序列。
4． 对题1图给出的x(n)要求：
(1) 画出x(－n)的波形；
x(n)[h1(n)h2(n)] h2(k) x(m)h1(nmk)
故系统是线性系统。
6． 给定下述系统的差分方程， 试判定系统是否是因果 稳定系统， 并说明理由。
1 N 1
（1） y(n)= N k 0 x(n－k)
（2） y(n)=x(n)+x(n+1)
n n0
（3） y(n)= x(k) k nn0
（4） y(n)=x(n－n0) （5） y(n)=ex(n)
n
1=n+1
m0
3
1=8－n
m n4
④ n>7时， y(n)=0
最后结果为 0 n<0或n>7
y(n)= n+1 0≤n≤3 8－n 4≤n≤7
y(n)的波形如题8解图（一）所示。 (2) y(n) =2R4(n)*［δ(n)－δ(n－2)］=2R4(n)－2R4(n－2)
=2［δ(n)+δ(n－1)－δ(n+4)－δ(n+5) y(n)的波形如题8解图（二）所示
故延时器是线性系统。
(4) y(n)=x(－n)
令输入为
输出为
x(n－n0)
y′(n)=x(－n+n0) y(n－n0)=x(－n+n0)=y′(n) 因此系统是线性系统。 由于

西安电子科技大学(高西全丁美玉第三版)数字信号处理第6章

西安电子科技大学(高西全丁美玉第三版)数字信号处理第6章

道， 设计巴特沃斯滤波器时， 对于3 dB截止频率λc进行归
一化最方便。
第５章
无限脉冲响应(IIR)数字滤波器的设 计
图5.1.5中①、 ②、 ③、 ④对应的4组频率变换公式：
p 频率变换公式： p 归一化低通边界频率： 1, s p s p
通过关系式（5.1.2）可由Ha(jΩ)指标确定数字滤波器
H(ejω)的指标（如ωp, ωs, αp, αs等）; 利用频率转换关系ω=ΩT 容易求出H(ejω)的各边界频率; 选用适当的设计方法可得到数 字滤波器的系统函数H（z）。 由（5.1.3）式知， 也可以采用脉冲响应不变法将等效
模拟滤波器Ha(s)转换成采样数字系统中数字滤波器的系统函
第５章
无限脉冲响应(IIR)数字滤波器的设 计
第5章 无限脉冲响应(IIR)数字 滤波器的设计
5.1 5.2 5.3 学习要点 例题 教材第6章习题与上机题解答
第５章
无限脉冲响应(IIR)数字滤波器的设 计
5.1 学 习 要 点
5.1.1 IIR数字滤波器设计的基本概念及基本设计方法 1． 滤波器设计指标参数定义及其描述 滤波器设计指标参数定义及其描述在教材中有详细的 介绍， 下面仅给出低通滤波器幅频特性函数和损耗函数描 述的滤波器指标参数的示意图， 如图5.1.1所示， 并给出 二者的换算关系。
为了使初学者对IIR数字滤波器设计方法有一个整体概念， 先抛开繁杂的设计过程和设计公式， 用图5.1.3归纳IIR数字滤 波器的一般设计方法。
第５章
无限脉冲响应(IIR)数字滤波器的设 计
图5.1.3
第５章
无限脉冲响应(IIR)数字滤波器的设 计
下面对图5.1.3中给出的五种设计方法及其学习要点进行简

数字信 处理 西安电子科技大学出版 高西全丁美玉 第三版 课后习题答案 全

数字信 处理 西安电子科技大学出版 高西全丁美玉 第三版 课后习题答案 全
y(n)=x(n)*h(n)
=x(n)*［2δ(n)+δ(n－1)+ δ(n－2) 1 2
=2x(n)+x(n－1)+ x(n－2)
将x(n)的表示式代入上式， 得到 1 y(n)=－2δ(n+2)－δ(n+1)－0.5δ(n2 )+2δ(n－1)+δ(n－2)
+4.5δ(n－3)+2δ(n－4)+δ(n－5)
k nn0
如果|x(n)|≤M， 则
第 1 章 时域离散信号和时域离散系统
（4）假设n0>0， 系统是因果系统， 因为n时刻输出只和n时刻以后的输入 有关。 如果|x(n)|≤M, 则|y(n)|≤M，
（5） 系统是因果系统， 因为系统的输出不取决于x(n)的未来值。 如果
|x(n)|≤M, 则|y(n)|=|ex(n)|≤e|x(n)|≤eM，
9． 证明线性卷积服从交换律、 结合律和分配律， 即证明下面等式成立： （1） x(n)*h(n)=h(n)*x(n) （2） x(n)*(h1(n)*h2(n))=(x(n)*h1(n))*h2(n) （3） x(n)*(h1(n)+h2(n))=x(n)*h1(n)+x(n)*h2(n) 证明： （1） 因为
（2） 因为ω=
,
所以
1
8
=16π, 这是无理数， 因此是非周期序列。
2π
第 1 章 时域离散信号和时域离散系统
* 4． 对题1图给出的x(n)要
1
2
求：
1
2
(1) 画出x(－n)的波形；
第 1 章 时域离散信号和时域离散系统
解：（1） x(－n)的波形如题4 (2) 将x(n)与x(－n)的波形对应相加， 再除以2， 得到xe(n)。 毫无疑问， 这是 一个偶对称序列。 xe(n)的波形如题4解图（二）所示。 (3) 画出xo(n)的波形如题4解图（三）所示。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

7.2687 1016 H a (s) 2 ( s 2 Re[ s1 ]s | s1 |2 )( s 2 2 Re[ s2 ]s | s2 |2 ) 7.2687 1016 ( s 2 1.6731104 s 4.7791108 )( s 2 4.0394 104 s 4.7790 108 )
3 2
所以
1 2 3 H a (s) 2 2 2 s s 1 3 1 3 s 2 2
1 3 a , b 对比可知， ， 套用公式， 得 2 2
c5
如上结果中，Ωc的值未代入相乘， 这样使读者能清楚地
看到去归一化后，3 dB截止频率对归一化系统函数的改变作用。
2． 设计一个切比雪夫低通滤波器， 要求通带截止频率 fp=3 kHz，通带最大衰减αp=0.2 dB，阻带截止频率fs=12 kHz, 阻带最小衰减αs=50 dB。 求出滤波器归一化系统函数G(p)和实 际的Ha(s)。 解: （1） 确定滤波器技术指标。 αp=0.2 dB, αs=50 dB, λp=1, Ωp=2πfp=6π×103 rad/s Ωs=2πfs=24π×103 rad/s
所以， 取N=3， 查教材中表6.2.1， 得到三阶巴特沃斯归一
化低通G(p)为
G ( p) 1 p3 2 p 2 2 p 1
(4) 频率变换。 将G(p)变换成实际高通滤波器系统函数H(s)：
s3 H (s) G( p) | c 3 2 2 3 p s 2 s 2 s c c c s
b (2) H a ( s ) ( s a)2 b 2
Ha(s)的极点为 s1=－a+jb, s2=－a－jb
将Ha(s)部分分式展开：
j j 2 2 H a (s) s ( a j b ) s ( a jb )
套用教材（6.3.4）式， 得到
H ( z)
教材第6章习题与上机题解答
1． 设计一个巴特沃斯低通滤波器， 要求通带截止频率
fp=6 kHz，通带最大衰减ap=3 dB， 阻带截止频率fs=12kHz， 阻带最小衰减as=25 dB。 求出滤波器归一化系统函数G(p)以 及实际滤波器的Ha(s)。 解: （1） 求阶数N。
N
lg ksp lg sp
1 3 1 3 s1 j , s2 j 2 2 2 2
3 3 j j 3 3 H a (s) 1 1 3 3 s j s j 3 2 2 2 H ( z) 1 e 3 j 3 z 1 1 e 3 j 3
2Hale Waihona Puke 1 z 1e aT cos(bT ) H ( z) 1 2e aT cos(bT ) z 1 e2aT z 2
这样， 如果遇到将
sa H a (s) ( s a)2 b 2
用脉冲响应不变法转换成数字滤波器时， 直接套用上面 的公式即可， 且对应结构图中无复数乘法器， 便于工程 实际中实现。
1 H a (s) 2 s s 1
1 (2) H a ( s ) 2 2s 3s 1
试采用脉冲响应不变法和双线性变换法将其转换为数字滤
波器。 设T=2 s。
解: Ⅰ. 用脉冲响应不变法 (1)
1 H a (s) 2 s s 1
方法一 直接按脉冲响应不变法设计公式， Ha(s)的极点为
(4) 将G(p)去归一化， 求得实际滤波器系统函数Ha(s)：
H a ( s) Q( p) |
p s
p
4 p
1.7368 ( s p pk )
k 1
4

p4
1.7368 ( s sk )
k 1 4
其中， sk=Ωppk=6π×103pk, k=1, 2, 3, 4。 因为p4=p1*, p3=p2*, 所以， s4=s1*, s3=s2*。 将两对共轭极点对应的因子相乘， 得 到分母为二阶因子的形式， 其系数全为实数。
式中 Ωc=2πfc=2π×20×103=4π×104 rad/s
4. 已知模拟滤波器的系统函数Ha(s)如下： (1)
sa H a (s) ( s a)2 b 2
(2)
b H a (s) ( s a)2 b 2
式中a、 b为常数， 设Ha(s)因果稳定， 试采用脉冲响应不变 法将其转换成数字滤波器H(z)。
1 e
( a jb )T
j 2
z
1

1 e( a jb )T z 1
j 2
通分并化简整理， 得到
z 1e aT sin(bT ) H ( z) 1 2e aT cos(bT ) z 1 e2aT z 2
5． 已知模拟滤波器的系统函数如下： (1)
100.1as p 1 102.5 1 ksp 17.794 0.1ap 0.3 10 1 10 s 1
s 2π 12 103 sp 2 3 p 2π 6 10
将ksp和λsp值代入N的计算公式, 得
lg17.794 N 4.15 lg 2
解: 该题所给Ha(s)正是模拟滤波器二阶基本节的两种典型
形式。 所以， 求解该题具有代表性， 解该题的过程， 就是 导出这两种典型形式的Ha(s)的脉冲响应不变法转换公式。 设 采样周期为T。 (1)
sa H a (s) ( s a)2 b 2
Ha(s)的极点为 s1=－a+jb, s2=－a－jb
将Ha(s)部分分式展开（用待定系数法）：
A1 A2 sa H a (s) 2 2 ( s a) b s s1 s s2 A1 ( s s2 ) A2 ( s s1 ) ( s a)2 b2 ( A1 A2 ) s A1s2 A2 s1 ( s a)2 b2
方法二 直接套用4题（2）所得公式。 为了套用公式，
先对Ha(s)的分母配方， 将Ha(s)化成4题中的标准形式：
b H a (s) c 2 2 ( s a) b
由于
2 2
c为一常数
2 2
1 3 1 3 s s 1 s s 2 4 2 2
(3) 求归一化系统函数G(p)
Q( p) 1
2
N 1
( p p )
k 1 k
N

1 1.7368 ( p pk )
k 1 4
其中， 极点pk由教材（6.2.46）式求出如下：
(2k 1) π (2k 1) π pk ch sin jch cos 2N 2N 1 1 1 1 arsh arsh 0.5580 N 4 0.2171
p s 2, as=15 dB s
(3) 设计相应的归一化低通G(p)。 题目要求采用巴特沃斯 类型， 故
10 1 ksp 0.18 0.1as 10 1
0.1ap
s sp 2 p
lg 0.18 N 2.47 lg sp lg 2 lg ksp
k 1, 2,3, 4
π π p1 ch0.5580sin j ch0.5580 cos 0.4438 j1.0715 8 8 3π 3π p2 ch0.5580sin j ch0.5580 cos 1.0715 j0.4438 8 8 5π 5π p3 ch0.5580sin j ch0.5580 cos 1.0715 j0.4438 8 8 7π 7π p4 ch0.5580sin j ch0.5580 cos 0.4438 j1.0715 8 8
也可得到分母多项式形式， 请读者自己计算。 3． 设计一个巴特沃斯高通滤波器， 要求其通带截止频率 fp=20 kHz， 阻带截止频率fs=10 kHz， fp处最大衰减为3 dB， 阻带最小衰减as=15 dB。 求出该高通滤波器的系统函数Ha(s)。
解: (1) 确定高通滤波器技术指标要求： p=20 kHz, ap=3 dB fs=10 kHz, as=15 dB (2) 求相应的归一化低通滤波器技术指标要求： 套用图 5.1.5中高通到低通频率转换公式②， λp=1, λs=Ωp/Ωs， 得到 λp=1, ap=3 dB
Ak 1/ 2 1/ 2 H ( z) s k T 1 ( a jb )T 1 ( a jb )T 1 1 e z 1 e z 1 e z k 1
按照题目要求， 上面的H(z)表达式就可作为该题的答案。 但在工程实际中， 一般用无复数乘法器的二阶基本节结构 来实现。 由于两个极点共轭对称， 所以将H(z)的两项通分 并化简整理， 可得
p s
c
s 5 3.2361 c s 4 5.2361 c2 s 3 5.2361 c3 s 2 3.2361 c4 s c5
c5
对分母因式形式， 则有
H a ( s) H a ( p) |
p
s
c
( s 2 0.6180 c s c2 )( s 2 1.6180 c s c2 )( s c )
G ( p)
( p p )
k 0 k
4
最后代入pk值并进行分母展开， 便可得到与查表相同的结果。 （3） 去归一化（即LP-LP频率变换）， 由归一化系统 函数G(p)得到实际滤波器系统函数Ha(s)。
由于本题中ap=3 dB， 即Ωc=Ωp=2π×6×103 rad/s， 因此
H a ( s) H a ( p) |
1 3 j 2 T 2
1 3 j 2 T 2
z 1