电大【高等数学基础】 导数与微分
- 格式:doc
- 大小:350.50 KB
- 文档页数:5

高等数学导数与微分高等数学是大学数学的一门重要课程,其中导数与微分是其核心内容之一。
导数与微分是数学中研究函数变化率的重要工具,它们在物理、经济学、工程学等领域中有着广泛的应用。
本文将从导数与微分的定义、性质以及应用等方面进行探讨。
导数是描述函数变化率的概念。
具体而言,对于给定的函数,其导数表示函数在某一点上的变化速率。
导数的定义是函数在某一点上的极限,即函数在该点附近随着自变量的微小变化而相应变化的极限值。
导数的计算可以通过求出函数的导数公式,或者利用极限的性质进行计算。
导数具有一些重要的性质。
首先,导数可以用来判断函数在某一点上的增减性。
如果函数在某一点的导数大于0,则函数在该点上是增函数;如果函数在某一点的导数小于0,则函数在该点上是减函数。
其次,导数还可以用来求函数的极值。
函数在极值点处的导数为0,因此可以通过求导数为0的点来确定函数的极值点。
此外,导数还可以用来研究函数的凹凸性、拐点等性质。
微分是导数的一种应用形式。
微分可以看作是导数的微小增量,是函数值的变化量与自变量的变化量之间的关系。
微分可以用来求函数在某一点的近似值,也可以用来求函数的最值。
微分的计算可以通过求导数公式,或者利用微分的定义进行计算。
微分的应用在物理学中有着广泛的应用,比如在运动学中,通过求速度、加速度的微分可以得到物体的位移和速度等信息。
导数与微分在实际问题中有着广泛的应用。
在物理学中,导数与微分可以用来描述物体的运动状态,并求解运动的规律。
在经济学中,导数与微分可以用来分析市场需求曲线、供给曲线等经济现象。
在工程学中,导数与微分可以用来求解最优化问题,比如求解最小曲面积或最小路径等。
导数与微分还在计算机科学、生物学等领域中有着重要的应用。
高等数学中的导数与微分是数学的重要概念,具有广泛的应用价值。
通过对导数与微分的研究,我们可以更好地理解函数的变化规律,并将其应用于实际问题的求解中。
导数与微分的理论基础和实际应用相互支撑,共同构成了数学中重要的一部分。


高等数学基础教材答案详解高等数学是大学阶段数学课程的重要组成部分,对于学生来说,理解并掌握其中的基础知识和解题方法至关重要。
本文将为大家提供高等数学基础教材中一些典型问题的答案详解,帮助读者更好地理解和应用这些知识。
1. 导数和微分导数是高等数学中的重要概念,它描述了函数在某一点的变化率。
在教材中常见的导数求解问题包括函数的基本求导法则、高阶导数、隐函数求导以及参数方程求导等。
我们以一个简单的例子来说明导数的求解过程。
例题:求函数f(x) = x^2在点x=2处的导数。
解答:根据导数的定义,导数可以通过求函数的极限来得到。
对于给定的函数f(x),我们需要求解极限lim┬(h→0)(f(x+h)−f(x))/h,其中x=2。
代入函数f(x) = x^2并按照极限的运算法则进行计算,化简等式后可得到结果f'(2) = 4。
2. 积分和定积分积分是确定函数与坐标轴围成的面积的数学方法,定积分是对函数在一个区间上的积分。
教材中的积分和定积分问题种类繁多,包括基本积分法、换元积分法、分部积分法、曲线面积计算以及旋转体体积计算等。
下面我们通过一个简单的例子来解释定积分的求解方法。
例题:计算函数f(x) = x^2在区间[0, 1]上的定积分。
解答:定积分的计算可以通过求解不定积分并应用区间的边界值来完成。
对于给定的函数f(x),首先求取不定积分∫(x^2)dx,得到F(x) = (x^3)/3 + C。
然后将区间的边界值代入不定积分的结果,即F(1) - F(0),计算出定积分的值为1/3。
3. 无穷级数和幂级数无穷级数和幂级数是高等数学中的重要概念,它们用于描述某些序列的求和。
在教材中,常见的问题涉及级数的收敛性判断、级数求和、幂级数的收敛半径等。
我们通过一个典型的无穷级数例题来说明相关问题的解答过程。
例题:判断级数∑(n=1)⁺∞(1)/(2^n)的收敛性,并给出其和。
解答:通过级数收敛性判别法,我们可以知道当级数的公比小于1时,级数收敛。

高等数学基础教材答案第二版《高等数学基础教材答案第二版》第一章导数与微分1.1 导数的定义与计算方法导数的定义:对于函数f(x),在点x处的导数表示为f'(x),可以用以下公式计算:f'(x) = lim(h→0) [(f(x+h) - f(x))/h]1.2 导数的几何意义与物理应用通过导数的计算,我们可以得到函数在某一点处的切线斜率,进而了解函数的增减性和凸凹性。
在物理学中,导数也可以表示速度、加速度等物理量。
第二章不定积分与定积分2.1 不定积分不定积分,又称原函数或反导数,可以通过求导数的逆运算得到。
不定积分的符号表示为∫f(x)dx。
2.2 定积分定积分是用来计算曲线下的面积或求解物理问题的有效工具。
定积分的符号表示为∫[a, b] f(x)dx,表示函数f(x)在区间[a, b]上的面积。
第三章一元函数的应用3.1 曲线的切线与法线曲线的切线可以通过求导数得到切线的斜率,进而确定切线方程。
法线垂直于切线,并且切线和法线的斜率乘积为-1。
3.2 最值与最值问题通过求导数可以找到函数的极值点,进而确定函数的最大值和最小值。
在实际问题中,最值问题经常出现,如求解最优化问题等。
第四章多元函数与偏导数4.1 多元函数的概念多元函数是指依赖于多个变量的函数,如f(x, y)。
多元函数的图像可以用三维坐标系表示。
4.2 偏导数的定义与计算偏导数表示多元函数对某个变量的导数,其他变量视为常数。
偏导数的符号表示为∂f/∂x。
第五章重积分与曲线积分5.1 二重积分二重积分是对平面区域上的函数进行求和。
可以通过迭代积分或转换为极坐标系下的积分进行计算。
5.2 曲线积分曲线积分是沿曲线对函数进行积分的操作。
根据曲线的参数方程或者标量函数方程进行计算。
第六章数项级数6.1 数列与数列的极限数列是指一系列按照一定顺序排列的数,可以通过递推公式给出。
数列的极限是指当n趋向于无穷大时,数列的变化趋势。






三一文库( )*电大考试*高等数学(1)学习辅导(一)第一章 函数⒈理解函数的概念;掌握函数)(x f y =中符号f ( )的含义;了解函数的两要素;会求函数的定义域及函数值;会判断两个函数是否相等。
两个函数相等的充分必要条件是定义域相等且对应关系相同。
⒉了解函数的主要性质,即单调性、奇偶性、有界性和周期性。
若对任意x ,有)()(x f x f =-,则)(x f 称为偶函数,偶函数的图形关于y 轴对称。
若对任意x ,有)()(x f x f -=-,则)(x f 称为奇函数,奇函数的图形关于原点对称。
掌握奇偶函数的判别方法。
掌握单调函数、有界函数及周期函数的图形特点。
⒊熟练掌握基本初等函数的解析表达式、定义域、主要性质和图形。
基本初等函数是指以下几种类型: ①常数函数:c y = ②幂函数:)(为实数ααx y =③指数函数:)1,0(≠>=a a a y x ④对数函数:)1,0(log ≠>=a a x y a⑤三角函数:x x x x cot ,tan ,cos ,sin ⑥反三角函数:x x x arctan ,arccos ,arcsin⒋了解复合函数、初等函数的概念,会把一个复合函数分解成较简单的函数。
如函数)1(arctan 2e x y +=可以分解uy e =,2v u =,w v arctan =,x w +=1。
分解后的函数前三个都是基本初等函数,而第四个函数是常数函数和幂函数的和。
⒌会列简单的应用问题的函数关系式。
例题选解 一、填空题⒈设)0(1)1(2>++=x x x xf ,则f x ()= 。
解:设x t 1=,则tx 1=,得 t t tt t f 2211111)(++=++= 故xx x f 211)(++=。
⒉函数x x x f -+-=5)2ln(1)(的定义域是 。
解:对函数的第一项,要求02>-x 且0)2ln(≠-x ,即2>x 且3≠x ;对函数的第二项,要求05≥-x ,即5≤x 。
高数大一导数和微分知识点在高等数学学科中,导数和微分是非常重要的概念和知识点。
导数用于描述函数在某一点上的变化率,而微分则是导数的一种具体形式。
本文将介绍导数和微分的基本概念、计算方法以及它们在实际问题中的应用。
一、导数的定义和性质导数描述了函数在某一点上的变化率。
函数f(x)在点x=a处的导数可以表示为f'(a),它的定义如下:f'(a) = lim [f(x) - f(a)] / (x - a) 当 x -> a时导数具有以下一些性质:1. 可导性:如果函数f(x)在点x=a处有导数,那么我们说函数在点x=a处可导。
2. 右导数和左导数:如果函数f(x)在点x=a处的右导数和左导数存在且相等,那么函数在点x=a处可导。
3. 常数导数:常数函数的导数为0。
4. 和差法则:(f+g)'(a) = f'(a) + g'(a),(f-g)'(a) = f'(a) - g'(a)。
5. 乘法法则:(f·g)'(a) = f'(a)·g(a) + f(a)·g'(a)。
6. 除法法则:(f/g)'(a) = (f'(a)·g(a) - f(a)·g'(a)) / (g(a))^2,其中g(a) ≠ 0。
7. 复合函数的导数:如果y=f(u)和u=g(x)都可导,则复合函数y=f(g(x))也可导,且导数为f'(g(x))·g'(x)。
二、导数的计算方法1. 基本函数的导数:- 常数函数的导数为0。
- 幂函数y=x^n的导数为y'=n·x^(n-1)。
- 三角函数的导数:正弦函数的导数为y'=cos(x),余弦函数的导数为y'=-sin(x),正切函数的导数为y'=sec^2(x)。
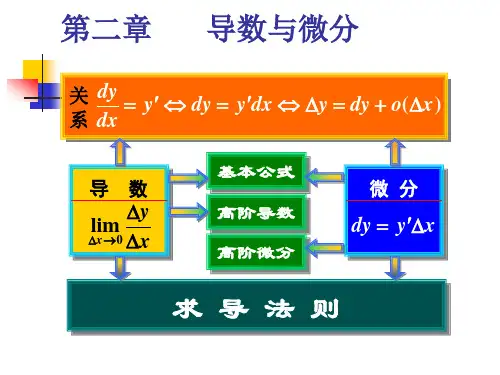
电视大学高等数学教材第一章导数与微分导数是数学中的重要概念,它在描述函数变化率、求解极值等方面有着广泛的应用。
微积分作为数学的重要分支,是研究变化与极限的工具之一。
本章内容将重点介绍导数和微分相关的概念、性质与应用。
1.1 导数的定义与计算导数表示函数在某一点的瞬时变化率,它的计算可以通过极限来实现。
尤其是涉及到多项式函数、指数函数、对数函数、三角函数等基本函数的导数计算。
此外,本节还将介绍导数的一些基本性质和常用的导数公式。
1.2 导数的应用导数在实际问题中的应用广泛,如求解最优化问题、曲线的切线方程与凹凸性判定等。
本节将通过具体的实际问题,展示导数在各个领域的应用,包括物理、经济等。
第二章不定积分与定积分不定积分与定积分是微积分的另一个重要分支,它们分别描述了函数的反变化和面积问题。
本章内容将围绕不定积分和定积分的定义、性质及计算方法展开。
2.1 不定积分不定积分是定积分的逆运算,也称原函数。
本节将介绍不定积分的定义与计算方法,其中包括基本积分公式、换元积分法、分部积分法等。
2.2 定积分定积分描述了函数在给定区间上的累计变化,它可以用于求解面积、长度等问题。
本节将介绍定积分的定义与计算方法,包括牛顿-莱布尼茨公式、换元积分法等。
第三章一元函数微分学进阶一元函数微分学是微积分的核心内容之一,本章将从导数的高阶性质、微分中值定理、泰勒公式等方面深入讲解一元函数微分学的进阶内容。
3.1 高阶导数与泰勒公式高阶导数描述了函数变化的更多细节,泰勒公式将函数展开为多项式,为研究函数性质提供了有力工具。
本节将介绍高阶导数的计算、泰勒公式的推导与应用。
3.2 微分中值定理与极值问题微分中值定理是导数与函数性质之间的重要关系,通过它可以证明函数的极值存在与求解。
本节将介绍拉格朗日中值定理、柯西中值定理等,以及求解极值问题的相关方法。
......(以下内容省略)通过以上小节的学习,你将了解到导数与微分、不定积分与定积分、一元函数微分学的高级应用等高等数学的核心知识点。
2) 导数与微分
070713.设
)(x f 在0x 可导,则=--→h
x f h x f h )
()2(lim
000
( ).
A
)(0x f ' B )(20x f ' C )(0x f '- D )(20x f '-
070113.设
)(x f 在0x 可导,则=--→h
x f h x f h 2)
()2(lim
000
( ).
(A) )(0x f ' (B) )(20x f ' (C) )(0x f '- (D) )(20x f '-
060113.设
x x f e )(=,则=∆-∆+→∆x f x f x )1()1(lim
( ).A e 2 B e C
080713.下列等式中正确的是( )
A
dx x x d 1
)1(2-= B dx x 2)x 1d(= C dx d x x 2)ln22(= D 050713.下列等式中正确的是( ). A.xdx d arctan )1(
2= B.
2
)1(dx d -= C.dx d x x
2)2ln 2
(= D.xdx x d cot )(tan =
A 先单调下降再单调上升
B 单调下降
C 先单调上升再单调下降
D 单调上升
060713. 函数
622+-=x x y 在区间)5,2(内满足( )
. A. 先单调下降再单调上升 B. 单调下降 C. 先单调上升再单调下降 D. 单调上升
080724.函数
2)2(2+-=x y 的单调减少区间是 .
080124.函数
1)(2-=x x f 的单调减少区间是 .
070724. 函数2
x
e y -=的单调减少区间是 .
070124.函数x y arctan =的单调增加区间是 .
060724.函数1)1(2++=x y 的单调增加区间是 . 060124.函数1)1(2++=x y 的单调减少区间是 .
050724.函数
)1ln(2x y +=的单调增加区间是 .
080732.设
2sin sin x e y x +=,求y ' 解:2sin 2sin cos 2cos )(sin )(x x x e x e y x x +='+'='
080132.设2
x xe
y =,求
y ' 解:2
22222)()(x
x x x e x e e x e x y +='+'='
070732.设2sin x e y x -=,求'y 解:x xe x x e y x x 2cos )().(sin sin 2sin -='-'='
070132.设x x y e cos ln +=,求'y 解:x x
x y e sin )(ln -'=' 060732.设
x x e y x ln tan -=,求y '.
x
x x x x 12-
解:由导数四则运算法则得
x x x x
x x x x x y ++=
'+'+'='ln 2cos 1
)(ln ln )()(tan 222
050733.设
2cos ln x y =,求d y .
解:
2222
2
2tan 2))(sin .(cos 1)(cos 1x x x x x
x y -='-='=
', dx x x dx y dy 2tan 2-='=
6 060734.设y
y x =()是由方程3e y e x y +=确定的函数,求d y .
解:等式两端求微分得:左端y e e
y y
d )(d ==, 右端dy y dx y x x 233
e )e (d +=+=
由此得
y y y x e y
d e d 3d 2x =+ 整理后得
x y e y y x
d 3
e d 2
-=
060134.设y
y x =()是由方程y x y e cos =确定的函数,求d y .
解:等式两端求微分得 左端y x x y x y d cos )(cos d )cos (d +==右端y y y
d e )e
(d ==
由此得
y y x x x y y d e d c o s d s i n =+- 整理后得 y d =
050734.设y
y x =()是由方程y
x
y x 2sin 2=
确定的函数,求'y 解:等式两端求微分得: 左端y y x ydx x y x
d cos sin 2)sin (d 22
+== 右端2
22)2(
d y
xdy
ydx y x -==
2
)2(-+=
y y
22
即曲线
2x y =上的点(
23,26)和点(2
3
,26-)到点A (0,2)的距离最短 08014某制罐厂要生产一种体积为V 的有盖圆柱形容器,问容器的底半径与高各为多少时用料最省?
解:设容器的底半径为r ,高为h ,则其表面积为r
V r rh r S
2π2π2π222+
=+=
2
2π4r V r S -
=', 由0='S ,得唯一驻点3
π
2V r =,此时3
π
4V h =。
由实际问题可知,当底半径3
π
2V r =与高3
π
4V h =时可使用料最省。
07074欲做一个底为正方形,容积为32立方米的长方体开口容器,怎样做法用料最省? 解: 设底边的边长为x ,高为h ,用材料为
y ,
由已知322
=h x
,2
32x
h =
,x x xh x y 12842
2+=+= 令012822=-='x x y ,解得4=x 是唯一驻点,此时24
32
2==h 。
由实际问题可知,4=x 是函数的极小值点,所以当4=x ,2=h 时用料最省。
07014某制罐厂要生产一种体积为V 的有盖圆柱形容器,问容器的底半径与高各为多少时用料最省?
同08014
06074在抛物线
x y 42=上求一点,使其与x 轴上的点)0,3(A 的距离最短.
解:设所求点P (x ,y ),则满足
x y 42=,点P 到点A 的距离之平方为
222 d 与x x d L
+-==22)3(在同一点取到最大值,为计算方便求L 的最大值点,
令01)3(2=+-=
'x L ,得25=
x ,由此解出2
10
±=y
即曲线x y =2上的点(
2
5,
2
10
)和(
25,2
10
-
)到点A (3,0)的距离最短。