8年级下册过关练习题

部编版八年级下册历史第四单元第12课民族大团结课后巩固练习一、选择题1．歌曲《爱我中华》谱写了56个民族交融相处，生生不息，共同铸造中华民族辉煌的历史篇章。

下列哪一政治制度的实行体现了中华民族大家庭的团结和兴盛？（）A．政治协商制度B．人民代表大会制度C．一国两制D．民族区域自治制度2．某年春节联欢晚会现场公布了这样一副对联，“上联，二十四个节气，乾坤竞秀。

下联，五十六朵奇葩，和睦共存。

横批，天人合一。

”新中国成立以来，我国为实现“五十六朵奇葩，和睦共存”而釆取的措施中不正确的是（）A．实行民族平等、民族团结、各民族共同繁荣的原则B．在少数民族聚居的地方实行民族区域自治制度C．实施西部大开发战略D．新中国成立后在少数民族地区实行了资本主义制度3．民族自治地方经济发展概况（）促进上表数据变化的原因有①民族区域自治制度的实行②对少数民族地区的民主改革与社会主义改造③党和政府采取优惠政策加强少数民族地区的经济建设④文化保护及西部大开发A．①②③B．②③④C．①③④D．①②③④4．民族区域自治制度下，各少数民族实行区域自治的前提是（）A．国家统一B．设置自治政府C．在国家统一领导下D．民族团结5．1957年3月25日，周恩来在谈及民族区域自治制度时说：“中国如果采取联邦制，就会在各民族间增加界墙，增加民族纠纷。

因为我国许多少数民族同汉族长期共同聚居在一个地区，有些地区……汉族都占很大比重，若实行严格的单一民族的联邦制，很多的人就要搬家……所以我们……要实行民族区域自治的政策。

”对此材料的理解，正确的是（）①联邦制不利于各个国家的民族团结与发展②在民族聚居区都要实现民族区域自治③民族区域自治制度是由我国历史与国情决定的④实现民族区域自治，有利于民族团结，有利于社会稳定A．①②B．①②③C．②③④D．③④6．下列有关民族区域自治制度的含义，理解不正确的是( )A．以国家统一、领士完整为前提B．以少数民族聚居区为基础C．少数民族自主地管理本民族，本地区的内部事务D．享有高度自治7．为实现各民族共同繁荣，新中国在少数民族地区采取了一系列措施。

部编版八年级语文下册第6课《恐龙无处不在》同步练习题（逐题解析）部编人教版八年级下册部编版八年级语文下册第6课《恐龙无处不在》同步练习题1.根据拼音写出汉字（1）鸟tún（______）目（2）chánchú（______）（______）（3）xié（______）带（4）潮xī（______）（5）领yù（______）（6）yǎn（______）射（7）二氧化guī（______）（8）排chì（______）【答案】(1).（1）臀(2).（2）蟾(3).蜍(4).（3）携(5).（4）汐(6).（5）域(7).（6）衍(8).（7）硅(9).（8）斥【解析】本题考查学生对字形的掌握情况，对汉字字形的正确书写能力。

这就要求学生平时的学习中注意字形的识记和积累，特别是形近字。

辨析字形既要注意平时的积累，也要联系整个词语的意思。

本题需要注意的字是：臀，蟾。

2.找出每组字形有误的一项，将序号写入括号（1）（______）A．尘埃B．至密C．繁盛D．熔化（2）（______）A．膨胀B．陨石C．流逝D．砥达【答案】(1).（1）B(2).（2）D【解析】本题考查学生根据词语意思选择正确字形，正确书写汉字能力。

这就要求学生平时的学习中注意字形的识记和积累，特别是形近字。

辨析字形既要注意平时的积累，也要联系整个词语的意思。

本题需要注意的词语是：致密：形容某一事或物精致紧密。

3.给加粗字注音并解释词语（1）天衣无缝________________（1）褶皱____________________（3）追溯____________________（4）劫难____________________【答案】(1).（1）fèng；比喻事物完善周密，找不出什么毛病。

(2).（2）zhězhòu；由于地壳运动，岩层受到挤压而形成的弯曲。

Unit 5Topic 2 【单元过关练】-2022-2023学年八年级英语下册单元复习过过过（仁爱版）（满分100分）一、单项选择(共15分，每小题1分）1．（2022·吉林长春·校考二模）The UK is _______ European country with a long history. Many tourists pay a visit to it every year.A．a B．an C．the D．/2．（2022春·八年级课时练习）—Did Ben do well in the ________?—Yes, he even got the highest grade in the class!A．concert B．exam C．discussion D．opening3．（2022春·重庆沙坪坝·八年级重庆南开中学校考期末）Tom made a(n) ________ to put in all his heart and we believe that he will make it.A．difference B．joke C．promise D．invitation4．（2022春·八年级单元测试）— Jack is a(n) ________ young man.— That’s true. He always feels nervous(紧张的) when he speaks in front of many people.A．friendly B．shy C．honest D．bored5．（2022春·吉林长春·八年级统考期末）Not ________ enjoys sports. But we must do sports to stay healthy. A．someone B．anyone C．everyone D．nobody6．（2022秋·八年级课时练习）—Jack ________ to take the examination because he was ill.—What a pity!A．expected B．failed C．meant D．thought7．（2022秋·广西贵港·八年级统考期末）The final exam is coming, so Tina has to ________ her lessons late into the night.A．review B．repeat C．report D．refuse8．（2022春·天津河北·八年级统考期末）It’s ________ to read the map when you can’t find the way. A．harmful B．helpful C．colourful D．beautiful9．（2021春·江苏扬州·八年级校考期中）You will find ________ to read some interesting story-books when you feel ________.A．it useful, terrible B．it helpless, badly C．that helpful, terribly D．that useful, bad10．（2022春·湖北武汉·八年级湖北省水果湖第一中学校考期中）— Which of the two dresses will you take?— I’ll take ________. One is for my cousin and the other is for my sister.A．either B．both C．all D．neither11．（2022春·八年级单元测试）I don’t like football. Tom doesn’t like it, ________ .A．too B．either C．also D．neither12．（2022春·广东深圳·八年级校考期中）My sibling is three years ________than me. He is my________brother. A．elder; elder B．older; elder C．older; older D．old; elder13．（2022春·八年级课时练习）In the New Year, I hope your life will ____________ happiness and good luck. A．be covered with B．be strict with C．be pleased with D．be filled with14．（2022春·八年级课时练习）________, several weeks later, I can swim very well.A．On the way B．In the way C．By the way D．In this way15．（2022秋·湖北武汉·八年级统考期末）—Please mind your steps, sir.—________.A．It doesn’t matter B．Thanks a lot C．Never mind D．Take it easy二．完形填空(共10分，每小题1分）（2021秋·广东梅州·八年级统考期末）通读下面短文，掌握其大意，然后在每小题所给的四个选项中，选出一个最佳答案，并将答题卡对应题目所选的选项涂黑。

最新北师大版八年级下册数学期末复习压轴题练习试题以及答案八年级下册数学期末压轴题1.在四边形ABCD中，∠BAC=∠ACD=90°，∠B=∠D．1) 证明四边形ABCD是平行四边形；2) 若AB=3cm，BC=5cm，AE=1/3 AB，点P从B点出发，以1cm/s的速度沿BC→CD→DA运动至A点停止，则从运动开始经过多少时间，使△BEP为等腰三角形？2.△XXX的XXX在直线m上，AC⊥BC，且AC=BC，△DEF的边FE也在直线m上，边DF与XXX重合，且DF=EF．1) 观察、思考，猜想并写出AB与AE所满足的数量关系和位置关系；2) 将△DEF沿直线m向左平移到图（2）的位置时，DE交AC于点G，连接AE，BG．猜想△BCG与△XXX能否通过旋转重合？请证明你的猜想．3.在△ABC中，AB=AC，CG⊥BA交BA的延长线于点G．一等腰直角三角尺按如图1所示的位置摆放，该三角尺的直角顶点为F，一条直角边与AC边在一条直线上，另一条直角边恰好经过点B．1) 观察、测量BF与CG的长度，猜想并写出BF与CG满足的数量关系，然后证明你的猜想；2) 当三角尺沿AC方向平移到图2所示的位置时，一条直角边仍与AC边在同一直线上，另一条直角边交BC边于点D，过点D作DE⊥BA于点E．此时请你通过观察、测量DE、DF与CG的长度，猜想并写出DE+DF与CG之间满足的数量关系，然后证明你的猜想；3) 当三角尺在（2）的基础上沿AC方向继续平移到图3所示的位置（点F在线段AC上，且点F与点C不重合）时，（2）中的猜想是否仍然成立？（不用说明理由）4.图1是边长分别为a和b（a＞b）的两个等边三角形纸片ABC和C′DE叠放在一起（C与C′重合）的图形．1) 操作：固定△ABC，将△C′DE绕点C按顺时针方向旋转30°，连结AD，BE，如图2；在图2中，线段BE与AD之间具有怎样的大小关系？证明你的结论；2) 操作：若将图1中的△C′DE绕点C按顺时针方向任意旋转一个角度，连结AD，BE，如图3；在图3中，线段BE 与AD之间具有怎样的大小关系？证明你的结论；3) 根据上面的操作过程，请你猜想当为多少度时，线段AD的长度最大？是多少？当为多少度时，线段AD的长度最小？是多少？（不要求证明）之间的数量关系，并说明理由；2）证明你所得到的猜想；3）若平行四边形ABCD的周长为20且a+b+c+d=10求平行四边形ABCD的面积．5、在△ACB和△AED中，已知AC=BC，AE=DE，∠ACB＝∠AED＝90°，点E在AB上，F是线段BD的中点，连接CE、FE。

人教版八年级数学下册《利用勾股定理解决折叠问题的技巧》练习题(附带答案）类型一 利用勾股定理解决三角形的折叠问题1．如图 △ABC 中 ∠ACB ＝90° AC ＝8 BC ＝6 将△ADE 沿DE 翻折使点A 与点B 重合 则CE 的长为 ．思路引领：设CE ＝x 则AE ＝BE ＝8﹣x 在Rt △BCE 中 由勾股定理可得62+x 2＝（8﹣x ）2 即可解得答案．解：设CE ＝x 则AE ＝BE ＝8﹣x在Rt △BCE 中 BC 2+CE 2＝BE 2∴62+x 2＝（8﹣x ）2解得x =74故答案为：74． 总结提升：本题考查直角三角形中的折叠问题 解题的关键是掌握折叠的性质 熟练应用勾股定理列方程解决问题．2．（2021秋•介休市期中）如图所示 有一块直角三角形纸片 ∠C ＝90° AC ＝8cm BC ＝6cm 将斜边AB 翻折 使点B 落在直角边AC 的延长线上的点E 处 折痕为AD 则CE 的长为 cm ．思路引领：根据勾股定理可将斜边AB 的长求出 根据折叠的性质知 AE ＝AB 已知AC 的长 可将CE 的长求出．解：在Rt △ABC 中∵∠C＝90°AC＝8cm BC＝6cm∴AB=√AC2+BC2=10cm根据折叠的性质可知：AE＝AB＝10cm∵AC＝8cm∴CE＝AE﹣AC＝2cm即CE的长为2cm故答案为：2．总结提升：此题考查翻折问题将图形进行折叠后两个图形全等是解决折叠问题的突破口．3．（2020秋•金台区校级期末）如图在△ABC中∠ACB＝90°点E F在边AB上将边AC沿CE翻折使点A落在AB上的点D处再将边BC沿CF翻折使点B落在CD的延长线上的点B′处（1）求∠ECF的度数；（2）若CE＝4 B′F＝1 求线段BC的长和△ABC的面积．思路引领：（1）由折叠可得∠ACE＝∠DCE=12∠ACD∠BCF＝∠B'CF=12∠BCB' 再根据∠ACB＝90°即可得出∠ECF＝45°；（2）在Rt△BCE中根据勾股定理可得BC=√41设AE＝x则AB＝x+5 根据勾股定理可得AE2+CE2＝AB2﹣BC2即x2+42＝（x+5）2﹣41 求得x=165得出AE的长和AB的长再由三角形面积公式即可得出S△ABC．解：（1）由折叠可得∠ACE＝∠DCE=12∠ACD∠BCF＝∠B'CF=12∠BCB'又∵∠ACB＝90°∴∠ACD+∠BCB'＝90°∴∠ECD+∠FCD=12×90°＝45°即∠ECF＝45°；（2）由折叠可得：∠DEC＝∠AEC＝90°BF＝B'F＝1 ∴∠EFC＝45°＝∠ECF∴CE＝EF＝4∴BE＝4+1＝5在Rt△BCE中由勾股定理得：BC=√BE2+CE2=√52+42=√41设AE＝x则AB＝x+5∵Rt△ACE中AC2＝AE2+CE2Rt△ABC中AC2＝AB2﹣BC2∴AE2+CE2＝AB2﹣BC2即x2+42＝（x+5）2﹣41解得：x=16 5∴AE=165AB＝AE+BE=165+5=415∴S△ABC=12AB×CE=12×415×4=825．总结提升：本题主要考查了折叠变换的性质、勾股定理、三角形面积等知识；熟练掌握折叠变换的性质由勾股定理得出方程是解题的关键．4．（2022秋•安岳县期末）如图在△ABC中∠C＝90°把△ABC沿直线DE折叠使△ADE与△BDE 重合．（1）若∠A＝34°则∠CBD的度数为；（2）当AB＝m（m＞0）△ABC的面积为2m+4时△BCD的周长为（用含m的代数式表示）；（3）若AC＝8 BC＝6 求AD的长．思路引领：（1）根据折叠可得∠1＝∠A＝34°根据三角形内角和定理可以计算出∠ABC＝56°进而得到∠CBD＝22°；（2）根据三角形ACB的面积可得12AC•BC＝2m+4 进而得到AC•BC＝4m+8 再在Rt△CAB中CA2+CB2＝BA2再把左边配成完全平方可得CA+CB的长进而得到△BCD的周长；（3）根据折叠可得AD＝DB设CD＝x则AD＝BD＝8﹣x再在Rt△CDB中利用勾股定理可得x2+62＝（8﹣x）2再解方程可得x的值进而得到AD的长．解：（1）∵把△ABC 沿直线DE 折叠 使△ADE 与△BDE 重合∴∠ABD ＝∠A ＝34°∵∠C ＝90°∴∠ABC ＝180°﹣90°﹣34°＝56°∴∠CBD ＝56°﹣34°＝22°故答案为：22°；（2）∵△ABC 的面积为2m +4∴12AC •BC ＝2m +4 ∴AC •BC ＝4m +8∵在Rt △CAB 中 CA 2+CB 2＝BA 2 AB ＝m∴CA 2+CB 2+2AC •BC ＝BA 2+2AC •BC∴（CA +BC ）2＝m 2+8m +16＝（m +4）2∴CA +CB ＝m +4∵AD ＝DB∴CD +DB +BC ＝m +4．即△BCD 的周长为m +4故答案为：m +4；（3）∵把△ABC 沿直线DE 折叠 使△ADE 与△BDE 重合∴AD ＝DB设CD ＝x 则AD ＝BD ＝8﹣x在Rt △CDB 中 CD 2+CB 2＝BD 2x 2+62＝（8﹣x ）2解得：x =74AD ＝8−74=254．总结提升：此题主要考查了图形的翻折变换 以及勾股定理 完全平方公式 关键是掌握勾股定理 以及折叠后哪些是对应角和对应线段．5．（2021秋•章丘区期中）（1）如图① Rt △ABC 的斜边AC 比直角边AB 长2cm 另一直角边BC 长为6cm 求AC 的长．（2）拓展：如图②在图①的△ABC的边AB上取一点D连接CD将△ABC沿CD翻折使点B的对称点E落在边AC上．①AE的长．②求DE的长．思路引领：（1）在Rt△ABC中由勾股定理可求AB的长即可求解；（2）①由折叠的性质可得∠DEC＝∠DBC＝90°DE＝DB EC＝BC＝6cm于是得到答案；②在Rt△ADE中由勾股定理可求DE的长．解：（1）设AB＝xcm则AC＝（x+2）cm∵AC2＝AB2+BC2∴（x+2）2＝x2+62解得x＝8∴AB＝8cm∴AC＝8+2＝10（cm）；（2）①由折叠的性质可得∠DEC＝∠DBC＝90°DE＝DB EC＝BC＝6cm∴∠AED＝90°AE＝AC﹣EC＝4（cm）；②设DE＝DB＝ycm则AD＝AB﹣BD＝（8﹣y）cm在Rt△ADE中AD2＝AE2+DE2∴（8﹣y）2＝42+y2解得：y＝3∴DE＝3（cm）．总结提升：本题考查了翻折变换折叠的性质勾股定理利用勾股定理列出方程是本题的关键．类型二利用勾股定理解决长方形的折叠问题6．（2022•纳溪区模拟）如图在矩形ABCD中AB＝5 AD＝3 点E为BC上一点把△CDE沿DE翻折 点C 恰好落在AB 边上的F 处 则CE 的长为 ．思路引领：利用勾股定理得出AF 的长度 再利用折叠的性质 在△BEF 中求解BE 的长 即可得出CE 的长度．解：在矩形ABCD 中 AB ＝5 AD ＝3 由折叠的性质可得：DF ＝DC ＝AB ＝5∴AF =√DF 2−AD 2=√52−32=4∴BF ＝AB ﹣AF ＝5﹣4＝1设CE ＝x 则：EF ＝CE ＝x BE ＝BC ﹣CE ＝3﹣x在Rt △BEF 中 由勾股定理可得：12+（3﹣x ）2＝x 2解得：x =53∴CE =53故答案为：53． 总结提升：本题考查了折叠的性质、矩形的性质和勾股定理等知识点 解题的关键是利用AF 求出BF 的长度．7．（2021•郯城县校级模拟）如图 在长方形ABCD 中 AB ＝3cm AD ＝9cm 将此长方形折叠 使点D 与点B 重合 折痕为EF 则△ABE 的面积为（ ）cm 2．A ．12B ．10C ．6D ．15思路引领：由长方形的性质得BAE ＝90° 再由折叠的性质得BE ＝ED 然后在Rt △ABE 中 由勾股定理得32+AE2＝（9﹣AE）2解得AE＝4（cm）即可求解．解：∵四边形ABCD是长方形∴∠BAE＝90°∵将此长方形折叠使点B与点D重合∴BE＝ED∵AD＝9＝AE+DE＝AE+BE∴BE＝9﹣AE在Rt△ABE中由勾股定理得：AB2+AE2＝BE2∴32+AE2＝（9﹣AE）2解得：AE＝4（cm）∴S△ABE=12AB•AE=12×3×4＝6（cm2）故选：C．总结提升：本题考查了翻折变换的性质、矩形的性质以及勾股定理等知识；熟练掌握翻折变换的性质和矩形的性质由勾股定理得出方程是解题的关键．8．（2020春•余干县校级期末）如图把长方形纸片ABCD沿EF折叠使点B落在边AD上的点B'处点A落在点A'处．（1）试说明B'E＝BF；（2）设AE＝a AB＝b BF＝c试猜想a b c之间的关系并说明理由．思路引领：（1）根据折叠的性质、平行的性质及等角对等边即可说明；（2）根据折叠的性质将AE、AB、BF都转化到直角三角形△A'B'E中由勾股定理可得a b c之间的关系．（1）证明：由折叠的性质得：B'F＝BF∠B'FE＝∠BFE在长方形纸片ABCD中AD∥BC∴∠B'EF＝∠BFE∴∠B'FE＝∠B'EF∴B'F＝B'E∴B'E＝BF．（2）解：a b c之间的关系是a2+b2＝c2．理由如下：由（1）知B'E＝BF＝c由折叠的性质得：∠A'＝∠A＝90°A'E＝AE＝a A'B'＝AB＝b．在△A'B'E中∵∠A'＝90°∴A'E2+A'B'2＝B'E2∴a2+b2＝c2．总结提升：本题考查了翻折变换的性质、矩形的性质、等腰三角形的判定、勾股定理等知识；灵活利用折叠的性质进行线段间的转化是解题的关键．9．（2020秋•罗湖区校级期末）如图把一张长方形纸片ABCD折叠起来使其对角顶点A与C重合D 与G重合若长方形的长BC为8 宽AB为4 求：（1）DE的长；（2）求阴影部分△GED的面积．思路引领：（1）设DE＝EG＝x则AE＝8﹣x在Rt△AEG中根据AG2+EG2＝AE2构建方程即可解决问题；（2）过G点作GM⊥AD于M根据三角形面积不变性AG×GE＝AE×GM求出GM的长根据三角形面积公式计算即可．解：（1）设DE＝EG＝x则AE＝8﹣x在Rt△AEG中AG2+EG2＝AE2∴16+x2＝（8﹣x）2解得x＝3∴DE＝3．（2）过G 点作GM ⊥AD 于M则12•AG ×GE =12•AE ×GM AG ＝AB ＝4 AE ＝CF ＝5 GE ＝DE ＝3 ∴GM =125∴S △GED =12GM ×DE =185．总结提升：本题主要考查了折叠的性质、勾股定理以及三角形面积不变性 灵活运用折叠的性质、勾股定理等几何知识点来分析、判断、推理是解题的关键．类型三 利用勾股定理解决正方形的折叠问题10．（2019•黔东南州一模）如图 将边长为6cm 的正方形纸片ABCD 折叠 使点D 落在AB 边中点E 处 点C 落在点Q 处 折痕为FH 则线段AF 的长为（ ）A ．32B ．3C ．94D ．154思路引领：由正方形的性质和折叠的性质可得EF ＝DE AB ＝AD ＝6cm ∠A ＝90° 由勾股定理可求AF 的长．解：∵将边长为6cm 的正方形纸片ABCD 折叠 使点D 落在AB 边中点E 处∴EF ＝DE AB ＝AD ＝6cm ∠A ＝90°∵点E 是AB 的中点∴AE ＝BE ＝3cm在Rt △AEF 中 EF 2＝AF 2+AE 2∴（6﹣AF ）2＝AF 2+9∴AF=9 4故选：C．总结提升：本题考查了翻折变换正方形的性质勾股定理利用勾股定理求线段的长度是本题的关键．11．如图将边长为8cm的正方形纸片ABCD折叠使点D落在BC边的中点E处点A落在点F处折痕为MN则线段CN的长是（）A．3cm B．4cm C．5cm D．6cm思路引领：由折叠的性质可得DN＝NE由中点的性质可得EC＝4cm结合正方形的性质可得∠BCD＝90°；设CN的长度为xcm则EN＝DN＝（8﹣x）cm接下来在直角△CEN中运用勾股定理就可以求出CN的长度．解：∵四边形MNEF是由四边形ADMN折叠而成的∴DN＝NE．∵E是BC的中点且BC＝8cm∴EC＝4cm．∵四边形ABCD是正方形∴∠BCD＝90°．设CN的长度为xcm则EN＝DN＝（8﹣x）cm由勾股定理NC2+EC2＝NE2得x2+42＝（8﹣x）2解得x＝3．故选：A．总结提升：本题考查翻折变换的问题折叠问题其实质是轴对称对应线段相等对应角相等找到相应的直角三角形利用勾股定理求解是解决本题的关键．第二部分专题提优训练1．（2022秋•慈溪市校级期中）在Rt△ABC中∠B＝90°AB＝4 BC＝8 D、E分别是边AC、BC上的点将△ABC沿着DE进行翻折点A和点C重合则EC＝．思路引领：设EC ＝x 在Rt △ABE 中 由勾股定理得42+（8﹣x ）2＝x 2 即可解得答案．解：设EC ＝x 则BE ＝8﹣x∵将△ABC 沿着DE 进行翻折 点A 和点C 重合∴AE ＝EC ＝x在Rt △ABE 中 AB 2+BE 2＝AE 242+（8﹣x ）2＝x 2解得x ＝5∴EC ＝5故答案为：5．总结提升：本题考查直角三角形中的翻折问题 解题的关键是掌握翻折的性质 能应用勾股定理列方程解决问题．2．（2021秋•靖江市期中）如图 在Rt △ABC 中 ∠C ＝90° D 是AB 的中点 AD ＝5 BC ＝8 E 是直线BC 上一动点 把△BDE 沿直线ED 翻折后 点B 落在点F 处 当FD ⊥BC 时 线段BE 的长为 ．思路引领：分点F 在BC 下方 点F 在BC 上方两种情况讨论 由勾股定理可BC ＝4 由平行线分线段成比例可得BD AD =BP BC =DP AC =12 求出FP 由勾股定理可求BE 的长． 解：若点F 在BC 下方时 DF 与BC 交于点P 如图1所示：∵D 是AB 的中点∴BD ＝AD ＝5∴AB ＝2AD ＝10∵∠C ＝90° BC ＝8∴AC =√AB 2−BC 2=√102−82=6∵点D 是AB 的中点∵FD ⊥BC ∠C ＝90°∴FD ∥AC∴BD AD =BP BC =DP AC =12 ∴BP ＝PC =12BC ＝4 DP =12AC ＝3∵△BDE 沿直线ED 翻折∴FD ＝BD ＝5 FE ＝BE∴FP ＝FD ﹣DP ＝5﹣3＝2在Rt △FPE 中 EF 2＝FP 2+PE 2∴BE 2＝22+（4﹣BE ）2解得：BE =52；若点F 在BC 上方时 FD 的延长线交BC 于点P 如图2所示：FP ＝DP +FD ＝3+5＝8在Rt △EFP 中 EF 2＝FP 2+EP 2∴BE 2＝64+（BE ﹣4）2解得：BE ＝10故答案为：52或10．总结提升：此题考查了折叠的性质、平行线的性质、直角三角形的性质以及勾股定理等知识 熟练掌握翻折变换的性质是解题的关键．3．如图 在Rt △ABC 中 AC ＝6 BC ＝8 D 为BC 上一点 将Rt △ABC 沿AD 折磨 点C 恰好落在AB 边上的E 点 求BD 的长．思路引领：由勾股定理求出AB＝10 由折叠的性质得出CD＝DE∠C＝∠AED＝90°AE＝AC＝6 得出BE＝AB﹣AE＝4 ∠BED＝90°设CD＝ED＝x则BD＝8﹣x在Rt△BDE中由勾股定理得出方程解方程即可．解：∵Rt△ABC中AC＝6 BC＝8∴AB=√62+82=10由折叠的性质得：CD＝DE∠C＝∠AED＝90°AE＝AC＝6∴BE＝AB﹣AE＝4 ∠BED＝90°设CD＝ED＝x则BD＝8﹣x在Rt△BDE中由勾股定理得：x2+42＝（8﹣x）2解得：x＝3∴BD＝8﹣3＝5．总结提升：本题考查了翻折变换的性质、勾股定理等知识；熟练掌握翻折变换的性质由勾股定理得出方程是解题的关键．4．（2018秋•襄汾县校级月考）如图在Rt△ABC中∠C＝90°AC＝8 BC＝6 按图中所示方法将△BCD沿BD折叠使点C落在边AB上的点C'处求AD的长及四边形BCDC′的面积．思路引领：利用勾股定理列式求出AB根据翻折变换的性质可得BC′＝BC C′D＝CD然后求出AC′设AD＝x表示出C′D、AC′然后利用勾股定理列方程求解即可求出AD；然后根据三角形的面积公式计算即可求出四边形BCDC′的面积．解：∵∠C＝90°AC＝8 BC＝6∴AB=√AC2+BC2=10由翻折变换的性质得BC′＝BC＝6 C′D＝CD∴AC′＝AB﹣BC′＝10﹣6＝4设CD＝x则C′D＝x AD＝8﹣x在Rt△AC′D中由勾股定理得AC′2+C′D2＝AD2即42+x2＝（8﹣x）2解得x＝3即CD＝3∴AD＝8﹣x＝5；由折叠可知：S△BCD＝S△BC′D∴四边形BCDC′的面积＝2S△BCD＝2×12×CD•BC＝3×6＝18．总结提升：本题考查了翻折变换的性质勾股定理此类题目熟记性质并利用勾股定理列出方程是解题的关键．5．（2021春•厦门期中）在矩形ABCD中AB＝3 BC＝4 E是AB上一个定点点F是BC上一个动点把矩形ABCD沿直线EF折叠点B的对应点B′落在矩形内部．若DB′的最小值为3 则AE＝53．思路引领：连接DE则DB′+EB′≥DE由EB′＝EB为定值故当D E B′三点共线时DB′最小利用勾股定理建立方程即可求解．解：如图1 连接DE由折叠性质可得：EB′＝EB∵DB′+EB′≥DE∴DB′≥DE﹣EB′＝DE﹣EB∵点E为定点∴EB为定值∴当D E B′三点共线时DB′最小且最小值为3∴DB′＝3如图2∵四边形ABCD 为矩形∴∠A ＝90° AD ＝BC ＝4设AE ＝x 则：EB ′＝EB ＝AB ﹣AE ＝3﹣x∴ED ＝EB ′+DB ′＝3﹣x +3＝6﹣x在Rt △AED 中 由勾股定理可得：x 2+42＝（6﹣x ）2解得：x =53∴AE =53故答案为：53． 总结提升：本题考查折叠的性质、矩形的性质、勾股定理等知识点 解题的关键是运用方程思想．6．（2021秋•城阳区校级月考）把一张矩形纸片（矩形ABCD ）按如图方式折叠 使顶点B 和点D 重合 折痕为EF ．若AB ＝3cm BC ＝5cm 则重叠部分△DEF 的面积是（ ）cm 2．A ．2B ．3.4C ．4D ．5.1思路引领：由矩形的性质得AD ＝BC ＝5cm CD ＝AB ＝3cm ∠A ＝90° 再由折叠的性质得A 'D ＝AB ＝3cm ∠A '＝∠A ＝90° AE '＝AE 设AE ＝xcm 则A ′E ＝xcm DE ＝（5﹣x ）cm 然后在Rt △A 'DE 中 由勾股定理得出方程 解方程 进而得出DE 的长 即可解决问题．解：∵四边形ABCD 是矩形 AB ＝3cm BC ＝5cm∴AD＝BC＝5cm CD＝AB＝3cm∠A＝90°由折叠的性质得：A'D＝AB＝3cm∠A'＝∠A＝90°AE'＝AE 设AE＝xcm则A′E＝xcm DE＝（5﹣x）cm在Rt△A'DE中由勾股定理得：A′E2+A′D2＝ED2即x2+32＝（5﹣x）2解得：x＝1.6∴DE＝5﹣1.6＝3.4（cm）∴△DEF的面积=12DE•CD=12×3.4×3＝5.1（cm2）故选：D．总结提升：此题考查了翻折变换的性质、矩形的性质、勾股定理以及三角形面积等知识熟练掌握翻折变换的性质和矩形的性质由勾股定理得出方程是解题的关键．7．（2017秋•金牛区校级月考）如图在矩形ABCD中E是AD的中点将△ABE沿BE折叠后得到△GBE 延长BG交CD于点F结果发现F点恰好是DC的中点若BC＝2√6则AB的长为？思路引领：连接EF由折叠性质得AE＝EG∠A＝∠EGB＝90°BG＝AB则∠EGF＝90°易证EG＝DE由矩形的性质得AB＝CD∠C＝∠D＝90°推出∠EGF＝∠D＝90°由HL证得Rt△EGF≌Rt△EDF得出FG＝FD求得CF＝DF＝FG=12CD=12AB BF＝BG+FG=32AB由勾股定理得出BC2+CF2＝BF2即可得出结果．解：连接EF如图所示：由折叠性质得：AE＝EG∠A＝∠EGB＝90°BG＝AB ∴∠EGF＝90°∵点E是AD的中点∴AE＝DE∴EG＝DE∵四边形ABCD是矩形∴AB＝CD∠C＝∠D＝90°∴∠EGF ＝∠D ＝90°在Rt △EGF 与Rt △EDF 中 {EG =ED EF =EF∴Rt △EGF ≌Rt △EDF （HL ）∴FG ＝FD∵F 点恰好是DC 的中点∴CF ＝DF ＝FG =12CD =12AB∴BF ＝BG +FG ＝AB +12AB =32AB在Rt △BCF 中 BC 2+CF 2＝BF 2即：（2√6）2+（12AB ）2＝（32AB ）2 解得：AB ＝2√3．总结提升：本题考查了折叠的性质、矩形的性质、全等三角形的判定与性质、勾股定理等知识 熟练掌握折叠的性质 证明三角形全等是解题的关键．8．（2018春•新抚区校级期中）如图 在矩形ABCD 中 已知AD ＝10 AB ＝8 将矩形ABCD 沿直线AE 折叠 顶点D 恰好落在BC 边上的F 处 求CE 的长．思路引领：先根据矩形的性质得AD ＝BC ＝10 AB ＝CD ＝8 再根据折叠的性质得AF ＝AD ＝10 EF ＝DE 在Rt △ABF 中 利用勾股定理计算出BF ＝6 则CF ＝BC ﹣BF ＝4 设CE ＝x 则DE ＝EF ＝8﹣x 然后在Rt △ECF 中根据勾股定理得到x 2+42＝（8﹣x ）2 再解方程即可得到CE 的长．解：∵四边形ABCD 为矩形∴AD ＝BC ＝10 AB ＝CD ＝8∵矩形ABCD 沿直线AE 折叠 顶点D 恰好落在BC 边上的F 处∴AF＝AD＝10 EF＝DE在Rt△ABF中∵BF=√AF2−AB2=6∴CF＝BC﹣BF＝10﹣6＝4设CE＝x则DE＝EF＝8﹣x在Rt△ECF中∵CE2+FC2＝EF2∴x2+42＝（8﹣x）2解得x＝3即CE＝3．总结提升：本题考查了折叠的性质：折叠是一种对称变换它属于轴对称折叠前后图形的形状和大小不变位置变化对应边和对应角相等．也考查了矩形的性质和勾股定理．9．（2018秋•通川区校级期中）将一张边长为2的正方形纸片ABCD对折设折痕为EF（如图（1））；再沿过点D的折痕将∠A翻折使得点A落在线段EF上的点H处（如图（2））折痕交AE于点G则EG 的长度是（）A．8﹣4√3B．4√3−6C．4﹣2√3D．2√3−3思路引领：由于正方形纸片ABCD的边长为2 所以将正方形ABCD对折后AF＝DF＝1 由折叠的性质得出AD＝DH＝2 AG＝GH在Rt△DFH中利用勾股定理可求出HF的长进而求出EH的长再设EG＝x在Rt△EGH中利用勾股定理即可求解．解：∵正方形纸片ABCD的边长为2∴将正方形ABCD对折后AE＝DF＝1∵△GDH是△GDA沿直线DG翻折而成∴AD＝DH＝2 AG＝GH在Rt△DFH中HF=√HD2−DF2=√22−12=√3∴EH＝2−√3在Rt△EGH中设EG＝x则GH＝AG＝1﹣x∴GH2＝EH2+EG2即（1﹣x）2＝（2−√3）2+x2解得x＝2√3−3．∴EG＝2√3−3．故选：D．总结提升：本题考查了正方形的性质折叠的性质勾股定理关键是学会用方程的思想方法解题．10．（2020秋•新都区校级月考）如图AD是△ABC的中线∠ADC＝45°把△ADC沿着直线AD对折点C落在点E的位置．如果BC＝6 那么以线段BE为边长的正方形的面积为（）A．6B．72C．12D．18思路引领：由题意易得BD＝CD＝DE＝3 再求出∠BDE＝90°然后根据勾股定理求出BE最后由正方形的面积进行求解即可．解：∵D是BC中点BC＝6∴BD＝CD＝3由折叠的性质得：CD＝DE＝3 ∠ADC＝∠ADE＝45°即∠CDE＝90°∴BD＝DE＝3 ∠BDE＝90°在Rt△BDE中由勾股定理得：BE=√BD2+DE2=√32+32=3√2∴以BE为边的正方形面积为：（3√2）2＝18故选：D．总结提升：本题考查了折叠的性质、勾股定理、正方形的面积计算等知识熟练掌握勾股定理及折叠的性质是解题的关键．。

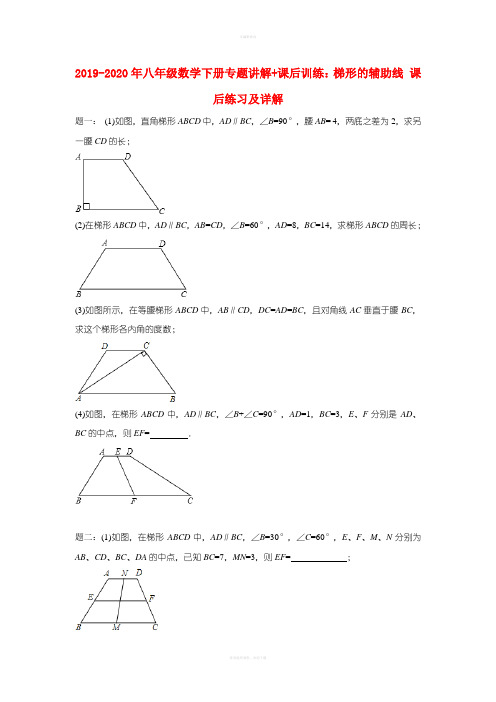
2019-2020年八年级数学下册专题讲解+课后训练：梯形的辅助线课后练习及详解题一：(1)如图，直角梯形ABCD中，AD∥BC，∠B=90°，腰AB= 4，两底之差为2，求另一腰CD的长；(2)在梯形ABCD中，AD∥BC，AB=CD，∠B=60°，AD=8，BC=14，求梯形ABCD的周长；(3)如图所示，在等腰梯形ABCD中，AB∥CD，DC=AD=BC，且对角线AC垂直于腰BC，求这个梯形各内角的度数；(4)如图，在梯形ABCD中，AD∥BC，∠B+∠C=90°，AD=1，BC=3，E、F分别是AD、BC的中点，则EF= ．题二：(1)如图，在梯形ABCD中，AD∥BC，∠B=30°，∠C=60°，E、F、M、N分别为AB、CD、BC、DA的中点，已知BC=7，MN=3，则EF= ；(2)如图，在梯形ABCD中，AD=DC，AB=DC，∠D=120°，对角线CA平分∠BCD，且梯形的周长为20，则梯形ABCD的面积为；(3)如图，等腰梯形ABCD中，AD∥BC，AD=3，AB= 4，BC=7，求∠B的度数；(4)如图，梯形ABCD中，AD∥BC，AC⊥BD，AD=3，BC=7，E在BC上，CE=2，则DE= ．题三：已知：等腰梯形的上底是2cm，腰长是4cm，一个底角是60°，则等腰梯形的下底是cm．题四：已知：等腰梯形的一个底角等于60°，它的两底分别为4cm和7cm，则它的周长为cm．题五：如图所示，在梯形ABCD中，AD∥BC，AB=CD，AC⊥BD，且AD= 4，BC=8，求AC的长．题六：如图，在梯形ABCD中，AD∥BC，对角线AC⊥BD，若AD=3，BC=7，求梯形ABCD 面积的最大值．题七：如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，点F是CD的中点，且AF ⊥AB，若AD=2.7，AF=4，AB=6，求CE的长．题八：如图，在梯形ABCD中，AB∥CD，∠A+∠B=90°，CD=5，AB=11，点M、N分别为AB、CD的中点，求线段MN的长．题九：如图，在梯形ABCD中，AD∥BC，∠ABC=90°，AB= 4，AD=3，BC=5，点M是边CD的中点，连接AM、BM．求△ABM的面积．题十：如图，已知直角梯形ABCD中，AD∥BC(AD＜BC)，∠B=90°，AB=AD+BC．点E 是CD的中点，点F是AB上的点，∠ADF= 45°，FE=a，梯形ABCD的面积为m．(1)求证：BF=BC；(2)求△DEF的面积(用含a、m的代数式表示)．题十一：以线段a=16，b=13为梯形的两底，c=10，d=6为腰画梯形，这样的梯形() A．只能画出一个B．能画出2个C．能画出无数个D．不能画出题十二：以线段a=5，b=10，c=15，d=20做梯形四边形，这样的梯形(不全等的)() A．至少能做3个B．恰好能做2个C．仅仅只能做1个D．一个也不能做梯形的辅助线课后练习参考答案题一：(1)2；(2)34；(3)60°，60°，120°，120°；(4)1．详解：(1)过D作DE⊥BC于E，∵AB⊥BC，DE⊥BC，AD∥BC，∴四边形ADEB是个矩形，∴AB=DE= 4，CE=BC AD=2，Rt△DEC中，CD===2；；(2)过A、D点作AE⊥BC于E，DF⊥BC于F，∵AB=CD，∠B=∠C，AE=DF，∴△ABE≌△DCF，∴BE=CF，∵AD=8，BC=14，BE=CF=3，又∵在Rt△ABE中，∠B=60°，∴AB=2BE=6，∴梯形ABCD的周长为8+14+6+6=34；(3)如图所示，过点C作CE∥AD，又DC∥AE，∴四边形AECD为平行四边形，又DC=AD=BC，∴四边形AECD为菱形，∴AE=CE=BC，∴∠EAC=∠ECA，∠CEB=∠B，∵∠B+∠CAB=90°，即3∠CAE=90°，∴∠CAE=30°，∴∠B=60°=∠DAB，∠D=∠DCB=120°；(4)过点E作AB、CD的平行线，与BC分别交于G，H，∵∠B+∠C=90°，∴∠EGH=∠B，∠EHG=∠C，∴∠EGH+∠EHG=90°，∴四边形ABGE和四边形CDEH都是平行四边形，△EGH为直角三角形，∵E、F分别是AD、BC的中点，∴BG=CH=0.5，GH=2，根据直角三角形中斜边上的中线是斜边的一半知，EF=GH=1，∴EF=1．题二：(1)4；(2)12；(3)60°；(4)5．详解：(1)过点N分别作NG∥AB，NH∥CD，得平行四边形ABGN和平行四边形DCHN，∴∠NGM+∠NHM=∠B+∠C=90°，GH=BC AD，MG=MH，∴GH=2MN=6，∴AD=76=1，∴EF= 4；(2)∵在梯形ABCD中，AB=DC，∴梯形ABCD是等腰梯形，∴∠D+∠DCB=180°，∵∠D=120°，∴∠B=∠DCB=60°，∵对角线CA平分∠BCD，∴∠ACB=30°，∵AD=DC，∴∠DAC=∠ACD=30°，∴∠BAC=90°，∴BC=2AB，∵梯形的周长为AD+DC+BC+AB=5AB=20，∴AB= 4，∴AC=4，BC=8，过点A作AE⊥BC于点E，∵AB= 4，AC=4，BC=8，∴AE=2，∴梯形ABCD的面积为(4+8)×2×=12；(3)过点A作AE∥DC交BC于E，∵AD∥BC，∴四边形AECD是平行四边形，∴EC=AD=3，DC=AE，∴BE=BC CE=73= 4，∴CD=AB= 4，∴AE=AB=BE= 4，∴△ABE是等边三角形，∴∠B=60°；(4)过D作DF∥AC交BC的延长线于F，∵AD∥BC，∴四边形ACFD是平行四边形，∴CF=AD=3，∵BC=7，∴BF=BC+CF=7+3=10，∵CE=2，∴BE=72=5，EF=2+3=5，∴BE=EF，又∵AC⊥BD，DF∥AC，∴∠BDF=90°，∴DE=BF=5．题三：6cm．详解：过D作DE∥AB交BC于E，∵DE∥AB，AD∥BC，∴四边形ABED是平行四边形，∴AD=BE=2cm，DE=AB=4cm，∠DEC=∠B=60°，AB=DE=DC，∴△DEC是等边三角形，∴EC=CD= 4cm，∴BC= 4cm+2cm=6cm．题四：17cm．详解：过上底顶点D作DE∥AB交BC于E，则四边形ABED是平行四边形，∴DE=AB，AD=BE，∵梯形的一个底角是60°，∴∠C=60°，又∵腰长AB=CD=DE，∴△CDE是等边三角形，∴CD=CE=BC BE=74=3cm，∴它的周长为3+7+3+4=17cm．题五：．详解：过D作DE∥AC交BC的延长线于E，∵AD∥BC，AB=CD，∴四边形ABCD是等腰梯形，∴ADEC是平行四边形，∴AD=CE，AC=DE，即可得出BE=BC+CE=BC+AD=12，又∵AC=BD，∴BD=ED，∴△BDE为等腰直角三角形，∴AC=BD=．题六：25．详解：过D作DE∥AC交BC延长线于E，∵AD∥BC，DE∥AC，∴四边形ACED是平行四边形，∴AD=CE，∴根据等底等高的三角形面积相等得出△ADC的面积等于△DCE的面积，即梯形ABCD的面积等于△BDE的面积，∵AC⊥BD，DE∥AC，∴∠BDE=90°，BE=3+7=10，∴此时△BDE的边BE边上的高越大，它的面积就越大，即当高是BE时最大，即梯形的最大面积是×10××10=25．题七：2.3．详解：延长AF、BC交于点G，∵AD∥BC，∴∠D=∠FCG，∠DAF=∠G，又DF=CF，∴△AFD≌△GFC，∴AG=2AF=8，CG=AD=2.7，∵AF⊥AB，AB=6，∴BG=10，∴BC=BG CG=7.3，∵AE=BE，∴∠BAE=∠B，∴∠EAG=∠AGE，∴AE=GE，∴BE=BG=5，∴CE=BC BE=2.3．题八：3．详解：如图，过D作DE∥BC，DF∥MN，∵在梯形ABCD中，AB∥CD，DE∥BC，∴CD=BE=5，AE=AB BE=115=6，∵M为AB的中点，∴MB=AM=AB=×11=5.5，ME=MB BE=5.55=0.5，∵N为DC的中点，∴DN=DC=×5=2.5，在四边形DFMN中，DC∥AB，DF∥MN，∴FM=DN=2.5，∴FE=FM+ME=2.5+0.5=3=AE，∴F为AE的中点，又∵DE∥BC，∴∠B=∠AED，∵∠A+∠B=90°，∴∠A+∠AED=90°，∴∠ADE=90°，即△ADE是直角三角形，∴DF=MN=AE=×6=3．题九：8．详解：延长AM交BC的延长线于点N，∵AD∥BC，∴∠DAM=∠N，∠D=∠MCN，∵点M是边CD的中点，∴DM=CM，∴△ADM≌△NCM(AAS)，∴CN=AD=3，AM=MN=AN，∴BN=BC+CN=5+3=8，∵∠ABC=90°，∴S△ABN=×AB•BN=×4×8=16，∴S△ABM=S△ABN=8，即△ABM的面积为8．题十：见详解．详解：(1)∵四边形ABCD是直角梯形，∴∠A=90°，∵∠ADF=45°，∴∠AFD= 45°，∴AD=AF，∵AB=AF+BF，AB=AD+BC，∴BF=BC；(2)连接FC，设AD=AF=x，BC=BF=y，连接CF，作DH⊥BC于H，易证四边形ABHD为矩形、△CDF为直角三角形，又∵E是CD中点，∴CD=2EF=2a，由勾股定理得x2+y2=2a2…①，由直角梯形的面积公式可得：(x+y)2=2m…②，由②①，得xy=m a2，∵S△DFC=S梯形ABCD S△AFD S△BFC=(x+y)2 x2 y2 = xy，∴S△DEF=S△DFC=m a2．题十一：D．详解：如图，过点B作BE∥AD，则出现平行四边形ABED和一个△BEC，∵AB=13，CD=16，AD=10，BC=6∴CE=3，BE=10，∵3+6＜10，∴BE，CE，BC不能构成三角形∴这样的梯形一个也不能作．故选D．题十二：C．详解：作DE∥AB，则DE=AB，①当a=5为上底，b=10为下底，c、d为腰时，105=5，与15，20不能构成三角形，故不满足题意；②当a=5为上底，b=15为下底，b、d为腰时，155=10，与10，20不能构成三角形，故不满足题意；③当a=5为上底，d=20为下底，b、c为腰时，205=15，与10，15可以构成三角形，故满足题意；④当b=10为上底，c=15为下底，a、d为腰时，1510=5，与5，20不能构成三角形，故不满足题意；⑤当b=10为上底，d=20为下底，a、c为腰时，2010=10，与5，15不能构成三角形，故不满足题意；⑥当c=15为上底，d=20 为下底，a、b为腰时，2015=5，与5，10不能构成三角形，故不满足题意；综上可得只有当a=5为上底，d=20为下底，b、c为腰时，满足题意，即以线段a=5，b=10，c=15，d=20做梯形四边形，这样的梯形(不全等的)只能做一个．故选C．.。

8.4“大气压强”知识过关练习题一、单选题1.带橡皮塞的口服液瓶，其吸管的横截面是如图所示的形状，做成这种形状的原因是（）A. 与众不同B. 增大嘴唇与吸管的摩擦C. 增大吸管的机械强度D. 让空气顺畅地进入瓶内2.你认为以下估测数据最符合实际的是（）A.梵净山顶的大气压约为1.5×105PaB.一名中学生的体重约为200kgC.从地上捡起物理书放在课桌上做功接近2JD.人的正常体温是39℃3.首先测出大气压强值的科学家是（）A. 阿基米德B. 帕斯卡C. 托里拆利D. 伽利略4.下列现象，不可能发生的是（）A. 水的沸点低于或者高于100℃B. -10℃的冰块放在0℃的水中，冰块会熔化C. 在敞开的锅中烧水，使水沸腾，再用猛火继续加热，则水的温度也不会升高D. 物体吸热，温度保持不变5.压强知识在生活和生产中应用广泛，下列关于压强的事例中解释正确的是（）A. 菜刀刀刃磨得很薄，是通过减小受力面积来减小压强B. “蛟龙号”载人深潜器在海水中下潜的过程中，受到海水的压强逐渐增大C. 用高压锅煮饭增大了液面气压，当锅内水沸腾的时候，温度仍然继续升高D. 火车进站时旅客不能越过安全黄线，原因是流体中流速大的地方压强大6.有关大气压的变化，下列说法错误的是( )A. 大气压的数值在不同的地方一般不同B. 同一地方大气压是不变化的C. 离海平面越高，大气压的数值越大D. 一个标准大气压等于76cm水银柱7.物理知识的应用为人们的生产、生活创造了许多自动化的设备，如下四幅图中均是利用相应的物理原理设计的自动化裝置，则下列关于它们的原理或结构说法中错误的是（）A. 利用了浮力、杠杆及连通器的知识B. 利用了大气压的知识C. 油量表为电压表改装而成D. 温度计内的测温液体是水银，而不能是酒精8.小华制成如图所示的“自动给水装置”，是用一个装满水的塑料瓶子倒放在盆景中，瓶口刚好被水浸没．其瓶中水面能高于盆内水面，主要是由于（）A. 瓶的支持力的作用B. 瓶的重力作用C. 水的浮力作用D. 大气压的作用9.“生活处处有物理，留心观察皆学问”．下面是小强的观察和他对现象的解释，其中正确的是（）A. “公共场所不要大声喧哗”是要求人们在公共场所说话音调放低些B. 炒菜时有“白气”冒出，这是汽化后的水蒸气C. 教室里一个开关能同时控制两只灯，两灯同时亮、同时灭，这两只灯是串联的D. 用吸管吸饮料是利用了大气压10.如图所示，甲、乙分别是酒精在标准大气压下熔化和沸腾时温度随时间变化的图像，下列说法中正确的是（）A.固态酒精是非晶体B.在-120℃时，酒精处于固态C.酒精温度计可以用来测量沸水的温度D.酒精在沸腾过程中温度升高11.第一位用实验的方法测出大气压强数值的科学家是（）A. 托里拆利B. 牛顿C. 伽利略D. 焦耳12.下面是对日常生活中一些数据的估计，其中最接近实际的是（）A. 一名中学生所受的重力约为50NB. 初中物理教科书的质量约1.8kgC. 人的正常步行速度约1.2m/sD. 古剑山山顶的大气压大约是1.2×105 Pa13.在做托里拆利实验时，测得管内、外水银面高度差是760毫米，然后再向水银槽里注入水银，使槽里水银面上升10毫米，则这时管内外水银面高度差为（）A. 770毫米B. 765毫米C. 760毫米D. 750毫米14.我国女科学家屠呦呦荣获2015年诺贝尔生理医学奖，为控制疟疾疫情，屠呦呦尝试用加热青蒿水溶液的方法使其沸腾，从而去除水分以提取药物，但提取药物的药效并不理想．她猜想：可能在高温的情况下，药物被破坏掉了．对此，可采用的方法是（）A. 用微火加热使溶液缓慢沸腾B. 用旺火加热缩短沸腾时间C. 减小容器内的气压降低溶液沸点D. 增大容器内的气压升高溶液沸点15.将图示的塑料挂衣钩按在竖直的墙或玻璃上，在钩上挂上几件衣服也不会掉下来，这是由于（）A. 大气压的作用B. 空气对它的浮力C. 玻璃或墙对它有吸引力D. 挂衣钩的惯性二、填空题16.我们利用金属钨作灯泡的灯丝，是因为钨的________ 高，不易熔断；饺子在水中怎么煮不会变黄变焦，而放在油锅却很快变黄变焦，是因为油的________ 高；17.小明同学一家假期到西藏去旅行，由于那里海拔较高, 他们在野炊时发现米饭煮不熟，这是因为________ .18.加油站都有这样的提示：请“熄火加油”、“禁止抽烟”、“不要使用手机”等．这是为了防止火花点燃汽油引起火灾，因为常温下液态的汽油容易发生的物态变化是________．我们利用金属钨作灯泡的灯丝，是因为钨的________高，不易熔断；饺子在水中怎么煮不会变黄变焦，而放在油锅中却很快变黄变焦，是因为油的________高．19.如图一款家用高压锅，其优点是很容易将食物煮熟煮烂，但是食物煮好后，即使断开电源很长时间也无法打开锅盖，为了能尽快开锅进食，可以稍稍打开顶部的减压阀，这时可以听到内部又沸腾了，这是因为内部液体上方的气压减小，导致液体的沸点________（填“升高”或“降低”），但这种做法很不安全，所以最好的做法应该是________.20.物理学在生产、生活中有着广泛的应用：用吸管吸取饮料，是利用________的知识；汽车发动机等热机工作时，将内能转化为________能；卫星通信是通过微波实现的，在真空中微波的传播速度与光速________（选填“相等”或“不相等”）．21.登山运动员在向高峰攀登时会出现“高原反应”，这除了高原缺氧、寒冷之外，还因为那里的大气压强比平原地区________(填“大”或“小”）得多.在高原上用普通锅难以煮熟食物，是因为普通锅的密封性能较差，锅内气压受外界大气压影响，使得水的沸点________(填“高于”或“低于”）100℃.22.如图所示是自制气压计，小红拿着它从1楼乘坐电梯到20楼，观察发现玻璃管内水柱的高度________（选填“升高”、“降低”或“不变”），说明大气压随高度的增加而________（选填“变大”、“变小”或“不变”），标准大气压的数值________ Pa．23.江西庐山的“云雾茶”历史悠久，文化源远流长．如图所示，在壶盖上开有一个小孔，其作用是在倒水时使壶内外的________相同；由于壶身和壶嘴构成________，方便装水和倒水，因而要求它们的高度相平．24.著名的________ 实验证明了大气压强的存在．托里拆利在玻璃管内装入________ 较大的水银做实验测出大气压强的值，若换用水完成该实验，则需要________ 玻璃管的长度（选填“减小”或“增大”）．25.生活中“吸”字表述的现象，其原因各不相同。

人教版八年级下册Unit 9 单元过关测试卷(741) 1.假如今年5月1日你和你的父母到聊城旅游了。

请根据下面表格提供的信息写一篇80词左右的英语短文，描述一下这次难忘的经历，并谈谈你的感受。

文章的开头已给出，不计入参考词汇：光岳楼Gu a ng yu e To we r, 铁塔th e Ir o n To we r,山陕会馆S ha n sh a nG u ild h a llM y p a r en ts an d I we n t to Lia o c h eng on M a y 1.2.Ta iwa n is in the s outh e a s t o f Ch in a．It is th e la rg es t is la nd in C h ina．It h a s a n a rea o f 36,000 sq ua r e k ilome te r s o r s o a nd ha s a p o pu la tio n o f mo r e th an 23,500,000. It is r ich in na tu r a l r e so u rc e s a nd f a mo us fo r its ba n an as, r ice a nd tea．O ve r h a lf o f th e ma in is land is c o ve r ed b y f o r e s t．Its s c en e r y is s o be au tif u l an d the we a th er is so p lea s a n t． A lot o f tr a ve le r s c o me fo r a vis it e ve r y ye a r．S un M o on La k e an d A li M ou n ta in a re ve r y f a mo u s p la c e s o f in te r e s t．Ta i p e i C ity is in th e n o rth o f the is la nd．It is th e la rg es t c ity o n th e is la n d．Th e r e a r e two a ir po r ts in Ta ip e i．Ta iwan h a s be en a p a r t o f C h in a s in ce a nc ie n t time s．Mo s t p eo p le on the is la n d c o me f ro m Fu jia n P ro vin c e a n d Gu a ng d on g P r o vin ce．N o w, ma n y Ta iwa n p eo p le c o me to th ema in la n d to bu ild f a c to r ie s a n d do b u s in e s s．Th e p eo p le on b o th s ide s o f th e s tr a its(海峡) h a ve a s tr o ng wish to u n ite th e mo th e r la n d．根据短文内(1)(2)(3)(4)(5)3.A f te r h a lf a ye a r's h a r d wo rk，Lin d a h a s ma d e g re a t p in ma th．4.Th e s o up is a little b it s a lty．If yo u p u t le s s s a lt，it will b e p．5.—Le t's ta k e s o me ph o to s．—O K．W he r e is yo u r c?6.—G ra c e is in tro ub le a nd s ad．—Le t's d o s o me th in g to e he r．7.—I a te my lu n c h with in on ly 7min u te s．—Wh y d id yo u e a t it in s uc h a r wa y？Tr a ve l is u s e fu l to us in a t lea s t th r e e wa ys．Fir s t，b y tr a ve lin g we c a n 1. th eb e a u tifu l sc e ne r y o fd iffe r e n t p la ce s．We can se e with o u r 2.e ye s ma n y p la c e s wh ichc a n be r e ad ab o u t in bo o k s，an d vis it s o mef a mo u s c itie s a nd s c en ic s p o ts． 3.，we will me e t pe o p le with d iff e r en t 4.an d se e s tr a ng e a nd d iff e r e n t th in g s 5.we tr a ve l．We c an g e t to k n o w the c u s to ms o f the pe op le in o the r c ou n tr ie s，6. d iff e r e nt f o o d s an d loc a l f la vo r s(当地风味) if we lik e．In th is wa y，we ca n u nd e r s tan d ho w 7.o th e r pe op le live．T h ir d，tr a ve l will n ot o n ly h e lp u s to g e t kno wle d ge o f 8. an d h is to r y，b u t a ls o h e lp u s 9. he a lth y a n d ma k e u s le s s na r r ow-min d e d(狭隘的)．With a ll the s e a d va n tag e s(优点) o f tr a ve l，it is no won de r th a t tra ve l h a s n o wb ec o me 10. tha n e ve r in C h ina．(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)9.这所学校超过四分之三的学生来自农村。

17.4反比例函数基础过关全练知识点1反比例函数的概念1.(2022江苏苏州草桥中学期中)下列函数中,变量y是x的反比例函数的是()A.y=x3B.y=3x+1C.y=3xD.y=3x2.【易错题】(2022湖南衡阳弘扬中学期中)已知y=(k-2)x k2−5是反比例函数,那么k的值是.知识点2反比例函数的图象与性质3.(2022云南中考)反比例函数y=6x的图象位于() A.第一、三象限 B.第一、四象限C.第二、三象限D.第二、四象限4.(2021山西期末)关于反比例函数y=-12x,下列说法不正确的是()A.函数图象经过点(3,-4)B.函数图象关于原点成中心对称C.函数图象位于第一、三象限D.当x<0时,y随x的增大而增大5.(2022河南南阳卧龙期中)已知点A(-1,y1),B(2,y2),C(1,y3),D(3,-2)都在双曲线y=kx上,则y1,y2,y3的大小关系是() A.y1>y2>y3 B.y1>y3>y2C.y3>y2>y1D.y2>y1>y36. (2022海南海口十中期中)在同一坐标系中,函数y =kx和y =kx +3(k ≠0)的图象大致是( )ABCD7.【分类讨论思想】(2022河南南阳桐柏思源实验学校第二次月考)已知点A (a ,y 1),B (a +1,y 2)在反比例函数y =m 2+1x(m 是常数)的图象上,且y 1<y 2,则a 的取值范围是( )A.a <0B.a >0C.0<a <1D.-1<a <0 8.【新独家原创】已知m =(−12)−1,则反比例函数y =m+3x的图象分布在第 象限.9.【教材变式·P56T1变式】(2022辽宁大连模拟)某长方体的体积为 1 000 cm 3,长方体的高h (单位:cm)随底面积S (单位:cm 2)的变化而变化,则h 关于S 的函数关系式为 ,它是 函数.10.(2022内蒙古呼和浩特中考)点(2a -1,y 1)、(a ,y 2)在反比例函数y =kx (k >0)的图象上,若0<y 1<y 2,则a 的取值范围是 . 知识点3 确定反比例函数的解析式11.(2022江苏苏州星湾中学期中)若点A (3,-6)在反比例函数y =kx 的图象上,则k 的值为( )A.-18B.18C.-2D.212.(2022海南中考)若反比例函数y =kx (k ≠0)的图象经过点(2,-3),则它的图象也一定经过的点是 ( )A.(-2,-3)B.(-3,-2)C.(1,-6)D.(6,1)13.【跨学科·物理】(2022河南南阳新野期中)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,图象如图所示,当气球内的气压大于120 kPa时,气球将爆炸,为了安全起见,气球的体积应()A.不小于54m3 B.小于54m3C.不小于45m3 D.小于45m314.(2022福建泉州安溪期中)如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数y=kx(k>0,x>0)的图象上,当m>1时,过点P分别作x轴、y 轴的垂线,垂足为A、B,过点Q分别作x轴、y轴的垂线,垂足为C、D,DQ交PA于点E,随着m的增大,四边形ACQE的面积()A.逐渐增大B.逐渐减小C.先减小后增大D.先增大后减小15.(2022福建中考)已知反比例函数y=kx的图象位于第二、四象限,则实数k的值可以是.(只需写出一个符合条件的实数)16.(2022湖北仙桃中考)在反比例函数y=k−1的图象的每一支上,y都随xx的增大而减小,且整式x2-kx+4是一个完全平方式,则该反比例函数的解析式为.(x>0) 17.【一题多变】(2022四川凉山州中考)如图,点A在反比例函数y=kx的图象上,过点A作AB⊥x轴于点B,若△OAB的面积为3,则k=.[变式一](2022湖南怀化中考)如图,直线AB交x轴于点C,交反比例函数y=a−1(a>1)的图象于A、B两点,过点B作BD⊥y轴,垂足为点D,若xS△BCD=5,则a的值为()A.8B.9C.10D.11[变式二](2022黑龙江齐齐哈尔中考)如图,点A是反比例函数y=k(x<0)x图象上一点,过点A作AB⊥y轴于点D,且D为线段AB的中点.若点C 为x轴上任意一点,且△ABC的面积为4,则k=.18.(2022河南南阳镇平期中)已知:反比例函数y=k的图象经过A(2,-4).x(1)求k的值.(2)这个函数的图象在哪几个象限?y随x的增大怎样变化?(3)画出函数的图象.(4)点B(-2,4),C(-1,5)在这个函数的图象上吗?19.(2022山东聊城实验中学期中)一辆汽车匀速通过某段公路,所需时,其图象为如图所示的一间t(h)与行驶速度v(km/h)满足函数关系:t=kv段曲线,且端点为A(40,1)和B(m,0.5).(1)求k和m的值;(2)若行驶速度不得超过50 km/h,则汽车通过该路段最少需要多少时间?能力提升全练20.【一题多解】(2022湖北武汉中考,6,)已知点A(x1,y1),B(x2,y2)在的图象上,且x1<0<x2,则下列结论一定正确的是() 反比例函数y=6xA.y1+y2<0B.y1+y2>0C.y1<y2D.y1>y221.(2022浙江舟山中考,15,)如图,在直角坐标系中,△ABC的顶点C 与原点O重合,点A在反比例函数y=k(k>0,x>0)的图象上,点B的坐标x为(4,3),AB与y轴平行,若AB=BC,则k=.22.(2022江苏常州中考,23,)如图,在平面直角坐标系xOy中,一次函数y=2x+b的图象分别与x轴、y轴交于点A、B,与反比例函数y=k(x>0)x的图象交于点C,连结OC.已知点B(0,4),△BOC的面积是2.(1)求b、k的值;(2)求△AOC的面积.23.【新考法】(2022河南中考,18,)如图,反比例函数y=k(x>0)的图x象经过点A(2,4)和点B,点B在点A的下方,AC平分∠OAB,交x轴于点C.(1)求反比例函数的表达式;(2)请用无刻度的直尺和圆规作出线段AC的垂直平分线;(要求:不写作法,保留作图痕迹)(3)线段OA与(2)中所作的垂直平分线相交于点D,连结CD,求证:CD∥AB.素养探究全练24.【模型观念】(2022内蒙古赤峰中考)阅读下列材料.定义运算:min|a,b|,当a≥b时,min|a,b|=b;当a<b时,min|a,b|=a.例如:min|-1,3|=-1;min|-1,-2|=-2.完成下列任务.(1)①min|(-3)0,2|=;②min|√14,-4|=.(2)如图,已知反比例函数y1=k和一次函数y2=-2x+b的图象交于A、Bx,−2x+b|=(x+1)(x-3)-x2,求这两个函数的解析两点.当-2<x<0时,min|kx式.答案全解全析基础过关全练1.C 根据反比例函数的定义,知符合题意的只有C.2.答案 -2解析 由题意得{k 2−5=−1,k −2≠0,解得k =-2.3.A 反比例函数y =6x 中,k =6>0,所以图象位于第一、三象限,故选A.4.C A.把x =3代入y =-12x得,y =-4,所以函数图象经过点(3,-4),故本选项正确;B.反比例函数的图象的两个分支关于原点成中心对称,故本选项正确;C.k =-12<0,所以函数图象位于第二、四象限,故本选项错误;D.k =-12<0,所以图象位于第二、四象限,且在每个象限内,y 随x 增大而增大,所以当x <0时,y 随x 的增大而增大,故本选项正确.故选C. 5.A ∵点D (3,-2)在双曲线y =kx 上,∴k =3×(-2)=-6<0,∴反比例函数的图象在第二、四象限,在每个象限内,y 随x 的增大而增大,∴A (-1,y 1)在第二象限,B (2,y 2),C (1,y 3)在第四象限, ∴y 1>0,0>y 2>y 3,∴y 1>y 2>y 3.故选A. 6.C 分两种情况讨论:①当k >0时,函数y =kx +3的图象在第一、二、三象限,函数y =kx 的图象在第一、三象限;②当k <0时,函数y =kx +3的图象在第一、二、四象限,函数y =kx 的图象在第二、四象限.只有C选项符合,故选C.7.D∵m2+1>0,∴反比例函数y=m 2+1x(m是常数)的图象在第一、三象限,在每个象限内,y随x的增大而减小.①当A(a,y1),B(a+1,y2)在同一象限时,∵y1<y2, ∴a>a+1,此不等式无解;②当点A(a,y1),B(a+1,y2)在不同象限时,∵y1<y2, ∴a<0,a+1>0,解得-1<a<0.故选D.8.答案一、三解析∵m=(−12)−1=-2,∴m+3=-2+3=1>0,∴函数y=m+3x的图象分布在第一、三象限.9.答案h=1 000S;反比例解析根据长方体的体积等于底面积乘高,可知函数关系式为h=1 000S,它是反比例函数.10.答案a>1解析因为k>0,所以反比例函数图象在第一、三象限,且在每个象限内,y随x的增大而减小.由0<y1<y2得,0<a<2a-1,解得a>1.故答案为a>1.11.A将点A(3,-6)代入y=kx得k=3×(-6)=-18,故选A.12.C∵反比例函数y=kx(k≠0)的图象经过点(2,-3),∴k=2×(-3)=-6,∵(-2)×(-3)=6≠-6,(-3)×(-2)=6≠-6,1×(-6)=-6,6×1=6≠-6,∴它的图象一定还经过的点是(1,-6),故选C.13.C设气球内气体的气压p(kPa)与气体体积V(m3)之间的关系式为p=k(k≠0),V,∵图象过点(1.6,60),∴k=96.∴p=96V当p=120时,V=4.∵图象在第一象限,p随V的增大而减小,故气球内的5m3,即气球的体积应气压小于或等于120 kPa时,体积应大于或等于45不小于4m3.故选C.514.A由题意得AC=m-1,CQ=n,则S四边形ACQE=AC·CQ=(m-1)n=mn-n.(k>0,x>0)的图象上,∴mn=k=4.∵P(1,4)、Q(m,n)在函数y=kx∴S四边形ACQE=AC·CQ=4-n,∵m>1时,n随m的增大而减小,∴S四边形ACQE=4-n随m的增大而增大.故选A.15.答案-3(答案不唯一)的图象位于第二、四象限,∴k<0,∴k的值可解析∵反比例函数y=kx以是-3.(答案不唯一)16.答案y=3x解析∵整式x2-kx+4是一个完全平方式,∴k=±4,的图象的每一支上,y都随x的增大而减小,∵反比例函数y=k−1x∴k-1>0,解得k>1,∴k=4,∴k-1=4-1=3,.∴反比例函数的解析式为y=3x17.答案 6解析∵△OAB的面积为3,点A在反比例函数y=k(x>0)的图象上,xOB·AB=3,即OB·AB=6,∴k=6.∴12),[变式一]D设B的横坐标为m,则B(m,a−1m∵BD ⊥y 轴,∴S △BCD =12m ·a−1m=5,解得a =11,故选D.[变式二]答案 -4 解析 如图,连结OA ,OB ,∵AB ⊥y 轴,∴AB ∥x 轴, ∴S △ABC =S △AOB , ∵△ABC 的面积为4, ∴S △AOB =4.∵D 为线段AB 的中点, ∴S △AOD =S △BOD ,∴S △AOD =2.根据反比例函数的比例系数k 的几何意义可得k =-4.18.解析 (1)∵反比例函数y =kx 的图象经过点A (2,-4),∴k =-4×2=-8.(2)由(1)知k =-8,∴反比例函数的解析式为y =-8x,∵-8<0,∴函数的图象在第二、四象限,在每个象限内,y 随x 的增大而增大. (3)函数图象如图.(4)∵-2×4=-8,-1×5=-5≠-8,∴点B 在函数图象上,点C 不在函数图象上.19.解析 (1)由题意得,函数t =k v的图象经过点(40,1),∴1=k40,解得k =40,∴函数关系式为t =40v,把(m ,0.5)代入t =40v,得0.5=40m,解得m =80.故k 的值为40,m 的值为80.(2)把v =50代入t =40v,得t =4050=0.8,∵t 随v 的增大而减小,∴汽车行驶速度不超过50 km/h 时,通过该路段最少需要0.8小时. 能力提升全练20.C 解法一:∵点A (x 1,y 1),B (x 2,y 2)是反比例函数y =6x 的图象上的两点,∴x 1y 1=x 2y 2=6.∵x 1<0<x 2,∴y 1<0<y 2.故选C.解法二:反比例函数y =6x 的大致图象如图所示.∵x 1<0<x 2,∴点A 在第三象限,点B 在第一象限,∴y 1<y 2.21.答案 32解析 由点B 的坐标为(4,3),可得OB =√42+32=5,∵AB ∥y 轴,AB =BC ,∴A 点的坐标为(4,8),∴k =4×8=32.22.解析 (1)∵一次函数y =2x +b 的图象过点B (0,4),∴b =4,∴一次函数的解析式为y =2x +4,∵OB =4,△BOC 的面积是2,∴12OB ·x C =2,即12×4×x C =2,∴x C =1,把x =1代入y =2x +4,得y =6,∴C (1,6),∵点C 在反比例函数y =k x(x >0)的图象上,∴k =1×6=6.(2)把y =0代入y =2x +4,得2x +4=0,解得x =-2,∴A (-2,0),∴OA =2,∴S△AOC=12×2×6=6.23.解析本题将尺规作图与反比例函数综合起来进行考查.(1)∵反比例函数y=kx(x>0)的图象经过点A(2,4),∴k=2×4=8.故反比例函数的表达式为y=8x.(2)如图,直线EF即为所作.(3)证明:如图,∵AC平分∠OAB,∴∠OAC=∠BAC.∵AC的垂直平分线交OA于点D,∴DA=DC,∴∠DAC=∠DCA.∴∠DCA=∠BAC.∴CD∥AB.素养探究全练24.解析(1)①1.②-4.(2)(x+1)(x-3)-x2=-2x-3,∵当-2<x<0时,min|kx,−2x+b|=-2x+b,∴-2x+b=-2x-3,∴b=-3,∴y2=-2x-3,当x=-2时,y2=1,∴A(-2,1).将A(-2,1)代入y1=kx 中,得k=-2,∴y1=-2x.。

部编八年级下册《钢铁是怎样炼成》练习题及参考答案2名著复习一、选择题1．依据《钢铁是怎样炼成的》中的情节，把批注续写完整。

情节一：保尔最爱读《牛虻》，书中塑造了一批英勇无畏，刚毅坚强，彻底献身于革命事业的革命者形象。

情节二：保尔失明了，他用硬纸板框中间卡出的缝限制铅笔进行写作，最终完成了《暴风雨所诞生的》。

（批注）读什么书，成长为什么人，保尔就是这样：____________________________ 2．下图是《钢铁是怎样炼成的》人物关系梳理图展示，请补充A、B两处空缺。

A是__________B是__________3．（活动二品读奋斗故事，汲取精神养分）“人最宝贵的东西是生命，生命属于人只有一次。

人的一生应该是这样度过的：当他回首往事的时候，他不会因为虚度年华而悔恨，也不会因为碌碌无为而羞耻。

这样，在临死的时候，他就能够说：‘我的整个生命和全部精力，都已经献给世界上最壮丽的事业——为人类的解放而斗争。

’”——《钢铁是怎样炼成的》上面这段话是______（人名）说的，在他的身上凝聚着那个时代最美好的精神品质——为理想而献身的精神、______的意志和______的高贵品质。

4．保尔瞻仰烈士公墓，怀着这样的思想：应该将整个生命和全部精力，都献给世界上最壮丽的事业一为__________________而斗争。

（《钢铁是怎样炼成的》）5．下面是某同学阅读《钢铁是怎样炼成的》一书时，整理的主人公保尔·柯察金的成长史。

将下列各阶段的标志性事件填写在思维导图的相应位置，正确的顺序是：_____。

（只填序号）A．解救朱赫来 B．铲雪筑路 C．打消“自杀”念头 D．加入骑兵部队6．请简要分析《钢铁是怎样炼成的》中保尔这一人物形象。

7．名著阅读。

“主题阅读”是名著阅读方法之一。

假如老师建议“做大写的人”的主题阅读，请从下面两部名著中任选一部，做简要分析。

（1）《傅雷家书》（2）《钢铁是怎样炼成的》8．保尔出生于贫困的铁路工人家庭，早年丧父，靠母亲替人洗衣做饭维持生计，却最终成为一个英雄、一位作家。