2009年普通高等学校招生全国统一考试(安徽卷WORD版)数学理科试题及标准答案

2009年普通高等学校招生全国统一考试（安徽卷）数学（理）试题第I 卷 (选择题 共50分)一.选择题：本大题10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）i 是虚数单位，若17(,)2ia bi ab R i+=+∈-，则乘积ab 的值是（B ） （A ）-15 （B ）-3 （C ）3 （D ）15 （2）若集合{}21|21|3,0,3x A x x B xx ⎧+⎫=-<=<⎨⎬-⎩⎭则A ∩B 是（D ） （A ） 11232x x x ⎧⎫-<<-<<⎨⎬⎩⎭或 (B) {}23x x <<(C) 122x x ⎧⎫-<<⎨⎬⎩⎭(D)112x x ⎧⎫-<<-⎨⎬⎩⎭（3）下列曲线中离心率为62的是（B ）（A ）22124x y -= （B ）22142x y -= （C ）22146x y -= （D ）221410x y -=(4)下列选项中，p 是q 的必要不充分条件的是（A ）（A ）p:a c +＞b+d , q:a ＞b 且c ＞d（B ）p:a ＞1,b>1， q:()(10)x f x a b a =-≠>的图像不过第二象限 （C ）p: x=1, q:2x x =（D ）p:a ＞1, q: ()log (10)a f x x a =≠>在(0,)+∞上为增函数 （5）已知{}n a 为等差数列，1a +3a +5a =105，246a a a ++=99.以n S 表示{}n a 的前n 项和，则使得n S 达到最大值的n 是（B ）（A ）21 （B ）20 （C ）19 （D ） 18 （6）设a ＜b,函数2()()y x a x b =--的图像可能是（C ）（7）若不等式组03434x x y x y ≥⎧⎪+≥⎨⎪+≤⎩所表示的平面区域被直线43y kx =+分为面积相等的两部分，则k 的值是（A ） （A ）73 （B ） 37 （C ）43 （D ） 34（8）已知函数()3sin cos (0)f x x x ωωω=+>，()y f x =的图像与直线2y =的两个相邻交点的距离等于π，则()f x 的单调区间是（C ）（A ）5[,],1212k k k Z ππππ-+∈ （B ）511[,],1212k k k Z ππππ++∈（C ）[,],36k k k Z ππππ-+∈ （D ）2[,],63k k k Z ππππ++∈（9）已知函数()f x 在R 上满足2()2(2)88f x f x x x =--+-，则曲线()y f x =在点(1,(1))f 处的切线方程是（A ）（A ）21y x =- （B ）y x = （C ）32y x =- （D ）23y x =-+（10）考察正方体6个面的中心，甲从这6个点中任意选两个点连成直线，乙也从这6个点中任意选两个点连成直线，则所得的两条直线相互平行但不重合的概率等于（D ） （A ）175 （B ） 275 （C ）375 （D ）475二．填空题：本大题共5小题，每小题5分，共25分，把答案填在答题卡的相应位置。

2009普通高等学校招生全国统一考试(全国卷H)数学(理科)本卷本12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项符合题 目要求的。

参考公式如果事件 A 、B 互斥，那么 P ( A+B )=P ( A )+P ( B )。

如果时间A 、B 相互独立，那么 P (A • B ) =P (A ) P ( B )。

如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中事件 A 恰好发生k次的概率 P n (k) H C ； p k (1 - p)n 上(k =0,1,2…，n)球的表面积公式2S =4二R 其中R 表示球的半径球的体积公式4 3V R 其中R 表示球的半径3一、选择题： 彳10i 1. =2 -iA . -2+4iB . -2-4iC . 2+4i 2.设集合A= :x x > 3? , B= xA . 0B . （3，4）C . （-2，1）D . （4，）3. 已知△ ABC 中，12cot A =，则 cosA =51251512A . —B . —C . - ----D . --131313134. 1 曲线y - 在点( 1，1)处的切线方程为：2x —1A . x -y -2 = 0B . x y -2 = 0C . x 4y - 5 = 0D . x _ 4y _ 5 = 0 5.已知正四棱柱 ABCD — A 1B 1C 1 D 1中，AA 二2AB ,E 为AA 1中点，则异面直线BE 与CD 1 所成角的余炫值为D . 2-4iX -1----- v x —4A. B .13応C . --------D .-1051056 .已知向量a= (2, 1), a b=10, a +b= s/2,则i ■b =A. B . C . 5 D . 257.设a =log3 二，b =log2、、3,c =log3. 2,则A. a b cB. a c bC. b a cD. b c aJT TT8 .若将函数y =ta n( 'X )^ 0)的图象向右平移一个单位长度后，与函数4 6y = tan(x 的图象重合，则「的最小值为61111A. B . C . D .-6 4 3 229.已知直线y=k(x，2)(k 0)与抛物线C: y =8x相交与A、B两点，F为C的焦点。

2009年普通高等学校招生全国统一考试理科数学（必修+选修Ⅱ） 本试卷分第卷（选择题）和第卷（非选择题）两部分．第卷1至2页，第卷3至4页．考试结束后，将本试卷和答题卡一并交回．第Ⅰ卷考生注意： 1．答题前，考生在答题卡上务必用0.5毫米黑色墨水签字笔将自己的姓名、准考证号、填写清楚 ，并贴好条形码．请认真核准条形码上的准考证号、姓名和科目． 2．每小题选出答案后，用2Ｂ铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．在试题卷上作答无效．．．．．．．．．． 3．本卷共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．参考公式： 如果事件A B ，互斥，那么 球的表面积公式 如果事件A B ，相互独立，那么 其中R 表示球的半径()()()P A B P A P B •=•球的体积公式 如果事件A 在一次试验中发生的概率是P ，那么 34π3V R =n 次独立重复试验中恰好发生k 次的概率其中R 表示球的半径一、选择题(1)设集合A=｛4，5，7，9｝，B=｛3，4，7，8，9｝，全集U=A B ，则集合[()u AB 中的元素共有（）（A ）3个 （B ）4个 （C ）5个 （D ）6个（2）已知1iZ＋=2+i,则复数z=（） （A ）-1+3i (B)1-3i (C)3+i (D)3-i (3) 不等式11X X +-＜1的解集为（ ）（A ）｛x }{}011x x x 〈〈〉 (B){}01x x 〈〈（C ）{}10x x -〈〈 (D){}0x x 〈(4)设双曲线22221x y a b-=（a ＞0,b ＞0）的渐近线与抛物线y=x 2+1相切，则该双曲线的离心率等于()（A （B ）2 （C （D(5) 甲组有5名男同学，3名女同学；乙组有6名男同学、2名女同学。

若从甲、乙两组中各选出2名同学，则选出的4人中恰有1名女同学的不同选法共有( )（A ）150种 （B ）180种 （C ）300种 (D)345种 （6）设a 、b 、c 是单位向量，且a ·b ＝0，则()()a c b c -•-的最小值为 ( )（A ）2- （B 2 （C ）1- (D)1（7）已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（ ）（A ）4 （B ）4 （C ）4 (D) 34（8）如果函数()cos 2y x φ＝3＋的图像关于点43π⎛⎫⎪⎝⎭，0中心对称，那么||ϕ的最小值为（A ）6π （B ）4π （C ）3π (D) 2π(9) 已知直线y=x+1与曲线y ln()x a =+相切，则α的值为( )(A)1 (B)2 (C) -1 (D)-2（10）已知二面角l αβ--为60，动点P 、Q 分别在面α、β内，PQ 到α的距离为P 、Q 两点之间距离的最小值为（ ）(A) (B)2 (C) （11）函数()f x 的定义域为R ，若(1)f x +与(1)f x -都是奇函数，则( )(A) ()f x 是偶函数 (B) ()f x 是奇函数 (C) ()(2)f x f x =+ (D) (3)f x +是奇函数12.已知椭圆22:12x C y +=的右焦点为F ,右准线为l ，点A l ∈，线段AF 交C 于点B ，若3FA FB =,则||AF =( )23第II 卷二、填空题：13. ()10x y -的展开式中，73x y 的系数与37x y 的系数之和等于 。

人才购物广场
公司简介：人才购物广场位于乌有市10大商业中心之一、4大城市副中心之
一的乌有商业区五角场北上海旗舰商业中心，是乌有市最大的商业项目之一。

项目占地2万平方米，总建筑面积近15万平方米。

人才购物广场是沁心万达集团在乌有投资的第一个项目，项目总投资为200万元,总建筑面积10万平方米，也是五角场最主要的核心建筑。

广场上划分为两层办公楼和大型停车场。

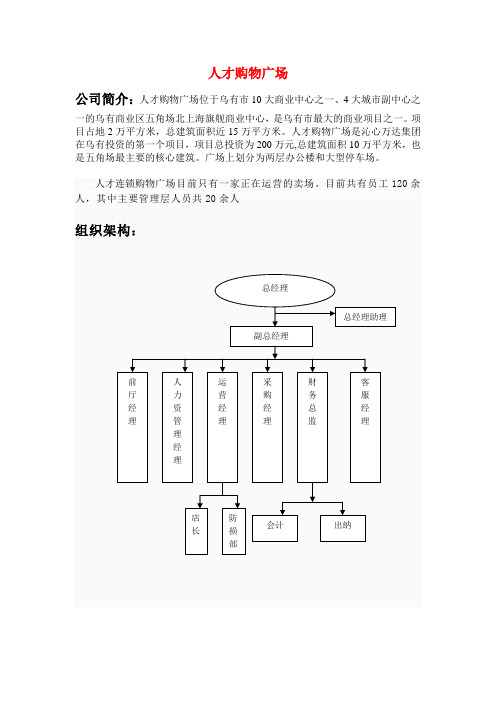
岗位职务：
总经理：公司最高领导
总经理助理：协助总经理处理好各项事务
副总经理：主要负责财务事物，监管采购和客户服务
前厅经理：主要负责客户接待和通知事项工作
人力资源管理经理：主要负责职工的考勤，岗位调动，培训开发，绩效考核以及薪酬管理的事物
运营经理：主管公司的日常运营和防损工作
采购经理：主要负责月初的采购货物和月末的盘点监管货物的质量检查
财务总监：主要负责公司的资金周转和运营状况
客服经理：主要负责客户的投诉，意见和建议反馈并及时做以回答和处理
店长：主要负责卖场的供货情况和安全防损工作
防损部：防损部员工主要负责公司安全工作和产品的保护
会计出纳：做好公司的每一笔账款记录并及时分析和汇报上级领导。

熟悉建筑结构抗震基本知识地震基本知识地震俗称地动，是一种具有突发性的自然现象。

地震按其发生的原因，主要有火山地震、陷落地震、人工诱发地震以及构造地震。

构造地震破坏作用大，影响范围广是房屋建筑抗震研究的主要对象。

在建筑抗震设计中，所指的地震是由于地壳构造运动（岩层构造状态的变动）使岩层发生断裂、错动而引起的地面振动，这种地面振动称为构造地震，简称地震。

地壳深处发生岩层断裂、错动的地方称为震源。

震源正上方的地面称为震中。

震中附近地面运动最激烈，也是破坏最严重的地区，叫震中区或极震区。

地面上某处到震源的距离叫震源距。

震源至地面的距离称为震源深度。

一般把震源深度小于60Km的地震称为浅源地震；60～300Km称为中源地震；大于300Km 成为深源地震。

中国发生的绝大部分地震均属于浅源地震。

地震波地震引起的振动以波的形式从震源向四周传播，这种波就称为地震波。

地震波按其在地壳传播的位置不同，分为体波和面波。

体波是在地球内部由震源向四周传播的波，分为纵波（P波）和横波（S波）。

纵波（P波）是由震源向四周传播的压缩波，介质质点的振动方向与波的传播方向一致，引起地面垂直振动，周期短、振幅小、波速快。

横波（S波）传播的是由震源向四周传播的剪切波，介质质点的振动方向与波的传播方向垂直，引起地面水平振动，周期长、振幅大、波速慢。

面波是体波经地层界面多次放射、折射形成的次生波。

面波的质点振动方向比较复杂，既引起地面水平振动又引起地面垂直振动。

当地震发生时，纵波首先到达，使房屋产生上下颠簸，接着横波到达，使范围产生水平摇晃，一般是当面波和横波都到达时，房屋振动最为激烈。

震级地震的震级是衡量一次地震大小的等级，用符号M表示。

地震的震级M，一般称为里氏震级。

1935年由里希特首先提出了震级的定义。

当震级相差一级，地面振动振幅增加约10倍，而能量增加近32倍。

一般说来，M＜2的地震，人们感觉不到，称为微震；M=2～4的地震称为有感地震；M＞5的地震，对建筑物就要引起不同程度的破坏，统称为破坏性地震；M＞7的地震称为强烈地震或大地震；M＞8的地震称为特大地震。

2009年安徽省高考数学试卷（理科）参考答案与试题解析一、选择题（共10小题，每小题5分，满分50分）1．（5分）（2009•安徽）i是虚数单位，若=a+bi（a，b∈R），则乘积ab的值是（）A．﹣15 B．﹣3 C．3 D．15【考点】复数相等的充要条件；复数代数形式的乘除运算．【专题】计算题．【分析】先根据两个复数相除的除法法则化简，再依据两个复数相等的充要条件求出a和b的值，即得乘积ab的值．【解答】解：∵===﹣1+3i=a+bi，∴a=﹣1，b=3，∴ab=﹣1×3=﹣3．故选B．【点评】本题考查两个复数相除的方法，以及两个复数相等的充要条件的应用．2．（5分）（2009•安徽）若集合A={x||2x﹣1|＜3}，B={x|＜0}，则A∩B是（）A．{x|﹣1＜x＜﹣或2＜x＜3} B．{x|2＜x＜3}C．{x|﹣＜x＜2} D．{x|﹣1＜x＜﹣}【考点】交集及其运算．【专题】综合题．【分析】集合A中的绝对值不等式可利用讨论2x﹣1的正负得到一个不等式组，求出不等式组的解集即可得到集合A；集合B中的其他不等式可转化为2x+1与x﹣3同号即同时为正或同时为负得到两个不等式组，分别求出解集即可得到集合B，求出两集合的交集即可．【解答】解：∵|2x﹣1|＜3，∴﹣3＜2x﹣1＜3，即，∴﹣1＜x＜2，又∵＜0，∴（2x+1）（x﹣3）＞0，即或，∴x＞3或x＜﹣，∴A∩B={x|﹣1＜x＜﹣}．故选D【点评】此题是以绝对值不等式和其他不等式的解法为平台，考查了求交集的运算，是一道中档题．3．（5分）（2009•安徽）下列曲线中离心率为的是（）A．B．C．D．【考点】双曲线的简单性质．【专题】计算题．【分析】通过验证法可得双曲线的方程为时，．【解答】解：选项A中a=，b=2，c==，e=排除．选项B中a=2，c=，则e=符合题意选项C中a=2，c=，则e=不符合题意选项D中a=2，c=则e=，不符合题意故选B【点评】本题主要考查了双曲线的简单性质．考查了双曲线方程中利用，a，b和c的关系求离心率问题．4．（5分）（2009•安徽）下列选项中，p是q的必要不充分条件的是（）A．p：a+c＞b+d，q：a＞b且c＞dB．p：a＞1，b＞1，q：f（x）=a x﹣b（a＞0，且a≠1）的图象不过第二象限C．p：x=1，q：x=x2D．p：a＞1，q：f（x）=log a x（a＞0，且a≠1）在（0，+∞）上为增函数【考点】必要条件、充分条件与充要条件的判断．【专题】简易逻辑．【分析】由题意根据必要条件、充分条件和充要条件的定义对ABCD四个选项进行一一判断，从而求解．【解答】解：A、∵q：a＞b且c＞d，∴a+c＞b+d，∴q⇒p，但p推不出q，p是q的必要不充分条件，故A正确；B、∵p：a＞1，b＞1，∴f（x）=a x﹣b（a＞0，且a≠1）的图象不过第二象限，但若b=1，a ＞1时f（x）的图象也不过第二象限，q推不出p，∴p是q的充分不必要条件，故B错误；C、∵x=1，∴x=x2，但当x=0时，x=x2，也成立，q推不出p，∴p是q的充分不必要条件，故C错误；D、∵a＞1，∴f（x）=log a x（a＞0，且a≠1）在（0，+∞）上为增函数，p是q的充要条件，故D错误；故选A．【点评】本小题主要考查了命题的基本关系及必要条件、充分条件和充要条件的定义，题中的设问通过对不等关系的分析，考查了命题的概念和对于命题概念的理解程度．5．（5分）（2009•安徽）已知{a n}为等差数列，a1+a3+a5=105，a2+a4+a6=99，以S n表示{a n}的前n项和，则使得S n达到最大值的n是（）A．21 B．20 C．19 D．18【考点】等差数列的前n项和．【专题】计算题．【分析】写出前n项和的函数解析式，再求此式的最值是最直观的思路，但注意n取正整数这一条件．【解答】解：设{a n}的公差为d，由题意得a1+a3+a5=a1+a1+2d+a1+4d=105，即a1+2d=35，①a2+a4+a6=a1+d+a1+3d+a1+5d=99，即a1+3d=33，②由①②联立得a1=39，d=﹣2，∴S n=39n+×（﹣2）=﹣n2+40n=﹣（n﹣20）2+400，故当n=20时，S n达到最大值400．故选：B．【点评】求等差数列前n项和的最值问题可以转化为利用二次函数的性质求最值问题，但注意n取正整数这一条件．6．（5分）（2009•安徽）设a＜b，函数y=（a﹣x）（x﹣b）2的图象可能是（）A．B．C．D．【考点】函数的图象．【专题】数形结合．【分析】根据所给函数式的特点，知函数值的符号取决于x的值与a的值的大小关系，当x≥a 时，y≤0，当x≤a时，y≥0，据此即可解决问题．【解答】解：∵y=（a﹣x）（x﹣b）2∴当x≥a时，y≤0，故可排除A、D；又当x≤a时，y≥0，故可排除C；故选B．【点评】本题主要考查了函数的图象，以及数形结合的数学思想方法，属于容易题．7．（5分）（2009•安徽）若不等式组所表示的平面区域被直线分为面积相等的两部分，则k的值是（）A．B．C．D．【考点】简单线性规划的应用．【专题】计算题；压轴题．【分析】先根据约束条件：，画出可行域，求出可行域顶点的坐标，再利用几何意义求面积即可．【解答】解：满足约束条件：，平面区域如图示：由图可知，直线恒经过点A（0，），当直线再经过BC的中点D（，）时，平面区域被直线分为面积相等的两部分，当x=，y=时，代入直线的方程得：k=，故选A．【点评】本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．8．（5分）（2009•安徽）已知函数f（x）=sinwx+coswx（w＞0），y=f（x）的图象与直线y=2的两个相邻交点的距离等于π，则f（x）的单调递增区间是（）A．[kπ﹣，kπ+]，k∈Z B．[kπ+，kπ+]，k∈ZC．[kπ﹣，kπ+]，k∈Z D．[kπ+，kπ+]，k∈Z【考点】两角和与差的正弦函数；正弦函数的单调性．【分析】先把函数化成y=Asin（ωx+φ）的形式，再根据三角函数单调区间的求法可得答案．【解答】解：f（x）=sinwx+coswx=2sin（wx+），（w＞0）．∵f（x）的图象与直线y=2的两个相邻交点的距离等于π，恰好是f（x）的一个周期，∴=π，w=2．f（x）=2sin（2x+）．故其单调增区间应满足2kπ﹣≤2x+≤2kπ+，k∈Z．kπ﹣≤x≤kπ+，故选C．【点评】本题主要考查三角函数单调区间的求法．求三角函数的周期、单调区间、最值都要把函数化成y=Asin（ωx+φ）的形式在进行解题．9．（5分）（2009•安徽）已知函数f（x）在R上满足f（1+x）=2f（1﹣x）﹣x2+3x+1，则曲线y=f（x）在点（1，f（1））处的切线方程是（）A．x﹣y﹣2=0 B．x﹣y=0 C．3x+y﹣2=0 D．3x﹣y﹣2=0【考点】利用导数研究曲线上某点切线方程；导数的几何意义．【专题】压轴题．【分析】对等式两边进行求导数，通过赋值求切线斜率；对等式赋值求切点坐标；据点斜式写出直线方程．【解答】解：∵f（1+x）=2f（1﹣x）﹣x2+3x+1∴f′（1+x）=﹣2f′（1﹣x）﹣2x+3∴f′（1）=﹣2f′（1）+3∴f′（1）=1f（1+x）=2f（1﹣x）﹣x2+3x+1∴f（1）=2f（1）+1∴f（1）=﹣1∴切线方程为：y+1=x﹣1即x﹣y﹣2=0故选A【点评】本题考查对数的几何意义，在切点处的对数值是切线斜率，求切线方程．10．（5分）（2009•安徽）考察正方体6个面的中心，甲从这6个点中任意选两个点连成直线，乙也从这6个点种任意选两个点连成直线，则所得的两条直线相互平行但不重合的概率等于（）A．B．C．D．【考点】古典概型及其概率计算公式．【专题】计算题；压轴题．【分析】先用组合数公式求出甲乙从这6个点中任意选两个点连成直线的条数共有C62，再用分步计数原理求出甲乙从中任选一条共有225种，利用正八面体找出相互平行但不重合共有共12对，代入古典概型的概率公式求解．【解答】解：甲从这6个点中任意选两个点连成直线，共有C62=15条，乙也从这6个点中任意选两个点连成直线，共有C62=15条，甲乙从中任选一条共有15×15=225种不同取法，因正方体6个面的中心构成一个正八面体，有六对相互平行但不重合的直线，则甲乙两人所得直线相互平行但不重合共有12对，这是一个古典概型，所以所求概率为=，故选D．【点评】本题的考点是古典概型，利用组合数公式和分步计数原理求出所有基本事件的总数，再通过正方体6个面的中心构成一个正八面体求出相互平行但不重合的对数，代入公式求解．二、填空题（共5小题，每小题5分，满分20分）11．（5分）（2009•安徽）若随机变量X～N（μ，σ2），则P（X≤μ）=．【考点】正态分布曲线的特点及曲线所表示的意义．【专题】计算题；作图题．【分析】由正态分布的图象规律知，其在x=μ左侧一半的概率为，故得P（ζ≤μ）的值．【解答】解：∵ζ服从正态分布N（μ，σ2），根据正态密度曲线的对称性可得∴曲线关于x=μ对称，P（X≤μ）=选填：．【点评】本题主要考查正态分布的图象，结合正态曲线，加深对正态密度函数的理解．12．（2009•安徽）以直角坐标系的原点为极点，x轴的正半轴为极轴，并在两种坐标系中取相同的长度单位．已知直线的极坐标方程为（ρ∈R），它与曲线（α为参数）相交于两点A和B，则|AB|=．【考点】点的极坐标和直角坐标的互化；参数方程化成普通方程．【专题】直线与圆．【分析】把参数方程、极坐标方程化为直角坐标方程，求出弦心距，再利用弦长公式求得弦长|AB|的值．【解答】解：直线的极坐标方程为（ρ∈R），化为直角坐标方程为x﹣y=0．曲线（α为参数）的普通方程为（x﹣1）2+（y﹣2）2=4，表示以（1，2）为圆心，半径等于2的圆．求得弦心距d==，故弦长为2=2=，故答案为．【点评】本题主要考查把参数方程、极坐标方程化为直角坐标方程的方法，直线和圆的位置关系，点到直线的距离公式，弦长公式的应用，属于基础题．13．（5分）（2009•安徽）程序框图（即算法流程图）如图所示，其输出结果是127．【考点】设计程序框图解决实际问题．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环计算a值，并输出满足条件a＞100的第一个a值，模拟程序的运行过程，用表格将程序运行过程中变量a的值的变化情况进行分析，不难给出答案．【解答】解：程序在运行过程中各变量的值如下表示：a 是否继续循环循环前1/第一圈 3 是第二圈7 是第三圈15 是第四圈31 是第五圈63 是第六圈127 否故最后输出的a值为：127故答案为：127【点评】根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是：：①分析流程图（或伪代码），从流程图（或伪代码）中即要分析出计算的类型，又要分析出参与计算的数据（如果参与运算的数据比较多，也可使用表格对数据进行分析管理）⇒②建立数学模型，根据第一步分析的结果，选择恰当的数学模型③解模．14．（5分）（2009•安徽）给定两个长度为1的平面向量和，它们的夹角为120°．如图所示，点C在以O为圆心，以1半径的圆弧AB上变动．若=x+y，其中x，y∈R，则x+y的最大值是2．【考点】向量在几何中的应用．【专题】计算题；压轴题．【分析】根据题意，建立坐标系，设出A，B点的坐标，并设∠AOC=α，则向量，且=x+y，由向量相等，得x，y的值，从而求得x+y的最值．【解答】解：建立如图所示的坐标系，则A（1，0），B（cos120°，sin120°），即B（﹣，）．设∠AOC=α，则=（cosα，sinα）．∵=x+y=（x，0）+（﹣，y）=（cosα，sinα）.∴∴x+y=sinα+cosα=2sin（α+30°）．∵0°≤α≤120°．∴30°≤α+30°≤150°．∴x+y有最大值2，当α=60°时取最大值2．答案：2【点评】本题是向量的坐标表示的应用，结合图形，利用三角函数的性质，容易求出结果．15．（5分）（2009•安徽）对于四面体ABCD，下列命题正确的序号是①④⑤．①相对棱AB与CD所在的直线异面；②由顶点A作四面体的高，其垂足是△BCD的三条高线的交点；③若分别作△ABC和△ABD的边AB上的高，则这两条高所在直线异面；④分别作三组相对棱中点的连线，所得的三条线段相交于一点；⑤最长棱必有某个端点，由它引出的另两条棱的长度之和大于最长棱．【考点】棱锥的结构特征．【专题】常规题型；压轴题．【分析】①根据三棱锥的结构特征判断．②根据对棱不一定相互垂直判断．③可由正四面体时来判断．④由棱中点两两连接构成平行四边形判断．⑤根据两边之和大于第三边判断．【解答】解：①根据三棱锥的结构特征知正确．②因为只有对棱相互垂直才行，所以不一定，不正确．③若分别作△ABC和△ABD的边AB上的高，若是正四面体时，则两直线相交，不正确．④因为相对棱中点两两连接构成平行四边形，而对棱的中点的连接正是平行四边形的对角线，所以三条线段相交于一点，故正确．⑤设图中CD是最长边．BC+BD＞CD，AC+AD＞CD若AC+BC≤CD 且AD+BD≤CD则AC+AD+BC+BD≤CD+CD，矛盾则命题成立．故答案为：①④⑤【点评】本题主要考查三棱锥的结构特征，通过作高，取中点连线，来增加考查的难度，即全面又灵活，是一道好题，属中档题．三、解答题（共6小题，满分75分）16．（12分）（2009•安徽）在△ABC中，sin（C﹣A）=1，sinB=．（Ⅰ）求sinA的值；（Ⅱ）设AC=，求△ABC的面积．【考点】解三角形．【专题】计算题．【分析】（I）利用sin（C﹣A）=1，求出A，C关系，通过三角形内角和结合sinB=，求出sinA的值；（II）通过正弦定理，利用（I）及AC=，求出BC，求出sinC，然后求△ABC的面积．【解答】解：（Ⅰ）因为sin（C﹣A）=1，所以，且C+A=π﹣B，∴，∴，∴，又sinA＞0，∴（Ⅱ）如图，由正弦定理得∴，又sinC=sin（A+B）=sinAcosB+cosAsinB=∴【点评】本小题主要考查三角恒等变换、正弦定理、解三角形等有关知识，考查运算求解能力．17．（12分）（2009•安徽）某地有A、B、C、D四人先后感染了甲型H1N1流感，其中只有A到过疫区．B肯定是受A感染的．对于C，因为难以断定他是受A还是受B感染的，于是假定他受A和受B感染的概率都是．同样也假定D受A、B和C感染的概率都是．在这种假定之下，B、C、D中直接受A感染的人数x就是一个随机变量．写出x的分布列（不要求写出计算过程），并求x的均值（即数学期望）．【考点】离散型随机变量的期望与方差．【专题】概率与统计．【分析】由题意知X的可能取值为1，2，3，分别求出相应的概率，由此能求出x的分布列和x的均值．【解答】解：由题意知X的可能取值为1，2，3，随机变量X的分布列是X 1 2 3PX的均值为EX=1×+2×+3×=．【点评】本题考查离散型随机变量的分布列和均值的求法，是中档题，在历年高考中都是必考题型．18．（13分）（2009•安徽）如图所示，四棱锥F﹣ABCD的底面ABCD是菱形，其对角线AC=2，BD=．AE、CF都与平面ABCD垂直，AE=1，CF=2．（1）求二面角B﹣AF﹣D的大小；（2）求四棱锥E﹣ABCD与四棱锥F﹣ABCD公共部分的体积．【考点】与二面角有关的立体几何综合题；棱柱、棱锥、棱台的体积．【专题】计算题．【分析】（1）连接AC、BD交于菱形的中心O，过O作OG⊥AF，G为垂足，连接BG、DG，根据定义可知∠BGD为二面角B﹣AF﹣D的平面角，在三角形BGD中求出此角即可；（2）连接EB、EC、ED，设直线AF与直线CE相交于点H，则四棱锥E﹣ABCD与四棱锥F﹣ABCD的公共部分为四棱锥H﹣ABCD，过H作HP⊥平面ABCD，P为垂足，然后求出HP，利用体积公式V=S菱形ABCD•HP求解即可．【解答】解：（1）解：连接AC、BD交于菱形的中心O，过O作OG⊥AF，G为垂足，连接BG、DG．由BD⊥AC，BD⊥CF得BD⊥平面ACF，故BD⊥AF．于是AF⊥平面BGD，所以BG⊥AF，DG⊥AF，∠BGD为二面角B﹣AF﹣D的平面角．由FC⊥AC，FC=AC=2，得∠FAC=，OG=．由OB⊥OG，OB=OD=，得∠BGD=2∠BGO=．（2）解：连接EB、EC、ED，设直线AF与直线CE相交于点H，则四棱锥E﹣ABCD与四棱锥F﹣ABCD的公共部分为四棱锥H﹣ABCD．过H作HP⊥平面ABCD，P为垂足．因为EA⊥平面ABCD，FC⊥平面ABCD，所以平面ACEF⊥平面ABCD，从而P∈AC，HP⊥AC．由+=+=1，得HP=．又因为S菱形ABCD=AC•BD=，故四棱锥H﹣ABCD的体积V=S菱形ABCD•HP=．【点评】本题考查空间位置关系，二面角平面角的作法以及空间几何体的体积计算等知识．考查利用综合法或向量法解决立体几何问题的能力．19．（12分）（2009•安徽）已知函数，讨论f（x）的单调性．【考点】利用导数研究函数的单调性．【专题】计算题；压轴题．【分析】先求出函数的定义域，然后求出导函数，设g（x）=x2﹣ax+2，二次方程g（x）=0的判别式△=a2﹣8，然后讨论△的正负，再进一步考虑导函数的符号，从而求出函数的单调区间．【解答】解：f（x）的定义域是（0，+∞），．设g（x）=x2﹣ax+2，二次方程g（x）=0的判别式△=a2﹣8．①当△=a2﹣8＜0，即时，对一切x＞0都有f′（x）＞0，此时f（x）在（0，+∞）上是增函数．②当△=a2﹣8=0，即时，仅对有f′（x）=0，对其余的x＞0都有f′（x）＞0，此时f（x）在（0，+∞）上也是增函数．③当△=a2﹣8＞0，即时，方程g（x）=0有两个不同的实根，，0＜x1＜x2．x （0，x1）x1（x1，x2）x2（x2，+∞）f'（x）+ 0 _ 0 +f（x）单调递增↗极大单调递减↘极小单调递增此时f（x）在上单调递增，在是上单调递减，在上单调递增．【点评】本题主要考查了利用导数研究函数的单调性，同时考查了转化的能力和分类讨论的数学思想，属于中档题．20．（13分）（2009•安徽）点P（x0，y0）在椭圆（a＞b＞0）上，x0=acosβ，y0=bsinβ，0＜．直线l2与直线l1：垂直，O为坐标原点，直线OP的倾斜角为α，直线l2的倾斜角为γ（Ⅰ）证明：点P是椭圆与直线l1的唯一交点；（Ⅱ）证明：tanα，tanβ，tanγ构成等比数列．【考点】直线与圆锥曲线的关系；等比关系的确定．【专题】圆锥曲线中的最值与范围问题．【分析】（Ⅰ）由，得y=，从而x=acosβ，由此能证明直线l1与椭圆有唯一交点P．（Ⅱ）tanα==tanβ，由此得tanαtanγ=tan2β≠0，从而能证明tanα，tanβ，tanγ构成等比数列．【解答】解：（Ⅰ）由，得y=，代入椭圆，得，将，代入上式，得x2﹣2acosβx+a2cos2β=0，从而x=acosβ，∴有唯一解，即直线l1与椭圆有唯一交点P．（Ⅱ）tanα==tanβ，l1的斜率为tan=，由此得tanαtanγ=tan2β≠0，∴tanα，tanβ，tanγ构成等比数列．【点评】本题考查直线与椭圆有唯一交点的证明，考查tanα，tanβ，tanγ构成等比数列的证明，解题时要认真审题，注意函数与方程思想的合理运用．21．（13分）（2009•安徽）首项为正数的数列{a n}满足a n+1=（a n2+3），n∈N+．（1）证明：若a1为奇数，则对一切n≥2，a n都是奇数；（2）若对一切n∈N+都有a n+1＞a n，求a1的取值范围．【考点】数列递推式；数列的函数特性．【专题】计算题；证明题．【分析】（1）首先在n=1时，知a1为奇数，再利用归纳法证明对一切n≥2，a n都是奇数；（2）先求出a n+1﹣a n的表达式，利用函数思想求解不等式a n+1﹣a n＞0，求出a n取值范围，利用归纳法求出a1的取值范围．【解答】（1）证明：已知a1是奇数，假设a k=2m﹣1是奇数，其中m为正整数，则由递推关系得a k+1==m（m﹣1）+1是奇数．根据数学归纳法，对任何n≥2，a n都是奇数．（2）法一：由a n+1﹣a n=（a n﹣1）（a n﹣3）知，a n+1＞a n当且仅当a n＜1或a n＞3．另一方面，若0＜a k＜1，则0＜a k+1＜=1；若a k＞3，则a k+1＞=3．根据数学归纳法得，0＜a1＜1⇔0＜a n＜1，∀n∈N+；a1＞3⇔a n＞3，∀n∈N+．综上所述，对一切n∈N+都有a n+1＞a n的充要条件是0＜a1＜1或a1＞3．法二：由a2=＞a1，得a12﹣4a1+3＞0，于是0＜a1＜1或a1＞3．a n+1﹣a n=﹣=，因为a1＞0，a n+1=，所以所有的a n均大于0，因此a n+1﹣a n与a n﹣a n﹣1同号．根据数学归纳法，∀n∈N+，a n+1﹣a n与a2﹣a1同号．因此，对一切n∈N+都有a n+1＞a n的充要条件是0＜a1＜1或a1＞3．【点评】此题主要考查数学归纳法求解有关数列的问题时的应用．。

2009年普通高等学校招生全国统一考试理科数学（必修+选修Ⅱ）本试卷分第错误！未找到引用源。

卷（选择题）和第错误！未找到引用源。

卷（非选择题）两部分．第错误！未找到引用源。

卷1至2页，第错误！未找到引用源。

卷3至4页．考试结束后，将本试卷和答题卡一并交回．第Ⅰ卷考生注意：1．答题前，考生在答题卡上务必用0.5毫米黑色墨水签字笔将自己的姓名、准考证号、填写清楚 ，并贴好条形码．请认真核准条形码上的准考证号、姓名和科目．2．每小题选出答案后，用2Ｂ铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．在试题卷上作答无效．．．．．．．．．． 3．本卷共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．参考公式：如果事件A B ，互斥，那么 球的表面积公式如果事件A B ，相互独立，那么 其中R 表示球的半径()()()P A B P A P B = 球的体积公式如果事件A 在一次试验中发生的概率是P ，那么 34π3V R = n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径一、选择题(1)设集合A=｛4，5，7，9｝，B=｛3，4，7，8，9｝，全集U=AB ，则集合[()u A B I 中的元素共有（A ）（A ）3个 （B ）4个 （C ）5个 （D ）6个解：{3,4,5,7,8,9}A B =，{4,7,9}(){3,5,8}U A B C A B =∴=故选A 。

也可用摩根律：()()()U U U C A B C A C B =（2）已知1iZ ＋=2+i,则复数z=（B ） （A ）-1+3i (B)1-3i (C)3+i (D)3-i 解：(1)(2)13,13z i i i z i =+⋅+=+∴=- 故选B 。

(3) 不等式11X X +-＜1的解集为（ D ）（A ）｛x }{}011x x x 〈〈〉 (B){}01x x 〈〈（C ）{}10x x -〈〈 (D){}0x x 〈解：验x=-1即可。

2009年普通高等学校招生全国统一考试（安徽卷）数学（理）试题第I 卷 (选择题 共50分)一.选择题：本大题10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）i 是虚数单位，若17(,)2ia bi ab R i+=+∈-，则乘积ab 的值是（B ） （A ）-15 （B ）-3 （C ）3 （D ）15 （2）若集合{}21|21|3,0,3x A x x B xx ⎧+⎫=-<=<⎨⎬-⎩⎭则A ∩B 是（D ） （A ） 11232x x x ⎧⎫-<<-<<⎨⎬⎩⎭或 (B) {}23x x <<(C) 122x x ⎧⎫-<<⎨⎬⎩⎭(D)112x x ⎧⎫-<<-⎨⎬⎩⎭（3（B ）（A ）22124x y -= （B ）22142x y -= （C ）22146x y -= （D ）221410x y -=(4)下列选项中，p 是q 的必要不充分条件的是（A ）（A ）p:a c +＞b+d , q:a ＞b 且c ＞d（B ）p:a ＞1,b>1， q:()(10)xf x a b a =-≠>的图像不过第二象限 （C ）p: x=1, q:2x x =（D ）p:a ＞1, q: ()log (10)a f x x a =≠>在(0,)+∞上为增函数 （5）已知{}n a 为等差数列，1a +3a +5a =105，246a a a ++=99.以n S 表示{}n a 的前n 项和，则使得n S 达到最大值的n 是（B ）（A ）21 （B ）20 （C ）19 （D ） 18 （6）设a ＜b,函数2()()y x a x b =--的图像可能是（C ）（7）若不等式组03434x x y x y ≥⎧⎪+≥⎨⎪+≤⎩所表示的平面区域被直线43y kx =+分为面积相等的两部分，则k 的值是（A ） （A ）73 （B ） 37 （C ）43 （D ） 34（8）已知函数()3sin cos (0)f x x x ωωω=+>，()y f x =的图像与直线2y =的两个相邻交点的距离等于π，则()f x 的单调区间是（C ）（A ）5[,],1212k k k Z ππππ-+∈ （B ）511[,],1212k k k Z ππππ++∈（C ）[,],36k k k Z ππππ-+∈ （D ）2[,],63k k k Z ππππ++∈（9）已知函数()f x 在R 上满足2()2(2)88f x f x x x =--+-，则曲线()y f x =在点(1,(1))f 处的切线方程是（A ）（A ）21y x =- （B ）y x = （C ）32y x =- （D ）23y x =-+（10）考察正方体6个面的中心，甲从这6个点中任意选两个点连成直线，乙也从这6个点中任意选两个点连成直线，则所得的两条直线相互平行但不重合的概率等于（D ） （A ）175 （B ） 275 （C ）375 （D ）475二．填空题：本大题共5小题，每小题5分，共25分，把答案填在答题卡的相应位置。