当前位置：文档之家 › 实对称矩阵的特征值和特征向量 (2)

实对称矩阵的特征值和特征向量 (2)

  • 格式：ppt
  • 大小：757.51 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

实对称矩阵特征值与特征向量的性质

实对称矩阵特征值与特征向量的性质
实对称矩阵的特征值与特征向量的性质
性质1：实对称矩阵的特征值都是实数。
设是n阶实对称矩阵A的特征值, (a1, a2 ,, an )T
是对应的特征向量,即A 两边取共轭，得
A (1)
A (aij )nn
A,
(a , 1
a 2
,
,
an
)T
,由于A为实对称阵，故
AT
AT
A,
（1）两端取转置，得：
2 4 2
1 2
2
A E 2 2 4 ( 2)2 ( 7)
2
4 2
1 2 2,3 7.
1 (2,1,0)T ,2 (2,0,1)T为属于特征值2的线性无关的特
征向量.
3 7的特征向量为3 (1，2， 2)T .
2 2 1
2
P 1
2
3
1
0
0 1
2 , 2
1 1 0
B 4 3 0 1 2 1,3 2.
1 0 2
对1 2 1,
2 1 0 1 0 1
B
E
4
1
2 0
0 1
0 0
1 0
2 , 1 (1,2, 1)T .
0
线性无关 的特征向 量只有一个
1 2 2 例：设A 2 2 4 ，求可逆阵P，使P1AP为对角阵。
1T A 11T .
1T A2 11T2.
21T2 11T2. (2 1)1T2 0.
1T2 0.
例：设1，1，1是三阶实对称方阵A的3个特征值，
1 （1，1，1）T,2 （2，2，1）T是A的属于特征值1的特
征向量，求A的属于特征值1的特征向量。
设A的属于特征值 1的特征向量为3 （x1，x2，x3）T ,

第二十二讲 实对称矩阵

第二十二讲 实对称矩阵

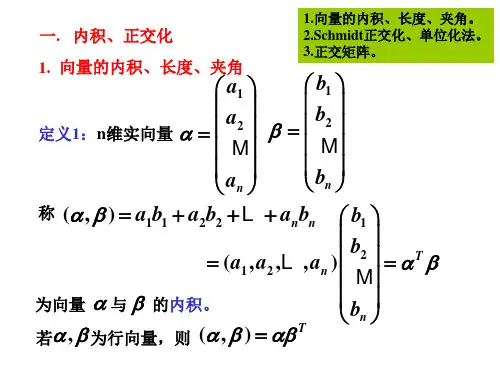
§22 实对称矩阵22.1 实对称矩阵的特征值与特征向量若矩阵满足则称为对称矩阵.本节主要讨论实对称矩阵的性质. 这类矩阵应用广泛，理论丰富、优美.一个实矩阵的特征值可能是虚数, 如但定理：实对称矩阵的特征值都是实数.证明：设实对称矩阵有则因故即为实数.22.1 实对称矩阵的特征值与特征向量属于不同特征值的特征向量线性无关, 对实对称矩阵有更强的结果. 定理：实对称矩阵的属于不同特征值的特征向量相互正交.证明：设与是实对称矩阵的两互异特征值(由前面定理是实数), 是相应特征向量, 即于是而故22.1 实对称矩阵的特征值与特征向量例：有特征值为分别属于的特征向量.易见与正交.22.2 实对称阵正交相似于对角阵回忆：矩阵可对角化有一组特征向量作为空间的基.故若是可对角化的实对称阵, 则存在的一组特征向量构成空间的单位正交基.事实上，定理：任何实对称阵正交相似于对角阵, 即对实对称阵存在正交阵使为对角阵.22.2 实对称阵正交相似于对角阵证明：对矩阵的阶数用数学归纳法.时结论成立. 假设结论对阶矩阵成立.对阶实对称阵设且则可扩充为的一组基, 进一步正交化，得一组标准正交基,记为则为正交阵，且22.2 实对称阵正交相似于对角阵由得且由归纳假设知, 对阶实对称矩阵存在正交阵使令则为正交阵, 且22.2 实对称阵正交相似于对角阵例：设求正交阵使为对角阵.22.2 实对称阵正交相似于对角阵解：因此的特征值是22.2 实对称阵正交相似于对角阵对可求出齐次线性方程组的一个基础解系:对可求出齐次线性方程组的一个基础解系:22.2 实对称阵正交相似于对角阵作正交化(只需对进行),22.2 实对称阵正交相似于对角阵再作单位化，得则为正交阵，且22.2 实对称阵正交相似于对角阵由前面定理知, 对任何实对称阵其中为正交阵，于是即22.2 实对称阵正交相似于对角阵注记：为到由特征向量张成的一维空间的投影矩阵.任意实对称阵可表示为秩投影矩阵的和.可类似证明：Schur定理：任意一个复方阵均酉相似于上三角阵，即对任何复方阵存在酉矩阵使为上三角阵.22.2 实对称阵正交相似于对角阵例：设是阶实对称阵，为的全部特征值，则存在实数满足对任意证明：因为实对称阵，故存在正交阵使则对任意记有令则22.2 实对称阵正交相似于对角阵例：设是实对称阵的最大特征值.求证：的对角线元素证明：因实对称，故存在正交阵使注意到其中令则22.3 实对称阵特征值和主元的关系矩阵特征值的符号与主元的符号一般无关，如特征值为 (两负)主元为 (两正)但对实对称阵而言，二者符号一致，如特征值为 (一正一负)主元为 (一正一负) 定理：实对称阵的正特征值数与正主元数相同.22.3 实对称阵特征值和主元的关系引理：设矩阵可逆，且则证明：假设则齐次线性方程组有非零解令则22.3 实对称阵特征值和主元的关系于是上式左边右边矛盾！故同理可证故22.3 实对称阵特征值和主元的关系定理的证明：由于实对称阵的主元数等于其非零特征值数，故不失一般性，可对可逆实对称阵讨论.设的正主元数为正特征值数为则其中是对角元为的下三角阵，为主元.又其中是正交阵，为特征值.22.3 实对称阵特征值和主元的关系于是22.3 实对称阵特征值和主元的关系令则可逆，且由引理知定理得证.注记：事实上，我们证明了惯性定理.22.3 实对称阵特征值和主元的关系小结：1.实对称阵的特征值都是实数.2.实对称阵属于不同特征值的特征向量相互正交.3.实对称阵正交相似于对角阵.4.实对称阵的正特征值数与正主元数相同.。

3.3实对称矩阵的特征值和特征向量 共14页

3.3实对称矩阵的特征值和特征向量 共14页

2

2

(2, 1) (1, 1)
1
3

3

(3 , (2,
2 2
) )
2

(3, 1) (1, 1)
1

s
s

(s , s1 ) (s1, s1 )
s1

(s , 2 ) (2 , 2 )
2

中的两个列向量，则 n T a1b1a2b2 anbn aibi i1
称为向量 与 的内积. 内积T 也可记作(, )
2. 内积的性质
(1) ( , ) = ( , ) ;
(2) (k , )= k( , );
(3) ( + , )= (, )+ ( , );
令 1 1
2

2

(2, 1) (1, 1)
1
3

3

(3 , (2,
2 ) 2 )
2

(3, 1) (1, 1)
1

s
s

(s , s1 ) (s1, s1 )
s1

(s , 2 ) (2 , 2 )
n
T ai2
i1
如果 || || = 1，则称 为单位向量.
0 ，则 1 为单位向量或标准化向量.
4. 长度的性质
(1) || || 0 , 且 || || = 0 = 0 ;
(2) || k || = | k | ·|| || ;
7.Th.: 设 1 , 2 , … , s 是一个正交向量组, 则1,2 , …,s
线性无关.

3.2 实对称矩阵与实二次型

3.2 实对称矩阵与实二次型
3.2 实对称矩阵与实二次型
一、 实对称矩阵的特征值与特征向量
定理3.6: 实对称矩阵的特征值一定是实数。 实对称矩阵的特征值一定是实数。 定理
为其任一特征值， λ 证明： 实对称， 证明：设A实对称， = a + bi为其任一特征值， 对应的特征 向量为 α + iβ ,
于是有 A(α + iβ ) = ( a + bi )(α + iβ ) 展开， 展开， Aα = aα − bβ , Aβ = bα + a β
2 + a n1 x1 x n + a n 2 x 2 x n + a n 3 x 3 x n + L + a nn x n
+ LL
= x1 ( a11 x + a12 x 2 + a13 x 3 + L + a1 n x n )
+ x 2 ( a 21 x1 + a 22 x + a 23 x 3 + L + a 2 n x n )
= ( x1 ,
x2 , L,
a11 a 12 = ( x1 x2 L xn ) a1n
a12 L a1n x1 a22 L a2 n x2 为实数） M （其中 a ij 为实数） L L a2 n L ann xn
个标准正交的特征向量。 注:求正交矩阵 Q 的关键是求矩阵 的n个标准正交的特征向量。 求正交矩阵 的关键是求矩阵A的 个标准正交的特征向量
具体步骤) 实对称矩阵对角化的实现: 具体步骤 实对称矩阵对角化的实现: (具体步骤 1）求出 A 的全部特征值 ） 的全部特征值; 2）对于每一个λi ，求出其对应的线性无关的特征向量 ） 求出其对应的线性无关的特征向量, 从而得出矩阵 A 的 n 个线性无关的 特征向量η 1 , η 2 ,..., η n . 均为单根时， 3) 当 λ i 均为单根时，将

实对称矩阵的特征值和特征向量

实对称矩阵的特征值和特征向量

A (aij )nn A (aij )nn
实对称矩阵的性质:
1.(定理4.12)实对称矩阵的特征值都是实数.
推论 实对称矩阵的特征向量都是实向量.
2.(定理4.13)实对称矩阵的属于不同特征值的特征向量正交.
定理4.4 矩阵的属于不同特征值的特征向量线性无关. 定理2.15 正交向量组必线性无关.
推论 实对称矩阵的属于不同特征值的特征向量线性无关. 3.实对称矩阵的属于ni重特征值的线性无关的特征向量恰有ni个. 4. n 阶实对称矩阵恰有n个线性无关的特征向量, 进而有n个单 位正交的特征向量. 5. 实对称矩阵必可对角化, 即 若A为实对称矩阵 , 则可逆矩阵P, 使P1 AP为对角矩阵 .
7.(定理4.14)若A为实对称矩阵 , 则正交矩阵Q, 使1.求A的所有互异的特征值 1 , 2 ,, m , 其中i的重数为ni , i 1,2,, m. 2.i , 解方程组(i E A) x 0, 求A的属于i的线性无关的特征向量 i1 , i 2 ,, ini . 3.利用Schmidt正交化方法将 i1 , i 2 , , ini 正交化, 再单位化, i 1,2, , m. 设所得的单位正交向量 组为1 , 2 , , n . 4.令Q ( 1 , 2 , , n ), 则Q为正交矩阵, 且 1 1 2 Q 1 AQ 2 m m
§4.3 实对称矩阵的特征值和特征向量 实对称矩阵: 对称的实矩阵. 共轭矩阵: 性质:
(1) A为实对称矩阵 A A AT . (2) AB A B , kB k B (k C ). (3)若A为实对称矩阵, 则 , R n , 有( A , ) ( , A ).

第25节实对称矩阵的特征值与特征向量

第25节实对称矩阵的特征值与特征向量

<定理2> 定理2> n阶矩阵 A与对角矩阵相似的充分必要
λi，矩阵 λi I − A 条件是对于每一个 条件是对于每一个 n重特征根 i
的秩是 n − ni . <推论> 推论> n阶矩阵 A与对角矩阵相似的充分必要 条件是对于每一个 λi ，其线性无关 条件是对于每一个 n重特征根 i 的特征向量个数为 ni .
§4.3 实对称矩阵的 特征值与特征向量
即矩阵 P 的列向量和对角矩阵中特征值的 位置要相互对应. 互对应. 2) 把矩阵 A 先对角化再求 Ak , 是计算矩阵的 幂的方法之一.
4
§4.3 实对称矩阵的 特征值与特征向量
向量内积 正交向量组 正交矩阵 实对称矩阵的特征值与特征向量 小结、 小结、作业、 作业、思考题
i =1
T 和 β 的内积. 的内积. 记作 (α , β ) 或 α β .
即 α T β = (α , β ) = ∑ ai bi
i =1
n
例如： 设 α = ( −1,1, 0, 2)T , β = (2, 0, −1, 3)T . 例如： 则向量 α 和 β 的内积
(4) α T α ≥ 0, 当且仅当 α = 0时，有α T α = 0. 其中 α , β , γ 为 R n中的任意向量. 中的任意向量.
3
4 6 0 例2 设 A = −3 −5 0 −3 −6 1
把特征值 λ1 = λ2 = 1 代入得齐次方程组
−3 x1 − 6 x2 = 0 ( I − A) x = 0, 即 −3 x1 + 6 x2 = 0 −3 x − 6 x = 0 1 2
= ( λ + 1)3

线性代数 实对称矩阵的特征值与特征向量

线性代数 实对称矩阵的特征值与特征向量

实对称矩阵的特征值与特征向量主要内容◼矩阵共轭的概念◼实对称矩阵的性质⚫矩阵共轭的概念定义(),ij m n A a ⨯=并称A 是A 的共轭矩阵.就是对它的每个元素取共轭. 记为对复数域上的矩阵(或向量)取共轭(1)kA k A =(2);A B A B +=+(3) ;AB AB =()(4) ;T T A A =(5);A A =()11.A A −−=(6)若A 可逆, 则(k 为复数)共轭矩阵的性质⚫实对称矩阵的特征值与特征向量定理1实对称矩阵的特征值都是实数, 相应的特征向量可取为实向量.证明：设λ是实对称矩阵A 的任意特征值，且x 是属于λ特征向量, xAx λ=上式两边取共轭,x Ax λ=即.x x A λ=由A 是实对称矩阵，,A A =即得故因此有.x x A λ=上式两边同时转置后、再右乘x , 得T T T T x A x x Ax x xλ===即T T x x x xλλ=T T x x x xλλ==右边左边即,λλ=说明λ是实数.这样当实对称矩阵的特征值都是实数时, 齐次方程组(λE −A )x =0是实系数的方程组, 因此必有实的基础解系, 所以对应的特征向量可取为实向量.而()1212T n n x x x x x x x x ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭012≠=∑=n i ix注意若A是一般的实矩阵而非对称的，则它的特征值与特征向量完全可能是复数.定理2证,A αλα=对第一个等式两边转置并右乘β, 设A 是实对称矩阵，特征值的特征向量必正交.则属于A 的不同设λ, μ是A 的两个不同特征值,α, β是分别属于λ,μ的特征向量，则有A βμβ=T T TA αβλαβ=得由于A =A T , A β=μβ，()0T λμαβ−=由于λ≠μ，代入上式左边并移项得，故αT β=0，即α与β正交. 证毕.定理2指出，实对称矩阵的属于不同特征值的特征向量不仅是线性无关的，是相互正交的.这为寻找实对称矩阵的正交特征向量组提供了方法. 而且。

3.3 实对称矩阵的特征值和特征向量

3.3 实对称矩阵的特征值和特征向量
i1 , i2 , ... , ini (i 1, 2, , m) .
Step3 利用施密特正交化方法，把向量组 i1 , i2 , ... , ini 正交化，得到正交向量组 i1 , i2 , ... , ini (i 1, 2, , m) . 再将所得正交向量组单位化，得到正交向量组 i1 , i2 , ... , ini (i 1, 2, , m) .
8
0
4
6

0 4 1 2

3
6
2
1

A为对称矩阵
A对称矩阵的特征值都是实数.
说明：若A是实数域上的对称矩阵，则
a11 a12 L
E A a21 a22 L
M
M
a1n a2n
M
an1 an2 L ann


1

,
0
2

2


T 2

T 1
1 1
1

1

0

1

1 2
1

1

0


1 2


1 2

1
再单位化得
1

(
1 2
,
1 2
,
0
)T
,
2

(
1 , 6
1, 6
2 )T 6
1
设特征值 3 对应的特征向量为
x = (x1 , x2 , x3)T , 由于实对称矩阵不同特征值对应的特征向量正交, 故
(1 , x) = x1 + x2 + x3 = 0

求实对称矩阵的特征值和特征

求实对称矩阵的特征值和特征

求实对称矩阵的特征值和特征求实对称矩阵的特征值和特征向量求实对称矩阵的特征值和特征向量是线性代数中一个基本的问题。

特征值和特征向量代表了矩阵在空间中的性质，具有重要的应用价值。

本文将系统地介绍求解实对称矩阵的特征值和特征向量的方法。

一、什么是实对称矩阵实对称矩阵指的是元素都为实数的方阵，其转置矩阵等于自己。

即，对于一个n阶实对称矩阵A，有A = A^T。

实对称矩阵在矩阵理论中非常重要，因为它们具有很多优秀性质，例如对称性和正交性等。

二、求实对称矩阵的特征值和特征向量的步骤特征向量代表的是方阵在某一方向上的拉伸效应，而特征值代表的则是这个拉伸效应的大小。

因此，求解实对称矩阵的特征值和特征向量可以从以下几个步骤入手：1. 求出矩阵的特征多项式设A为一个n阶实对称矩阵，则其特征多项式为：f(λ) = det(λI - A)其中λ为待求的特征值，I为n阶单位矩阵。

求出特征多项式后，我们可以通过对其进行分解，从而求出矩阵的特征值。

2. 求解特征值将特征多项式f(λ)分解为：f(λ) = (λ-λ1)(λ-λ2)…(λ-λn)其中λ1, λ2, …, λn为n个特征值，可以通过求解f(λ)=0的方程组得到。

特别地，由于我们在求解过程中使用的是实对称矩阵，因此得到的所有特征值都是实数。

3. 求解特征向量求解特征向量的方法有很多种。

一种比较简单的方法是，对于矩阵A的每一个特征值λi，解出下面的方程组：(A-λiI)xi = 0其中xi为λi对应的特征向量。

由于A是实对称矩阵，因此这个方程组的解可以通过高斯消元或LU分解等方式求解。

4. 将特征向量规范化在求解出特征向量后，为了便于后续的处理，需要将它们进行规范化。

具体地，我们将特征向量xi除以其模长，使得其模长等于1。

即：||xi|| = 1这样做的好处是，保证了特征向量之间的正交性，也就是说它们构成了一个规范正交基。

三、总结求解实对称矩阵的特征值和特征向量是线性代数中一个重要的问题。

第三节 实对称矩阵的特征值与特征向量

第三节 实对称矩阵的特征值与特征向量
[a 3 , b1] b1
2
[a 2 , b1] b1
2
2
b1
b1 +
[a 3 , b2] b2
2
b2
b1= a1
[a 2 , b1 ] b1
2
[a 3 , b1] b1
b1
a 2 在 b1 上的 投影向量
a 3 在b1上的 投影向量
b1
例3
设 a 1 = (1, − 1, − 1) , 求求求向量
α 1 ,α 2 ,L ,α s 两两正交。 两两正交。
正交单位向量组： 两两正交， 正交单位向量组： 求求实向量 α 1 ,α 2 ,L ,α s 两两正交， 标准正交向量组） 且每个向量长度全为1。 （标准正交向量组） 且每个向量长度全为 。
1( i = j ) 即 (α i ,α j ) = 0( i ≠ j )
1 0 1 0 1 0
x1 = −x3 , ∴ x2 = 0.
−1 取 a3 = 0 即可 即可. 1
− 1 令 x3 = 1，得基础解系 ξ = 0 . 1
2. Schmidt正交化、单位化法。 正交化、单位化法。 正交化 定义5： 定义 ： 正交向量组： 正交向量组：求求实向量
定理：正交向量组是线性无关的。 定理：正交向量组是线性无关的。
线性无关。 设a1 , a 2 , L , a r 为正交向量组 , 则a1 ,L, a r 线性无关。 定理 T 证 设λ1 a1 + λ 2 a 2 + L + λ r a r = 0 两端左乘 a 1 : T T T T ⇒ λ1 a 1 a 1 = 0 ⇒ λ1 a1 a1 + λ 2 a1 a 2 + L + λ r a1 a r = 0

实对称矩阵的特征值和特征向量

实对称矩阵的特征值和特征向量
由于对称矩阵A的特征值 i 为实数,所以齐次
线性方程组
(A i E)x 0 是实系数方程组,由 A i E 0知必有实的基础解
系, 从 而 对 应 的 特 征 向 量 可以 取 实 向 量.
P4/12
§3 实对称矩阵的特征值和特征向量
定理3.10 设1, 2是对称矩阵的两个特征值, p1, p2是对应的特征向量. 若1 2, 则p1, p2正交.
二、用正交矩阵将对称矩阵对角化的步骤
1) 作 E A 0 求诸i, i = 1, 2, …, m
2) 解 (iE A)x 0 得基础解系
i1 ,i 2 ,L , r i,nri i r (i E A)
3) 正交化得 i1 ,i 2 ,L i,nri
4) 单位化得 ij
§3 实对称矩阵的特征值和特征向量
一、对称矩阵的性质 二、利用正交矩阵将对称矩阵对角化的方法
1
§3 实对称矩阵的特征值和特征向量
一、对称矩阵的性质
本节所提到的对称矩阵, 除非特别说 明, 均指实对称矩阵．
定理3.9 对称矩阵的特征值为实数.
证明 设复数为对称矩阵A的特征值 ,复向量x为
对应的特征向量,
P8/12
§3 实对称矩阵的特征值和特征向量
将1 = 3代入(EA) x = 0, 得基础解系 a1 = (2, 1, 0)T, a2 = (2, 0, 1)T.
将其正交化：
b1 = a1,
b2
a2

a2 b1
, ,
b1 b1

b1

2, 0,1T

4 2,1, 0T
例3.6 设三阶对称阵A的特征值1 = 0, 2 = 1(二重). 属于1的特征向量为a1 = (0, 1, 1)T, 求A. 解 对应于2 = 1的线性无关的特征向量有两个, 设为a2, a3. 则a2, a3均a1与正交, 即满足

线性代数3.3实对称矩阵的特征值和特征向量

线性代数3.3实对称矩阵的特征值和特征向量

05
实对称矩阵的应用举例
在二次型中的应用
二次型的标准型
通过实对称矩阵的正交变换，可 以将二次型化为标准型，从而简 化问题的求解。
二次型的正定性
利用实对称矩阵的特征值性质， 可以判断二次型的正定性，进而 解决优化问题。
二次曲面分类
实对称矩阵的特征值和特征向量 可用于二次曲面的分类，如椭球 面、双曲面等。
1. 求出矩阵$A$的特征多项式$f(lambda)$。
3. 对于每个特征值$lambda_i$，求出对应的特征向量 $alpha_{i1}, alpha_{i2}, ldots, alpha_{ik}$，其中$k$是 $lambda_i$的重数。
5. 计算$P^{-1}AP = Lambda$，其中$Lambda = text{diag}(lambda_1, lambda_2, ldots, lambda_n)$。
线性代数3.3实对称 矩阵的特征值和特征
向量
目录
• 引言 • 实对称矩阵的应用举例 • 总结与展望
01
引言
课程背景与目标
课程背景
线性代数是数学的一个重要分支，广泛应用于各个学科领域。实对称矩阵作为一 类特殊的矩阵，具有很多重要的性质和应用。特征值和特征向量是矩阵理论中的 核心概念，对于理解矩阵的性质和解决实际问题具有重要意义。
迭代法
通过构造迭代序列来逼近特 征值和特征向量，如幂法、 反幂法等。
特征值与矩阵性质的关系
特征值与矩阵的行列式
矩阵的所有特征值的乘积等于其行列式 的值。
特征值与矩阵的秩
如果矩阵至少有一个非零特征值，则 其秩大于等于1；如果矩阵所有特征
值都为零，则其秩为零。
特征值与矩阵的迹

对称矩阵的特征值和特征向量二-新

对称矩阵的特征值和特征向量二-新

17
跳转到第一页
对 2E A X 0的系数矩阵2E A施行初等行变换, 化为行最简形矩阵
2 E A 0 1 0 1 0 0
2 2 0
2 3 2
0 1 2 0 0 4
1 1 2
0 2 4
3.求正交矩阵P , 使得P 1 AP为对角矩阵
13
跳转到第一页
例1 利用正交矩阵将对称矩阵A 对角化
2 2 0 A 2 1 2 0 2 0
解: 第一步,求矩阵A的特征值
2
E A

2 0
2 0 1 2 2

14
跳转到第一页
2
12
跳转到第一页
三、 利用正交矩阵将实对称矩阵对角化的方法 利用正交矩阵将实对称矩阵对角化， 其具体步骤为：
1.求A的全部特征值1 , 2 , , n
2.由 i E A x 0(i 1, 2 , n), 求出A 的属于i的极大线性无关特征向量组, 并将极大线性无关特征向量组中的特征向量 正交化、单位化.
*证 对实对称矩阵的阶数,采用数学归纳法证明. 当k =1,A为1阶实对称矩阵,A a , 有E 1 , 使得E 1 AE =E T AE = 1 , 其中1 a .定理成立. 假设k =n-1定理成立.
7
当k =n, 设A为n阶实对称矩阵, 第一步 构建一个正交矩阵M , 设1是属于A的特征值1的一个单位特征向量, 使用施密特方法选n-1个非零向量 2 , , n , 使得1 , 2 , , n , 为正交单位向量组, 以1 , 2 , , n , 为列向量构建一个正交矩阵M , M (1 , 2 , , n )

实对称矩阵特征值和特征向量

实对称矩阵特征值和特征向量
2. 内积的性质
(1) ( , ) = ( , ) ;
(2) (k , )= k( , );
(3) ( + , )= (, )+ ( , );
(4) ( , ) 0 , 且( ,)= 0 = 0 .
其中 , , 为 Rn 中的任意列向量，k R .
P13-2
第三章
3.Def.: 设 = (a1 , a2 , … , an)T Rn ，称 ( , ) T
s1
( s (2
, ,
2 2
) )
2
( s (1
, ,
1 1
) )
1
例1 求与向量组
1 = (1, 1, 1)T ,2 = (1, -2, -3)T ,3 = (1, 2, 2)T
等价的一个正交单位向量组.P13-6第三章Fra bibliotek例2 已知
1 1, 1, 1T , 2 1, 1, 3T
求 3 使之与1 , 2 都正交.
2
2
(2 , 1 ) (1, 1)
1
3
3
(3 , 2 ) (2 , 2 )
2
(3 , 1 ) (1, 1)
1
s
s
( s , s1 ) ( s1 , s1 )
s1
( (
s 2
, ,
2 2
) )
2
( s (1
, ,
1 1
) )
1
则 1 , 2 , … , s 是一个正交向量组, 且
{ 1 , 2 , … , s } { 1 , 2 , … , s }
Q-1AQ 成为对角矩阵.
四、实对称矩阵对角化方法
例1 求正交矩阵 P , 使 P-1AP 为对角矩阵.

3.3实对称矩阵的特征值和特征向量(简)

3.3实对称矩阵的特征值和特征向量(简)

1 1 Q AQ n
2

实对称矩阵的特征值的性质 一、 定理3.12 实对称矩阵的特征值都是实数. 则 说明： 若A是实数域上的 对称矩阵，
a 11
E A
a 21 a n1
n
a 12

a1n a2n
| A | | E A |
） 移项得： （| A | 1 | E A | 0 即 2 | E A | 0 | E A | 0
例 4 . 设矩阵 A 与 B 相似 , 1 其中 A 2 3 1 4 3 1 2 2 , B 0 a 0 0 2 0 0 0 , b
T

1 ( T ) T 1 T A T A T ( A ) T
( 2 ) 2( T )
( 1 2 )( T ) 0 1 2
0
T
即

定理3.14 设A是n阶实对称矩阵, 则存在n阶正交
a 22
an2

n2
a nn
nm
( 1 ) 1 ( 2 )
...( m )
1 , 2 , ..., m 都是实数.
定理3.13 实对称矩阵的 对应于不同特征值的 特征向量 是相互正交的. A是实对称矩阵, A的两个特征值 1 , 2 1 2 则 A 1 A 2 证
1 1 1 1
1, 2 ,
1
两两正交.再将它们单位化.
1
2 1 1 1 2 2 2 1 0
6 1 2 2 1 6 32 2 3 2 6

3.3 实对称矩阵的特征值和特征向量

3.3 实对称矩阵的特征值和特征向量

0 2 3
1
2
0
解
E A 2
0
2
2
2
( 1)( 2 )( 5 )
特征值:
3 1 1, 2 2 , 3 5
0
特征向量分别为:
1 , 2 , 3 不同， 1 , 2 , 3 两两正交， 现把它们单位化. 2 1 2 3 3 3 1 1 1 1 3 32 1 1 1 2 2 2 1 3 3 3 3 3 1 2 2 2 1 3 3 3 则 1 , 2 , 3 是单位正交向量组 . 2 x3
1 1 1 , 3 0 0 1
也即 x1 + x2 + x3 = 0
2
x1 x 2 x 3
解得其基础解系为
1 1 0 1 0 1
3
解 设特征值 3 对应的特征向量为
则 x 必与 1 正交， 即 x 1 0 .
T
也即 x1 + x2 + x3 = 0
2
1 1 1 , 3 0 0 1
x1 x x2 x3
令 3） Q ( 1 , 2 , , n ）， 则正交矩阵
Q
1
Q 使得
AQ Λ
例3 求一个三阶实对称矩阵A, 它的特征值为6,3,3,
且对应于6的一个特征向量为1 (1,1,1) .
T
析
实对称矩阵一定可以对角化， 6
则存在可逆矩阵 P， 有 P

4.3 实对称矩阵的特征值特征向量

4.3 实对称矩阵的特征值特征向量

用α i与上式两边内积运算得：α
得 k 1α
i Tα 1+k2α i Tα 2+…+kiα i Tα
i
T(k
1α 1+k2α 2+…+ksα s)=0,
Tα s=(i=1,2,…,s)
i+…+ksα i
又 α iTα j=0 (i≠j) 所以有： kiα iTα i=0 (i=1,2,…,s) 又 α i≠0 得α iTα i>0 因此： ki＝0 （i=1,2,…s）,则 α 1,α 2,…α s线性无关。
可得:
x1T T x2 T Q Q x T n
x1
x2

xn
T x1T x1 x1 x2 T T x2 x1 x 2 x2 T x Tx x n x2 n 1 ∵Q为正交矩阵等价于 QTQ＝I

(3)∣α Tβ |≤‖α ‖‖β ‖
即是
a1b1 a2b2 an bn
a
i 1
n
2 i
bi2
i 1
n
此不等式称柯西－布涅可夫斯基不等式,下面证明此不等式 证明: (1)当α与β线性相关时,有α＝kβ或β＝kα,显然有
∣αTβ|＝‖α‖‖β‖
(2)当α与β线性无关时，对任一实数x, 有: xα+β≠0 因此恒有 ‖xα+β‖>0 即有 ‖xα+β‖2＝（xα+β）T(xα+β) ＝(xαT+βT)( xα+β) ＝(αTα)x2+(αTβ+βTα)x+βTβ ＝(αTα)x2+(2αTβ)x+βTβ>0 所以有 恒成立.

线性代数(第二版)第三节实对称矩阵的特征值和特征向量

线性代数(第二版)第三节实对称矩阵的特征值和特征向量

二、实对称矩阵对角化方法
根据定理 4.14 ，任一实对称矩阵 A 都可以对角
化. 因此，对 A 的任一 ni 重特征值 i，齐次方程组
( iE – A )X = 0 的基础解系中必含有 ni 个线性无关
的向量，它们都是 A 的属于 i 的特征值(
定 定 理 理 44 ..11 00
定 定 理 理 44 ..11 00
+ – –
A … A ) ) + 的 的 r s 秩 秩 =
等 等 n ,于 于知n n这 – –
样的 n n ii ..
特
征
向
量
共
可
得
n 个.
矩 矩
定 定 理 理
4 4 .. 1 1 2 2
实 实 对 对 称 称 矩 矩 阵 阵 的 的 特 特 征 征 值 值 都 都 是 是 实 实 数 数 ..
由 阵 阵 r 1 ( ( + ii rE E 2
+ – –
A … A ) ) + 的 的 r s 秩 秩 =
等 等 n ,于 于 知
这样的 n n – – n n ii ..
特
征
向
量
共
可
得
n 个.
矩 矩
定 定 理 理
4 4 .. 1 1 2 2
实 实 对 对 称 称 矩 矩 阵 阵 的 的 特 特 征 征 值 值 都 都 是 是 实 实 数 数 ..
证 证 法 法 二 二 利 利 用 用 性 性 质 质
设
A 的互不相等的特征值为
1 , … ,
s,
它们的重数依次为
r1 , …
根据
定 定 理 理
4 4 .. 1 1 0 0 及 及 定 定 理 理

实对称矩阵的特征值和特征向量

实对称矩阵的特征值和特征向量

把 1(2,1,0)T 2(2,0,1)T
正交化：
11(2,1, 0)T
2
2
12TT111
(2,0,1)T
4(2,1,0)T(2,4,1)T
5
55
将 1,2,3单位化，得到
21 1 12 2
5(2,1,0)T 5
5(2,4,5)T 15
1 0 1
1 0 1
1 11

2(0,1,1)T 2
32 3 322
(1,0, 0)T 2(0,1,1)T
2
一、 实对称矩阵特征值的性质
定理4.12 实对称矩阵的特征值都是实数。
证明：设 A是n阶实对称矩阵， 0是矩阵 A的在复数 域上的任一特征值，属于 0 的特征向量为
(a 1,a2, ,an)T
则 A0 ( 0 )，于是，两边取复数共轭得到

在不计排列顺序情况下，这种对角化形式是唯一的。
（实对称矩阵A 的标准形！！）
例2 对矩阵 2 2 2 A 2 1 4 2 4 1
求一正交阵 Q , 使 Q1AQ 成对角矩阵。 解： 矩阵 A的特征多项式为
22 2 2 2 0 d eE tA ()2 142 1 3
A 0 A 0 A 0 (4.11)
实对称矩阵特征值的性质
对最后一式取复数转置， 得到
TA0T
定理4.12 实对称矩阵 的特征值都是实数。
两边再右乘 ， 得到 T A 0 T 0 T 0 T ( 0 0 ) T 0
1
Q TA Q Q 1A Q
于是 AQQT

2 2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

证明：设 1 ，2 是实对称矩阵 A 的不同特征值， 1 ，
2分别是属于特征值 1 ，2 的特征向量。
于是 A1 11 (1 0) ， A2 22 (2 0)
对上面第一式两边左乘

T 2
，
ห้องสมุดไป่ตู้
得到
2T
A1

1
T 2
1
而
（4.12）

T 2
A1

第一步 对给定实对称矩阵 A ， 解特征方程，
det(E A) 0
求出 A 的所有特征值, 设 A 的所有不同的特征值为
1, 2 , , m
其中 i 为 ni 重的，n1 n2 nm n ； 第二步 对每个 i , 解齐次线性方程组 (i E A) X 0
的属于 1 的 记 Q1 是以 1
为
第一列任意正交矩阵。把 Q1 分块为 Q1 (1,Q0 )， 其中
Q0 为 n (n 1) 矩阵。
则
Q11 AQ1

Q1T
AQ1


1T
Q0T
A(1,Q0 )


1T
Q0T
A1 A1
注意到
A1 11 1T1 1, A AT
是实对称矩阵，特征值 1 2 1 （二重）对应特征 向量 (2, 1, 2)T , (1 2, 0)T 和 3 8 对应特征向量 (1, 0, 1)T
都正交。 当然，(2, 1, 2)T , (1 2, 0)T 彼此不正交，但可以通过
标准正交化方法 把它们化为标准正交组。
定理4.14 设 A 是阶 n 实对称矩阵, 则 存在正交阵 Q , 使 QT AQ Q1AQ 为对角阵.
求出它的一个基础解系 i1,i2 , ,ini (i 1,2, , m) ； 第三步 利用施米特正交化方法，把 i1,i2 , ,ini
正交化，得到正交向量组 i1, i2 , , ini ，
再把 i1, i2 , , ini 单位化，得到一个 标准正交组 i1, i2, , ini ， (i 1,2, , m) ；
( AT 2
)T
1

( A 2
)T
1

(2 2 )T
1

2
T 2
1
于是有
1
T 2
1

2
T 2
1

(1

2
)
T 2
1

0
这样，由1

2 得到

T 2
1

0，即 1
与
2
是正交的。
【注】实对称矩阵 A 的属于不同特征值的
特征向量相互正交的线性无关组。 例1 在§4.1中里4中，矩阵 3 2 4 A 2 0 2 4 2 3
证明： 对矩阵 A 的阶数 n 用数学归纳法。 当 n 1 时, 定理结论显然成立. 假设对于所有 n 1 阶实对称矩阵来说定理成立。
下面证明对于阶实对称矩阵来说定理成立。
设 1 是 A 的一个特征值，1 是属于特征值 1 的特征
向量,
显然单位向量 1

1
1
1
也是
A
特征向量. 故不妨设1是单位向量，

A 0 A 0 A 0 (4.11)
实对称矩阵特征值的性质
对最后一式取复数转置， 得到
T A 0 T
两边再右乘 ， 得到
定理4.12 实对称矩阵 的特征值都是实数。
T A 0 T 0 T 0 T (0 0 ) T 0
注意：它们都是属于 i 的线性无关特征向量！！
第四步 令 Q (11,12 , ,1n1 , ,m1,m2 , ,mnm ) ，
则 Q 是正交阵, QT AQ Q1AQ 为对角阵， 且
n1 n2
nm
QT AQ Q1AQ diag(1, ,1 ,2 , ,2 , ,m , ,m )
附注： 矩阵 主对角线元素（特征值！）排列顺序
与 Q 中正交列向量组（特征向量！）排列顺序相对应。
及1与Q0 的各列向量都正交， 所以
1T
Q0T
AQ0 AQ0

Q11 AQ1

1
0
0 Q0T AQ0



1
0
0 A1
其中 A1 Q0T AQ0 为 n 1 阶实对称矩阵。 根据归纳法假设， 对 A1 存在 n 1 阶正交矩阵 Q2 使得
Q21A1Q2 Q2T A1Q2 diag(2 , 3 , , n )
令
Q3

1 0
0 Q2

,
Q

Q1Q3
，
则 Q3,Q 均为 n 阶正交矩阵， 并且
Q 1 A Q

Q31 (Q11 A Q1 )Q3


1 0
0 Q2
1


1
0
0 1 A1 0
0 Q2


1 0
0 Q2 1


由于 T 2 0 ，所以有
0 0 0 0 0 这样，0 是实数。由 0 的任意性，实对称矩阵 A 的 特征值都是实数。
附注：进一步地有，实对称矩阵 A 的属于特征值的 特征向量都是实数向量。
定理4.13 实对称矩阵 A 的属于不同
特征值的特征向量相互正交。
1
0
0 A1

1 0
0 Q2



1
0
0 Q2T A1Q2
diag(1, 2 , 3, , n )
这表明 Q 1 AQ 为对角矩阵。 根据数学归纳法原理，
对任意 n 阶实对称矩阵定理结论成立。
二、 实对称矩阵对角化方法
根据定理4.14，任意一个实对称矩阵都可以对角化。 具体步骤如下:
§3.3 实对称矩阵特征值和特征向量
实数域上的对称矩阵简称为实对称矩阵。
这类矩阵的最大优点是特征值都是实数，永远可以对角化。
一、 实对称矩阵特征值的性质
定理4.12 实对称矩阵的特征值都是实数。
证明：设 A 是n 阶实对称矩阵，0是矩阵 A 的在复数 域上的任一特征值，属于 0 的特征向量为
(a1, a2 , , an )T 则 A 0 ( 0) ，于是，两边取复数共轭得到