反比例练习(1)

一、选择题1、在同一坐标系中，一次函数y k x k=-和反比例函数2ky x=的图像大致位置可能是下图中的 （ ）A B C D 2.已知113x y-=，则55x xy y x xy y +---的值为（ ）A. 72- B. 72 C. 27 D. ―27 3、如图1，已知动点P 在函数()102y x x=>的图像上运动，PM x ⊥轴于点,M PN y ⊥轴于点N ，线段,PM PN 分别与直线:1AB y x =-+交于点E F、，则BEAF ⋅的值为A 、4B 、2C 、1D 、12（ ） 4、如图2，有一块直角三角形纸片，两直角边6,8AC cm BC cm ==，现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合。

则CD 等于 （ ）A 、2cmB 、3cmC 、4cmD 、5cm二、填空题（试一试，你一定能成功哟！）1.当x________时，分式x -13有意义；当x_________时，分式242--x x 的值是0. (1)2.计算： 02131312）（）（---+--=_________________. 3.若关于x 的分式方程22233m x x -=--无解，则常数m 的值为 。

(2) 4.如图3，A,B 两点的坐标分别是(-3,0),(0,4),M 是y 轴上一点，沿AM 折叠，AB 刚好落在x 轴上AB ’处，那么直线AM 的解析式是 。

5、已知方程131112-=--+x x k x 有增根，则增根是 。

6、若关于x 的分式方程211=--x m 的解为正数，则m 的取值范围 。

(3) 7. 已知反比例函数y=xm 3-和正比例函数y=（5－m ）x 的图像均在第一、三象限，则m的取值范围是 。

8.写出一个反比例函数，使得这个反比例函数的图像在第一、三象限，这个函数是 。

三、解答题（认真解答,一定要细心哟!）1、先化简代数式()()222222a b a b aba b a b a b a b ⎛⎫+--÷ ⎪-+-+⎝⎭，然后请你自取一组,a b 的值代入求值。

八年级辅导资料六：（反比例函数综合练习一）一．选择题1．面积为4的矩形一边为x ，另一边为y ，则y 与x 的变化规律用图象大致表示为 （ ）2.下列各点中，在函数x y 2-=的图像上的是（ ）A 、（2，1） B 、（-2，1） C 、（2，-2） D 、（1，2） 3.反比例函数y ＝xn 5+图象经过点（2，3），则n 的值是（ ）．A 、－2 B 、－1 C 、0 D 、1 4.若反比例函数y ＝x k（k ≠0）的图象经过点（－1，2），则这个函数的图象一定经过点（ ）．A 、（2，－1）B 、（－21，2） C 、（－2，－1） D 、（21，2）5.已知甲、乙两地相距s （km ），汽车从甲地匀速行驶到乙地，则汽车行驶的时间t （h ）与行驶速度v （km/h ）的函数关系图象大致是（ ）6.一次函数y ＝kx －k ，y 随x 的增大而减小，那么反比例函数y ＝x k满足（ ）． A 、当x ＞0时，y ＞0 B 、在每个象限内，y 随x 的增大而减小C 、图象分布在第一、三象限D 、图象分布在第二、四象限7.已知反比例函数y ＝x m21-的图象上有A （x 1，y 1）、B （x 2，y 2）两点，当x 1＜x 2时，y 1＜y 2，则m 的取值范围是（ ）．A 、m ＜0B 、m ＞0C 、m ＜21D 、m ＞218．如图，一次函数与反比例函数的图象相交于A 、B 两点，则图中使反比例函数的值小于一次函数的值的x 的取值范围是（ ）．A 、x ＜－1B 、x ＞2C 、－1＜x ＜0或x ＞2D 、x ＜－1或0＜x ＜2二．填空题9.某种灯的使用寿命为1000小时，它的可使用天数y 与平均每天使用的小时数x 之间的函数关系式为 .10．已知反比例函数x ky =的图象分布在第二、四象限，则在一次函数b kx y +=中，y 随x 的增大而 （填“增大”或“减小”或“不变”）．11.若反比例函数y ＝x b 3-和一次函数y ＝3x ＋3的图象有两个交点，且有一个交点的纵坐标为6，则b ＝ ．v /(km/h)v /(km/h)v /(km/h)A ．B ．C ． ．12.反比例函数22)12(-+=k x k y 在每个象限内y 随x 的增大而增大，则k= .13. 若m ＜－1，则下列函数：①()0 x x my =;② y =－mx+1; ③ y = mx; ④ y =(m + 1)x 中，y 随x 增大而增大的是___________。

yxO CBA反比例函数练习一、填空1.已知反比例函数ky x=的图象经过（1，－2）．则k = ． 2.写出一个反比例函数的解析式，使它的图象不经过第一、三象限，则该函数是____________．3.已知反比例函数2k y x-=，其图象在第一、第三象限内，则k 。

4. 已知y 与x 成反比例，当x=5时，y=-1，那么当y=3时，x=________；5. 点(231)P m -，在反比例函数1y x =的图象上，则m = ．6. 如果反比例函数22-=m mxy 在每个象限内，y 随x 的增大而增大，则m = ．7. ）若点A(m ，－2)在反比例函数4y x=的图像上，则当函数值y ≥－2时，自变量x 的取值范围是___________.8. 若反比例函数y=(2m-1)22m x- 的图象在第一、三象限,则函数的解析式为___________.9.如图所示,点B 是反比例函数y=k x图象上一点,过点B 分别作x 轴、y •轴的垂线,如果构成的矩形面积是4,那么反比例函数的解析式是 ．10.已知点（x 1，－1），（x 2，2），（x 3，4），在函数ｙ＝kx(k<0)的图象上，则x 1，x 2，x 3从小到大排列为 ．二、选择11.下列函数中，y 是x 反比例函数的是 （ ）A 2x y =B 12y x =+C 12y x=- D 2xy =-12.已知反比例函数的图像经过点（2，-3），则它的图象一定也经过 （ ） A (－2,－3) B (3,－2) C (－1，-6) D （6，1） 13.矩形面积为4，它的长y 与宽x 之间的函数关系用图象大致可表示为14.若反比例函数ky x=的图象经过点(3)m m ，，其中0m ≠，则此反比例函数的图象在（ ）A ．第一、二象限B ．第一、三象限C ．第二、四象限D ．第三、四象限15.已知反比例函数xy 1=，下列结论中不正确的是（ ）A.图象经过点（－1，－1）B.图象在第一、三象限C.当1>x 时，10<<yD.当0<x 时，y 随着x 的增大而增大 16.如图,点P 是x 轴上的一个动点,过点P 作x 轴的垂线PQ 交双曲线于点Q,连结OQ, 当点P 沿x 轴正半方向运动时,Rt △QOP 面积( ) A.逐渐增大 B.逐渐减小 C.保持不变 D.无法确定三、解答题17. 在压力不变的情况下，某物体承受的压强()p Pa 是它的受力面积()2S m 的反比例函数，其图象如图所示。

反比例函数练习一一．选择题（共22小题）1．（2015春•泉州校级期中）下列函数中，y是x的反比例函数的为（）A．y=2x+1 B．C．D．2y=x2．（2015春•兴化市校级期中）函数y=k是反比例函数，则k的值是（）A．﹣1 B．2 C．±2 D．±3．（2015春•衡阳县期中）若y=（m﹣1）x|m|﹣2是反比例函数，则m的值为（）A．m=2 B．m=﹣1 C．m=1 D．m=04．（2014•汕尾校级模拟）若y与x成反比例，x与z成反比例，则y是z的（）A．正比例函数B．反比例函数C．一次函数D．不能确定5．（2014春•常州期末）反比例函数（m为常数）当x＜0时，y随x的增大而增大，则m的取值范围是（）A．m＜0 B．C．D．m≥6．（2015•贺州）已知k1＜0＜k2，则函数y=和y=k2x﹣1的图象大致是（）A．B． C．D．7．（2015•滦平县二模）在同一直角坐标系中，函数y=kx+k与y=（k≠0）的图象大致为（）A．B．C．D．8．（2015•上海模拟）下列函数的图象中，与坐标轴没有公共点的是（）A．B．y=2x+1 C．y=﹣x D．y=﹣x2+19．（2015•宝安区二模）若ab＞0，则函数y=ax+b与函数在同一坐标系中的大致图象可能是（）A．B．C．D．10．（2015•鱼峰区二模）若方程=x+1的解x0满足1＜x0＜2，则k可能是（）A．1 B．2 C．3 D．611．（2012•颍泉区模拟）如图，有反比例函数y=，y=﹣的图象和一个圆，则图中阴影部分的面积是（）第11题图第12题图A．πB．2πC．4πD．条件不足，无法求12．（2010•深圳）如图所示，点P（3a，a）是反比例函数y=（k＞0）与⊙O的一个交点，图中阴影部分的面积为10π，则反比例函数的解析式为（）A．y=B．y=C．y=D．y=13．（2014•随州）关于反比例函数y=的图象，下列说法正确的是（）A．图象经过点（1，1）B．两个分支分布在第二、四象限C．两个分支关于x轴成轴对称D．当x＜0时，y随x的增大而减小14．（2014•昆明）如图是反比例函数y=（k为常数，k≠0）的图象，则一次函数y=kx﹣k 的图象大致是（）A．B．C．D．15．（2014•天水）已知函数y=的图象如图，以下结论：①m＜0；②在每个分支上y随x的增大而增大；③若点A（﹣1，a）、点B（2，b）在图象上，则a＜b；④若点P（x，y）在图象上，则点P1（﹣x，﹣y）也在图象上．其中正确的个数是（）A．4个B．3个C．2个D．1个16．（2014•杭州）函数的自变量x满足≤x≤2时，函数值y满足≤y≤1，则这个函数可以是（）A．y=B．y=C．y=D．y=17．（2014•阜新）反比例函数y=在每个象限内的函数值y随x的增大而增大，则m的取值范围是（）A．m＜0 B．m＞0 C．m＞﹣1 D．m＜﹣118．（2015•凉山州）以正方形ABCD两条对角线的交点O为坐标原点，建立如图所示的平面直角坐标系，双曲线y=经过点D，则正方形ABCD的面积是（）第18题图第19题图A．10 B．11 C．12 D．1319．（2015•眉山）如图，A、B是双曲线y=上的两点，过A点作AC⊥x轴，交OB于D 点，垂足为C．若△ADO的面积为1，D为OB的中点，则k的值为（）A．B．C．3 D．420．（2014•绥化）如图，过点O作直线与双曲线y=（k≠0）交于A、B两点，过点B作BC⊥x轴于点C，作BD⊥y轴于点D．在x轴上分别取点E、F，使点A、E、F在同一条直线上，且AE=AF．设图中矩形ODBC的面积为S1，△EOF的面积为S2，则S1、S2的数量关系是（）第20题图第21题图A．S1=S2B．2S1=S2C．3S1=S2D．4S1=S2 21．（2014•抚顺）如图，在平面直角坐标系中，点A是x轴正半轴上的一个定点，点P是双曲线y=（x＞0）上的一个动点，PB⊥y轴于点B，当点P的横坐标逐渐增大时，四边形OAPB的面积将会（）A．逐渐增大B．不变C．逐渐减小D．先增大后减小22．（2014•重庆）如图，反比例函数y=﹣在第二象限的图象上有两点A、B，它们的横坐标分别为﹣1，﹣3，直线AB与x轴交于点C，则△AOC的面积为（）A．8 B．10 C．12 D．24二．填空题（共4小题）23．（2015•锦江区一模）已知y=（a﹣1）是反比例函数，则a=．24．（2014•江西模拟）已知反比例函数的解析式为y=，则最小整数k=．25．（2013•路北区二模）函数y=，当y≥﹣2时，x的取值范围是（可结合图象求解）．26．（2014•贵阳）若反比例函数的图象在其每个象限内，y随x的增大而增大，则k的值可以是．（写出一个符合条件的值即可）三．解答题（共4小题）27．（2014春•东城区校级期中）已知反比例函数y=﹣（1）说出这个函数的比例系数；（2）求当x=﹣10时函数y的值；（3）求当y=6时自变量x的值．28．（2013春•汉阳区校级期中）已知函数y=（5m﹣3）x2﹣n+（n+m），（1）当m，n为何值时是一次函数？（2）当m，n为何值时，为正比例函数？（3）当m，n为何值时，为反比例函数？29．（2013•德宏州）如图，是反比例函数y=的图象的一支．根据给出的图象回答下列问题：（1）该函数的图象位于哪几个象限？请确定m的取值范围；（2）在这个函数图象的某一支上取点A（x1，y1）、B（x2，y2）．如果y1＜y2，那么x1与x2有怎样的大小关系？30．（2014•苏州）如图，已知函数y=（x＞0）的图象经过点A、B，点A的坐标为（1，2），过点A作AC∥y轴，AC=1（点C位于点A的下方），过点C作CD∥x轴，与函数的图象交于点D，过点B作BE⊥CD，垂足E在线段CD上，连接OC、OD．（1）求△OCD的面积；（2）当BE=AC时，求CE的长．答案：一．选择题（共22小题）1．C 2．D 3．B 4．A 5．C 6．C 7．B 8．A 9．C 10．C 11．B 12．D 13．D 14．B 15．B 16．A 17．D 18．C 19．B20．B 21．C 22．C二．填空题（共4小题）23．-1 24．1 25．x≤-2或x＞0 26．-1（答案不唯一）三．解答题（共4小题）27．28．29．30．。

正反比例练习题（1）一、判断下面两种相关联的量成不成比例，如果成比例，成什么比例。

11、分数的大小一定，它的分子和分母（）比例。

12、全班人数一定，出勤人数和出勤率（）比例。

13、正方体一个面的面积和它的表面积（）比例。

14、在一定的时间里，做一个零件所用的时间和做零件的个数（）比例。

15、圆的半径和面积（）比例。

16、圆锥体的高一定，圆锥的底面半径和它的体积（）比例。

17、4X=8Y，X和Y（）比例。

18、车轮的直径一定，所行的路程和车轮的转数（）比例。

19、圆柱的底面半径一定，圆柱的高和圆柱的体积（）比例。

20、分数值一定，分子和分母（）比例。

21、正方形的边长和面积（）比例。

22、小麦的总重量一定，出粉率和面粉的重量（）比例。

23、三角形的面积一定，底和高（）比例。

24、要行一段路程，已行的和未行的路程（）比例。

25、长方形的长一定，宽和周长（）比例。

26、圆的半径和周长（）比例。

27、总产量一定，单产量和数量（）比例。

28、在同一时间里，杆高和影长（）比例。

29、做一项工程，工作效率和工作时间（）比例。

30、汽车从甲地到乙地，行车时间和速度（）比例。

二、判断题，对的打√，错的打ⅹ。

1、速度和时间成反比例。

（）2、圆的半径一定，圆的面积和兀不成比例（）3、三角形的底一定，它的面积和高不成比例。

（）4、正方形的边长和面积成正比例。

（）5、出盐率一定，盐的重量和海水的重量成正比例。

（）正反比例练习题（2）一、判断。

1、方砖的边长一定，要铺地面积和用砖块数成正比例（）2、用瓷砖铺地，要用的砖数一定，要铺地的平方米数和每平方米用砖的数量成正比例（）3、要铺地的总面积一定，每块方砖的边长与需要的块数成正比例（）4、一个比例的两个内项分别是25和0.4，它的两个外项的积一定是10。

（）5、梯形的面积一定，高和上下底的和成反比例（）6、圆的半径一定，圆的面积和兀不成比例（）7、加工时间一定，加工零件个数和加工每个零件所需的时间成反比例（）8、南京到北京，所行驶的路程和速度不成比例（）9、出盐率一定，盐的重量和海水重量成正比例。

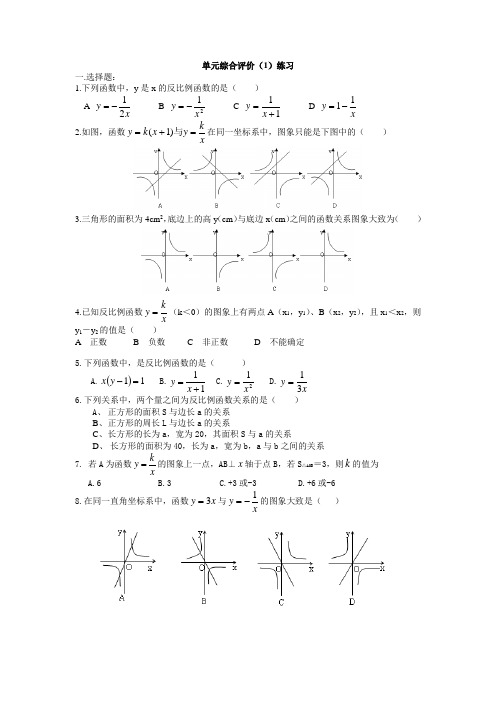
单元综合评价（1）练习一.选择题：1.下列函数中，y 是x 的反比例函数的是（ ） A x y 21-= B 21xy -= C 11+=x y D x y 11-= 2.如图，函数x k y x k y =+=与)1(在同一坐标系中，图象只能是下图中的（ ）3.三角形的面积为4cm 2，底边上的高y （cm ）与底边x （cm ）之间的函数关系图象大致为（ ）4.已知反比例函数xk y =（k ＜0）的图象上有两点A （x 1，y 1）、B （x 2，y 2），且x 1＜x 2，则y 1－y 2的值是（ ）A 正数B 负数C 非正数D 不能确定5.下列函数中，是反比例函数的是（ ）A.()11=-y xB.11+=x yC.21xy = D.x y 31= 6.下列关系中，两个量之间为反比例函数关系的是（ ）A 、 正方形的面积S 与边长a 的关系B 、 正方形的周长L 与边长a 的关系C 、 长方形的长为a ，宽为20，其面积S 与a 的关系D 、 长方形的面积为40，长为a ，宽为b ，a 与b 之间的关系7. 若A 为函数k y x=的图象上一点，AB ⊥x 轴于点B ，若S △AOB ＝3，则k 的值为 A.6 B.3 C.+3或-3D.+6或-6 8.在同一直角坐标系中，函数x y 3=与xy 1-=的图象大致是（ ）9.反比例函数xm y 32+=，当x >0时，y 随x 的增大而增大，那么m 的取值范围是（ ） A.m >23- B.m <23- C.m >23 D.m <23 10.若反比例函数xk y =的图象经过点（-1，2），则这个函数的图象一定经过点（ ） A.（2，-1） B.⎪⎭⎫ ⎝⎛-2,21 C.（-2，-1） D.⎪⎭⎫ ⎝⎛2,21 11.设()()2211,,,y x B y x A 是反比例函数x y 2-=图象上的两点，若1x <2x <0则1y 与2y 之间的关系是( )A.2y <1y <0B.1y <2y <0C.2y >1y >0D.1y >2y >012.当x <0时，反比例函数xy 31-= （ ） A.图象在第二象限内，y 随x 的增大而减小；B.图象在第二象限内，y 随x 的增大而增大；C.图象在第三象限内，y 随x 的增大而减小；D.图象在第三象限内，y 随x 的增大而增大.13.函数k kx y +=与xk y =在同一坐标系中的图象如图所示，则k 的取值范围为（ ） A.k >0 B.k <0 C.-1<k <0 D.k <-1第13题 第14题14.某乡的粮食总产量为a 吨，设该乡平均每人占有粮食为y 吨，人口数为x人，y 与x 的函数关系的图象为（ ）.15.如果y 是z 的反比例函数，z 是x 的反比例函数，那么y 是x 的（ ）A .一次函数B .反比例函数C .正比例函数D .反比例或正比例函数二.填空题：1.在函数xk y =中，当2=x 时，3-=y .则此函数的解析式为 . 2． 若关于x 、y 的函数42-=k x y 是反比例函数，则=k .3．双曲线xy 8=与直线x y 2=的交点坐标为 . 4.若反比例函数3y x=的图象上有两点1(2 )A y ，，2(3 )B y ，，则1y ______2y （填“>”或“=”或“<”）.5.如图（7），P 是反比例函数图象在第二象限上的一点，且矩形PEOF 的面积为8，则反比例函数的表达式是＿＿＿＿＿＿＿＿＿＿.（7） （8）6.如图（8）是一次函数1y kx b =+和反比例函数2m y x =的图象，•观察图象写出12yy >时，x 的取值范围是＿＿＿＿＿＿＿＿＿＿＿.7.函数y =xk (k ＞0)的图象上两点A (x 1, y 1)和B (x 2, y 2),且x 1＞x 2＞0，分别过A 、B 向x 轴作AA 1⊥x 轴于A 1，BB 1⊥x 轴于B 1，则O AA S 1∆_________O BB S 1∆ (填“＞”“=”或“＜”)，若O AA S 1∆=2，则函数解析式为_________.8.设有反比例函数xk y 1+=，（x 1，y 1）、（x 2，y 2）为其图象上两点，若x 1＜0＜x 2，y 1＞y 2，则k 的取值范围 .三.解答题：1.如图，正比例函数y ＝kx （k ＞0）与反比例函数x k y =的图象相交于Ａ、Ｃ两点，过Ａ作x 轴的垂线交x 轴于Ｂ，连接BC ，求△ABC 的面积.2.如图，一次函数的图象与x 轴、y 轴分别交于A 、B 两点，与反比例函数的图象交于C 、D 两点，如果A 点的坐标为(2，0)，点C 、D 分别在第一、三象限，且OA =OB =AC =BD ，试求一次函数和反比例函数的解析式.Ox y A C B3.如图，正方形OABC 的面积为4，点Ｏ为坐标原点，点Ｂ在函数xk y =(k ＞0，x ＞0)的图象上，点Ｐ（m ，n ）是函数x k y =(k ＞0，x ＞0)的图象上任意一点，过点Ｐ分别作x 轴、y 轴的垂线，垂足分别为Ｅ、Ｆ，并设矩形OEPF 和正方形OABC示：考虑点Ｐ在点Ｂ的左侧或右侧两种情况） （1）求Ｂ点坐标和k 的值；（2）当Ｓ＝1.5时，求点Ｐ的坐标； （3）写出Ｓ关于m 的函数关系式.。

六年级反比例的练习题1. 某书店每本书的售价与购买数量成反比例关系，购买5本该书时需要25元，请问购买8本该书需要多少元？解析：购买5本书需要25元，即书的售价与购买数量的乘积等于常数，设该常数为k，则有 5 × 25 = k。

要求购买8本书的价格，即 8 ×x = k，其中x为该书的售价。

解方程可得 x = 5 × 25 ÷ 8 = 15.625。

所以购买8本该书需要15.625元。

2. 一辆汽车以60千米的时速行驶，需要6小时到达目的地。

请问以80千米的时速行驶，需要多少小时能够到达同样的目的地？解析：行驶的路程与速度成反比例关系，即路程与时间的乘积为常数。

假设常数为k，则有 60 × 6 = k。

要求以80千米的时速行驶的时间，即 80 × x = k，其中x为所需时间。

解方程可得 x = 60 × 6 ÷ 80 = 4.5。

所以以80千米的时速行驶，需要4.5小时能够到达同样的目的地。

3. 一个邮递员每天送快递，每天送100个快递需要2个小时。

请问如果他每天送150个快递，需要多少小时？解析：送快递的数量与所需时间成反比例关系，即数量与时间的乘积为常数。

设常数为k，则有 100 × 2 = k。

要求送150个快递所需时间，即 150 × x = k，其中x为所需时间。

解方程可得 x = 100 × 2 ÷ 150 =1.3333。

所以送150个快递需要1.3333小时。

4. 一辆汽车行驶了240千米所用的时间为4小时，请问行驶480千米需要多少小时？解析：行驶的路程与时间成反比例关系，即路程与时间的乘积为常数。

假设常数为k，则有 240 × 4 = k。

要求行驶480千米所需时间，即480 × x = k，其中x为所需时间。

解方程可得 x = 240 × 4 ÷ 480 = 2。

反比例函数练习题（1）一、填空题：1、函数9x y =-和函数2y x =的图象有 个交点；2、反比例函数k y x =的图象经过（－32，5）点、（,3a -）及（10,b ）点，则k ＝ ，a ＝ ，b ＝ ；3、若反比例函数1232)12(---=k k xk y 的图象经过二、四象限，则k = _______5、已知正比例函数y kx =与反比例函数3y x=的图象都过A （m ，1），则m ＝ ，正比例函数与反比例函数的解析式分别是 、 ； 6、设有反比例函数，、为其图象上的两点，若时，，则的取值范围是___________7、如图是反比例函数ky x=的图象，则k 与0的大小关系是k 0. 8、函数2y x =-的图象，在每一个象限内，y 随x 的增大而 ； 9、反比例函数()0ky k x=>在第一象限内的图象如图，点M 是图象上一点， MP 垂直x 轴于点P ，如果△MOP 的面积为1，那么k 的值是 ；10．已知点A （72m -,5m -）在第二象限，且m 为整数，则过A 的反比例函数的关系式为___________.11．正比例函数(2)y m x =-的图象与反比例函数1m y x+=的图象的一个交点是A ，点A 的横坐标是2，则此反比例函数的关系式为_________________. 12．已知反比例函数52)32(--=kx k y 的图象在所在的每一个象限内y 随着x 的增大而增大，则=k．13．请写出一个当自变量x <0时，函数值y 随x 的增大而增大的反比例函数 二、选择题14、下列函数中，是反比例函数的是（ ）A. y x =-2B. y x =-12C. y x=-11D. y x =1215、 函数ykx =-与y k x=（k ≠0）的图象的交点个数是（ ） A. 0 B. 1 C. 2 D. 不确定 16、在同一直角坐标系中，x y 2-=与)0(<=k xky 的交点个数是 A ．3 B ．2 C ．1 D ．017．向高为H 的圆柱形水杯中注水，已知水杯底面半径为2，那么注水量y 与水深x 的函数图象是( )19．已知函数xky =（K <0）经过P 1(1x ，1y )，P 2(2x ，2y )，如果y 2<y 1<0，那么 ( ) A ．012<<x xB ．021<<x x C ．012>>x x D ．021>>x x20．已知点P 1(a ，b )在函数xky =(k ≠0)的图象上，那么不在此图象上的点是 A ．P1(b ，a)B ．P2(－a ，－b)C ．P ３(a 1，－b1)21．如图所示的图象的函数关系式只能是（ ） A.y x = B .1y x=C . 2y x =22．在函数xky =(k ＞0)的图象上有三点A 1(x 1, 12223(x 3, y 3 ),已知x 1＜x 2＜0＜x 3,则下列各式中,正确的是 ( ) A.y 1＜y 2＜y 3 B.y 3＜y 2＜y 1 C. y 2＜ y 1＜y 3 D.y 3＜y 1＜y 224、若y 与－3x 成反比例，x 与4z成正比例，则y 是z 的（）A 、 正比例函数B 、 反比例函数C 、 一次函数D 、 不能确定25、若反比例函数22)12(--=mx m y 的图象在第二、四象限，则m 的值是（ ）A 、 －1或1B 、小于12的任意实数 C 、 －1 Ｄ、 不能确定26、如果矩形的面积为6cm 2，那么它的长y cm 与宽x cm 之间的函数关系用图象表示大致（ ）D27、在同一直角坐标平面内，如果直线1y xk =2k x的关系一定是（）A 、1k <0， 2k >0 B 、1k >0， 2k <0 C 、1k 、2k 同号D 、1k 、2k 异号28、已知反比例函数()0k y k x=<的图象上有两点A(1x ，1y )，B(2x ，2y )，且21x x <，则21y y -的值是（ ）A 、正数 B 、 负数 C 、 非正数 D 、 不能确定 29、在同一坐标系中，函数ky =和3y kx =+的图象大致是 （ ）1、如图，Rt △ABO 的顶点A 是双曲线ky x=与直线()1y x k =--+在第二象限的交点，AB ⊥x轴于B 且S △ABO=32 （1）求这两个函数的解析式 （2）求直线与双曲线的两个交点A ，C 的坐标和△AOC 的面积。

反比例函数练习（1）一、判断题 1．当x 与y 乘积一定时，y 就是x 的反比例函数，x 也是y 的反比例函数（ ） 2．如果一个函数不是正比例函数，就是反比例函数 （ ）3．y 与2x 成反比例时y 与x 并不成反比例（ ） 二．填空题4．已知三角形的面积是定值S ，则三角形的高h 与底a 的函数关系式是h =__________,这时h 是a 的__________；5．如果y 与x 成反比例，z 与y 成正比例，则z 与x 成____ ___； 6．如果函数222-+=k kkx y 是反比例函数，那么k =________，此函数的解析式是____ ____；7． 有一面积为60的梯形，其上底长是下底长的31，若下底长为x ，高为y ，则y与x 的函数关系是______________ 三、选择题： 8．如果函数12-=m x y 为反比例函数，则m 的值是 （ ）A1- B 0 C 21D 19．李老师骑自行车上班，最初以某一速度匀速行进，中途由于自行车故障，停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速行进，结果准时到校。

在课堂上，李老师请学生画出自行车行进路程s 千米与行进时间t 的函数图像的示意图，同学们画出的示意图如下，你认为正确的是（ ）10、下列函数中，y 是x 反比例函数的是（ ）（A ） 12+=x y （B ）22x y = （C ）x y 51=（D ）x y =2四．辨析题（1）兄弟二人分吃一碗饺子，每人吃饺子的个数如下表：①写出兄吃饺子数y 与弟吃饺子数x 之间的函数关系式（不要求写xy 的取值范围）.②虽然当弟吃的饺子个数增多时，兄吃的饺子数(y )在减少，但y 与x 是成反例吗？（2）水池中有水若干吨，若单开一个出水口，水流速v 与全池水放光所用时t 如下表：①写出放光池中水用时t(小时)与放水速度v(吨/小时)之间的函数关系.②这是一个反比例函数吗？ ③与（1）的结论相比，可见并非反比例函数有可能“函数值随自变量增大而减小”，反之，所有的反比例函数都是“函数值随自变量的增大而减小吗？这个问题，你可以提前探索、尝试，也可以预习下一课时”反比例函数的图象和性质，也可以等到下一节课我们共同解决.五．已知□ABCD 中，AB = 4，AD = 2，E 是AB 边上的一动点，设AE=x ，DE 延长线交CB 的延长线于F ，设CF =y ，求y 与x 之间的函数关系。

反比例专项练习30题（有答案）1．下表中，x与y成反比例，那么☆表示的数是（）x 5 ☆y 120 150A．3B．4C．6.252．以下四幅图象中，表示成反比例的是（）A．B．C．D．3．a与b成反比例的条件是（）A．a÷b=c（c一定）B．c×a=b（c一定）C．a×b=c（c一定）D．a×c=b（b一定）4．成反比例的两种量在变化过程中，一种量扩大，另一种量（）A．扩大B．缩小C．不变5．下列关系式中x、y 都不为0，则x与y不是成反比例关系的是（）A．x=B．y=3÷x C．x=×πD．x=6．表示a和b这两种量成反比例的关系式是（）A．a+b=8 B．a﹣b=8 C．a×b=8 D．a÷b=8 7．下列各式中，a和b成反比例的是（）A．9a=6b B．a×=1 C．a×8=8．长方形的面积一定，长和宽（）A．成正比例B．成反比例C．不成比例9．表示a与b成反比例关系式的式子是（）A．a+b=8 B．a﹣b=8 C．a=5b D．a b=710．已知=，那么A和B（）A．成反比例B．成正比例C．不成比例D．无法确定11．如果5a=3b，那么a和b（）关系．A．成正比例B．成反比例C．不成比例12．4X﹣5Y=0，（X、Y不等于0），X和Y（）A．成正比例B．成反比例C．不成比例13．a与b（）A．成正比例B．成反比例C．不成比例14．教室里的面积一定，教室里的人数和每人占地的面积（）A．成反比例B．成正比例C．不成比例D．无法确定是否成比例15．关于正反比例的判断，以下说法正确的是（）A．三角形的面积一定，它的底和高成反比例B．一个人的身高与体重成反比例C．圆的半径和面积成正比例16．已知a与b成反比例，b与c成反比例，那么a与c的关系是（）A．正比例B．反比例C．不成比例D．无法确定17．x和y成反比例关系的是（）A．x+y=100 B．x：5=3：y C．20x=5y18．如果=，那么x和y（）A．成正比例B．成反比例C．不成比例19．A÷C=B，当A一定时，B与C成反比例．_________．20．六年级同学排队做广播操，每行人数和排成的行数成_________比例；出油率一定，花生油的质量和花生的质量，成_________比例；3x=y，x和y成_________比例；实际距离一定，图上距离和比例尺成_________比例．21．如果AB=K+2（K一定），那么A和B成反比例．_________．22．一项工程的总量一定，已经完成的工作量与剩下的工作量成反比例．_________．23．x与y成反比例关系，根据条件完成下表．x 15 20 30 40y 400 240 200 10024．用36米长的篱笆围一个长方形的鸡舍，围成的长和宽成反比例．_________．25．假如ab+13=37，那么a与b成反比例．_________．26．直角三角形的两个锐角大小成反比例．_________．27．圆周长计算公式为C=2πr，当C一定，π和r 成反比例．_________．28．已知x和y是成反比例关系，根据表中的条件填写下表．x 2_________40_________y 5_________0.1_________29．运一批货物，每天运的吨数和需要的天数如下表：每天运的吨数300 150 100 75 60 50需要的天数 1 2 3 4 5 6（1）写出几组这两组量中的对应的两个数的积，并比较积的大小．（2）说明这个积表示什么？（3）表中相关联的两个量成反比例吗？为什么？30．观察下面的两个表，然后回答问题．（1）上表中各有哪两种相关联的量？（2）在各表的两种相关的量中，一种量是怎样随着另一种量的变化而变化的？它们的变化规律各有什么特征？（3）哪个表中的两种量成正比例关系？哪个表中的两种量成反比例关系？参考答案：1．150☆=5×120，50☆=600，☆=4；故选：B．2．A、图象表示的两个量的比值一定，不属于反比例的意义；B、图象分成两部分，一部分是一个量随另一个量的增加而增加，而另一部分是一个量随另一个量的增加而减少，不属于反比例的意义，C、图象中两个量对应的数的乘积是600，是一定的，符合反比例的意义，D、两个量对应的数的乘积是不一定的，属于不符合反比例的意义，故选：C．3．两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做反比例关系．只有a×b=（定量），a与b才成反比例．只有C选项符合反比例的意义．故选：C4．成反比例的两种量在变化过程中，一种量扩大，另一种量缩小，变化方向应该相反；故选：B．5．A、因为x=，则有xy=4（一定），所以x和y成反比例；B、因为y=3÷x，则有xy=3（一定），所以x和y成反比例；C、因为x=×π，则有xy=π（一定），所以x和y成反比例；D、因为x=，则有=4（一定），所以x和y成正比例；故选：D6．A，因为a=b=8（一定），是a、b的和一定，所以a、b不成比例；B，a﹣b=8（一定），是a、b的差一定，所以a、b不成比例；C，a×b=8（一定），是a、b的乘积一定，所以a、b成反比例；D，a÷b=8（一定），是a、b的比值一定，所以a、b成正比例；故选：C7．选项A，因为9a=6b，则=，无法确定a和b的乘积是否一定，则不成反比例；选项B，因为a×=1，则ab=3（值一定），所以a和b成反比例；选项C，因为a×8=，则=40，无法确定a和b的乘积是否一定，则不成反比例；故答案为：B8．根据长方形的面积公式，长×宽=长方形的面积（一定），符合反比例的意义xy=k（一定），所以长方形的面积一定，长和宽成反比例．故选B9．选项A，由a+b=8，不能判定a和b成什么比例；选项B，由a﹣b=8，不能判定a和b成什么比例；选项C，由a=5b可得=5（定值），所以a和b成正比例；选项D，因为ab=7（定值），则a和b成反比例；故答案为：D10．=，AB=3×5=15（一定），所以A与B成反比例，故选：A11．5a=3b，那么：a：b=；是个定值，一个因数一定，积和另一个因数成正比例．故答案选：A12．因为4X﹣5Y=0，则4x=5y，x：y=5：4（一定），所以x和y成正比例；故选：A13．，﹣=0，=，ab=3（一定），故选：B14．人数×每人占地的面积=教室里的面积，教室里的面积一定，也就是这两种量的乘积一定，所以成反比例；故选A．15．A、因为三角形的面积=底×高÷2，所以底×高=三角形的面积×2（一定），即底和高的乘积一定，符合反比例的意义，所以三角形的面积一定，它的底和高成反比例；B、因为一个人的身高和体重的乘积不是一定的，比值也不是一定的，所以一个人的身高与体重不成比例；C、因为圆的面积=π×半径的平方，即圆的面积÷半径的平方=π（一定），所以圆的面积与半径的平方成正比例，但圆的面积与半径不成比例；故选：A16．因为a和b成反比例，所以ab=k1（一定），则b=，因为，b和c成反比例，所以bc=k2（一定），把b=，代入式子bc=k2（一定），得出：a：c=（一定），是a和c对应的比值一定，所以a和c成正比例；故选：A17．A、x+y=100，是和一定，既不符合正比例的意义也不符合反比例的意义，所以x和y不成反比例；B、x：5=3：y，xy=15（一定），符合反比例的意义，所以x和y成反比例；C、20x=5y，x：y=0.25（一定），符合正比例的意义，不符合反比例的意义，所以x和y成正比例，不成反比例；故选：B18．因为=；所以4x=4.5y；x：y=4.5：4；x：y=1.125（一定）；可以看出，x和y是两个相关联的变化的量，它们相对应的比值是1.125，是一定的，所以x和y成正比例关系．故选：A19．因为：A÷C=B，所以：B×C=A（一定）；可以看出，B和C是两种相关联的量，B随C的变化而变化，A是一定的，也就是B与C相对应数的乘积一定，所以B与C成反比例关系．故答案为：正确20．六年级同学排队做广播操，每行人数和排成的行数成反比例；出油率一定，花生油的质量和花生的质量，成正比例；3x=y，x和y成正比例；实际距离一定，图上距离和比例尺成正比例．21．如果AB=K+2（K一定），k一定，那么k+2也是一定的，可以看出，A和B是两种相关联的量，A随B的变化而变化．k+2是一定的，也就是A与B相对应数的乘积一定，符合反比例的意义．所以A与B成反比例关系．故答案为：正确．22．一项工程的总量一定，已经完成的工作量与剩下的工作量成反比例．×．23．15×400=6000，6000÷20=300，6000÷240=25，6000÷40=150，6000÷100=60；故答案为：x 15 20 25 30 40 60y 400 300 240 200 150 10024．因为长方形的长+宽=篱笆的总长度×（一定），是长和宽对应的和一定，不是乘积一定，所以围成的长和宽不成比例．故判断为：错误25．因为ab+13=37，则：ab=24（一定），所以a和b成反比例；故答案为：正确．26．直角三角形的两个锐角大小成反比例．×．27．圆周长计算公式C=2πr中，2π是一定的，当C一定，那么r也是一定的，这样在这个关系式中，所有的量都是一定的，所以当C一定，π和r不成任何比例，所以“当C一定，π和r 成反比例”是错误的．28．因为2×5=10，所以10÷=50，10÷0.1=100，10÷40=0.25，10÷=12，故答案为：50，100，0.25，1229．（1）300×1=300，150×2=300，100×3=300，75×4=300，60×5=300，50×6=300，因为积都是300，所以积相等；（2）每天运的吨数×需要的天数=这批货物的总吨数，所以这个积表示这批货物的总吨数；（3）因为表中相对应的两个数的乘积一定，符合反比例的意义，所以成反比例关系30.（1）根据题干分析可得，上表左边两种相关联的量是路程与时间；左边表格中两种相关联的量是速度与时间；据此即可解答；（2）左边表格中：路程随着时间的变化而变化，右边表格中：时间随着速度的变化而变化；（3）左边表格：20÷1=40÷2=60÷3=20，所以速度一定时，路程与速度成正比例；右边表格：60×1=30×2=20×3=60，所以路程一定时，速度与时间成反比例。