8角度调制习题及答案0
- 格式:doc
- 大小:377.50 KB
- 文档页数:8

一.填空 1.对DSB —SC 信号,当采用插入导频法进行载波同步时,插入的条件是( )。
2.残留边带滤波器的传输特性H (w )应该是( )。
3.AM 系统在( )情况下会出现门限效应。
4.什么是门限效应?AM 信号瞎用包络检波法为什么会产生门限效应? 5.在残留边带调制系统中,为了不失真地恢复信号,其传输函数H (w )应满足( )。
6.在解调过程中,( )的解调方式会产生门限效应,产生门限效应的原因是( )。
7.当调频指数满足( )时称为窄带调频。
8.相干解调器由( )和( )组成,信号与噪声可以分开处理,故没有门限效应。
9.门限效应是由包络检波器的( )作用所引起的。
10.什么是频分复用? 填空答案:1.载频处、正交插入2.在载频两边具有互补对称特性 3.在包络检波时且小信噪比时4小信噪比时,解调输出信号无法与噪声分开,有用信号“淹没”在噪声中,这时候输出信噪比不是按比例地随着输入信噪比下降,而是急剧恶化。
这种现象称为门限效应。
5.H ()()c c H H ωωωωωω++-=≤常数, 6.非相干解调 非线性应用 7.1f m <<8.相乘器 低通滤波器 9.非线性解调 10.利用调制技术将各路信息信号调制到不同载频上,使各路信号的频谱搬移到各自的子通道内,合成后送入信道传输。
在接收端,采用一系列不同中心频率的带通滤波器分离出各路已调信号,解调后恢复各路相应的基带信号。
1.常见的幅度调制方式:(调幅<AM>)、(双边带<DSB>)、(单边带<SSB>)、(残留边带<VSB>)。
2.如果把语音信号0.3-3.4kHZ 直接通过天线发射,那么天线的长度为(22km ) 3.基带信号控制高频载波的过程叫(调制)4.要保证Ao+f (t )总是正的,对于所有的t ,必须要求( )5.( )越大,说明这种调制制度的抗干扰性能越好。




第七章 思考题与习题7.1 什么是角度调制?解:用调制信号控制高频载波的频率(相位),使其随调制信号的变化规律线性变化的过程即为角度调制。
7.2 调频波和调相波有哪些共同点和不同点,它们有何联系?解:调频波和调相波的共同点调频波瞬时频率和调相波瞬时相位都随调制信号线性变化,体现在m f MF ∆=;调频波和调相波的不同点在:调频波m f m f k V Ω∆=与调制信号频率F 无关,但f m f k V M Ω=Ω与调制信号频率F 成反比;调相波p p m M k V Ω=与调制信号频率F 无关,但m f m f k V Ω∆=Ω与调制信号频率F 成正比;它们的联系在于()()d t t dtϕω=,从而具有m f MF ∆=关系成立。
7.3 调角波和调幅波的主要区别是什么?解:调角波是载波信号的频率(相位)随调制信号的变化规律线性变化,振幅不变,为等福波;调幅波是载波信号的振幅随调制信号的变化规律线性变化,频率不变,即高频信号的变化规律恒定。
7.4 调频波的频谱宽度在理论上是无限宽,在传送和放大调频波时,工程上如何确定设备的频谱宽度? 解:工程上确定设备的频谱宽度是依据2m BW f =∆确定7.5为什么调幅波调制度 M a 不能大于1,而调角波调制度可以大于1?解:调幅波调制度 M a 不能大于,大于1将产生过调制失真,包络不再反映调制信号的变化规律;调角波调制度可以大于1,因为f fcmmV M k V Ω=。
7.6 有一余弦电压信号00()cos[]m t V t υωθ=+。
其中0ω和0θ均为常数,求其瞬时角频率和瞬时相位解: 瞬时相位 00()t t θωθ=+ 瞬时角频率0()()/t d t dt ωθω==7.7 有一已调波电压1()cos()m c t V A t t υωω=+,试求它的()t ϕ∆、()t ω∆的表达式。
如果它是调频波或调相波,它们相应的调制电压各为什么?解:()t ϕ∆=21A t ω,()()12d t t A t dtϕωω∆∆==若为调频波,则由于瞬时频率()t ω∆变化与调制信号成正比,即()t ω∆=()f k u t Ω=12A t ω,所以调制电压()u t Ω=1fk 12A t ω 若为调相波,则由于瞬时相位变化()t ϕ∆与调制信号成正比,即 ()t ϕ∆=p k u Ω(t )所以调制电压()u t Ω=1pk 21A t ω 由此题可见,一个角度调制波可以是调频波也可以是调相波,关键是看已调波中瞬时相位的表达式与调制信号:与调制信号成正比为调相波,与调制信号的积分成正比(即瞬时频率变化与调制信号成正比)为调频波。


第6章角度调制与解调电路6.1已知调制信号38cos(2π10)V u t Ω=⨯,载波输出电压6o ()5cos(2π10)V u t t =⨯,3f 2π10rad/s V k =⨯ ,试求调频信号的调频指数f m 、最大频偏m f ∆和有效频谱带宽BW ,写出调频信号表示式[解]3m 3m 2π108810Hz2π2πf k U f Ω⨯⨯∆===⨯3m33632π1088rad2π102(1)2(81)1018kHz ()5cos(2π108sin 2π10)(V)f f o k U m BW m F u t t t Ω⨯⨯===Ω⨯=+=+⨯==⨯+⨯6.2已知调频信号72()3cos[2π105sin(2π10)]V o u t t t =⨯+⨯,3f 10πrad/s V k = ,试:(1)求该调频信号的最大相位偏移f m 、最大频偏m f ∆和有效频谱带宽BW ;(2)写出调制信号和载波输出电压表示式。
[解](1)5f m =5100500Hz=2(+1)2(51)1001200Hzm f f m F BW m F ∆==⨯==+⨯=(2)因为mf f k U m Ω=Ω,所以352π1001V π10f m fm U k ΩΩ⨯⨯===⨯,故27()cos 2π10(V)()3cos 2π10(V)O u t t u t t Ω=⨯=⨯6.3已知载波信号m c ()cos()o u t U t ω=,调制信号()u t Ω为周期性方波,如图P6.3所示,试画出调频信号、瞬时角频率偏移()t ω∆和瞬时相位偏移()t ϕ∆的波形。
[解]FM ()u t 、()t ω∆和()t ϕ∆波形如图P6.3(s)所示。
6.4调频信号的最大频偏为75kHz ,当调制信号频率分别为100Hz 和15kHz 时,求调频信号的fm 和BW 。
[解]当100Hz F =时,37510750100m f f m F ∆⨯===2(1)2(7501)100Hz 150kHzf BW m F =+=+⨯=当15kHz F =时,33751051510m f f m F ∆⨯===⨯32(51)1510Hz 180kHzBW =+⨯⨯=6.5已知调制信号3()6cos(4π10)V u t t Ω=⨯、载波输出电压8()2cos(2π10)V o u t t =⨯,p 2rad /V k =。



第5章 角度调制与解调思 考 题8.1 已知载波f c =100MH Z ,载波电压振幅U cm =5V ,调制信号u Ω(t )= ( cos2π×103t +2cos2π×500t )V 。
试写出下述条件调频波的数学表达式:(1) 频灵敏度K f =1kH Z /V 。
(2)频偏△f m =20kH Z 。
解:(1)⎥⎦⎤⎢⎣⎡+=⎰Ωtt fc cm t FM dt u k t U u 0)()(cos ω⎥⎦⎤⎢⎣⎡⨯⋅⨯+⨯⋅⨯+⨯⨯⨯=⎥⎦⎤⎢⎣⎡⨯+⨯+=⎰⎰t t t tdt ktdt kt f t t ffc 5002sin 50022000102sin 10210001010014.32cos 55002cos 2102cos 2cos 53363πππππππ()t t t 5002sin 64.0102sin 16.01028.6cos 538⨯+⨯+⨯=ππ(2)因为max )(2t u k f f m m Ω=∆=∆πω 所以V KHz t u f k m f /8.622102014.32)(23max=⨯⨯⨯=∆=Ωπ所以()tt t dt t u k t U t u tfc cm FM 5002sin 40102sin 101028.6cos 5)(cos )(380⨯+⨯+⨯=⎥⎦⎤⎢⎣⎡+=⎰Ωππω8.2 载波振荡频率f c =25MH Z ,振幅U cm =4V ;调制信号为单频余弦波,频率为F =400H Z ;最大频偏△f m =10kH Z 。
(1) 分别写出调频波和调相波的数学表达式。
(2) 若调制频率变为2 kH Z ,其他参数均不变,再分别写出调频波和调相波的数学表达式。
解:(1)因为F m f f m ⋅=∆,所以rad KHzKHzFfm mf 254.010==∆=所以:()()()tt Ft t f t m t U t u c f c cm FM 38105.2sin 251057.1cos 42sin 252cos 4sin cos )(⨯+⨯=+=Ω+=ππω()()tt t m t U t u P c cm PM 38105.2sin 251057.1cos 4cos cos )(⨯+⨯=Ω+=ω(2)如果F=2KHz ,则radKHzKHz m m P f 5210===近而可写出调频波和调相波的数学表达式:()()()tt Ft t f t m t U t u c f c cm FM 38105.2sin 51057.1cos 42sin 52cos 4sin cos )(⨯+⨯=+=Ω+=ππω()()tt t m t U t u P c cm PM 38105.2sin 51057.1cos 4cos cos )(⨯+⨯=Ω+=ω8.3若调频波的中心频率f c =100MH Z ,最大频偏△f m =75kH Z ,求最高调制频率F max 为下列数值时的m f 和带宽:(1) F max =400 H Z ;(2) F max =3kH Z ;(3) F max =15kH Z 。
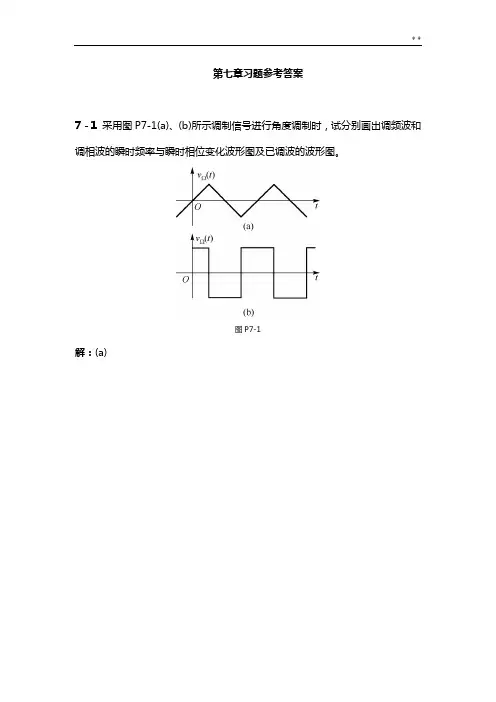
第七章习题参考答案7-1采用图P7-1(a)、(b)所示调制信号进行角度调制时,试分别画出调频波和调相波的瞬时频率与瞬时相位变化波形图及已调波的波形图。
图P7-1解:(a)(b)图P7-1J7-2有一调角波数学表示式)10cos 03.010sin(12=48t t -v V ,试问这是调频波求 中心角频率,调制角频率以及最大角频偏?[参考答案: rad/s 300=Δm ω] 解:一个角度调制波既可以是调频波又可以是调相波,关键是看已调波中瞬时相位)(Δt φ的表达式与调制信号的关系,与调制信号成正比为调相波,与调制信号的积分成正比为调频波。
由调角波的表达式)10cos 03.010sin(12=48t t -v 得知t t φ410cos 03.0=)(Δ-, 若调制信号t ωV sin =m Ωv ,则)10cos 03.010sin(12=48t t -v 为调频波。
中心频率为rad/s 108C =ω,调制角频率为rad/s 10=4Ω,最大角频偏300rad/s =rad/s 10×0.03==Δ4f m ΩM ω7-3 一个调频波的载波频率是10MHz ~7,频偏为00kHz 2,调制频率为0kHz 1,求调制指数。
若调制频率降为0Hz 2,求调制指数。
[参考答案:20=f1M ,4f210=M ]解:由于调制频率为0kHz 1,属于单音调制。
ΩV k M mΩf f =,又3m Ωf m 10×200×π2==ΔV k ω, 所以 20=10×10×π210×200×π2=33f1M 当调制频率为20Hz 时,433f210=20×π210×200×π2=M 7-4 一个调相波的载波频率是10MHz ~7,调制指数是20。
调制频率同上题,求角频偏。
[参考答案:rad/s 10×26.1=Δ6m1ω,rad/s 10×5.2=Δ3m2ω] 解:同样属于单音调制。
《通信原理》习题参考答案第四章4-1. 已知线性调制信号表示式如下:(1) t t c ωcos cos Ω(2) ()t t c ωcos sin 5.01Ω+式中,ωc =6Ω。
试分别画出它们的波形图和频谱图。
解:(1)t Ωcos 和t c ωcos 的波形分别如下:t c ωcos 的频谱为:()()[]c c ωωδωωδπ-++ ∴t t c ωcos cos Ω的频谱为:()()[]()()[]{}c c ωωδωωδπωδωδππ-++*Ω-+Ω+21()()()()[]c c c c ωωδωωδωωδωωδπ-Ω-+-Ω+++Ω-++Ω+=2()()()()[]c Ω-+Ω-+Ω++Ω+=75572ωδωδωδωδπ(2) ()t Ω+sin 5.01和t c ωcos 的波形分别如下:两波形相乘可得到如下波形:()t t t t t c c c ωωωcos sin 5.0cos cos sin 5.01Ω+=Ω+ ∵t c ωcos 的频谱为:()()[]c c ωωδωωδπ-++t Ωsin 的频谱为:()()[]Ω--Ω+ωδωδπj∴()t t c ωcos sin 5.01Ω+的频谱如下:()()[]()()[]()()[]{}c c c c j ωωδωωδπωδωδππωωδωωδπ-++*Ω--Ω++-++215.0()()[]()()()()[]{}c c c c c c jωωδωωδωωδωωδπωωδωωδπ-Ω---Ω+++Ω--+Ω++-++=4 ()()[]()()()()[]{}Ω--Ω-+Ω+-Ω++Ω-+Ω+=7557466ωδωδωδωδπωδωδπj频谱图如下:4-3. 已知调制信号()()()t t t m ππ4000cos 2000cos +=载波为t π410cos ,进行单边带调制,试确定该单边带信号的表达式,并画出频谱图。
《无线通信》练习册答案(总12页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题一一、填空题:1、无线通信系统主要由_发射机 __接收机和__天线_三大部分组成。
2、无线通信方式主要有__单工_ _ __和__半双工_三种方式。
3、无线通信的波长、频率是根据λ=c/f_公式计算的。
4、高频的频率范围___________,波长范围_____________。
P15—165、甚高频的频率范围___________,波长范围_____________。
P15—166、超高频的频率范围___________,波长范围_____________。
P15—167、特高频的频率范围___________,波长范围_____________。
P15—168、无线通信的形式有_移动_和_固定_两种。
二、名词解释:1、频段:把无线电频率划分为若干个区域,每个区域称为频段。
2、单工通信:通信的双方同时只能单方向工作的方式3、双工通信:通信的双方可同时双方向工作的方式4、半双工通信:通信的一方为单工通信方式,而另一方为双工通信方式。
三、判断题:1、无线通信是利用无线电波来传输信息的。
(√)2、无线通信是在移动中进行通信的。
(Χ)3、无线通信的通信方式有两种。
(Χ)4、无线通信的通信形式有两种。
(Χ)5、超短波通信是指频率在3MHz~3000MHz。
( Χ)6、超短波通信是指波长在100m~10cm。
(Χ)7、移动通信的频率在VHF和UHF频段。
(√)习题二一、填空题:1、调制按调制信号不同分类有_模拟信号_和数字信号_两种。
2、调制按载波信号不同分类有_模拟信号和_数字信号_两种。
3、调制按调制器实现功能分类有_线形__和__非线形_两种。
4、调频波的瞬时频率ω(t)=_____________________。
P532—P5365、调频波的瞬时频移Δω(t)=_____________________。
数字调制技术习题解答第1题解:第2题解:s b R b /48008=,sb R R R b b B /160038log :8288===码元传输速率为 Hz B MASK 320016002:=×=带宽为HzB Hz B B FSK PSK ASK 3200200284002002)1(888=××==×==)(/60020038log )2(288三者相同s bit B R B b =×==2328log 2log163828log 2log )3(2288228=====×==M r r M M r ASK PSKFSK第4题解:(设每个码元内包含两个载波)HzB Hz f ASK c 200010002)1()(1071070276=×=×=×=载波频率(2)结果如下:t610140cos ×π第6题解:发0时,载频为2400Hz ,画图时,用每个码元中包含2个载波周期代替。
发1时,载频为4800Hz ,画图时,用每个码元中包含4个载波周期代替。
结果如下:第7题解:(1)传码率,带宽Baud 6102×MHz B ASK22=,MHz f MHz f 15,1021==。
f1(2)MHz f f B FSK9||10221262=−+××=第8题解:(注意以下两点)(1) 强调相位突变的概念,相位突变为180度的反相!!(2) 码元的宽度为,而载波周期为b b f T /1=f T /1=,需比较两者关系后再画图。
第9题解:在数字调相2PSK信号中,若码元速率为1200Baud,载波为1800HZ,波形如图所示,画出该二相差分移相信号的相位偏移和二进制绝对码的波形。
第10题解:如下图所示的波形,问题:(1)若此信号是绝对相移信号,它所对应可能的二进制数字信号序列是什么?(2)若此信号是相对相移信号,且已知相邻相位差为0时对应“1”码元,相差π时对应“0”码元,它所对应的二进制数字序列是什么?(3)若此信号是相对相移信号,且已知相邻相位差为π时对应“1”码元,相差0时对应“0”码元,它所对应的二进制数字序列是什么?(4)上述三个问题说明了什么?解:(1)两种可能的序列:1,0,0,1,0以及0,1,1,0,1(2)序列为:1,0,1,0,0(3)序列为:0,1,0,1,1(4)第二种情况为“0变1不变”第三种情况为“1变0不变”,说明了规则不是惟一的,只有当发送端与接收端规则一致时,才能正确解调出原信号。
第8章 角度调制与解调思 考 题8.1 已知载波f c =100MH Z ,载波电压振幅U cm =5V ,调制信号u Ω(t )= ( cos2π×103t +2cos2π×500t )V 。
试写出下述条件调频波的数学表达式:(1) 频灵敏度K f =1kH Z /V 。
(2)频偏△f m =20kH Z 。
解:(1)⎥⎦⎤⎢⎣⎡+=⎰Ωtt f c cm t FM dt u k t U u 0)()(cos ω⎥⎦⎤⎢⎣⎡⨯⋅⨯+⨯⋅⨯+⨯⨯⨯=⎥⎦⎤⎢⎣⎡⨯+⨯+=⎰⎰t t t tdt k tdt k t f t tf f c 5002sin 50022000102sin 10210001010014.32cos 55002cos 2102cos 2cos 5336003πππππππ()t t t 5002sin 64.0102sin 16.01028.6cos 538⨯+⨯+⨯=ππ(2)因为max )(2t u k f f m m Ω=∆=∆πω所以V KHz t u f k m f /8.622102014.32)(23max =⨯⨯⨯=∆=Ωπ所以()tt t dt t u k t U t u tf c cm FM 5002sin 40102sin 101028.6cos 5)(cos )(380⨯+⨯+⨯=⎥⎦⎤⎢⎣⎡+=⎰Ωππω8.2 载波振荡频率f c =25MH Z ,振幅U cm =4V ;调制信号为单频余弦波,频率为F =400H Z ;最大频偏△f m =10kH Z 。
(1) 分别写出调频波和调相波的数学表达式。
(2) 若调制频率变为2 kH Z ,其他参数均不变,再分别写出调频波和调相波的数学表达式。
解:(1)因为F m f f m ⋅=∆,所以rad KHz KHz F f m m f 254.010==∆=所以:()()()tt Ft t f t m t U t u c f c cm FM 38105.2sin 251057.1cos 42sin 252cos 4sin cos )(⨯+⨯=+=Ω+=ππω()()t t t m t U t u P c cm PM 38105.2sin 251057.1cos 4cos cos )(⨯+⨯=Ω+=ω(2)如果F=2KHz ,则rad KHzKHzm m P f 5210=== 近而可写出调频波和调相波的数学表达式:()()()tt Ft t f t m t U t u c f c cm FM 38105.2sin 51057.1cos 42sin 52cos 4sin cos )(⨯+⨯=+=Ω+=ππω()()t t t m t U t u P c cm PM 38105.2sin 51057.1cos 4cos cos )(⨯+⨯=Ω+=ω8.3若调频波的中心频率f c =100MH Z ,最大频偏△f m =75kH Z ,求最高调制频率F max 为下列数值时的m f 和带宽:(1) F max =400 H Z ;(2) F max =3kH Z ;(3) F max =15kH Z 。
解:(1)rad KHzKHzF f m m f 5.1874.075max ==∆=,()KHz F f BW m 8.1502max =+∆= (2)rad KHz KHzF f m m f 25375max ==∆=,()KHz F f BW m 1562max =+∆= (3)rad KHzKHzF f m m f 51575max ==∆=,()KHz F f BW m 1802max =+∆=8.4 设调角波的表达式为u (t )=5cos(2×106πt +5cos2×103πt )V 。
(1) 求载频f C 、调制频率F 、调制指数m 、最大频偏△f m 、最大相偏△ϕm 和带宽。
(2) 这是调频波还是调相波?求相应的原调制信号(设调频时K f =2kHz/V ,调相时K p=1rad/v)。
解:(1)MHz f C C 1210226=⨯==πππω,KHz F 1210223=⨯=Ω=πππ rad m 5=,KHz KHz F m f f m 515=⨯=⋅=∆,()KHz KHz KHz BW 12152=+= rad m m 5==∆ϕ(2)可能是调频波,也可能是调相波。
如果看成调频波:t t u π3102sin 5.2)(⨯-=Ω 如果看成调相波:t t u π3102cos 5)(⨯=Ω8.5 若调角波的调制频率F =400Hz ,振幅U Ωm =2.4V ,调制指数m=60rad 。
(1) 求最大频偏△f m 。
(2) 当F 降为250Hz ,同时U Ωm 增大为3.2V 时,求调频和调相情况下调制指数各变为多少?解:(1)KHz KHz mF f m 244.060=⨯==∆ (2)由V KHz k U k m f mf f /10=Ω=Ω得所以可得当F 降为250Hz ,同时U Ωm 增大为3.2V 时rad m f 12825.02.310=⨯=由V rad k U k m P m P P /25==Ω得所以可得当F 降为250Hz ,同时U Ωm 增大为3.2V 时rad m P 802.325=⨯= 8.6 若载波u c(t)=10cos2π×50×106tV ,调制信号为u Ω(t)=5sin2π×103tV ,且最大频偏△f m =12kHz ,写出调频波的表达式。
解:由题可知:rad Ff m U mf C cm 12102101038=∆=⨯=Ω==ππω 所以:()t m t U t u f C cm FM Ω+=sin cos )(ω()t t 38102sin 1210cos 10⨯+=ππ8.7 用正弦调制的调频波的瞬时频率为f (t)=(106+104cos2π×103t)Hz ,振幅为10V ,试求:(1) 该调频波的表达式。
(2) 最大频偏△f m 、调频指数m f 、带宽和在1Ω负载上的平均功率。
(3) 若将调制频率提高为2×103Hz ,f(t)中其他量不变,△f m 、m f 、带宽和平均功率有何变化?解:(1)由题得:)102cos 1010(2)()(3406t dt t t tt⨯+==⎰⎰ππωϕt t 36102sin 10102⨯+⨯=ππ 所以()t t t u FM ππ36102sin 10102cos 10)(⨯+⨯=(2)WR U P KHzF f BW rad KKF f m KHz t u f L cm av m m f m 5021002122)(21011010)(2max max ====+∆===∆===∆Ω(3)不变W p KHzKHz BW radm KHzf av f m 5024)210(2521010==+====∆ 8.8 调制信号为余弦波,当频率F =500Hz 、振幅U Ωm =1V 时,调角波的最大频偏△f m1=200Hz 。
若U Ωm =1V ,F =1kHz ,要求将最大频偏增加为△f m2=20kHz 。
试问:应倍频多少次(计算调频和调相两种情况)?解:根据题目已知的条件可得rad F f m m m P f 4.05002001==∆==(1)对于调频波由Ω⋅=Ωmf f U k m 得k f =2×3.14×200,所以在U Ωm =1V ,F =1kHz时,KHz F U k f mf m 2.0100010001200=⨯⨯=∙Ω⋅=∆Ω,所以要将最大频偏增加为△f m2=20kHz ,则应倍频100次。
(2)对于调相波由m P P U k m Ω=得k p =0.4,所以在U Ωm =1V ,F =1kHz 时,KHz F U k f m P m 4.0114.0=⨯⨯=⋅⋅=∆Ω,所以要将最大频偏增加为△f m2=20kHz ,则应倍频50次。
8.9在变容管直接调频电路中,如果加到变容管的交流电压振幅超过直流偏压的绝对值,则对调频电路有什么影响?答:如果加到变容管的交流电压振幅超过直流偏压的绝对值,则在信号的一个周期内的某些时间,变容二极管有可能会正向导通,则失去结电容随反偏电压变化的特性,因而不能实现调频。
8.10双失谐回路斜率鉴频器的一只二极管短路或开路,各会产生什么后果?如果一只二极管极性接反,又会产生什么会果?答:如果一只二极管开路,则电路相当于单失谐回路鉴频器;如果一只二极管短路,则输出的低频调制信号中将叠加有调幅-调频波;如果一只二极管接反,则两检波器输出电压大小相等,极性相同,在输出端相互抵消,输出电压为零。
习图5—1中,0360MHz f =,变容管的3γ=,0.6V V Ω=,cos v t Ω=Ω。
(1)分析电路工作原理,画出交流等效电路。
(2)已知当6V Q V =-时,20pF jQ C =。
求2?L = (3)求m f ∆及调制灵敏度(/m Q f V ∆)。
解:(1)该电路是1C 、2C 、变容二极管和电感L 组成的电容三端式振荡器。
当v Ω改变变容管反向偏置电压时,变容管j C 随之变化,从而振荡频率随v Ω规律变化而实现调频。
(2)12120.51pF 0.513C C C C C ===++ 203'0.33pF 1203jQ jQCC C C C ∑==≈++262120110.59μH (2)'(236010)0.3310L f C ππ-∑===⨯⨯⨯⨯(3)0(1)j j r DC C v V γ=+ ()c o s r Q v t V V t Ω=+Ω 0(1cos )cos (1)j j jQ Q DC C C m t V V tV γγ-Ω==+Ω+Ω+其中 00(1)j Q DC C V V γ=+ 110.1560.6 6.6Q D V m V V Ω===≈++ j j CC C C C ∑=+()t ωωω=====0ω==0v Ω=时的载频)11jQ jQC p C C =≈+ 20.016jQCp C C =≈+()t ωω=将()t ω在cos 0t Ω=处展开成泰勒级数,有:220222202220012111()[1cos (1)cos ]24211111[1(1)cos (1)cos 2]82282cos cos 2t p m t p m t p m p m t p m t t t ωωωγγγωγγγγγωωωω==+Ω+--Ω+=+--+Ω+--Ω+=+∆+∆Ω+∆Ω+习图5—2中,哪个电路能实现包络检波?哪个电路能实现鉴频?01f 和02f 如何配置?解:(a )图中两谐振回路的谐振曲线如图所示。