第2章解直角三角形复习课教案

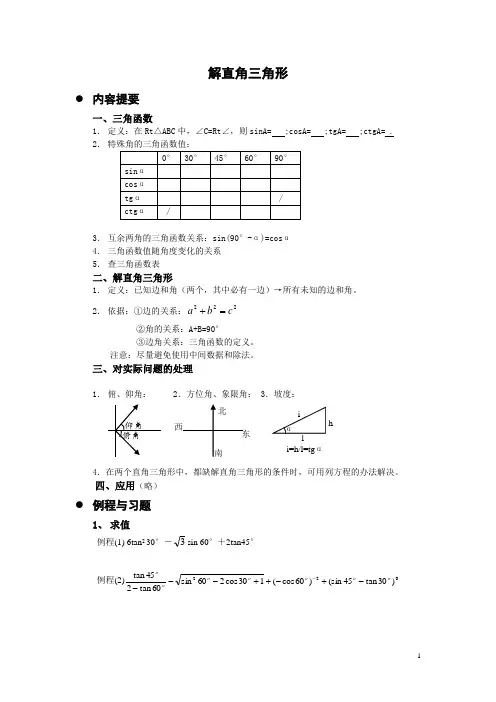
解直角三角形● 内容提要一、三角函数1． 定义：在Rt △ABC 中，∠C=Rt ∠，则sinA= ;cosA= ;tgA= ;ctgA= . 2．3． 互余两角的三角函数关系：sin(90°-α)=cos α 4． 三角函数值随角度变化的关系 5． 查三角函数表二、解直角三角形1． 定义：已知边和角（两个，其中必有一边）→所有未知的边和角。

2． 依据：①边的关系：222c b a =+ ②角的关系：A+B=90°③边角关系：三角函数的定义。

注意：尽量避免使用中间数据和除法。

三、对实际问题的处理1． 俯、仰角： 2．方位角、象限角： 3．坡度：4．在两个直角三角形中，都缺解直角三角形的条件时，可用列方程的办法解决。

四、应用（略）● 例程与习题1、 求值例程(1) 6tan 2 30°－3sin 60°＋2tan45°例程(2)022)30tan 45(sin )60cos (130cos 260sin 60tan 245tan o o o o o oo-+-++----α h i i=h/l=tg α习题(1)40cos 450sin )60cos 50cos 40(cos 60tan 50tan 40tan 222+++-∙∙习题(2)0)12(60tan 45tan 30cos 2-+-+ 习题(3)sin 30cos 45cos 60sin 45︒-︒︒-︒习题(4)2(tan 45)︒习题(5)sin 353tan 3012sin 60cos55︒︒--+︒︒2、 解答题例题（1）、如图，在Rt ABC ∆中，90BCA ∠=︒，CD 是中线，5,4BC CD ==，求AC 的长。

习题（1）、如图，在Rt ABC ∆中，90BCA ∠=︒，CD 是中线，6,5BC CD ==，求sin ,cos ACD ACD ∠∠和tan ACD ∠。

解直角三角形复习课教案富顺县怀德镇大城九年制学校—王甸健教学目标1、复习解直角三角形的有关概念、依据和分类。

2、灵活运用勾股定理、直角三角形中两锐角互余、锐角三角函数及恰当的添加辅助线解直角三角形。

使学生会用解直角三角形的有关知识解决实际问题。

3、通过解题活动提高学生分析问题、解决问题的能力以及计算能力，增强数学应用意识。

教学重难点1、重点：把实际问题中的已知条件和未知元素，化归到某个直角三角形中解决。

2、难点：把实际问题转化为解直角三角形的数学问题。

教学过程一、复习回顾，知识梳理1、定义：什么是解直角三角形？由直角三角形中除直角外的已知元素，求未知元素的过程，叫做解直角三角形.2、单元知识网络3、解直角三角形4、30°，45°，60°的三角函数值5、在解直角三角形中，经常接触的名称：23112160︒45︒45︒30︒二、例题精讲 运用提升例1 已知：如图，在△ABC 中，AB=6，∠B=60°，∠C=45°，AD ⊥BC 于点D ，求BC 的长.练习1： 将已知条件改变，不给AD ⊥BC 于点D 。

已知：如图，在△ABC 中，AB=6，∠B=60°，∠C=45°，求BC 的长.例2 已知：如图，在△ABC 中，AB=6，∠ABE=60°，∠C=45°，求BC的长.练习2： 已知：如图，AD ⊥BC 于点D ，BC=4，∠C=45°，∠ABD=60°，求AD 的长.练习3：若把练习1图形再次变形，将已知条件改为：如图：BC=4，∠C=45°，∠ABE=60°.求点A 到BC 的距离.你能求解吗？三、课堂小结1、本节课我们复习了解直角三角形的方法及应用它解决一些实际问题。

2、解直角三角形要熟练运用三角函数的定义和勾股定理. 要观察图形，了解直角三角形边、角之间的关系，还要注意挖掘隐含条件。

解直角三角形的复习课教案（ 1）执教者：上海市园南中学姚春花教学目标： 掌握直角三角形的基本方法，能灵活运用锐角三角比解直角三角形。

并在解题过程中渗透化归方程等数学思想。

通过习题的变式， 让学生感悟图形间的联系，以及知识的本质。

通过一题多解，培养学生的发散思维。

教学重点与难点 ：寻找合适的方法灵活求解直角三角形。

教学过程 ： 一、回顾与思考1、在 Rt △ABC 中，∠ C=90°， b=2，c= 2 2 ,则∠ B=度； a=2、在 Rt △ABC 中，∠ C=90°，∠ A=3 0°， AB=3，则 AC= ；∠ B=度、在 Rt △ABC 中，∠ B=90°， sin A= 3， a=3，则 c= ；b=3 54、在 Rt △ABC 中，∠ A=60°∠ B=75°， AB=8，则 AC=归纳：1、解一个直角三角形要具备什么样的条件？生：除直角外，已知三角形的两个元素（其中至少有一个条件与边有关） ，才能解这个直角三角形。

2、解直角三角形运用到哪些定理或定义？（依据） ①勾股定理 ②锐角三角比 ③两锐角互余（以上四题均给出图形，教师根据学生的回答，让学生回顾知识）归纳：解直角三角形首先要根据题目给出图形， 其次关键在于正确选用只含有一个未知数的三角比的式子。

3、你能归纳出解一般三角形的思路吗？ 构造有效的直角三角形二、小试牛刀1、已知在 Rt △ABC 中，∠ ACB=9 0°， CD 是斜边 AB 上的高，AB=10， tan A3，求 AC 的长 C4A BD归纳：常用解法：①寻找 Rt△（根据三角比）②转化角（等角的同名三角比相等）③设元（列方程求解）2、已知，如图，在△ ABC 中，∠ A=3 0°，F 为 AC上一点，且 AF : FC 4 : 1, EF ⊥ AB，E 为垂足，联结 EC，求 tan∠CEB 的值。

《解直角三角形复习》教案单位：泸县一中 年级： 九 学科： 数 学 设计者：_______ 时间：2015年 4月14日【学习目标】：1. 巩固三角函数的概念,巩固用直角三角形边之比来表示某个锐角的三角函数.2. 熟记30°，45°, 60°角的三角函数值.会计算含有特殊角的三角函数的值，会由一个特殊锐角的三角函数值，求出它的对应的角度.3.掌握直角三角形的边角关系，会运用勾股定理，直角三角形的两锐角互余及锐角三角函数解直角三角形.4.会用解直角三角形的有关知识解决简单的实际问题.【教学重点】：从实际问题中提炼图形，将实际问题数学化，将抽象问题具体化。

【教学难点】：运用解直角三角形的知识灵活、恰当地选择关系式解决实际问题。

【教学过程】： 一、考点梳理：1.锐角三角函数的定义在Rt △ABC 中,∠C=90°,∠A ,∠B ,∠C 的对边分别为a ,b ,c.2、特殊角的三角函数值三角函数 角α sin α cos αtan α30°45°60°1sin =A A A ∠=∠———————————的、正弦函数：的=A A A ∠=∠———————————的2、余弦函数：cos 的=A A A ∠=∠———————————的3、正切函数：tan 的3、解直角三角形的定义及类型(1)定义：一般地，在直角三角形中，除直角外，共有 5 个元素，即______条边和______个锐角．由直角三角形中除直角外的已知元素，求出其余未知元素的过程，叫做解直角三角形． 4、解直角三角形的应用（1）仰角和俯角在视线与水平线所成的角中,视线在水平线 的叫做仰角,在水平线 的叫做俯角.(2）方位角一般以观察者的位置为中心，南北方向线与目标方向线之间的夹角叫方位角。

如下图：OA 方向用方位角表示为 ；OB 方向用方位角表示为 。

（3）坡角、坡度坡角：指坡面与水平线的夹角，如图中的坡度：指坡面的垂直高度与水平距离的比，如图中的i =1:1.5表示AF 与BF 的比 坡角与坡度的关系：二、基础巩固：1. 如图,在Rt △ABC 中,∠C=90°,BC=3,AC=4,那么cos A 的值等于( )2.河堤横断面如图所示,堤高BC=6 m,迎水坡AB 的坡度为 ,则AB 的长为( )3.4A 4.3B 3.5C 4.5D 3.12A m .43B m .53C m .63D m3.如图，在Rt △ABC 中，∠ACB =90°,D 为AB 的中点，CD =5,AC =6,则cos B 的值是（ ）第1题图 第2题图5．在△ABC 中，sin C ＝，∠BAC ＝105°，AC ＝2cm ，求BC 的长．三、能力提升：探究1：为了响应市人民政府“形象重于生命”的号召，在甲建筑物上从A 点到E 点挂一长为 米的宣传条幅，在乙建筑物的顶部D 点测得条幅顶端A 点的仰角为60°,测得条幅底端E 点的俯角为45°。

解直角三角形（复习）一、教学目标：1、熟练掌握直角三角形中蕴含的三种等量关系。

2、能运用三角函数解决与直角三角形有关的简单的实际问题。

3、体会数形结合思想以及转化思想在解决数学问题中的应用。

二、教学重难点：特殊三角函数值的应用及运用锐角三角函数解决简单的实际问题。

三、教学用具：多媒体、导学案 四、教学过程设计： （一）、问题思索：有人说，数学家就是不用爬树或把树砍倒就能够知道树高的人．小敏想知道校园内一棵大树的高（如图），你能帮助小敏设计出测量大树的高度的方案吗？（二）、回顾旧知： 1、锐角三角比(1) sinA=(2) cosA=(3) tanA=2、特殊角的三角比：(1) 已知一边和一锐角，解直角三角形； (2) 已知两边，解直角三角形。

（三）、热点回顾：1. 在△ABC 中，∠C =90°，BC=5，AC=12， 则cosA 等于（ ）a BAC1312.512.135.122.D C B A2．计算：3. 物化大厦离小伟家60m ，小伟从自家的窗中眺望大厦，并测得大厦顶部的仰角为45°，大厦底部的俯角为30°，求该大厦的高度。

（四）、跟踪练习：3．在Rt △ABC 中，∠C ＝90°,已知：c ＝12，∠B =60° 解直角三角形。

1. 一个钢球沿坡角31°的斜坡向上滚动了5米，此时钢球距地面的高度是（ ）米． ．5sin 315cos315tan 311:m α∠=ＡＤ2.如图所示，铁路的路基横断面是等腰梯形，斜坡的坡度为 的水平宽度为 ，基面AD 宽为2m ，则AE= ，4、如图，小明想测量塔CD的高度。

他在A处仰望塔顶，测得仰角为45゜，再往塔的方向前进50m至B处，测得仰角为60゜，那么该塔有多高？（小明的身高忽略不计）（五）、通过本节课的复习，你有哪些新的收获？（六）、快乐达标：1、在Rt △ABC 中，∠C ＝90°． (1)已知：32=a ，2=b ，求∠A 、∠B ，c ；(2)已知：32sin =A ，6=c ，求a 、b ；2、已知：如图，Rt △ABC 中，∠A ＝30°，∠C ＝90°， ∠BDC ＝60°，BC ＝6cm ．求AD 的长．。

温馨提示：此材料是教师讲课的教案，学生学习的学案，上课时的笔记，课后的复习资料，请同学们装订保管。

发给同学们后请通过研读课本资料，并在同学和老师帮助下完成，并达到能讲的水平。

解直角三角形复习课教学案一、学习目标：运用三角函数的概念以及有关直角三角形的概念解直角三角形；经历探究直角三角形边角关系的过程，应用于解决有关的实际问题；形成数形结合的分析方法和应用意识。

（学生课后体会）二、重难点：理解并掌握直角三角形边角之间的关系；如何应用直角三角形的边角关系解决有关实际问题。

（学生课后检测是否到达要求）三、课前预习：阅读教材第86----104页（学生自行安排时间）四、教具准备：多媒体课件五、学习过程：（一）、知识结构（二）、知识要点回顾1、在Rt△ABC中，∠C为直角，∠A、∠B为锐角，它们所对的边分别为c 、a、b ，其中除直角c 外，其余的5个元素之间有以下关系：⑴三边之间的关系：⑵锐角之间的关系⑶边角之间的关系：2、特殊锐角的三角函数3、正弦、余弦和正切、余切的性质4、同角三角函数关系:（1）平方关系:（2）倒数关系:（3）商数关系:5、互余角三角函数之间的关系:（三）、例题讲解例1、求下列各式的值1、2sin30°+3tan30°+cot45°2、cos245°+ tan60°cos30°3、 例2、求锐角A 的值1、 已知 tanA= 3 ，求锐角A .2、已知2cosA - 3 = 0 ,求锐角A 的度数 .例3、确定值、角的范围、1、 在Rt △ABC 中∠C=90°，当 锐角A>45°时，sinA 的值（） (A)0＜sinA ＜ 23 (B) 23＜sinA ＜1(C) 0＜sinA ＜ 22 (D) 22＜sinA ＜12、当∠A 为锐角，且cotA 的值小于 3 时，∠A （ ）(A)0°＜∠A ＜30° (B)30°＜∠A ＜90°(C) 0°＜∠A ＜60° (D)60°＜∠A ＜90°（四）、课堂测试1. 在△ABC 中∠C=90° ,∠B=2∠A . 则cosA=______2. 若tan(β+20°）= ,为锐角.则β=______ 3、3.已A 是锐角且tanA=3,则 4、在Rt △ABC 中，∠C=90°,cosB= ,则sinB 的值为5、5.已知 0°<ａ< 45 °锐角,化简 =______6. tana.tan20°=1,则a= 度例题4 在Rt △ABC 中，∠C=90°：oo oo 30sin 45cos 30sin 45cos +-3__sin 2cos 2cos sin =+-A A AA 32a a cos sin 21- A Bb ac ┏ C⌒ 对边邻边 斜边⑴已知∠A 、 c, 则a=__________;b=_________。