专题由递推关系求数列的通项公式含答案

`式已知递推公式求通项公].p)i (a [p a p)i (p a pa p)(pa pa p 1p 2n )i (a a 1p .)()(pa a p p1q a }p1q a {p1q a p p1q a p 1q 1p q a 1p q pa a 11n 1i i11n n 1n 1i 1i 1nn 1n nn 1n 1n 1n 1n 1i 1n n 1n 1n n 1n 1n 1n ∑∑∑-=--=+++++-=++++=+=+=≠≥+==+=-+-+-+=-+-≠=+=f f n f f n f n f ，从而利用叠加法易得，，变形为，则两边同时除以若；，，则显然若不是常数，其中为公比的等差数列为首项，是以显然）（，变为，则两边同加上若为公差的等差数列；为首项，，则显然是以若）常见形式：（p x a x a qx a x a x x p p x a 1x a 1x x x x 0b x a -d cx dcx b ax x dca b aa a )2(2n 1n 21n 11n 211n 11n 21212n n 1n 通项公式求解，然后再利用等比数列可以用待定系数法求解，其中则有若通项公式求解，然后再利用等差数列可以用待定系数法求解，其中则有若，，令此方程的两个根为）（，即，令典型例子：不动点法--=--≠+-=-==-+++=++=++++用待定系数法求得、，，则其通项公式为若用待定系数法求得、，）（则其通项公式若，，令此方程两根为，特征方程为性递推式的好方法特征根法是专用来求线特征根法B A Bx Axa x x B A x Bn A a ,x x x x q px x qa pa a .)3(n2n1n 21n1n 21212n 1n 2n +=≠+==+=+=++.4然后用数学归纳法去证的规律猜出一个结果，简单说就是根据前几项）数学归纳法（公式，马上迎刃而解！，只需联系正切二倍角看起来似乎摸不着头脑：东西，看看下面的例子三角函数是个很奇妙的）联系三角函数（2nn 1n a1a 2a 5-=+递推新值的过程。

如何由递推公式求通项公式高中数学递推数列通项公式的求解是高考的热点之一，是一类考查思维能力的题型，要求考生进行严格的逻辑推理。

找到数列的通项公式，重点是递推的思想：从一般到特殊，从特殊到一般；化归转换思想，通过适当的变形，转化成等差数列或等比数列，达到化陌生为熟悉的目的。

下面就递推数列求通项的基本类型作一个归纳，以供参考。

类型一：1()nna a f n 或1()n na g n a 分析：利用迭加或迭乘方法。

即：112211()()+()nnnnna a a a a a a a ……或121121n n n nna a a a a a a a ……例1.(1)已知数列na 满足11211,2nna a a nn，求数列n a 的通项公式。

（2）已知数列n a 满足1(1)1,2nn n a a s ，求数列n a 的通项公式。

解：（1）由题知：121111(1)1nna a nnn n nn 112211()())n n n n na a a a a +(a -a a (1)111111()()()121122n n nn ……312n（2）2(1)n n s n a 112(2)nn s na n两式相减得：12(1)(2)n nna n a na n 即：1(2)1n na n n a n 121121n n nn n a a a a a a a a (121)121nn n n……n类型二：1(,(1)0)nn a pa q p q pq p 其中为常数，分析：把原递推公式转为：1(),1nnq a tp a t p其中t=，再利用换元法转化为等比数列求解。

例2.已知数列n a 中，11,123n n a a a ，求n a 的通项公式。

解：由123nn a a 可转化为：132(3)n na a 令3,nn b a 11n+1n则b =a +3=4且b =2b n b 1是以b =4为首项，公比为q=2的等比数列11422n n bn即123n na 类型三：1()(nn a pa f n 其中p 为常数)分析：在此只研究两种较为简单的情况，即()f x 是多项式或指数幂的形式。

已知数列的递推公式求通项公式的方法
1.累加法：递推关系式为1()n n a a f n +-=采用累加法。

“累加法”实为等差数列通项公式的推导方法。

2.累乘法:递推关系式为
1()n n
a f n a +=采用累乘法。

“累乘法”实为等比数列通项公式的推导方法 3.构造法：递推关系式为(1)1n n a pa q +=+,(2)1n
n n a pa q +=+,
都可以通过恒等变形，构造出等差或等
比数列，利用等差或等比数列的定义进行解题，其中的构造方法可通过待定系数法来进行。

4. 和化项法：递推关系式为()n S f n =或()n n S f a =一般利用11,
1
,2
n n n S n a S S n -=⎧
=⎨-≥⎩进行转化。

例1.已知12a = , 1n a +=2132n n a -+⋅
求数列{}n a 的通项公式.
例2.已知11,a = 11
n n n a a n +=⋅
+，
求数列{}n a 的通项公式
例3.已知11,a =123n n a a +=+，
求数列{}n a 的通项公式
例5.已知43n n S a =+，
求数列{}n a 的通项公式.
例4.已知11,a =123n n n a a +=+，
求数列{}n a 的通项公式
例6.已知113
n n a S +=
，11a =,
求数列{}n a 的通项公式。

递推数列求通项公式的典型方法1、 a n+1=a n +f （n ）型 累加法:a n =（a n -a n-1）+（a n-1-a n-2）+…＋（a 2-a 1）+ a 1 =f （n-1）+f （n-2）+…f （1）+ a1例1 已知数列｛a n ｝满足a 1=1,a n+1=a n +2n （n ∈N *）, 求a n 解: a n =（a n -a n-1）+（a n-1-a n-2）+…＋（a 2-a 1）+ a 1 =2n-1+2n-2+…+21+1=2n -1（n ∈N *）例 在数列{n a }中，31=a ,)1(11++=+n n a a n n ，求通项公式n a .解：原递推式可化为：1111+-+=+n n a a n n则,211112-+=a a 312123-+=a a413134-+=a a ，……，nn a a n n 1111--+=-逐项相加得：n a a n 111-+=.故na n 14-=2、)(1n g a ann =+型累积法:112211.....a a aa a a a a n n n n n ---=所以()()()()11...321a g n g n g n g a n ---=∴例2:已知数列｛a n ｝满足()*1N n n a ann ∈=+,.11=a 求n a解:112211...a a aa a a a a n n n n n ---==()()()()!11...321-=---n n n n ()()+∈-=∴N n n a n !1例2 设数列{n a }是首项为1的正项数列，且0)1(1221=+-+++n n n n a a na a n （n=1,2,3…），则它的通项公式是n a =▁▁▁（2000年高考15题）. 解：原递推式可化为：)]()1[(11n n n n a a na a n +-+++=0 ∵ n n a a ++1＞0，11+=+n na a n n 则,43,32,21342312===a a a a a a ……，nn a a n n 11-=- 逐项相乘得：n a a n 11=，即n a =n1. 3．q pa a n n +=+1型（p,q 为常数）方法：（1）⎪⎪⎭⎫⎝⎛-+=-++111p q a p p q a n n ，再根据等比数列的相关知识求n a . (2)()11-+-=-n n n n a a p a a 再用累加法求n a .(3)111++++=n n n n n p qp a p a ,先用累加法求n n p a 再求n a 例3．已知{}n a 的首项a a =1（a 为常数），()2,21≥∈=+-n N n a a n n ，求n a解 设()λλ-=--12n n a a ，则1-=λ ()1211+=+∴-n n a a{}1+∴n a 为公比为2的等比数列。

由递推公式求数列通项公式常见题型及解法对于由递推公式所确定的数列通项公式问题,通常可通过对递推公式变形,转化成等差数列或等比数列加以解决,也可以通过构造法把问题转化后予以解决.下面分类举例说明.一,%+l=%+-厂(n)型累加法:%=(一%～1)+(n一l一%一2)+…+(oa一.I)+nl=-厂(n一1)+_厂(n一2)+…+f(1)+01.例1在数列{}中,已知+=,=2,求通项公式.解:已知递推式化为…_l__一:+%+12+I’又tan(a+c)=号,tanAtanC=2+厂,tanA+tanC=3+,/一.由IanA+tanc=+,[tanAtanC=2+,v/3.解得tanA=1,tanC=2+,/丁或tanA=2+,/,tanC=1.所以A=45.,B=60.,C=75.或A=75o.B=60..C=45..当=45咐,.=8c==8,6=Ac=每=4,c=4+4_当=75.时,.=8,b=4,厂一(x/一1),c=8(,/一1).【解题反思】此题将三角形,正弦定理,三角形内角和,方程思想等知识巧妙24基础教育论坛[2011年第2期j即一--1=1,%+1’所以一1=1,l:1,啦Z啦Z111111啦劬一2’’一l一2n’将以上(n一1)个式子相加,得1一1=_2211l+..’1,—_22”‘即an=争++寺++…+一(一一.21一所以=一=.2练习:已知数列{%}满足n.=1,+.=n+2n(孔∈N).求血,结合,对学生的综合能力的运用是一个很大的考验,只有熟练掌握了三角的基本公式和基本方法技巧,才能运用自如,完整解答问题.三,有益的启示《考试说明》明确提出:要在”突出数学基础知识,基本技能,基本思想方法的考查”的同时,”重视数学基本能力和综合能力的考查”,”注重数学应用意识和创新意识的考查”,由此可见,坚持和加强在知识的交汇点处命题势在必行.在知识的交汇处命题,一方面数学学科知识之间的纵横交融,渗透综合的鲜明特点,将正,余弦定理与向量,解析几何,立体几何,数列,不等式,数列,方程等重要知识有效交汇于一体;另一方面,可有效考查学生的各类方法技能和重要数学思想的合理运用,把对学生的数学思维能力和综合应用能力的考查融合在对学生双基考二,+l=_厂(n)?型累积法:=—旦L?上…??塑?c—l(一2nl.,所以=-厂(n一1(n一2(n一3)一1)01.例2求数列.t=_『1,%=_}.%一(n≥2)的通项公式.解:当n≥2时,=堕?盟?a4…??L.al0l啦%一1【即%=面可×}:一4,l2—1’当n=l,=}=所以r(n∈N+)?查之中,因此我们必须高度重视,积极应对.数学知识交汇题,一般具有背景清晰且内涵丰富,新颖脱俗且思路灵活的特点,这就需要我们在熟练掌握数学基础知识和基本技能的基础上,深刻理解题意, 洞察内在联系,准确选择方法,要依据题设条件,合理进行变换,灵活进行转化,严谨完善解题.正弦定理,余弦定理在高考中,一般不单设试题,而是融于其他知识当中去考查,学生学习中应重视四大数学思想方法的培养.在运用定理时,要注重与其他知识的交汇,多角度联想,观察和分析问题,教师要教给学生学习的方法, 让学生学会学习,真正做到与其他知识融会贯通,切实提高学生分析问题,解决问题的能力,,促进其思维能力的发展和提高.练习:已知数列{吼}满足土上_=n (11,∈N+),ot=l,求n,1.三,%+I--,pa~+叮型方法:1)+小t?),.’,再根据等比数列的相关知识求(2)+.～%=p(%一an一)再用累加法求.(争一,先用累加法求争,再求?例3在数列{}中,a.=1,当n≥2时,有%=3一1+2,求.解法1:设+A=3(%l+A),即有=3～1+2A,对比=3l+2,得A=1.于是%+I=3(1+1),数列{+}是以a.+l=2为首项,以3为公比的等比数列,所以有=2?3一1.解法2:由已知递推式,得%+l=3%+2,%=3a.一l+2(n≥2).上述两式相减,得%+l～:3(%一%一1),因此,数列{%+.一nJl}是以o.2一a=4. 为首项,以3为公比的等比数列.所以+l一=4?3’,即3一%=4?3,所以%=2?3’1.练习:已知{}的首项n.=n(a为常数),;2a.一1(n∈N+,n≥2),求‰四,%+l=p%+/(n)型例4设数列{}满足,a=1,=一一J+2n一1(n≥2),求通项公式%.解:设6=+An,+曰,则%=b一An—B,%一l=6一l—A(一1)一B,所以b一An—B=an=1[6-I--A(n一1)一B]+2n一1,即b=1b—j+(A+2)n+(}A+一-).设所以b=16且b=%一4n+6.厶由于il6}是以3为首项,以为公比的等比数列,所以有b=3丁._由此得:一;:十4n.6.【说明】通过引入一些尚待确定的系数转化命题结构,经过变形与比较,把问题转化成基本数列(等差或等比数列). 五,+f:p%+q型例5已知b≠O,b≠士1,伪=,=了’+-+(n≥2),写出用/1,和b表示%的通项公式,解:将已知递推式两边乘以(1+6)”,得(1+6)=6(1+6)’an+l+,又设‰=(1+6),于是,原递推式化为n=bxT,仿类型三,可解得%=b—b=‘故%:.【说明】对于递推式+.=p+g,可两边除以q’,得争+上争’争,引入辅助数列6争,得n+争6n+,然后可归结为类型三.g六,+2p%+j+口型方法:待定系数法,设%+.一衄(一一%),构造等比数列.例6已知数列{}中,=1啦=2,+=++,求%.解:在%+2=%+l+两边减去+l,得%+2一+I:一一(+l一).所以{%+一%{是以02一n.=l为首项,以一为公比的等比数列.所以%+一=(一})..令E式=1,2,3,:一.(一1),再把这(n一1)个等式累加,得%一o=1 (一})+(_丁1)+?+(一})一=囊[1(一】.以;1哼((一}-11..t:,线性分式型..例7.(倒数法)已知数列{}中,a.: },+J=打,求{}的通项公式-解:j一::+2,所以{}是以为-NN,公差为2的等差数列,即l_:丁5+2(一1):,jj所以丁?练习:已知数列{}中,a.=1,=精,求{%}的通项公式?解.=}:击,所以f专}是以1为首项,公差为2的等差数列.所以=l+2(一1)_2,卜l,即Sn?所以=一一丁一1一=一fl(,n=1),删{2n1一2n3(.1一一…等差,等比数列是两类最基本的数列,是数列部分的重点,自然也是高考考查的热点,而考查的目的在于测试学生灵活运用知识的能力,这个”灵活”往往集中在”转化”的水平上.转化的目的是化陌生为熟悉,当然首先是等差,等比数列,根据不同的递推公式,采用相应的变[2011年第2期]基础教育论坛●_’r4:=A得解Il,l0一扛一2++A一2A一2。

三项递推关系求通项要求一个递推关系的通项，需要知道递推关系的初始条件和递推公式。

以下是三种常见的递推关系的通项求解方法：1. 线性递推关系：假设线性递推关系为 a_n = p*a_(n-1) + q*a_(n-2)，其中p和q为常数，a_n为第n项的值。

我们需要知道的初始条件为 a_0和 a_1。

假设通项形如a_n = x^n，其中x为常数。

将其代入递推关系，得到：x^n = p*x^(n-1) + q*x^(n-2)整理，得到特征方程：x^2 - p*x - q = 0解特征方程，得到x1和x2，这两个根就是递推关系的通项的形式。

2. 非线性递推关系：假设递推关系为 a_n = f(a_(n-1), a_(n-2))，其中f为一个函数。

我们需要知道的初始条件为 a_0 和 a_1。

通常情况下，求非线性递推关系的通项比较困难，没有统一的解法。

需要根据具体的递推关系和函数f的性质来进行分析和求解。

3. 递归递推关系：递归递推关系是一种常见的递推关系形式，常用于定义数列的递推关系。

比如斐波那契数列的递推关系为：F_n = F_(n-1) + F_(n-2)，初始条件为 F_0 = 0 和 F_1 = 1。

可以通过数学归纳法证明，斐波那契数列的通项为F_n = (φ^n - (-φ)^(-n)) / √5，其中φ=(1+√5)/2为黄金分割比。

总结来说，要求一个递推关系的通项，需要根据具体的递推关系形式进行分析和解决。

对于线性递推关系，可以通过特征方程解得通项表达式；对于非线性递推关系，需要具体问题具体分析；对于递归递推关系，可以通过数学归纳法证明通项的形式。

由递推公式求通项的9种方法1．a n ＋1＝a n ＋f (n )型把原递推公式转化为a n ＋1－a n ＝f (n )，再利用累加法(逐差相加法)求解，即a n ＝a 1＋(a 2－a 1)＋(a 3－a 2)＋…＋(a n －a n －1)＝a 1＋f (1)＋f (2)＋f (3)＋…＋f (n －1)．[例1] 已知数列{a n }满足a 1＝12，a n ＋1＝a n ＋1n 2＋n，求a n . [解] 由条件，知a n ＋1－a n ＝1n 2＋n ＝1n (n ＋1)＝1n －1n ＋1，则(a 2－a 1)＋(a 3－a 2)＋(a 4－a 3)＋…＋(a n －a n －1)＝⎝⎛⎭⎫1－12＋⎝⎛⎭⎫12－13＋⎝⎛⎭⎫13－14＋…＋⎝ ⎛⎭⎪⎫1n －1－1n ， 所以a n －a 1＝1－1n. 因为a 1＝12，所以a n ＝12＋1－1n ＝32－1n. 2．a n ＋1＝f (n )a n 型把原递推公式转化为a n ＋1a n＝f (n )，再利用累乘法(逐商相乘法)求解，即由a 2a 1＝f (1)，a 3a 2＝f (2)，…，a n a n －1＝f (n －1)，累乘可得a n a 1＝f (1)f (2)…f (n －1)．[例2] 已知数列{a n }满足a 1＝23，a n ＋1＝n n ＋1·a n，求a n . [解] 由a n ＋1＝n n ＋1·a n ，得a n ＋1a n ＝n n ＋1， 故a n ＝a n a n －1·a n －1a n －2·…·a 2a 1·a 1＝n －1n ×n －2n －1×…×12×23＝23n .即a n ＝23n . 3．a n ＋1＝pa n ＋q (其中p ，q 均为常数，pq (p －1)≠0)型对于此类问题，通常采用换元法进行转化，假设将递推公式改写为a n ＋1＋t ＝p (a n ＋t )，比较系数可知t ＝q p －1，可令a n ＋1＋t＝b n ＋1换元即可转化为等比数列来解决．[例3] 已知数列{a n }中，a 1＝1，a n ＋1＝2a n ＋3，求a n .[解] 设递推公式a n ＋1＝2a n ＋3可以转化为a n ＋1－t ＝2(a n －t )，即a n ＋1＝2a n －t ，则t ＝－3.故递推公式为a n ＋1＋3＝2(a n ＋3)．令b n ＝a n ＋3，则b 1＝a 1＋3＝4，且b n ＋1b n ＝a n ＋1＋3a n ＋3＝2. 所以{b n }是以b 1＝4为首项，2为公比的等比数列．所以b n ＝4×2n －1＝2n ＋1，即a n ＝2n ＋1－3. 4．a n ＋1＝pa n ＋q n (其中p ，q 均为常数，pq (p －1)≠0)型(1)一般地，要先在递推公式两边同除以q n ＋1，得a n ＋1qn ＋1＝p q ·a n q n ＋1q ，引入辅助数列{b n }⎝⎛⎭⎪⎫其中b n ＝a n q n ，得b n ＋1＝p q ·b n ＋1q ，再用待定系数法解决；(2)也可以在原递推公式两边同除以pn ＋1，得a n ＋1p n ＋1＝a n p n ＋1p ·⎝ ⎛⎭⎪⎫q p n ，引入辅助数列{b n }⎝ ⎛⎭⎪⎫其中b n ＝a n p n ，得b n ＋1－b n ＝1p ⎝ ⎛⎭⎪⎫q p n ，再利用叠加法(逐差相加法)求解．[例4] 已知数列{a n }中，a 1＝56，a n ＋1＝13a n ＋⎝⎛⎭⎫12n ＋1，求a n . [解] 法一：在a n ＋1＝13a n ＋⎝⎛⎭⎫12n ＋1两边乘以2n ＋1，得2n ＋1·a n ＋1＝23(2n ·a n )＋1. 令b n ＝2n ·a n ，则b n ＋1＝23b n ＋1， 根据待定系数法，得b n ＋1－3＝23(b n －3)． 所以数列{b n －3}是以b 1－3＝2×56－3＝－43为首项， 以23为公比的等比数列． 所以b n －3＝－43·⎝⎛⎭⎫23n －1，即b n ＝3－2⎝⎛⎭⎫23n .于是，a n ＝b n 2n ＝3⎝⎛⎭⎫12n －2⎝⎛⎭⎫13n . 法二：在a n ＋1＝13a n ＋⎝⎛⎭⎫12n ＋1两边乘以3n ＋1，得 3n ＋1a n ＋1＝3n a n ＋⎝⎛⎭⎫32n ＋1.令b n ＝3n ·a n ，则b n ＋1＝b n ＋⎝⎛⎭⎫32n ＋1.所以b n －b n －1＝⎝⎛⎭⎫32n ，b n －1－b n －2＝⎝⎛⎭⎫32n －1，…， b 2－b 1＝⎝⎛⎭⎫322.将以上各式叠加，得b n －b 1＝⎝⎛⎭⎫322＋…＋⎝⎛⎭⎫32n －1＋⎝⎛⎭⎫32n . 又b 1＝3a 1＝3×56＝52＝1＋32， 所以b n ＝1＋32＋⎝⎛⎭⎫322＋…＋⎝⎛⎭⎫32n －1＋⎝⎛⎭⎫32n ＝1·⎣⎡⎦⎤1－⎝⎛⎭⎫32n ＋11－32＝2⎝⎛⎭⎫32n ＋1－2， 即b n ＝2⎝⎛⎭⎫32n ＋1－2.故a n ＝b n 3n ＝3⎝⎛⎭⎫12n －2⎝⎛⎭⎫13n . 5．a n ＋1＝pa n ＋an ＋b (p ≠1，p ≠0，a ≠0)型这种类型一般利用待定系数法构造等比数列，即令a n ＋1＋x (n ＋1)＋y ＝p (a n ＋xn ＋y )，与已知递推式比较，解出x ，y ，从而转化为{a n ＋xn ＋y }是公比为p 的等比数列．[例5] 设数列{a n }满足a 1＝4，a n ＝3a n －1＋2n －1(n ≥2)，求a n .[解] 设递推公式可以转化为a n ＋An ＋B ＝3[a n －1＋A (n －1)＋B ]，化简后与原递推式比较，得⎩⎪⎨⎪⎧2A ＝2，2B －3A ＝－1，解得⎩⎪⎨⎪⎧A ＝1，B ＝1. 令b n ＝a n ＋n ＋1.(*)则b n ＝3b n －1，又b 1＝6，故b n ＝6·3n －1＝2·3n ， 代入(*)式，得a n ＝2·3n －n －1.6．a n ＋1＝pa r n (p >0，a n >0)型这种类型一般是等式两边取对数后转化为a n ＋1＝pa n ＋q 型数列，再利用待定系数法求解．[例6] 已知数列{a n }中，a 1＝1，a n ＋1＝1a ·a 2n(a >0)，求数列{a n }的通项公式． [解] 对a n ＋1＝1a ·a 2n的两边取对数， 得lg a n ＋1＝2lg a n ＋lg 1a. 令b n ＝lg a n ，则b n ＋1＝2b n ＋lg 1a. 由此得b n ＋1＋lg 1a ＝2⎝⎛⎭⎫b n ＋lg 1a ，记c n ＝b n ＋lg 1a，则c n ＋1＝2c n ， 所以数列{c n }是以c 1＝b 1＋lg 1a ＝lg 1a为首项，2为公比的等比数列． 所以c n ＝2n －1·lg 1a. 所以b n ＝c n －lg 1a ＝2n －1·lg 1a －lg 1a＝lg ⎣⎡⎦⎤a ·⎝⎛⎭⎫1a 2n －1＝lg a 1－2n ， 即lg a n ＝lg a 1－2n ，所以a n ＝a 1－2n .7．a n ＋1＝Aa n Ba n ＋C(A ，B ，C 为常数)型 对于此类递推数列，可通过两边同时取倒数的方法得出关系式[例7] 已知数列{a n }的首项a 1＝35，a n ＋1＝3a n 2a n ＋1，n ＝1,2,3，…，求{a n }的通项公式． [解] ∵a n ＋1＝3a n 2a n ＋1，∴1a n ＋1＝23＋13a n，∴1a n ＋1－1＝13⎝⎛⎭⎫1a n －1. 又1a 1－1＝23， ∴⎩⎨⎧⎭⎬⎫1a n －1是以23为首项，13为公比的等比数列， ∴1a n －1＝23·13n －1＝23n ， ∴a n ＝3n 3n ＋2. 8.)(1n f a a n n =++型 由原递推关系改写成),()1(2n f n f a a n n -+=-+然后再按奇偶分类讨论即可例8.已知数列{}n a 中，,11=a .21n a a n n =++求n a 解析：.21n a a n n =++2212+=+++n a a n n ，故22=-+n n a a 即数列{}n a 是奇数项和偶数项都是公差为2的等差数列，⎩⎨⎧∈≥-=∴*,1,1,N n n n n n n a n 且，为偶数为奇数 9.)(1n f a a n n =⋅+型将原递推关系改写成)1(12+=+⋅+n f a a n n ，两式作商可得,)()1(2n f n f a a n n +=+然后分奇数、偶数讨论即可 例9.已知数列{}n a 中，,2,311n n n a a a =⋅=+求{}n a 解析：⎪⎩⎪⎨⎧∈≥⋅⋅=+-N n n n n a n n n ,1,231,23221，为偶数为奇数。

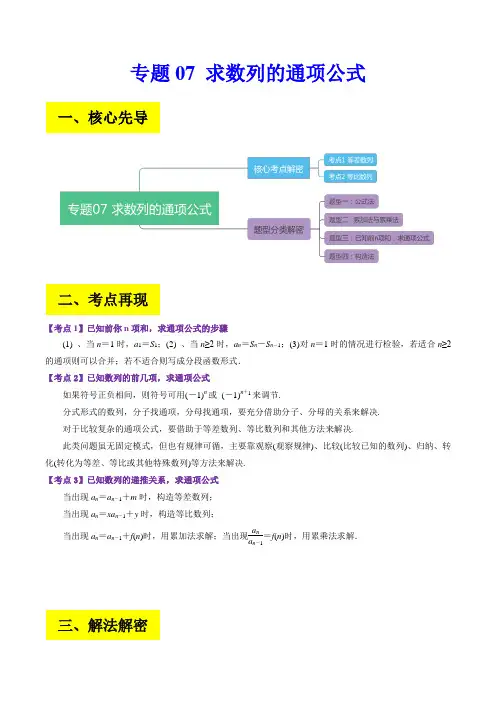
专题07 求数列的通项公式【考点1】已知前你n 项和，求通项公式的步骤(1) 、当n ＝1时，a 1＝S 1；(2) 、当n ≥2时，a n ＝S n －S n －1；(3)对n ＝1时的情况进行检验，若适合n ≥2的通项则可以合并；若不适合则写成分段函数形式． 【考点2】已知数列的前几项，求通项公式如果符号正负相间，则符号可用(－1)n 或 (－1)n＋1来调节.分式形式的数列，分子找通项，分母找通项，要充分借助分子、分母的关系来解决. 对于比较复杂的通项公式，要借助于等差数列、等比数列和其他方法来解决.此类问题虽无固定模式，但也有规律可循，主要靠观察(观察规律)、比较(比较已知的数列)、归纳、转化(转化为等差、等比或其他特殊数列)等方法来解决. 【考点3】已知数列的递推关系，求通项公式当出现a n ＝a n －1＋m 时，构造等差数列； 当出现a n ＝xa n －1＋y 时，构造等比数列； 当出现a n ＝a n －1＋f (n )时，用累加法求解；当出现a na n －1＝f (n )时，用累乘法求解．三、解法解密 二、考点再现一、核心先导若数列{}n a 满足1n n a a an b ++=+，则数列{}{}221,n n a a -都是公差为a 的等差数列，若数列{}n a 满足()10,0,1n t n n a a a b a b b ++⋅=⋅≠≠≠，则数列{}{}221,n n a a -都是公比为b 的等比数列.题型一:公式法例1、（2022·全国·武功县普集高级中学模拟预测（理））记n S 为各项均为正数的等比数列{}n a 的前n 项和，378S =，312a =，则5a =（ ）A ．14B ．18C ．1D ．2【变式训练1-1】、（2022·广西·模拟预测（理））在等比数列{}n a 中，若253,6a a ==，则11a =___________. 例2、（2022·浙江台州·模拟预测）已知公差为2的等差数列{}n a 中，3a ，4a ，7a 成等比数列. (1)求n a ；(2)设2n an n b a =+，求数列{}n b 的前n 项和n S .【答案】(1)25n a n =-【变式训练2-1】、（2022·上海松江·二模）在等差数列{}n a 中，已知1210a a +=，34530a a a ++=． (1)求数列{}n a 的通项公式；(2)若数列{}n n a b +是首项为1，公比为3的等比数列，求数列{}n b 的前n 项和n S ．题型二:累加法与累乘法(一) 、用累加法求数列的通项公式例3、（2022·上海市控江中学高二期末）己知数列{}n a 满足111,2(,1)n n a a a n n n +==+∈≥N ，则其通项公式n a =________．【答案】2n n 1-+ 【解析】 【分析】利用累加法即可求出数列{}n a 的通项公式. 【详解】因为12n n a a n +=+，所以12n n a a n +-=，所以212a a -=，324a a -=，436a a -=，…，()121n n a a n --=-，把以上1n -个式子相加，得()()()()()213243124621n n a a a a a a a a n -++++++++---=--……， 即()()122212n n a n a +---=，所以2211nn n a an n =-+=-+.故答案为：2n n 1-+.【变式训练3-1】、在数列{}n a 中,112a =,12141n n a a n +-=-,则该数列的通项公式n a = ． 【分析】题目已知条件是1()(2n n a a f n n --=≥,且n *∈N ）形式,用叠加原理求解.【解析】因为121111()4122121n n a a n n n +-==---+,所以运用累加法即可得到：1122111111111()()()[(1)()()](1)23352321221n n n n a a a a a a n n n ----+-++-=-+-++-=----,所以11143(1)22142n n a a n n -=+-=--,故应填4342n n --． 【点评】当1()(2n n a a f n n --=≥,且n *∈N ）满足一定条件时,可用1()n n n a a a -=-+12()n n a a ---+…211()a a a -+来求通项n a ,这种方法通常叫累加法. 本题用到裂项相消求和,相消时应注意消去的项规律,及消去哪些项,保留哪些项,于是前n 项的和变成首尾若干少数项之和.还有不少同学会出现的错误,认为21d n n =-或21d n n =+是常数,实际上21d n n =-或21d n n=+是个变量,n 变化d 随之改变.【变式训练3-2】、（2022·浙江柯桥·高二期末）已知等差数列{}n a 中，16a =，前5项的和为590S =，数列{}n b 满足11b =，()*12N n n n b b n +-=∈．(1)求数列{}n a ，{}n b 的通项公式；(2)记n n n c a b =-，求数列{}n c 的前n 项和n T ．【答案】(1)()6N*n a n n =∈，()*21N n n b n =-∈；(2)()()211234224234665n n n n n n T n n n ++⎧+-+≤⎪=⎨--+≥⎪⎩. 【解析】 【分析】（1）利用等差数列求和公式可得6d =，进而可得()6N*n a n n =∈，再利用累加法可求n b ，即得； （2）由题可得()()62142615n n n n n n n c a b n n ⎧-+≤⎪=-=⎨--≥⎪⎩，然后利用分组求和法即得.(1)设公差为d ，由题设可得5456902d ⨯⨯+=， 解得6d =，所以()6N*n a n n =∈； 当2n ≥时，2123221111222222n n n n n b b b b b b b b ----=⎫⎪-=⎪⇒-=++⋅⋅⋅+⎬⋅⋅⋅⋅⋅⋅⎪⎪-=⎭，∴122112nn n b -==--，当1n =时，11b =（满足上述的n b ），所以()*21N n n b n =-∈．(2)∵()()62142615n n n n n n n c a b n n ⎧-+≤⎪=-=⎨--≥⎪⎩．当4n ≤时，()()21271361222nn n T c c c n =++⋅⋅⋅+=++⋅⋅⋅++-++⋅⋅⋅+⎡⎤⎣⎦ ()()212761212nn n -++=-- 213422n n n +=+-+．当5n ≥时，()()561234222313761nn n T c c c n ⎡⎤=++⋅⋅⋅+=+++⋅⋅⋅+-++⋅⋅⋅+⎣⎦()()()54212463234122n n n ---+=+--1223466n n n +=--+．综上所述：()()211234224234665n n n n n n T n n n ++⎧+-+≤⎪=⎨--+≥⎪⎩． (二) 、用累乘法求数列的通项公式例4、（2022·安徽黄山·一模）已知数列{}n a 满足12a =，()1221n n n a a n ++=+，则20211232020a a a a a =+++⋅⋅⋅+___________.【答案】10111010【解析】 【分析】利用累乘法可求得数列{}n a 的通项公式，利用错位相减法可求得122020+++a a a ，即可求得所求代数式的值. 【详解】因为数列{}n a 满足12a =，()1221n n n a a n ++=+，则()1221n n n a a n ++=+，所以，当2n ≥时，()()132112121232421223n n n n n a a a a a n a a a n--+⨯⨯=⋅⋅⋅⋅=⨯⨯⨯⨯=+⋅， 12a =也满足()112n n a n -=+⋅，所以，对任意的N n *∈，()112n n a n -=+⋅.令122020S a a a =+++，则012201922324220212S =⨯+⨯+⨯++⨯，可得1220192020222322020220212S =⨯+⨯++⨯+⨯，上述两个等式作差得()20191220192020202020202122222202122202122020212S --=++++-⨯=+-⨯=-⨯-，所以，202012202020202a a a S +++==⨯，因此，2020202120201232020202221011=202021010a a a a a ⨯=+++⋅⋅⋅+⨯. 故答案为：10111010. 例5、（2021·河北·沧州市一中高三阶段练习）已知数列{}n a 中，112a =，且满足1(1)n n na n a +=+. (1)求数列{}n a 的通项公式；(2)设112n n n b a λ+⎛⎫=-⎪⎝⎭，若对任意的*N n ∈，数列{}n b 是单调递减数列，求实数λ的取值范围. 【答案】(1)2n na = (2)1,3∞⎛⎫+ ⎪⎝⎭【解析】 【分析】（1）利用累乘法求得n a . （2）由10n nb b 分离常数λ，结合函数的性质求得λ的取值范围.(1)依题意0n a ≠，故11n n a n a n ++=，从而11n n a n a n -=-，2n ≥， 故3212112n n n a a a a na a a a -⋅==，2n n a =， 当1n =时，上式也符合，所以2n n a =. (2)由（1）知，112221n n n n b a n λλ+⎛⎫⎛⎫=-=-⎪ ⎪+⎝⎭⎝⎭， 若对任意的*N n ∈，数列{}n b 是单调递减数列，则1422021n n n b b n n λ+⎛⎫-=--<⎪++⎝⎭对任意的*N n ∈恒成立， 即4221maxn n λ⎛⎫>- ⎪++⎝⎭， 又()()4222221123n n n n n n n-==++++++， 因为函数()20y x x x=+>在区间()0,2上单调递减， 在()2,+∞上单调递增，所以由对勾函数的性质可知，当1n =或2n =时，23n n++取得最小值6， 即4221n n -++取得最大值13，故实数λ的取值范围为1,3∞⎛⎫+ ⎪⎝⎭.【变式训练5-1】、数列{}n a 中，前n 项和为n S ， 2nn na S = (1)求数列{}n a 的通项公式；学=科网 (2)令2112n n n n n S S b S S ++++=+，证明： 12223n n b b b n <+++<+.【解析】(1) 2nn na S =， ()()11122n n n a S n ---=≥，两式相减得： ()1122n n n n a na a --=-， 整理得： ()()121n n n a n a --=-， （叠乘法）因为()1132n n a n n a n --=≥-，所以3221a a =， 4332a a =，…， 112n n a n a n --=-， 相乘得21na n a =-，且当n =1、2时，满足此式， 所以()21n a n a =-.(2) ()()()()()()22222112212122n n n a n na b n na n n a +++=++++ 22n nn n +=++， 因为n b 2>，所以122n b b b n +++>；222211211222n n nb n n n n n n +=++=++-+⎛⎫=+- ⎪+⎝⎭ 12111112213242nb b b n n n +++⎛⎫=+-+-+⋯+- ⎪+⎝⎭ 11122123212n n n n ⎛⎫=++--<+ ⎪++⎝⎭.【变式训练5-2】、（2022·吉林·东北师大附中模拟预测）已知数列{}n a 中，11a =，n S 是数列{}n a 的前n 项和，且32n n a S n =+. (1)求数列{}n a 的通项公式： (2)证明：12123nn S S S ++⋅⋅⋅+<. 【答案】(1)()12n n n a +=(2)证明见解析 【分析】（1）利用n a 与n S 关系可推导得到111n n a n a n -+=-，利用累乘法即可求得n a ；题型三:已知前n 项和，求通项公式例6、（2022·湖南·安仁县第一中学模拟预测）已知数列{}n a 中，前n 项的和为n S ，且34n n S a =- (1)求数列{}n a 的通项公式； (2)如果123123n n a a a a ++++<92-823n⎛⎫⨯⎪⎝⎭恒成立，求n 最小值. nna ++，解不等式即可， nna ++12()23n n -++⨯32)312n -++⨯212()32()]3n -+++n⎫⎪⎭，【变式训练6-1】、（2022·四川资阳·一模（理））已知数列{}n a 的前n 项和为n S ，满足3232S a =+，且12n n a S a =+．(1)求{}n a 的通项公式； (2)数列{}n b 满足11231232n nna b b b b +++++=-，求{}n b 的前n 项和n T ． 2q为公比的等比数列，2得13a a +122n -=⋅=n nna b ++=3131n n b b --+++=，2n ≥12，符合b 1212222n nn b ++=+++121231222n n n 012111112222n n n T T --==++++-题型四:构造法例7、（2022·安徽·合肥市第十一中学高二期末）已知数列{}n a 满足13a =，()*121N n n a a n +=+∈.(1)求证：数列{}1n a +是等比数列； (2)求数列{}n a 的通项公式及前n 项的和n S . 【答案】(1)证明见解析； (2)121n n a +=-，224n n S n +=--. 【解析】 【分析】 （1）证明出1121n n a a ++=+，即可证得结论成立； （2）由（1）的结论并确定数列{}1n a +的首项和公比，可求得数列{}n a 的通项公式，再利用分组求和法可求得n S . (1)证明：因为数列{}n a 满足13a =，()*121N n n a a n +=+∈，则()1121n n a a ++=+，且114a +=，则218a +=，3116a +=，，以此类推可知，对任意的N n *∈，10n a +>，所以，1121n n a a ++=+，故数列{}1n a +为等比数列. (2)解：由（1）可知，数列{}1n a +是首项为4，公比为2的等比数列，则111422n n n a -++=⨯=，所以，121n n a +=-，因此，()()()()()23412341212121212222n n n S n ++=-+-+-++-=++++-()222122412n n n n +-=-=---.【变式训练7-1】、（2022·江苏镇江·高二期末）已知数列{}n a 满足111,21,.n n a a a n N *+==+∈(1)证明数列{}1n a +是等比数列，并求数列{}n a 的通项公式； (2)令(1)n n b n a =+，求数列{}n b 的前n 项和.n T【答案】(1)证明见解析，21nn a =-(2)1(1)2 2.n n T n +=-⋅+ 【解析】 【分析】（1）根据等比数列的定义证明数列{}1n a +是以2为首项，2为公比的等比数列，进而求解得答案； （2）根据错位相减法求和即可. (1)解：数列{}n a 满足111,21,.n n a a a n N *+==+∈112(1)n n a a ++=+，∴数列{}1n a +是以112a +=为首项，2为公比的等比数列， 11222n n n a -∴+=⋅=，即21n n a =-；∴21nn a =-(2) 解：(1)2n n n b n a n =+=⋅，231222322n n T n ∴=⋅+⋅+⋅++⋅，23412122232(1)22n n n T n n +=⋅+⋅+⋅++-⋅+⋅，2311112(21)22222222221n nn n n n n T n n n ++++-∴-=++++-⋅=-⋅=--⋅-，1(1)2 2.n n T n +∴=-⋅+A 组 基础巩固1．（2022·广西北海·一模（理））在等差数列{}n a 中，38a =，712a =，则12a =（ ） A ．19 B ．18C ．17D ．20【答案】C【分析】利用已知条件列方程组求出1,a d ，从而可求出12a . 【详解】设等差数列{}n a 的公差为d ，则由题意可得1128612a d a d +=⎧⎨+=⎩，解得161a d =⎧⎨=⎩， 所以1211161117a a d =+=+=， 故选：C.2．（2022·全国·模拟预测（文））在数列{}n a 中，()()()111,11N n n a n n a a n *+=+-=∈，则2022a =（ ）A ．40432022B ．20212022C ．40402021D ．20202021()21111111111212a a a n n n n ⎛⎫⎛⎫⎛⎫++-+=-+-++-+ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭3．（2022·广西·模拟预测（文））在等比数列{}n a 中，124a a +=，若1a 、22a +、3a 成等差数列，则{}n a 的公比为（ ） A ．2 B ．3C ．4D ．5【答案】B4．（2010·山西临汾·模拟预测（文））已知等差数列{}n a 的公差是2，若1a ，3a ，4a 成等比数列，则2a 等于（ ） A ．6- B ．4- C ．8- D ．10-【答案】A【分析】利用等比中项，结合等差数列通项公式列方程求解即可. 【详解】解：因为等差数列{}n a 的公差为2，且1a ，3a ，4a 成等比数列， 所以2314a a a =，即()()()2222224a a a +=-+， 解得26a =- ， 故选：A5．（2022·山西大附中三模（理））已知等差数列{}n a 的各项均为正数，其前n 项和为n S ，且满足652317a S a a ==，，则12a =（ ）A ．28B ．30C ．32D ．35【答案】D【分析】根据等差数列基本量的计算可得公差和首项的值,进而代入即可求解.【详解】设公差为d 且0d >，由652317a S a a ==，，得()()111115172510230a d a a d a d a d d d +=⎧=⎧⎪+=++⇒⎨⎨=⎩⎪>⎩， 故1211123335a a d =+=+=， 故选：D6．（2022·广东·肇庆市外国语学校模拟预测）若数列{}n a 满足121n n a a +=-，则称{}n a 为“对奇数列”．已知正项数列{}1n b +为“对奇数列”，且12b =，则n b =（ ）A ．123n -⨯B ．12n -C ．12n +D ．2n【答案】D【分析】根据题意可得()11211n n b b ++=+-，进而可得{}n b 为等比数列，再求得通项公式即可.【详解】由题意得()11211n n b b ++=+-，所以12n n b b +=，又12b =，所以{}n b 是首项为2，公比为2的等比数列，所以1222n nn b -=⨯=．故选：D ．7．（2022·四川·成都七中模拟预测（文））设数列{}n a 满足11,1n n n a a a ++=-且112a =，则2022a =（ ）A ．2-B ．13-C ．12D ．38．（2020·云南·昆明一中模拟预测（理））已知等比数列{}n a 的前n 项和为()*3n n S a n =+∈N ，则实数a 的值是（ ） A ．3- B ．3 C ．1- D ．1【答案】C【分析】先求出1a 23,a a ，由2213a a a 解得即可；【详解】等比数列{}n a 的前n 项和为()*3n n S a n =+∈N ，当1n =时，可得1113a a S +==，可得13a a =+，当2n ≥时，113n n S a --=+，则()1113323n n n n n n a S S a a ---==-=⋅-++所以213123236,2318a a --=⋅==⋅=因为{}n a 为等比数列， 所以2213a a a ，即()66183a ⨯=+解得1a =-，经检验符合题意. 故选：C ．9．（2022·吉林·东北师大附中模拟预测（文））等差数列{}n a 中，1239a a a ++=，4516a a +=，则6a =（ ） A ．9 B ．10 C ．11 D ．12【答案】C【分析】根据条件求出1,a d 即可.【详解】因为1231339a a a a d ++=+=，4512716+=+=a a a d ， 所以可解得1a 1,d 2，所以61511011a a d =+=+=， 故选：C10．（2022·江苏省木渎高级中学模拟预测）已知数列{}n a 满足：①先单调递减后单调递增：②当3n =时取得最小值．写出一个满足条件的数列{}n a 的通项公式n a =_________．【答案】()()2*3N n n a n =-∈【分析】利用数列单调性的定义进行判断，从而得到数列的最值.【详解】设()()2*3N n a n n =-∈，则()212n a n +=-，()()2122325n n a a n n n +-=---=-，当120152,n n n n a a +-=-≤<≤，数列单调递减，当1503,2n n n a a n +-=->≥，数列单调递增，即1234a a a a >><<⋅⋅⋅， 可得当3n =时数列取得最小值，故答案为：()()2*3N n n a n =-∈11．（2022·河南开封·模拟预测（理））在等比数列{}n a 中，n S 为其前n 项和，若33a =，39S =，则{}n a 的公比为______．12．（2022·陕西西安·模拟预测（文））已知等差数列{}n a 的公差1d =，且3a ，5a ，6a 成等比数列． (1)求数列{}n a 的通项公式； (2)求数列{}n a 的前n 项和为n S ．13．（2022·河南·模拟预测（理））若数列{}n a 满足11a =，12n n a a n +-=． (1)求{}n a 的通项公式；(2)证明：121112na a a +++<． ()2112(1)2(2)21a a a n n ++-+=-+-+++222(1)2n n -+⋅-=12=<； 111=-， 2311111111111112231n n a a a a n n ⎛⎫++=++++<+-+-++- ⎪-⎝⎭12n=-<12na ++<； 21n n -+.B 组 能力提升14．（2023·江西景德镇·模拟预测（理））已知数列{}n a 为等差数列，数列{}n b 为等比数列且公比2q .数列{}n a 和数列{}n b 的前n 和分别为n S 和n T ，且满足222n n T S +=，则等差数列{}n a 的通项公式为_____________. 【答案】42n a n =-【分析】分别令1,2,3n =，得到224468222T S T S T S+=⎧⎪+=⎨⎪+=⎩，设{}n a 的公差为d ，化简得到114275634740a d a d -=⎧⎨-=⎩，解方程组可得答案.【详解】由已知得，令1,2,3n =得，222244446868222222T S T S T S T S T S T S ⎧+==-⎧⎪⎪+=⇒=-⎨⎨⎪⎪+==-⎩⎩，根据等比数列求和公式，得到2141613,15,63T b T b T b ===，故12141832152632b S b S b S =-⎧⎪=-⎨⎪=-⎩428225(2)221(2)S S S S -=-⎧⇒⎨-=-⎩，设{}n a 的公差为d ，则1111462105108282422142a d a d a d a d +-=+-⎧⎨+-=+-⎩，化简得111427562347404a d a a d d ⎧-==⎧⇒⎨⎨-==⎩⎩，42n a n =-故答案为：42n a n =-15．（2022·广西·模拟预测（文））已知等比数列{}n a 满足31352,4a a a a +=+=，则79a a +=___________. 16．（2022·河南省叶县高级中学模拟预测（文））已知数列{}n a 为等比数列，1272a a +=，2336a a +=，则4a =______. 【答案】6【分析】设等比数列{}n a 的首项为1a ，公比为q ，由题意可得到11(1)72(1)36a q a q q +=⎧⎨+=⎩，能求出1a 和q ，即可求出答案【详解】解：设等比数列{}n a 的首项为1a ，公比为q ，由题意可得1211223117236a a a a q a a a q a q +=+=⎧⎨+=+=⎩即11(1)72(1)36a q a q q +=⎧⎨+=⎩， 易得10q +≠，所以两式相除，解得12q =， 将12q =代入1(1)72a q +=可得148a =，所以3416a a q ==， 故答案为：617．（2022·云南民族大学附属中学模拟预测（理））若数列{}n a 满足12a =，()*121N n n n a a a n ++++=∈，则其前2020项和为___________. 【答案】675【分析】利用分组求和法求得正确答案. 【详解】12a =，121n n n a a a ++++=()()()2020123456720182019202016731675S a a a a a a a a a a a ∴=+++++++⋯⋯+++=+⨯=故答案为：67518．（2022·安徽·全椒县第八中学模拟预测（理））雪花曲线是由瑞典人科赫（Koch ）于1904年提出的一种分形曲线，其形态似雪花，故称雪花曲线，又称科赫雪花．雪花曲线是由等边三角形开始，把三角形的每条边三等分，并在每条边三等分后的中段向外作新的等边三角形，但要去掉与原三角形叠合的边．接着对所得新图形的每条边继续上述过程，即在每条边三分后的中段，向外画新的“尖形”．不断重复这样的过程，便产生了雪花曲线．下图分别是0、1、2、3级的雪花曲线，若第0级的等边三角形边长等于1，则第4级的雪花曲线周长等于______．19．（2020·全国·模拟预测（文））记数列{}n a 的前n 项和为n S ，若11a =，12n n a S +=（n 为正整数），则数列{}n a 的通项公式为________．故答案为：21,123,2n n n a n -=⎧=⎨⋅≥⎩. 20．（2022·浙江宁波·一模）南宋的数学家杨辉“善于把已知形状、大小的几何图形的求面积、体积的连续量问题转化为离散量的垛积问题”，在他的专著《详解九章算法•商功》中，杨辉将堆垜与相应立体图形作类比，推导出了三角垛、方垛、刍童垛等的公式，例如三角垛指的是如图顶层放1个，第二层放3个，第三层放6个，第四层放10个第n 层放n a 个物体堆成的堆垛，则1210111a a a +++=__________． 【答案】2011【分析】由累加法即可求得n a ，再利用裂项相消法即可求解. 【详解】由题可知：1231,3,6a a a ===，即有()12n n a a n n --=≥， 所以121321()()()n n n a a a a a a a a -=+---+++(1)12342n n n +=+++++=，当n=1成立 所以1222(1)1n a n n n n ==-++，所以121011122222222223341011a a a +++=-+-+-++- 22021111=-=. 故答案为：201121．（2022·全国·高三专题练习）已知数列{}n a 的前n 项和31n S n =-，数列{}n b 满足11b =-，()121n n b b n +=+-. (1)求数列{}n a 、{}n b 的通项公式. (2)若n nn a b c n⋅=，求数列{}n c 的前n 项和n T . 【答案】(1)2,13,2n n a n =⎧=⎨≥⎩，22n b n n =-(23)n ++-符合上式，∴n b =2,36,n n -=⎧=⎨-⎩C 组 真题实战练22．（2019·全国·高考真题（理））已知各项均为正数的等比数列{}n a 的前4项和为15，且53134a a a =+，则3a = A ．16 B ．8C ．4D ．2【答案】C【解析】利用方程思想列出关于1,a q 的方程组，求出1,a q ，再利用通项公式即可求得3a 的值．【详解】设正数的等比数列{an }的公比为q ，则2311114211115,34a a q a q a q a q a q a ⎧+++=⎨=+⎩， 解得11,2a q =⎧⎨=⎩，2314a a q ∴==，故选C ．【点睛】本题利用方程思想求解数列的基本量，熟练应用公式是解题的关键．23．（2021·全国·高考真题（文））记n S 为等比数列{}n a 的前n 项和.若24S =，46S =，则6S =（ ） A ．7 B ．8 C ．9 D ．10【答案】A【分析】根据题目条件可得2S ，42S S -，64S S -成等比数列，从而求出641S S -=，进一步求出答案. 【详解】∵n S 为等比数列{}n a 的前n 项和， ∴2S ，42S S -，64S S -成等比数列 ∴24S =，42642S S -=-= ∴641S S -=， ∴641167S S =+=+=. 故选：A.24．（2012·全国·高考真题（理））已知等差数列{}n a 的前n 项和为55,5,15n S a S ==,则数列11n n a a +⎧⎫⎨⎬⎩⎭的前100项和为 A ．100101B ．99101C ．99100D ．101100【答案】A【详解】设等差数列{a n }的首项为a 1，公差为d. ∵a 5＝5，S 5＝15，∴1145{545152a d a d +=⨯+=⇒111a d =⎧⎨=⎩⇒a n ＝n. ∴11n n a a +⋅＝()11+n n ＝111n n -+，S 100＝112⎛⎫- ⎪⎝⎭＋1123⎛⎫- ⎪⎝⎭＋…＋11100101⎛⎫- ⎪⎝⎭＝1－1101＝100101. 25．（2014·全国·高考真题（理））等比数列{}n a 中，452,5a a ==，则数列{}lg n a 的前8项和等于 A ．6 B ．5 C ．4 D ．3【答案】C【详解】试题分析：利用等比数列的性质可得a 1a 8=a 2a 7=a 3a 6=a 4a 5=10．再利用对数的运算性质即可得出． 解：∵数列{a n }是等比数列，a 4=2，a 5=5， ∴a 1a 8=a 2a 7=a 3a 6=a 4a 5=10． ∴lga 1+lga 2+…+lga 8 =lg （a 1a 2…×a 8） ==4lg10 =4． 故选C ．考点：等比数列的前n 项和．26．（2014·天津·高考真题（文））设{}n a 是首项为1a ，公差为-1的等差数列，n S 为其前n 项和，若124,,S S S 成等比数列，则1a =（ ） A ．2 B ．-2C ．12D ．12-【答案】D 【分析】把已知2214S S S 用数列的首项1a 和公差d 表示出来后就可解得1a ．，【详解】因为124S S S ，，成等比数列，所以2214S S S ，即211111(21)(46).2a a a a -=-=-，故选D.【点睛】本题考查等差数列的前n 项和，考查等比数列的性质，解题方法是基本量法．本题属于基础题． 27．（2010·湖北·高考真题（文））已知等比数列{}n a 中，各项都是正数，且1321,,22a a a 成等差数列，则91078a a a a +=+ A ．12+ B ．12- C ．322+ D ．322-【答案】C【详解】试题分析：由已知3122a a a =+，所以21112a q a a q =+，因为数列{}n a 的各项均为正，所以21q =+，222910787878322a a a q a q q a a a a ++===+++．故选C ．考点：等差数列与等比数列的性质．28．（2015·浙江·高考真题（理））已知{}n a 是公差d 不为零的等差数列，其前n 项和为n S ，若348,,a a a 成等比数列，则 A ．140,0a d dS >> B ．140,0a d dS << C ．140,0a d dS >< D ．140,0a d dS <>【答案】B【详解】∵等差数列，，，成等比数列，∴，∴，∴，，故选B.考点：1.等差数列的通项公式及其前项和；2.等比数列的概念29．（2019·全国·高考真题（理））记Sn 为等差数列{an }的前n 项和，12103a a a =≠，，则105S S =___________. 【答案】4.【分析】根据已知求出1a 和d 的关系，再结合等差数列前n 项和公式求得结果. 【详解】因213a a =，所以113a d a +=，即12a d =，所以105S S =11111091010024542552a d a a a d⨯+==⨯+． 【点睛】本题主要考查等差数列的性质、基本量的计算．渗透了数学运算素养．使用转化思想得出答案．30．（2019·全国·高考真题（文））记n S 为等差数列{}n a 的前n 项和，若375,13a a ==，则10S =___________.31．（2008·四川·高考真题（文））设数列{}n a 中，112,1+==++n n a a a n ，则通项n a = ___________． 21⎤++++⎦)1+ 故应填【考点】：此题重点考察由数列的递推公式求数列的通项公式；抓住1n n a a +=32．（2014·广东·高考真题（文））等比数列{}n a 的各项均为正数，且154a a =，则2122232425log log log log log a a a a a ++++=_____.【答案】5.【详解】试题分析：由题意知21534a a a ==，且数列{}n a 的各项均为正数，所以32a =，()()()223512345152433352a a a a a a a a a a a a a ∴=⋅⋅=⋅==，()521222324252123452log log log log log log log 25a a a a a a a a a a ∴++++===．考点：1．考查等比数列的基本性质；2．对数的基本运算．33．（2015·安徽·高考真题（理））已知数列{}n a 是递增的等比数列，14239,8a a a a +==，则数列{}n a 的前n 项和等于 . 2q ，项和1n a S =等比数列的性质；2.等比数列的前34．（2014·江苏·高考真题）在各项均为正数的等比数列{}n a 中，若21a =，8642a a a =+，则6a 的值是_______. 【答案】4【详解】试题分析：设等比数列{}n a 的公比为100q a >>，．∵8642a a a =+，∴7511123=+a q a q a q ，化为4220q q --=，解得22q =．∴261254124a a q a q ===⨯=．故答案为4．考点：等比数列的通项公式.35．（2015·全国·高考真题（理））n S 为数列{n a }的前n 项和.已知n a ＞0，22n n a a +=43n S +.（Ⅰ）求{n a }的通项公式； （Ⅱ）设11n n n b a a +=,求数列{n b }的前n 项和. 1n （Ⅱ））根据数列的递推关系，利用作差法即可求11n a +，利用裂项法即可求数列121n +++本题主要考查数列的通项公式以及数列求和的计算，利用裂项法是解决本题的关键．36．（2021·全国·高考真题）记n S 是公差不为0的等差数列{}n a 的前n 项和，若35244,a S a a S ==． （1）求数列{}n a 的通项公式n a ； （2）求使n n S a >成立的n 的最小值．37．（2021·全国·高考真题（文））设{}n a 是首项为1的等比数列，数列{}n b 满足3nn na b =．已知1a ，23a ，39a 成等差数列．（1）求{}n a 和{}n b 的通项公式；（2）记n S 和n T 分别为{}n a 和{}n b 的前n 项和．证明：2nn S T <． 113n n --+++121111333-⎫+++⎪⎭n ，230121*********323333n n n -⎫⎛⎫++++-++++=⎪ ⎪⎭⎝⎭0101233--+++113---n n 2111111212233-----+++n n ， ⑧ 311212233---+++nn ． ⑨211133-⎫++-⎪⎭n 123--⨯n n ． 03<⨯nn．113n n --+++3213n n -+++2111133333n n n n =++++-1)323n nn-⋅，3(134n n --1n b c ++=：导函数法 23+++=nx x x )()(1'1n x x ⎡⎤⎤-⎣⎦1-++=n nx1-n ，所以2112311111233333n n n T b b b b n -⎡⎤⎛⎫⎛⎫=++++=+⨯+⨯++⋅=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦12111(1)11133333113n nn n f +⎛⎫⎛⎫+-+ ⎪ ⎪⎛⎫⎝⎭⎝⎭⋅=⨯ ⎪⎝⎭⎛⎫- ⎪⎝⎭' 13113311(1)4334423n nnn n n +⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+-+=-+⎢⎥ ⎪ ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦，下同方法二． 【整体点评】本题主要考查数列的求和，涉及到等差数列的性质，错位相减法求数列的和，考查学生的数学运算能力，是一道中档题，其中证明不等式时采用作差法，或者作商法要根据式子得结构类型灵活选择，关键是要看如何消项化简的更为简洁.（2）的方法一直接作差后利用错位相减法求其部分和，进而证得结论；方法二根据数列的不同特点，分别利用公式法和错位相减法求得,n n S T ,然后证得结论,为最优解；方法三采用构造数列裂项求和的方法，关键是构造1()3αβ⎛⎫=+ ⎪⎝⎭nn c n ，使1+=-n n n b c c ，求得n T 的表达式，这是错位相减法的一种替代方法，方法四利用导数方法求和，也是代替错位相减求和法的一种方法. 38．（2014·全国·高考真题（理））已知数列{}n a 满足111,31n n a a a +==+. (1)证明12n a ⎧⎫+⎨⎬⎩⎭是等比数列，并求{}n a 的通项公式；(2)证明：121113 (2)n a a a +++<. 【答案】（1）证明见解析，113322n n a -+=；（2）证明见解析. 【详解】试题分析：本题第（1）问，证明等比数列，可利用等比数列的定义来证明，之后利用等比数列，求出其通项公式；对第（2）问，可先由第（1）问求出1na ，然后转化为等比数列求和，放缩法证明不等式. 试题解析：（1）证明：由131n n a a +=+得1113()22n n a a ++=+，所以112312n n a a ++=+，所以12n a ⎧+⎫⎨⎬⎩⎭是等比数列，首项为11322a +=，公比为3，所以12n a +=1332n -⋅，解得n a =312n-. （2）由（1）知：n a =312n -，所以1231n n a =-， 因为当1n ≥时，13123n n --≥⋅，所以1113123n n -≤-⋅，于是11a +21a +1na =31(1)23n -32<，+1n a 32<. 【易错点】对第（1）问，构造数列证明等比数列不熟练；对第（而找不到思路，容易想到用数学归纳法证明而走弯路考点：本小题考查等比数列的定义、数列通项公式的求解、数列中不等式的证明等基础知识，考查同学们的逻辑推理能力，考查分析问题与解决问题的能力。

递推数列题型分类归纳解析各种数列问题在很多情形下，就是对数列通项公式的求解。

特别是在一些综合性比较强的数列问题中，数列通项公式的求解问题往往是解决数列难题的瓶颈。

我现在总结出几种求解数列通项公式的方法，希望能对大家有帮助。

类型1 )(1n f a a n n +=+解法：把原递推公式转化为)(1n f a a n n =-+，利用累加法(逐差相加法)求解。

例1. 已知数列{}n a 满足211=a ，nn a a n n ++=+211，求n a 。

解：由条件知：111)1(1121+-=+=+=-+n n n n n n a a n n 分别令)1(,,3,2,1-⋅⋅⋅⋅⋅⋅=n n ，代入上式得)1(-n 个等式累加之，即)()()()(1342312--+⋅⋅⋅⋅⋅⋅+-+-+-n n a a a a a a a a)111()4131()3121()211(nn --+⋅⋅⋅⋅⋅⋅+-+-+-=所以na a n 111-=-211=a ，nn a n 1231121-=-+=∴类型2 n n a n f a )(1=+ 解法：把原递推公式转化为)(1n f a a nn =+，利用累乘法(逐商相乘法)求解。

例2:已知数列{}n a 满足321=a ，n n a n n a 11+=+，求n a 。

解：由条件知11+=+n n a a n n ，分别令)1(,,3,2,1-⋅⋅⋅⋅⋅⋅=n n ，代入上式得)1(-n 个等式累乘之，即 1342312-∙⋅⋅⋅⋅⋅⋅∙∙∙n n a a a a a a a a nn 1433221-⨯⋅⋅⋅⋅⋅⋅⨯⨯⨯=n a a n 11=⇒ 又321=a ，na n 32=∴类型3 q pa a n n +=+1（其中p ，q 均为常数，)0)1((≠-p pq ）。

解法（待定系数法）：把原递推公式转化为：)(1t a p t a n n -=-+，其中pqt -=1，再利用换元法转化为等比数列求解。