模糊逻辑

模糊逻辑与传统逻辑的比较与分析逻辑学是研究推理和思维规律的学科，而其中的两种重要的分支是模糊逻辑和传统逻辑。

本文将对这两种逻辑进行比较与分析，探讨它们的差异、应用领域以及各自的优缺点。

一、模糊逻辑模糊逻辑是基于模糊理论的一种逻辑系统，它适用于描述现实生活中的不确定性和模糊性。

相比传统逻辑只有真和假的二值范围，模糊逻辑允许命题具有连续的真值，这使得推理更加灵活。

模糊逻辑通过模糊集合和模糊关系来表达模糊性，其中模糊集合允许元素在某种程度上属于该集合，而模糊关系则将元素之间的关系表示为程度。

与传统逻辑相比，模糊逻辑具有以下优点：1. 表达能力更强：由于模糊逻辑能够处理模糊和不确定的信息，它能够更好地捕捉到现实世界的复杂性和多样性。

2. 适应性更强：在一些领域中，传统逻辑无法很好地应对琐碎和复杂的问题，而模糊逻辑能够根据不同情况进行适应，提供更加准确的推理结果。

3. 推理灵活性更高：传统逻辑中的命题只能是真或假，而模糊逻辑中的模糊命题可以有不同的真值，从而使得推理更加灵活。

然而，模糊逻辑也存在一些不足之处：1. 真值的不确定性：由于模糊逻辑中命题的真值是在0到1之间连续变化的，这导致真值的确定度比传统逻辑中的真假更加模糊，从而在某些情况下可能引起歧义。

2. 计算复杂性增加：模糊逻辑中的计算涉及到模糊集合和模糊关系的运算，这使得计算的复杂性增加，对计算资源的需求更高。

二、传统逻辑传统逻辑是逻辑学的基础，也是最为常见的逻辑推理模式。

它基于二值逻辑，即命题的真值只能是真或假，不允许出现中间值。

传统逻辑使用命题、命题连接词和推理规则进行推理，能够处理确定性的问题。

与模糊逻辑相比，传统逻辑具有以下特点：1. 简单明确：传统逻辑是一种严密的推理系统，其命题和推理规则具有明确的定义，使得推理过程更加简单和清晰。

2. 精确性高：由于传统逻辑只处理确定性的命题，其推理过程具有较高的精确性，不容易产生歧义。

3. 计算效率高：传统逻辑的推理过程较为简单，不涉及模糊集合和模糊关系的运算，计算效率较高。

什么是计算机模糊逻辑请解释模糊逻辑的基本原理和应用计算机模糊逻辑是一种用于处理模糊性问题的逻辑推理方法。

相比于传统的二进制逻辑，在模糊逻辑中，概念之间的划分不再是非黑即白的严格边界，而是允许存在不确定的灰色区域。

模糊逻辑的基本原理是基于模糊集合论，通过引入隶属度来描述某个元素对一个模糊集合的隶属关系程度。

模糊逻辑的应用广泛，包括人工智能、控制系统、数据挖掘等领域。

一、模糊逻辑的基本原理模糊逻辑是由美国学者洛特菲尔德于1965年提出的，它的核心思想是将传统二值逻辑中的真假划分扩展到连续的隶属度范围上。

模糊逻辑使用隶属度函数来描述一个元素对某个模糊集合的隶属关系程度，其中隶属度值介于0和1之间。

通过引入模糊集合和隶属度函数的概念，模糊逻辑能够处理那些无法用精确逻辑方式表达的问题。

模糊逻辑的基本原理可以总结为以下几点：1. 模糊集合：模糊集合是一种包含隶属度函数的数学概念，它用来描述元素对某个概念的隶属程度。

与传统的集合不同，模糊集合中的元素不再具有明确的边界，而是在某个隶属度范围内模糊存在。

2. 隶属度函数：隶属度函数是模糊集合的核心，它将元素与某个概念的隶属程度关联起来。

隶属度函数通常采用曲线来表示，曲线的高度代表了隶属度的程度。

常用的隶属度函数包括三角函数、高斯函数等。

3. 模糊逻辑运算：模糊逻辑引入了一系列运算符来处理模糊集合，包括交集、并集、补集等。

这些运算符可以用来进行逻辑推理和决策。

二、模糊逻辑的应用模糊逻辑在人工智能、控制系统、数据挖掘等领域有着广泛的应用。

1. 人工智能：模糊逻辑为人工智能提供了处理不确定性问题的方法。

在模糊逻辑中，可以使用模糊推理来进行模糊推断、模糊分类等任务。

例如，在模糊控制系统中，可以使用模糊规则来推断控制器的输出，以实现对模糊系统的控制。

2. 控制系统：模糊逻辑在控制系统中可以用于处理模糊输入、输出和规则的控制。

通过使用模糊控制器，可以有效地处理那些难以用数学模型精确描述的系统。

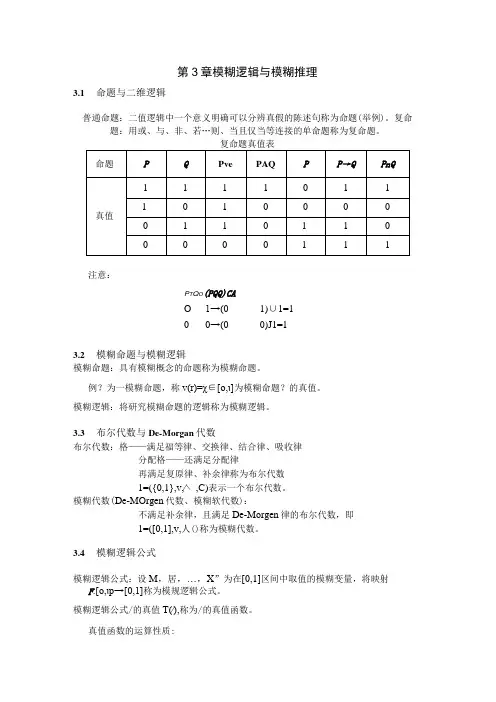
第3章模糊逻辑与模糊推理3.1命题与二维逻辑普通命题：二值逻辑中一个意义明确可以分辨真假的陈述句称为命题(举例)。

复命题：用或、与、非、若…则、当且仅当等连接的单命题称为复命题。

注意：P T Q O(PQQ)CAO 1→(01)∪1=10 0→(00)J1=13.2模糊命题与模糊逻辑模糊命题：具有模糊概念的命题称为模糊命题。

例？为一模糊命题，称v(r)=χ∈[o,ι]为模糊命题？的真值。

模糊逻辑：将研究模糊命题的逻辑称为模糊逻辑。

3.3布尔代数与De-Morgan代数布尔代数：格——满足福等律、交换律、结合律、吸收律分配格——还满足分配律再满足复原律、补余律称为布尔代数1=({0,1},v,∕∖,C)表示一个布尔代数。

模糊代数(De-MOrgen代数、模糊软代数)：不满足补余律，且满足De-Morgen律的布尔代数，即1=([0,1],v,人()称为模糊代数。

3.4模糊逻辑公式模糊逻辑公式：设M，居，…，X”为在[0,1]区间中取值的模糊变量，将映射F:[o,ιp→[0,1]称为模规逻辑公式。

模糊逻辑公式/的真值T(∕),称为/的真值函数。

真值函数的运算性质:T(F)=I-T(F)T(F vF)=max(T(F),T(F))T(F A F)=min(T(FXnF))T(F→F)=min(1,I-T(F)+T(F))了真——F 中一切赋值均为T(F)≥J2 /假——尸中一切赋值均为TX 产)<g1 .模糊逻辑函数的分解例：模糊逻辑函数/(x,y,z)=0V 取丫兀由，确定/(x,y,z)在〃=2处于第一级时变量的取值范围。

解：为满足了处于第一级，则Jf(X,y,z)≥6 于是，疝≥%或xyz ≥见或xyz≥a i 则有：x≥i -a↑x≥a↑y≥∖-a[或y≥a↑z≥a 1 [z≤∖-a↑2 .模糊逻辑函数范式——标准型析取形式：∕=∑n/∙»=17=1 合取形式：F=<=1j=1举例：f(x,y,z)=[(xVy)A V[(xvz)A y]=(xvy)v(xvz)v(yvz)3.5 语言变量及其集合描述自然语言：具有模糊性，灵活。

模糊逻辑在机器学习中的应用第一章：引言1.1 背景介绍机器学习是人工智能领域的重要分支，通过分析大量数据和模式识别来进行决策和预测。

然而，在现实世界中，存在不确定性和模糊性的事件很常见，传统的二进制逻辑往往不能很好地处理这些问题。

1.2 模糊逻辑的概念模糊逻辑是一种基于模糊集合理论的数学工具，它能够处理不确定和模糊性的问题。

相比于传统的二进制逻辑，模糊逻辑的输出是一个连续的值，表示事物的模糊程度。

第二章：模糊逻辑基础2.1 模糊集合模糊集合是一种广义的集合，其中每个元素都具有隶属度。

隶属度表示了元素与集合之间的模糊程度，取值范围在0到1之间。

2.2 模糊关系模糊关系是一种描述元素之间模糊关联的数学模型，它可以用来表示模糊规则和决策。

2.3 模糊推理模糊推理是基于模糊规则进行决策和推断的过程，通过对输入进行模糊化处理，然后应用模糊关系进行推理，最终获得模糊输出。

第三章：模糊逻辑在机器学习中的应用3.1 模糊聚类聚类是一种将相似数据点分组的技术，模糊聚类将元素隶属于不同的类别，以反映元素与不同类别之间的模糊程度。

模糊聚类可以用于图像分割、文本挖掘等领域。

3.2 模糊分类传统的分类算法往往将数据点划分为离散的类别，而模糊分类将数据点划分为多个模糊类别，以反映数据点属于不同类别的模糊程度。

模糊分类可以应用于识别模糊边界的问题。

3.3 模糊决策决策问题往往伴随着不确定性，模糊决策可以通过将不确定性考虑在内，生成一组模糊决策规则来处理不确定性和模糊性的问题。

模糊决策在风险评估、金融分析等领域有着广泛的应用。

第四章：模糊逻辑与经典机器学习算法的融合4.1 模糊逻辑与神经网络在神经网络中，模糊逻辑可以用来表示神经元的激活函数，增强神经网络对模糊数据的处理能力。

模糊神经网络在模式识别和预测分析等领域具有较好的性能。

4.2 模糊逻辑与支持向量机支持向量机是一种经典的机器学习算法，通过寻找超平面将不同类别的样本点分隔开。

什么是模糊算法初步了解模糊逻辑模糊算法初步了解模糊逻辑随着科技和人工智能的不断发展，越来越多的算法被广泛运用于各种应用领域中。

其中，模糊算法就是其中之一。

那么，什么是模糊算法？下面就让我们一起来初步了解一下模糊逻辑吧。

一、什么是模糊算法？在传统的计算机模型中，逻辑关系是非常明确的——要么是真，要么是假。

这种二元逻辑虽然简单明了，但是却无法处理那些带有不确定性的问题，比如人类语言中那些含糊不清的描述。

而模糊逻辑则提供了一种计算模型，使得计算机能够处理那些不确定的信息。

模糊算法就是基于模糊逻辑的一种算法。

它本质上是一种模糊推理系统，通过对数据进行模糊化处理，使得模糊的数据能够被计算机所理解。

在模糊算法中，一个变量的取值不再是明确的，而是一个模糊的概念，其取值不仅可以是0或1，还可以是介于0和1之间的任何实数。

这种算法能够处理那些难以用精确数据来描述的问题，如模糊控制、图像处理、语言识别等。

二、模糊逻辑的基本概念模糊逻辑是一种可以处理模糊性的逻辑。

在模糊逻辑中，一个命题的真值不再是只有真和假两种取值，而能够取任意介于0和1之间的实数值。

具体来说，模糊逻辑中的三个基本概念是模糊集、隶属度函数和模糊关系。

1. 模糊集模糊集是指定义在某个数学空间上的一类不精确的集合。

与传统集合不同的是，模糊集可以包括一些元素，它们的隶属度是介于0和1之间的实数值，即一个元素属于模糊集的程度。

比如，我们可以定义一个“年轻人”模糊集，其隶属度可以根据不同年龄段来定义。

2. 隶属度函数隶属度函数是一个数学函数，它可以将一个元素与一个模糊集进行联系。

其输出是该元素与该模糊集之间的隶属度，可以理解为描述该元素在该模糊集中所占的比重。

例如，一个“温和”的隶属度函数可能如下表示：___________///________________0.2 0.5 1其中，数值0.2表示隶属度在0.2时的取值，0.5表示隶属度在0.5时的取值，1表示隶属度在1时的取值。

简述模糊逻辑的原理及应用1. 模糊逻辑的原理模糊逻辑是一种处理不确定性的逻辑系统，它与传统的二值逻辑不同，允许命题的真值范围在0和1之间连续变化。

模糊逻辑的原理基于模糊集合理论，将模糊概念引入逻辑推理中。

1.1 模糊概念在传统的二值逻辑中，一个命题的真值只能是0或1，即假或真。

而在模糊逻辑中，一个命题的真值可以是介于0和1之间的任何数值，表示命题的模糊程度。

例如，对于命题“这个苹果是红色的”，在二值逻辑中只能是真或假，而在模糊逻辑中可以是0.8，表示这个苹果的红色程度为80%。

1.2 模糊集合模糊逻辑中的模糊概念可以通过模糊集合来表示。

模糊集合是一种将元素的隶属度（即属于该集合的程度）表示为0到1之间的数值的数学概念。

例如，对于集合A表示“高个子人”的模糊集合，一个人的身高可以有不同程度地属于这个集合，如0.7表示这个人身高高度的程度为70%。

1.3 模糊逻辑运算模糊逻辑运算是对模糊概念进行推理和运算的方法。

常用的模糊逻辑运算包括模糊与、模糊或、模糊非等。

例如，对于命题“这个苹果既酸又甜”，可以通过模糊与来计算这个命题的模糊程度，假设酸度为0.8，甜度为0.6，则命题的模糊程度为0.6。

2. 模糊逻辑的应用模糊逻辑在实际应用中具有广泛的应用价值，以下列举了几个常见的应用领域。

2.1 模糊控制模糊控制是模糊逻辑在控制系统中的应用。

传统的控制系统通常基于精确的数学模型和准确的输入输出关系，而模糊控制则可以处理不确定性和模糊性的问题。

例如，模糊控制可以根据当前的温度和湿度来调节空调的工作状态，使室内温度保持在一个舒适的范围内。

2.2 模糊推理模糊推理是模糊逻辑在人工智能领域中的应用。

在传统的推理系统中，逻辑规则通常是二值的，而模糊推理则可以处理模糊概念的推理问题。

例如，假设有一个模糊推理系统用于判断一个人的健康状况，系统可以根据一些模糊规则和输入的模糊数据来判断这个人的健康状况是好、一般还是差。

2.3 模糊识别模糊识别是模糊逻辑在模式识别领域中的应用。

数学中的模糊数学与模糊逻辑数学作为一门严谨的学科，几乎在每个人的学习生涯中都会接触到。

然而，在实际应用中，我们常常会遇到一些不确定、模糊的问题。

为了更好地解决这类问题，数学家们引入了模糊数学与模糊逻辑的概念。

本文将探讨数学中的模糊数学与模糊逻辑的基本原理和应用。

一、模糊数学的基本原理模糊数学是对现实世界中不确定性问题的数学描述与处理方法的研究。

它针对真实世界中事物属性的模糊性，引入了隶属度的概念，用来描述事物属性的模糊程度。

在模糊数学中，一个模糊数可以用一个隶属函数来表示，该函数将取值范围映射到[0,1]之间，表示某个数值与一个模糊概念之间的关联程度。

模糊数的运算是模糊数学的核心内容之一。

在模糊数学中，模糊数之间可以进行加、减、乘、除等基本运算。

这些运算的结果也是一个模糊数，用来描述事物属性的不确定性。

二、模糊数学的应用领域1. 模糊控制模糊控制是模糊数学的一种重要应用。

它通过对输入和输出之间的关系建立模糊规则，并根据规则进行推理和决策，实现对复杂系统的控制。

相比于传统的控制方法，模糊控制在处理不确定性和模糊性的问题上具有较大的优势，适用于很多实际工程项目。

2. 模糊聚类模糊聚类是一种聚类分析方法，用于将具有模糊性质的数据进行分类。

传统的聚类方法在处理模糊数据时存在局限性，而模糊聚类能够克服这些问题。

它通过计算数据点与聚类中心之间的相似性来确定聚类结果，能够更好地适应模糊性、不确定性的数据。

3. 模糊决策在实际决策中，常常会遇到多个因素相互影响、信息不完全的情况。

模糊决策方法通过引入模糊数学的概念，将各个因素的不确定性进行量化，并通过模糊推理来得出最终的决策结果。

这种方法可以有效地应对实际决策中的不确定性、模糊性问题。

三、模糊逻辑的基本原理模糊逻辑是一种扩展了传统二值逻辑的逻辑系统。

与传统二值逻辑只有真和假两种取值不同，模糊逻辑引入了隶属度的概念，使命题在真和假之间具有连续性。

在模糊逻辑中，命题的真值（隶属度）表示命题的可信度或确定程度。

模糊逻辑发展现状
模糊逻辑是一种处理模糊信息的数学工具，旨在处理现实生活中存在的不确定和模糊性问题。

它的发展可以追溯到1965年，当时美国的研究者洛特菲尔德首次提出了模糊逻辑的概念。

模糊逻辑与传统的布尔逻辑相比，更能够处理模糊和不确定的信息。

布尔逻辑中，命题只有真和假两种取值，而模糊逻辑允许命题在真和假之间的连续取值，以表示事物的模糊性质。

模糊逻辑的发展经历了几个重要的阶段。

在20世纪70年代，模糊逻辑理论开始得到广泛的应用，并在控制系统、人工智能、模式识别等领域展示了巨大的潜力。

然而，在模糊逻辑的发展过程中也存在一些争议。

一些学者认为，模糊逻辑的表达能力有限，难以处理复杂的问题。

另一些学者则持相反观点，认为模糊逻辑可以更好地解释人类的思维方式，并在实际问题中有广泛的应用前景。

近年来，随着技术的发展和应用领域的扩大，模糊逻辑在各个领域取得了更多的突破。

例如，在控制领域，模糊控制方法已被广泛应用于工业控制和机器人技术中，取得了良好的效果。

在人工智能领域，模糊推理和模糊决策也被应用于专家系统和决策支持系统中。

总的来说，模糊逻辑在科学研究和实际应用中都发挥着重要作用。

尽管仍然存在一些问题和挑战，但其在处理模糊和不确定信息方面的优势使其具有广阔的应用前景。

未来的发展将进一
步加强模糊逻辑的理论基础，提高其处理能力，并拓展其在更多领域的应用。

模糊逻辑算法解析及其使用场景随着人工智能技术的不断发展，模糊逻辑成为了一种重要的算法模型。

模糊逻辑算法的特点是可以将模糊信息进行量化，从而更加准确地进行推理和决策。

本文从模糊逻辑算法的定义、原理和使用场景三个方面进行探讨。

一、模糊逻辑算法的定义模糊逻辑算法是一种处理模糊性信息的数学模型，其核心在于将模糊信息映射成数值，从而实现对该信息的处理。

与传统的布尔逻辑算法不同，模糊逻辑算法允许信息的值域在 0 到 1 之间取任意值，因此可以处理更加复杂的信息，具有更广泛的适用性。

二、模糊逻辑算法的原理模糊逻辑算法的核心在于“隶属度函数”的使用。

隶属度函数是一种将模糊信息映射到实数域的函数，通常用符号μ(x) 表示。

μ(x) 的值代表了某个元素 x 对于一个集合 A 的隶属程度，也就是 x 属于 A 的程度。

例如，在描述“温度”的情形下，我们可以定义一个温度集合 A，然后将任一温度值 x 映射到数值μ(x) ∈ [0,1] 上，表示该值对于集合 A 的隶属程度。

μ(x) 的值越大，x 就越符合集合A 的要求。

根据隶属度函数，我们可以定义出一种新的逻辑运算符号：模糊集合运算。

例如，假设我们有两个温度集合 A 和 B，同时我们有一个温度值 x。

我们可以用μA(x) 和μB(x) 两个值分别表示 x 对于 A 和 B 的隶属度，然后定义出一个“模糊 AND 运算符”：μA(x) ∧ μB(x)。

与传统的 AND 非常相似，当且仅当μA(x) ∧ μB(x) = min(μA(x), μB(x)) > 0 时，x 属于集合A ∩ B。

类似地，我们可以定义出模糊 OR、模糊 NOT 等运算符。

通过这些运算符的组合，我们可以处理模糊信息，实现对于不确定性的判断和决策。

三、模糊逻辑算法的使用场景1. 控制系统模糊逻辑算法在控制系统中应用广泛。

例如，在温度控制的场景下，我们可以根据隶属度函数将温度值映射到数值上，然后根据这个数值执行具体的控制策略。

模糊逻辑算法应用实例
模糊逻辑算法是一种能够处理不确定性问题的算法，具有很强的适应性和容错性。

在实际应用中，模糊逻辑算法被广泛应用于控制系统、图像处理、自动化、人工智能等领域。

以下是几个模糊逻辑算法应用实例。

1. 温度控制系统
在温度控制系统中，传统的控制方法是使用二元逻辑，即只有“开”和“关”两种状态。

然而，在实际控制过程中，存在诸多不确定性因素，如环境温度的波动、设备的工作状态等，这些都会导致传统控制方法的失效。

而模糊逻辑算法可以将这些不确定性因素纳入考虑范围，通过模糊控制器来实现更加精准的温度控制。

2. 图像处理
在图像处理中，模糊逻辑算法可以用来进行边缘检测、图像分割等操作。

由于图像中存在很多灰度值相近的像素点，在传统的二元逻辑中，很难对这些像素进行准确的分类和处理。

而模糊逻辑算法可以通过模糊分类器，将像素点分为模糊的不同类别，从而实现更加精细的图像处理。

3. 汽车安全控制系统
在汽车安全控制系统中，模糊逻辑算法可以用来对车辆的速度、加速度、制动力等参数进行控制。

由于在实际行驶中，各种因素都会影响车辆的行驶状态，如路面情况、天气状况等，因此，传统的二元逻辑控制方法难以满足复杂的控制需求。

而模糊逻辑算法可以通过模
糊控制器，实现对车辆的精细控制，从而提高车辆的安全性和驾驶体验。

综上所述，模糊逻辑算法在不确定性问题处理中具有很大的优势，在实际应用中有着广泛的应用前景。

从入门到精通模糊逻辑算法原理详解模糊逻辑是一种基于模糊集的推理方法，在人工智能领域应用广泛。

本文旨在从入门到精通地详细解释模糊逻辑算法原理。

一、什么是模糊逻辑在传统逻辑中，一个命题只能是真或假。

然而，在现实生活中，很多概念存在模糊性，比如“高矮胖瘦”等。

模糊逻辑就是一种能够处理这些模糊性的逻辑。

模糊逻辑的基础是模糊集理论，即一种介于绝对真和绝对假之间的数学符号。

模糊集把命题的真实性定义为一个0到1之间的实数，表示命题成立的程度。

例如，“这个苹果是红色的”这个命题是部分正确和部分错误的，可以用0.8表示。

二、模糊逻辑的算法原理模糊逻辑的算法原理主要包括模糊集的表示、模糊逻辑运算和模糊推理三个部分。

1. 模糊集的表示模糊集可以用数学函数形式来表示，常用的有三角形、梯形、高斯等函数形式。

以三角形为例，其函数形式如下：$$\mu _{A}(x)=\left\{\begin{matrix}0& \ x<x_0 \\\frac{x-x_0}{x_1-x_0} & \ x_0≤x<x_1\\1&\ x_1≤x≤x_2\\\frac{x_3-x}{x_3-x_2} &\ x_2<x≤x_3\\0& \ x>x_3\end{matrix}\right.$$其中，$x_0$ 和 $x_3$ 表示集合 $A$ 的边界，$x_1$ 和 $x_2$ 表示集合 $A$ 的顶点。

2. 模糊逻辑运算模糊逻辑运算包括交、并、补、差等。

设 $A$ 和 $B$ 为模糊集，其模糊逻辑运算如下：交运算：$A\cap B$，表示两个模糊集的交集。

通常用 $T$ 表示其高峰值。

并运算：$A\cup B$，表示两个模糊集的并集。

通常用 $S$ 表示其面积。

补运算：$\bar{A}$，表示模糊集 A 的补集。

通常用 $1-A$ 表示。

差运算：$A-B$，表示模糊集 A 减去模糊集 B 后的剩余部分。

经典逻辑和模糊逻辑之间的关系
模糊逻辑是布尔运算的扩展。

经典逻辑坚持所有事物都可以用二元项（0或1，黑或白，是或否）来表达，而模糊逻辑用真实度替代了布尔真值。

这些陈述表示实际上接近于日常人们的问题和语意陈述，因为“真实”和结果在多数时候是部分（非二元）的和/或不精确的（不准确的，不清晰的，模糊的）。

模糊逻辑基于人们根据不精确和非数字信息做出决策的观察。

模糊模型或集合是表示模糊性和不精确信息的数学方法（因此术语模糊）。

这些模型具有识别、表示、操纵、解释和利用模糊和缺乏确定性的数据和信息的能力。

经典逻辑只允许结论为真或假。

然而，也有一些具有可变答案的命题，例如在要求一群人识别颜色时可能会发现。

在这种情况下，真理是从不精确或部分知识进行推理的结果，其中抽样答案被映射到频谱上。