第八章 第一节 欧拉法
- 格式:ppt
- 大小:272.00 KB
- 文档页数:19



欧拉法原理欧拉法是一种常用的数值解微分方程的方法,它是由瑞士数学家欧拉提出的。
在物理、工程、计算机等领域,微分方程是一种常见的数学工具,用来描述系统的变化规律。
而欧拉法可以通过离散化微分方程,将连续的变化过程转化为离散的计算步骤,从而求得近似解。
在本文中,我们将介绍欧拉法的原理及其应用。
首先,我们来看看欧拉法的原理。
对于一个一阶常微分方程dy/dx=f(x,y),我们可以通过欧拉法来进行数值解。
假设我们要求解的区间为[x0,xn],步长为h,则我们可以将区间[x0,xn]等分为n段,每一段的长度为h。
然后,我们从初始点x0开始,根据微分方程dy/dx=f(x,y)的斜率f(x0,y0)计算出下一个点的纵坐标y1=y0+hf(x0,y0)。
然后,我们以(x1,y1)作为新的起点,重复上述步骤,直到得到整个区间上的近似解。
欧拉法的原理其实就是将微分方程中的导数转化为差分形式,从而得到离散的计算步骤。
虽然欧拉法是一种简单粗暴的数值解法,但在一些简单的微分方程问题中,它仍然是一种有效的数值解法。
当然,欧拉法也有它的局限性,比如对于刚性方程或者高阶微分方程,欧拉法可能会出现精度不足的问题。
接下来,我们来看看欧拉法的应用。
在物理学中,欧拉法常常用来模拟运动的轨迹。
比如在自由落体运动中,我们可以通过欧拉法来计算物体的位置随时间的变化规律。
在工程领域,欧拉法也常常用来求解控制系统的动态响应。
在计算机领域,欧拉法也是常见的数值计算方法,比如在游戏物理引擎中,欧拉法可以用来模拟物体的运动轨迹。
总之,欧拉法是一种常见的数值解微分方程的方法,它通过离散化微分方程,将连续的变化过程转化为离散的计算步骤,从而求得近似解。
虽然欧拉法有其局限性,但在一些简单的微分方程问题中,它仍然是一种有效的数值解法。
在物理、工程、计算机等领域,欧拉法都有着广泛的应用。
希望本文能够对读者对欧拉法有所帮助。
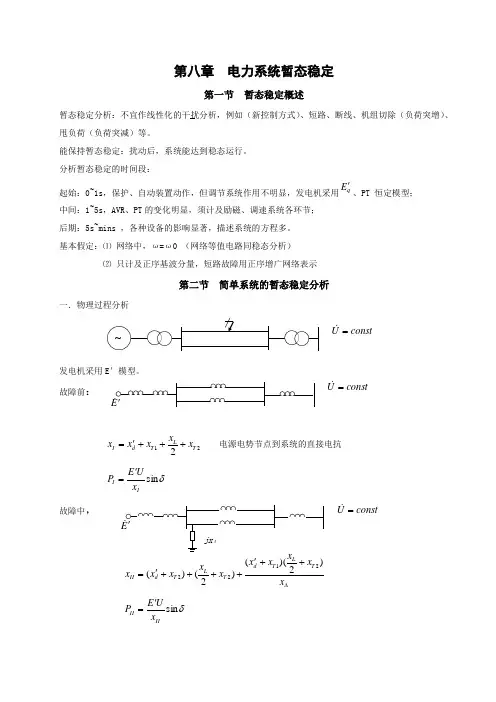
第八章 电力系统暂态稳定第一节 暂态稳定概述暂态稳定分析:不宜作线性化的干扰分析,例如(新控制方式)、短路、断线、机组切除(负荷突增)、甩负荷(负荷突减)等。
能保持暂态稳定:扰动后,系统能达到稳态运行。
分析暂态稳定的时间段:起始:0~1s ,保护、自动装置动作,但调节系统作用不明显,发电机采用qE '、PT 恒定模型;中间:1~5s ,AVR 、PT 的变化明显,须计及励磁、调速系统各环节; 后期:5s~mins ,各种设备的影响显著,描述系统的方程多。
基本假定:⑴ 网络中,ω=ω0 (网络等值电路同稳态分析) ⑵ 只计及正序基波分量,短路故障用正序增广网络表示第二节 简单系统的暂态稳定分析一.物理过程分析发电机采用E ’模型。
故障前:221T LT dI x x x x x +++'= 电源电势节点到系统的直接电抗 δsin II x UE P '= 故障中,∆++'++++'=x xx x x x x x x T LT dT LT dII )2)(()2()(2122δsin IIII x UE P '=故障切除后:功角特性曲线为故障发生后的过程为:运行点变化 原因 结果a →b 短路发生 PT>PE, 加速,ω上升,δ增大 b →c ω上升,δ增大 ω>ω0 ,动能增加c →e 故障切除 PT<PE, 开始减速,但ω>ω0 ,δ继续增大 e →f 动能释放 减速,当ωf =ω0,动能释放完毕,δm 角达最大 f →k PT<PE, 减速δ,减小 经振荡后稳定于平衡点k 结论: 若最大摇摆角h m δδ<,系统可经衰减的振荡后停止于稳定平衡点k,系统保持暂态稳定,反之,系统不能保持暂态稳定。
暂态稳定分析与初始运行方式、故障点条件、故障切除时间、故障后状态有关。
电力系统暂态稳定分析是计算电力系统故障及恢复期间内各发电机组的功率角i δ的变化情况(即δ–t曲线),然后根据i δ角有无趋向恒定(稳定)数值,来判断系统能否保持稳定,求解方法是非线性微分方程的数值求解。





1欧拉法求微分方程方法说明欧拉(Euler)法是解常微分方程初值问题(4.1)最简单的数值方法,其具体做法是,将区间[a,b]进行N等分:,步长.并将式(4.1)写成等价的积分形式(4.2)再对式(4.2)右端积分用矩形公式计算,则有, (4.3)在式(4.3)右端取,舍去余项。
则得,作为的近似值。
在式(4.3)右端取,舍去余项,则得作为的近似值.一般地,在式(4.3)右端取舍去余项,则得(4.4)作为的近似值.式(4.4)为欧拉法计算公式.我们知道微分方程的解是平面上的一族积分曲线,这族曲线中过点的积分曲线就是初值问题式(4.1)的解.欧拉法的几何意义是,过点引斜率为的积分曲线的切线,此切线与直线的交点为,再过点引以为斜率的切线与直线的交点为,依此类推,从出发,作以为斜率的切线,此切线与直线交点为.于是便得到过点的一条折线,见图4.1.过的积分曲线则用此折线来代替.因此,这种方法亦称折线法.图4.1例:用欧拉法求微分方程[]2',(0)1,0.1,0,1x y y y h y 区间为=-==欧拉法流程图如下:欧拉法程序如下: clear;clc;x1=0; x2=1; h=0.1; x0=0; y0=1;N=(x2-x1)/h;%要计算的次数 x(1)=x0; y(1)=y0; for n=1:Nx(n+1)=x(n)+h;y(n+1)=y(n)+h*(y(n)-2*x(n)/y(n)); end X=x Y=y2改进欧拉法求微分方程方法说明由于欧拉法采用矩形公式计算积分产生较大截断误差.改进欧拉法(又称改进折线法)是采取梯形公式来计算式(4.3)右端积分,则有(5.1)在式(5.1)右端取,舍去余项,则得将作为的近似值.在式(5.1)右端再取,舍去余项,则得将作为的近似值.一般地,在式(5.1)右端取,舍去余项.则得(5.2)将作为的近似值.式(5.2)为改进欧拉法计算公式.流程图如下:例:用改进欧拉法求微分方程[] 2',(0)1,0.1,0,1xy y y hy区间为=-==改进欧拉法程序如下:clear;clc;x1=0;x2=1;h=0.1;x0=0;y0=1;p(1)=0;N=(x2-x1)/h;x(1)=x0;y(1)=y0;for n=1:Nx(n+1)=x(n)+h;y(n+1)=y(n)+h*(y(n)-2*x(n)/y(n));p(n+1)=y(n)+h*(y(n+1)-2*x(n)/y(n+1));y(n+1)=(y(n+1)+p(n+1))/2;endX=xY=y3斐波那契法求极值方法说明斐波那契法原理类似于黄金分割法,只是搜索区间的缩短率不再采用黄金分割数0.618。


第八章常微分方程初值问题的解法在科学与工程问题中,常微分方程描述物理量的变化规律,应用非常广泛. 本章介绍最基本的常微分方程初值问题的解法,主要针对单个常微分方程,也讨论常微分方程组的有关技术.8.1引言本节介绍常微分方程、以及初值问题的基本概念,并对常微分方程初值问题的敏感性进行分析.8.1.1 问题分类与可解性很多科学与工程问题在数学上都用微分方程来描述,比如,天体运动的轨迹、机器人控制、化学反应过程的描述和控制、以及电路瞬态过程分析,等等. 这些问题中要求解随时间变化的物理量,即未知函数y(t),t表示时间,而微分方程描述了未知函数与它的一阶或高阶导数之间的关系. 由于未知函数是单变量函数,这种微分方程被称为常微分方程(ordinary differential equation, ODE),它具有如下的一般形式①:g(t,y,y′,⋯,y(k))=0 ,(8.1) 其中函数g: ℝk+2→ℝ. 类似地,如果待求的物理量为多元函数,则由它及其偏导函数构成的微分方程称为偏微分方程(partial differential equation, PDE). 偏微分方程的数值解法超出了本书的范围,但其基础是常微分方程的解法.在实际问题中,往往有多个物理量相互关联,它们构成的一组常微分方程决定了整个系统的变化规律. 我们先针对单个常微分方程的问题介绍一些基本概念和求解方法,然后在第8.5节讨论常微分方程组的有关问题.如公式(8.1),若常微分方程包含未知函数的最高阶导数为y(k),则称之为k阶常微分方程. 大多数情况下,可将常微分方程(8.1)写成如下的等价形式:y(k)=f(t,y,y′,⋯,y(k−1)) ,(8.2) 其中函数f: ℝk+1→ℝ. 这种等号左边为未知函数的最高阶导数y(k)的方程称为显式常微分方程,对应的形如(8.1)式的方程称为隐式常微分方程.通过简单的变量代换可将一般的k阶常微分方程转化为一阶常微分方程组. 例如对于方程(8.2),设u1(t)=y(t),u2(t)=y′(t),⋯,u k(t)=y(k−1), 则得到等价的一阶显式常微分方程组为:{u1′=u2u2′=u3⋯u k′=f(t,u1,u2,⋯,u k).(8.3)本书仅讨论显式常微分方程,并且不失一般性,只需考虑一阶常微分方程或方程组.例8.1 (一阶显式常微分方程):试用微积分知识求解如下一阶常微分方程:y′=y .[解] 采用分离变量法进行推导:①为了表达式简洁,在常微分方程中一般省略函数的自变量,即将y(t)简记为y,y′(t)简记为y′,等等.dy dt =y ⟹ dy y=dt , 对两边积分,得到原方程的解为:y (t )=c ∙e t ,其中c 为任意常数.从例8.1看出,仅根据常微分方程一般无法得到唯一的解. 要确定唯一解,还需在一些自变量点上给出未知函数的值,称为边界条件. 一种边界条件设置方法是给出t =t 0时未知函数的值:y (t 0)=y 0 .在合理的假定下,从t 0时刻对应的初始状态y 0开始,常微分方程决定了未知函数在t >t 0时的变化情况,也就是说这个边界条件可以确定常微分方程的唯一解(见定理8.1). 相应地,称y (t 0)=y 0为初始条件,而带初始条件的常微分方程问题:{y ′=f (t,y ),t ≥t 0y (t 0)=y 0 . (8.4)为初值问题(initial value problem, IVP ).定理8.1:若函数f (t,y )关于y 满足李普希兹(Lipschitz )条件,即存在常数L >0,使得对任意t ≥t 0,任意的y 与y ̂,有:|f (t,y )−f(t,y ̂)|≤L |y −y ̂| ,(8.5) 则常微分方程初值问题(8.4)存在唯一的解.一般情况下,定理8.1的条件总是满足的,因此常微分方程初值问题的解总是唯一存在的. 为了更清楚地理解这一点,考虑f (t,y )的偏导数ðf ðy 存在,则它在求解区域内可推出李普希兹条件(8.5),因为f (t,y )−f (t,y ̂)=ðf ðy (t,ξ)∙(y −y ̂) , 其中ξ为介于y 和y ̂之间的某个值. 设L 为|ðf ðy (t,ξ)|的上界,(8.5)式即得以满足.对公式(8.4)中的一阶常微分方程还可进一步分类. 若f (t,y )是关于y 的线性函数,f (t,y )=a (t )y +b (t ) ,(8.6) 其中a (t ),b (t )表示自变量为t 的两个一元函数,则对应的常微分方程为线性常微分方程,若b (t )≡0, 则为线性齐次常微分方程. 例8.1中的方程属于线性、齐次、常系数微分方程,这里的“常系数”是强调a (t )为常数函数.8.1.2 问题的敏感性对常微分方程初值问题,可分析它的敏感性,即考虑初值发生扰动对结果的影响. 注意这里的结果(解)是一个函数,而不是一个或多个值. 由于实际应用的需要,分析常微分方程初值问题的敏感性时主要关心t →∞时y (t )受影响的情况,并给出有关的定义. 此外,考虑到常微分方程的求解总与数值算法交织在一起、以及历史的原因,一般用“稳定”、“不稳定”等词汇说明问题的敏感性.定义8.1:对于常微分方程初值问题(8.4),考虑初值y 0的扰动使问题的解y (t )发生偏差的情形. 若t →∞时y (t )的偏差被控制在有界范围内,则称该初值问题是稳定的(stable ),否则该初值问题是不稳定的(unstable ). 特别地,若t →∞时y (t )的偏差收敛到零,则称该初值问题是渐进稳定的(asymptotically stable ).关于定义8.1,说明两点:● 渐进稳定是比稳定更强的结论,若一个问题是渐进稳定的,它必然是稳定的. ● 对于不稳定的常微分方程初值问题,初始数据的扰动将使t →∞时的结果误差无穷大. 因此为了保证数值求解的有效性,常微分方程初值问题具有稳定性是非常重要的.例8.2 (初值问题的稳定性): 考察如下“模型问题”的稳定性:{y ′=λy,t ≥t 0y (t 0)=y 0 . (8.7)[解] 易知此常微分方程的准确解为:y (t )=y 0e λ(t−t 0). 假设初值经过扰动后变为y 0+Δy 0,对应的扰动后解为y ̂(t )=(y 0+Δy 0)e λ(t−t 0),所以扰动带来的误差为Δy (t )=Δy 0e λ(t−t 0) .根据定义8.1,需考虑t →∞时Δy (t )的值,它取决于λ. 易知,若λ≤0,则原问题是稳定的,若λ>0,原问题不稳定. 而且当λ<0时,原问题渐进稳定.图8-1分三种情况显示了初值扰动对问题(8.7)的解的影响,从中可以看出不稳定、稳定、渐进稳定的不同含义.对例8.2中的模型问题,若考虑参数λ为一般的复数,则问题的稳定性取决于λ的实部,若Re(λ)≤0, 则问题是稳定的,否则不稳定. 例8.2的结论还可推广到线性、常系数常微分方程,即根据f (t,y )中y 的系数可确定初值问题的稳定性. 对于一般的线性常微分方程(8.6),由于方程中y 的系数为关于t 的函数,仅能分析t 取某个值时的局部稳定性.例8.3 (局部稳定性): 考察如下常微分方程初值问题的稳定性:{y ′=−10ty,t ≥0y (0)=1 . (8.8)[解] 此常微分方程为线性常微分方程,其中y 的系数为a (t )=−10t . 当t ≥0时,a (t )≤0,在定义域内每个时间点上该问题都是局部稳定的.事实上,方程(8.8)的解析为y (t )=e −5t 2,初值扰动Δy 0造成的结果误差为Δy (t )=Δy 0e −5t 2. 这说明初值问题(8.8)是稳定的.对于更一般的一阶常微分方程(8.4),由于其中f (t,y )可能是非线性函数,分析它的稳定性非常复杂. 一种方法是通过泰勒展开用一个线性常微分方程来近似它,再利用线性常微分方程稳定性分析的结论了解它的局部稳定性. 具体的说,在某个解函数y ∗(t)附近用一阶泰勒展开近似f (t,y ),f (t,y )≈f (t,y ∗)+ðf ðy(t,y ∗)∙(y −y ∗) 则原微分方程被局部近似为(用符号z 代替y ): 图8-1 (a) λ>0对应的不稳定问题, (b) λ=0对应的稳定问题, (c) λ<0对应的渐进稳定问题. (a) (b) (c)z′=ðfðy(t,y∗)∙(z−y∗)+f(t,y∗)这是关于未知函数z(t)的一阶线性常微分方程,可分析t取某个值时的局部稳定性. 因此,对于具体的y∗(t)和t的取值,常微分方程初值问题(8.4)的局部稳定性取决于ðfðy(t,y∗)的实部的正负号. 应注意的是,这样得到的关于稳定性的结论只是局部有效的.实际遇到的大多数常微分方程初值问题都是稳定的,因此在后面讨论数值解法时这常常是默认的条件.8.2简单的数值解法与有关概念大多数常微分方程都无法解析求解(尤其是常微分方程组),只能得到解的数值近似. 数值解与解析解有很大差别,它是解函数在离散点集上近似值的列表,因此求解常微分方程的数值方法也叫离散变量法. 本节先介绍最简单的常微分方程初值问题解法——欧拉法(Euler method),然后给出数值解法的稳定性和准确度的概念,最后介绍两种隐格式解法.8.2.1 欧拉法数值求解常微分方程初值问题,一般都是“步进式”的计算过程,即从t0开始依次算出离散自变量点上的函数近似值. 这些离散自变量点和对应的函数近似值记为:t0<t1<⋯<t n<t n+1<⋯y 0,y1,⋯y n,y n+1,⋯其中y0是根据初值条件已知的. 相邻自变量点的间距为 n=t n+1−t n, 称为步长.数值解法通常使用形如y n+1=G(y n+1,y n,y n−1,…,y n−k)(8.9) 的计算公式,其中G表示某个多元函数. 公式(8.9)是若干个相邻时间点上函数近似值满足的关系式,利用它以及较早时间点上函数近似值可算出y n+1. 若公式(8.9)中k=0,则对应的解法称为单步法(single-step method),其计算公式为:y n+1=G(y n+1,y n) .(8.10) 否则,称为多步法(multiple-step method). 另一方面,若函数G与y n+1无关,即:y n+1=G(y n,y n−1,…,y n−k),则称为显格式方法(explicit method),否则称为隐格式方法(implicit method). 显然,显格式方法的计算较简单,只需将已得到的函数近似值代入等号右边,则可算出y n+1.欧拉法是一种显格式单步法,对初值问题(8.4)其计算公式为:y n+1=y n+ n f(t n,y n) , n=0,1,2,⋯.(8.11) 它可根据数值微分的向前差分公式(第7.7节)导出. 由于y′=f(t,y),则y′(t n)=f(t n,y(t n))≈y(t n+1)−y(t n)n,得到近似公式y(t n+1)≈y(t n)+ n f(t n,y(t n)),将其中的函数值换为数值近似值,则得到欧拉法的递推计算公式(8.11). 还可以从数值积分的角度进行推导,由于y(t n+1)=y(t n)+∫y′(s)dst n+1t n =y(t n)+∫f(s,y(s))dst n+1t n,用左矩形公式近似计算其中的积分(矩形的高为s=t n时被积函数值),则有y(t n+1)≈y(t n)+ n f(t n,y(t n)) ,将其中的函数值换为数值近似值,便得到欧拉法的计算公式.例8.4 (欧拉法):用欧拉法求解初值问题{y ′=t −y +1y (0)=1. 求t =0.5时y (t )的值,计算中将步长分别固定为0.1和0.05.[解] 在本题中,f (t,y )=t −y +1, t 0=0, y 0=1, 则欧拉法计算公式为:y n+1=y n + (t n −y n +1) , n =0,1,2,⋯当步长h=0.1时,计算公式为y n+1=0.9y n +0.1t n +0.1; 当步长h=0.05时,计算公式为y n+1=0.95y n +0.05t n +0.05. 两种情况的计算结果列于表8-1中,同时也给出了准确解y (t )=t +e −t 的结果.表8-1 欧拉法计算例8.4的结果 h=0.1h=0.05 t ny n y (t n ) t n y n t n y n 0.11.000000 1.004837 0.05 1.000000 0.3 1.035092 0.21.010000 1.018731 0.1 1.002500 0.35 1.048337 0.31.029000 1.040818 0.15 1.007375 0.4 1.063420 0.41.056100 1.070320 0.2 1.014506 0.45 1.080249 0.5 1.090490 1.106531 0.25 1.023781 0.5 1.098737 从计算结果可以看出,步长取0.05时,计算的误差较小.在常微分方程初值问题的数值求解过程中,步长 n ,(n =0,1,2,⋯)的设置对计算的准确性和计算量都有影响. 一般地,步长越小计算结果越准确,但计算步数也越多(对于固定的计算区间右端点),因此总计算量就越大. 在实际的数值求解过程中,如何设置合适的步长达到准确度与效率的最佳平衡是很重要的一个问题.8.2.2数值解法的稳定性与准确度在使用数值方法求解初值问题时,还应考虑数值方法的稳定性. 实际的计算过程中都存在误差,若某一步的解函数近似值y n 存在误差,在后续递推计算过程中,它会如何传播呢?会不会恶性增长,以至于“淹没”准确解?通过数值方法的稳定性分析可以回答这些问题. 首先给出稳定性的定义.定义8.2:采用某个数值方法求解常微分方程初值问题(8.4),若在节点t n 上的函数近似值存在扰动δn ,由它引起的后续各节点上的误差δm (m >n )均不超过δn ,即|δm |≤|δn |,(m >n),则称该方法是稳定的.在大多数实际问题中,截断误差是常微分方程数值求解中的主要计算误差,因此我们忽略舍入误差. 此外,仅考虑稳定的常微分方程初值问题.考虑单步法的稳定性,需要分析扰动δn 对y n+1的影响,推导δn+1与δn 的关系式. 以欧拉法为例,先考虑模型问题(8.7),并且设Re(λ)≤0. 此时欧拉法的计算公式为②:y n+1=y n + λy n =(1+ λ)y n ,由y n 上的扰动δn 引起y n+1的误差为:δn+1=(1+ λ)δn ,要使δn+1的大小不超过δn ,则要求|1+ λ|≤1 . (8.12)② 对于稳定性分析以及后面的一些场合,由于只考虑一步的计算,将步长 n 记为 .。
欧拉法、梯形法和龙格-库塔一、解方程:= 8x(2-y)y(0)=1二、算出方程的解析解为:y= 2 -三、实验原理:1.欧拉法原理:将区间[a,b]分成n段.那么方程在第x i点有y'(x i) = f(x i,y(x i)).再用向前差商近似代替导数则为:.在这里.h是步长.即相邻两个结点间的距离。
因此可以根据xi点和yi点的数值计算出y i+1来:.i=0,1,2,n这就是欧拉格式.若初值y i+ 1是已知的.则可依据上式逐步算出数值解y1,y2……..yn2.梯形法原理:将向前欧拉公式中的导数f(xi,yi)改为微元两端f(xi,yi)和f(xi+1,yi+1)的平均.即梯形公式。
3.龙格-库塔方法的基本思想:在区间[xn,xn+1]内多取几个点.将他们的斜率加权平均.作为导数的近似。
令初值问题表述如下。
则.对于该问题的RK4由如下方程给出:其中这样.下一个值(y n+1)由现在的值(y n)加上时间间隔(h)和一个估算的斜率的乘积决定。
该斜率是以下斜率的加权平均:k1是时间段开始时的斜率;k2是时间段中点的斜率.通过欧拉法采用斜率k1来决定y在点tn + h/2的值;k3也是中点的斜率.但是这次采用斜率k2决定y值;k4是时间段终点的斜率.其y值用k3决定。
当四个斜率取平均时.中点的斜率有更大的权值:RK4法是四阶方法.也就是说每步的误差是h5阶.而总积累误差为h4阶。
四、欧拉法、梯形法和龙格-库塔的实现代码:h=0.1;x=0:h:1;y1=zeros(size(x));y1(1)=1;y2=zeros(size(x));y2(1)=1;y3=zeros(size(x));y3(1)=1;for i1=2:length(x)y1(i1) = y1(i1-1) + h*8*x(i1-1)*(2-y1(i1-1));%欧拉法 m1= 8*x(i1-1)*(2-y2(i1-1));%梯形法m2 =8*x(i1)*(2-y2(i1-1)+h*m1);y2(i1)=y2(i1-1)+h*(m1+m2)/2;%梯形法公式k1=8*x(i1-1)*(2-y2(i1-1)); %龙格-库塔k2=8*(x(i1-1)+h/2)*(2-(y2(i1-1)+h*k1/2));k3=8*(x(i1-1)+h/2)*(2-(y2(i1-1)+h*k2/2));k4=8*(x(i1-1)+h)*(2-(y2(i1-1)+h*k3));y3(i1)=y3(i1-1)+(k1+2*k2+2*k3+k4)*h/6; %龙格-库塔公式endy4=2-exp(-4*(x.^2));%解析解plot(x,y1,x,y2,x,y3,x,y4)%解析解与数值解图像legend('y1','y2','y3','y4')plot(x,y4-y1,x,y4-y2,x,y4-y3)% 解析解与数值解误差图像legend('y4-y1','y4-y2','y4-y3')五、图像:1.解析解y4与各个数值解y1,y2,y3的图像:(1)当步长h=0.1时:(2)当步长h=0.05时:(3)当步长h=0.01时:结论:三个图中.方程的解析解都是y4。
第8章 常微分方程数值解法本章主要内容:1.欧拉法、改进欧拉法. 2.龙格-库塔法。
3.单步法的收敛性与稳定性。
重点、难点一、微分方程的数值解法在工程技术或自然科学中,我们会遇到的许多微分方程的问题,而我们只能对其中具有较简单形式的微分方程才能够求出它们的精确解。
对于大量的微分方程问题我们需要考虑求它们的满足一定精度要求的近似解的方法,称为微分方程的数值解法。
本章我们主要讨论常微分方程初值问题⎪⎩⎪⎨⎧==00)(),(yx y y x f dx dy的数值解法。
数值解法的基本思想是:在常微分方程初值问题解的存在区间[a,b]内,取n+1个节点a=x 0<x 1<…<x N =b (其中差h n = x n –x n-1称为步长,一般取h 为常数,即等步长),在这些节点上把常微分方程的初值问题离散化为差分方程的相应问题,再求出这些点的上的差分方程值作为相应的微分方程的近似值(满足精度要求)。
二、欧拉法与改进欧拉法欧拉法与改进欧拉法是用数值积分方法对微分方程进行离散化的一种方法。
将常微分方程),(y x f y ='变为()*+=⎰++11))(,()()(n xn x n n dtt y t f x y x y1.欧拉法(欧拉折线法)欧拉法是求解常微分方程初值问题的一种最简单的数值解法。
欧拉法的基本思想:用左矩阵公式计算(*)式右端积分,则得欧拉法的计算公式为:Nab h N n y x hf y y n n n n -=-=+=+)1,...,1,0(),(1 欧拉法局部截断误差11121)(2++++≤≤''=n n n n n x x y h R ξξ或简记为O (h 2)。
我们在计算时应注意欧拉法是一阶方法,计算误差较大。
欧拉法的几何意义:过点A 0(x 0,y 0),A 1(x 1,y 1),…,A n (x n ,y n ),斜率分别为f (x 0,y 0),f (x 1,y 1),…,f (x n ,y n )所连接的一条折线,所以欧拉法亦称为欧拉折线法。