Euler法和改进的Euler法实验报告
- 格式:doc
- 大小:257.99 KB
- 文档页数:6

常微分方程数值解实验报告学院:数学与信息科学专业:信息与计算科学姓名:郑思义学号:201216524课程:常微分方程数值解实验一:常微分方程的数值解法1、分别用Euler 法、改进的Euler 法(预报校正格式)和S —K 法求解初值问题。
(h=0.1)并与真解作比较。
⎩⎨⎧=++-=10(1y')y x y 1.1实验代码:%欧拉法function [x,y]=naeuler(dyfun,xspan,y0,h)%dyfun 是常微分方程,xspan 是x 的取值范围,y0是初值,h 是步长 x=xspan(1):h:xspan(2); y(1)=y0;for n=1:length(x)-1y(n+1)=y(n)+h*feval(dyfun,x(n),y(n)); end%改进的欧拉法function [x,m,y]=naeuler2(dyfun,xspan,y0,h)%dyfun 是常微分方程,xspan 是x 的取值范围,y0是初值,h 是步长。
%返回值x 为x 取值,m 为预报解,y 为校正解 x=xspan(1):h:xspan(2); y(1)=y0;m=zeros(length(x)-1,1); for n=1:length(x)-1 k1=feval(dyfun,x(n),y(n)); y(n+1)=y(n)+h*k1; m(n)=y(n+1);k2=feval(dyfun,x(n+1),y(n+1)); y(n+1)=y(n)+h*(k1+k2)/2; end%四阶S —K 法function [x,y]=rk(dyfun,xspan,y0,h)%dyfun 是常微分方程,xspan 是x 的取值范围,y0是初值,h 是步长。
x=xspan(1):h:xspan(2); y(1)=y0;for n=1:length(x)-1 k1=feval(dyfun,x(n),y(n));k2=feval(dyfun,x(n)+h/2,y(n)+(h*k1)/2); k3=feval(dyfun,x(n)+h/2,y(n)+(h*k2)/2); k4=feval(dyfun,x(n)+h,y(n)+h*k3);y(n+1)=y(n)+(h/6)*(k1+2*k2+2*k3+k4);end%主程序x=[0:0.1:1];y=exp(-x)+x;dyfun=inline('-y+x+1');[x1,y1]=naeuler(dyfun,[0,1],1,0.1);[x2,m,y2]=naeuler2(dyfun,[0,1],1,0.1);[x3,y3]=rk(dyfun,[0,1],1,0.1);plot(x,y,'r',x1,y1,'+',x2,y2,'*',x3,y3,'o');xlabel('x');ylabel('y');legend('y为真解','y1为欧拉解','y2为改进欧拉解','y3为S—K解','Location','NorthWest');1.2实验结果:x 真解y 欧拉解y1 预报值m 校正值y2 S—K解y30.0 1.0000 1.0000 1.0000 1.00000.1 1.0048 1.0000 1.0000 1.0050 1.00480.2 1.0187 1.0100 1.0145 1.0190 1.01870.3 1.0408 1.0290 1.0371 1.0412 1.04080.4 1.0703 1.0561 1.0671 1.0708 1.07030.5 1.1065 1.0905 1.1037 1.1071 1.10650.6 1.1488 1.1314 1.1464 1.1494 1.14880.7 1.1966 1.1783 1.1945 1.1972 1.19660.8 1.2493 1.2305 1.2475 1.2500 1.24930.9 1.3066 1.2874 1.3050 1.3072 1.30661.0 1.3679 1.3487 1.3665 1.3685 1.36792、选取一种理论上收敛但是不稳定的算法对问题1进行计算,并与真解作比较。

实验报告实验项目名称常微分方程的数值解法实验室数学实验室所属课程名称微分方程数值解实验类型上机实验实验日期2013年3月11日班级10信息与计算科学学号2010119421姓名叶达伟成绩实验概述:【实验目的及要求】运用不同的数值解法来求解具体问题,并通过具体实例来分析比较各种常微分方程的数值解法的精度,为以后求解一般的常微分方程起到借鉴意义。
【实验原理】各种常微分方程的数值解法的原理,包括Euler法,改进Euler法,梯形法,Runge-Kutta方法,线性多步方法等。
【实验环境】(使用的软硬件)Matlab软件实验内容:【实验方案设计】我们分别运用Euler法,改进Euler法,RK方法和Adams隐式方法对同一问题进行求解,将数值解和解析解画在同一图像中,比较数值解的精度大小,得出结论。
【实验过程】(实验步骤、记录、数据、分析)我们首先来回顾一下原题:对于给定初值问题:1. 求出其解析解并用Matlab画出其图形;2. 采用Euler法取步长为0.5和0.25数值求解(2.16),并将结果画在同一幅图中,比较两者精度;3. 采用改进Euler法求解(2.16),步长取为0.5;4. 采用四级Runge-Kutta法求解(2.16),步长取为0.5;5. 采用Adams四阶隐格式计算(2.16),初值可由四级Runge-Kutta格式确定。
下面,我们分五个步骤来完成这个问题:步骤一,求出(2.16)式的解析解并用Matlab 画出其图形; ,用Matlab 做出函数在上的图像,见下图:00.51 1.52 2.53 3.54 4.550.511.522.533.5x 1015y=exp(1/3 t 3-1.2t)exact solution图一 初值问题的解析解的图像步骤二,采用Euler 法取步长为0.5和0.25数值求解(2.16),并将结果画在同一幅图中,比较两者精度;我们采用Euler 法取步长为0.5和0.25数值求解,并且将数值解与解析解在一个图中呈现,见下图:00.51 1.52 2.53 3.54 4.550.511.522.533.5x 1015Numerical solution of Euler and exact solutionexact solution h=0.5h=0.25图二 Euler 方法的计算结果与解析解的比较从图像中不难看出,采用Euler 法取步长为0.5和0.25数值求解的误差不尽相同,也就是两种方法的计算精度不同,不妨将两者的绝对误差作图,可以使两种方法的精度更加直观化,见下图:00.51 1.52 2.53 3.54 4.550.511.522.533.5x 1015Absolute error of numerical solution and exact solutionh=0.5h=0.25图三 不同步长的Euler 法的计算结果与解析解的绝对误差的比较 从图像中我们不难看出,步长为0.25的Euler 法比步长为0.5的Euler 法的精度更高。

微分方程数值解法实验报告2篇微分方程数值解法实验报告(一)在实际科学与工程问题中,我们经常会遇到微分方程的求解。
然而,许多微分方程往往没有解析解,这就需要我们利用数值方法来获得近似解。
本篇实验报告将介绍两种常见的微分方程数值解法:欧拉方法和改进的欧拉方法。
一、欧拉方法欧拉方法是最简单的微分方程数值解法之一。
其基本原理为离散化微分方程,将微分方程中的导数用差商代替。
设要求解的微分方程为dy/dx = f(x, y),步长为h,则可用以下公式进行递推计算:y_{n+1} = y_n +hf(x_n, y_n)二、算法实现为了对欧拉方法进行数值实验,我们以一阶线性常微分方程为例:dy/dx = x - y, y(0) = 1步骤如下:(1)选择合适的步长h和求解区间[a, b],这里我们取h=0.1,[a, b] = [0, 1];(2)初始化y_0 = 1;(3)利用欧拉方法递推计算y_{n+1} = y_n + 0.1(x_n - y_n);(4)重复步骤(3),直到x_n = 1。
三、实验结果与讨论我们通过上述步骤得到了在[0, 1]上的近似解y(x)。
下图展示了欧拉方法求解的结果。
从图中可以看出,欧拉方法得到的近似解与精确解有一定的偏差。
这是因为欧拉方法只是通过递推计算得到的近似解,并没有考虑到更高阶的误差。
所以在需要高精度解时,欧拉方法并不理想。
四、改进的欧拉方法针对欧拉方法的不足,我们可以考虑使用改进的欧拉方法(也称为改进的欧拉-柯西方法)。
它是通过利用前后两个步长欧拉方法得到的结果作为差商的中间项,从而提高了求解精度。
一阶线性常微分方程的改进欧拉方法可以表示为:y_{n+1} = y_n + h(f(x_n, y_n) + f(x_{n+1}, y_n + hf(x_n,y_n)))/2五、算法实现与结果展示将改进的欧拉方法应用于前述的一阶线性常微分方程,我们同样选择h=0.1,[a, b] = [0, 1]。

微分方程数值解实验报告实验目的:掌握微分方程数值解的基本方法,能够利用计算机编程求解微分方程。
实验原理:微分方程是自然科学与工程技术中常见的数学模型,它描述了变量之间的关系及其随时间、空间的变化规律。
解微分方程是研究和应用微分方程的基础,但有很多微分方程无法找到解析解,只能通过数值方法进行求解。
本实验采用欧拉方法和改进的欧拉方法求解微分方程的初值问题:$$\begin{cases}\frac{dy}{dt}=f(t,y)\\y(t_0)=y_0\end{cases}$$其中,$f(t,y)$是给定的函数,$y(t_0)=y_0$是已知的初值条件。
欧拉方法是最基本的数值解法,其步骤如下:1.给定$t_0$和$y_0$2.计算$t_{i+1}=t_i+h$,其中$h$是步长3. 计算$y_{i+1}=y_i+hf(t_i,y_i)$4.重复步骤2、3直到达到终止条件改进的欧拉方法是对欧拉方法进行改进,通过利用函数$y(t)$在$t+\frac{1}{2}h$处的斜率来更准确地估计$y_{i+1}$,其步骤如下:1.给定$t_0$和$y_0$2.计算$t_{i+1}=t_i+h$,其中$h$是步长3. 计算$y_*=y_i+\frac{1}{2}hf(t_i,y_i)$4. 计算$y_{i+1}=y_i+hf(t_i+\frac{1}{2}h,y_*)$5.重复步骤2、3、4直到达到终止条件实验步骤:1.编写程序实现欧拉方法和改进的欧拉方法2.给定微分方程和初值条件3.设置步长和终止条件4.利用欧拉方法和改进的欧拉方法求解微分方程5.比较不同步长下的数值解与解析解的误差6.绘制误差-步长曲线,分析数值解的精度和收敛性实验结果:以一阶常微分方程$y'=3ty+t$为例,给定初值$y(0)=1$,取步长$h=0.1$进行数值求解。
利用欧拉方法求解微分方程得到的数值解如下:\begin{array}{cccc}t & y_{\text{exact}} & y_{\text{Euler}} & \text{误差} \\ \hline0.0&1.000&1.000&0.000\\0.1&1.035&1.030&0.005\\0.2&1.104&1.108&0.004\\0.3&1.212&1.217&0.005\\0.4&1.360&1.364&0.004\\0.5&1.554&1.559&0.005\\0.6&1.805&1.810&0.005\\0.7&2.131&2.136&0.005\\0.8&2.554&2.560&0.006\\0.9&3.102&3.107&0.006\\1.0&3.807&3.812&0.005\\\end{array}利用改进的欧拉方法求解微分方程得到的数值解如下:\begin{array}{cccc}t & y_{\text{exact}} & y_{\text{Improved Euler}} & \text{误差} \\\hline0.0&1.000&1.000&0.000\\0.1&1.035&1.035&0.000\\0.2&1.104&1.103&0.001\\0.3&1.212&1.211&0.001\\0.4&1.360&1.358&0.002\\0.5&1.554&1.552&0.002\\0.6&1.805&1.802&0.003\\0.7&2.131&2.126&0.005\\0.8&2.554&2.545&0.009\\0.9&3.102&3.086&0.015\\1.0&3.807&3.774&0.032\\\end{array}误差-步长曲线如下:实验结论:通过对比欧拉方法和改进的欧拉方法的数值解与解析解的误差,可以发现改进的欧拉方法具有更高的精度和收敛性。


实验课程名称数值计算方法实验项目名称 Euler 方法年级 09级专业信息与计算科学学生姓名姜露学号 0907010200理学院实验时间:2011 年 5 月 30日学生实验室守则一、按教学安排准时到实验室上实验课,不得迟到、早退和旷课。
二、进入实验室必须遵守实验室的各项规章制度,保持室内安静、整洁,不准在室内打闹、喧哗、吸烟、吃食物、随地吐痰、乱扔杂物,不准做与实验内容无关的事,非实验用品一律不准带进实验室。
三、实验前必须做好预习(或按要求写好预习报告),未做预习者不准参加实验。
四、实验必须服从教师的安排和指导,认真按规程操作,未经教师允许不得擅自动用仪器设备,特别是与本实验无关的仪器设备和设施,如擅自动用或违反操作规程造成损坏,应按规定赔偿,严重者给予纪律处分。
五、实验中要节约水、电、气及其它消耗材料。
六、细心观察、如实记录实验现象和结果,不得抄袭或随意更改原始记录和数据,不得擅离操作岗位和干扰他人实验。
七、使用易燃、易爆、腐蚀性、有毒有害物品或接触带电设备进行实验,应特别注意规范操作,注意防护;若发生意外,要保持冷静,并及时向指导教师和管理人员报告,不得自行处理。
仪器设备发生故障和损坏,应立即停止实验,并主动向指导教师报告,不得自行拆卸查看和拼装。
八、实验完毕,应清理好实验仪器设备并放回原位,清扫好实验现场,经指导教师检查认可并将实验记录交指导教师检查签字后方可离去。
九、无故不参加实验者,应写出检查,提出申请并缴纳相应的实验费及材料消耗费,经批准后,方可补做。
十、自选实验,应事先预约,拟订出实验方案,经实验室主任同意后,在指导教师或实验技术人员的指导下进行。
十一、实验室内一切物品未经允许严禁带出室外,确需带出,必须经过批准并办理手续。
学生所在学院:理学院专业:信息与计算科学班级:091。

用Euler法和改进的Euler法求u' -5u(0 < t w,,(0)=1的数值解,步长h=0.1, 0.05,并比较两个算法的精度。
解:1) 当步长h=0.1 时编写程序如下所示clf clear clc%直接求解微分方程y=dsolve( 'Dy=-5*y' , 'y(0)=1' , 't' )%Euler 法h=0.1;t=0:h:1; n=length(t);u=zeros(1,n); u(1)=1;zbu(1,1)=t(1); zbu(2,1)=u(1);for i=2:nf=-5*u(i-1); u(i)=u(i-1)+h*f;zbu(1,i)=t(i); zbu(2,i)=u(i);endzbu%改进的Euler 法v=zeros(1,n);v0=zeros(1,n); v(1)=1;zbv(1,1)=t(1); zbv(2,1)=v(1);for i=2:n f=-5*v(i-1); v0(i)=v(i-1)+h*f; v(i)=v(i-1)+h/2*(f-5*v0(i)); zbv(1,i)=t(i); zbv(2,i)=v(i);end zbvplot(t,u, 'r*' , 'markersize' ,10)hold on,plot(t,v, 'r.' , 'markersize' ,20)hold on,ezplot(y,[0,1])hold on,title( 'Euler 法和改进的Euler 法比较(h=0.1 )),grid onlegend( 'Euler 法’,'?改进的Euler 法','解析解')%解真值h=0.1;t=O:h:1;n=len gth(t);for i=1: ny(i)=1/exp(5*t(i)); %通过第一部分程序直接解得的解析解zby(1,i)=t(i);zby(2,i)=y(i);endzby我们可以得到计算后的结果图像如图一所示EulBr法和改进的Eutgr法比较)0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.9 09 1图1 Euler法和改进的Euler法比较(h=0.1)同时,我们得到Euler法,改进的Euler法和解析解的在各点处数值分别如下所示:t坐标0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 欧拉 1.0000 0.5000 0.2500 0.1250 0.0625 0.0313 0.0156 0.0078 0.0039 0.0020 0.0010 改进欧拉 1.0000 0.6250 0.3906 0.2441 0.1526 0.0954 0.0596 0.0373 0.0233 0.0146 0.0091 真值 1.0000 0.6065 0.3679 0.2231 0.1353 0.0821 0.0498 0.0302 0.0183 0.0111 0.0067 表1 Euler法和改进的Euler法在各点数值比较(h=0.1)为了比较Euler法和改进的Euler法的算法精度,在这里我们利用相对误差的概念进行评判。

微分方程数值解实验报告微分方程数值解实验报告一、引言微分方程是数学中一类重要的方程,广泛应用于各个科学领域。
在实际问题中,往往难以得到微分方程的解析解,因此需要借助数值方法来求解。
本实验旨在通过数值解法,探索微分方程的数值解及其应用。
二、数值解法介绍常用的微分方程数值解法有欧拉法、改进欧拉法、四阶龙格-库塔法等。
在本实验中,我们将采用改进欧拉法进行数值解的求取。
改进欧拉法是一种一阶的显式迭代法,其基本思想是将微分方程的导数用差商来近似表示,并通过迭代逼近真实解。
具体迭代公式如下:\[y_{n+1} = y_n + h \cdot f(x_n + \frac{h}{2}, y_n + \frac{h}{2} \cdot f(x_n, y_n))\]其中,\(y_n\)表示第n步的近似解,\(h\)表示步长,\(f(x_n, y_n)\)表示微分方程的导数。
三、实验步骤1. 确定微分方程及初始条件在本实验中,我们选择经典的一阶常微分方程:\[y' = -2xy\]并给定初始条件\(y(0) = 1\)。
2. 设置步长和迭代次数为了得到较为准确的数值解,我们需要合理选择步长和迭代次数。
在本实验中,我们将步长设置为0.1,迭代次数为10。
3. 迭代计算数值解根据改进欧拉法的迭代公式,我们可以通过编写计算程序来求解微分方程的数值解。
具体计算过程如下:- 初始化:设定初始条件\(y_0 = 1\),并给定步长\(h = 0.1\)。
- 迭代计算:使用改进欧拉法的迭代公式,通过循环计算得到\(y_1, y_2, ...,y_{10}\)。
- 输出结果:将计算得到的数值解输出,并进行可视化展示。
四、实验结果与分析通过以上步骤,我们得到了微分方程的数值解\(y_1, y_2, ..., y_{10}\)。
将这些数值解进行可视化展示,可以更直观地观察到解的变化趋势。
根据实验结果,我们可以发现随着迭代次数的增加,数值解逐渐逼近了真实解。

一、实验目的1. 理解普里姆算法的基本原理和步骤。
2. 掌握使用C语言实现普里姆算法的方法。
3. 熟悉最小生成树的概念及其在实际应用中的重要性。
4. 通过实验验证普里姆算法的正确性和效率。
二、实验环境1. 操作系统:Windows 102. 编程语言:C语言3. 开发环境:Visual Studio三、实验原理普里姆算法是一种贪心算法,用于在加权无向图中寻找最小生成树。
最小生成树是指一个无向图的所有顶点构成的树,其边权值之和最小。
普里姆算法的基本思想是从某个顶点开始,逐步增加边,直到包含所有顶点为止。
四、实验步骤1. 定义邻接矩阵:首先定义一个二维数组表示图的邻接矩阵,其中元素表示两个顶点之间的边权值。
2. 初始化数据结构:定义一个结构体表示顶点,包含顶点的编号和距离。
初始化一个数组存储所有顶点的结构体。
3. 选择起始顶点:选择一个顶点作为起始顶点,将其距离设置为0,其余顶点的距离设置为无穷大。
4. 遍历邻接矩阵:对于每个顶点,遍历其邻接矩阵,找到距离最小的边,将其加入最小生成树中,并更新相邻顶点的距离。
5. 重复步骤4:重复步骤4,直到所有顶点都被加入最小生成树中。
6. 输出结果:输出最小生成树的边和权值。
五、实验代码```c#include <stdio.h>#include <stdlib.h>#define MAXVEX 6#define INF 10000typedef struct {int adjvex; // 邻接顶点的位置int lowcost; // 与adjvex顶点相连的边的权值} MinNode;typedef struct {char vexs[MAXVEX]; // 顶点表MinNode adjmatrix[MAXVEX][MAXVEX]; // 邻接矩阵int numVertexes, numEdges; // 图中当前顶点的数量和边的数量} MGraph;void CreateMGraph(MGraph G) {int i, j, k, w;printf("请输入顶点数量和边数量:\n");scanf("%d %d", &G->numVertexes, &G->numEdges);printf("请输入顶点信息:\n");for (i = 0; i < G->numVertexes; i++) {scanf("%s", G->vexs[i]);}for (i = 0; i < G->numVertexes; i++) {G->adjmatrix[i][j].adjvex = 0;G->adjmatrix[i][j].lowcost = INF;}}for (k = 0; k < G->numEdges; k++) {printf("请输入边(%d)的两个顶点和权值:\n", k + 1); scanf("%d %d %d", &i, &j, &w);G->adjmatrix[i][j].adjvex = j;G->adjmatrix[i][j].lowcost = w;G->adjmatrix[j][i].adjvex = i;G->adjmatrix[j][i].lowcost = w;}}void Prim(MGraph G, int u) {int min, i, j, k;MinNode adjvex;int visited[MAXVEX] = {0}; // 标记顶点是否被访问过visited[u] = 1;printf("%c ", G.vexs[u]); // 输出起始顶点for (i = 1; i < G.numVertexes; i++) {min = INF;k = u;if (visited[j] == 0 && G.adjmatrix[k][j].lowcost < min) { min = G.adjmatrix[k][j].lowcost;adjvex = G.adjmatrix[k][j];k = j;}}printf("%c ", G.vexs[k]); // 输出当前顶点visited[k] = 1;G.adjmatrix[u][k].lowcost = INF;G.adjmatrix[k][u].lowcost = INF;}}int main() {MGraph G;int u;printf("请输入起始顶点编号:\n");scanf("%d", &u);CreateMGraph(&G);Prim(G, u);return 0;}```六、实验结果1. 输入顶点数量和边数量:6 82. 输入顶点信息:A B C D E F3. 输入边(1)的两个顶点和权值:0 1 14. 输入边(2)的两个顶点和权值:0 2 25. 输入边(3)的两个顶点和权值:1 2 36. 输入边(4)的两个顶点和权值:1 3 67. 输入边(5)的两个顶点和权值:2 3 48. 输入边(6)的两个顶点和权值:2 4 59. 输入边(7)的两个顶点和权值:3 4 710. 输入边(8)的两个顶点和权值:4 5 811. 输入起始顶点编号:0实验结果:A B C D E F七、实验总结通过本次实验,我们成功实现了普里姆算法,并验证了其在实际应用中的有效性。

CENTRAL SOUTH UNIVERSITY 数值分析实验报告Euler 方法与改进的Euler 方法的应用一、问题背景在工程和科学技术的实际问题中,常需求解微分方程,但常微分方程中往往只有少数较简单和典型的常微分方程(例如线性常系数常微分方程等)可求出其解析解,对于变系数常微分方程的解析求解就比较困难,而一般的非线性常微分方程的求解困难就更不用说了。
大多数情况下,常微分方程只能用近似方法求解。
这种近似解法可分为两大类:一类是近似解析法,如级数解法、逐次逼近法等;另一类是数值解法,它给出方程在一些离散点上的近似值。
二、数学模型在具体求解微分方程时,需具备某种定解条件,微分方程和定解条件合在一起组成定解问题。
定解条件有两种:一种是给出积分曲线在初始点的状态,称为初始条件,相应的定解问题称为初值问题。
另一类是给出积分曲线首尾两端的状态,称为边界条件,相应的定解问题称为边值问题。
在本文中主要讨论的是给定初值条件的简单Euler 方法和改进的Euler 方法来求解常微分方程。
三、算法及流程Euler 方法是最简单的一种显式单步法。
对于方程()y x f dxdy ,= 考虑用差商代替导数进行计算,取离散化点列nh x x n +=0,L n ,2,1,0=则得到方程的近似式()()()()n n n n x y x f hx y x y ,1≈-+ 即()n n n n y x hf y y ,1+=+ 得到简单Euler 方法。
具体计算时由0x 出发,根据初值,逐步递推二得到系列离散数值。
简单Euler 方法计算量小,然而精度却不高,因而我们可以构造梯形公式()()[]η=++=+++0111,,2y y t f y t f h y y n n n n n n 其中()N a b h -=。
这是一个二阶方法,比Euler 方法精度高。
但是上述公式右边有1+n y ,因而是隐式差分方程,可以用迭代方法计算1+n y 。
_改进欧拉方法范文改进欧拉方法的方法有很多,并且可以从多个方面进行改进。
在下面的文本中,将介绍三种常见的改进方法:改进的欧拉方法、修正的欧拉方法和改进的欧拉方法。
改进的欧拉方法(Improved Euler Method)是一种将欧拉方法进行改进的方法,它通过对函数的斜率进行线性插值来提高计算精度。
具体来说,改进的欧拉方法使用欧拉方法所计算出的斜率与下一个时间步上使用欧拉方法所计算出的斜率的平均值来计算下一个时间步的值。
改进的欧拉方法的迭代公式如下:y(i+1)=y(i)+(1/2)*h*(f(t(i),y(i))+f(t(i+1),y(i)+h*f(t(i),y(i ))))其中,i表示当前时间步,i+1表示下一个时间步,h表示时间步长,t(i)表示当前时间,t(i+1)表示下一个时间,y(i)表示在当前时间步处的函数值,y(i+1)表示下一个时间步处的函数值,f(t,y)表示在时间t处函数的斜率。
修正的欧拉方法(Modified Euler Method)是在改进的欧拉方法的基础上进行改进的方法,它通过对两个时间步使用欧拉方法所计算出的斜率的平均值来计算下一个时间步的值。
修正的欧拉方法的迭代公式如下:y(i+1)=y(i)+h*f(t(i)+1/2*h,y(i)+1/2*h*f(t(i),y(i)))其中,i表示当前时间步,i+1表示下一个时间步,h表示时间步长,t(i)表示当前时间,y(i)表示在当前时间步处的函数值,y(i+1)表示下一个时间步处的函数值,f(t,y)表示在时间t处函数的斜率。
改进的欧拉方法(Heun's method)是一种通过将两个时间步的斜率进行加权平均来计算下一个时间步的值的方法。
改进的欧拉方法的迭代公式如下:y(i+1)=y(i)+(1/2)*h*(f(t(i),y(i))+f(t(i+1),y(i)+h*f(t(i),y(i ))))其中,i表示当前时间步,i+1表示下一个时间步,h表示时间步长,t(i)表示当前时间,t(i+1)表示下一个时间,y(i)表示在当前时间步处的函数值,y(i+1)表示下一个时间步处的函数值,f(t,y)表示在时间t处函数的斜率。
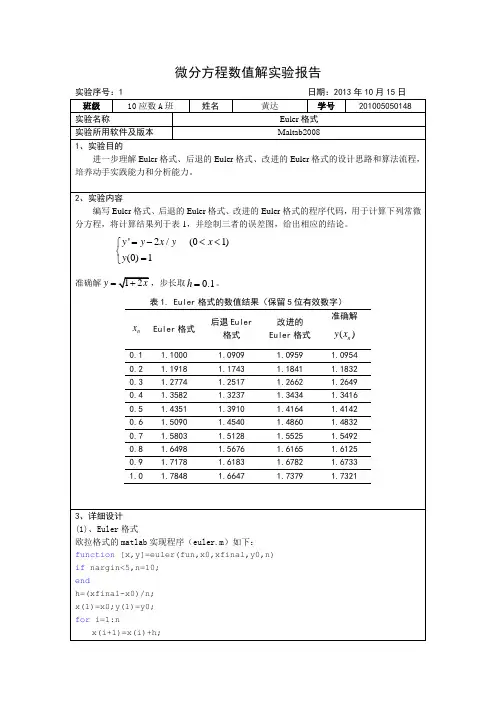
佛山科学技术学院实 验 报 告课程名称 数值分析 实验项目 常微分方程问题初值问题数值解法 专业班级 姓 名 学 号 指导教师 陈剑 成 绩 日 期一. 实验目的1、理解如何在计算机上实现用Euler 法、改进Euler 法、Runge -Kutta 算法求一阶常微分方程初值问题⎩⎨⎧=∈='1)(],[),,()(y a y b a x y x f x y 的数值解。
2、利用图形直观分析近似解和准确解之间的误差。
二、实验要求(1) 按照题目要求完成实验内容; (2) 写出相应的Matlab 程序;(3) 给出实验结果(可以用表格展示实验结果); (4) 分析和讨论实验结果并提出可能的优化实验。
(5) 写出实验报告。
三、实验步骤1、用Matlab 编写解常微分方程初值问题的Euler 法、改进Euler 法和经典的四阶Runge-Kutta 法。
2、给定初值问题⎪⎩⎪⎨⎧=≤≤-=;1)1(,21,1')1(2y x xy x y⎪⎩⎪⎨⎧=≤≤++-=31)0(10,25050')2(2y x x x y y 要求:(a )用Euler 法和改进的Euler 法(步长均取h=0.05)及经典的四阶Runge-Kutta 法(h=0.1)求(1)的数值解,并打印)10,....2,1,0(1.01=+=i i x 的值。
(b) 用经典的四阶Runge-Kutta 方法解(2),步长分别取h=0.1, 0.05,0.025,计算并打印)10,....2,1,0(1.0==i i x 个点的值,与准确解25031)(x e x y x +=-比较,并列表写出在x=0.2,0.5,0.8处,对于不同步长h 下的误差,讨论同一节点处,误差随步长的变化规律。
(c )用Matlab 绘图函数绘制(2)的精确解和近似解的图形。
四、实验结果 %Euler.mfunction y = Euler(x0,xn,y0,h) %Euler 法解方程f_xy ; %x0,y0为初始条件; %x0,xn 为求值区间; %h 为步长; %求区间个数: n = (xn-x0)/h;%矩阵x 存储n+1个节点: x = [x0:h:xn]';%矩阵y 存储节点处的值: y = [y0;zeros(n,1)];%矩阵y_存储节点处导数值: y_(1)= f_xy(x0,y0); y_ = [y_(1);zeros(n,1)];%进行迭代(欧拉法迭代;求导数): for i = 2:n+1y (i) = y(i-1)+h*y_(i-1); y_(i) = f_xy(x(i),y(i)); end%Imp_Euler.mfunction y = Imp_Euler(x0,xn,y0,h)%改进的Euler法解方程f_xy;%x0,y0为初始条件;%x0,xn为求值区间;%h为步长;%求区间个数:n = (xn-x0)/h;%矩阵x存储n+1个节点:x = [x0:h:xn]';%矩阵y存储节点处的值:y = [y0;zeros(n,1)];%矩阵y_存储节点处导数值:y_(1)= f_xy(x0,y0);y_ = [y_(1);zeros(n,1)];%使用改进Euler法求值(欧拉法求近似;近似点导数;梯形校正;求导):for i = 2:n+1y_l = y(i-1) + h*y_(i-1);y_l = f_xy(x(i),y_l);y(i) = y(i-1) + (h/2)*(y_(i-1)+y_l);y_(i)= f_xy(x(i),y(i));end%R_Kutta4.mfunction y = R_Kutta4(x0,xn,y0,h)%Runger_Kutta法解方程f_xy;%x0,y0为初始条件;%x0,xn为求值区间;%h为步长;%求区间个数:n = (xn-x0)/h;%矩阵x存储n+1个节点:x = [x0:h:xn]';%矩阵y存储节点处的值:y = [y0;zeros(n,1)];%矩阵k1,k2,k3,k4存储各节点(中点)数值:k1(1)= f_xy(x0,y0);k1 = [k1(1);zeros(n,1)];k2(1)= f_xy(x0+h/2,y0+h*k1(1)/2);k2 = [k2(1);zeros(n,1)];k3(1)= f_xy(x0+h/2,y0+h*k2(1)/2);k3 = [k3(1);zeros(n,1)];k4(1)= f_xy(x0+h,y0+h*k3(1));k4 = [k4(1);zeros(n,1)];for i= 2:n+1y(i) = y(i-1)+(h/6)*(k1(i-1)+2*k2(i-1)+2*k3(i-1)+k4(i-1));k1(i)= f_xy(x(i),y(i));k2(i)= f_xy(x(i)+h/2,y(i)+h*k1(i)/2);k3(i)= f_xy(x(i)+h/2,y(i)+h*k2(i)/2);k4(i)= f_xy(x(i)+h,y(i)+h*k3(i));end(a):%f_xy.mfunction y_=f_xy(x,y)%求解第五次作业第一题的点(x,y)处的导数;y_ = 1/(x^2) - y/x;%run521.mclc,clear;x0 = 1;xn = 2;h = 0.05;y0 = 1;%便于显示出x,与y对应:x = [x0:h:xn]';y = Euler(x0,xn,y0,h);YE =[x,y];y = Imp_Euler(x0,xn,y0,h); YIE= [x,y];h = 0.1;x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); YRK= [x,y];(b): %f_xy.mfunction y_=f_xy(x,y) %求第二个方程的导数: y_ = -50*y+50*(x^2)+2*x;%run522.mclc,clear; x0 = 0; xn = 1; y0 = 1/3; %步长0.1: h = 0.1; x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); y_r= f_Real(x); Y1 = [x,y,y_r];%步长0.05: h = 0.05; x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); y_r= f_Real(x); Y2 = [x,y,y_r]; %步长0.025: h = 0.025; x = [x0:h:xn]';y = R_Kutta4(x0,xn,y0,h); y_r= f_Real(x); Y3 = [x,y,y_r];五、讨论分析(a)从结果可以看出使用RK 方法,步长较大但是结果也更加精确; (b)分析求值结果的误差,可以发现当步长取0.1时,误差是超级大的(10^8数量级),但是当步长缩小一半取0.05时,误差就很小了,再缩小一半,误差就更小了。
《数值计算方法》实验7报告班级:学号: 姓名: 成绩:1. 实验名称实验7 常微分方程的Euler 方法与改进的Euler 方法2. 实验题目取步长h =0.2,用Euler 方法和改进的Euler 方法求初值问题2',[0,1](0)1y y x x y y ⎧=-∈⎪⎨⎪=⎩的数值解,并将计算结果与解析解y =3. 实验目的掌握求解常微分方程的Euler 方法,熟悉改进的Euler 方法.4. 基础理论对于初值问题0'(,),[,]()y f x y x a b y a y =∈⎧⎨=⎩取节点i x a ih =+,则求解其数值解的Euler 公式为1(,),(0,1,,)n n n n y y hf x y n N +=+=改进的Euler 公式(也叫预报-校正法)为111(,)[(,)(,)]2n n n n n n n n n n y y hf x y h y y f x y f x y +++=+⎧⎪⎨=++⎪⎩ 5. 实验环境操作系统:Windows xp ;6. 实验过程第一步,确定好初值;先借Euler 公式求得一个初步的近似值,并且称之为预报值。
第二步,因为预报值精度低,所以要用它代替梯形公式右端的值,重新使用梯形公式计算一次,就得到了校正值。
7. 结果与分析精确解 Euler 方法改进Euler 方法x y ye[k] |ye[k]-y|ym[k] |ym[k]-y|0.0 1.000000 1.000000 0.000000 1.0000 00 0.0000000.2 1.095445 1.200000 0.104555 1.186667 0.0912220.4 1.183216 1.373333 0.190117 1.348312 0.1650960.6 1.264911 1.531495 0.266584 1.493704 0.2287930.8 1.341641 1.681085 0.339444 1.627861 0.2862211.0 1.414214 1.826948 0.412735 1.754205 0.339991Press any key to continue根据结果,可以得出,使用Euler公式计算方便,计算量少,然而,它的精度比较低。
常微分方程的数值解法实验报告实验报告:常微分方程的数值解法摘要:常微分方程(ODE)是描述动力学系统中物理量随时间变化的数学方程,广泛应用于自然科学和工程领域。
然而,对于一些复杂的非线性ODE,很难找到解析解。
因此,我们需要数值解法来求解这些方程。
本实验报告将介绍四种常见的常微分方程数值解法,分别是欧拉法、改进的欧拉法、四阶龙格-库塔法和自适应步长的龙格-库塔法,并通过数值实验比较它们的精度和效率。
1.引言在实际问题中,许多物理量的变化规律可以由常微分方程描述。
然而,对于复杂的非线性ODE,很难找到解析解。
因此,为了解决这类问题,我们需要借助数值方法来求解。
2.方法本实验采用四种常见的常微分方程数值解法:欧拉法、改进的欧拉法、四阶龙格-库塔法和自适应步长的龙格-库塔法。
(1)欧拉法是最简单的数值解法,通过将微分方程转化为差分方程,使用离散的步长来近似微分方程。
(2)改进的欧拉法在欧拉法的基础上进行了改进,使用预估-校正的方法来提高精度。
(3)四阶龙格-库塔法是一种经典的数值解法,通过利用不同步长处的斜率来近似微分方程,具有较高的精度。
(4)自适应步长的龙格-库塔法是在四阶龙格-库塔法的基础上改进而来的,根据步长的大小自适应地选择不同的步长,同时保证精度和效率。
3.实验设计为了比较这四种数值解法的精度和效率,我们设计了两个实验。
实验一是求解一阶常微分方程:dy/dx = -2x,初始条件y(0) = 1,解析解为y = 1 - x^2、实验二是求解二阶常微分方程:d^2y/dx^2 + y = 0,初始条件y(0) = 0,dy/dx(0) = 1,解析解为y = sin(x)。
4.结果与分析实验一中,比较四种数值解法在不同步长下的近似解和解析解,计算其误差。
实验结果表明,四阶龙格-库塔法和自适应步长的龙格-库塔法具有较高的精度,而欧拉法和改进的欧拉法的精度较低。
实验二中,我们比较四种数值解法在不同步长下的近似解和解析解,并计算其误差。
用Euler法和改进的Euler法求u’=-5u(0≤t≤1),u(0)=1的数值解,步长h=0.1,0.05,并比较两个算法的精度。
解:
1)当步长h=0.1时
编写程序如下所示
clf
clear
clc
%直接求解微分方程
y=dsolve('Dy=-5*y','y(0)=1','t')
%Euler法
h=0.1;
t=0:h:1;
n=length(t);
u=zeros(1,n);
u(1)=1;
zbu(1,1)=t(1);
zbu(2,1)=u(1);
for i=2:n
f=-5*u(i-1);
u(i)=u(i-1)+h*f;
zbu(1,i)=t(i);
zbu(2,i)=u(i);
end
zbu
%改进的Euler法
v=zeros(1,n);
v0=zeros(1,n);
v(1)=1;
zbv(1,1)=t(1);
zbv(2,1)=v(1);
for i=2:n
f=-5*v(i-1);
v0(i)=v(i-1)+h*f;
v(i)=v(i-1)+h/2*(f-5*v0(i));
zbv(1,i)=t(i);
zbv(2,i)=v(i);
end
zbv
plot(t,u,'r*','markersize',10)
hold on,
plot(t,v,'r.','markersize',20)
hold on,
ezplot(y,[0,1])
hold on,
title('Euler法和改进的Euler法比较(h=0.1)),
grid on
legend('Euler法','¸改进的Euler法','解析解')
%解真值
h=0.1;
t=0:h:1;
n=length(t);
for i=1:n
y(i)=1/exp(5*t(i)); %通过第一部分程序直接解得的解析解
zby(1,i)=t(i);
zby(2,i)=y(i);
end
zby
我们可以得到计算后的结果图像如图一所示
图1 Euler法和改进的Euler法比较(h=0.1)
同时,我们得到Euler法,改进的Euler法和解析解的在各点处数值分别如下所示:
t坐标0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
改进欧拉 1.0000 0.6250 0.3906 0.2441 0.1526 0.0954 0.0596 0.0373 0.0233 0.0146 0.0091
表1 Euler法和改进的Euler法在各点数值比较(h=0.1)为了比较Euler法和改进的Euler法的算法精度,在这里我们利用相对误差的概念进行评判。
对于Euler法和改进的Euler法的每个的估计值有:
相对误差=|估计值-真值 |
真值
从而我们可以通过计算得到如下的相对误差表:
t坐标0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
改进欧拉0 0.0305 0.0618 0.0942 0.1275 0.1618 0.1972 0.2336 0.2712 0.3099 0.3498 表2 Euler法和改进的Euler法在各点相对误差比较(h=0.1)为了评定算法精度,我们对每种算法的在所有点处的相对误差求平均,可以得到Euler法的平均相对误差为0.5443,改进的Euler法的平均相对误差为0.1670。
由此我们可以得出改进的欧拉法的算法进度更高。
2)当步长h=0.05时
程序编写如下
clf
clear
clc
%直接求解微分方程
y=dsolve('Dy=-5*y','y(0)=1','t')
%Euler法
h=0.01;
t=0:h:1;
n=length(t);
u=zeros(1,n);
u(1)=1;
zbu(1,1)=t(1);
zbu(2,1)=u(1);
for i=2:n
f=-5*u(i-1);
u(i)=u(i-1)+h*f;
zbu(1,i)=t(i);
zbu(2,i)=u(i);
end
zbu
%改进的Euler法
v=zeros(1,n);
v0=zeros(1,n);
v(1)=1;
zbv(1,1)=t(1);
zbv(2,1)=v(1);
for i=2:n
f=-5*v(i-1);
v0(i)=v(i-1)+h*f;
v(i)=v(i-1)+h/2*(f-5*v0(i));
zbv(1,i)=t(i);
zbv(2,i)=v(i);
end
zbv
plot(t,u,'r*','markersize',10)
hold on,
plot(t,v,'r.','markersize',20)
hold on,
ezplot(y,[0,1])
hold on,
title('Euler法和改进的Euler法比较(h=0.1)),
grid on
legend('Euler法','¸改进的Euler法','解析解')
%解真值
h=0.01;
t=0:h:1;
n=length(t);
for i=1:n
y(i)=1/exp(5*t(i)); %通过第一部分程序直接解得的解析解 zby(1,i)=t(i);
zby(2,i)=y(i);
end
zby
计算后的结果图像为
图1 Euler法和改进的Euler法比较(h=0.05)
同时,我们得到Euler法,改进的Euler法和解析解的在各点处数值分别如下所示:
t坐标0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50
改进欧拉 1.0000 0.7813 0.6104 0.4768 0.3725 0.2910 0.2274 0.1776 0.1388 0.1084 0.0847
t坐标0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 1.00
改进欧拉0.0662 0.0517 0.0404 0.0316 0.0247 0.0193 0.0150 0.0118 0.0092 0.0072
此时,求出两种算法的相对误差的平均值分别为:
Euler法改进的Euler法
0.2960 0.0321
由此可见改进的Euler法的算法精度高于Euler法。
由以上的分析我们可以得出如下结论:
1. Euler法和改进的Euler法相比较,改进的Euler法的计算精度更高,相对误差
也比较小。
因此在求解微分方程的数值解时,改进的Euler法优于Euler法。
2. 在上述两种方法中当步长h越小则计算精度越高,相对误差较小。
因此,计
算能力允许的范围内,选取步长越小可以得到更加精确的结果。
3. 在利用这两种方法计算数值解的过程中,前一次迭代的结果会对下一轮求得
的数值产生影响。
因此,一旦上一轮迭代所得的结果有偏差,下一轮结果的
偏差将大于上一轮的偏差。
因此会导致伴随迭代次数的增加而产生更大的偏
差。