风速模型

在进行深入探讨Weibull分布风速模型基本构成参数及其作用之前，我们先来简单了解一下Weibull分布。

Weibull分布是由瑞典数学家瓦尔德玛·魏布尔于1951年提出的，用来描述风速、风力等自然现象的统计分布。

1. Weibull分布的基本特征Weibull分布是一种连续概率分布，其密度函数为：\[ f(x;\lambda,k) = \frac{k}{\lambda}\left(\frac{x}{\lambda}\right)^{k-1} e^{-(x/\lambda)^k} \]其中，\( x>0 \)，\( \lambda>0 \)为比例参数，\( k>0 \)为形状参数。

Weibull分布的平均值、方差和标准差分别为：\[ \text{E}[X] = \lambda \Gamma(1+\frac{1}{k}) \]\[ \text{Var}[X] = \lambda^2 \left[ \Gamma(1+\frac{2}{k}) -(\Gamma(1+\frac{1}{k}))^2 \right] \]\[ \text{Std}[X] = \lambda \sqrt{\left[ \Gamma(1+\frac{2}{k}) - (\Gamma(1+\frac{1}{k}))^2 \right]} \]其中，\( \Gamma \)为Gamma函数。

2. Weibull分布的构成参数Weibull分布的构成参数包括比例参数\( \lambda \)和形状参数\( k \)。

比例参数\( \lambda \)反映了分布的尺度，它决定了分布的位置，即控制了平均值的大小。

形状参数\( k \)决定了分布的形状，描述了分布的偏斜性。

当\( k>1 \)时，分布呈现右偏态，当\( k<1 \)时，分布呈现左偏态，当\( k=1 \)时，分布呈现对称性。

3. Weibull分布的作用Weibull分布在风能、风电等领域得到了广泛的应用。

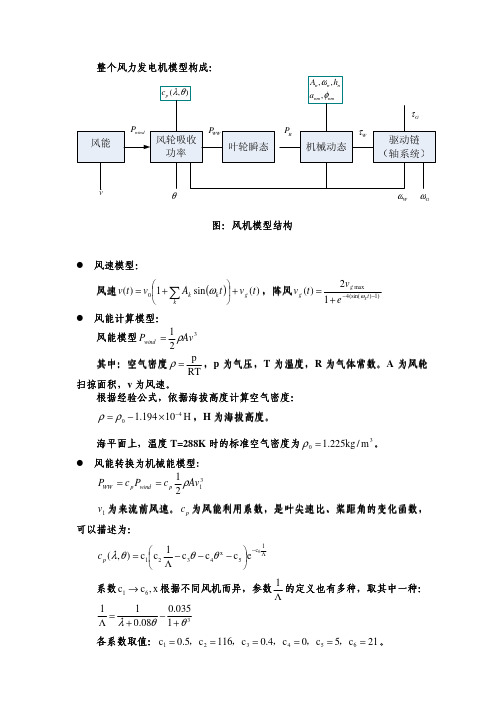
一、风力发电模型1风速数学模型一年当中的大部分时间中风速都是比较平稳的，风速在0~25m/s 之间发生的概率较高。

研究表明，绝大多数地区的年平均风速都可以采用威布尔分布函数来表示])exp[()(1k k cv c v c k v -=）（ϕ 其中v 是平均风速，c 是尺度系数，它反映的是该地区平均风速的大小；另一个形状系数k,它能够反映风速分布的特点，对应威布尔分布密度函数的形状，取值范围一般在1.8到2.3之间。

在有些研究中为了考察暂态过程中风速的变化情况，也可以风速分解，采用四分量模型，即：基本风、阵风、渐变风和随机风。

2单个风电场模型风力发电场输出功率的变化主要源于风速和风向的波动、风力发电机组的故障停运等，而坐落在同一风力发电场的不同风机具有几乎相同的风速、风向，因此可以假设同一风力发电场内所有风机的风速和风向相同，然后根据风力发电机组的功率特性曲线求出单个风机的输出功率，所有风机功率之和乘以一个表示尾流效应的系数即为该风力发电厂的输出功率。

其中，t SW 为风机轮毂高度处的风速，co r ci ,V V V ，以及r P 为别为风机启动风速、额定风速、切除风速以及风机额定功率。

在此基础上，引入了风机停运模型来模拟风力发电机组的故障停运：风力发电机组具有一定的故障率。

当风机处于检修状态时，输出为零；当风机处于运行状态时，输出功率由风力发电场风速决定二、光伏发电模型1，光伏发电系统是由光伏电池板、控制器、电能存储和变换等环节构成的发电与电能变换系统。

2，光伏发点输出功率模型其中，P 为输出功率，mod η为该小时环境温度下的模块效率，A 为光照总面积，wr η为配线效率系数，pc η为功率调节系统的效率，tilt I 为倾斜面的光照，l horisconta I 为水平面的光照，R 为l horisconta I 到tilt I 的折算系数，sd η为模块的标准效率，m f 为匹配系数，β为效率改变的温度系数，cell T 为环境温度。

河南能源鹤煤热电2x135MW机组低氮改造工程《SOFA风量测量装置》数学计算模型航天环境工程有限公司二〇一五年七月六日（一）、概述河南能源鹤煤热电2x135MW机组低氮改造工程锅炉SOFA风量实施在线监测。

每台锅炉的SOFA风量测量装置包括：罗斯蒙特差压变送器4只，靠背管测速装置4套。

本文提供风量的计算的数学模型。

（二）、风量计算数学模型SOFA风量计算数学模型如下：(差压变送器量程建议为0-1000pa)Q=Kc KA3.6=23.96032575KcA3.6 (km3/h)式中：Q—SOFA风道风量，单位 k m3/hKc—风速测量装置流量系数,暂取0.839ΔP—变送器输出差压，单位Pat—SOFA风温度,单位 ℃ （可取各侧二次风箱温度）Pa—SOFA风道内静压,单位Pa. （可取各侧二次风箱压力）KA—风速测量装置安装处截面积, 单位m2各角SOFA风参数设置如下:序号 测点名称 安装处风道尺寸流速系数(Kc)截面积 总系数K备注SOFA 风量 #1 SOFA风流量0.9 1.086 0.839 0.9774 70.73421114 #2 SOFA风流量0.9 1.086 0.8390.9774 70.73421114 #3 SOFA风流量0.9 1.086 0.8390.9774 70.73421114 #4 SOFA风流量0.9 1.086 0.8390.9774 70.73421114（三）、小信号切除及系统阻尼加装要求1．小信号切除功能风量计算，因涉及开根号，故应加装小信号切除功能，建议当变送器输出电流小于或等于4.2mA，认为风速为零。

2．系统阻尼加装要求为了确保显示的稳定性，系统应加装软件阻尼。

建议系统采样速率取用1次/秒，采用前8秒钟平均值进行显示。

基于核密度估计的风速建模方法作者：马强刘波安宗文来源：《风能》2016年第01期风能作为一种清洁可再生资源，正在被越来越多的国家用以发电并作为改善能源结构的一种措施。

风能具有的随机性、波动性及间歇性特点将对风电机组的安全稳定运行带来影响；同时，风速预测也是风功率预测的关键步骤之一。

目前，风速模型主要从概率分布角度出发对其随机性进行描述，当研究短周期或某些特殊时段的风速分布特性时，由于气候变化等随机因素影响的明显增强，将会导致两峰甚至多峰风速分布情况的出现。

因此，对于多峰风速分布情况，如何对其进行有效的风速分布描述及建立相应的风速模型，具有一定的研究意义。

基于此，本文针对风速分布可能呈现单峰、双峰或多峰的特性，提出一种基于核密度估计建立风速模型的方法。

通过MATLAB对实测风速进行核密度估计并绘制概率密度估计值曲线；利用权重系数组合多个正态分布对概率密度估计值曲线进行拟合，从而获得风速的概率密度函数；由概率密度函数生成随机风速样本并通过残差值和确定系数对拟合精度进行检验。

核密度估计为了获得总体概率密度分布，常用的方法有参数法和非参数法。

参数法由样本的频率直方图轮廓假设总体的概率密度分布，并通过样本对分布参数进行估计。

如图1所示，样本的频率直方图轮廓呈单峰状，近似正态分布。

因此假设总体服从正态分布，并通过样本对正态分布参数μ，σ进行估计得到总体的概率密度分布，如图2所示。

参数法依赖于对总体分布的假设，并且对分布参数进行估计时所涉及函数常为多元函数，需使用最大似然估计等方法借助编程计算获得参数估计值，过程相对复杂。

威布尔模型、权重系数组合模型都属于参数法。

非参数法则根据某一点处概率密度值与该点附近包含样本个数间的关系对其进行估计，无需假设总体分布及参数估计，引用经验密度函数f（x）作为总体密度函数的一个非参数估计，如式（1）所示：式中，n为样本总数；h i表示每个区间的长度，称为带宽；n i为该带宽內样本点个数。