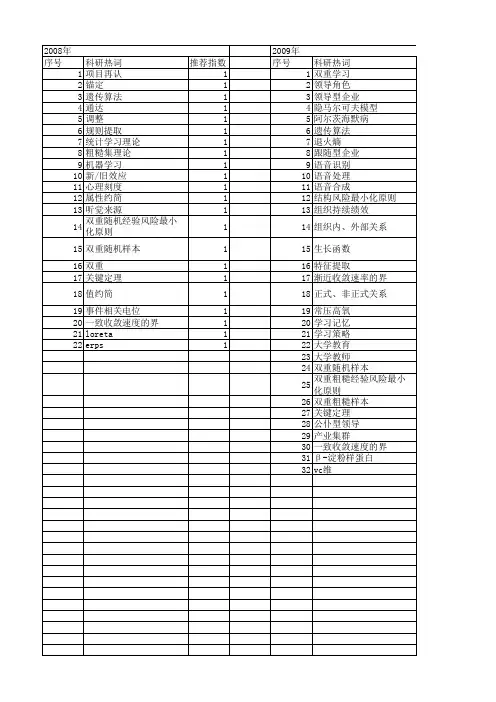
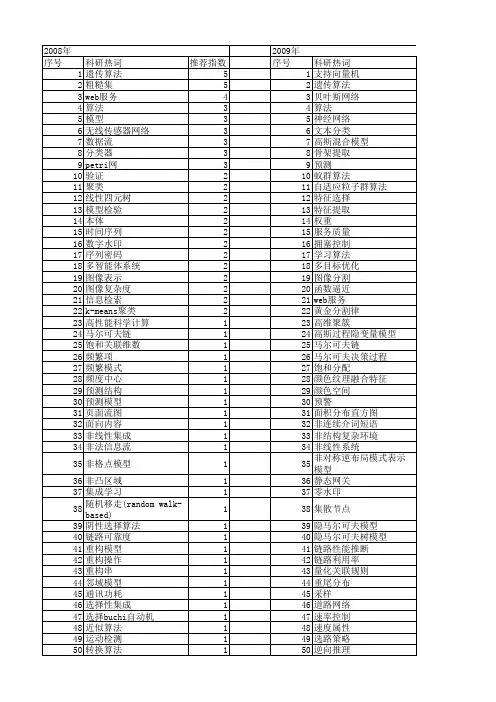
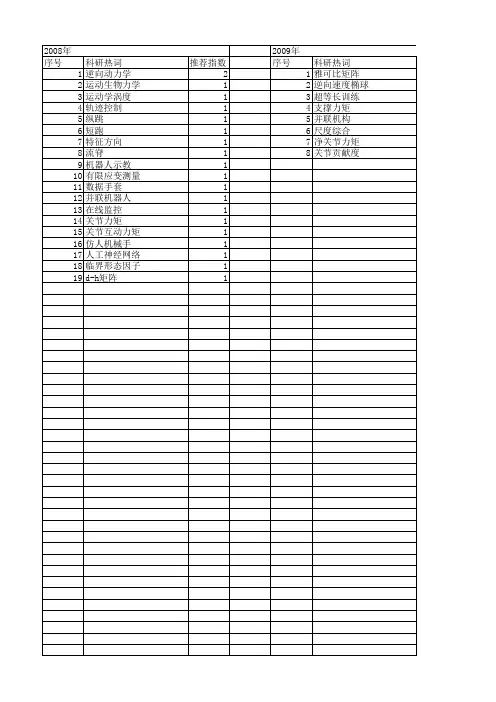
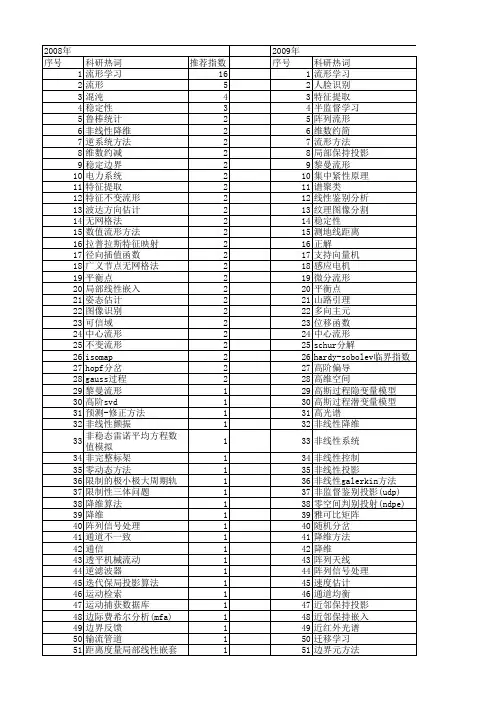
【计算机科学】_高斯过程隐变量模型_期刊发文热词逐年推荐_20140724

2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
科研热词 推荐指数 项目再认 1 锚定 1 遗传算法 1 通达 1 调整 1 规则提取 1 统计学习理论 1 粗糙集理论 1 机器学习 1 新/旧效应 1 心理刻度 1 属性约简 1 听觉来源 1 双重随机经验风险最小化原则 1 双重随机样本 1 双重 1 关键定理 1 值约简 1 事件相关电位 1 一致收敛速度的界 1 loreta 1 erps 1
1 1 1 1 1 1 1
53 严肃游戏 54 东道国当地网络 55 tau蛋白质类
1 1 1ຫໍສະໝຸດ 2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 风能产业 领导公平 零树 陷阱 遗忘 过程 迁移学习 跨领域 跨国创业 试错 认知障碍 虚拟现实 自然交互 自主创新能力 能源组合 管理创新 程序公平 稀疏表示 科研思维 社会网络 现代机器 演化 海外网络 海外人才 模仿 机械原理 探索性学习 投资组合理论 战略性新兴产业 情感倾向性 当地资源获取 开发性学习 小波 学习效应 学习成本 字典学习 多态现象,遗传 图像压缩 国际知识学习 反生产行为 双重选择 双元型组织 创新人才培养 创新 创业成长 创业企业 公共政策创新 全球学习 全球动态演化 光伏发电 健身游戏 伦理型领导
53 54 55 56 57 58 59
2011年 科研热词 绩效 民营化 嵌入性 外资股东 儿童 产业集群 阿尔茨海默病 量子角动态旋转 速度经济 通勤交通 连接关系 近似动态规划 过滤 负相关学习 规则分类学习 行政性协调 老年斑 结构嵌入 组织域 累计权值 精神卫生 粗糙集 粗糙熵阈值 管理能力 神经元形态 相对核 生产成本控制情报系统 生产性服务网络 特质理解 特征选择 满意度指标 效价线索 支持向量机集成 扰动 情绪线索 性别 归纳式学习 属性约简 对比研究 学习障碍 学习记忆 回转窑 双重结构 双重学习 动态约简 加速遗传算法 创新绩效 分类器组合 关系嵌入 免疫 克隆选择算法 信息技术 推荐指数 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

粗糙近似 粗糙关系特征 粒度计算 简图 符号化模型检测 移动对象数据库 移动agent 神经网络集成 确定有限自动机 知识表达 着色时间petri网 相空间重构 相关反馈 盲信号分离 疫苗 用户兴趣模型 生成树 独立分量分析 特征选择 特征词聚类 特征约简 特征提取 灵活规划 渐进网格 混沌技术 混沌吸引子 混合系统 消息通信 浮点遗传算法 测试路径 测试场景 测试中介 流数据挖掘 死锁预防 模糊随机变量 模糊聚类 模糊深隐马尔可夫模型 模型误差 概率粗糙集 概率密度估计 概念格 植入(l,d)问题 梯形子模式 格点量子色动力学 查询优化 柔性制造系统 构件集成测试 构件组合 构件消息自动机 构件回归测试 构件变更 构件元数据 构件 机器视觉
路由算法 路由模型 路由安全 路由协议 路径规划 资源调度模型 资源调度 费米矩阵 贝叶斯算法 语义分析 词性标注 证据丢失 访问直径 访问控制 设计立方体 订单管理 计算网格 视频编码 视差估计 规则学习 覆盖网组播 裁剪策略 行为语义 蛋白质结构预测 蛋白质折叠 蚁群算法 自适应细菌agent 自适应 自然语言理解 自然语言处理 自动web服务合成 能量有效性 背景建模 聚类中心 耦合系数 群体"软件人" 置信度 网络配置 网络安全态势感知 网络安全 网络均衡模型 网格资源 网格计算 网格简化 网格信任模型 网格 综述 维结构 结构连接算法 细-线程 线性模型 线性反馈移位寄存器 约简 索引
107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160

2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
2011年 科研热词 逆向工程 运动生成 运动学 超声检测机器人 设计 核函数 多关节摄动 位姿误差补偿 高斯过程隐变量模型 高斯过程 非线性降维 隐变量模型 逆向运动学 运动数据 运动学分析 虚拟人 自适应 聚类 方草压捆机 插秧机 打结器 强制推秧机构 姿态样本 农业机械 典型姿态 共轭凸轮 仿真 下意识行为 pik算法 推荐指数 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 1 1 1 1 1 1 1 1 1 13年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
科研热词 通用后置 运动学模型 运动学仿真 轨迹规划 踝关节康复机器人 距舟关节 足内侧纵弓 生物力学 柔索驱动 枕颈交界区 枕寰枢复合体 有限元模型 数值解法 并联机构 并联机器人 多轴机床 全微分 任意结构 三维运动 simmechanics
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
科研热词 逆向动力学 运动生物力学 运动学涡度 轨迹控制 纵跳 短跑 特征方向 流脊 机器人示教 有限应变测量 数据手套 并联机器人 在线监控 关节力矩 关节互动力矩 仿人机械手 人工神经网络 临界形态因子 d-h矩阵

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
辛数值流形时间子域法 距离保持投影 趋势分析 超平面 走时非对称项 贝叶斯规则 语音情感识别 语义距离 词汇分布 计算机辅助几何设计 计算机视觉 视频理解 表情识别 行为识别 螺旋理论 薄板弯曲 自适应观测器 自相合 自由曲面 脑电 脑机接口 背景图像 背景减除 联络 统一框架 结构动力响应 终端滑模控制 线性近邻传递算法 线性流形 线性分类方法 等距离映射 等距映射算法 等距映射 突变控制 突变判据 空间基础框架 稳健性 积分变换bochner-martinelli 积分偏移 离散系统 短信聚类 相空间非传统hamilton 直推式学习 白噪声 生物力学 球体退化八叉树网格(sdog) 特殊正交矩阵 特征融合 特征抽取 特征向量 特征函数 物理覆盖 灌浆压力 潜艇
资源空间模型 谐波平衡法 语义邻域 计算机应用 解码 解析解 视频摘要 观测器 蚁群聚类算法 范式 节能过渡 舌像分析 自适应算法 自适应控制 自组织映射 自动剖分 脉冲宽度调制 联合对角化 网格自适应 网格 编码 维数约简 维数约筒 维数分裂法 维数 统一电能质量调节器 线性判别分析(lda) 线性二次型调节器 粒子滤波 算术编码 等距特征映射 等距映射 等度降维 等变化性 空间特征向量 空间 空时 稳定流形 积分流形 神经网络 碰撞振动 相空间重构 相干信号 相对阶 相对梯度 直推式支持张量机 直接估计梯度 盲信源分离 目标跟踪 理论预测 环状流形 特殊欧氏群 特征核函数 物理非线性

科研热词 抑郁症 海马 静息状态 磁共振成像 支持向量机 高斯过程隐变量模型 静息态 雇佣关系 随机森林 长时程增强 部分可观马尔可夫决策过程 谷氨酸 蛋白酪氨酸激酶 脑部微量透析 脑结构 脑白质 结构风险最小化原则 组织绩效 粒度 离群点检测 离散化 神经网络 神经影像学 相关性 田纳西-伊斯曼 环境动荡性 激进式公司创业 渐进式公司创业 海马齿状回 概率主成分分析 样本信息熵 时间序列 故障诊断 故障原型 探索式学习 强关系 弱关系 属性重要性 局部一致性 局部fisher判别分析 学习记忆 多属性规则 外显记忆测验 场兴奋性突触后电位 图像水印 因子分析 回归估计 周期性分析 员工期望所得 匹配律 动物实验模型 动态能力
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68
半监督学习 半条件随机域模型 功能连接 利用式学习 初始聚类中心 分类回归树 分类 典型相关分析 不明确识别 ycrcb色度空间 vc维 l-范数 k-均值 k-means聚类 glivenko-cantelli类 adaboost
科研热词 推荐指数 抑郁症 3 粗糙集 2 面部动态表情 1 静息态 1 集成推理 1 隐马尔科夫模型 1 降维 1 邻域模型 1 遥感傅里叶变换红外光谱 1 选择性集成 1 自然语言处理 1 自助法 1 脑白质 1 肤色检测 1 肤色分布 1 维数约简 1 统计最复杂性 1 纤维丛 1 神经网络 1 磁共振成像 1 知识管理系统 1 病例对照研究 1 激进式公司创业 1 渐进式公司创业 1 流形学习 1 概率神经网络 1 植食性昆虫 1 杏仁核 1 机器学习 1 易挥发性有机化合物 1 明确识别 1 时延故障测试 1 文本段落划分 1 故障分析 1 探索式学习 1 战略互联网 1 成对约束 1 情绪 1 性能检测 1 强关系 1 弱关系 1 弥散张量成像 1 布尔可满足性 1 层次化电路 1 局部主成分分析 1 害虫防治 1 定性分析 1 学习行为 1 基于规则推理 1 基于案例推理 1 圆形分类器 1 反向传播人工神经网络 1

推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
科研热词 遗传算法 矩阵的秩 特征子集选择 模拟 概念矩阵 概念格 无标度特性 扩张矩阵 形式概念分析 多光谱图像 复杂网络 基因调控网络 哈斯图 动力学稳定性 入侵检测 光谱色彩管理 主成分分析 中间空间
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
2011年 科研热词 门限方案 蛋白质二级结构预测 组合公钥 种子矩阵 混合svm方法 复合金字塔模型 ecc复合定理 自动文摘 独立段群 正交投影 无向图 文档句权重 并发程序 小波分解 小样本问题 分类器 几何攻击 人脸识别 主题句抽取 不变质心 不变特征矩阵 rijndael加密 petri网 推荐指数 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
2014年 科研热词 评估指标 网络拓扑 粗糙集 相似度 混合模型 权重因子 弹性路由层 层次分析法 协同过滤 冷启动 决策 供应商选择 优化 ip重路由 推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

Байду номын сангаас
科研热词 推荐指数 流形学习 21 降维 3 局部线性嵌入 3 人脸识别 3 非线性降维 2 维数约简 2 维数约减 2 特征提取 2 流形 2 拉普拉斯特征映射 2 isomap 2 高阶svd 1 降维算法 1 迭代保局投影算法 1 运动检索 1 运动捕获数据库 1 边际费希尔分析(mfa) 1 距离度量局部线性嵌套 1 资源空间模型 1 谱图 1 视频摘要 1 蚁群聚类算法 1 舌像分析 1 自组织映射 1 维数约筒 1 线性投影 1 线性判别分析(lda) 1 纤维丛 1 等度降维 1 直推式支持张量机 1 直接估计梯度 1 环状流形 1 特征核函数 1 混合模型 1 步态识别 1 步态能量图 1 正则化最小二乘 1 正交边际费希尔分析(omfa) 1 模式识别 1 模型选择 1 最近特征线 1 最大差异延展算法 1 时序关联共生 1 数据挖掘 1 故障诊断 1 手写体数字识别 1 张量镜头 1 张量局部判别投影 1 带权多维尺度变换 1 局部线性逼近 1 局部嵌入 1 局部多维尺度变换(lmds) 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76
局部坐标排列 局部判别投影 局部几何特性 局部光滑逼近 局部主成分分析 小世界邻域 姿态变化 奇异值 多维尺度变换 多流形 多模态 多姿态人耳识别 图像检索 双向参考索引 动态切空间排列 切距离 内在流形 保局投影 人脸图像处理 人耳识别 不相关边际费希尔分析(umfa) web资源描述 l-isomap k-均值

特征矢量 特征提取 炎症 混淆交叉 混沌优化 混沌 混合遗传算法 海森矩阵 洪水灾情 水下航行器 比例积分微分神经元网络(pidnn) 正则化最小二乘 正交交叉 模糊神经网络 模糊推理 模拟退火算法 模拟退火 模拟进化算法 模拟植物生长 概率神经网络 样本空间分析 标准竞争 权值调整 权值直接确定 机组组合 机械手 朴素贝叶斯分类器 有监督局部线性嵌入 最近特征线 最小最大模块化网络 最小二乘支持向量机回归 最小二乘支持向量机 族群进化算法 族群经验学习机制 数据挖掘 数据建模 改进 支持向量机树 支持向量回归 操作风险 拟牛顿法 感知器 总体优化 快速留一法 径流预测 径流 影响图 彩色图像分割 归一化编辑距离 强化学习 张量局部判别投影 异常检测 带权多维尺度变换 差分进化
迭代最近点算法 迭代保局投影算法 进化计算 进化规划 过程神经元 轨迹规划 轨迹模式 距离度量局部线性嵌套 距离学习 超分辨 贪婪算法 贝叶斯网络 谱图 调制识别 评价模型 认知 计算经济学 衍生算法 蒙特卡罗分析 自适应局部学习 自适应kalman滤波 自组织映射 育种算法 聚类算法 聚类 联合树 网络效应 网络安全 维数约筒 维数约减 结构风险最小化 组合优化 线性降维 线性搜索 线性投影 纤维丛 精度评价 粗糙集 粒子群优化(pso) 粒子群优化 管道腐蚀 算法收敛性 等级预测 稳健性 移动自组网 码书设计 石油需求 短期负荷预测 知识库 矢量量化 相对值务件互信息 直接估计梯度 病毒进化遗传算法 病例对照研究
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 154 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106

高斯过程原理范文高斯过程是一种概率结果预测方法，它通过对变量之间的相关性进行建模，可以在给定一些已知观测值的情况下，预测未来的结果。

高斯过程是贝叶斯方法中的一种，它更注重对不确定性的处理和建模，适用于很多实际问题的解决。

本文将介绍高斯过程的原理和应用。

高斯过程的本质是定义了一个随机函数，其取值在任意给定的样本点处服从高斯分布。

这样，通过对样本点之间的距离和相关性进行建模，就可以预测未知点的取值了。

高斯过程最重要的两个性质是平稳性和正定核函数。

平稳性指的是高斯过程的均值和方差都是常数，并且不依赖于观测的位置；正定核函数则是用来度量样本点之间的相关性，它必须是正定的函数。

高斯过程可以用来解决回归问题和分类问题。

在回归问题中，给定一些样本点的观测值，我们可以通过高斯过程预测未知点的取值，并给出该预测的不确定性。

预测的不确定性可以用方差或置信区间来表示，这样就可以进行评估和决策了。

在分类问题中，我们可以将观测值分为两类，然后通过高斯过程对未知点进行分类，并计算出其属于一些类别的概率。

这样就可以判断未知点属于哪个类别了。

高斯过程的应用非常广泛，可以用于信号处理、机器学习、地质勘探等领域。

在信号处理中，高斯过程可以用来对信号进行建模和预测，从而实现信号的降噪和滤波。

在机器学习中，高斯过程被用来进行监督学习和强化学习，可以在给定一些观测值的情况下，对未知数据进行预测和决策。

在地质勘探中，高斯过程可以用来研究地下的油气储量和物性分布，从而指导油气勘探的工作。

高斯过程有很多的优点，使得它成为一个非常有用的工具。

首先，高斯过程是一种非参数的方法，不需要对模型进行显式的建模和参数估计，因此可以避免过拟合和欠拟合问题。

其次，高斯过程可以同时预测结果的取值和不确定性，这使得其预测结果更加可靠和可解释。

此外，高斯过程的数学理论非常成熟，有很多的推导和证明可以参考，使得其应用更加可靠和稳定。

总之，高斯过程是一种非常有用的概率结果预测方法，可以在很多实际问题中发挥作用。

53 54 55 56
fcm聚类 dna计算 cidoccrm adaboost
1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71
图像表示 因子分析 回归 向量编码 动态信息扩充 函数分布 关注点多维分离 不确定性 不完备知识 web服务 web信息提取 uml rough集理论 plc petri网 object-z ik-tableau dom树扩展 dezert-smarandache理论
科研热词 线性四元树 图像表示 图像复杂度 需求工程模式 需求工程 遗传算法 适应性构件 软件产品线 语言模型 评标 访问历史 融合 绒毛 真实感建模 界面关系模型 用户兴趣模型 特征 模糊聚类 模式复用 梯形子模式 构件模型 机器视觉 有限状态机 映射 时态关系数据库 时态xml 文本聚类 搜索空间 搜索 布局问题 工程项目 层次模型 实时绘制 定制 大词汇量连续语音识别 多智能体 多值逻辑 复用过程框架 声学模型 地理本体 发夹结构 分类器 产品线实现 二值图像 主动服务 个性化 与或图 不可移动文物 三维植物建模 xml tnam hmax特征
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52

推荐指数 3 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139
2009年 科研热词 单片机 bp神经网络 虚拟仪器 航天器 labview 鲁棒最小二乘 高斯光斑 飞航导弹 频率跟踪 预测模型 非正弦 雨量传感器 集成测试系统 重型卡车 通用示波器 通信功能 选矿过程 连续碳酸化分解 边缘网络 软测量 软件解决方案 转鼓供水 车载监控系统 质量特性 质量测试 质量 质心计算 贝叶斯网络 自动驾驶仪系统 自动 自主研发 绝对辐射计 结构相似度 系统设计 粒子群优化算法 管道机器人 等精度测频. 稳态精度 稳像火控系统 科技工作者 硬件加速 电能质量 电机协调 电定标 环境工程 推荐指数 3 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92

科研热词 高斯过程回归 高斯过程 高斯过程隐变量模型 高斯混合模型 高斯机器学习 高斯回归 预警 预处理 非线性滤波 连续状态空间 进化策略 近似模型 轴承 自适应预测 结构可靠度 结构优化设计 监测数据 瓦斯浓度 注塑成型 沙漠腹地 模型不确定性 桥梁工程 悬索桥 性能退化 工艺参数优化 小波包熵 容积卡尔曼滤波 多智能体系统 基于模型的强化学习 地下水含盐量 响应面法 偏离值 人工神经网络
2008年 序号 1 2 3 4
科研热词 高斯过程回归 隐性函数 贝叶斯估计 故障识别
推荐指数 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
科研热词 高斯过程 近红外光谱 补偿 维数灾 糖度 矩阵行列式的对数 番茄汁 有效酸度 最小二乘支持向量机 数值实验 强化学习 幂级数展开 图像去噪 回归 函数分布 svm分类 ls-svm回归
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38
2011年 科研热词 推荐指数 高斯过程 3 高斯过程回归 2 预测有效度 1 非线性预测控制 1 集成 1 采矿工程 1 近红外光谱 1 软测量 1 蒙特卡罗交叉验证 1 自适应自然梯度法 1 翼型设计 1 经验模态分解 1 系统 1 瓦斯浓度 1 灰色关联聚类分析 1 步态识别 1 正设计 1 模糊聚类 1 概率积分法 1 最小二乘支持向量机 1 时间序列 1 无信息变量去除 1 插值 1 开采沉陷 1 建模 1 定量分析 1 多尺度核 1 地表移动参数 1 在线高斯过程 1 反设 1 区间预测 1 偏最小二乘回归 1 micky-glass 1 hammerstein-wiener模型 1 cst参数化方法 1 cstr建模 1 bp神经网络 1 bagging算法 1

2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
科研热词 推荐指数 调和映射 2 高斯调频 1 高斯曲率 1 高斯分布 1 首次失效时间 1 非高斯结构反应 1 通信信号 1 超越率 1 调制识别 1 说话人确认 1 语音序列分类 1 蚁群算法 1 神经网络 1 相似性 1 特征矢量 1 演化方程 1 混沌映射 1 混合自动重传请求(harq) 1 混合神经网络 1 正交频分复用(ofdm) 1 次序均衡评分 1 模型预测控制 1 概率分布规整 1 核 1 极小浸入 1 支持向量回归 1 度分布 1 平均群超尺寸 1 局部固定核 1 多输入多输出系统 1 变分方法 1 功能因子 1 初始条件 1 分歧指标 1 低密度奇偶校验(ldpc)码 1 tv模型 1 sar成像 1 mfcc 1 hermite矩模型 1 hammerstein模型 1 gmm评分函数 1 gmm-ubm 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83
支持向量数据描述 支持向量描述鉴别分析 操作条件反射 恒虚警 延迟系统辨识 广义高斯混合模型 峰值衰减形态 局部距离保持 局部加权投影回归 安全系数 孤立点检测 子频带转换 姿态平衡控制 姿态估计 多径衰落 多尺度几何分析 增量学习 图像增强 围岩变形 反走样 单载波频域均衡 动态神经网络 分层条件随机场 全频带转换 信息熵 信息流 仿生自主学习系统 人脸识别 二维映射神经元模型 乳腺x线图像 三维信号映射

107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156类 统计线性回归 粒子群优化 稀疏表示 禁带 相关噪声 盲源分离 目标识别 特征点 熵能 流形学习 波达方向估计 棘波检测 核方法 核密度估计 期望最大化算法 斑点噪声 数字水印 广义高斯分布 尺度参数 多速率 均值漂移 图论 图像配准 图像复原 后验概率 双树复小波变换 参数估计 匹配追踪 分布估计算法 凸优化 免疫网络算法 信息融合 优化 人工免疫 交互多模型 retinex k均值聚类 黑色素瘤 黄土沟壑区 鲁棒性 鲁棒估计 高阶循环累积量 高斯过程隐变量模型 高斯脉冲 高斯背景噪声 高斯算法 高斯白噪声 高斯滤波器 高斯混合模型(gmm) 高斯混合 高斯消去法
科研热词 高斯混合模型 粒子滤波 图像去噪 图像处理 遗传算法 目标跟踪 支持向量机 图像分割 高斯过程 高斯曲率 高斯分布 运动目标检测 超宽带 计算机视觉 自适应阈值 磁化等离子体光子晶体 独立分量分析 特征提取 混沌映射 混合高斯模型 正交频分复用 时域有限差分法 无线传感器网络 小波变换 多目标跟踪 图像增强 去噪 光子晶体 em算法 高阶统计量 高斯滤波 高斯混合尺度模型 高斯模型 高斯核函数 高斯尺度空间 高斯噪声 高斯函数 高分辨距离像 预测 非线性非高斯 非线性 降噪 递归最小二乘 边缘检测 贝叶斯估计 说话人识别 语音识别 识别 认知无线电 视频水印 视觉特征 节点定位

第47卷第2期Vol.47No.2计算机工程Computer Engineering2021年2月February 2021多尺度多核高斯过程隐变量模型周培春1，吴兰岸2（1.玉林师范学院计算机科学与工程学院，广西玉林537000；2.南宁师范大学计算机与信息工程学院，南宁530299）摘要：高斯过程隐变量模型(GPLVM)作为一种无监督的贝叶斯非参数降维模型,无法有效利用数据所包含的语义标记信息,同时其建模过程中假设观测变量的各特征相互独立,忽略了特征之间的空间结构信息。

为解决上述问题,采用图像池化操作获得不同尺度的特征表示,利用线性投影方式将不同尺度的图像投影到低维隐空间进行特征融合,并将融合特征和数据标记分别作为输入和输出,构建多尺度多核高斯过程隐变量模型(MSMK -GPLVM),通过图像数据与数据标记的关联实现模型监督学习,同时对GPLVM 和线性投影权重矩阵进行联合学习以提高分类性能。

实验结果表明,MSMK -GPLVM 能够有效利用图像空间结构信息和语义标记信息,相比其他隐变量模型具有更强的数据降维和分类能力。

关键词：高斯过程；隐变量；降维；语义信息；空间信息开放科学（资源服务）标志码（OSID ）：中文引用格式：周培春，吴兰岸.多尺度多核高斯过程隐变量模型［J ］.计算机工程，2021，47（2）：285-292.英文引用格式：ZHOU Peichun ，WU Lan ’an.Multi -scale multi -kernel Gaussian process latent variable model ［J ］.Computer Engineering ，2021，47（2）：285-292.Multi-Scale Multi-Kernel Gaussian Process Latent Variable ModelZHOU Peichun 1，WU Lan ’an 2（1.School of Computer Science and Engineering ，Yulin Normal College ，Yulin ，Guangxi 537000，China ；2.School of Computer and Information Engineering ，Nanning Normal University ，Nanning 530299，China ）【Abstract 】As an unsupervised Bayesian non -parameter dimension reduction model ，the Gaussian Process Latent Variable Model （GPLVM ）fails to efficiently utilize semantic label information of data.Moreover ，it just assumes that the features of all observed variables are independent in modeling ，and thus ignores the spatial information among the features.To address the two issues ，this paper proposes a Multi -Scale Multi -Kernel Gaussian Process Latent Variable Model （MSMK -GPLVM ）.The model projects the images of different scales into a low -dimensional latent space through linear projection for feature fusion.A MSMK -GPLVM is constructed by taking the fused features as the input and the data labels as the output ，and it realizes supervised learning through the connection between image data and data labels ，and jointly learns the GPLVM and linear projection weight matrix to improve the classification performance.Experimental results show that MSMK -GPLVM can effectively utilize the spatial structure information of images and the semantic label pared with other latent variable models ，it has better performance in dimension reduction and classification.【Key words 】Gaussian process ；latent variable ；dimension reduction ；semantic information ；spatial information DOI ：10.19678/j.issn.1000-3428.00565560概述在机器学习和模式识别任务中，图像数据作为一种特殊的数据形式广泛应用于人脸识别［1］、表情识别［2］、年龄估计［3］等场景中，而此类数据通常具有较高的维度导致机器学习模型计算复杂度高且容易产生过拟合等维数灾难问题。

一种基于高斯隐变量模型的分类算法王秀美;高新波;李洁【期刊名称】《计算机学报》【年(卷),期】2012(35)12【摘要】高斯过程隐变量模型是近年来新兴的无监督降维方法,它可以找到高维数据的低维流形结构.但是由于高斯过程隐变量模型是无监督的概率降维方法,所以当数据集中的样本有类别标记信息时,高斯过程隐变量模型不能利用这些监督信息,实现分类的任务.为了使高斯过程隐变量模型可以处理分类任务,文中提出了一种监督的高斯过程隐变量模型分类模型.通过最大化后验似然的方法确定观测数据在隐空间的坐标,同时可以完成分类任务.实验结果证明了该模型可以有效地用于分类.%Gaussian process latent variable model is a new probabilistic approach for dimensionality reduction. It can obtain a low-dimensional manifold of a data set in an entirely unsupervised way. However, when there is some supervised information in the data set, Gaussian process latent variable model cannot use this information for supervised tasks, e. G. , classification and regression learning. For this purpose, a supervised Gaussian process latent variable model for classification is developed. The maximum-a-posterior algorithm is employed to estimate all latent variables position. Compared with the traditional Gaussian process latent variable model, the supervised version of this model shows more advantages in experiments.【总页数】7页(P2661-2667)【作者】王秀美;高新波;李洁【作者单位】西安电子科技大学电子工程学院西安710071;西安电子科技大学电子工程学院西安710071;西安电子科技大学电子工程学院西安710071【正文语种】中文【中图分类】TP181【相关文献】1.一种基于改进高斯过程隐变量模型的多角度人脸识别算法 [J], 刘剑;龚志恒;吴成东;高恩阳2.基于免疫克隆高斯过程隐变量模型的SAR目标特征提取与识别 [J], 张向荣;缑丽敏;李阳阳;冯婕;焦李成3.一种基于高斯过程隐变量模型的表情识别方法 [J], 潘武生;黄玉水4.一种基于选择性卷积特征和最大后验高斯混合模型的细粒度图像分类算法 [J], 解冰; 朱宏擎5.基于高斯过程隐变量模型的滚动轴承故障识别 [J], 尹爱军;石波;谭建;李海珠因版权原因，仅展示原文概要，查看原文内容请购买。

基于判别特征加权的GPLVM算法
王秀美;高新波
【期刊名称】《计算机科学》
【年(卷),期】2009(36)3
【摘要】高斯过程隐变量模型是最近提出的比较流行的无监督降维方法.但是,它是一种无监督的机器学习算法,没有突出类结构,使得结果不能有效地表示类别信息.因此,提出一种利用判别特征值对高斯过程隐变量模型进行加权的算法,该算法不仅能够加强模型在低维流形上的判别性,而且能很好地保持类内的流形结构.
【总页数】4页(P189-192)
【作者】王秀美;高新波
【作者单位】西安电子科技大学电子工程学院,西安,710071;西安电子科技大学电子工程学院,西安,710071
【正文语种】中文
【中图分类】TP3
【相关文献】
1.一种改进了的基于遗传算法的维特征加权改进FCM算法 [J], 韦相;汤兴华
2.特征加权组稀疏判别投影分析算法 [J], 郑建炜;黄琼芳;杨平;王万良;马文龙
3.基于模糊判别准则和特征加权模板匹配的字符识别 [J], 郑宗良
4.基于特征加权的代理判别模型模式识别方法 [J], 潘海洋;郑近德;郭雨怡
5.基于多卷积核通道特征加权双目立体匹配算法 [J], 郑秋梅;温阳;王风华
因版权原因，仅展示原文概要，查看原文内容请购买。