下载文档原格式
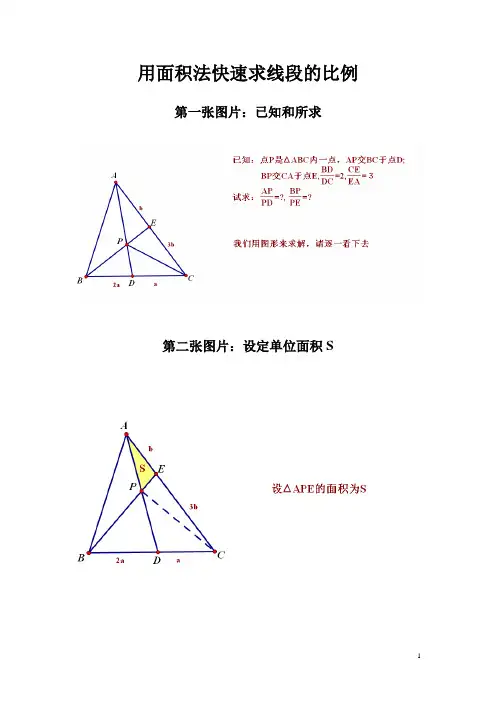
用面积法快速求线段的比例第一张图片：已知和所求
第二张图片：设定单位面积S
第三张图片：根据线段的比例关系求第一个三角形的面积
第四张图片：根据线段的比例关系求第二一个三角形的面积
第五张图片：根据线段的比例关系求第三一个三角形的面积
第六张图片：根据线段的比例关系求最后两个三角形的面积
第七张图片：列出所有小三角形的面积
第八张图片：根据面积的比例关系求出线段的比例
第九张图片：由具体的数字推广到抽象一般
第十张图片：我们也可走另外一条道路
第十一张图片：别忘了我们的拐杖
END。
八年级数学竞赛例题专题讲解：面积法阅读与思考平面几何学的产生源于人们测量土地面积的需要，面积关联着几何图形的重要元素边与角．所谓面积法是指借助面积有关的知识来解决一些直接或间接与面积问题有关的数学问题的一种方法．有许多数学问题，虽然题目中没有直接涉及面积，但由于面积联系着几何图形的重要元素，所以借助于有关面积的知识求解，常常简捷明快．用面积法解题的基本思路是：对某一平面图形面积，采用不同方法或从不同角度去计算，就可得到一个含边或角的关系式，化简这个面积关系式就可得到求解或求证的结果．下列情况可以考虑用面积法：（1）涉及三角形的高、垂线等问题；（2）涉及角平分线的问题．例题与求解【例1】如图，从等边三角形内一点向三边作垂线，已知这三条垂线段的长分别为1，3，5，则这个等边三角形的边长为______________．(全国初中数学联赛试题) 解题思路：从寻求三条垂线段与等边三角形的高的关系入手．等腰三角形底边上任一点到两腰距离之和等于一腰上的高，那么等边三角形呢？等腰梯形呢？【例2】如图，△AOB中，∠O＝，OA＝OB，正方形CDEF的顶点C在DA上，点D在OB上，点F在AB上，如果正方形CDEF的面积是△AOB的面积的，则OC：OD等于( )A．3：1 B．2：1C．3：2 D．5：3解题思路：由面积关系，可能想到边、角之间的关系，这时通过设元，即可把几何问题代数化来解决．【例3】如图，在□ABCD中，E为AD上一点，F为AB上一点，且BE＝DF，BE与DF交于G，求证：∠BGC＝∠DGC.（长春市竞赛试题）解题思路：要证∠BGC＝∠DGC，即证CG为∠BGD的平分线，不妨用面积法寻找证题的突破口．【例4】如图，设P为△ABC内任意一点，直线AP，BP，CP交BC，CA，AB于点D、E、F.求证：（1）；（2）.（南京市竞赛试题）解题思路：过P点作平行线，产生比例线段.【例5】如图，在△ABC中，E，F，P分别在BC，CA，AB上，已知AE，BF，CP相交于一点D，且，求的值.解题思路：利用上例的结论，通过代数恒等变形求值.（黄冈市竞赛试题）【例6】如图，设点E，F，G，H分别在面积为1的四边形ABCD的边AB，BC，CD，DA上，且（是正数），求四边形EFGH的面积．（河北省竞赛试题）解题思路：连对角线，把四边形分割成三角形，将线段的比转化为三角形的面积比．线段比与面积比的相互转化，是解面积问题的常用技巧．转化的基本知识有：(1) 等高三角形面积比，等于它们的底之比；(2) 等底三角形面积比，等于它们的高之比；(3) 相似三角形面积比，等于它们相似比的平方．能力训练1．如图，正方形ABCD的边长为4cm，E是AD的中点，BM⊥EC，垂足为M，则BM＝______.（福建省中考试题）2．如图，矩形ABCD中，P为AB上一点，AP＝2BP，CE⊥DP于E，AD＝，AB＝，则CE＝__________.（南宁市中考试题）第1题图第2题图第3题图3．如图，已知八边形ABCDEFGH中四个正方形的面积分别为25，48，121，114，PR＝13，则该八边形的面积为____________.（江苏省竞赛试题） 4. 在△ABC中，三边长为，，，表示边上的高的长，，的意义类似，则(＋＋)的值为____________. （上海市竞赛试题）5．如图，△ABC的边AB＝2，AC＝3，Ⅰ，Ⅱ，Ⅲ分别表示以AB，BC，CA为边的正方形，则图中三个阴影部分的面积之和的最大值是__________.（全国竞赛试题） 6．如图，过等边△ABC内一点P向三边作垂线，PQ＝6，PR＝8，PS＝10，则△ABC的面积是 ( )．A. B.C.D.（湖北省黄冈市竞赛试题）第5题图第6题图第7题图7．如图，点D是△ABC的边BC上一点，若∠CAD＝∠DAB＝，AC＝3，AB＝6，则AD的长是( )．A．2 B. C.3 D.8．如图，在四边形ABCD中，M，N分别是AB，CD的中点，AN，BN，DM，CM划分四边形所成的7个区域的面积分别为，，，，，，，那么恒成立的关系式是( )．A.+=B.+=C.+= D．+=9．已知等边△ABC和点P，设点P到△ABC三边AB，AC，BC的距离分别为，，，△ABC的高为．若点P在一边BC上（如图1），此时，可得结论：＋＋＝.请直接用上述信息解决下列问题：当点P在△ABC内（如图2）、点P在△ABC外（如图3）这两种情况时，上述结论是否还成立？若成立．请给予证明；若不成立，，，与之间又有怎样的关系？请写出你的猜想，不需证明．（黑龙江省中考试题）10.如图，已知D，E，F分别是锐角△ABC的三边BC，CA，AB上的点，且AD、BE、CF相交于P点，AP＝BP＝CP＝6，设PD＝，PE＝，PF＝，若，求的值．（“希望杯”邀请赛试题）11.如图，在凸五边形ABCDE中，已知AB∥CE，BC∥AD，BE∥CD，DE∥AC，求证：AE∥BD.（加拿大数学奥林匹克试题）12.如图，在锐角△ABC中，D，E，F分别是AB，BC，CA边上的三等分点. P，Q，R分别是△ADF，△BDE，△CEF的三条中线的交点.(1) 求△DEF与△ABC的面积比；(2) 求△PDF与△ADF的面积比；(3) 求多边形PDQERF与△ABC的面积比.13．如图，依次延长四边形ABCD的边AB，BC，CD，DA至E，F，G，H，使，若，求的值．（上海市竞赛试题）14.如图，一直线截△ABC的边AB，AC及BC的延长线分别交于F，E，D三点，求证：．（梅涅劳斯定理）15．如图，在△ABC中，已知，求的值.（“华罗庚金杯”少年数学邀请赛试题）。
巧用比例解决面积问题2,如图,在三角形ABC中,BC和CE分别是两边上的中线,并且BD⊥CE,BD=4,CE=6,那么△ABC的面积为多少?【解】连接DE,则DE∥BC,且DE=½BC, S△ADE=S△DEB=½S△BCD,S梯形BCDE=¾S△ABC,作DF∥EC,与BC延长线交于F,则BD⊥DF,EC=DF,且S梯形=S△BDF=½•4•6BCDE=12,∴S△ABC=16 【完】3,如图,四边形ABCD为普通凸四边形,如何过A点作一条直线,把四边形ABCD分成面积相等的两个部分?【解】如图2,连接AC,过B点作BE∥AC,交DC延长线于E,连接AE,则S△ACE=S△ABC,故S梯形ABCD=S△ADE,取DE的中点F,连接AF,则有S△ADF=S△AEF=½S△ADE=½S梯形ABCD,故直线AF 为所求的直线｡【完】(面积问题)4,如图,延长△ABC的三边分别至D､E､F点,使得BD=αAB,CE=αBC,AF=αAC,求S△DEF:S△ABC｡【解】如图2,连接AE,BF,CD,设S△ABC=X,则S△ACE=S△BCD=S△ABF=αX;S△AEF=S△CDE=S△BDF=α²X;∴S△DEF=X+3αX+3α²X,即S△DEF:S△ABC=1+α+α²【完】5.(1)如图1,在D､E､F分别在△ABC的AB､AC､BC边上,且DE∥BC,EF∥AB,△EFC的面积为S1,△ADE面积为S2,四边形DEFB的面积为S,证明:S²=4S1•S2;(2)如图2,已知平行四边形DEFG的四个顶点在△ABC的三边上,若△ADG､△BDE､△GFC的面积分别为2､3､5,求△ABC的面积｡【证明】(1)过A作AN⊥BC,交DE于M,交BC于N,过E作EP⊥BC,交BC于P,则S2=½DE•AM,S=DE•MN,S1=½CF•MN,由四边形DEFG为平行四边形知,△ADE∽△EFC,△AME∽△EPC,且MN=EP,于是DE:FC=AE:EC=AM:EP,∴AM•FC= DE•EP=DE•MN,∴4S1•S2=4·½•CF•MN•½DE•AM=CF·AM·DE·MN=(DE·MN)²=S²【证毕】(2)如图4,过G点作GK∥AB,交BC于K，∵GF=DE,∠GFK=∠DEB，∠B=∠GKF，∴△GKF≌△DEB,故△GFK的面积为5，△CGK的面积为3+5=8，根据(1)中的结论,平行四边形DGKB的面积的平方为:4•2•8=64，∴平行四边形DGKB的面积为8，故△ABC的面积为:2+8+8=18 【完】6,如图1,在梯形ABCD中,AD∥BC,CE是∠BCD的角平分线,且CE⊥AB于E,BE=2AE,若四边形AECD的面积为1,求梯形ABCD的面积｡【解】如图2分别延长CD､BA,交于F点,∵ CE是∠BCD的角平分线,且CE⊥AB,∴△BCF为等腰三角形,且CB=CF,又BE=EF=2AE,∴FA=AE,FA:FB=1:4,S△ADF::S△BCF=1:16,设S△ADF=X,则S△BCF=16X,S△ECF=8X,于是有:8X=X+1,X=1/7,∴S梯形ABCD=1+8•1/7=15/7【完】7,如图1,在四边形ABCD中,AB∥CD,AB+CD=BC,点P为AD的中点,如果AB=X,CD=Y,且Y>X,那么在BC边上是否存在一点Q,使得PQ所在直线将四边形ABCD分成相等的两部分?【解】如图2,延长CD至F,使得DF=X,延长BA至E,使得AE=Y,则BE∥CF,且BE=CF=X+Y,又BE=BC=X+Y,所以BCFE为菱形,连接BF,交AD于N点,则△ABN≌△DFN,于是DN=NA,故N和P点重合,且P为BF的中点｡设P到各边的距离为Z,在BC边上取Q 点,使得BQ=Y,连接PQ,S四边形ABQP=S△ABP+S△BPQ=½X•Z+½Y•Z=½Z•(X+Y);S四边形PQCD=S△PQC+S△PCD=½X•Z+½Y•Z=½Z•(X+Y),故直线PQ将四边形ABCD分成相等的两部分｡综上所述,在BC边上存在一点Q,使得PQ所在直线将四边形ABCD分成相等的两部分｡【完】8,如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC､△ADF､△BEF的面积分别记为S△ABC､S△ADF､S△BEF,且S△ABC=12｡则S△ADF-S△BEF=?【解】如图2,连接CF,设S△BEF=x,S△ADF=y,则S△CFE=2x,S△CFD=2x,∵ S△ABD=S△BCD,∴S△ABF=3x;∵ 2S△ABE=S△ACE,∴2(3x+x)=2x+2y,解得:y=3x;又S△ABC=12,∴x+2x+y+y+3x=12,即12x=12,x=1,y=3;∴S△ADF-S△BEF=y-x=2｡【完】9,如图,已知正方形ABCD的边长为1,M､N为BD所在直线上的两点,且AM=√5,∠MAN=135°,则四边形AMCN的面积为多少?【解】如图2,连接AC,与MN交于P点,则AP=√2/2,MP=3√2/2,MB=√2;因为∠MAN=135º,∴∠ANM+AMN=45°,而∠NAD+∠AND=45°,∴∠NAD=∠AMN,从而∠AND=∠MAD,于是△ADN∽△ABM∽△AMN,ND:AD=AB:MB,ND=1/MB=√2/2,所以MN=MP+PD+ND=5√2/2,S四边形AMCN=2·½·5√2/2·√2/2=5 【完】10,如图,正六边形ABCDEF的边长为2√3cm,P为正六边形内一点,则点P到各边距离之和为多少?【解】如图2,连接PA､PB､PC､PD､PE､PF,则正六边形ABCDEF被分成了六个三角形,设P到六个边的距离之和为xcm,那么这六个三角形面积之和为:½·2√3·x=√3x;另一方面,正六边形的面积为:6·½·2√3·√3=18,∴√3x=18,x=6√3,即点P到各边距离之和为6√3 【完】11,如图,E､F分别为矩形ABCD的边,AB､BC的中点,连接AF､CE,交于点G,则S四边形∶ S矩形ABCD等于多少?AGCD【解】如图2,连接BG,设AD=a,AB=b,S△AEG=x,S△CFG=y,则S△BEG=x,S△BFG=y,2x+y=ab/4,x+2y=ab/4,于是3(x+y)=ab/2,得到:x+y=ab/6,S四边形AGCD=ab-2(x+y)=2ab/3,故S∶ S矩形ABCD=2∶3 【完】四边形AGCD12,如图,正方形ABCD,点P是对角线AC上一点,连接BP,过P作PQ⊥BP,PQ交CD于Q,若AP=CQ=2,求正方形ABCD的面积｡【解】如图2,过P作AD的平行线,交AB于M,交CD于N,过P作PL⊥AD,交AD于L｡则PM=PL=ND,MB=PN,∠NPQ=∠MBP,∴△NPQ≌△MBP,得到:PM=NQ,故NQ=ND=√2,CD=2+2√2,S正方形ABCD=(2+2√2)²=12+8√2 【完】13,△ABC所在平面上的点P,使得△PAB､△PBC､△PAC的面积相等,这样的点P的个数为多少?【解】如图1,取AB的三等分点D,E,BC的三等分点F,G,CA的三等分点H,I,连接DG､HE､IF,则三线交于一点P,连接PA,PB,PC,由于AI:AC=1:3,所以S△PAB:S△ABC=1:3,即S△PAB=S△ABC/3,同理,S△PAC=S△PBC=S△ABC/3,故这样的P点符合要求;如图2,过点C作CP∥AB,过点B作BP∥AC,CP和BP交于P点｡连接PA,PB,PC｡则S△PAC=S△PAB=S△PBC=½S△ABC,这样的点P有三个,均符合要求｡综上所述,符合要求的P点共有4个｡【完】14,如图,设点E､F､G､H分别在面积为1的四边形ABCD的边AB､BC､CD､DA上,且AE∶EB=BF∶FC=CG∶GD=DH∶HA=k(k是正数),求四边形EFGH的面积【解】如图14-2,连接BD,∵AH∶AD=1∶(1+k),AE∶AB=k∶(k+1)∴S△AEH∶S△ABD=k∶(1+k) ²,即S△AEH=kS△ABD/(1+k) ²;同理,S△CFG=kS△CBD/(1+k) ²,故S△AEH+S△CFG=(S△ABD+kS△CBD)k/(1+k) ²=S四边形ABCD•k/(1+k) ²= k/(1+k) ²;同理,S△DHG+S△BEF= k/(1+k) ²,于是:S△AEH+S△CFG +S△DHG+S△BEF=2k/(1+k) ²,故S四边形EFGH=S四边形ABCD-(S△AEH+S△CFG +S△DHG+S△BEF)=1-2k/(1+k) ²=(1+k²)/(1+k)²【完】15,如图15-1,设凸四边形ABCD的一组对边AB､CD的中点分别为K､M,求证:S四边形=S△ABM+S△CDKABCD【解】如图15-2,分别过D､M､C作BA的垂线DE､MF､CG,垂足分别为E､F､G,S△ADK=½•AK•DE;S△BCK=½•BK•CG;由于AK=BK,∴S△ADK+S△BCK=½AK•(DE+CG),在梯形DEGC中,FM为其中位线,∴FM=½(DE+CG),故S△ADK+S△BCK=AK•FM=½•2AK•FM=½•AB•FM=S△AMB,所以,S四边形=(S△ADK+S△BCK)+S△CDK =S△ABM+S△CDK 【证毕】ABCD16,如图16-1,在梯形ADEB中,∠D=∠E=90°,△ABC是等边三角形,且点C在DE上,如果AD=7,BE=11,求△ABC的面积｡【解】如图16-2,过A作BE的垂线AF,垂足分别为F,设DC=x,CE=y,17,如图17-1,矩形ABCD的面积为1,边AB､AD的中点分别为E､F,连接EC､ED､FB､FC,交点如图所示,求四边形CGHI的面积S四边形CGHI｡【解】如图17-2,分别延长BF､CD,交于点M;延长DE､CB交于N,连接CH｡则因为F､E 分别为AD､AB的中点,所以F､E分别为BM､DN的中点,且D､B分别为CM､CN的中点｡于是得到下列比例关系:18,如图18-1,D､E､F分别为△ABC的三边AB､BC､CA上的点,且BD∶DA=AF∶FC=CE∶EB=1∶3,连接AE､BF､CD,AE分别交BF､CE于H､I,CD､BF 交于点G,求S△GHI∶S△ABC｡【解】如图18-2,连接AG､BI､CH,设S△AFH=x,S△CEI=y, S△BDG=z, S△CIH=m,S△BIG=n,S△AGH=p,则S△CFH=3x,S△BEI=3y,S△ADG=3z,根据题意,有:S△ABC = x+3x+y+3y+z+3z+m+n+p+ S△GHI =4(x+y+z)+(m+n+p) + S△GHI;……①比较△AFG和△CFG,有:S△GHI+m+3x=3(p+x),即3p=m+S△GHI ;同理,3m=n+S△GHI;3n=p+S△GHI;此三式相加,得:3(m+n+p)=(m+n+p)+3S△GHI,即:m+n+p=1.5S△GHI;……②又比较△ABF和△BCF,有:4y+m+n+3x+ S△GHI =3(4z+p+x),即:3p+12z=4y+m+n+ S△GHI;同理,3m+12x=4z+p+n+S△GHI;3n+12y=4x+p+m+S△GHI;此三式相加,得:3(m+n+p)+12(x+y+z)=3S△GHI+2(m+n+p)+4(x+y+z),整理,得:8(x+y+z)=3 S△GHI-(m+n+p)= 3S△GHI-1.5S△GHI=1.5S△GHI,即4(x+y+z)=0.75S△GHI;……③将②､③代入①,得:S△ABC =0.75S△GHI +1.5S△GHI + S△GHI =3.25 S△GHI故S△GHI∶S△ABC=4∶13 【完】19,如图18-1,四边形ABCD和CHFG都是正方形,边长分别为a和b,四边形CDEH为长方形,S△ADO∶S△FOH=1∶8,求a∶b的值｡【解法一】过点O分别作OM⊥AE于M､ON⊥EF于N,则S△ADO=½a•OM,S△FOH=½b•ON;∵OM∶EH=AM∶AE,得:AM=OM•(a+b)/a;∵OM∶EF=DM∶DE,得:OM∶(a+b)=(AM-a)∶b,于是:AM=a+[b•OM/(a+b)],∴a+[b•OM/(a+b)]= OM•(a+b)/a,化简,得:OM=a2(a+b)/(a2+b2+ab);同理,ON= b2(a+b)/(a2+b2+ab);所以S△ADO∶S△FOH=[a•a2(a+b)/(a2+b2+ab)]∶[b•b2(a+b)/(a2+b2+ab)]=1∶8,化简,得:a3∶b3=1∶8,故:a∶b=1∶2 【完】【解法二】如图19-3,连接AF,OE,则A､C､F在同一直线上｡由“燕尾定理”※,S△AEO∶S△AFO=EH∶HF=a∶b;S△AFO∶S△EFO=AD∶DE=a∶b,∴(S△AEO•S△AFO)∶(S△AFO•S△EFO)=a2∶b2,即S△AEO∶S△EFO=a2∶b2,∵AE=EF=a+b,∴OM∶ON= a2∶b2,故S△ADO∶S△FOH=(a•OM)∶(b•ON)=a3∶b3=1∶8,因此,a∶b=1∶2 【完】※注:“燕尾定理”及其证明:如图19-4,点O为△ABC内任意一点,连接AO,BO,CO,并延长AO交BC于D,则S△ABO∶S△ACO=BD∶DC证明方法:如图19-4,分别过C､B作AD的垂线,与AD(或AD延长线)交于E､F,则BF∥CE,∴△BDF∽△CDE,BF∶CE=BD∶DC;S△ABO∶S△ACO=½•AO•BF∶½•AO•CE=BF∶CE=BD∶DC｡【证毕】“燕尾定理”､“鸟头原理”常被运用于求图形面积的问题,如何发现､构造并利用这些定理是解决面积问题的关键｡。
师生园地２０２２年４月下半月㊀㊀㊀面积法在初中数学解题中的应用◉辽宁省大连市第五十一中学㊀穆永强１引言面积法解题的基本思想是以 面积 当作思维起点,将题目中的已知量与未知量通过面积公式联系起来,这样显得更为简洁与直观,有助于学生快速理清思路,使其充分体会到面积法的妙用与价值．２应用面积法证明线段相等问题证明线段相等是一类较为常见的平面几何类问题,虽然运用常规方法能够证明,但有时,过程较为繁琐㊁步骤较多,有时学生容易陷入到思维障碍当中,影响他们的解题自信．对此,教师可以指导学生应用面积法证明线段相等的问题,使其转变解题思路,帮助他们找到正确的证明流程与方法．图１例１㊀如图１,已知在等腰三角形A B C 中,A B 和A C 相等,点D 在B C 边上,其中D B 的长度与D C 相等,D E 垂直于A B ,垂点是E ,D F 垂直于A C ,垂点为F ,请尝试证明D E 与D F 相等．分析:学生通过初步审题与观察图形,发现虽然题设中给出的条件较多,也极具条理性,不过他们一时间难以想到用何种方法来证明这两条线段相等,以至于陷入到困境当中．教师可提示学生应用面积法进行证明．具体证明方法如下:因为B D ＝C D ,所以әA B D 的面积同әA C D 的面积相等,得出１２A B D E ＝１２A C D E ,又因为AB ＝AC ,所以DE ＝DF ．虽然本题可以使用全等三角形的相关知识进行证明,不过采用面积法思路更为简洁,既可以培养学生一题多解的意识,还能够让他们感受到面积法的优势,扩充认知范围．３应用面积法准确求出线段长度求线段长度是数学解题训练中的惯设题目,贯穿于小学㊁初中㊁高中整个教学阶段,虽然这类题目大多数难度都不是特别大,不过部分题目中给出的隐藏条件难以发现,影响解题的正常进行．此时,教师在教学中,应指引学生尝试应用面积法来处理此类题目,使其通过面积的拆分准确求出线段长度,帮助他们建立解题自信．图２例２㊀如图２所示,在三角形A B C 中,B C ＝９０c m ,A D 为高,A D ＝６０c m ,正方形P Q MN 的顶点Q ,M 在BC 边上,顶点P ,N 分别在边A B ,A C 上,其中AD 垂直于B C ,垂点是D ,同正方形的边P N 相交于点E ,那么正方形P Q MN 的边长是多少?分析:学生读完题目后,发现题目中给出的具体数据仅限于三角形,似乎与正方形的关系不大,所以他们很难找准切入点,极易遇到解题障碍,所以教师可引导学生应用面积法,并结合方程相关知识求解．设正方形的边长是x c m ,因为１２ˑB C ˑA D ＝１２ˑP N ˑA E ＋１２ˑB Q ˑP Q ＋１２ˑC M ˑMN ＋P Q ２,代入相关数据可得,１２ˑ９０ˑ６０＝x ２ˑ(６０－x )＋１２ˑP Q (B Q ＋C M )＋P Q ２,由此得１２ˑ９０ˑ６０＝x２ˑ(６０－x )＋x ２ˑ(９０－x )＋x ２,将这个方程化简,解得的x 值即为正方形的边长．在本例中,常规解法是用相似三角形的相似比等于对应高线的比列出比例式求得结果,这里用面积的拆分求解有异曲同工之妙,可以有效活化学生的解题思路．４应用面积法求得线段长度的和不少平面几何类问题都与线段有一定的联系,除０９Copyright ©博看网. All Rights Reserved.２０２２年４月下半月㊀师生园地㊀㊀㊀㊀求一条线段的长度以外,还会求几条线段的总长,这类题目难度通常较大,学生处理起来颇费周折．为此,教师在教学中,可以引导学生尝试应用面积法求几条线段长度的和,使其通过拆分面积及面积公式顺利求得正确答案．图３例３㊀如图３所示,已知梯形A B C D 中,A D ʊB C ,A B ＝D C ,对角线A C 与B D 相交于点O ,E 为B C 上的一个动点(E 不与B ,C 两点重合),在点E 运动过程中,如果点E 到A C ,B D 的垂线段分别是E Q ,E P ,而B C ＝８,B D ＝６,梯形的高DF 的长度是３,求E P ＋E Q 的和．分析:本题涉及的元素较多,线段较为复杂,还存在一个动点,结果要求两条线段之和,对学生来说难度相对较大,不易找到突破口．应用面积法的解答方法如下:因为四边形A B C D 是一个等腰梯形,对角线A C 与B D 相交于点O ,据此能证明әO B C 是一个等腰三角形,又因为点E 是梯形下底上的一个动点,点E 到A C ,B D 的垂线段分别是E Q ,E P ,作辅助线延长B D 至H ,与C H 垂直,再根据等腰三角形底边上一点到两腰的距离之和等于一腰上的高这一性质,得出E P ＋E Q ＝C H ．因为S әD B C ＝１２B C D F ＝１２B DC H ,由已知条件,求得C H ＝４,E P ＋E Q 的和是４．本案例,由于点E 是动点学生觉得无从下手,只要证明定理 等腰三角形底边上一点到两腰的距离之和等于一腰上的高 ,再结合同一个三角形面积的不同表示问题就轻松解决．５应用面积法求证线段比例等式求证线段比例也是初中数学解题教学中的一类常见题型,由于涉及到比例难度相对较大,对学生的解题能力与思维水平要求较高,通常要用到代数方面的知识,他们很难轻松证明．教师可引领学生巧妙采用面积法证明线段的比例等式,主要通过构建面积这一载体 ,证明几何图形的线段比例等式关系,显得清晰又直观．例４㊀已知在әA B C 中,D 是B C 上的一点,设点E 是A D 的中点,连接B E ,并延长与A C 交于点F ,假设B D ʒC D ＝２ʒ１,求证A F ʒF C ＝２ʒ３．分析:首先,根据题意画出图形,如图４,把点C 与点E 连接起来．设әC E D 的面积是x ,因为A E ＝D E ,所以әA E C 的面积也是x ．又因为B D ʒC D ＝２ʒ１,图４可得әB E D 的面积是２x ,又因A E ＝D E ,可得әA E B 的面积也是２x ．设әE F C 的面积为y ,则A F F C ＝S әA B F S әB F C ＝３x －y３x ＋y①A F F C ＝S әA E F S әE F C ＝x －yy②由式①㊁②式联立,可得x ＝５３y ．所以A F F C ＝S әA E F S әE F C ＝x －y y ＝５３y －y y ＝２３yy＝２３,即A F ʒF C ＝２ʒ３成立．本题采用面积法证明线段的比例等式十分巧妙,借助面积这一纽带,清楚地证明几何图形中线段比例的等式关系,使学生的解题思路变得愈加开阔．６应用面积法有效解决函数问题在求解初中函数类试题时,除运用待定系数法之外,还经常用到数形结合法,而面积法就属于数形结合思想的一种．有时,借助面积法也可以有效解决函数问题．例５㊀如果一次函数y ＝４x ＋b 的图象与两个坐标轴之间围成一个面积为８的三角形,求该一次函数的解析式．图５分析:本题虽然是一道代数题,但其求解过程要利用三角形的面积．为此,利用函数式找出两直角边的长即可．如图５所示．列出算式１２ˑ|b |ˑ|b |４＝８,解之得b ＝８,或b ＝－８,所以该一次函数的解析式为y ＝４x ＋８,或y ＝４x －８．本例结合面积法处理代数中的一次函数类题目,其实是对数形结合思想的巧妙应用,以此增进数与形之间的关系,使其掌握更多解题方法,优化他们的解题思路．总的来说,在初中数学解题教学活动中,教师很有必要把面积法的思想融会贯通至解题实践中,引领学生学会转变解题思路,思维变得发散与开阔起来,使其通过面积法的有效应用,将一些比较抽象㊁难懂㊁复杂的数学试题变得直观㊁易懂与简单,这对培养学生的解题能力㊁数学思想等均有着相当积极的意义．Z １９Copyright ©博看网. All Rights Reserved.。
小学数学解题技巧：用比例法巧求面积小学数学解题技巧 2009-07-26 13:15:00 阅读178 评论0 字号：大中小学习中常遇到一些求面积的几何题，但条件比较隐蔽，用常规思路解答，常常无从入手。
如果从两种相关联的量之间的比例关系入手去分析问题，往往能帮助我们巧妙地解答。
例1：在三角形ABC中，AD垂直于BC，BE垂直于AC，如图1。
AD=7厘米，BE=8厘米，AC＋BC=21厘米，三角形ABC的面积是多少平方厘米？[分析与解] 因为三角形的面积等于底乘高除以2，当三角形的面积一定时，底和高成反比例，从三角形ABC的面积＝BC×AD÷2＝AC×BE÷2可得到：BC×AD＝AC×BE，AC:BC＝AD:BE＝8:7；又从AC＋BC＝21（厘米）可得，AC＝21×＝9.8（厘米），所以三角形ABC的面积是9.8×8÷2＝39.2（平方厘米）或BC＝21×＝11.2（厘米），所以三角形ABC的面积是11.2×7÷2＝39.2（平方厘米）。
例2：在三角形ABC中，三角形CDE的面积是15平方分米，三角形BCE的面积是30平方分米，三角形ADF的面积是35平方分米，三角形ABF的面积是20平方分米，三角形AEF的面积是多少平方分米？[分析与解] 因为三角形的面积除以底等于高的一半，所以当高一定时，面积与底成正比例；又因为三角形CDE底边DE上的高与三角形BCE底边BE上的高相同，所以，DE:BE＝S△CDE:S△BCE＝15:30＝1:2；同样道理可知，从DE:BE＝1:2得：S△AED:S△ABE＝1:2；S△AED:S△ABD＝1:(1＋2)＝1:3。
设三角形AED的面积是x平方分米，则x:(35＋20)＝1:3 解之得：x＝，所以三角形AEF的面积是35－＝（平方分米）。
面积法在初中数学解题中的应用数学是中学阶段基础教育的主要学科之一，对启发学生思维、开发学生智力、培养逻辑能力等方面都有举足轻重的作用。
其中，平面几何又是中学数学学科中重要的内容。
学习平面几何相关知识有助于帮助学生形成良好的几何思维习惯，同时能有效培育和提升学生的数学演绎和推理能力。
平面几何在中国也拥有十分悠久的发展历史，同样，平面几何中的面积问题与平面几何一样历史悠久，从溯源的角度上看，面积还是几何学的起源之一。
面积及面积法在日常生活中的运用随处可见，与生活息息相关、紧密相连。
文章围绕面积法在初中数学解题中的应用展开研究，从面积简史、面积及面积法的基本概念入手，结合解题实例，详细分析面积法在初中数学解?}过程中的巧妙应用。
在中学数学中，关于面积和面积法相关知识的教学已达到一定深度。
通过对面积和面积法的学习，一方面能够使学生更好、更直观地学习、理解和掌握数学知识，另一方面通过面积法，构建“数形结合”几何模型，能够将中学数学中一些较为抽象和代数化知识进行更为直观、具象的几何解释。
这些都对培养学生的数学品质，理解数学思想，提升和强化学生具象思维和直觉思维等大有裨益。
对此，有必要更加深入地研究和探索面积及面积法的相关发展历程、概念，以及其在中学数学解题中的巧妙运用，来增强中学生数学思维的灵活性，提高学生的数学素养。
一、与面积相关内容的概述（一）中国古代数学的面积发展史面积的发展史最早可以追溯到古埃及时期，其在中国的发展也同样历史悠久、源远流长。
与其他古代文明相比，面积在中国数学史上的发展有着独特的风格和特色，其在中国古代的实际运用主要在于对田垄、土地的测量。
早在公元前2世纪，中国古代的数学家就著有《算术书》，该书是中国数学史上首次系统性地提出和阐释面积相关的算题，其中就包括对田地的测量以及土地税征收等，以及与实际生产生活密切联系的面积问题。
在之后的历史发展中，又相继有《九章算术》《九章算术注》《孙子算经》《缀术》等相关著作问世。
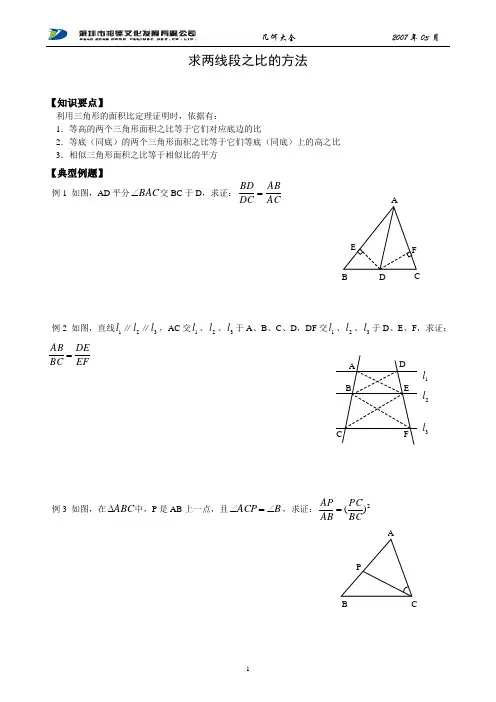
求两线段之比的方法【知识要点】利用三角形的面积比定理证明时，依据有：1．等高的两个三角形面积之比等于它们对应底边的比2．等底（同底）的两个三角形面积之比等于它们等底（同底）上的高之比 3．相似三角形面积之比等于相似比的平方【典型例题】例1 如图，AD 平分BAC ∠交BC 于D ，求证：ACABDC BD =例2 如图，直线1l ∥2l ∥3l ，AC 交1l 、2l 、3l 于A 、B 、C 、D ，DF 交1l 、2l 、3l 于D 、E 、F ，求证：EFDEBC AB =例3 如图，在ABC ∆中，P 是AB 上一点，且B ACP ∠=∠，求证：2)(BCPC AB AP =B DCA DBECF1l2l3lB C例4 已知：AD 是ABC ∆的中线，经过点B 的直线与AD 相交于E ，与AC 相交于F ，求证：EFBEAF AC =【经典练习】1．已知：如图，ABC ∆中，E 为AB 的中点，作□BCDE ，由C 向AB 、DE 上作垂线CF 、CG ，求证：CF AE CG BC ⋅=⋅2．已知：菱形ABCD 中，︒=∠30D ，求证：BD AC AD ⋅=23．已知圆内接四边形ABCD 的两条对角线相交于点P ，且AB=CP ，求证：BC DC AD AB ⋅=⋅CGD4．已知：如图，梯形ABCD 中，AB ∥CD ，BD AE ⊥于E ，AC DF ⊥于F ，BD CG ⊥于G ，AC BQ ⊥于Q ，求证：BQ CG DF AE ⋅=⋅5．在ABC ∆中，BC AD ⊥于D ，且ABC h AD ∆=,外接圆的半径为R ，求证：Rh AC AB 2=⋅6．已知：在□ABCD 中，E 为对角线AC 上一点，AB EF ⊥于F ，AD EG ⊥于G ，求证：EG AD EF AB ⋅=⋅AB。
10第 10 讲 倍数关系和巧连辅助线求解直线型本讲知识点汇总：一、如果两个长方形的长相等，那么它们的面积的比等于它们宽之比。
二、过三角形一个项点的直线将三角形分为两个小三角形，则这两个小三角形面积之 比等于该直线分对边所得的两条线段长度之比，这是由两个小三角形有共同的高决定的。
三、面积和线段是对应成比例的，有的时候可以利用面积的比求线段的长度。
四、在解题的过程中运用辅助线帮助我们计算。
注意：辅助线只是一种辅助的工具， 我们真正用来解题的是各种直线形的知识，只有对这些知识非常地熟悉，才有可能想到如 何连结辅助线，进而真正解决问题。
迄今为止， 同学们已经学会了很多图形计算面积的方法， 在计算这些面积的时候， 只要 知道相应线段的长度， 然后利用公式即可以计算。
例如计算长方形的面积： 只需知道长方形 的长和宽即可利用长方形的面积 =长 X 宽进行计算。
但很多时候，题目中并不给出长和宽， 那怎么来求面积呢 ?我们来看下面这个例题。
对于长方形，我们总结出：如果两个长方形的长（宽）相等，那么它们的面积的比等于 它们宽（长）之比。
例如：如图所示的长方形 ABCD 与长方形 BEFC 宽BC 相同，那么长方形ABCD 的面积：长方形 BEFC 的面积 =AB ： BE 。
D C F准备 1、如图，有 9 个小长方形，其中 5 个小长方形的面积分别为 平方米。
其余 4 个长方形的面积分别是多少平方米？41281620准备 2、如图，有 7 个小长方形，其中的 5 个小长方形的面积分别为 20、4、6、8、10 平方厘米，求阴影长方形的面积是多少平方厘米？204、8、12、16、 20 46准备3 、如图，一个长方形被分成4 个不同的三角形，红色的面积是9 平方厘米，黄色三角形的面积是21平方厘米，绿色三角形的面积是10平方厘米，那么黄色三角形的面积多少平方厘米？从上面的准备题可以看出，求一个图形的面积不一定要通过公式，有些时候我们也可以利用图形各部分之间的面积关系进行计算。
