当前位置：文档之家 › 主成分分析法MATLAB的实现

主成分分析法MATLAB的实现

  • 格式：doc
  • 大小：151.00 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

主成分分析 MATLAB代码

主成分分析 MATLAB代码
T=L(:,1)+L(:,2)+L(:,3)+L(:,4); %计算T统计量
%特征向量图(效果等价于主成分载荷图)
figure(4); %创造第二个图形窗口
e1=-E(:,1);e2=-E(:,2); %提取特征向量并转换符号
Co2=Co1+A(:,2).^2; %提取2个主成分的公因子方差
Co3=Co2+A(:,3).^2; %提取3个主成分的公因子方差
Co4=Co3+A(:,4).^2; %提取4个主成分的公因子方差
Rz=cov(F); %计算协方差矩阵
Rz=corrcoef(F); %计算相关系数矩阵
Rz=corrcoef(Z); %计算相关系数矩阵
%计算非标准化数据协方差矩阵的三种方法
Covz=Z'*Z/(n-1); %计算协方差矩阵
Covz=cov(Z); %计算协方差矩阵
%计算主成分得分相关系数的四种方法
Rz=F'*F/(n-1); %计算相关系数矩阵
grid on %添加网格
%几个用于检验的语句
%计算再生相关系数矩阵
Rp=H*H'; %计算再生相关矩阵
Re=R-Rp; %计算相关矩阵的残差矩阵
%综合得分
S=Z(:,1)+Z(:,2)+Z(:,3)+Z(:,4) %非标准化得分四列加和
S1=F(:,1)*eigv(1)^0.5+F(:,2)*eigv(2)^0.5+F(:,3)*eigv(3)^0.5+F(:,4)*eigv(4)^0.5
%计算T平方统计量(2)
eigv=diag(G); %提取角矩阵的对角线元素

matlab主成分分析案例

matlab主成分分析案例

1•设随机向量X= (X i , X 2, X 3)T 的协方差与相关系数矩阵分别为1 4，R4 25分别从，R 出发，求X 的各主成分以及各主成分的贡献率并比较差异况。

解答： >> S=[1 4;4 25];>> [P C,vary,ex plain ed]=p cacov(S); 总体主成分分析：>> [P C,vary,ex plain ed]=p cacov(S) 主成分交换矩阵： PC =-0.1602 -0.9871 -0.9871 0.1602 主成分方差向量： vary = 25.6491 0.3509各主成分贡献率向量 explained = 98.6504 1.3496则由程序输出结果得出，X 的主成分为: Y 1=-0.1602X 1-0.9871X 2 Y 2=-0.9871X 1+0.1602X 2两个主成分的贡献率分别为：98.6504%, 1.3496%;贝U 若用第一个主成分代替原 来的变量，信息损失率仅为1.3496，是很小的。

2.根据安徽省2007年各地市经济指标数据，见表 5.2，求解： (1) 利用主成分分析对17个地市的经济发展进行分析，给出排名; (2) 此时能否只用第一主成分进行排名？为什么？1 0.8 0.8 11.0000 0.9877 0.9980 0.9510 0.9988 0.9820 0.4281 0.9999解答：(1)>> clear>> A=[491.70,380.31,158.39,121.54,22.74,439.65,344.44,17.43;21.12,30.55,6.40,12.40,3.31,21.17,17.71,2.03;1.71,2.35,0.57,0.68,0.13,1.48,1.36,-0.03;9.83,9.05,3.13,3.43,0.64,8.76,7.81,0.54;64.06,77.86,20.63,30.37,5.96,63.57,52.15,4.71;30.38,46.90,9.19,9.83,17.87,28.24,21.90,3.80;31.20,70.07,8.93,18.88,33.05,31.17,26.50,2.84;79.18,62.09,20.78,24.47,3.51,71.29,59.07,6.78;47.81,40.14,17.50,9.52,4.14,45.70,34.73,4.47;104.69,78.95,29.61,25.96,5.39,98.08,84.81,3.81;21.07,17.83,6.21,6.22,1.90,20.24,16.46,1.09;214.19,146.78,65.16,41.62,4.39,194.98,171.98,11.05;31.16,27.56,8.80,9.44,1.47,28.83,25.22,1.05;12.76,14.16,3.66,4.07,1.57,11.95,10.24,0.73;6.45,5.37,2.39,2.20,0.40,5.97,4.79,0.52;39.43,44.60,15.17,15.72,3.27,36.03,27.87,3.48;5.02,3.62,1.63,1.42,0.53,4.45,4.04,0.02];得到的相关系数矩阵为：>> R=corrcoef(A)R =0.9877 1.0000 0.9884 0.9947 0.5438 0.9885 0.9835 0.94850.9988 0.9884 1.0000 0.9824 0.4294 0.9984 0.9948 0.94620.9820 0.9947 0.9824 1.0000 0.5051 0.9829 0.9763 0.93910.4281 0.5438 0.4294 0.5051 1.0000 0.4311 0.4204 0.45570.9999 0.9885 0.9984 0.9829 0.4311 1.0000 0.9986 0.95300.9980 0.9835 0.9948 0.9763 0.4204 0.99861.0000 0.95690.9510 0.9485 0.9462 0.9391 0.4557 0.9530 0.9569 1.0000计算特征值与特征向量：>> [v,d]=eig(corrcoef(A))V 一-0.3723 0.1179 0.1411 -0.2543 -0.0459 0.5917 -0.5641 0.3041-0.3741 -0.0343 0.1606 0.2247 -0.1514 -0.6284 -0.1535 0.5841-0.3719 0.1152 0.1957 -0.1954 -0.6909 -0.1351 0.0383 -0.5244-0.3713 0.0096 0.2368 0.7875 0.2168 0.2385 0.0303 -0.2845-0.1949 -0.9689 -0.0004 -0.1242 0.0119 0.0628 0.0151 -0.0593-0.3725 0.1143 0.1222 -0.2302 0.0924 0.2259 0.7946 0.2988-0.3716 0.1272 0.0353 -0.3800 0.6591 -0.3521 -0.1557 -0.3428-0.3613 0.0596 -0.9185 0.1165 -0.0872 0.0302 0.0022 -0.0096d =7.11350 00 00 0 0.77700.08100 0.02370 0.00410 0 0 0 0.00000 0 0.0001各主成分贡献率:>> w=sum(d)/sum(sum(d))计算各个主成分得分:>> F=[A-ones(17,1)*mean(A)]*v(:,8)224.3503 -24.0409 -40.0941 -35.9075 4.7573 -12.6102 -2.85731.8038 -13.9012 13.4541 -29.3847 62.3383 -23.3175 -32.4285 -38.1309 -14.8637 -39.1675>> [F1,I1]=sort(F,'descend')F1按从大到小的顺序给个主成分得分排名: F1 = 224.35030.8892 0.0971 0.0000 0.00000.0101 0.0030 0.0005 0.00010.000662.338313.45414.75731.8038 -2.8573 12.6102 13.9012 14.8637 23.3175 24.0409 29.3847 32.4285 35.9075 38.1309 39.1675 -40.0941I1 给出各个名次的序号：I1 =1121058769161321114415173 >> [F2,I2]=sort(I1)F2 =34567891011121314151617I2 给出个城市排名，即所求排名：I2 =1111714476583122101315916（2）由于第一主成分的贡献率大于80%，其他各成分贡献率都太小，所以只能用第一主成分进行排名。

matlab主成分分析案例

matlab主成分分析案例

1.设随机向量X=（X 1，X 2，X 3）T 的协方差与相关系数矩阵分别为⎪⎪⎭⎫ ⎝⎛=∑25441，⎪⎪⎭⎫⎝⎛=18.08.01R 分别从∑，R 出发，求X 的各主成分以及各主成分的贡献率并比较差异况。

解答：>> S=[1 4;4 25];>> [PC,vary,explained]=pcacov(S); 总体主成分分析：>> [PC,vary,explained]=pcacov(S) 主成分交换矩阵： PC =-0.1602 -0.9871 -0.9871 0.1602 主成分方差向量： vary = 25.6491 0.3509各主成分贡献率向量 explained = 98.6504 1.3496则由程序输出结果得出，X 的主成分为： Y 1=-0.1602X 1-0.9871X 2 Y 2=-0.9871X 1+0.1602X 2两个主成分的贡献率分别为：98.6504%，1.3496%；则若用第一个主成分代替原来的变量，信息损失率仅为1.3496，是很小的。

2.根据安徽省2007年各地市经济指标数据，见表5.2，求解： （1）利用主成分分析对17个地市的经济发展进行分析，给出排名； （2）此时能否只用第一主成分进行排名？为什么？解答：（1）>> clear>> A=[491.70,380.31,158.39,121.54,22.74,439.65,344.44,17.43;21.12,30.55,6.40,12.40,3.31,21.17,17.71,2.03;1.71,2.35,0.57,0.68,0.13,1.48,1.36,-0.03;9.83,9.05,3.13,3.43,0.64,8.76,7.81,0.54;64.06,77.86,20.63,30.37,5.96,63.57,52.15,4.71;30.38,46.90,9.19,9.83,17.87,28.24,21.90,3.80;31.20,70.07,8.93,18.88,33.05,31.17,26.50,2.84;79.18,62.09,20.78,24.47,3.51,71.29,59.07,6.78;47.81,40.14,17.50,9.52,4.14,45.70,34.73,4.47;104.69,78.95,29.61,25.96,5.39,98.08,84.81,3.81;21.07,17.83,6.21,6.22,1.90,20.24,16.46,1.09;214.19,146.78,65.16,41.62,4.39,194.98,171.98,11.05;31.16,27.56,8.80,9.44,1.47,28.83,25.22,1.05;12.76,14.16,3.66,4.07,1.57,11.95,10.24,0.73;6.45,5.37,2.39,2.20,0.40,5.97,4.79,0.52;39.43,44.60,15.17,15.72,3.27,36.03,27.87,3.48;5.02,3.62,1.63,1.42,0.53,4.45,4.04,0.02];得到的相关系数矩阵为：>> R=corrcoef(A)R =1.0000 0.9877 0.9988 0.9820 0.4281 0.9999 0.9980 0.95100.9877 1.0000 0.9884 0.9947 0.5438 0.98850.9835 0.94850.9988 0.9884 1.0000 0.9824 0.4294 0.99840.9948 0.94620.9820 0.9947 0.9824 1.0000 0.5051 0.98290.9763 0.93910.4281 0.5438 0.4294 0.5051 1.0000 0.43110.4204 0.45570.9999 0.9885 0.9984 0.9829 0.4311 1.00000.9986 0.95300.9980 0.9835 0.9948 0.9763 0.4204 0.99861.0000 0.95690.9510 0.9485 0.9462 0.9391 0.4557 0.95300.9569 1.0000计算特征值与特征向量：>> [v,d]=eig(corrcoef(A))v =-0.3723 0.1179 0.1411 -0.2543 -0.0459 0.5917-0.5641 0.3041-0.3741 -0.0343 0.1606 0.2247 -0.1514 -0.6284-0.1535 0.5841-0.3719 0.1152 0.1957 -0.1954 -0.6909 -0.13510.0383 -0.5244-0.3713 0.0096 0.2368 0.7875 0.2168 0.23850.0303 -0.2845-0.1949 -0.9689 -0.0004 -0.1242 0.0119 0.06280.0151 -0.0593-0.3725 0.1143 0.1222 -0.2302 0.0924 0.22590.7946 0.2988-0.3716 0.1272 0.0353 -0.3800 0.6591 -0.3521-0.1557 -0.3428-0.3613 0.0596 -0.9185 0.1165 -0.0872 0.03020.0022 -0.0096d =7.1135 0 0 0 0 0 0 00 0.7770 0 0 0 0 0 00 0 0.0810 0 0 0 0 00 0 0 0.0237 0 0 0 00 0 0 0 0.0041 00 00 0 0 0 0 0.0006 0 00 0 0 0 0 00.0000 00 0 0 0 0 0 0 0.0001各主成分贡献率：>> w=sum(d)/sum(sum(d))w =0.8892 0.0971 0.0101 0.0030 0.0005 0.00010.0000 0.0000计算各个主成分得分：>> F=[A-ones(17,1)*mean(A)]*v(:,8)F =224.3503-24.0409-40.0941-35.90754.7573-12.6102-2.85731.8038-13.901213.4541-29.384762.3383-23.3175-32.4285-38.1309-14.8637-39.1675>> [F1,I1]=sort(F,'descend')F1按从大到小的顺序给个主成分得分排名：F1 =224.350362.338313.45414.75731.8038-2.8573-12.6102-13.9012-14.8637-23.3175-24.0409-29.3847-32.4285-35.9075-38.1309-39.1675-40.0941I1给出各个名次的序号：I1 =1121058769161321114415173>> [F2,I2]=sort(I1)F2 =1234567891011121314151617I2给出个城市排名，即所求排名：I2 =1111714476583122101315916（2）由于第一主成分的贡献率大于80%，其他各成分贡献率都太小，所以只能用第一主成分进行排名。

主成分分析报告matlab程序

主成分分析报告matlab程序

主成分分析报告matlab程序主成分分析报告 Matlab 程序在数据分析和处理的领域中，主成分分析（Principal Component Analysis，PCA）是一种常用且强大的工具。

它能够将多个相关变量转换为一组较少的不相关变量，即主成分，同时尽可能多地保留原始数据的信息。

在 Matlab 中，我们可以通过编写程序来实现主成分分析，这为我们的数据处理和理解提供了极大的便利。

主成分分析的基本思想是找到数据中的主要方向或模式。

这些主要方向是通过对数据的协方差矩阵进行特征值分解得到的。

最大的特征值对应的特征向量就是第一主成分的方向，第二大的特征值对应的特征向量就是第二主成分的方向，以此类推。

在 Matlab 中，我们首先需要导入数据。

假设我们的数据存储在一个名为｀data` 的矩阵中，每一行代表一个观测值，每一列代表一个变量。

｀｀｀matlabdata ＝ load(＇your_data_filetxt'）；％替换为您的数据文件路径｀｀｀接下来，我们需要对数据进行中心化处理，即每个变量减去其均值。

｀｀｀matlabcentered_data ＝ data repmat(mean(data)， size(data, 1)， 1)；｀｀｀然后，计算协方差矩阵。

｀｀｀matlabcov_matrix ＝ cov(centered_data)；｀｀｀接下来进行特征值分解。

｀｀｀matlabV, D ＝ eig(cov_matrix)；｀｀｀｀V` 是特征向量矩阵，｀D` 是对角矩阵，其对角元素是特征值。

我们对特征值进行从大到小的排序，并相应地对特征向量进行重新排列。

｀｀｀matlablambda, index ＝ sort(diag(D)，＇descend'）；sorted_V ＝ V(：， index)；｀｀｀此时，｀sorted_V` 的每一列就是一个主成分的方向。

为了计算每个观测值在主成分上的得分，我们可以使用以下代码：｀｀｀matlabprincipal_components ＝ centered_data sorted_V;｀｀｀我们还可以计算每个主成分解释的方差比例。

使用Matlab进行高维数据降维与可视化的方法

使用Matlab进行高维数据降维与可视化的方法

使用Matlab进行高维数据降维与可视化的方法数据降维是数据分析和可视化中常用的技术之一，它可以将高维数据映射到低维空间中，从而降低数据的维度并保留数据的主要特征。

在大数据时代，高维数据的处理和分析变得越来越重要，因此掌握高维数据降维的方法是一项关键技能。

在本文中，我们将介绍使用Matlab进行高维数据降维与可视化的方法。

一、PCA主成分分析主成分分析（Principal Component Analysis，PCA）是一种常用的降维方法，它通过线性变换将原始数据映射到新的坐标系中。

在新的坐标系中，数据的维度会减少，从而方便进行可视化和分析。

在Matlab中，PCA可以使用`pca`函数来实现。

首先，我们需要将数据矩阵X 传递给`pca`函数，并设置降维后的维度。

`pca`函数将返回一个降维后的数据矩阵Y和对应的主成分分析结果。

```matlabX = [1 2 3; 4 5 6; 7 8 9]; % 原始数据矩阵k = 2; % 降维后的维度[Y, ~, latent] = pca(X, 'NumComponents', k); % PCA降维explained_variance_ratio = latent / sum(latent); % 各主成分的方差解释比例```通过这段代码，我们可以得到降维后的数据矩阵Y，它的维度被减少为k。

我们还可以计算出每个主成分的方差解释比例，从而了解每个主成分对数据方差的贡献程度。

二、t-SNE t分布随机邻域嵌入t分布随机邻域嵌入（t-distributed Stochastic Neighbor Embedding，t-SNE）是一种非线性的高维数据降维方法，它能够有效地保留数据样本之间的局部结构关系。

相比于PCA，t-SNE在可视化高维数据时能够更好地展现不同类别之间的差异。

在Matlab中，t-SNE可以使用`tsne`函数来实现。

我们同样需要将数据矩阵X 传递给`tsne`函数，并设置降维后的维度。

Matlab主成分分析：详解+实例

Matlab主成分分析：详解+实例
主成分分析(PCA)中我们的目标是找到 一个能使个体差异达到最大的变量线性 组合。
主成分分析
总结:
主 原始变量 目标
成
X1, , Xm
主成分
Z1, ,Zp
分
线性组合
分
Z1, , Zp 互不相关
析 的
信息不重合 按‘重要性’排序
求解主 成分
思
Z1, , Zp
想 Var(Z1) Var(Z2 ) Var(Zp )
r
i r 2(z j , xi )，
j1
这里r(z j , xi )表示zj 与 xi 的相关系数。
主成分分析
1 2 0
例1 设 x [ x1, x2 , x3 ]T 且 R 2 5 0
0 0 0
则可算得1 5.8284，2 0.1716，如果我们仅取第
一个主成分，由于其累积贡献率已经达到97.14%， 似乎很理想了，但如果进一步计算主成分对原变量的
c1 x1+ c2 x2+… +cp xp
我们希望选择适当的权重能更好地区分学生的 成绩. 每个学生都对应一个这样的综合成绩, 记 为s1, s2,…, sn , n为学生人数. 如果这些值很分散, 表明区分好, 即是说, 需要寻找这样的加权, 能使 s1, s2,…, sn 尽可能的分散, 下面来看的统计定义.
x5:交通和通讯,
x6:娱乐教育文化服务,
x7:居住,
x8:杂项商品和服务.
对居民消费数据做主成分分析.
聚类分析
聚类分析
聚类分析
计算的Matlab程序如下:
clc,clear load czjm1999.txt
%把原始数据保存在纯文本文件czjm1999.txt中

主成分分析报告PCA(含有详细推导过程以及案例分析报告matlab版)

主成分分析法(PCA)在实际问题中，我们经常会遇到研究多个变量的问题，而且在多数情况下，多个变量之间常常存在一定的相关性。

由于变量个数较多再加上变量之间的相关性，势必增加了分析问题的复杂性。

如何从多个变量中综合为少数几个代表性变量，既能够代表原始变量的绝大多数信息，又互不相关，并且在新的综合变量基础上，可以进一步的统计分析，这时就需要进行主成分分析。

I. 主成分分析法(PCA)模型（一）主成分分析的基本思想主成分分析是采取一种数学降维的方法，找出几个综合变量来代替原来众多的变量，使这些综合变量能尽可能地代表原来变量的信息量，而且彼此之间互不相关。

这种将把多个变量化为少数几个互相无关的综合变量的统计分析方法就叫做主成分分析或主分量分析。

主成分分析所要做的就是设法将原来众多具有一定相关性的变量，重新组合为一组新的相互无关的综合变量来代替原来变量。

通常，数学上的处理方法就是将原来的变量做线性组合，作为新的综合变量，但是这种组合如果不加以限制，则可以有很多，应该如何选择呢？如果将选取的第一个线性组合即第一个综合变量记为1F ，自然希望它尽可能多地反映原来变量的信息，这里“信息”用方差来测量，即希望)(1F Var 越大，表示1F 包含的信息越多。

因此在所有的线性组合中所选取的1F 应该是方差最大的，故称1F 为第一主成分。

如果第一主成分不足以代表原来p 个变量的信息，再考虑选取2F 即第二个线性组合，为了有效地反映原来信息，1F 已有的信息就不需要再出现在2F 中，用数学语言表达就是要求0),(21=F F Cov ，称2F 为第二主成分，依此类推可以构造出第三、四……第p 个主成分。

（二）主成分分析的数学模型对于一个样本资料，观测p 个变量p x x x ,,21，n 个样品的数据资料阵为：⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=np n n p p x x x x x x x x x X212222111211()p x x x ,,21=其中：p j x x x x nj j j j ,2,1,21=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛= 主成分分析就是将p 个观测变量综合成为p 个新的变量（综合变量），即⎪⎪⎩⎪⎪⎨⎧+++=+++=+++=ppp p p p p p p p x a x a x a F x a x a x a F x a x a x a F 22112222121212121111 简写为：p jp j j j x x x F ααα+++= 2211p j ,,2,1 =要求模型满足以下条件：①j i F F ,互不相关（j i ≠，p j i ,,2,1, =）②1F 的方差大于2F 的方差大于3F 的方差，依次类推③.,2,1122221p k a a a kp k k ==+++于是，称1F 为第一主成分，2F 为第二主成分，依此类推，有第p 个主成分。

matlab中主成分分析的函数1


练习：应用 MATLAB 内部的数据 cities.mat 进行分析。该数据是 美国 329 个城市反映生活质量的 9 项指标的数据。这 9 项指标分别为： 气候、住房、健康状况、犯罪、交通、教育、艺术、娱乐和经济。
例 2：从协方差矩阵或相关系数矩阵出发求解主成分
表：128 名成年男子身材的六项指标的相关系数矩阵
功能：运用协方差矩阵或相关系数矩阵进行主成分分析 格式：PC=pcacov(X) [PC,latent,explained]=pcacov(X)
说明：[PC,latent,explained]=pcacov(X)通过协方差矩阵 X 或 相关系数矩阵进行主成分分析，返回主成分(PC)、协方差矩阵 X 的特 征值(latent)和每个特征向量表征在观测量总方差中所占的百分数 (explained)（即是主成分的贡献向量）。 3. pcares 函数
%为了更加直观，以元胞数组的形式显示结果 %result1=cell(n+1,4);%定义一个 n+1 行，4 列的元胞数组 result1(1,:)={'特征值','差值','贡献率','累积贡献率'} result1（2:7,1）=num2cell(latent);%存放特征值 result1（2:6,2）=num2cell(-diff(latent));%存放特征值之间 的差值 result1（2:7,3：4） =num2cell([explained ,cumsum(explained )]);%存放(累积)贡献率 %以元胞数组的形式显示前 3 个主成分表达式 s={'标准化变量';'身高（x1）’;’坐高(x2)’;’ 胸围(x3)’;’ 手臂长(x4)’;’肋 围(x5) ’；‘腰围(x6)’} result1（：,1）=s; result1（1,2:4）={‘主成分 prin1','主成分 prin2', '主成分 prin3'};

聚类分析 主成分分析和典型相关分析 含matlab程序


∑ ∑ E(βˆ1)
=
E⎜⎛ ⎝
n i=1
ki
yi
⎟⎞ ⎠
=
n
ki E( yi )
i=1
n
n
n
∑ ∑ ∑ = ki E(β0 + β1xi ) = β0 ki + β1 ki xi
i=1
i=1
i=1
所以
∑ ∑ n
n
ki =
xi − x
n
=0
i=1
∑ i=1 (xi − x)2
i=1
n
∑ ∑ n
n
ki xi =
同样可以证明
∑ Var(βˆ0
)
=
σ
2[
1 n
+
x2 ]
n
(xi − x)2
i =1
（8）
-231-
且 βˆ0 是 β0 的线性无偏的最小方差估计量。
2.2.3 其它性质 用最小二乘法拟合的回归方程还有一些值得注意的性质：
1．残差和为零。 残差
ei = yi − yˆi ， i = 1,2,L, n
则
n
∑ Q(βˆ0 , βˆ1)
=
min
β0 ,β1
Q(
β
0
,
β1
)
=
i=1
( yi
− βˆ0
− βˆ1xi )2
显然 Q(β0 , β1) ≥ 0 ，且关于 β0 , β1 可微，则由多元函数存在极值的必要条件得
∑ ∂Q
∂β 0
n
= −2 ( yi
i=1
− β0
− β1xi ) = 0
∑ ∂Q
∂β 1
d

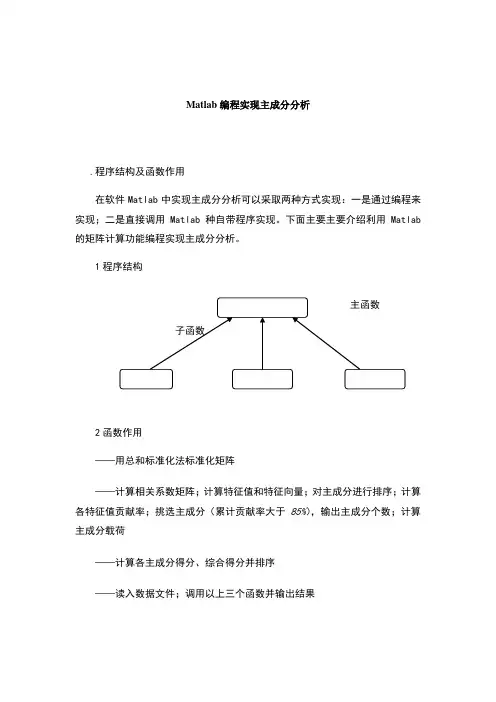
主成分分析matlab程序

Matlab编程实现主成分分析.程序结构及函数作用在软件Matlab中实现主成分分析可以采取两种方式实现：一是通过编程来实现；二是直接调用Matlab种自带程序实现。

下面主要主要介绍利用Matlab 的矩阵计算功能编程实现主成分分析。

1程序结构2函数作用——用总和标准化法标准化矩阵——计算相关系数矩阵；计算特征值和特征向量；对主成分进行排序；计算各特征值贡献率；挑选主成分（累计贡献率大于85%），输出主成分个数；计算主成分载荷——计算各主成分得分、综合得分并排序——读入数据文件；调用以上三个函数并输出结果3.源程序总和标准化法标准化矩阵%,用总和标准化法标准化矩阵function std=cwstd(vector)cwsum=sum(vector,1); %对列求和[a,b]=size(vector); %矩阵大小,a为行数,b为列数for i=1:afor j=1:bstd(i,j)= vector(i,j)/cwsum(j);endend计算相关系数矩阵%function result=cwfac(vector);fprintf('相关系数矩阵:\n')std=CORRCOEF(vector) %计算相关系数矩阵fprintf('特征向量(vec)及特征值(val)：\n')[vec,val]=eig(std) %求特征值(val)及特征向量(vec)newval=diag(val) ;[y,i]=sort(newval) ; %对特征根进行排序，y为排序结果，i为索引fprintf('特征根排序：\n')for z=1:length(y)newy(z)=y(length(y)+1-z);endfprintf('%g\n',newy)rate=y/sum(y);fprintf('\n贡献率：\n')newrate=newy/sum(newy)sumrate=0;newi=[];for k=length(y):-1:1sumrate=sumrate+rate(k);newi(length(y)+1-k)=i(k);if sumrate> break;endend %记下累积贡献率大85%的特征值的序号放入newi中fprintf('主成分数：%g\n\n',length(newi));fprintf('主成分载荷：\n')for p=1:length(newi)for q=1:length(y)result(q,p)=sqrt(newval(newi(p)))*vec(q,newi(p));endend %计算载荷disp(result)%,计算得分function score=cwscore(vector1,vector2);sco=vector1*vector2;csum=sum(sco,2);[newcsum,i]=sort(-1*csum);[newi,j]=sort(i);fprintf('计算得分：\n')score=[sco,csum,j]%得分矩阵：sco为各主成分得分；csum为综合得分；j为排序结果%function print=cwprint(filename,a,b);%filename为文本文件文件名，a为矩阵行数(样本数)，b为矩阵列数(变量指标数)fid=fopen(filename,'r')vector=fscanf(fid,'%g',[a b]);fprintf('标准化结果如下：\n')v1=cwstd(vector)result=cwfac(v1);cwscore(v1,result);4.程序测试例题原始数据中国大陆35个大城市某年的10项社会经济统计指标数据见下表。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

MATLAB
结
课
作
业
指导老师：张肃
班级：信管121
姓名：桂亚东
学号：4118
利用Matlab 编程实现主成分分析
概述
Matlab 语言是当今国际上科学界 (尤其是自动控制领域) 最具影响力、也是
最有活力的软件。

它起源于矩阵运算，并已经发展成一种高度集成的计算机语言。

它提供了强大的科学运算、灵活的程序设计流程、高质量的图形可视化与界面设计、与其他程序和语言的便捷接口的功能。

Matlab 语言在各国高校与研究单位起着重大的作用。

主成分分析是把原来多个变量划为少数几个综合指标的一种统计分析方法，从数学角度来看，这是一种降维处理技术。

主成分分析计算步骤
① 计算相关系数矩阵
⎥⎥⎥⎥⎥⎦⎤
⎢⎢⎢⎢
⎢⎣⎡=pp p p p p r r r r r r r r r R ΛM M M M ΛΛ212222111211 （1） 在（3.5.3）式中，r ij （i ，j=1，2，…，p ）为原变量的xi 与xj 之间的相关系数，其计算公式为
∑∑∑===----=
n
k n
k j kj
i ki
n
k j kj i ki
ij x x
x x
x x x x
r 1
1
2
2
1
)()
()
)(( （2）
因为R 是实对称矩阵（即r ij =r ji ），所以只需计算上三角元素或下三角元素即可。

② 计算特征值与特征向量
首先解特征方程0=-R I λ，通常用雅可比法（Jacobi ）求出特征值
),,2,1(p i i Λ=λ，并使其按大小顺序排列，即0,21≥≥≥≥p
λλλΛ；然后分别求
出对应于特征值i λ的特征向量),,2,1(p i e i Λ=。

这里要求i e =1，即112
=∑=p
j ij e ，其
中ij e 表示向量i e 的第j 个分量。

③ 计算主成分贡献率及累计贡献率 主成分i z 的贡献率为
),,2,1(1
p i p
k k
i
Λ=∑=λ
λ
累计贡献率为
)
,,2,1(11
p i p
k k
i
k k
Λ=∑∑==λ
λ
一般取累计贡献率达85—95%的特征值m λλλ,,,21Λ所对应的第一、第二，…，第m （m ≤p ）个主成分。

④ 计算主成分载荷 其计算公式为
)
,,2,1,(),(p j i e x z p l ij i j i ij Λ===λ （3）
得到各主成分的载荷以后，还可以按照（3.5.2）式进一步计算，得到各主成分的得分
⎥⎥⎥⎥⎦⎤⎢⎢⎢
⎢⎣⎡=nm n n m m z z z z z z z z z Z ΛM M M M ΛΛ212222111211 （4） 2.函数作用
——用总和标准化法标准化矩阵
——计算相关系数矩阵；计算特征值和特征向量；对主成分进行排序；计算各特征值贡献率；挑选主成分（累计贡献率大于85%），输出主成分个数；计算主成分载荷
——计算各主成分得分、综合得分并排序 ——读入数据文件；调用以上三个函数并输出结果
3.源程序
总和标准化法标准化矩阵
%,用总和标准化法标准化矩阵 function std=cwstd(vector)
cwsum=sum(vector,1); %对列求和
[a,b]=size(vector); %矩阵大小,a 为行数,b 为列数 for i=1:a for j=1:b
std(i,j)= vector(i,j)/cwsum(j); end end
计算相关系数矩阵
%
function result=cwfac(vector);
fprintf('相关系数矩阵:\n')
std=CORRCOEF(vector) %计算相关系数矩阵
fprintf('特征向量(vec)及特征值(val)：\n')
[vec,val]=eig(std) %求特征值(val)及特征向量(vec)
newval=diag(val) ;
[y,i]=sort(newval) ; %对特征根进行排序，y为排序结果，i为索引fprintf('特征根排序：\n')
for z=1:length(y)
newy(z)=y(length(y)+1-z);
end
fprintf('%g\n',newy)
rate=y/sum(y);
fprintf('\n贡献率：\n')
newrate=newy/sum(newy)
sumrate=0;
newi=[];
for k=length(y):-1:1
sumrate=sumrate+rate(k);
newi(length(y)+1-k)=i(k);
if sumrate> break;
end
end %记下累积贡献率大85%的特征值的序号放入newi中fprintf('主成分数：%g\n\n',length(newi));
fprintf('主成分载荷：\n')
for p=1:length(newi)
for q=1:length(y)
result(q,p)=sqrt(newval(newi(p)))*vec(q,newi(p));
end
end %计算载荷
disp(result)
%,计算得分
function score=cwscore(vector1,vector2);
sco=vector1*vector2;
csum=sum(sco,2);
[newcsum,i]=sort(-1*csum);
[newi,j]=sort(i);
fprintf('计算得分：\n')
score=[sco,csum,j]
%得分矩阵：sco为各主成分得分；csum为综合得分；j为排序结果
%
function print=cwprint(filename,a,b);
%filename为文本文件文件名，a为矩阵行数(样本数)，b为矩阵列数(变量指标数) fid=fopen(filename,'r')
vector=fscanf(fid,'%g',[a b]);
fprintf('标准化结果如下：\n')
v1=cwstd(vector)
result=cwfac(v1);
cwscore(v1,result);
4.程序测试
原始数据
中国大陆35个大城市某年的10项社会经济统计指标数据见下表。

运行结果
>> cwprint('',35,10)
fid =
6
数据标准化结果如下：
v1 =
相关系数矩阵: std =
特征向量(vec)：
vec =
特征值(val)
val =
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
特征根排序：
各主成分贡献率：
newrate =
第一、二主成分的载荷：
1
3
7
5
6
3
7
7
9
6
第一、二、三、四主成分的得分：score =
5 9 4
6 6 2
8 3 4
6 1 7
9 5 4
8 0 8 0。