特殊角的三角函数值及计算

特殊三角函数值对照表（特殊角的三角函数值）《特殊角的三角函数值》是人教版数学九年级下册第二十八章的内容，特殊三角函数值一般指在0，30°，45°，60°，90°，180°角下的正余弦值。

这些角度的三角函数值是经常用到的。

并且利用两角和与差的三角函数公式，可以求出一些其他角度的三角函数值。

具体的三角函数值如下表：扩展资料：黄金三角函数介绍：α=18°(π/10) sinα=(√5-1)/4 cosα=√(10+2√5)/4tαnα=√(25-10√5)/5cscα=√5+1 secα=√(50-10√5)/5 cotα=√(5+2√5)α=36°(π/5) sinα=√(10-2√5)/4 cosα=(√5+1)/4tαnα=√(5-2√5)cscα=√(50+10√5)/5 secα=√5-1 cotα=√(25+10√5)/5α=54°(3π/10) sinα=(√5+1)/4 cosα=√(10-2√5)/4 tαnα=√(25+10√5)/5是数学中属于初等函数中的超越函数的一类函数。

它们的本质是任意角的集合与一个比值的集合的变量之间的映射。

通常的三角函数是在平面直角坐标系中定义的，其定义域为整个实数域。

另一种定义是在直角三角形中，但并不完全。

扩展资料：三角函数在复数中有重要的应用。

三角函数也是物理学中的常用工具。

它有六种基本函数函数名正弦余弦正切余切正割余割符号 sin cos tan cot sec csc正弦函数sin（A）=a/c余弦函数cos（A）=b/c正切函数tan（A）=a/b余切函数cot（A）=b/a其中a为对边，b为邻边，c为斜边特殊角的值如下表：在直角三角形中，任意一锐角∠A的对边与斜边的比叫做∠A 的正弦，记作sinA（由英语sine一词简写得来），即sinA=∠A的对边/斜边。

扩展资料：sinα = tanα × cosα（即sinα / cosα = tanα ）cosα = cotα × sinα （即cosα / sinα = cotα）tanα = sinα × secα (即tanα / sinα = secα)sin ( α ± β ) = sinα · cosβ ± cosα · sinβsin ( α + β + γ ) = sinα · cosβ · cosγ +cosα · sinβ · cosγ + cosα · cosβ · sinγ - sinα · sinβ · sinγcos ( α ± β ) = cosα cosβ ∓ sinβ sinαtan ( α ± β ) = ( tanα ± tanβ ) / ( 1 ∓ tanα tanβ )完整初中三角函数值表如下图所示：常见的三角函数有正弦函数、余弦函数和正切函数。

三角函数的特殊角度在数学中，三角函数是研究角度和边长关系的重要工具。

三角函数有很多特殊的角度，它们的取值可以用简单的分数或根号表示。

本文将探讨三角函数中的特殊角度，包括正弦、余弦和正切。

一、正弦函数的特殊角度1. 特殊角度π/6：正弦函数sin(π/6) = 1/2，即 sin(30°) = 1/2。

这是一个非常常见的角度，它出现在很多问题中。

2. 特殊角度π/4：正弦函数sin(π/4) = √2/2，即sin(45°) = √2/2。

这个角度同样非常常见，经常用于讨论直角三角形中的比例关系。

3. 特殊角度π/3：正弦函数sin(π/3) = √3/2，即sin(60°) = √3/2。

这个角度出现在六边形等问题中，具有重要的几何意义。

二、余弦函数的特殊角度1. 特殊角度π/3：余弦函数cos(π/3) = 1/2，即 cos(60°) = 1/2。

与正弦函数π/6 相互补，也具有重要的几何意义。

2. 特殊角度π/4：余弦函数cos(π/4) = √2/2，即cos(45°) = √2/2。

与正弦函数π/4 相等。

3. 特殊角度π/6：余弦函数cos(π/6) = √3/2，即cos(30°) = √3/2。

与正弦函数π/3 相互补，也具有重要的几何意义。

三、正切函数的特殊角度1. 特殊角度π/4：正切函数tan(π/4) = 1，即 tan(45°) = 1。

这是一个非常重要的角度，经常出现在直角三角形中的问题中。

2. 特殊角度π/6：正切函数tan(π/6) = √3/3，即tan(30°) = √3/3。

与余切函数的值互为倒数。

3. 特殊角度π/3：正切函数tan(π/3) = √3，即tan(60°) = √3。

与余切函数的值互为倒数。

特殊角度在数学和实际问题中有广泛的应用。

通过熟练掌握这些特殊角度的三角函数值，我们能够更快地解决数学问题，并在实际应用中灵活运用。

三角函数值大全（1）特殊角三角函数值sin0=0,sin15=（√6-√2)/4 ,sin30=1/2,sin45=√2/2,sin60=√3/2,sin75=(√6+√2)/2 ,sin90=1,sin105=√2/2*(√3/2+1/2)sin120=√3/2sin135=√2/2sin150=1/2sin165=（√6-√2)/4sin180=0sin270=-1sin360=0cos0=1cos30= 二分之根号3cos45= 二分之根号2cos60=cos90=0tan0=0tan30= 三分之根号3tan45=1tan60= 根号3tan90=无cot0=无cot30= 根号3cot45=1cot60= 三分之根号3cot90=0（2）0°～90°的任意角的三角函数值，查三角函数表。

（3）锐角三角函数值的变化情况（i）锐角三角函数值都是正值（ii）当角度在0°～90°间变化时，正弦值随着角度的增大（或减小）而增大（或减小）余弦值随着角度的增大（或减小）而减小（或增大）正切值随着角度的增大（或减小）而增大（或减小）余切值随着角度的增大（或减小）而减小（或增大）（iii）当角度在0°≤α≤90°间变化时，0≤sinα≤1, 1≥cosα≥0,当角度在0°< α<90°间变化时，tanα>0, cotα>0.附：三角函数值表sin1= sin2= sin3=sin4= sin5= sin6=sin7= sin8= sin9=sin10= sin11= sin12=sin13= sin14= sin15=sin16= sin17= sin18=sin19= sin20= sin21=sin22= sin23= sin24=sin25= sin26= sin27=sin28= sin29= sin30=sin31= sin32= sin33=sin34= sin35= sin36=sin37= sin38= sin39=sin40= sin41= sin42=sin43= sin44= sin45=sin46= sin47= sin48=sin52= sin53= sin54= sin55= sin56= sin57= sin58= sin59= sin60= sin61= sin62= sin63= sin64= sin65= sin66= sin67= sin68= sin69= sin70= sin71= sin72= sin73= sin74= sin75= sin76= sin77= sin78= sin79= sin80= sin81= sin82= sin83= sin84= sin85= sin86= sin87= sin88= sin89=sin90=1cos1= cos2= cos3= cos4= cos5= cos6= cos7= cos8= cos9= cos10= cos11= cos12= cos13= cos14= cos15=cos19= cos20= cos21= cos22= cos23= cos24= cos25= cos26= cos27= cos28= cos29= cos30= cos31= cos32= cos33= cos34= cos35= cos36= cos37= cos38= cos39= cos40= cos41= cos42= cos43= cos44= cos45= cos46= cos47= cos48= cos49= cos50= cos51= cos52= cos53= cos54= cos55= cos56= cos57= cos58= cos59= cos60= cos61= cos62= cos63= cos64= cos65= cos66= cos67= cos68= cos69= cos70= cos71= cos72= cos73= cos74= cos75=cos79= cos80= cos81= cos82= cos83= cos84= cos85= cos86= cos87= cos88= cos89=cos90=0tan1= tan2= tan3= tan4= tan5= tan6= tan7= tan8= tan9= tan10= tan11= tan12= tan13= tan14= tan15= tan16= tan17= tan18= tan19= tan20= tan21= tan22= tan23= tan24= tan25= tan26= tan27= tan28= tan29= tan30= tan31= tan32= tan33= tan34= tan35= tan36= tan37= tan38= tan39= tan40= tan41= tan42=tan43= tan44= tan45= tan46= tan47= tan48= tan49= tan50= tan51= tan52= tan53= tan54= tan55= tan56= tan57= tan58= tan59= tan60= tan61= tan62= tan63= tan64= tan65= tan66= tan67= tan68= tan69= tan70= tan71= tan72= tan73= tan74= tan75= tan76= tan77= tan78= tan79= tan80= tan81= tan82= tan83= tan84= tan85= tan86= tan87= tan88= tan89=tan90=无取值。

三角函数特殊角三角函数是数学中常见的函数类型之一，而在三角函数中，特殊角是指能够通过明确的数值计算得出精确值的角度。

特殊角是三角函数的重要概念之一，在解决各种数学问题中具有重要作用。

本文将重点讨论一些常见的三角函数特殊角及其计算方法。

正弦函数和余弦函数在三角函数中，最常见的两个函数是正弦函数和余弦函数。

在单位圆上，我们定义特殊角为0度、30度、45度、60度和90度时，正弦函数和余弦函数的数值如下：•当角度为0度时，正弦函数的值为0，余弦函数的值为1。

•当角度为30度时，正弦函数的值为1/2，余弦函数的值为√3/2。

•当角度为45度时，正弦函数的值为√2/2，余弦函数的值也为√2/2。

•当角度为60度时，正弦函数的值为√3/2，余弦函数的值为1/2。

•当角度为90度时，正弦函数的值为1，余弦函数的值为0。

正切函数另一个常见的三角函数是正切函数。

在特殊角中，我们定义角度为0度、45度和90度时，正切函数的数值如下：•当角度为0度时，正切函数的值为0。

•当角度为45度时，正切函数的值为1。

•当角度为90度时，正切函数的值为不存在，因为在这个角度上正切函数的值趋近于无穷大。

应用举例特殊角在数学问题中有很多应用，例如在三角形的计算中，我们可以通过特殊角来求解各种未知量。

又如在物理学中，特殊角的概念也被广泛运用，例如在力学问题中，根据特殊角可以方便地计算各种受力方向与大小之间的关系。

总结特殊角是三角函数中的重要概念，通过熟练掌握特殊角的数值和计算方法，可以帮助我们更好地理解和运用三角函数。

特殊角的认识不仅在数学问题中有应用，也可以在其他学科领域中发挥重要作用。

因此，对于特殊角的理解和掌握具有重要意义。

特殊角的三角函数运算三角函数是数学中常见的函数，它们在解决各种角度相关问题时起着重要作用。

特殊角是指具有特定角度值的角，包括0度、30度、45度、60度和90度等常用角。

本文将介绍特殊角的三角函数运算，包括正弦函数、余弦函数和正切函数。

1. 正弦函数的特殊角运算正弦函数是一个周期函数，它的周期是360度或2π弧度。

在特殊角中，我们常用的是0度、30度、45度、60度和90度的正弦值。

- 0度的正弦值为0；- 30度的正弦值为1/2；- 45度的正弦值为√2/2；- 60度的正弦值为√3/2；- 90度的正弦值为1。

2. 余弦函数的特殊角运算余弦函数也是一个周期函数，它的周期同样是360度或2π弧度。

下面是特殊角中常用的余弦值。

- 0度的余弦值为1；- 30度的余弦值为√3/2；- 45度的余弦值为√2/2；- 60度的余弦值为1/2；- 90度的余弦值为0。

3. 正切函数的特殊角运算正切函数是正弦函数和余弦函数的比值，因此其值与它们相对应的特殊角有关。

- 0度的正切值为0；- 30度的正切值为√3/3；- 45度的正切值为1；- 60度的正切值为√3；- 90度的正切值不存在。

特殊角的三角函数运算在解决各种实际问题中起着重要作用。

这些特殊角的数值容易记忆，并且它们的三角函数数值也具有规律性，便于在计算中应用。

通过掌握特殊角的运算结果，我们可以更加高效地解决各种三角函数相关问题。

总结：特殊角的三角函数运算能够帮助我们解决各种与角度相关的问题。

正弦函数、余弦函数和正切函数是常见的三角函数，它们在特殊角中具有固定的数值，并且具有一定的规律性。

通过熟练掌握特殊角的三角函数运算结果，我们可以更加高效地进行各种相关计算。

以上就是特殊角的三角函数运算的相关内容，希望对您有帮助！。

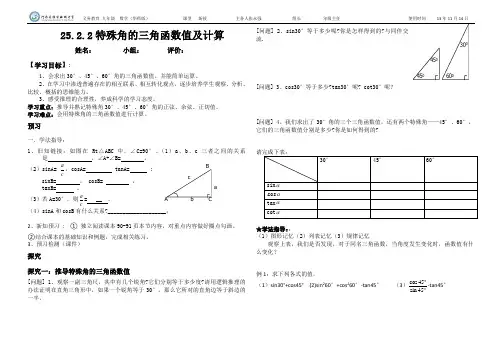
义务教育 九年级 数学（华师版） 课型 新授 主备人张永强 组长 年级主任 使用时间 13年11月14日25.2.2特殊角的三角函数值及计算姓名： 小组： 评价：【学习目标】:1、会求出30°、45°、60°角的三角函数值。

并能简单运算。

2、在学习中渗透普遍存在的相互联系、相互转化观点，逐步培养学生观察、分析、比较、概括的思维能力。

3、感受推理的合理性，养成科学的学习态度。

学习重点：推导并熟记特殊角30°、45°、60°角的正弦、余弦、正切值。

学习难点：会用特殊角的三角函数值进行计算。

预习一．学法指导：1、旧知链接：如图在 Rt △ABC 中，∠C=90°。

（1）a 、b 、c 三者之间的关系是 ，∠A+∠B= 。

（2）sinA= ca ，cosA= tanA= ; sinB= ， cosB= ，tanB= 。

（3）若A=30°，则ca= __ 。

（4）sinA 和cosB 有什么关系?____________________；2、新知预习 : ① 独立阅读课本90-91页本节内容，对重点内容做好圈点勾画。

②结合课本的基础知识和例题，完成相关练习。

3、预习检测（课件）探究探究一：推导特殊角的三角函数值[问题] 1、观察一副三角尺，其中有几个锐角?它们分别等于多少度?请用逻辑推理的办法证明在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

[问题] 2、sin30°等于多少呢?你是怎样得到的?与同伴交流.[问题] 3、cos30°等于多少?tan30°呢? cot30°呢？[问题] 4、我们求出了30°角的三个三角函数值，还有两个特殊角——45°、60°，它们的三角函数值分别是多少?你是如何得到的?请完成下表：★学法指导：：（1）图形记忆（2）列表记忆（3）规律记忆观察上表，我们是否发现，对于同名三角函数，当角度发生变化时，函数值有什么变化？例1：求下列各式的值．（1）sin30°+cos45° (2)sin 260°+cos 260°-tan45° （3）cos 45sin 45︒︒-tan45°30° 45° 60° sin α cos α tan α cot αb A B Ca ┌c┌┌300600450450阳光高效课堂导学稿探究二：利用特殊角的三角函数值求角。

特殊三角函数怎么求计算公式有哪些
三角函数是数学学习中的一个重点，那幺，特殊三角函数怎幺求呢？有哪些计算公式呢？下面小编整理了一些相关信息，供大家参考！
1 特殊三角函数怎幺算特殊三角函数是性质特殊的一类三角函数的总称，主要包括正弦三角函数、余弦三角函数、正切三角函数、余切三角函数、正割三角函数、和余割三角函数。

从等腰直角三角形开始
两腰是1 斜边就是√2
算出a=sin45°=1/√2
再由边长为2 的等边三角形高是√3
算出b=sin30°=1/2
c=sin60°=√3/2
利用和差公式就可以算出
sin15°=sin(45°-30°)=ac-ab=(√3-1)/√2/2
sin75°=sin(45°+30°)=ac+ab=(√3+1)/√2/2
这样就有每隔15°的三角函数值了
sin15°=(√3-1)/√2/2
sin30°=1/2
sin45°=1/√2
sin60°=√3/2
sin75°=(√3+1)/√2/2
1 特殊三角函数相关公式在平面直角坐标系xOy 中，从点O 引出一条射线。