北京交通大学(最优控制理论与算法研究生课程)第一章 最优控制概述
- 格式:ppt
- 大小:1.99 MB
- 文档页数:30






最优化理论与算法(数学专业研究生)第一章引论前言一、历史与现状最优化理论最早可追忆到古老的极值问题,但成为一门独立的学科则是在 20世纪四十年月末至五十年月初。
其奠定性工作包含FritzJohn最优性条件( 1948),Kuhn-Tucker最优性条件(1951),和Karush最优性条件(1939)。
近几十年来最优化理论与算法发展十分快速,应用也愈来愈宽泛。
现在已形成一个相当宏大的研究领域。
对于最优化理论与方法,狭义的主要指非线性规划的有关内容,而广义的则涵盖:线性规划、非线性规划、动向规划、整数规划、几何规划、多目标规划、随机规划甚至还包含变分、最优控制等动向优化内容。
本课程所波及的内容属于前者。
二、最优化问题的一般形式1、无拘束最优化问题minf(x)()xR n2、拘束最优化问题minf(x)c i(x)0,i E()st..i Ic i(x)0,这里E和I均为指标集。
§数学基础一、范数向量范数xx1x2maxx i(l范数)()ni1x i(l1范数)()n1(x i2)2(l2范数)()i11/30n1x p(x i p)p(l p范数)()i11x A(x T Ax)2(A正定)(椭球范数)()事实上1-范数、2-范数与范数分别是p-范数当p=1、2和p时情况。
2.矩阵范数定义方阵A的范数是指与A有关系并记做A的一个非负数,它拥有以下性质:①对于A0都有A0,而A0时A0;②对于随意k R,都有kA kA;③AB A B;④AB A B;若还进一步知足:⑤Ax p A x p则称之为与向量范数p相协调(相容)的方阵范数。
若令AxAmaxx (这里x是某一直量范数)()x0可证这样定义的范数是与向量范数相协调的,往常称之为由向量范数引诱的方阵范数。
特别地,对方阵A(a ij)nn,有:nA1max a ijj1inA max a iji1j1A2(A T A)2((列和的最大者)()(行和的最大者)()T表示A T A的特点值的最大者)(1.11) AA称为谱范数(注:方阵A的特点值的模的最大者称为A的谱半径,记为(A))。

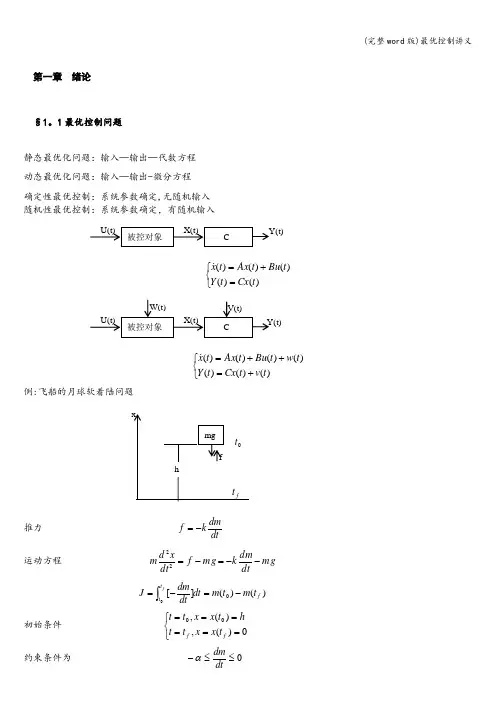
第一章 绪论§1。
1最优控制问题静态最优化问题:输入—输出—代数方程 动态最优化问题:输入—输出-微分方程 确定性最优控制:系统参数确定,无随机输入 随机性最优控制:系统参数确定,有随机输入⎩⎨⎧=+=)()()()()(t Cx t Y t Bu t Ax t x⎩⎨⎧+=++=)()()()()()()(t v t Cx t Y t w t Bu t Ax t x例:飞船的月球软着陆问题推力 dtdmkf -= 运动方程 mg dt dmk mg f dtx d m --=-=22 )()(][00f t t t m t m dt dtdmJ f-=-=⎰ 初始条件 ⎩⎨⎧======0)(,)(,00f f t x x t t ht x x t t约束条件为 0≤≤-dtdmα求min J§1.2最优控制的数学模型一 控制系统的数学模型(集中参数系统)直接法建立:动力学、运动学的基本定律,即解析法.间接法建立:通过“辩识"的途径确定系统的结构与参数.)),(),(()(t t u t x f t x= 其中 T n t x t x t x t x )](,)(),([)(21 =,T r t u t u t u t u )](,)(),([)(21 =,],,[21n f f f f = )(t x 为n 维状态向量,)(t u 为r 维控制向量,f 为n 维函数向量。
二 目标集通过)(t u 使)(t x 由)(0t x 到)(f t x ,其中)(0t x 为初始状态,并且通常为已知;)(f t x 为终端状态,即控制所要求达到的目标。
一般来说对终端状态的要求可用如下的约束条件表示:0)),((,0)),((21≤=f f f f t t x g t t x g 。
三 容许控制i u 具有不同的物理属性,一般有r 1,2i u i ,,=≤α,即在控制域U 内。


最优控制先修课程:常微分方程,最优化方法最优控制问题是具有特殊数学结构的一类最优化问题,在科学、工程和管理乃至人文领域都存在大量的最优控制问题。
最优控制研究动态系统在各种约束条件下,寻求目标泛函取极值的最优控制函数与最优状态轨线的数学理论和方法,它是静态最优化在无穷维空间的扩展。
希望学生通过本课程的学习,能够结合实际背景,建立最优控制的模型,理解求解最优控制的三大类基本方法的数学思想,灵活地掌握这些方法的基本过程,并能解释计算结果的意义。
主要内容如下:最优控制问题及其建模;数学基础;变分法及其在最优控制的应用;极小值原理及其应用;动态规划方法及其应用;应用。
最优控制一、课程基本信息 1.先修课程:数学系本科包括到大三的全部课程 2.面向对象:理学院数学系各专业 3.推荐教学参考书:吴沧浦,《最优控制的理论与方法》,国防工业出版社,2000 王朝珠等,《最优控制理论》,科学出版社,2003 邢继祥等,《最优控制应用基础》,科学出版社,2003 W. L. Brogan, Modern C ontrol Theor y, (3th eidition), Prentice-Hall, Englew ood C liffs,1991 二、课程的性质和任务本课程是数学与应用数学专业本科生高年级选修课程之一。
从数学的角度,最优控制问题是最优化问题中具有特殊结构的一类问题。
就问题的来源看,它又是控制问题。
最优控制研究动态系统在各种约束条件下寻求使目标泛函取极值的最优控制函数和最优状态轨线的数学理论和方法。
最优控制问题涉及范围广跨度大,几乎理工医农,管理军事乃至人文经法领域,都存在着大量此类问题。
最优化已是寻求最优系统和结构,挖掘系统潜力的有力武器,学会求解最优控制问题,是应用数学工作者的最基本素养之一。
通过本课程的主要任务是,从各个教学环节引导学生认识不同数学问题的特点和相应数学模型的结构,自己学会分析实际问题,建立各种数量之间的联系,写出正确的合理的最优控制的模型;领会求解最优控制问题解法是如何提出的数学思想,并学会如何根据这些思想来构成相应方法的技巧;学会能正确地解释计算结果的物理意义的能力。

最优控制理论教学大纲
一、引言
最优控制理论是控制工程领域中的重要分支,旨在寻找使系统性能
达到最优的控制策略。
本教学大纲旨在为学生提供最优控制理论的基
础知识和应用技能,使他们能够在实际工程中灵活应用最优控制理论,提高工程系统的性能。
二、最优控制理论概述
1. 最优控制概念
2. 最优控制问题分类
3. 最优控制理论的历史发展
三、最优控制理论基础知识
1. 动态规划理论
2. 变分法
3. 极大值原理
4. 动态系统建模
四、最优控制理论应用
1. 线性二次型最优控制问题
2. Pontryagin最小原理
3. 最优控制在机器人控制中的应用
4. 预测控制
五、最优控制理论实践案例
1. 飞行器自动驾驶控制
2. 汽车智能驾驶系统
3. 工业生产过程中的最优控制应用
六、教学方法
1. 理论讲解结合实例分析
2. 班级讨论和小组作业
3. 实验室实践操作和仿真演示
七、评估方式
1. 期中考试
2. 课堂作业
3. 期末大作业
八、参考教材
1. "Optimal Control Theory: An Introduction" by Donald E. Kirk
2. "Optimal Control Applications in Electric Power Systems" by Louie Wei
通过本教学大纲的学习,学生将全面掌握最优控制理论的基础知识和应用技能,为将来从事控制工程领域的工作打下坚实基础。
愿学生们在学习过程中努力钻研,不断提升自我,在最优控制理论领域取得优异成绩!。
《最优控制》课程教学⼤纲《最优控制》课程教学⼤纲课程代码:060142002课程英⽂名称:Optimal Control课程总学时:32 讲课:32 实验:0 上机:0适⽤专业:⾃动化专业⼤纲编写(修订)时间:2017.11⼀、⼤纲使⽤说明(⼀)课程的地位及教学⽬标《最优控制》是现代控制理论的重要组成部分,它已⼴泛应⽤于军事和⼯业及经济领域中,例如空间技术、系统⼯程、⼈⼝理论、经济管理、决策及⼯业过程控制等等。
并在各个领域取得了显著的成果。
本课程是⾃动化专业的⼀门选修课,其基本任务和教学⽬标是要求⾃动化专业学⽣掌握最优控制理论及应⽤的基础知识及解最优控制问题的常⽤⽅法,了解最优控制的发展⽅向,为将来的专业发展打下⼀定的基础。
(⼆)知识、能⼒及技能⽅⾯的基本要求1.基本知识:初步掌握最优控制的基础理论,如最优控制问题的概念、最优控制的数学描述、解决最优控制问题⽅法及⼆次型性能指标最优控制问题。
2.基本理论和⽅法:初步掌握解决最优控制问题的⼀些基本⽅法,如古典变分原理,庞德⾥亚⾦极⼤(⼩)值原理和贝尔曼动态规划⽅法。
3.基本技能:利⽤最优控制理论和⽅法能够解决的实际最优控制问题。
(三)实施说明1.教学⽅法:从基本教育出发,站在培养⼈才的⾼度上,来看待本课程所应承担的责任。
在讲授具体内容时,要分清每⼀部分内容在本课程中所处的地位,这样才能在⼤纲实施过程中得⼼应⼿。
要提⾼学⽣的基本素质,要求学⽣化被动吸收为主动索取知识。
2.教学⼿段:本课程属于技术基础课,在教学中采⽤电⼦教案、CAI课件及多媒体教学系统等先进教学⼿段,以确保在有限的学时内,全⾯、⾼质量地完成课程教学任务。
为了提⾼教学效果,可采⽤多环节教学⽅式,如课程讲授、课堂提问及课前预习和课后阅读。
对于每次课堂讲授,原则上采⽤两个层次讲解,即⼀是提出研究的问题;⼆是介绍解决问题的各种⽅法及其存在的优缺点,培养学⽣创新思维意识。
通过课堂提问,在课堂上调动学⽣积极性,促进其思考,提⾼教与学互动性。