下载文档原格式
Inverse ManipulatorKinematicsAlgebraic solution by reduction to polynomialOutline2 Introduction IntroductionIntroductionThe Inverse kinematic is the basis of robot trajectory planning and control.5IntroductionExample :6Algebraic solution by reduction to polynomialOutline7SolvabilitySolvabilityFor the 6 DOF Puma 560 manipulator,we have:How to find the 6 joint variablesHere we might have 12 equations to solve for 6 independent variables. Constraints should be utilized.6 equations for 6 unknown variables9SolvabilityDifficulty: these 6 equations are nonlinear and transcendental equations.obtain the solution.whereSolvability11SolvabilitySolvabilityThe dexterous workspace is only one point(the origin). The There is no dexterous workspace. The reachable SolvabilityFor most industry robots, there is limitation for the joint variable range, thus the workspace is reduced.Only one attainable orientationIf a manipulator has less than 6 DOF, it can’t attain general goal position and orientation in 3D space.Workspace also depends on the tool-frame transformation.Solvability15There might be multiple solution in solving kinematic equations.Two possible solution for the same position and orientation.How to choose possible solution?Solvability” solution.The number of solutions depends on the number of and the allowable ranges of motion of the joints, also, it can be a function of other link parameters (link length, link twist, link offset, joint angle).Solvability2. Multiple solutions17The PUMA 560 can reach certain goals with 8different solutions.+Due to the limits of joints range, some of these 8 solutions could be inaccessible.SolvabilitySolvabilityAlgebraic solution by reduction to polynomial Outline20Manipulator Subspace21workspace is a portion of an n‐DOF subspacesubspace : planeworkspace : a subset of the plane{workspace} ⊂{subspace} ⊂{space}Manipulator Subspaceof a manipulator?Giving an expression for a manipulator’s wrist frame {w}to be free to take on all possible values.Manipulator SubspaceThe subspace of is given by:233R planar manipulatorAs are allowed to take on arbitrary values, the subspace is generatedNOTE : Link lengths and joints limits restrict the workspace of the manipulator to be a subset of this subspace.Algebraic solution by reduction to polynomial Outline24Algebraic vs. GeometricGiven the transformation matrix, solved for25Algebraic vs. GeometricD-H TableAlgebraic vs. GeometricThe transformation matrix can be computed viaand we haveAlgebraic vs. GeometricSpecification of the goal points can be accomplished by specifying three parameters: ..The transformation is assumed to have the following structurewhereThe above four nonlinear equations are used to solve for (unknown)Algebraic vs. GeometricThe parameters is How to solve for according thefollowing equations:Algebraic vs. Geometric1.Algebraic solution 30The is the only unknown parameter.Algebraic vs. GeometricStep1.In the solution algorithm, the above constraintshould be checked to determine whether a solution exist or not. If the constrain is not Algebraic vs. Geometric1.Algebraic solution Here, the choice of signs in the solution of corresponds to Algebraic vs. Geometric33Based on the solution of , we can get:whereAlgebraic vs. Geometricwe haveAlgebraic vs. GeometricNote:If a choice of sign is made in the solution of ,it will affect and thus affectStep5. Based on the fact that The solution of can be obtained.Algebraic vs. Geometric36solved for by using the tools of plane geometry.can utilize plane geometry directly to find a solution.Algebraic vs. Geometricconsidering the solid triangle, the “” can be applied to solve for as:37PossibleconfigurationThe other possible solution can be obtained by settingAlgebraic vs. Geometric2. Geometric solutionTo solve for , we find the express for angleand .38and can be solved via:then can be solved as:Algebraic vs. Geometric39the solution of can Algebraic solution by reduction to polynomial Outline40Algebraic solution by reduction to polynomialexpression in terms of a single variable.This is a very important geometric substitution used often in solving kinematic equations. These substitution convert transcendental equations into polynomial equations in Algebraic solution by reduction to polynomialGiven a transcendental equation try to solve for42Solutions:(when )Algebraic solution by reduction to polynomial Outline43Inverse manipulator kinematicsThe Unimation Puma 560 Industry Robot44Inverse manipulator kinematicsReview : D-H table45Inverse manipulator kinematicsReview : Transformation of each link.46Inverse manipulator kinematicsReview : Transformation of all link47whereInverse manipulator kinematics: Given the goal point and orientation specified by:(Known: Numerical value)Solve forInverse manipulator kinematics Separating out 1 unknown parameter How to solve ?Inverse manipulator kinematics2. Inverting to be obtain50 whereInverse manipulator kinematicsCheck the (2,4) elements on both sides ,we have Inverse manipulator kinematicsIntroduce the trigonometric(三角恒等变换) substitutions:52whereThen it can be obtained that:Inverse manipulator kinematics3. The left side of the following equation is known53Inverse manipulator kinematicsTaking square of the above two equations, and adding the results together, it can be obtained thatInverse manipulator kinematicsThe above equation depends only on , then similar steps can be followed to solve for as:4. Consider the following equationhave been solved, but is unknownInverse manipulator kinematics56Eq.(3.11) in Chapter3Check elements (1,4) and (2,4) on both sides, we haveInverse manipulator kinematics 57Inverse manipulator kinematics585. Now the left side of the following equation is knownEq.(3.11) in Chapter3Check the elements (1,3) and (3,3), it can be obtained thatInverse manipulator kinematics ca can be solved as:Case2.,The manipulator is in a singular configurationas axis 4 and 6 line up and cause the same motion of the last link of the robot. Thus is chosen arbitrarily.Inverse manipulator kinematics606. Consider the following equation again:andCheck the elements (1,3) and (3,3), it can be obtained thatInverse manipulator kinematics 61Hence, we can solve for as7. Applying the same method one more time, we havewhereCheck the elements (3,1) and (1,1), it can be obtained thatInverse manipulator kinematics62Thus we can solve for aswe can obtain eight sets of possible solutions, some of them will be discarded due to the joint angle limitsInverse manipulator kinematics63Summary1、原则：等号两端的矩阵中对应元素相等，列出相关方）、从含变量少的左边开始，如，向右递推，直到）、选择等号左边或右边矩阵中等于常数或仅含有一个变量的元素，列出相应元素对应的方程或方程组。
一、课程基本情况介绍《机器人学导论》是由计算机科学技术学院开设的一门研究生课程。
课程负责人是计算机科学技术学院研究员、博士生导师，智能机器人研究院副院长，市智能信息重点实验室副主任，少年科学院首席顾问。
先后主持国家自然科学基金、科技创新2030“新一代人工智能”重大项目、市科委重大专项等20余项科研项目。
在机器人、人工智能、智能装备等方面进行了系统深入的研究，发表学术论文150余篇（包括CVPR、ICCV、NeurIPS、AAAI、TIP等顶级期刊/会议论文50余篇），申请发明专利50余项。
自2004年入职以来，先后开设了《大学物理》、《机器人学》、《工程伦理》等本科生和研究生课程，并创新性地将人工智能技术和产业发展等思政元素融入到教学实践中，教学和科研成果获得了2021年市计算机学会教学成果一等奖、2018年罗马尼亚科学院奖、2017年中国国际工业博览会特等奖、2016年教育部技术发明二等奖等。
他始终坚持“培养学生是我们的本分”，以潜心治学来要求自己，也影响学生。
坚守做科研要甘守寂寞、淡泊名利、持之以恒，做“纯粹”的学问。
二、课程思政教学开展情况介绍党的十八大以来，面对新一轮科技革命和产业变革形势，党中央和国务院审时度势，发布和实施了《新一代人工智能发展规划》，制定和实施了人工智能发展国家战略。
作为人工智能重要载体的机器人，被誉为“制造业皇冠顶端的明珠”，是衡量一个国家创新能力和产业竞争力的重要标志，已成为全球新一轮科技和产业革命的重要切入点。
经过多年的持续积累，我国在人工智能和机器人领域取得重要进展，部分领域关键技术实现重要突破。
但我国机器人整体发展水平与发达国家相比仍存在差距，缺少重大原创成果，在基础理论、核心算法以及关键元器件等方面尚存在差距，机器人领域的尖端人才远远不能满足需求。
如何深入挖掘机器人学导论课程蕴含的思想政治教育资源，引导广大学生爱国和爱党、爱社会主义高度统一，将爱国热情与报国行动有机结合，成为该课程思政改革的指导思想。
机器人学导论第4章操作臂逆运动学机器人学导论第4章操作臂逆运动学主要内容是探讨机器人操作臂的逆运动学问题。
逆运动学是指在已知末端点的位置和姿态的情况下，求解机器人各个关节的角度。
在机器人操作中，逆运动学是非常重要的，因为它能够帮助我们确定机器人应该如何运动来达到所需的目标位置和姿态。
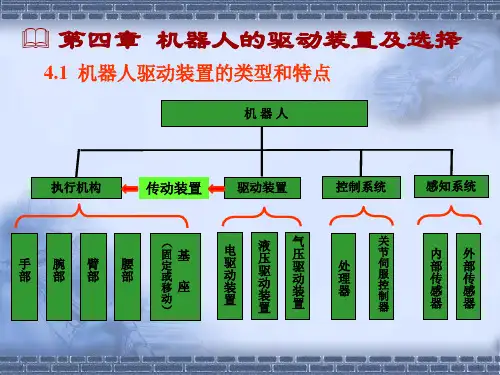
在本章中，首先介绍了机器人操作臂的结构和坐标系的选择。
机器人操作臂通常由多个关节组成，每个关节可以旋转或者移动。
不同的坐标系选择会对逆运动学的求解产生影响，因此在选择坐标系时需要仔细考虑。
接下来，本章介绍了机器人操作臂逆运动学的求解方法。
逆运动学的求解通常需要解决一系列非线性方程组，因此有多种方法可以用来求解逆运动学问题。
其中包括解析法和数值法。
解析法是通过解析求解方程组来得到逆运动学解的方法，它的优点是计算速度快，但是只适用于简单的机器人结构。
数值法则是通过迭代计算的方法来逼近逆运动学解，它的优点是适用范围广，但是计算速度较慢。
在解析法中，本章介绍了两种常见的求解方法，分别是几何法和代数法。
几何法通过几何关系来求解逆运动学，它的思想是将机器人操作臂的各个关节看作一个几何图形，通过解几何问题来求解逆运动学。
代数法则是通过建立机器人操作臂的关系方程组来求解逆运动学，它的优点是可以求解更复杂的机器人结构。
在数值法中，本章介绍了两种常见的数值方法，分别是迭代法和优化法。
迭代法通过不断重复迭代来逼近逆运动学解，它的思想是通过不断调整关节的角度来使得末端点的位置和姿态逐步趋向于目标值。
优化法则是通过建立逆运动学问题的优化模型来求解逆运动学解，它的优点是可以考虑更多的约束条件和目标函数。
最后，本章还介绍了一些逆运动学问题的特殊情况，比如奇异位置和工作空间。
奇异位置是指在一些位置上，机器人操作臂的自由度降低，这会导致逆运动学问题无解或者存在无穷多解。
工作空间是指机器人操作臂能够到达的所有位置和姿态构成的空间，工作空间的大小和形状对逆运动学的求解也会产生影响。
