对数函数及其性质同步练习1

对数函数及其性质（第三课时）1、若log a 2＜1，则实数a 的取值范围是( )A ．(1,2)B ．(0,1)∪(2，＋∞)C ．(0,1)∪(1,2)D ．(0，12)2、若log a 2<log b 2<0，则下列结论正确的是( )A ．0<a<b<1B ．0<b<a<1C ．a>b>1D ．b>a>13、已知函数f(x)＝2log 12x 的值域为[－1,1]，则函数f(x)的定义域是( )A ．[22，2]B ．[－1,1]C ．[12，2] D ．(－∞，22]∪[2，＋∞)4、若函数f(x)＝a x ＋log a (x ＋1)在[0,1]上的最大值和最小值之和为a ，则a 的值为() A.14 B.12 C ．2 D ．45、函数f(x)＝log a [(a －1)x ＋1]在定义域上( )A ．是增函数B ．是减函数C ．先增后减D ．先减后增6、设a ＝lge ，b ＝(lg e)2，c ＝lg e ，则( )A ．a>b>cB ．a>c>bC ．c>a>bD ．c>b>a7、已知0＜a ＜1,0＜b ＜1，如果a logb(x －3)＜1，则x 的取值范围是________．8、f(x)＝log 21＋x a －x 的图象关于原点对称，则实数a 的值为________．9、函数y ＝log a x 在[2，＋∞)上恒有|y|＞1，则a 取值范围是________．10、已知f(x)＝⎩⎨⎧6－a x －4a x<1log a x x≥1是R 上的增函数，求a 的取值范围．11、解下列不等式．(1)log 2(2x ＋3)＞log 2(5x －6)；(2)log x 12＞1.12、函数f(x)＝log 12(3x 2－ax ＋5)在[－1，＋∞)上是减函数，求实数a 的取值范围．13、求下列函数的反函数：（1）y=0.2－x +1；（2）y=log a （4－x ）.14、 已知函数y=log a （1－a x ）（a ＞0，a ≠1）.（1）求函数的定义域与值域；（2）求函数的单调区间；（3）证明函数图象关于y=x 对称.15、 已知函数f （x ）=（21）x （x ＞0）和定义在R 上的奇函数g （x ）.当x ＞0时，g （x ）=f （x ），试求g （x ）的反函数.16、 探究函数y=log 3（x+2）的图象与函数y=log 3x 的图象间的关系.17、函数log (1)a y x =-(01)a a >≠且的反函数的图象经过点（1，4），求a 的值.18、 求函数y = log 4 (7 + 6 x – x 2)的单调区间和值域.。

2.2.2　对数函数及其性质课后篇巩固提升基础巩固1.y=2x与y=log2x的图象关于( )A.x轴对称B.直线y=x对称C.原点对称D.y轴对称y=2x与y=log2x互为反函数,故函数图象关于直线y=x对称.2.函数y=ln(1-x)的图象大致为( )(-∞,1),且函数在定义域上单调递减,故选C.3.已知函数y=log a(x+c)(a,c为常数,且a>0,a≠1)的图象如图所示,则下列结论成立的是( )A.a>1,c>1B.a>1,0<c<1C.0<a<1,c>1D.0<a<1,0<c<1y=log a (x+c )的图象是由y=log a x 的图象向左平移c 个单位长度得到的,结合题图知0<c<1.根据单调性易知0<a<1.4.已知a>0且a ≠1,函数y=log a x ,y=a x ,y=x+a 在同一坐标系中的图象可能是( )函数y=a x 与y=log a x 的图象关于直线y=x 对称,再由函数y=a x 的图象过(0,1),y=log a x 的图象过(1,0),观察图象知,只有C 正确.5.已知a=,b=log 2,c=lo ,则( )2-1313g 1213A.a>b>cB.a>c>bC.c>b>aD.c>a>b0<a=<20=1,b=log 2<log 21=0,c=lo >lo =1,∴c>a>b.故选D .2-1313g 1213g 12126.若对数函数f (x )的图象经过点P (8,3),则f = .(12)f (x )=log a x (a>0,a ≠1),则log a 8=3,∴a 3=8,∴a=2.∴f (x )=log 2x ,故f =log 2=-1.(12)1217.将y=2x 的图象先 ,再作关于直线y=x 对称的图象,可得到函数y=log 2(x+1)的图象( )A.先向上平移一个单位长度B.先向右平移一个单位长度C.先向左平移一个单位长度D.先向下平移一个单位长度,可求出解析式或利用几何图形直观推断.8.已知函数f (x )=直线y=a 与函数f (x )的图象恒有两个不同的交点,则a 的取值范围{log 2x ,x >0,3x ,x ≤0,是 .f (x )的图象如图所示,要使直线y=a 与f (x )的图象有两个不同的交点,则0<a ≤1.9.作出函数y=|log 2x|+2的图象,并根据图象写出函数的单调区间及值域.y=log 2x 的图象,如图甲.再将y=log 2x 在x 轴下方的图象关于x 轴对称翻折到x 轴上方(原来在x 轴上方的图象不变),得函数y=|log 2x|的图象,如图乙;然后将y=|log 2x|的图象向上平移2个单位长度,得函数y=|log 2x|+2的图象,如图丙.由图丙得函数y=|log 2x|+2的单调递增区间是[1,+∞),单调递减区间是(0,1),值域是[2,+∞).10.已知对数函数y=f(x)的图象经过点P(9,2).(1)求y=f(x)的解析式;(2)若x∈(0,1),求f(x)的取值范围.(3)若函数y=g(x)的图象与函数y=f(x)的图象关于x轴对称,求y=g(x)的解析式.设f(x)=log a x(a>0,且a≠1).由题意,f(9)=log a9=2,故a2=9,解得a=3或a=-3.又因为a>0,所以a=3.故f(x)=log3x.(2)因为3>1,所以当x∈(0,1)时,f(x)<0,即f(x)的取值范围为(-∞,0).g1(3)因为函数y=g(x)的图象与函数y=log3x的图象关于x轴对称,所以g(x)=lo x.3能力提升1.函数y=log a(x+2)+1(a>0,且a≠1)的图象过定点( )A.(1,2)B.(2,1)C.(-2,1)D.(-1,1)x+2=1,得x=-1,此时y=1.2.若函数f (x )=log 2x 的反函数为y=g (x ),且g (a )=,则a=( )14A.2 B.-2 C. D.-1212,得g (x )=2x .∵g (a )=,∴2a =,∴a=-2.14143.若函数f (x )=log 2(x 2-ax-3a )在区间(-∞,-2]上是减函数,则实数a 的取值范围是( )A.(-∞,4)B.(-4,4]C.(-∞,4)∪[2,+∞)D.[-4,4)t (x )=x 2-ax-3a ,则由函数f (x )=log 2t 在区间(-∞,-2]上是减函数,可得函数t (x )在区间(-∞,-2]上是减函数,且t (-2)>0,所以有-4≤a<4,故选D .4.已知函数f (x )=a x +log a (x+1)在[0,1]上的最大值与最小值之和为a ,则a 的值等于( )A. B.2 C.3D.1213y=a x 与y=log a (x+1)在[0,1]上的单调性相同,所以f (x )在[0,1]上的最大值与最小值之和为f (0)+f (1)=(a 0+log a 1)+(a 1+log a 2)=a ,整理得1+a+log a 2=a ,即log a 2=-1,解得a=.故选A .125.已知a=log 23.6,b=log 43.2,c=log 43.6,则a ,b ,c 的大小关系为 .a==2log 43.6=log 43.62,又函数y=log 4x 在区间(0,+∞)上是增函数,3.62>3.6>3.2,log 43.6log 42∴log 43.62>log 43.6>log 43.2,∴a>c>b.6.已知a>0且a ≠1,则函数y=a x 与y=log a (-x )在同一直角坐标系中的图象只能是下图中的 (填序号).方法一)首先,曲线y=a x 位于x 轴上方,y=log a (-x )位于y 轴左侧,从而排除①③.其次,从单调性考虑,y=a x 与y=log a (-x )的增减性正好相反,又可排除④.故只有②满足条件.(方法二)若0<a<1,则曲线y=a x 下降且过点(0,1),而曲线y=log a (-x )上升且过点(-1,0),所有选项均不符合这些条件.若a>1,则曲线y=a x 上升且过点(0,1),而曲线y=log a (-x )下降且过点(-1,0),只有②满足条件.(方法三)如果注意到y=log a (-x )的图象关于y 轴的对称图象为y=log a x 的图象,又y=log a x 与y=a x 互为反函数(两者图象关于直线y=x 对称),则可直接选②.7.已知函数f (x )是定义在R 上的奇函数,若当x ∈(0,+∞)时,f (x )=lg x ,则满足f (x )>0的x 的取值范围是 .f (x )的解析式为f (x )=其图象如右图所示.{lg x ,x >0,0,x =0,-lg (-x ),x <0,由函数图象可得不等式f (x )>0时,x 的取值范围为(-1,0)∪(1,+∞).-1,0)∪(1,+∞)8.设函数f (x )=ln(ax 2+2x+a )的定义域为M.(1)若1∉M ,2∈M ,求实数a 的取值范围;(2)若M=R ,求实数a 的取值范围.由题意M={x|ax 2+2x+a>0}.由1∉M ,2∈M 可得{a ×12+2×1+a ≤0,a ×22+2×2+a >0,化简得解得-<a ≤-1.{2a +2≤0,5a +4>0,45所以a 的取值范围为.(-45,-1](2)由M=R 可得ax 2+2x+a>0恒成立.当a=0时,不等式可化为2x>0,解得x>0,显然不合题意;当a ≠0时,由二次函数的图象可知Δ=22-4×a×a<0,且a>0,即化简得解得a>1.{4-4a 2<0,a >0,{a 2>1,a >0,所以a 的取值范围为(1,+∞).9.已知函数f (x )=log 2(a 为常数)是奇函数.1+ax x -1(1)求a 的值与函数f (x )的定义域;(2)若当x ∈(1,+∞)时,f (x )+log 2(x-1)>m 恒成立,求实数m 的取值范围.∵函数f (x )=log 2是奇函数,1+axx -1∴f (-x )=-f (x ).∴log 2=-log 2.1-ax -x -11+ax x -1即log 2=log 2,∴a=1.ax -1x +1x -11+ax 令>0,解得x<-1或x>1.1+x x -1所以函数的定义域为{x|x<-1或x>1}.(2)f (x )+log 2(x-1)=log 2(1+x ),当x>1时,x+1>2,∴log 2(1+x )>log 22=1.∵x ∈(1,+∞),f (x )+log 2(x-1)>m 恒成立,∴m ≤1.故m 的取值范围是(-∞,1].。

5.3对数函数的图像和性质课时过关·能力提升1.若log3a<0则A.a>1,b>0B.0<a<1,b>0C.a>1,b<0D.0<a<1,b<0解析:由函数y=log3x,y的图像(图略)知,0<a<1,b<0.答案:D2.已知a=log23+则的大小关系是A.a=b<cB.a=b>cC.a<b<cD.a>b>c解析:a=log23+因此a=b.而log2所以a=b>c,故选B.答案:B3.已知函数f(x)=ln x,g(x)=lg x,h(x)=log3x,直线y=a(a>0)与这三个函数图像的交点的横坐标分别为x1,x2,x3,则x1,x2,x3的大小关系是()A.x2<x3<x1B.x1<x3<x2C.x2<x1<x3D.x3<x1<x2解析:根据对数函数的图像与性质,可知当底数大于1时,在x轴上方,底数越大,函数图像越靠近x轴,分别作出f(x),g(x),h(x)的大致图像,如图所示.由图可知直线y=a(a>0)与f(x),g(x),h(x)的图像交点的横坐标x1,x2,x3的大小关系是x1<x3<x2,故选B.答案:B4.已知f(x)-是R上的减函数,则a的取值范围是()A.(0,1) B解析:∵由题意知f(x)=log a x(x≥1)是减少的, ∴0<a<1,且f(1)=0.又由题意知f(x)=(3a-1)x+4a(x<1)是减少的, ∴3a-1<0.∴a又f(x)-在(-∞,+∞)上是减函数,∴(3a-1)×1+4a≥0.∴a≥∴a∈答案:C5.已知y=log a(2-ax)在[0,1]上是关于x的减函数,则a的取值范围是()A.(0,1)B.(1,2)C.(0,2)D.[2,+∞)解析:令u=2-ax,∵a>0,且a≠1,∴u=2-ax在[0,1]上是关于x的减函数.又y=log a(2-ax)在[0,1]上是关于x的减函数,∴函数y=log a u是关于u的增函数,且对x∈[0,1]时,u=2-ax恒为正数.∴a>1,且x∈[0,1]时,u min=2-a>0.∴1<a<2.答案:B6.对任意实数a,b,定义运算“*”如下:a*b则函数的值域为A.[0,+∞)B.(-∞,0]C解析:在同一平面直角坐标系中分别画出y=l和y=log2x这两个函数的图像,如图所示.由图可得f(x)-的值域为(-∞,0].答案:B7.若函数f(x)-且则实数的取值范围是A.(-1,0)∪(0,1)B.(-∞,-1)∪(1,+∞)C.(-1,0)∪(1,+∞)D.(-∞,-1)∪(0,1)解析:由分段函数的表达式知,需要对a的正负进行分类讨论.由f(a)>f(-a),得或--即或解得a>1或-1<a<0.答案:C8.已知函数f(x)=|lg x|.若0<a<b,且f(a)=f(b),则a+b的取值范围是()A.(1,+∞)B.[1,+∞)C.(2,+∞)D.[2,+∞)解析:作出函数f(x)=|lg x|的图像,如图.由图可知0<a<1<b,则-lg a=lg b,从而lg ab=0,ab=1,即a设g(a)=a+b=a由于0<a<1,则g(a)在(0,1)上是减少的,于是g(a)>g(1)=2.答案:C9.函数y=log3(x2-2x)的递减区间是.解析:令u=x2-2x(x>2或x<0),则y=log3u,且y=log3u是增函数,u=x2-2x(x>2或x<0)的递减区间是(-∞,0),故y=log3(x2-2x)的递减区间是(-∞,0).答案:(-∞,0)10.已知a>0,a≠1,指数函数y当∈(0,+∞)时,有y>1,解关于x的不等式log a(x-1)≤log a(x2+x-6).解:∵y在x∈(0,+∞)时,有y>1,故0<a<1.于是由log a(x-1)≤log a(x2+x-6),得---解得2<x≤故原不等式的解集为{x|2<x≤11.★已知实数x满足4x-10·2x+16≤0,求函数y=(log3x)2-log的值域解:不等式4x-10·2x+16≤0可化为(2x)2-10·2x+16≤0,即(2x-2)(2x-8)≤0.从而有2≤2x≤8,即1≤x≤3.所以0≤log3x≤1.因为函数y=(log3x)2-log可化为y=(log3x)2-所以所求函数的值域为12.★已知函数f(x)=log a(ax2-x),是否存在实数a,使它在区间[2,4]上是增加的?如果存在,说明a可取哪些值;如果不存在,说明理由.解:存在实数a满足题意.设g(x)=ax2-x.当a>1时,为使函数y=f(x)=log a(ax2-x)在区间[2,4]上是增加的,只需g(x)=ax2-x在区间[2,4]上是增加的,故应满足-解得a所以a>1.当0<a<1时,为使函数y=f(x)=log a(ax2-x)在区间[2,4]上是增加的,只需g(x)=ax2-x在区间[2,4]上是减少的.故-无解,此时a不存在.综上,当a>1时,函数f(x)=log a(ax2-x)在区间[2,4]上是增加的.。

4.4.2 对数函数的图象和性质刷新题夯基础题组一 对数(型)函数的图象1.(2020山西康杰中学高一上期中)为了得到函数f (x )=log 2x 的图象,只需将函数g (x )=log 2x8的图象( )A.向上平移3个单位长度B.向下平移3个单位长度C.向左平移3个单位长度D.向右平移3个单位长度2.在同一平面直角坐标系中,y =2x 与y =log 2(-x )的图象可能是( )3.(2020河南省实验中学高一上期中)函数f (x )=lg(|x |-1)的大致图象是( )题组二 对数函数的性质及其应用4.(2020天津红桥高一上期末)函数f (x )=log a (x -1)+2(a >0,a ≠1)的图象恒过定点 ( )A.(2,2)B.(2,3)C.(1,0)D.(2,1)5.(2021河北石家庄正定一中高一上期中)函数f (x )=√1-lnx 的定义域是 ( ) A.(0,e)B.(0,e]C.[e,+∞)D.(e,+∞)6.已知a =log 23-1,(12)b=5,c =log 32,则a ,b ,c 的大小关系为( )A.c <b <aB.b <a <cC.a <c <bD.a <b <c7.(2020北京平谷高一上期末)已知a ,b ∈R,那么“3a <3b ”是“lo g 13a >lo g 13b ”的 ( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件8.(2020四川成都外国语学校高一上期中)函数f(x)=lo g1(x2-2x-3)的单调递增区间2是.9.(2020湖南醴陵一中高一上期中)若log0.5(m-1)>log0.5(3-m),则m的取值范围是.10.函数f(x)=log a(x+√x2+2a2)是奇函数,则a=.11.已知函数f(x)=lg(x+1),解不等式0<f(1-2x)-f(x)<1.),其中0<a<1.12.设函数f(x)=log a(1-ax(1)证明:f(x)是(a,+∞)上的减函数;(2)若f(x)>1,求x的取值范围..13.已知函数f(x)=log21-x1+x(1)求函数f(x)的定义域;(2)讨论函数f(x)的奇偶性;(3)证明:函数f(x)在定义域上单调递减.题组三 对数函数的最大(小)值与值域问题14.(2020广东东莞高一上期末)下列函数中,与函数f (x )=x +1(x ∈R)的值域不相同的是( ) A.y =x (x ∈R)B.y =x 3(x ∈R)C.y =ln x (x >0)D.y =e x (x ∈R)15.(2021河北石家庄正定一中高一上期中)函数f (x )=log 2(x 2-2x +3)的值域为 ( )A.[0,+∞)B.[1,+∞)C.RD.[2,+∞)16.(2020北京通州高一上期末)已知函数f (x )=log a x (a >0,且a ≠1)在[1,4]上的最大值与最小值的和是2,则a 的值为 .17.(2020天津河东高一上期末)已知x 满足√3≤3x ≤9. (1)求x 的取值范围;(2)求函数y =(log 2x -1)(log 2x +3)的值域.18.已知函数f (x )=log 2x.(1)若f (a )>f (2),求a 的取值范围; (2)求y =log 2(2x -1)在[2,14]上的最值.题组四 反函数19.(2020北京西城高一上阶段测试)函数y =(1a )x与y =log b x 互为反函数,则a 与b 的关系是( )A.ab =1B.a +b =1C.a =bD.a -b =120.函数y =a x (a >0,且a ≠1)的反函数的图象过点(√a ,a ),则a 的值为 ( ) A.2 B.12 C.2或12 D.321.若函数y=f(x)是函数y=3x的反函数,则f(12)的值为.刷新题培素养题组一对数函数的图象1.(2020北京石景山高一上期末,)在同一平面直角坐标系中,函数f(x)=x a(x≥0),g(x)=log a x 的图象可能是()2.(2020河北承德高一上期末,)已知函数f(x)=a x-1+log b x-1(a>0且a≠1,b>0且b≠1),则f(x)的图象过定点()A.(0,1)B.(1,1)C.(1,0)D.(0,0)3.(2020河北唐山一中高一上期中,)函数y=xln|x||x|的图象是()题组二对数函数单调性的应用4.(2020河南信阳高级中学高一上期中,)已知函数f(x)=log a(-x2-2x+3)(a>0,a≠1),若f(0)<0,则此函数的单调递减区间是()A.(-∞,-1]B.[-1,+∞)C.[-1,1)D.(-3,-1]5.(2020福建厦门外国语学校高一上期中,)已知函数f(x)=log3(1-ax),若f(x)在(-∞,2]上为减函数,则实数a的取值范围为()A.(0,+∞)B.(0,12) C.(1,2) D.(-∞,0)6.(多选)()若a>b>0,0<c<1,则()A.log c a<log c bB.c a>c bC.a c>b cD.log c(a+b)>07.(2020山东青岛二中高一上期末,)已知函数f(x)的定义域为R,图象恒过点(1,1),对任意x 1<x2,都有f(x1)-f(x2)x1-x2>-1,则不等式f[log2(2x-1)]<2-log2(2x-1)的解集为 ()A.(0,+∞)B.(log23,+∞)C.(-∞,0)∪(0,log23) D.(0,log23)8.(2020浙江浙北G2高一上期中联考,)已知函数f (x )=|lg x |+2,若实数a ,b 满足b >a >0,且f (a )=f (b ),则a +2b 的取值范围是 . 9.()已知函数f (x )={log a x +m ,0<x <1,-x +2,x ≥1(a >0,a ≠1)在定义域内单调递减,若|f (2m )|>f (a ),求实数m 的取值范围.10.(2020安徽淮北第一中学高一月考,)已知函数f (x )=log a (a x -1)(a >0,且a ≠1).(1)当a =12时,求函数f (x )的定义域;(2)当a >1时,求关于x 的不等式f (x )<f (1)的解集;(3)当a =2时,若不等式f (x )-log 2(1+2x )>m 对任意实数x ∈[1,3]恒成立,求实数m 的取值范围.题组三 对数函数的最大(小)值与值域问题 11.(2020山东泰安高一上期末,)若函数f (x )={2x +2,x ≤1,log 2(x -1),x >1在(-∞,a ]上的最大值为4,则a 的取值范围为 ( ) A.[0,17] B.(-∞,17] C.[1,17] D.[1,+∞)12.()若函数f (x )=log 2[kx 2+(2k -1)x +14]的值域为R,则实数k 的取值范围为 .13.(2020河南周口高一上期末调研,)若函数f (x )={(2-a )x +2a ,x <1,1+lnx ,x ≥1的值域为R,则实数a的取值范围是 . 14.(2020安徽屯溪一中高一上期中,)已知函数f (x )=(13)x,函数g (x )=log 3x.(1)若g (mx 2+2x +m )的定义域为R,求实数m 的取值范围;(2)当x ∈[-1,1]时,求函数y =[f (x )]2-2af (x )+3的最小值h (a );(3)是否存在实数m ,n ,使得函数y =2x +log 3 f (x 2)的定义域为[m ,n ],值域为[4m ,4n ]?若存在,求出m ,n 的值;若不存在,请说明理由.题组四 对数函数的综合运用 15.()已知函数f (x )=ln(x +√x 2+1)+1,若实数a 满足f (-a )=2,则f (a )等于 ( )A.1B.0C.-1D.-216.(2020山东济南高一上期末,)已知函数f (x )=log 32-x2+x ,若f (a )+f (a -1)>0,则实数a 的取值范围是 ( )A.(-∞,12)B.(-1,12) C.(-2,2) D.(-1,2) 17.(多选)(2020山东泰安高一上期末,) 若定义域为[0,1]的函数f (x )同时满足以下三个条件:(i)对任意的x ∈[0,1],总有f (x )≥0; (ii)f (1)=1;(iii)若x 1≥0,x 2≥0,x 1+x 2≤1,则有f (x 1+x 2)≥f (x 1)+f (x 2),就称f (x )为“A 函数”.下列定义在[0,1]上的函数中,是“A 函数”的有 ( ) A.f (x )=lo g 12(x +1) B.f (x )=log 2(x +1) C.f (x )=x D.f (x )=2x -118.(2020山东烟台高一上期末,)已知函数f (x )=ln kx -1x+1为奇函数.(1)求实数k 的值;(2)判断并证明函数f (x )的单调性;(3)若存在α,β∈(1,+∞),使得函数f (x )在区间[α,β]上的值域为[ln (mα-m2),ln (mβ-m2)],求实数m 的取值范围.答案全解全析刷新题夯基础1.A g (x )=log 2x8=log 2x -log 28=log 2x -3,所以只需将函数g (x ) =log 2x8的图象向上平移3个单位长度,即可得到函数f (x )=log 2x 的图象,故选A .2.B 因为y =2x 的图象为过点(0,1)的递增的指数函数图象,故排除选项C,D;y =log 2(-x )的图象为过点(-1,0)的递减的对数型函数图象,故排除选项A,故选B .解题模板 函数图象的辨识可从以下方面入手:根据函数的定义域,判断图象的左右位置,根据函数的值域,判断图象的上下位置;根据函数的单调性,判断图象的变化趋势;根据函数的奇偶性,判断图象的对称性;根据函数的特征点,排除不符合要求的图象.3.B 解法一:由题可知,当x >0时, f (x )=lg(x -1),其图象可由函数y =lg x 的图象向右平移1个单位得到;当x <0时, f (x )=lg(-x -1)=lg[-(x +1)],其图象可由函数y =lg x 的图象先关于y 轴做翻折变换,再向左平移1个单位得到,结合选项可知B 正确.故选B .解法二:易知f (x )的定义域为(-∞,-1)∪(1,+∞),又f (-x )=lg(|-x |-1)=lg(|x |-1)=f (x ),所以f (x )是偶函数,因此C,D 错误.当x >0时, f (x )=lg(x -1),是(1,+∞)上的增函数,故选B .4.A 由对数函数的性质可知,当x =2时, f (2)=2,故函数f (x )=log a (x -1)+2(a >0,a ≠1)的图象恒过定点(2,2).故选A .5.B 要使函数f (x )=√1-lnx 有意义,需满足{1-lnx ≥0,x >0,解得0<x ≤e .因此函数的定义域为(0,e],故选B .6.B 由(12)b=5,得b =lo g 125=-log 25,又a =log 23-1=-log 23,所以-log 25<-log 23<0<log 32,即b <a <c ,故选B .7.B 由3a<3b⇒a <b ,因为a ,b 的正负不明确,所以“3a<3b”不一定能推出“lo g 13a >lo g 13b ”;由lo g 13a >lo g 13b ⇒0<a <b ⇒3a <3b ,所以“3a <3b ”是“lo g 13a >lo g 13b ”的必要不充分条件.故选B .8.答案 (-∞,-1)解析 由x 2-2x -3>0,得x <-1或x >3,因此函数f (x )的定义域为(-∞,-1)∪(3,+∞),记为D.设u =x 2-2x -3,则y =lo g 12u ,易知y =lo g 12u 是定义域内的减函数,又u =(x -1)2-4在(-∞,1]上单调递减,在[1,+∞)上单调递增, ∴f (x )的单调递增区间为(-∞,1]∩D =(-∞,-1). 9.答案 (1,2)解析 ∵y =log 0.5x 是定义域内的减函数,∴log 0.5(m -1)>log 0.5(3-m )⇔{m -1>0,3-m >0,m -1<3-m ,即{m >1,m <3,m <2,∴1<m <2,即m 的取值范围是(1,2). 10.答案√22解析 ∵函数f (x )的定义域为R,且为奇函数,∴f (0)=0,即log a √2a 2=0, ∴√2a 2=1,又a >0,∴a =√22. 经验证,当a =√22时, f (x )为奇函数. 11.解析 不等式0<f (1-2x )-f (x )<1, 即0<lg(2-2x )-lg(x +1)=lg 2-2xx+1<1. 由{2-2x >0,x +1>0得-1<x <1. 由0<lg 2-2xx+1<1,得1<2-2xx+1<10.因为x +1>0,所以x +1<2-2x <10x +10,解得-23<x <13. 由{-1<x <1,-23<x <13得-23<x <13,故不等式的解集为(-23,13). 12.解析 (1)证明:任取x 1,x 2∈(a ,+∞),不妨令0<a <x 1<x 2,g (x )=1-ax ,则g (x 1)-g (x 2)=(1-a x 1)-(1-ax 2)=a (x 1-x 2)x 1x 2<0,∴g (x 1)<g (x 2).又∵0<a <1,∴f (x 1)>f (x 2), ∴f (x )是(a ,+∞)上的减函数. (2)∵log a (1-ax )>1,且0<a <1, ∴0<1-ax <a ,∴1-a <a x <1.∵0<a <1,∴1-a >0,从而a <x <a1-a .∴x的取值范围是(a,a1-a).13.解析(1)要使函数f(x)=log21-x1+x 有意义,需满足1-x1+x>0,解得-1<x<1,即函数的定义域为(-1,1).(2)函数f(x)为奇函数.证明:函数f(x)的定义域为(-1,1),任取x∈(-1,1),都有f(-x)=log21+x1-x =-log21-x1+x=-f(x),则函数f(x)为奇函数.(3)证明:由(1)可知, f(x)的定义域为(-1,1), 任取x1,x2∈(-1,1),不妨设-1<x1<x2<1,则f(x1)-f(x2)=log21-x11+x1-log21-x21+x2=log2(1-x11+x1×1+x21-x2)=log21+x2-x1-x1x21-(x2-x1)-x1x2,又x1<x2,所以x2-x1>0, 则有1+x2-x1-x1x21-(x2-x1)-x1x2>1,故f(x1)-f(x2)=log21+x2-x1-x1x21-(x2-x1)-x1x2>log21=0,故函数f(x)在定义域上单调递减.14.D易知f(x)的值域为R.A,B,C选项中各函数的值域均为R,不符合题意;选项D中函数的值域为(0,+∞),与f(x)的值域不同,故选D.15.B∵x2-2x+3=(x-1)2+2≥2,∴f(x)=log2(x2-2x+3)≥log22=1,因此,函数f(x)的值域是[1,+∞),故选B.16.答案 2解析①当a>1时, f(x)=log a x在(0,+∞)上为增函数,所以f(x)=log a x在[1,4]上的最大值为log a4,最小值为log a1;②当0<a<1时, f(x)=log a x在(0,+∞)上为减函数,所以f(x)=log a x在[1,4]上的最大值为log a1,最小值为log a4.故有log a1+log a4=2,即log a4=2,所以a =2,故答案为2. 17. 解析 (1) ∵√3≤3x ≤9, ∴312≤3x ≤32,由于指数函数y =3x 在R 上单调递增, ∴12≤x ≤2.因此,x 的取值范围是[12,2].(2)由(1)得12≤x ≤2,∴-1≤log 2x ≤1.令t =log 2x ,则y =(t -1)(t +3)=t 2+2t -3,其中t ∈[-1,1]. ∵函数y =t 2+2t -3的图象开口向上,且对称轴为直线t =-1, ∴函数y =t 2+2t -3在t ∈[-1,1]上单调递增,∴当t =1时,y 取得最大值,为0;当t =-1时,y 取得最小值,为-4. ∴函数y =(log 2x -1)(log 2x +3)的值域为[-4,0]. 18.解析 (1)∵f (x )=log 2x 为增函数,f (a )>f (2), ∴a >2,即a 的取值范围是(2,+∞). (2)∵2≤x ≤14, ∴3≤2x -1≤27,∴log 23≤log 2(2x -1)≤log 227.∴函数f (x )=log 2(2x -1)在[2,14]上的最小值为log 23,最大值为log 227. 19.A 由函数y =(1a )x与y =log b x 互为反函数得1a =b ,化简得ab =1,故选A . 20.B 解法一:函数y =a x (a >0,且a ≠1)的反函数为y =log a x (a >0,且a ≠1), 故y =log a x 的图象过点(√a ,a ),则a =log a √a =12.解法二:∵函数y =a x (a >0,且a ≠1)的反函数的图象过点(√a ,a ),∴函数y =a x (a >0,且a ≠1)的图象过点(a ,√a ),∴a a=√a =a 12,即a =12. 21.答案 -log 32解析 易得y =f (x )=log 3x , ∴f (12)=log 312=-log 32.刷新题培素养1.D选项A中两条曲线都不是函数y=x a(x≥0)的图象;选项B中,y=x a(x≥0)中a>1,y=log a x(x>0)中0<a<1,不符合;选项C中,y=x a(x≥0)中0<a<1,y=log a x(x>0)中a>1,不符合;选项D中,y=x a(x ≥0)中0<a<1,y=log a x(x>0)中0<a<1,符合,故选D.2.C当x=1时, f(x)=f(1)=a0+log b1-1=1+0-1=0,∴f(x)的图象过定点(1,0).故选C.解题模板解决函数图象过定点问题,应从定值入手,如a0=1,log b1=0,由此确定定点.3.B当x>0时,y=xln|x||x|=ln x,排除C,D;当x<0时,y=xln|x||x|=-ln(-x),又y=-ln(-x)与y=ln x的图象关于原点对称,故选B.4.D由f(0)<0得log a3<0,因此0<a<1.由-x2-2x+3>0得x2+2x-3<0,解得-3<x<1.因此函数f(x)的定义域为(-3,1).设u=-x2-2x+3=-(x+1)2+4,∴当x∈(-3,-1]时,u=-x2-2x+3单调递增,当x∈[-1,1)时,u=-x2-2x+3单调递减,而0<a<1,即y=logau单调递减,∴f(x)的单调递减区间为(-3,-1],故选D.5.B设y=log3u,u=1-ax.由f(x)在(-∞,2]上为减函数,且y=log3u是增函数知,u=1-ax是减函数,∴-a<0,即a>0.由1-ax>0得ax<1,又a>0,∴x<1a,即f(x)的定义域为(-∞,1a),∴(-∞,2]⊆(-∞,1a )⇒2<1a,结合a>0,得0<a<12,因此a的取值范围是(0,12),故选B.警示求含对数函数的复合函数的单调性时,既要考虑到内、外两层函数的单调性,还要考虑到函数的定义域,即单调区间是函数定义域的子集,要防止因忽略定义域导致解题错误.6.AC选项A中,因为0<c<1,所以y=log c x为单调递减函数,由a>b>0得log c a<log c b,故A正确; 选项B中,因为0<c<1,所以y=c x为单调递减函数,由a>b>0,得c a<c b,故B错误;选项C中,因为a>b>0,0<c<1,所以(ab )c>1,所以a c>b c,故C正确;选项D 中,取c =12,a +b =2,则log c (a +b )=lo g 122=-1<0,故D 错误.故选AC .7.D 由对任意x 1<x 2,都有f (x 1)-f (x 2)x 1-x 2>-1,可得[f (x 1)+x 1]-[f (x 2)+x 2]x 1-x 2>0,令R (x )=f (x )+x ,则函数R (x )=f (x )+x 在R 上是增函数. 不等式f [log 2(2x -1)]<2-log 2(2x -1), 即f [log 2(2x -1)]+log 2(2x -1)<2=f (1)+1, 即log 2(2x -1)<1,所以0<2x -1<2, 即0<x <log 23, 故选D .解题模板 解决含有未知函数的不等式,往往要构造函数,运用单调性解题,构造函数时要充分考虑题中的条件f (x 1)-f (x 2)x 1-x 2>-1,平时要积累构造函数的经验.8.答案 (3,+∞)解析 f (x )的图象如图所示,因为f (a )=f (b ),所以结合图象可得0<a <1<b ,于是lg a =-lg b ,则b =1a ,所以a +2b =a +2a , 设g (a )=a +2a (0<a <1).因为g (a )在(0,1)上为减函数,所以g (a )>g (1)=3,即a +2a >3,所以a +2b 的取值范围是(3,+∞). 9.解析 由函数f (x )在定义域内单调递减, 可知{0<a <1,log a 1+m ≥1,即{0<a <1,m ≥1.由m ≥1得2m ≥2,故f (2m )=-2m +2, 由0<a <1得f (a )=log a a +m =1+m ,∴|f (2m )|>f (a )⇔|-2m +2|>m +1,又m ≥1, ∴2m -2>m +1,解得m >3, 故m 的取值范围是(3,+∞).10.解析 (1)当a =12时, f (x )=lo g 12(12-1),故12-1>0,解得x <0,故函数f (x )的定义域为(-∞,0).(2)由题意知, f (x )=log a (a x -1)(a >1),其定义域为(0,+∞),易知f (x )为(0,+∞)上的增函数, 由f (x )<f (1)得{x >0,x <1,∴不等式的解集为(0,1).(3)设g (x )=f (x )-log 2(1+2x)=log 22x -12+1,x ∈[1,3],设t =2x -12+1=1-22+1,易知t =1-22+1为增函数,又y =log 2t 为定义域内的增函数,所以g (x )在[1,3]上单调递增,故g (x )min =g (1)=log 213.∵f (x )-log 2(1+2x )>m 对任意实数x ∈[1,3]恒成立, ∴m <g (x )min =log 213, 即m ∈(-∞,log 213).11.C 易知f 1(x )=2x +2在(-∞,1]上单调递增, f 2(x )=log 2(x -1)在(1,+∞)上单调递增.作出f (x )的大致图象,如图所示.由图可知, f (1)=4, f (17)=4,所以a 的取值范围为[1,17]. 12.答案 [0,14]∪[1,+∞)解析 设u =kx 2+(2k -1)x +14的值域为A ,y =log 2u 的定义域为B ,则B =(0,+∞). 当k =0时,u =-x +14,A =R,则A ∩B =(0,+∞),函数f (x )的值域为R,符合题意; 当k ≠0时,依题意得k >0,B ⊆A ,因此(2k -1)2-4×k ×14≥0,解得k ≤14或k ≥1, 此时k 的取值范围是(0,14]∪[1,+∞).综上所述,实数k 的取值范围为[0,14]∪[1,+∞). 13.答案 [-1,2)解析 当x ≥1时,ln x ≥0,从而1+ln x ≥1. 设x <1时,y =(2-a )x +2a 的值域为B ,则(-∞,1)⊆B.因此{2-a >0,(2-a )×1+2a ≥1,解得-1≤a <2.故a 的取值范围是[-1,2).14.解析 (1)由题意知mx 2+2x +m >0对任意实数x 恒成立, 当m =0时显然不满足, ∴{m >0,Δ=22-4m 2<0,∴m >1.∴实数m 的取值范围为(1,+∞). (2)当x ∈[-1,1]时, f (x )∈[13,3]. 令f (x )=t (t ∈[13,3]),则y =t 2-2at +3=(t -a )2+3-a 2,∴h (a )={28-6a 9,a <13,3-a 2,13≤a ≤3,12-6a ,a >3.(3)存在.∵y =2x +log 3 f (x 2)=2x +log 3(13)x2=2x -x 2=-(x -1)2+1≤1,∴4n ≤1, ∴n ≤14,∴函数在[m ,n ]上单调递增, ∴{2m -m 2=4m ,2n -n 2=4n . 又∵m <n ,∴m =-2,n =0.15.B 设g (x )=ln(x +√x 2+1),易知其定义域为R,且g (-x )=ln(-x +√(-x )2+1)=ln √2=-ln(x +√x 2+1)=-g (x ), 所以g (x )为奇函数.因为f (-a )=g (-a )+1=2,所以g (-a )=1,从而g (a )=-1, 所以f (a )=g (a )+1=-1+1=0,故选B .16.B 由题可知f (x )=log 32-x2+x 的定义域满足2-x2+x >0⇒(x -2)(2+x )<0,解得-2<x <2. 又f (x )+f (-x )=log 3(2-x2+x ·2+x 2-x )=log 31=0,故f (x )为奇函数.又f (x )=log 32-x2+x =log 3(-1+42+x ),且y =-1+42+x 在(-2,2)上为减函数,故f (x )为减函数.f (a )+f (a -1)>0,即f (a )>-f (a -1)=f (1-a ), 所以{-2<a <2,-2<a -1<2,a <1-a ,所以a ∈(-1,12).故选B .17.CD 选项A 中, f (1)=lo g 12(1+1)=-1,故f (x )=lo g 12(x +1)不是“A 函数”.选项B 中,若x 1≥0,x 2≥0,x 1+x 2≤1,则f (x 1)+f (x 2)=log 2(x 1+1)+log 2(x 2+1)=log 2(x 1x 2+x 1+x 2+1)≥log 2(x 1+x 2+1)=f (x 1+x 2),不满足(iii),故f (x )=log 2(x +1)不是“A 函数”.选项C 中,f (x )显然满足(i)(ii),又f (x 1+x 2)=x 1+x 2=f (x 1)+f (x 2),所以f (x )=x 是“A 函数”.选项D 中, f (x )显然满足(i)(ii),因为f (x 1+x 2)=2x 1+x 2-1, f (x 1)+f (x 2)=2x 1+2x 2-2,所以f (x 1+x 2)-[f (x 1)+f (x 2)]=2x 1+x 2-2x 1-2x 2+1=(2x 1-1)(2x 2-1),又x 1,x 2∈[0,1],所以2x 1-1≥0,2x 2-1≥0,从而f (x 1+x 2)≥f (x 1)+f (x 2),因此, f (x )=2x -1是“A 函数”.故选CD . 18.解析 (1)因为函数f (x )=ln kx -1x+1为奇函数,所以f (x )+f (-x )=0, 即ln kx -1x+1+ln -kx -1-x+1=ln (kx -1)(-kx -1)(x+1)(-x+1)=ln 1-k 2x 21-x 2=0对定义域内任意x 恒成立,所以k 2=1,即k =±1,显然k ≠-1,所以k =1. 经验证,k =1符合题意.(2)f (x )在(-∞,-1),(1,+∞)上均为增函数.证明:由(1)知f (x )=ln x -1x+1,其定义域为(-∞,-1)∪(1,+∞), 任取x 1,x 2∈(1,+∞),不妨设x 1<x 2,则f (x 1)-f (x 2)=ln x 1-1x 1+1-ln x 2-1x 2+1=ln (x 1-1)(x 2+1)(x 1+1)(x 2-1),因为(x 1-1)(x 2+1)-(x 1+1)(x 2-1)=2(x 1-x 2)<0,且(x 1+1)(x 2-1)>0,(x 1-1)·(x 2+1)>0, 所以0<(x 1-1)(x 2+1)(x 1+1)(x 2-1)<1,所以f (x 1)-f (x 2)=ln (x 1-1)(x 2+1)(x 1+1)(x 2-1)<0,即f (x 1)<f (x 2),所以f (x )在(1,+∞)上为增函数. 同理, f (x )在(-∞,-1)上为增函数. (3)由(2)知f (x )在(1,+∞)上为增函数,又因为函数f (x )在[α,β]上的值域为[ln (mα-m2),ln (mβ-m2)],所以m >0,且{ln α-1α+1=ln (mα-m2),ln β-1β+1=ln (mβ-m2), 所以{α-1α+1=mα-m2,β-1β+1=mβ-m 2,即α,β是方程x -1x+1=mx -m2的两个不等实根,问题等价于方程mx 2-(1-m2)x +1-m2=0在(1,+∞)上有两个不等实根,令h (x )=mx 2-(1-m2)x +1-m2,x ∈(1,+∞),易知h (x )为二次函数,其图象的对称轴为直线x =12m -14, 则{m >0,12m -14>1,Δ=[-(1-m 2)]2-4m (1-m2)>0,ℎ(1)=m >0, 即{m >0,0<m <25,m >2或m <29,解得0<m <29.。

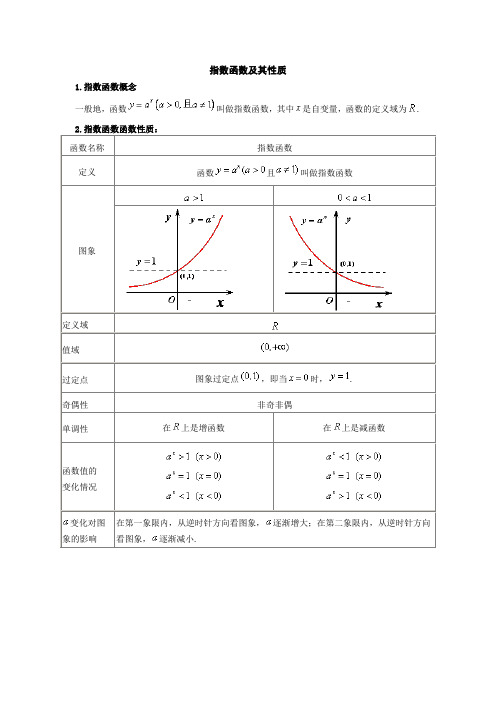
指数函数及其性质1.指数函数概念一般地，函数叫做指数函数，其中是自变量，函数的定义域为.且图象过定点，即当.在在变化对图在第一象限内，从逆时针方向看图象，看图象，对数函数及其性质1.对数函数定义一般地，函数叫做对数函数，其中是自变量，函数的定义域.且图象过定点，即当时，上是增函数上是减函数变化对图在第一象限内，从顺时针方向看图象，看图象，指数函数习题一、选择题 1．定义运算a ⊗b ＝⎩⎪⎨⎪⎧a (a ≤b )b (a >b )，则函数f (x )＝1⊗2x的图象大致为( )2．函数f (x )＝x 2－bx ＋c 满足f (1＋x )＝f (1－x )且f (0)＝3，则f (b x )与f (c x)的大小关系是( )A ．f (b x )≤f (c x)B ．f (b x )≥f (c x)C ．f (b x )>f (c x)D ．大小关系随x 的不同而不同3．函数y ＝|2x－1|在区间(k －1，k ＋1)内不单调，则k 的取值范围是( ) A ．(－1，＋∞) B ．(－∞，1) C ．(－1,1) D ．(0,2)4．设函数f (x )＝ln [(x －1)(2－x )]的定义域是A ，函数g (x )＝lg(a x－2x－1)的定义域是B ，若A ⊆B ，则正数a 的取值范围( ) A ．a >3 B ．a ≥3 C ．a > 5D ．a ≥ 55．已知函数f (x )＝⎩⎪⎨⎪⎧(3－a )x －3，x ≤7，a x －6，x >7.若数列{a n }满足a n ＝f (n )(n ∈N *)，且{a n }是递增数列，则实数a 的取值范围是( ) A ．[94，3)B ．(94，3)C ．(2,3)D ．(1,3)6．已知a >0且a ≠1，f (x )＝x 2－a x，当x ∈(－1,1)时，均有f (x )<12，则实数a 的取值范围是( )A ．(0，12]∪[2，＋∞)B ．[14，1)∪(1,4]C ．[12，1)∪(1,2]D ．(0，14)∪[4，＋∞)二、填空题7．函数y ＝a x(a >0，且a ≠1)在[1,2]上的最大值比最小值大a2，则a 的值是________．8．若曲线|y |＝2x＋1与直线y ＝b 没有公共点，则b 的取值范围是________．9．(2011·滨州模拟)定义：区间[x 1，x 2](x 1<x 2)的长度为x 2－x 1.已知函数y ＝2|x |的定义域为[a ，b ]，值域为[1,2]，则区间[a ，b ]的长度的最大值与最小值的差为________．三、解答题10．求函数y ＝211．(2011·银川模拟)若函数y ＝a 2x ＋2a x－1(a >0且a ≠1)在x ∈[－1,1]上的最大值为14，求a 的值．12．已知函数f (x )＝3x ，f (a ＋2)＝18，g (x )＝λ·3ax －4x的定义域为[0,1]． (1)求a 的值；(2)若函数g (x )在区间[0,1]上是单调递减函数，求实数λ的取值范围．1.解析：由a ⊗b ＝⎩⎪⎨⎪⎧a (a ≤b )b (a >b )得f (x )＝1⊗2x＝⎩⎪⎨⎪⎧2x(x ≤0)，1 (x >0).答案：A2. 解析：∵f (1＋x )＝f (1－x )，∴f (x )的对称轴为直线x ＝1，由此得b ＝2. 又f (0)＝3，∴c ＝3.∴f (x )在(－∞，1)上递减，在(1，＋∞)上递增．若x ≥0，则3x ≥2x ≥1，∴f (3x )≥f (2x)．若x <0，则3x <2x <1，∴f (3x )>f (2x)．∴f (3x )≥f (2x)． 答案：A3.解析：由于函数y ＝|2x－1|在(－∞，0)内单调递减，在(0，＋∞)内单调递增，而函数在区间(k －1，k ＋1)内不单调，所以有k －1<0<k ＋1，解得－1<k <1. 答案：C4. 解析：由题意得：A ＝(1,2)，a x －2x >1且a >2，由A ⊆B 知a x －2x>1在(1,2)上恒成立，即a x －2x －1>0在(1,2)上恒成立，令u (x )＝a x －2x －1，则u ′(x )＝a x ln a －2x ln2>0，所以函数u (x )在(1,2)上单调递增，则u (x )>u (1)＝a －3，即a ≥3. 答案：B5. 解析：数列{a n }满足a n ＝f (n )(n ∈N *)，则函数f (n )为增函数，注意a 8－6>(3－a )×7－3，所以⎩⎪⎨⎪⎧a >13－a >0a 8－6>(3－a )×7－3，解得2<a <3.答案：C6. 解析：f (x )<12⇔x 2－a x <12⇔x 2－12<a x ，考查函数y ＝a x 与y ＝x 2－12的图象，当a >1时，必有a －1≥12，即1<a ≤2，当0<a <1时，必有a ≥12，即12≤a <1，综上，12≤a <1或1<a ≤2.答案：C7. 解析：当a >1时，y ＝a x 在[1,2]上单调递增，故a 2－a ＝a 2，得a ＝32.当0<a <1时，y ＝ax在[1,2]上单调递减，故a －a 2＝a 2，得a ＝12.故a ＝12或32.答案：12或328. 解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．曲线|y |＝2x＋1与直线y ＝b 的图象如图所示，由图象可得：如果|y |＝2x＋1与直线y ＝b 没有公共点，则b 应满足的条件是b ∈[－1,1]． 答案：[－1,1]9. 解析：如图满足条件的区间[a ，b ]，当a ＝－1，b ＝0或a ＝0，b ＝1时区间长度最小，最小值为1，当a ＝－1，b ＝1时区间长度最大，最大值为2，故其差为1. 答案：110. 解：要使函数有意义，则只需－x 2－3x ＋4≥0，即x 2＋3x －4≤0，解得－4≤x ≤1. ∴函数的定义域为{x |－4≤x ≤1}．令t ＝－x 2－3x ＋4，则t ＝－x 2－3x ＋4＝－(x ＋32)2＋254，∴当－4≤x ≤1时，t max ＝254，此时x ＝－32，t min ＝0，此时x ＝－4或x ＝1.∴0≤t ≤254.∴0≤－x 2－3x ＋4≤52.∴函数y ＝1()2[28，1]．由t ＝－x 2－3x ＋4＝－(x ＋32)2＋254(－4≤x ≤1)可知，当－4≤x ≤－32时，t 是增函数，当－32≤x ≤1时，t 是减函数．根据复合函数的单调性知：y ＝1()2在[－4，－32]上是减函数，在[－32，1]上是增函数．∴函数的单调增区间是[－32，1]，单调减区间是[－4，－32]．11. 解：令a x＝t ，∴t >0，则y ＝t 2＋2t －1＝(t ＋1)2－2，其对称轴为t ＝－1.该二次函数在[－1，＋∞)上是增函数．①若a >1，∵x ∈[－1,1]，∴t ＝a x ∈[1a，a ]，故当t ＝a ，即x ＝1时，y max ＝a 2＋2a －1＝14，解得a ＝3(a ＝－5舍去)． ②若0<a <1，∵x ∈[－1,1]，∴t ＝a x∈[a ，1a ]，故当t ＝1a，即x ＝－1时，y max ＝(1a＋1)2－2＝14.∴a ＝13或－15(舍去)．综上可得a ＝3或13.12. 解：法一：(1)由已知得3a ＋2＝18⇒3a＝2⇒a ＝log 32.(2)此时g (x )＝λ·2x －4x， 设0≤x 1<x 2≤1，因为g (x )在区间[0,1]上是单调减函数，所以g (x 1)－g (x 2)＝(2x 1－2x 2)(λ－2x 2－2x 1)>0恒成立，即λ<2x 2＋2x 1恒成立．由于2x 2＋2x 1>20＋20＝2，所以实数λ的取值范围是λ≤2. 法二：(1)同法一．(2)此时g (x )＝λ·2x －4x，因为g (x )在区间[0,1]上是单调减函数，所以有g ′(x )＝λln2·2x －ln4·4x＝ln2[－2·(2x )2＋λ·2x ]≤0成立．设2x ＝u ∈[1,2]，上式成立等价于－2u 2＋λu ≤0恒成立． 因为u ∈[1,2]，只需λ≤2u 恒成立， 所以实数λ的取值范围是λ≤2.对数与对数函数同步练习一、选择题1、已知32a =，那么33log 82log 6-用a 表示是（ ）A 、2a -B 、52a -C 、23(1)a a -+D 、 23a a -2、2log (2)log log a a a M N M N -=+，则NM的值为（ ） A 、41B 、4C 、1D 、4或13、已知221,0,0x y x y +=>>，且1l o g (1),l o g ,l o g 1y aa a x m n x+==-则等于（ ）A 、m n +B 、m n -C 、()12m n +D 、()12m n -4、如果方程2lg (lg5lg7)lg lg5lg70x x +++= 的两根是,αβ，则αβ 的值是（ ）A 、lg5lg 7B 、lg 35C 、35D 、3515、已知732log [log (log )]0x =，那么12x -等于（ ）A 、13 B C D 6、函数2lg 11y x ⎛⎫=- ⎪+⎝⎭的图像关于（ ）A 、x 轴对称B 、y 轴对称C 、原点对称D 、直线y x =对称7、函数(21)log x y -=的定义域是（ ）A 、()2,11,3⎛⎫+∞ ⎪⎝⎭B 、()1,11,2⎛⎫+∞ ⎪⎝⎭C 、2,3⎛⎫+∞ ⎪⎝⎭D 、1,2⎛⎫+∞ ⎪⎝⎭8、函数212log (617)y x x =-+的值域是（ ）A 、RB 、[)8,+∞C 、(),3-∞-D 、[)3,+∞ 9、若log 9log 90m n <<，那么,m n 满足的条件是（ ）A 、 1 m n >>B 、1n m >>C 、01n m <<<D 、01m n <<<10、2log 13a <，则a 的取值范围是（ ）A 、()20,1,3⎛⎫+∞ ⎪⎝⎭B 、2,3⎛⎫+∞ ⎪⎝⎭C 、2,13⎛⎫ ⎪⎝⎭D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭11、下列函数中，在()0,2上为增函数的是（ ）A 、12log (1)y x =+ B 、2log y =C 、21log y x = D 、2log (45)y x x =-+ 12、已知()log x+1 (01)a g x a a =>≠且在()10-，上有()0g x >，则1()x f x a +=是（ ）A 、在(),0-∞上是增加的B 、在(),0-∞上是减少的C 、在(),1-∞-上是增加的D 、在(),0-∞上是减少的 二、填空题13、若2log 2,log 3,m n a a m n a +=== 。

高中数学 2.2.3 对数函数的图象和性质 第1课时同步练习 湘教版必修11．已知f (x )是对数函数，且满足f (x ＋6)＝f (x )＋f (6)，其中x ＞0，则x 的值为( )．A ．6B ．56C ．65D ．不存在 2．函数f (x )＝12ln x 的反函数为( )． A ．12e x y =(x ＞0) B ．y ＝e 2x (x ∈R )C ．1210x y =(x ＞0)D ．y ＝102x (x ＞0)3．若函数y ＝f (x )的反函数图象过点(1,5)，则函数y ＝f (x )的图象必过点( )．A ．(1,1)B ．(1,5)C ．(5,1)D ．(5,5)4．函数y ＝2－x ＋1(x ＞0)的反函数是( )．A ．y ＝log 2(x ＋1)B ．y ＝－log 2(x ＋1)C ．y ＝log 2(x －1)D ．y ＝－log 2(x －1)5．已知函数y ＝e x 的图象与函数y ＝f (x )的图象关于直线y ＝x 对称，则( )．A ．f (2x )＝e 2x (x ∈R )B ．f (2x )＝ln 2·ln x (x ＞0)C ．f (2x )＝2e x (x ∈R )D ．f (2x )＝ln x ＋ln 2(x ＞0)6．已知f (x )，g (x )是两个对数函数，且f (3)＝2g (9)，f (1)＋g (4)＝12，则f (x )，g (x )的解析式分别是( )．A ．f (x )＝log 2x ，g (x )＝log 16xB ．f (x )＝log 16x ，g (x )＝log 2xC ．f (x )＝log 2x ，g (x )＝log 4xD ．f (x )＝log 4x ，g (x )＝log 2x7．函数f (x )＝1x＋3的反函数是__________． 8．已知函数2x m y x -=+的反函数的图象经过点(2,3)，则m ＝__________. 9．函数()ax b f x x c +=+(a ，b ，c 是常数)的反函数是312x y x -=+，求a ，b ，c 的值． 10．已知函数f (x )是对数函数，且f (4)＝1，函数y ＝f (x )－1的反函数是g (x )．(1)求g (x )；(2)求g (－x )在区间[0,2]上的最值．参考答案1.答案：C解析：设f(x)＝log a x(a＞0且a≠1)，依题意有log a(x＋6)＝log a x＋log a6，于是x＋6＝6x，解得65x=，故选C．2.答案：B解析：将x与y换位得x＝12ln y，所以2x＝ln y， y＝e2x，故反函数是y＝e2x(x∈R)．3.答案：C解析：由互为反函数的两函数图象间的关系知f(x)的图象必过(5,1)，选C．4.答案：D解析：将x与y换位得x＝2－y＋1，于是x－1＝2－y，－y＝log2(x－1)，∴y＝－log2(x－1)，即反函数是y＝－log2(x－1)．选D．5.答案：D解析：y＝f(x)是y＝e x的反函数，∴f(x)＝ln x，f(2x)＝ln 2x＝ln x＋ln 2 (x＞0)．6.答案：A解析：依题意，可设f(x)＝log a x(a＞0且a≠1)，g(x)＝log b x(b＞0，且b≠1)．∴log32log91 log1log42a ba b=⎧⎪⎨+=⎪⎩，，因此log32log916a bb=⎧⎨=⎩，，解得2,16.ab=⎧⎨=⎩故f(x)＝log2x，g(x)＝log16x，选A．7.答案：13 yx=-解析：由x＝1y＋3解得13yx=-，故反函数是13yx=-.8.答案：－7解析：依题意，原函数的图象经过点(3,2)，则3232m-=+，所以m＝－7.9.解：312xyx-=+，解得原函数()212133x x f x x x +--==--. 又()ax b f x x c+=+， ∴a ＝－2，b ＝－1，c ＝－3.10. 解：(1)设f (x )＝log a x (a ＞0且a ≠1)， 则log a 4＝1，解得a ＝4.这时f (x )＝log 4x . y ＝log 4x －1，由x ＝log 4y －1，解得y ＝4x ＋1，故g (x )＝4x ＋1.(2)g (－x )＝4－x ＋1＝114x -⎛⎫ ⎪⎝⎭，当x ∈[0,2]时，x －1∈[－1,1]，故g (－x )的最大值是1144-⎛⎫= ⎪⎝⎭，最小值是11144⎛⎫= ⎪⎝⎭.。

高中数学《对数函数图像与性质》精选练习（含详细解析）一、选择题1.给出下列函数:(1)y=log2(x-1). (2)y=log x2x.(3)y=log(e+1)x. (4)y=4log33x.(5)y=log(3+π)x. (6)y=lg5x.(7)y=lgx+1.其中是对数函数的个数为( )A.1B.2C.3D.42.已知对数函数f(x)过点(2,4),则f()的值为( )A.-1B.1C.D.3.函数f(x)=log a(x+2)+1(a>0,且a≠1)的图象必经过点( )A.(1,-1)B.(1,0)C.(-1,1)D.(0,1)4函数y=的定义域是( )A.(-∞,1]B.(0,1]C.[-1,0)D.(-1,0]5.如图所示,曲线是对数函数f(x)=log a x的图象,已知a取,,,,则对应于C1,C2,C3,C4的a值依次为( )A.,,,B.,,,C.,,,D.,,,6.函数f(x)=的定义域是( )A.(-1,+∞)B.[-1,+∞)C.(-1,1)∪(1,+∞)D.[-1,1)∪(1,+∞)7.已知a>0且a≠1,则函数y=log a x和y=(1-a)x在同一直角坐标系中的图象可能是下列图象中的( )A.(1)(2)B.(2)(3)C.(3)(4)D.(1)(2)(3)二、填空题(每小题5分,共15分)8若函数y=f(x)是函数y=a x(a>0且a≠1)的反函数,且f(2)=1,则f(x)= .9若对数函数f(x)=log a x+(a2-4a-5),则a= .10已知集合A={x|y=log2(x-1)},B={y|y=2x+1,x∈A},则A∩B= .11若函数y=log a+3的图象恒过定点P,则P点坐标为.12.函数f(x)=log2(1+4x)-x,若f(a)=b,则f(-a)= .三、解答题13.已知函数y=log a(x+3)-(a>0,a≠1)的图象恒过定点A,若点A也在函数f(x)=3x+b的图象上,求b的值.14已知函数f(x)=log2.(1)求证:f(x1)+f(x2)=f.(2)若f=1,f(-b)=,求f(a)的值.15若函数y=log a(x+a)(a>0且a≠1)的图象过点(-1,0).(1)求a的值.(2)求函数的定义域.16已知f(x)=|log3x|.(1)画出函数f(x)的图象.(2)讨论关于x的方程|log3x|=a(a∈R)的解的个数.参考答案与解析1【解析】选 B.由对数函数的概念可知(1)(2)(4)(6)(7)都不符合对数函数形式的特点,只有(3)(5)符合.2【解析】选B.设f(x)=logax,由f(x)过点(2,4),则loga2=4,即a4=2,解得a=,所以f(x)=lo x,所以f()=lo=1.3【解析】选C.当x+2=1时,f(x)=loga (x+2)+1=loga1+1=1,即x=-1时,f(-1)=1,故函数恒过定点(-1,1).4【解析】选B.要使函数有意义,必须lo(2x-1)≥0,则0<2x-1≤1,即1<2x≤2,解得0<x≤1,故函数的定义域为(0,1].5【解析】选A.先排C1,C2底的顺序,底都大于1,当x>1时图低的底大,C1,C2对应的a分别为,.然后考虑C3,C4底的顺序,底都小于1,当x<1时底大的图高,C3,C4对应的a分别为,.综合以上分析,可得C1,C2,C3,C4的a值依次为,,,.故选A.6【解析】选C.解不等式组可得x>-1,且x≠1,故定义域为(-1,1)∪(1,+∞).7【解析】选B.当0<a<1时,1-a>0,函数y=logax在(0,+∞)上是减函数.函数y=(1-a)x在R上是增函数.图(3)符合此要求.当a>1时,1-a<0,函数y=logax在(0,+∞)上是增函数.函数y=(1-a)x在R上是减函数.图(2)符合此要求.8【解析】由题意知f(x)=loga x,又f(2)=1,所以loga2=1,所以a=2,f(x)=log2x.答案:log2x9【解析】由对数函数的定义可知,解得a=5.答案:510【解析】由题知x-1>0,解得x>1,所以y=2x+1>2+1=3,所以A∩B=(3,+∞).答案:(3,+∞)11【解析】因为y=logat的图象恒过(1,0), 所以令=1,得x=-2,此时y=3,所以该函数过定点(-2,3).答案:(-2,3)12【解析】因为f(a)=log2(1+4a)-a=b,所以log2(1+4a)=a+b,所以f(-a)=log2(1+4-a)+a=log2+a=log2(1+4a)-log222a+a=a+b-2a+a=b.答案:b13【解析】当x+3=1,即x=-2时,对任意的a>0,且a≠1都有y=loga1-=0-=-,所以函数y=loga(x+3)-的图象恒过定点A,若点A也在函数f(x)=3x+b的图象上,则-=3-2+b,所以b=-1.14【解析】(1)左边=f(x1)+f(x2)=log2+log2=log2=log2.右边=log2=log2.所以左边=右边.(2)因为f(-b)=log2=-log2=,所以f(b)=-,利用(1)可知:f(a)+f(b)=f,所以-+f(a)=1,解得f(a)=.15【解析】(1)将(-1,0)代入y=loga (x+a)(a>0,a≠1)中,有0=loga(-1+a),则-1+a=1,所以a=2.(2)由(1)知y=log2(x+2),x+2>0,解得x>-2,所以函数的定义域为{x|x>-2}.16【解析】(1)函数f(x)=对应的函数f(x)的图象为:(2)设函数y=|log3x|和y=a.当a<0时,两图象无交点,原方程解的个数为0个.当a=0时,两图象只有1个交点,原方程只有1解.当a>0时,两图象有2个交点,原方程有2解.。

2.2.2 对数函数及其性质(一)自主学习1．掌握对数函数的概念、图象和性质．2．能够根据指数函数的图象和性质得出对数函数的图象和性质，把握指数函数与对数函数关系的实质．1．对数函数的定义：一般地，我们把函数y ＝log a x (a >0，且a ≠1)叫做________________，其中x 是自变量，函数的定义域是(0，＋∞)．a >10<a <1(0，＋∞)对数函数y ＝log a x (a >0且a ≠1)和指数函数________________________互为反函数．对点讲练对数函数的图象【例1】 下图是对数函数y ＝log a x 的图象，已知a 值取3，43，35，110，则图象C 1，C 2，C 3，C 4相应的a 值依次是( )A. 3、43、35、110B.3、43、110、35C.43、3、35、110D.43、3、110、35规律方法 (1)y ＝log a x (a >0，且a ≠1)图象无限地靠近于y 轴，但永远不会与y 轴相交． (2)设y 1＝log a x ，y 2＝log b x ，其中a >1，b >1(或0<a <1，0<b <1)，则当x >1时，“底大图低”，即若a >b ，则y 1<y 2.当0<x <1时，“底大图高”，即若a >b ，则y 1>y 2.(3)在同一坐标系内，y ＝log a x (a >0，且a ≠1)的图象与y ＝log 1ax (a >0，且a ≠1)的图象关于x 轴(即y ＝0)对称．变式迁移1 借助图象求使函数y ＝log a (3x ＋4)的函数值恒为负值的x 的取值范围．对数函数的单调性的应用【例2】 比较下列各组中两个值的大小：(1)log 0.52.7，log 0.52.8； (2)log 34，log 65； (3)log a π，log a e (a >0且a ≠1)．变式迁移2 若a ＝log 3π，b ＝log 76，c ＝log 20.8，则( )A ．a >b >cB ．b >a >cC ．c >a >bD ．b >c >a求函数的定义域【例3】 求下列函数的定义域：(1)y ＝3log 2x ； (2)y ＝log 0.5(4x －3)； (3)y ＝log (x ＋1)(2－x )．规律方法 求与对数函数有关的函数定义域时，除遵循前面已学习过的求函数定义域的方法外，还要对这种函数自身有如下要求：一是要特别注意真数大于零；二是要注意对数的底数；三是按底数的取值应用单调性，有针对性的解不等式．变式迁移3 求下列函数的定义域．(1)y ＝1lg (x ＋1)－3； (2)y ＝log a (4x －3)(a >0，且a ≠1)．1．对数函数单调性等重要性质要借助图象来理解与掌握．2．比较对数值的大小要用函数单调性及中间“桥梁”过渡．另外还要注意底数是否相同．3．掌握对数函数不但要清楚对数函数自身的图象和性质，还要结合指数函数的图象和性质来对比掌握．4．对数函数的单调性与指数函数的单调性大同小异．课时作业一、选择题1．已知函数f (x )＝11－x的定义域为M ，g (x )＝ln(1＋x )的定义域为N ，则M ∩N 等于( )A ．{x |x >－1}B ．{x |x <1}C ．{x |－1<x <1}D ．∅ 2．若log a 2<log b 2<0，则( )A ．0<a <b <1B ．0<b <a <1C ．a >b >1D ．b >a >1 3．以下四个数中的最大者是( )A ．(ln 2)2B ．ln(ln 2)C ．ln 2D ．ln 24．函数y ＝a x 与y ＝－log a x (a >0且a ≠1)在同一坐标系中的图象形状只能是( )二、填空题5．函数f (x )＝lg (4－x )x －3的定义域为______________．6．若指数函数f (x )＝a x则不等式log a (x －1)<07．函数y ＝log a (x ＋2)＋3的图象过定点__________． 三、解答题8．求下列函数的定义域：(1)y ＝ 32x －1－127；(2)y ＝－lg (1－x )；(3)y ＝11－log a (x ＋a )(a >0，a ≠1)．9．已知f (x )＝log a 1＋x1－x(a >0，a ≠1)，(1)求f (x )的定义域； (2)求使f (x )>0的x 的取值范围； (3)判断f (x )的奇偶性．2.2.2 对数函数及其性质(一) 答案自学导引 1．对数函数2．(1,0) (－∞，0) [0，＋∞) (0，＋∞) (－∞，0] x 轴3．y ＝a x (a >0且a ≠1) 对点讲练【例1】 A [过(0,1)作平行于x 轴的直线，与C 1，C 2，C 3，C 4的交点的坐标为(a 1,1)，(a 2,1)，(a 3,1)，(a 4,1)，其中a 1，a 2，a 3，a 4分别为各对数的底，显然a 1>a 2>a 3>a 4，所以C 1，C 2，C 3，C 4的底值依次由大到小．]变式迁移1 解 当a >1时，由题意有 0<3x ＋4<1，即－43<x <－1.当0<a <1时，由题意有3x ＋4>1，即x >－1.综上，当a >1时，－43<x <－1；当0<a <1时，x >－1.【例2】 解 (1)∵0<0.5<1，∴对数函数y ＝log 0.5x 在(0，＋∞)上是减函数． 又∵2.7<2.8，∴log 0.52.7>log 0.52.8.(2)∵y ＝log 3x 在(0，＋∞)上是增函数， ∴log 34>log 33＝1.∵y ＝log 6x 在(0，＋∞)上是增函数， ∴log 65<log 66＝1. ∴log 34>log 65.(3)当a >1时，y ＝log a x 在(0，＋∞)上是增函数． ∵π>e ，∴log a π>log a e.当0<a <1时，y ＝log a x 在(0，＋∞)上是减函数． ∵π>e ，∴log a π<log a e.综上可知，当a >1时，log a π>log a e ； 当0<a <1时，log a π<log a e.变式迁移2 A [利用界值法可得a ＝log 3π>log 33＝1,0<b ＝log 76<log 77＝1，c ＝log 20.8<log 21＝0，故a >b >c .]【例3】 解 (1)∵该函数是奇次根式，要使函数有意义，只要对数的真数是正数即可， ∴定义域是{x |x >0}．(2)要使函数y ＝log 0.5(4x －3)有意义， 必须log 0.5(4x －3)≥0＝log 0.51，∴0<4x －3≤1.解得34<x ≤1.∴定义域是⎩⎨⎧⎭⎬⎫x |34<x ≤1.(3)由⎩⎪⎨⎪⎧x ＋1>0x ＋1≠12－x >0，得⎩⎪⎨⎪⎧x >－1x ≠0，x <2即0<x <2或－1<x <0，所求定义域为(－1,0)∪(0,2)．变式迁移3 解 (1)由⎩⎪⎨⎪⎧lg (x ＋1)－3≠0x ＋1>0，得⎩⎪⎨⎪⎧x ＋1≠103x >－1， ∴x >－1且x ≠999，∴函数的定义域为{x |x >－1且x ≠999}． (2)log a (4x －3)≥0.(*)当a >1时，(*)可化为log a (4x －3)≥log a 1， ∴4x －3≥1，x ≥1.当0<a <1时，(*)可化为 log a (4x －3)≥log a 1，∴0<4x －3≤1，34<x ≤1.综上所述，当a >1时，函数定义域为[1，＋∞)，当0<a <1时，函数定义域为⎝⎛⎦⎤34，1. 课时作业1．C [由题意知M ＝{x |x <1}， N ＝{x |x >－1}．故M ∩N ＝{x |－1<x <1}．]2．B [由底数与对数函数的图象关系(如图)可知y ＝log a x ，y ＝log b x 图象的大致走向．再由对数函数的图象规律：从第一象限看，自左向右底数依次增大．∴选B.] 3．D [∵0<ln 2<1，∴ln(ln 2)<0，(ln 2)2<ln 2，而ln 2＝12ln 2<ln 2.∴最大的数是ln 2.] 4．A5．{x |x <4，且x ≠3}解析 ⎩⎪⎨⎪⎧4－x >0x －3≠0解得x <4，且x ≠3，所以定义域为{x |x <4，且x ≠3}． 6．{x |1<x <2}解析 由题可知a ＝1.2，∴log 1.2(x －1)<0， ∴log 1.2(x －1)<log 1.21，解得x <2， 又∵x －1>0，即x >1，∴1<x <2. 故原不等式的解集为{x |1<x <2}． 7．(－1,3)8．解 (1)由32x －1－127≥0得，x ≥－1.∴所求定义域为[－1，＋∞)．(2)由－lg(1－x )≥0得，⎩⎪⎨⎪⎧1－x ≤11－x >0，即x ∈[0,1)∴所求定义域为[0,1)．(3)1－log a (x ＋a )>0时，函数有意义， 即log a (x ＋a )<1① 当a >1时，－a <－1由①得，⎩⎪⎨⎪⎧x ＋a <ax ＋a >0解得－a <x <0.∴定义域为(－a,0)． 当0<a <1时，－1<－a <0. 由①得，x ＋a >a .∴x >0. ∴定义域为(0，＋∞)．故所求定义域是：当0<a <1时，x ∈(0，＋∞)； 当a >1时，x ∈(－a,0)．9．解 (1)由1＋x1－x>0，得－1<x <1.故所求的定义域为(－1,1)．(2)①当a >1时，由log a 1＋x1－x>0＝log a 1得1＋x 1－x>1，∴0<x <1. ②当0<a <1时，由log a 1＋x1－x>0＝log a 1得0<1＋x 1－x<1，∴－1<x <0.故当a >1时，所求范围为0<x <1； 当0<a <1时，所求范围为－1<x <0.(3)f (－x )＝log a 1－x1＋x＝log a (1＋x 1－x)－1＝－f (x )∴f (x )为奇函数．。

指数函数及其性质1.指数函数概念一般地，函数叫做指数函数，其中是自变量，函数的定义域为.且图象过定点，即当.在在变化对图在第一象限内，从逆时针方向看图象，看图象，对数函数及其性质1.对数函数定义一般地，函数叫做对数函数，其中是自变量，函数的定义域.且图象过定点，即当时，上是增函数上是减函数变化对图在第一象限内，从顺时针方向看图象，看图象，指数函数习题一、选择题 1．定义运算a ⊗b ＝⎩⎪⎨⎪⎧a (a ≤b )b (a >b )，则函数f (x )＝1⊗2x的图象大致为( )2．函数f (x )＝x 2－bx ＋c 满足f (1＋x )＝f (1－x )且f (0)＝3，则f (b x )与f (c x)的大小关系是( )A ．f (b x )≤f (c x)B ．f (b x )≥f (c x)C ．f (b x )>f (c x)D ．大小关系随x 的不同而不同3．函数y ＝|2x－1|在区间(k －1，k ＋1)内不单调，则k 的取值范围是( ) A ．(－1，＋∞) B ．(－∞，1) C ．(－1,1) D ．(0,2)4．设函数f (x )＝ln [(x －1)(2－x )]的定义域是A ，函数g (x )＝lg(a x－2x－1)的定义域是B ，若A ⊆B ，则正数a 的取值范围( ) A ．a >3 B ．a ≥3 C ．a > 5D ．a ≥ 55．已知函数f (x )＝⎩⎪⎨⎪⎧(3－a )x －3，x ≤7，a x －6，x >7.若数列{a n }满足a n ＝f (n )(n ∈N *)，且{a n }是递增数列，则实数a 的取值范围是( ) A ．[94，3)B ．(94，3)C ．(2,3)D ．(1,3)6．已知a >0且a ≠1，f (x )＝x 2－a x，当x ∈(－1,1)时，均有f (x )<12，则实数a 的取值范围是( )A ．(0，12]∪[2，＋∞)B ．[14，1)∪(1,4]C ．[12，1)∪(1,2]D ．(0，14)∪[4，＋∞)二、填空题7．函数y ＝a x(a >0，且a ≠1)在[1,2]上的最大值比最小值大a2，则a 的值是________．8．若曲线|y |＝2x＋1与直线y ＝b 没有公共点，则b 的取值范围是________．9．定义：区间[x 1，x 2](x 1<x 2)的长度为x 2－x 1.已知函数y ＝2|x |的定义域为[a ，b ]，值域为[1,2]，则区间[a ，b ]的长度的最大值与最小值的差为________．三、解答题10．求函数y＝211．若函数y＝a2x＋2a x－1(a>0且a≠1)在x∈[－1,1]上的最大值为14，求a的值．12．已知函数f(x)＝3x，f(a＋2)＝18，g(x)＝λ·3ax－4x的定义域为[0,1]．(1)求a的值；(2)若函数g(x)在区间[0,1]上是单调递减函数，求实数λ的取值范围．1.解析：由a ⊗b ＝⎩⎪⎨⎪⎧a (a ≤b )b (a >b )得f (x )＝1⊗2x＝⎩⎪⎨⎪⎧2x(x ≤0)，1 (x >0).答案：A2. 解析：∵f (1＋x )＝f (1－x )，∴f (x )的对称轴为直线x ＝1，由此得b ＝2. 又f (0)＝3，∴c ＝3.∴f (x )在(－∞，1)上递减，在(1，＋∞)上递增．若x ≥0，则3x ≥2x ≥1，∴f (3x )≥f (2x)．若x <0，则3x <2x <1，∴f (3x )>f (2x)．∴f (3x )≥f (2x)． 答案：A3.解析：由于函数y ＝|2x－1|在(－∞，0)内单调递减，在(0，＋∞)内单调递增，而函数在区间(k －1，k ＋1)内不单调，所以有k －1<0<k ＋1，解得－1<k <1. 答案：C4. 解析：由题意得：A ＝(1,2)，a x －2x >1且a >2，由A ⊆B 知a x －2x>1在(1,2)上恒成立，即a x －2x －1>0在(1,2)上恒成立，令u (x )＝a x －2x －1，则u ′(x )＝a x ln a －2x ln2>0，所以函数u (x )在(1,2)上单调递增，则u (x )>u (1)＝a －3，即a ≥3. 答案：B5. 解析：数列{a n }满足a n ＝f (n )(n ∈N *)，则函数f (n )为增函数，注意a 8－6>(3－a )×7－3，所以⎩⎪⎨⎪⎧a >13－a >0a 8－6>(3－a )×7－3，解得2<a <3.答案：C6. 解析：f (x )<12⇔x 2－a x <12⇔x 2－12<a x ，考查函数y ＝a x 与y ＝x 2－12的图象，当a >1时，必有a －1≥12，即1<a ≤2，当0<a <1时，必有a ≥12，即12≤a <1，综上，12≤a <1或1<a ≤2.答案：C7. 解析：当a >1时，y ＝a x 在[1,2]上单调递增，故a 2－a ＝a 2，得a ＝32.当0<a <1时，y ＝ax在[1,2]上单调递减，故a －a 2＝a 2，得a ＝12.故a ＝12或32.答案：12或328. 解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．曲线|y |＝2x＋1与直线y ＝b 的图象如图所示，由图象可得：如果|y |＝2x＋1与直线y ＝b 没有公共点，则b 应满足的条件是b ∈[－1,1]． 答案：[－1,1]9. 解析：如图满足条件的区间[a ，b ]，当a ＝－1，b ＝0或a ＝0，b ＝1时区间长度最小，最小值为1，当a ＝－1，b ＝1时区间长度最大，最大值为2，故其差为1. 答案：110. 解：要使函数有意义，则只需－x 2－3x ＋4≥0，即x 2＋3x －4≤0，解得－4≤x ≤1. ∴函数的定义域为{x |－4≤x ≤1}．令t ＝－x 2－3x ＋4，则t ＝－x 2－3x ＋4＝－(x ＋32)2＋254，∴当－4≤x ≤1时，t max ＝254，此时x ＝－32，t min ＝0，此时x ＝－4或x ＝1.∴0≤t ≤254.∴0≤－x 2－3x ＋4≤52.∴函数y ＝1()2[28，1]． 由t ＝－x 2－3x ＋4＝－(x ＋32)2＋254(－4≤x ≤1)可知，当－4≤x ≤－32时，t 是增函数，当－32≤x ≤1时，t 是减函数．根据复合函数的单调性知：y ＝1()2在[－4，－32]上是减函数，在[－32，1]上是增函数．∴函数的单调增区间是[－32，1]，单调减区间是[－4，－32]．11. 解：令a x＝t ，∴t >0，则y ＝t 2＋2t －1＝(t ＋1)2－2，其对称轴为t ＝－1.该二次函数在[－1，＋∞)上是增函数．①若a >1，∵x ∈[－1,1]，∴t ＝a x ∈[1a，a ]，故当t ＝a ，即x ＝1时，y max ＝a 2＋2a －1＝14，解得a ＝3(a ＝－5舍去)． ②若0<a <1，∵x ∈[－1,1]，∴t ＝a x∈[a ，1a ]，故当t ＝1a，即x ＝－1时，y max ＝(1a＋1)2－2＝14.∴a ＝13或－15(舍去)．综上可得a ＝3或13.12. 解：法一：(1)由已知得3a ＋2＝18⇒3a＝2⇒a ＝log 32.(2)此时g (x )＝λ·2x －4x， 设0≤x 1<x 2≤1，因为g (x )在区间[0,1]上是单调减函数，所以g (x 1)－g (x 2)＝(2x 1－2x 2)(λ－2x 2－2x 1)>0恒成立，即λ<2x 2＋2x 1恒成立．由于2x 2＋2x 1>20＋20＝2，所以实数λ的取值范围是λ≤2. 法二：(1)同法一．(2)此时g (x )＝λ·2x －4x，因为g (x )在区间[0,1]上是单调减函数，所以有g ′(x )＝λln2·2x －ln4·4x＝ln2[－2·(2x )2＋λ·2x ]≤0成立．设2x ＝u ∈[1,2]，上式成立等价于－2u 2＋λu ≤0恒成立． 因为u ∈[1,2]，只需λ≤2u 恒成立， 所以实数λ的取值范围是λ≤2.对数与对数函数同步练习一、选择题1、已知32a =，那么33log 82log 6-用a 表示是（ ）A 、2a -B 、52a -C 、23(1)a a -+ D 、 23a a -2、2log (2)log log a a a M N M N -=+，则NM的值为（ ） A 、41B 、4C 、1D 、4或13、已知221,0,0x y x y +=>>，且1l o g (1),l o g ,l o g 1y aa a x m n x+==-则等于（ ）A 、m n +B 、m n -C 、()12m n +D 、()12m n -4、如果方程2lg (lg5lg7)lg lg5lg70x x +++= 的两根是,αβ，则αβ 的值是（ ）A 、lg5lg 7B 、lg 35C 、35D 、351 5、已知732log [log (log )]0x =，那么12x -等于（ ）A 、13 B C D 6、函数2lg 11y x ⎛⎫=- ⎪+⎝⎭的图像关于（ ）A 、x 轴对称B 、y 轴对称C 、原点对称D 、直线y x =对称7、函数(21)log x y -=的定义域是（ ）A 、()2,11,3⎛⎫+∞ ⎪⎝⎭B 、()1,11,2⎛⎫+∞ ⎪⎝⎭C 、2,3⎛⎫+∞ ⎪⎝⎭D 、1,2⎛⎫+∞ ⎪⎝⎭8、函数212log (617)y x x =-+的值域是（ ）A 、RB 、[)8,+∞C 、(),3-∞-D 、[)3,+∞ 9、若log 9log 90m n <<，那么,m n 满足的条件是（ ）A 、 1 m n >>B 、1n m >>C 、01n m <<<D 、01m n <<<10、2log 13a <，则a 的取值范围是（ ）A 、()20,1,3⎛⎫+∞ ⎪⎝⎭B 、2,3⎛⎫+∞ ⎪⎝⎭C 、2,13⎛⎫ ⎪⎝⎭D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭11、下列函数中，在()0,2上为增函数的是（ ）A 、12log (1)y x =+ B 、2log y =C 、21log y x = D 、2log (45)y x x =-+ 12、已知()log x+1 (01)a g x a a =>≠且在()10-，上有()0g x >，则1()x f x a +=是（ ）A 、在(),0-∞上是增加的B 、在(),0-∞上是减少的C 、在(),1-∞-上是增加的D 、在(),0-∞上是减少的 二、填空题13、若2log 2,log 3,m n a a m n a +=== 。