中考数学复习第三单元函数及其图象第14课时二次函数同步训练

课时训练(十四)二次函数的综合应用(限时:70分钟)1.[2018·玉林]如图K14-1,一段抛物线y=-x2+4(-2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1;将C1绕点A1旋转180°得到C2,顶点为D2;C1与C2组成一个新的图像,垂直于y轴的直线l与新图像交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),x1,x2,x3均为正数,设t=x1+x2+x3,则t的取值范围是()图K14-1A.6<t≤8B.6≤t≤8C.10<t≤12D.10≤t≤122.如图K14-2,O为坐标原点,边长为的正方形OABC的顶点A在x轴的正半轴上,将正方形OABC绕顶点O顺时针旋转75°,使点B落在某抛物线的图像上,则该抛物线的解析式为()图K14-2A.y=x2B.y=-x2C.y=-x2D.y=-3x23.如图K14-3,在平面直角坐标系内,二次函数y=ax2+bx(a≠0),一次函数y=ax+b(a≠0)以及反比例函数y=(k≠0)的图像都经过点A,其中一次函数的图像与反比例函数的图像还交于另一点B,且一次函数与x 轴,y轴分别交于点C,D.若点A的横坐标为1,该二次函数的对称轴是直线x=2,则下列结论:①b=-4a;②a+b>k;③8a+4b>k;④a+2b>4k.其中正确结论的个数是()图K14-3A.1个B.2个C.3个D.4个4.如图K14-4,平面直角坐标系中,抛物线y=x2-2x+3交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP的面积为S.当y≤3时,S随x变化的图像大致是()图K14-46.如图K14-7,在平面直角坐标系xOy中,A(-3,0),B(0,1),形状相同的抛物线C n(n=1,2,3,4,…)的顶点在直线AB上,其对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…,那么这些抛物线称为“美丽抛物线”,根据上述规律,抛物线C2的顶点坐标为;若这些“美丽抛物线”与抛物线y=-x2+1形状相同,试写出抛物线C10的解析式.图K14-77.如图K14-8,曲线BC是反比例函数y=(4≤x≤6)的一部分,其中B(4,1-m),C(6,-m),抛物线y=-x2+2bx的顶点记作A.图K14-8(1)求k的值;(2)判断点A是否可与点B重合;(3)若抛物线与曲线BC有交点,求b的取值范围.8.在平面直角坐标系中,直线y=x+4与x,y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,并与x 轴交于另一点C(点C在点A的右侧),点P是抛物线上的一个动点.(1)求抛物线的解析式及点C的坐标.(2)若点P在第二象限内,过点P作PD⊥x轴于点D,交AB于点E,当点P运动到什么位置时,PE最长?最长是多少?图K14-99.[2018·金华、丽水]如图K14-10,抛物线y=ax2+bx(a≠0)过点E(10,0),矩形ABCD的边AB在线段OE 上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.(1)求抛物线的函数表达式.(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.图K14-10参考答案1.D[解析] 旋转后的抛物线的解析式为y=(x-4)2-4=x2-8x+12,∵x1,x2,x3均为正数,∴点P1(x1,y1),P2(x2,y2)在第四象限,根据对称性可知:x1+x2=8,∵2≤x3≤4,∴10≤x1+x2+x3≤120,即10≤t≤12.2.B[解析] 如图,作BE⊥x轴于点E,连接OB,设抛物线的解析式为y=ax2,由题意可知∠AOE=75°,∵∠AOB=45°,∴∠BOE=30°,∵OA=,∴OB=2,∴BE=OB=1,∴OE=-=,∴点B的坐标为(,-1),代入y=ax2得a=-,∴y=-x2.3.B[解析] ①对称轴为直线x=-=2,∴b=-4a,故结论正确;②∵一次函数与反比例函数的图像都经过点A,∴x=1时,a+b=k,故结论错误;③由图像可知,x=2时,4a+2b>,∴8a+4b>k,故结论正确;④a+2b=-+2b=b,4k=4(a+b)=4-+b=3b,∵二次函数图像开口向下,∴a<0,∴b=-4a>0,∴b<3b,∴a+2b<4k,故结论错误.4.B[解析] 当y=0时,x2-2x+3=0,解得x1=2,x2=6,∴点B的坐标为(2,0),点C的坐标为(6,0);当x=0时,y=x2-2x+3=3,则点A的坐标为(0,3).抛物线的对称轴为直线x=4,点A关于直线x=4的对称点为(8,3),利用待定系数法可求出直线AC的解析式为y=-x+3.过点P作PD∥y轴交AC于点D,如图,设点P的坐标为x,x2-2x+3,则点D的坐标为x,-x+3,当0≤x≤6时,DP=-x+3-x2-2x+3=-x2+x,∴S=OC·DP=-x2+x,当6<x≤8时,DP=x2-2x+3--x+3=x2-x,∴S=OC·DP=x2-x.5.3+[解析] 连接CM,∵抛物线的解析式为y=x2-2x-3,∴点D的坐标为(0,-3),∴OD的长为3,设y=0,则0=x2-2x-3,解得:x=-1或3,∴A(-1,0),B(3,0),∴AO=1,BO=3,∵AB为半圆的直径,∴AB=4,CM=2,OM=1,在Rt△COM中,OC=-=,∴CD=CO+OD=3+.6.(3,2)y=-(x-144)2+49[解析] 设直线AB的解析式为y=kx+b,则-解得:故直线AB的解析式为y=x+1,∵抛物线C2的顶点的横坐标为3,且顶点在直线AB上,∴抛物线C2的顶点坐标为(3,2).∵对称轴与x轴的交点的横坐标依次为:2,3,5,8,13,21,34,55,89,144…∴从第3个数开始,每个数都是前两个数的和,∴抛物线C10的顶点的横坐标为144,则纵坐标为×144+1=49,∴抛物线C10的顶点坐标为(144,49),∵抛物线C10与抛物线y=-x2+1的形状相同,∴抛物线C10的解析式为y=-(x-144)2+49.7.解:(1)∵B(4,1-m),C(6,-m)在反比例函数y=的图像上,∴k=4(1-m)=6×(-m),解得m=-2,∴k=4×[1-(-2)]=12.(2)∵m=-2,∴B(4,3),∵抛物线y=-x2+2bx=-(x-b)2+b2,∴A(b,b2).若点A与点B重合,则有b=4,且b2=3,显然不成立,∴点A不与点B重合.(3)当抛物线经过点B(4,3)时,有3=-42+2b×4,解得b=,显然抛物线右半支经过点B;当抛物线经过点C(6,2)时,有2=-62+2b×6,解得b=,这时仍然是抛物线右半支经过点C,∴b的取值范围为≤b≤.8.解:(1)∵直线y=x+4与x,y轴分别交于A,B两点,∴A(-4,0),B(0,4),将点A,B的坐标代入抛物线解析式得:解得:-则抛物线的解析式为y=-x2-3x+4,令-x2-3x+4=0,解得:x1=-4,x2=1,∴点C的坐标为(1,0).(2)设P点横坐标为m,则纵坐标为-m2-3m+4,E点纵坐标为m+4,则PE=-m2-3m+4-(m+4)=-m2-3m+4-m-4=-m2-4m=-(m+2)2+4,(-4<m<0)当m=-2时,PE有最大值4,此时点P的纵坐标为6,故当点P运动到(-2,6)时,PE最长,最长为4.9.解:(1)设抛物线的函数表达式为y=ax(x-10).∵当t=2时,AD=4,∴点D的坐标是(2,4).∴4=a×2×(2-10),解得a=-.∴抛物线的函数表达式为y=-x2+x.(2)由抛物线的对称性得BE=OA=t,∴AB=10-2t.当x=t时,y=-t2+t.∴矩形ABCD的周长=2(AB+AD)=2--=-t2+t+20=-(t-1)2+.∵-<0,0<1<10,∴当t=1时,矩形ABCD的周长有最大值,最大值是.(3)连接DB,取DB的中点,记为P,则P为矩形ABCD的中心,由矩形的对称性知,平分矩形ABCD面积的直线必过点P.连接OD,取OD中点Q,连接PQ.当t=2时,点A,B,C,D的坐标分别为(2,0),(8,0),(8,4),(2,4).结合图像知,当点G,H分别落在线段AB,DC上且直线GH过点P时,直线GH平分矩形ABCD的面积.∵AB∥CD,∴线段OD平移后得到线段GH,线段OD的中点Q平移后的对应点是P.∴抛物线的平移距离=OG=DH=QP.在△OBD中,PQ是中位线,∴PQ=OB=4.所以抛物线向右平移的距离是4.。

江苏省昆山市2017年中考数学专题复习14《二次函数图像与性质》编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（江苏省昆山市2017年中考数学专题复习14《二次函数图像与性质》）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为江苏省昆山市2017年中考数学专题复习14《二次函数图像与性质》的全部内容。

2017年中考数学专题练习14《二次函数图像与性质》【知识归纳】1．一般地，形如 的函数叫做二次函数，当a ，b 时,是一次函数． 2．二次函数y ＝ax 2＋bx ＋c 的图象是 ，对称轴是直线x= ，顶点坐标是（ ， ）. 3．抛物线的开口方向由a 确定,当a ＞0时，开口 ;当a ＜0时，开口 ；a 的值越 ，开口越 ．4．抛物线与y 轴的交点坐标为 ．当c ＞0时，与y 轴的 半轴有交点；当c ＜0时，与y 轴的 半轴有交点；当c ＝0时,抛物线过 ． 5．若a ＞0，当x ＝2ba -时，y 有最小值，为 ； 若a ＜0，当x ＝2ba-时，y 有最大值，为 ．6．当a ＞0时，在对称轴的左侧，y 随x 的增大而 ，在对称轴的右侧，y 随x 的增大而 ；当a ＜0时，在对称轴的左侧，y 随x 的增大而 ，在对称轴的右侧．y 随x 的增大而 ． 7．当m ＞0时,二次函数y ＝ax 2的图象向 平移 个单位得到二次函数y ＝a （x ＋m ）2的图象；当k ＞0时,二次函数y ＝ax 2的图象向 平移 个单位得到二次函数y ＝ax 2＋k 的图象．平移的口诀：左“ ”右 “ ”；上“ ”下“ ”． 【基础检测】1．（2016•兰州)二次函数y=x 2﹣2x+4化为y=a （x ﹣h ）2+k 的形式，下列正确的是（ )A ．y=（x ﹣1)2+2 B ．y=（x ﹣1)2+3 C ．y=（x ﹣2）2+2 D ．y=(x ﹣2)2+4 2.当x 为实数时,代数式x 2﹣2x ﹣3的最小值是 ．3．（2016•永州)抛物线y=x 2+2x+m ﹣1与x 轴有两个不同的交点，则m 的取值范围是( ）A ．m ＜2B ．m ＞2C ．0＜m≤2 D．m ＜﹣24。

人教版九年级上册数学22.1.4 二次函数y=ax²+bx+c的图象
和性质同步练习
一、单选题
解析式为，则，的值为（ ）
A ．，
B ．，
C ．，
D ．，
8．已知二次函数的图象大致如图所示．下列说法正确的是（ ）
A ．
B ．当时，
C ．
D ．若在函数图象上，当时，二、填空题
y =23x bx c ++b c 6b =1c =-18b =-23
c =6b =5c =-18b =-29
c =()20y ax bx c a =++≠20
a b -=13x -<<0
y <0
a b c ++>()()1122,,,x y x y 12x x <12
y y <
配方得：y ＝
当x ＜－1时，y 随x 增大而 ；
当x ＝－1时，y 最大值为 ；
当x ＞－1时，y 随x 增大而 ．
18．求出下列抛物线的开口方向，对称轴和顶点坐标．
（1）
(1)求这个二次函数的表达式；
(2)点是直线下方抛物线上的顶点，求2241y x x =--+2245
y x x =-+P BC
20．如图，二次函数的图象与轴交于，两点，
与
轴交于点，为抛物线的顶点．
(1)求此二次函数的解析式；
(2)求的面积；
(3)在其对称轴右侧的抛物线上是否存在一点，使是等腰三角形？若存在，请直接写出点的坐标；若不存在，请说明理由．
()20y ax bx c a =++≠x ()1,0A -()3,0B y ()0,3C D CDB △P PDC △P
参考答案：。

3.3 二次函数y=ax²的图像与性质同步训练2024-2025学年鲁教版（五四制）数学九年级上册一、单选题1．二次函数y＝﹣（x+3）2+9的图象的顶点坐标是（）A．（﹣3，9）B．（3，9）C．（9，3）D．（9，﹣3）2．抛物线y=x2−2x−a上有A(−4,y1)、B(2,y2)两点，则y1和y2的大小关系一定为（）A．y2<y1B．y1<y2C．y2<y1<0D．y1<y2<0 3．对于二次函数y=−(x−2)2−7，下列说法正确的是（）A．图象开口向上B．对称轴是直线x=−2C．当x>2时，y随x的增大而减小D．当x<2时，y随x的增大而减小4．函数y=12x2+1与y=12x2的图象的不同之处是（）A．对称轴B．开口方向C．顶点D．形状5．若A(−2,y1),B(1,y2),C(2,y3)是抛物线y=2(x−1)2+a上的三点，则y1,y2,y3为的大小关系为（）A．y1>y2>y3B．y1>y3>y2C．y3>y2>y1D．y3>y1>y2 6．已知二次函数y=−2(x−3)2+1，下列说法正确的是（）A．图象的对称轴为x=−3B．图象的顶点坐标为(3,1)C．函数的最大值是−1D．函数的最小值是−17．如图，平面直角坐标系中的二次函数图象所对应的函数解析式可能为（）A．y=−12x2B．y=−12(x+1)2C．y=−12(x−1)2−1D．y=−12(x+1)2−1二、填空题8．抛物线y=−3(x−5)2+5的顶点坐标是．9．已知y=√−2(x−3)2+36，则当x=时，y有最大值是．10．已知二次函数y＝﹣8（x+m）2+n的图象的顶点坐标是(﹣5，﹣4)，那么一次函数y＝mx+n的图象经过第象限．11．已知点A（x1，5），B（x2，5），（x1≠x2）都在抛物线y=a(x−2)2+3上，则x1+x2= ，(x1+x2)时，y= ．当x=12三、解答题12．已知抛物线y=−2(x+2)2+11．(1)确定抛物线开口方向及对称轴；(2)当x为何值时，二次函数取得最大值或最小值，并求出这个最大值或最小值？13．已知函数y=(m+3)x m2+3m−2是关于x的二次函数．(1)求m的值．(2)当m为何值时，该函数图象的开口向下？(3)当m为何值时，该函数有最小值？(4)试说明函数图象的增减性．14．如图是二次函数y1=3x2−1的图象，根据图象回答下列问题：2(1)二次函数y=x²的图象与y1的图象有什么相同和不同（各写出两条）；(2)若有一个二次函数的图象与y1的图象形状相同，且不经过第三、四象限，写出一个符合条件的二次函数的表达式．15．二次函数y＝x2的图象如图所示，请将此图象向右平移1个单位，再向下平移4个单位．（1）请直接写出经过两次平移后的函数解析式；（2）请求出经过两次平移后的图象与x轴的交点坐标，并指出当x满足什么条件时，函数值小于0？（3）若A（x1，y1），B（x2，y2）是经过两次平移后所得的函数图象上的两点，且x1＜x2＜0，请比较y1、y2的大小关系．（直接写结果）16．小强同学想画出二次函数y=−2x2−4x的图象，并根据图象研究它的性质．(1)请你帮小强先将该二次函数化成y=a(x−ℎ)2+k形式（在下面空白处写出过程），并完成下表，然后在平面直角坐标系中画出它的图象．x…−72−3−10132…y…−212−600−6−212…(2)根据图象回答问题：①该图象是一条抛物线，它的对称轴是_______；①该图象的顶点坐标为_______，该函数有最_______值（填大、小）；①当x_______时，y随x的增大而减小．。

课时训练(十四)二次函数的综合应用(限时:70分钟)1.[2018·玉林]如图K14-1,一段抛物线y=-x2+4(-2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1;将C1绕点A1旋转180°得到C2,顶点为D2;C1与C2组成一个新的图像,垂直于y轴的直线l与新图像交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),x1,x2,x3均为正数,设t=x1+x2+x3,则t的取值范围是 ()图K14-1A.6<t≤8B.6≤t≤8C.10<t≤12D.10≤t≤122.如图K14-2,O为坐标原点,边长为2的正方形OABC的顶点A在x轴的正半轴上,将正方形OABC绕顶点O顺时针旋转75°,使点B落在某抛物线的图像上,则该抛物线的解析式为()图K14-2x2D.y=-3x2A.y=2x2B.y=-1x2C.y=-123.如图K14-3,在平面直角坐标系内,二次函数y=ax2+bx(a≠0),一次函数y=ax+b(a≠0)以及反比例函数y=(k≠0)的图像都经过点A,其中一次函数的图像与反比例函数的图像还交于另一点B,且一次函数与x轴,y轴分别交于点C,D.若点A 的横坐标为1,该二次函数的对称轴是直线x=2,则下列结论:①b=-4a;②a+b>k;③8a+4b>k;④a+2b>4k.其中正确结论的个数是()图K14-3A.1个B.2个C.3个D.4个4.如图K14-4,平面直角坐标系中,抛物线y=1x2-2x+3交x轴于点B,C,交y轴于点A,点P(x,y)是抛物线上的一个动点,连接PA,AC,PC,记△ACP的面积为S.当y≤ 时,S随x变化的图像大致是 ()图K14-4图K14-55.如图K14-6,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A,B,C,D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2-2x-3,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为.图K14-66.如图K14-7,在平面直角坐标系xOy中,A(-3,0),B(0,1),形状相同的抛物线C n(n=1,2, , ,…)的顶点在直线AB上,其对称轴与x轴的交点的横坐标依次为2, ,5,8,1 ,…,那么这些抛物线称为“美丽抛物线”,根据上述规律,抛物线C2的顶点坐标为;若这些“美丽抛物线”与抛物线y=-x2+1形状相同,试写出抛物线C10的解析式.图K14-77.如图K14-8,曲线BC是反比例函数y=( ≤x≤6)的一部分,其中B(4,1-m),C(6,-m),抛物线y=-x2+2bx的顶点记作A.图K14-8(1)求k的值;(2)判断点A是否可与点B重合;(3)若抛物线与曲线BC有交点,求b的取值范围.8.在平面直角坐标系中,直线y=x+4与x,y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,并与x轴交于另一点C(点C在点A的右侧),点P是抛物线上的一个动点.(1)求抛物线的解析式及点C的坐标.(2)若点P在第二象限内,过点P作PD⊥x轴于点D,交AB于点E,当点P运动到什么位置时,PE最长?最长是多少?图K14-99.[2018·金华、丽水]如图K14-10,抛物线y=ax2+bx(a≠0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B 的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.(1)求抛物线的函数表达式.(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.图K14-10参考答案1.D[解析] 旋转后的抛物线的解析式为y=(x-4)2-4=x2-8x+12, ∵x1,x2,x3均为正数,∴点P1(x1,y1),P2(x2,y2)在第四象限,根据对称性可知:x1+x2=8,∵2≤x3≤ ,∴10≤x1+x2+x3≤120,即10≤t≤12.2.B[解析] 如图,作BE⊥x轴于点E,连接OB,设抛物线的解析式为y=ax2,由题意可知∠AOE=75°,∵∠AOB= 5°,∴∠BOE= 0°,∵OA=,∴OB=2,OB=1,∴BE=12∴OE=2-2=,∴点B的坐标为(,-1),代入y=ax2得a=-1,∴y=-1x2.=2,3.B[解析] ①对称轴为直线x=-2∴b=-4a,故结论正确;②∵一次函数与反比例函数的图像都经过点A , ∴x=1时,a+b=k ,故结论错误; ③由图像可知,x=2时,4a+2b>2, ∴8a+4b>k ,故结论正确;④a+2b=- +2b=7 b ,4k=4(a+b )=4- +b =3b ,∵二次函数图像开口向下,∴a<0,∴b=-4a>0,∴7b<3b ,∴a+2b<4k ,故结论错误.4.B [解析] 当y=0时,1x 2-2x+3=0,解得x 1=2,x 2=6,∴点B 的坐标为(2,0),点C 的坐标为(6,0);当x=0时,y=1x 2-2x+3=3,则点A 的坐标为(0,3).抛物线的对称轴为直线x=4,点A 关于直线x=4的对称点为(8,3), 利用待定系数法可求出直线AC 的解析式为y=-12x+3.过点P 作PD ∥y 轴交AC 于点D ,如图,设点P 的坐标为x ,1x 2-2x+3,则点D 的坐标为x ,-12x+3,当0≤x ≤6时,DP=-12x+3-1 x 2-2x+3=-1 x 2+2x , ∴S=12OC ·DP=-x 2+2x ,当6<x ≤8时,DP=1x 2-2x+3--12x+3=1x 2-2x ,∴S=12OC ·DP= x 2-2x.5.3+ [解析] 连接CM ,∵抛物线的解析式为y=x2-2x-3,∴点D的坐标为(0,-3),∴OD的长为3,设y=0,则0=x2-2x-3,解得:x=-1或3, ∴A(-1,0),B(3,0),∴AO=1,BO=3,∵AB为半圆的直径,∴AB=4,CM=2,OM=1,在Rt△COM中,OC=2-2=,∴CD=CO+OD=3+.6.(3,2)y=-(x-144)2+49[解析] 设直线AB的解析式为y=kx+b,则-0,1,解得:1,1,故直线AB的解析式为y=1x+1,∵抛物线C2的顶点的横坐标为3,且顶点在直线AB上,∴抛物线C2的顶点坐标为(3,2).∵对称轴与x轴的交点的横坐标依次为:2, ,5,8,1 ,21, ,55,8 ,1 …∴从第3个数开始,每个数都是前两个数的和,∴抛物线C10的顶点的横坐标为144,则纵坐标为1×144+1=49,∴抛物线C10的顶点坐标为(144,49),∵抛物线C 10与抛物线y=-x 2+1的形状相同, ∴抛物线C 10的解析式为y=-(x-144)2+49.7.解:(1)∵B (4,1-m ),C (6,-m )在反比例函数y=的图像上, ∴k=4(1-m )=6×(-m ),解得m=-2,∴k=4×[1-(-2)]=12.(2)∵m=-2,∴B (4,3),∵抛物线y=-x 2+2bx=-(x-b )2+b 2, ∴A (b ,b 2).若点A 与点B 重合,则有b=4,且b 2=3,显然不成立,∴点A 不与点B 重合.(3)当抛物线经过点B (4,3)时,有3=-42+2b×4, 解得b=18,显然抛物线右半支经过点B ;当抛物线经过点C (6,2)时,有2=-62+2b×6, 解得b=16,这时仍然是抛物线右半支经过点C ,∴b 的取值范围为1 8≤b ≤16.8.解:(1)∵直线y=x+4与x ,y 轴分别交于A ,B 两点,∴A (-4,0),B (0,4),将点A ,B 的坐标代入抛物线解析式得:16 0, ,解得:- , ,则抛物线的解析式为y=-x 2-3x+4,令-x2-3x+4=0,解得:x1=-4,x2=1,∴点C的坐标为(1,0).(2)设P点横坐标为m,则纵坐标为-m2-3m+4,E点纵坐标为m+4,则PE=-m2-3m+4-(m+4)=-m2-3m+4-m-4=-m2-4m=-(m+2)2+4,(-4<m<0) 当m=-2时,PE有最大值4,此时点P的纵坐标为6,故当点P运动到(-2,6)时,PE最长,最长为4.9.解:(1)设抛物线的函数表达式为y=ax(x-10).∵当t=2时,AD=4,∴点D的坐标是(2,4).∴4=a×2×(2-10),解得a=-1.∴抛物线的函数表达式为y=-1x2+52x.(2)由抛物线的对称性得BE=OA=t,∴AB=10-2t.当x=t时,y=-1t2+52t.∴矩形ABCD的周长=2(AB+AD)=2(10-2)-1252=-12t2+t+20=-12(t-1)2+ 12.∵-1<0,0<1<10,2∴当t=1时,矩形ABCD的周长有最大值,最大值是 1.2(3)连接DB,取DB的中点,记为P,则P为矩形ABCD的中心,由矩形的对称性知,平分矩形ABCD面积的直线必过点P.连接OD,取OD中点Q,连接PQ.当t=2时,点A,B,C,D的坐标分别为(2,0),(8,0),(8,4),(2,4).结合图像知,当点G,H分别落在线段AB,DC上且直线GH过点P时,直线GH平分矩形ABCD的面积.∵AB∥CD,∴线段OD平移后得到线段GH,线段OD的中点Q平移后的对应点是P.∴抛物线的平移距离=OG=DH=QP.在△OBD中,PQ是中位线,OB=4.∴PQ=12所以抛物线向右平移的距离是4.11。

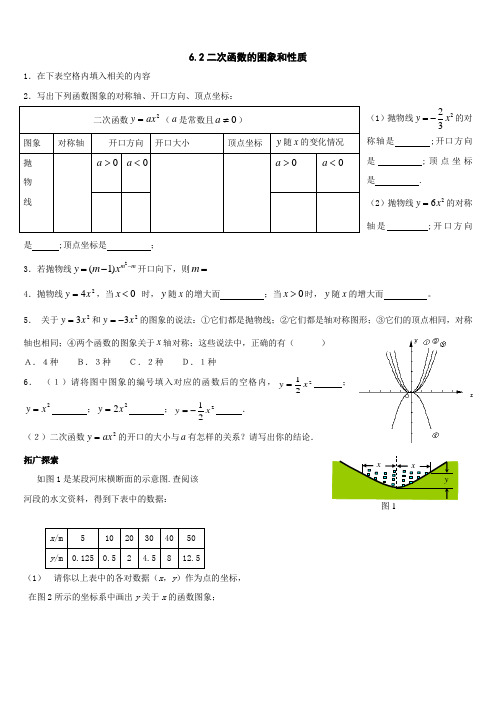
6.2二次函数的图象和性质1．在下表空格内填入相关的内容2．写出下列函数图象的对称轴、开口方向、顶点坐标：（1）抛物线223y x =-的对称轴是 ;开口方向是 ;顶点坐标是 .（2）抛物线26y x =的对称轴是 ;开口方向是 ;顶点坐标是 ； 3．若抛物线2(1)mmy m x -=-开口向下，则______=m4．抛物线24x y =，当0x < 时，y 随x 的增大而 ；当0x >时，y 随x 的增大而 。

5． 关于23x y =和23x y -=的图象的说法：①它们都是抛物线；②它们都是轴对称图形；③它们的顶点相同，对称轴也相同；④两个函数的图象关于x 轴对称；这些说法中，正确的有（ ） Ａ．４种 Ｂ．３种 Ｃ．２种 Ｄ．１种6． （１）请将图中图象的编号填入对应的函数后的空格内，221x y = ；2x y = ；22x y = ；221x y -= ．（２）二次函数2ax y =的开口的大小与a 有怎样的关系？请写出你的结论． 拓广探索如图1是某段河床横断面的示意图.查阅该 河段的水文资料，得到下表中的数据：x /m 5 10 20 30 40 50y /m 0.125 0.5 2 4.5 8 12.5（1） 请你以上表中的各对数据（x ，y ）作为点的坐标， 在图2所示的坐标系中画出y 关于x 的函数图象；二次函数2ax y =（a 是常数且0≠a ）图象 对称轴 开口方向 开口大小顶点坐标 y 随x 的变化情况 抛 物 线0>a 0<a0>a0<axxy图1（2）①填写下表：②根据所填表中数据呈现的规律，猜想出用x 表示y 的 二次函数的表达式： . （3）当水面宽度为36米时，一艘吃水深度 （船底部到水面的距离）为1.8米的货船能否在 这个河段安全通过？为什么？基础训练二1．在下表空格内填入相关的内容2.完成下列填空：（1）抛物线532+-=x y 的对称轴是 ;开口方向是 ;顶点坐标是 .这条抛物线可以看作是由抛物线23x y -=向 平移 个单位长度得到的。

1.2二次函数的图象知识点分类训练一．二次函数的图象1．在同一坐标系中，二次函数y＝ax2+bx与一次函数y＝bx﹣a的图象可能是（）A．B．C．D．2．某同学在用描点法画二次函数y＝ax2+bx+c的图象时，列出了下面的表格：x…﹣2﹣1012…y…﹣11﹣21﹣2﹣5…由于粗心，他算错了其中一个y值，则这个错误的数值是（）A．﹣11B．﹣2C．1D．﹣5二．二次函数图象与系数的关系3．如图所示是二次函数y＝ax2+bx+c图象的一部分，图象过A点（3，0），二次函数图象对称轴为x＝1，给出四个结论：①b2＞4ac；②bc＜0；③2a+b＝0；④a+b+c＝0，其中正确结论有（）个．A．0B．1C．2D．34．如图，已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＞0；②b﹣a＞c；③4a+2b+c＞0；④3a＞﹣c；⑤a+b＞m（am+b）（m≠1的实数）．其中正确结论的有（）A．①②③B．②③⑤C．②③④D．③④⑤5．如图，抛物线y＝ax2+bx+c（a≠0）过点（﹣1，0）和点（0，﹣3），且顶点在第四象限，设P＝a+b+c，则P的取值范围是（）A．﹣3＜P＜﹣1B．﹣6＜P＜0C．﹣3＜P＜0D．﹣6＜P＜﹣3 6．如图，二次函数y＝ax2+bx+c（a≠0）的图象的对称轴是直线x＝1，则以下四个结论中：①abc＞0，②2a+b＝0，③4a+b2＜4ac，④3a+c＜0．正确的个数是（）A．1B．2C．3D．47．如图，若a＜0，b＞0，c＜0，则抛物线y＝ax2+bx+c的大致图象为（）A．B．C．D．8．已知二次函数y＝ax2+bx+c的图象如图所示，有以下结论：①abc＞0，②a﹣b+c＜0，③2a＝b，④4a+2b+c＞0，⑤若点（﹣2，y1）和（﹣，y2）在该图象上，则y1＞y2．其中正确的结论是（填入正确结论的序号）．9．如图，二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于A、B两点，与y轴交于点C，对称轴是直线x＝﹣1，点B的坐标为（1，0）．下面的四个结论：①AB＝4；②b2﹣4ac＞0；③ab＜0；④a﹣b+c＜0，其中正确的结论是（填写序号）．三．二次函数图象上点的坐标特征10．若二次函数y＝|a|x2+bx+c的图象经过A（m，n）、B（0，y1）、C（3﹣m，n）、D（，y2）、E（2，y3），则y1、y2、y3的大小关系是（）A．y1＜y2＜y3B．y1＜y3＜y2C．y3＜y2＜y1D．y2＜y3＜y1 11．已知（﹣3，y1），（﹣2，y2），（1，y3）是抛物线y＝﹣3x2﹣12x+m上的点，则（）A．y3＜y2＜y1B．y3＜y1＜y2C．y2＜y3＜y1D．y1＜y3＜y2 12．已知二次函数y＝ax2﹣2ax+1（a＜0）图象上三点A（﹣1，y1），B（2，y2）C（4，y3），则y1、y2、y3的大小关系为（）A．y1＜y2＜y3B．y2＜y1＜y3C．y1＜y3＜y2D．y3＜y1＜y2 13．已知点A（x1，y1），B（x2，y2）均在抛物线y＝ax2+2ax+4（0＜a＜3）上，若x1＜x2，x1+x2＝1﹣a，则（）A．y1＞y2B．y1＜y2C．y1＝y2D．y1与y2大小不能确定14．已知函数y＝x2﹣2mx+2021（m为常数）的图象上有三点：A（x1，y1），B（x2，y2），C （x3，y3），其中x1＝﹣+m，x2＝+m，x3＝m﹣1，则y1、y2、y3的大小关系是（）A．y1＜y3＜y2B．y3＜y1＜y2C．y1＜y2＜y3D．y2＜y3＜y1 15．已知A（x1，2022），B（x2，2022）是二次函数y＝ax2+bx+5（a≠0）的图象上两点，则当x＝x1+x2时，二次函数的值是（）A．B．C．2022D．516．若直线y＝x+m与抛物线y＝x2+3x有交点，则m的取值范围是（）A．m≥﹣1B．m≤﹣1C．m＞1D．m＜117．已知函数y＝﹣（x﹣1）2图象上两点A（2，y1），B（a，y2），其中a＞2，则y1与y2的大小关系是y1y2（填“＜”、“＞”或“＝”）18．当x＝m和x＝n（m≠n）时，二次函数y＝x2﹣2x+3的函数值相等，当x＝m+n时，函数y＝x2﹣2x+3的值为．19．已知点（﹣1，m）、（2，n）在二次函数y＝ax2﹣2ax﹣1的图象上，如果m＞n，那么a0（用“＞”或“＜”连接）．20．如果点A（﹣1，4）、B（m，4）在抛物线y＝a（x﹣1）2+h上，那么m的值为．21．已知二次函数y＝ax2﹣2ax+c（a＜0）图象上的两点（x1，y1）和（3，y2），若y1＞y2，则x1的取值范围是．22．已知二次函数y＝ax2+bx+c中，自变量x与函数y的部分对应值如下表：x…﹣2023…y…8003…当x＝﹣1时，y＝．23．二次函数y＝ax2+bx+c（a≠0）的函数值y与自变量x之间的部分对应值如下表：x…﹣2﹣1012…y…﹣7﹣1355…则的值为．24．已知点A（a，m）、B（b，m）、P（a+b，n）为抛物线y＝x2﹣2x﹣2上的点，则n＝．25．已知二次函数y＝a（x﹣1）2﹣4的图象经过点（3，0）．（1）求a的值；（2）若A（m，y1）、B（m+n，y2）（n＞0）是该函数图象上的两点，当y1＝y2时，求m、n之间的数量关系．四．二次函数图象与几何变换26．抛物线y＝x2+4x+5是由抛物线y＝x2+1经过某种平移得到，则这个平移可以表述为（）A．向左平移1个单位B．向左平移2个单位C．向右平移1个单位D．向右平移2个单位27．二次函数y＝x2的图象平移后经过点（2，0），则下列平移方法正确的是（）A．向左平移2个单位，向下平移2个单位B．向左平移1个单位，向上平移2个单位C．向右平移1个单位，向下平移1个单位D．向右平移2个单位，向上平移1个单位28．二次函数y＝﹣2x2+4x+1的图象如何移动就得到y＝﹣2x2的图象（）A．向左移动1个单位，向上移动3个单位B．向右移动1个单位，向上移动3个单位C．向左移动1个单位，向下移动3个单位D．向右移动1个单位，向下移动3个单位29．将抛物线y＝2（x﹣1）2+2向左平移3个单位，再向下平移4个单位，那么得到的抛物线的表达式为．30．将抛物线y＝ax2+bx﹣1向上平移3个单位长度后，经过点（﹣2，5），则8a﹣4b﹣11的值是．31．把抛物线y＝2x2﹣4x+3向左平移1个单位长度，得到的抛物线的解析式为．32．将抛物线y＝ax2+bx+c向左平移2个单位，再向下平移5个单位，得到抛物线y＝x2+4x ﹣1，则a+b+c＝．33．已知二次函数y1＝x2+2x﹣3的图象如图所示．将此函数图象向右平移2个单位得抛物线y2的图象，则阴影部分的面积为．34．如图，将函数y＝（x﹣2）2+1的图象沿y轴向上平移得到一条新函数的图象，其中点A（1，m），B（4，n）平移后的对应点分别为点A'、B'．若曲线段AB扫过的面积为9（图中的阴影部分），则新图象的函数表达式是．35．如图，抛物线y1＝﹣x2+2向右平移1个单位得到抛物线y2，回答下列问题：（1）抛物线y2的顶点坐标；（2）阴影部分的面积S＝；（3）若再将抛物线y2绕原点O旋转180°得到抛物线y3，求抛物线y3的解析式．36．把抛物线y＝x2平移得到抛物线m，抛物线m经过点A（﹣6，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线y＝x2交于点Q．（1）求顶点P的坐标；（2）写出平移过程；（3）求图中阴影部分的面积．参考答案一．二次函数的图象1．解：由方程组得ax2＝﹣a，∵a≠0∴x2＝﹣1，该方程无实数根，故二次函数与一次函数图象无交点，排除B．A：二次函数开口向上，说明a＞0，对称轴在y轴右侧，则b＜0；但是一次函数b为一次项系数，图象显示从左向右上升，b＞0，两者矛盾，故A错；C：二次函数开口向上，说明a＞0，对称轴在y轴右侧，则b＜0；b为一次函数的一次项系数，图象显示从左向右下降，b＜0，两者相符，故C正确；D：二次函数的图象应过原点，此选项不符，故D错．故选：C．2．解：由函数图象关于对称轴对称，得（﹣1，﹣2），（0，1），（1，﹣2）在函数图象上，把（﹣1，﹣2），（0，1），（1，﹣2）代入函数解析式，得，解得，函数解析式为y＝﹣3x2+1当x＝2时，y＝﹣11，故选：D．二．二次函数图象与系数的关系3．解：由图象知和x轴有两个交点，∴Δ＝b2﹣4ac＞0，∴b2＞4ac，故①正确；由图象知，图象与y轴交点在x轴的上方，且二次函数图象对称轴为x＝1，∴c＞0，∵﹣＝1，a＜0，∴b＞0，即bc＞0，2a+b＝0，∴②不正确，③正确；由图象知，当x＝1时y＝ax2+bx+c＝a×12+b×1+c＝a+b+c＞0，∴④不正确，综合上述：正确的个数是2，故选：C．4．解：①∵对称轴在y轴的右侧，∴ab＜0，由图象可知：c＞0，∴abc＜0，故①不正确；②当x＝﹣1时，y＝a﹣b+c＜0，∴b﹣a＞c，故②正确；③由对称知，当x＝2时，函数值大于0，即y＝4a+2b+c＞0，故③正确；④∵x＝﹣＝1，∴b＝﹣2a，∵a﹣b+c＜0，∴a+2a+c＜0，3a＜﹣c，故④不正确；⑤当x＝1时，y的值最大．此时，y＝a+b+c，而当x＝m时，y＝am2+bm+c，所以a+b+c＞am2+bm+c（m≠1），故a+b＞am2+bm，即a+b＞m（am+b），故⑤正确．故②③⑤正确．故选：B．5．解：∵抛物线y＝ax2+bx+c（c≠0）过点（﹣1，0）和点（0，﹣3），∴0＝a﹣b+c，﹣3＝c，∴b＝a﹣3，∵当x＝1时，y＝ax2+bx+c＝a+b+c，∴P＝a+b+c＝a+a﹣3﹣3＝2a﹣6，∵顶点在第四象限，a＞0，∴b＝a﹣3＜0，∴a＜3，∴0＜a＜3，∴﹣6＜2a﹣6＜0，即﹣6＜P＜0．故选：B．6．解：①根据抛物线开口向下可知：a＜0，因为对称轴在y轴右侧，所以b＞0，因为抛物线与y轴正半轴相交，所以c＞0，所以abc＜0，所以①错误；②因为抛物线对称轴是直线x＝1，即﹣＝1，所以b＝﹣2a，所以b+2a＝0，所以②正确；③∵b＝﹣2a，∴b2＝4a2，如果4a+b2＜4ac，那么4a+4a2＜4ac，∵a＜0，∴c＜1+a，而根据抛物线与y轴的交点，可知c＞1，∴结论③错误；④当x＝﹣1时，y＜0，即a﹣b+c＜0，因为b＝﹣2a，所以3a+c＜0，所以④正确．所以正确的是②④，共2个．故选：B．7．解：∵a＜0，∴抛物线的开口方向向下，故第三个选项错误；∵c＜0，∴抛物线与y轴的交点为在y轴的负半轴上，故第一个选项错误；∵a＜0、b＞0，对称轴为x＝＞0，∴对称轴在y轴右侧，故第四个选项错误．故选：B．8．解：∵二次函数开口向下，且与y轴的交点在x轴上方，∴a＜0，c＞0，∵对称轴为x＝1，∴﹣＝1，∴b＝﹣2a＞0，∴abc＜0，故①、③都不正确；∵当x＝﹣1时，y＜0，∴a﹣b+c＜0，故②正确；由抛物线的对称性可知抛物线与x轴的另一交点在2和3之间，∴当x＝2时，y＞0，∴4a+2b+c＞0，故④正确；∵抛物线开口向下，对称轴为x＝1，∴当x＜1时，y随x的增大而增大，∵﹣2＜﹣，∴y1＜y2，故⑤不正确；综上可知正确的为②④，故答案为：②④．9．解：∵抛物线对称轴是直线x＝﹣1，点B的坐标为（1，0），∴A（﹣3，0），∴AB＝4，故选项①正确；∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，故选项②正确；∵抛物线开口向上，∴a＞0，∵抛物线对称轴在y轴左侧，∴a，b同号，∴ab＞0，故选项③错误；当x＝﹣1时，y＝a﹣b+c此时最小，为负数，故选项④正确；故答案为：①②④．三．二次函数图象上点的坐标特征10．解：∵经过A（m，n）、C（3﹣m，n），∴二次函数的对称轴x＝，∵B（0，y1）、D（，y2）、E（2，y3）与对称轴的距离B最远，D最近，∵|a|＞0，∴y1＞y3＞y2；故选：D．11．解：抛物线的对称轴为直线x＝﹣＝﹣2，∵a＝﹣3＜0，∴x＝﹣2时，函数值最大，又∵﹣3到﹣2的距离比1到﹣2的距离小，∴y3＜y1＜y2．故选：B．12．解：y＝ax2﹣2ax+1（a＜0），对称轴是直线x＝﹣＝1，即二次函数的开口向下，对称轴是直线x＝1，即在对称轴的右侧y随x的增大而减小，A点关于直线x＝1的对称点是D（3，y1），∵2＜3＜4，∴y2＞y1＞y3，故选：D．13．解：将点A（x1，y1），B（x2，y2）分别代入y＝ax2+2ax+4（0＜a＜3）中，得：y1＝ax12+2ax1+4﹣﹣﹣﹣①，y2＝ax22+2ax2+4﹣﹣﹣﹣②，②﹣①得：y2﹣y1＝（x2﹣x1）[a（3﹣a）]，因为x1＜x2，3﹣a＞0，则y2﹣y1＞0，即y1＜y2．故选：B．14．解：y＝x2﹣2mx+2021＝（x﹣m）2﹣m2+2021，∴抛物线开口向上，对称轴为：直线x＝m，当x＞m时，y随x的增大而增大，由对称性得：x1＝﹣+m与x＝m+的y值相等，x3＝m﹣1与x＝m+1的y值相等，且，∴+m＜m+1＜m+，∴y2＜y3＜y1；故选：D．15．解：∵A（x1，2022），B（x2，2022）是二次函数y＝ax2+bx+5（a≠0）的图象上两点，又∵点A、B的纵坐标相同，∴A、B关于对称轴x＝﹣对称，∴x＝x1+x2＝﹣，∴a+b（﹣）+5＝5；故选：D．16．解：令x+m＝x2+3x，则x2+2x﹣m＝0，令△＝22﹣4×1×（﹣m）≥0，解得，m≥﹣1，故选：A．17．解：∵函数y＝﹣（x﹣1）2，∴函数的对称轴是直线x＝1，开口向下，∵函数图象上两点A（2，y1），B（a，y2），a＞2，∴y1＞y2，故答案为：＞．18．解：∵当x＝m和x＝n（m≠n）时，二次函数y＝x2﹣2x+3＝（x﹣1）2+2的函数值相等，∴以m、n为横坐标的点关于直线x＝1对称，则＝1，∴m+n＝2，∵x＝m+n，∴x＝2，函数y＝4﹣4+3＝3．故答案为3．19．解：∵二次函数的解析式为y＝ax2﹣2ax﹣1，∴该抛物线对称轴为x＝1，∵|﹣1﹣1|＞|2﹣1|，且m＞n，∴a＞0．故答案为：＞．20．解：由点A（﹣1，4）、B（m，4）在抛物线y＝a（x﹣1）2+h上，得（﹣1，4）与（m，4）关于对称轴x＝1对称，m﹣1＝1﹣（﹣1），解得m＝3，故答案为：3．21．解：∵y1＞y2，∴a﹣2ax1+c＞9a﹣6a+c，∴a﹣2ax1﹣3a＞0，∵a＜0，∴函数y＝a﹣2ax1﹣3a开口向下，令a﹣2ax1﹣3a＝0，解得x1＝﹣1或3，画出函数图象示意图：由图象可得，当﹣1＜x＜3时，a﹣2ax1﹣3a＞0，∴x1的取值范围是﹣1＜x1＜3，故答案为：﹣1＜x1＜3．22．解：依据表格可知抛物线的对称轴为x＝1，∴当x＝﹣1时与x＝3时函数值相同，∴当x＝﹣1时，y＝3．故答案为：3．23．解：∵x＝1、x＝2时的函数值都是﹣1相等，∴此函数图象的对称轴为直线x＝﹣＝＝，即＝﹣．故答案为：﹣．24．解：∵抛物线解析式为y＝x2﹣2x﹣2＝（x﹣1）2﹣3，∴该抛物线的对称轴是直线x＝1，又∵点A（a，m）和B（b，m）关于直线x＝1对称，∴＝1，∴a+b＝2，把（2，n）代入抛物线的解析式得，n＝22﹣2×2﹣2＝﹣2．故答案是：﹣2．25．解：（1）将（3，0）代入y＝a（x﹣1）2﹣4，得0＝4a﹣4，解得a＝1；（2）方法一：根据题意，得y1＝（m﹣1）2﹣4，y2＝（m+n﹣1）2﹣4，∵y1＝y2，∴（m﹣1）2﹣4＝（m+n﹣1）2﹣4，即（m﹣1）2＝（m+n﹣1）2，∵n＞0，∴m﹣1＝﹣（m+n﹣1），化简，得2m+n＝2；方法二：∵函数y＝（x﹣1）2﹣4的图象的对称轴是经过点（1，﹣4），且平行于y轴的直线，∴m+n﹣1＝1﹣m，化简，得2m+n＝2．四．二次函数图象与几何变换26．解：原抛物线的顶点为（0，1），新抛物线的顶点为（﹣2，1），∴是抛物线y＝x2+1向左平移2个单位得到，故选：B．27．解：A、平移后的解析式为y＝（x+2）2﹣2，当x＝2时，y＝14，本选项不符合题意．B、平移后的解析式为y＝（x+1）2+2，当x＝2时，y＝11，本选项不符合题意．C、平移后的解析式为y＝（x﹣1）2﹣1，当x＝2时，y＝0，函数图象经过（2，0），本选项符合题意．D、平移后的解析式为y＝（x﹣2）2+1，当x＝2时，y＝1，本选项不符合题意．故选：C．28．解：二次函数y＝﹣2x2+4x+1的顶点坐标为（1，3），y＝﹣2x2的顶点坐标为（0，0），∴向左移动1个单位，向下移动3个单位．故选：C．29．解：抛物线y＝2（x﹣1）2+2向左平移3个单位，再向下平移4个单位得到y＝2（x﹣1+3）2+2﹣4＝2（x+2）2﹣2．故得到抛物线的解析式为y＝2（x+2）2﹣2．故答案为：y＝2（x+2）2﹣2．30．解：将抛物线y＝ax2+bx﹣1向上平移3个单位长度后，表达式为：y＝ax2+bx+2，∵经过点（﹣2，5），代入得：4a﹣2b＝3，则8a﹣4b﹣11＝2（4a﹣2b）﹣11＝2×3﹣11＝﹣5，故答案为：﹣5．31．解：∵y＝2x2﹣4x+3＝2（x﹣1）2+1，∴向左平移1个单位长度得到的抛物线的解析式为y＝2（x+1﹣1）2+1＝2x2+1，故答案为：y＝2x2+1．32．解：平移后的抛物线y＝x2+4x﹣1＝（x+2）2﹣5，顶点为（﹣2，﹣5），根据平移规律，得原抛物线顶点坐标为（0，0），又平移不改变二次项系数，∴原抛物线解析式为y＝x2，∴a＝1，b＝c＝0，∴a+b+c＝1，故答案为1．33．解：由题意知，y1＝x2+2x﹣3＝（x+1）2﹣4，则顶点坐标是（﹣1，﹣4）．所以，阴影部分的面积为：2×4＝8．故答案是：8．34．解：∵函数y＝（x﹣2）2+1的图象过点A（1，m），B（4，n），∴m＝（1﹣2）2+1＝，n＝（4﹣2）2+1＝3，∴A（1，），B（4，3），过A作AC∥x轴，交B′B的延长线于点C，则C（4，），∴AC＝4﹣1＝3，∵曲线段AB扫过的面积为9（图中的阴影部分），∴AC•AA′＝3AA′＝9，∴AA′＝3，即将函数y＝（x﹣2）2+1的图象沿y轴向上平移3个单位长度得到一条新函数的图象，∴新图象的函数表达式是y＝（x﹣2）2 +4．故答案是：y＝（x﹣2）2 +4．35．解：（1）读图找到最高点的坐标即可．故抛物线y2的顶点坐标为（1，2）；（2）把阴影部分进行平移，可得到阴影部分的面积即为图中两个方格的面积＝1×2＝2；（3）由题意可得：抛物线y3的顶点与抛物线y2的顶点关于原O成中心对称．所以抛物线y3的顶点坐标为（﹣1，﹣2），于是可设抛物线y3的解析式为：y＝a（x+1）2﹣2．由对称性得a＝1，所以y3＝（x+1）2﹣2．36．解：（1）平移的抛物线解析式为y＝（x+6）x＝x2+3x＝（x+3）2﹣，所以顶点P的坐标为（﹣3，﹣）；（2）把抛物线y＝x2先向左平移3个单位，再向下平移个单位即可得到抛物线y＝（x+3）2﹣；（3）图中阴影部分的面积＝S△OPQ＝×3×9＝．。

二次函数命题点分类集训(时间：120分钟 共26题 答对______题)命题点1 二次函数的性质1. (湘潭)抛物线y ＝2(x －3)2＋1的顶点坐标是( )A. (3，1)B. (3，－1)C. (－3，1)D. (－3，－1)2. (衢州)二次函数y ＝ax 2＋bx ＋c (a ≠0)图象上部分点的坐标(x ，y )对应值列表如下：x… －3 －2 －1 0 1 … y…－3－2－3－6－11…则该函数图象的对称轴是( ) A. 直线x ＝－3 B. 直线x ＝－2 C. 直线x ＝－1 D. 直线x ＝03. (兰州)二次函数y ＝x 2－2x ＋4化为y ＝a (x －h )2＋k 的形式，下列正确的是( )A. y ＝(x －1)2＋2B. y ＝(x －1)2＋3C. y ＝(x －2)2＋2D. y ＝(x －2)2＋44. (玉林)抛物线y ＝12x 2，y ＝x 2，y ＝－x 2的共同性质是：①都是开口向上；②都以点(0，0)为顶点；③都以y 轴为对称轴；④都关于x 轴对称．其中正确的个数有( )A. 1个B. 2个C. 3个D. 4个5. (来宾)已知函数y ＝－x 2－2x ，当________时，函数值y 随x 的增大而增大． 命题点2 二次函数图象的平移6. (上海)如果将抛物线y ＝x 2＋2向下平移1个单位，那么所得新抛物线的表达式是( )A. y ＝(x －1)2＋2B. y ＝(x ＋1)2＋2C. y ＝x 2＋1D. y ＝x 2＋37. (2015临沂)要将抛物线y ＝x 2＋2x ＋3平移后得到抛物线y ＝x 2，下列平移方法正确的是( )A. 向左平移1个单位，再向上平移2个单位B. 向左平移1个单位，再向下平移2个单位C. 向右平移1个单位，再向上平移2个单位D. 向右平移1个单位，再向下平移2个单位8. (眉山)若抛物线y ＝x 2－2x ＋3不动，将平面直角坐标系．．．．．．．．xOy 先沿水平方向向右平移1个单位，再沿铅直方向向上平移3个单位，则原抛物线图象的解析式应变为( )A. y ＝(x －2)2＋3B. y ＝(x －2)2＋5C. y ＝x 2－1D. y ＝x 2＋49. (滨州)在平面直角坐标系中，把一条抛物线先向上平移3个单位长度，然后绕原点旋转180°得到抛物线y ＝x 2＋5x ＋6，则原抛物线的解析式是( )A. y ＝－(x －52)2－114B. y ＝－(x ＋52)2－114C. y ＝－(x －52)2－14D. y ＝－(x ＋52)2＋14命题点3 二次函数图象与系数的关系10. (2015泰安)某同学在用描点法画二次函数y ＝ax 2＋bx ＋c 图象时，列出了下面的表格：x … －2 －1 0 1 2 … y…－11－21－2－5…由于粗心，他算错了其中一个y 值，则这个错误的数值是( ) A. －11 B. －2 C. 1 D. －511. (黄石)以x 为自变量的二次函数y ＝x 2－2(b －2)x ＋b 2－1的图象不经过第三象限，则实数b 的取值范围是( )A. b ≥54B. b ≥1或b ≤－1C. b ≥2D. 1≤b ≤212. (遂宁)已知直线y ＝bx －c 与抛物线y ＝ax 2＋bx ＋c 在同一直角坐标系中的图象可能是( )13. (义乌)抛物线y ＝x 2＋bx ＋c (其中b ，c 是常数)过点A (2，6)，且抛物线的对称轴与线段y ＝0(1≤x ≤3)有交点，则c 的值不可能是( )A. 4B. 6C. 8D. 1014. (常德)二次函数y ＝ax 2＋bx ＋c (a ≠0)的图象如图所示，下列结论：①b <0；②c >0；③a ＋c <b ；④b 2－4ac >0，其中正确的个数是( )A. 1B. 2C. 3D. 4第14题图 15. (2014扬州)如图，抛物线y ＝ax 2＋bx ＋c (a >0)的对称轴是过点(1，0)且平行于y 轴的直线，若点P (4，0)在该抛物线上，则4a －2b ＋c 的值为________．第15题图命题点4 二次函数图象与方程、不等式16. (宿迁)若二次函数y ＝ax 2－2ax ＋c 的图象经过点(－1，0)，则方程ax 2－2ax ＋c ＝0的解为( )A. x 1＝－3，x 2＝－1B. x 1＝1，x 2＝3C. x 1＝－1，x 2＝3D. x 1＝－3，x 2＝117. (泸州)若二次函数y ＝2x 2－4x －1的图象与x 轴交于A (x 1，0)、B (x 2，0)两点，则1x 1＋1x 2的值为________．18. (2017原创)如图，直线y ＝x ＋m 和抛物线y ＝x 2＋bx ＋c 都经过点A (1，0)和B (3，2)，不等式x 2＋bx ＋c ＞x ＋m 的解集为____________．第18题图命题点5 二次函数的实际应用 19. (台州)竖直上抛的小球离地高度是它运动时间的二次函数．小军相隔1秒依次竖直向上抛出两个小球．假设两个小球离手时离地高度相同，在各自抛出后1.1秒时到达相同的最大离地高度．第一个小球抛出后t 秒时在空中与第二个小球的离地高度相同，则t ＝________．20. (扬州)某电商销售一款夏季时装，进价40元/件，售价110元/件，每天销售20件，每销售一件需缴纳电商平台推广费用a 元(a >0)．未来30天，这款时装将开展“每天降价1元”的夏令促销活动，即从第1天起每天的单价均比前一天降1元．通过市场调研发现，该时装单价每降1元，每天销量增加4件．在这30天内，要使每天缴纳电商平台推广费用后的利润随天数t (t · 为正整数．．．．)的增大而增大，a 的取值范围应为________． 21. (青岛8分)如图，需在一面墙上绘制几个相同的抛物线型图案，按照图中的直角坐标系，最左边的抛物线可以用y ＝ax 2＋bx (a ≠0)表示．已知抛物线上B ，C 两点到地面的距离均为34 m ，到墙边OA 的距离分别为12 m ，32m.(1)求该抛物线的函数关系式，并求图案最高点到地面的距离；(2)若该墙的长度为10 m ，则最多可以连续绘制几个这样的抛物线型图案？第21题图22. (成都8分)某果园有100棵橙子树，平均每棵树结600个橙子，现准备多种一些橙子树以提高果园产量，但是如果多种树，那么树之间的距离和每一棵树所接受的阳光就会减少．根据经验估计，每多种一棵树，平均每棵果树就会少结5个橙子，假设果园多种x 棵橙子树．(1)直接写出平均每棵树结的橙子数y (个)与x 之间的关系式；(2)果园多种多少棵橙子树时，可以使橙子的总产量最大？最大为多少个？23. (十堰8分)一茶叶专卖店经销某种品牌的茶叶，该茶叶的成本价是80元/kg ，销售单价不低于120元/kg ，且不高于180元/kg.经销一段时间后得到如下数据：销售单价x (元/kg) 120 130 … 180 每天销量y (kg)10095…70设y 与x 的关系是我们所学过的某一种函数关系．(1)直接写出y 与x 的函数关系式，并指出自变量x 的取值范围； (2)当销售单价为多少时，销售利润最大？最大利润是多少？命题点6 二次函数综合题24. (宁波10分)如图，已知抛物线y ＝－x 2＋mx ＋3与x 轴交于点A ，B 两点，与y 轴交于点C ，点B 的坐标为(3，0)．(1)求m 的值及抛物线的顶点坐标；(2)点P 是抛物线对称轴l 上的一个动点，当PA ＋PC 的值最小时，求点P 的坐标．第24题图25. (百色12分)正方形OABC 的边长为4，对角线相交于点P ，抛物线L 经过O 、P 、A 三点，点E 是正方形内的抛物线上的动点．(1)建立适当的平面直角坐标系，①直接写出O ，P ，A 三点坐标；②求抛物线L 的解析式；(2)求△OAE 与△OCE 面积之和的最大值．第25题图 26. (无锡10分)已知二次函数y ＝ax 2－2ax ＋c (a >0)的图象与x 轴的负半轴和正半轴分别交于A 、B 两点，与y 轴交于点C ，它的顶点为P ，直线CP 与过点B 且垂直于x 轴的直线交于点D ，且CP ∶PD ＝2∶3.(1)求A 、B 两点的坐标；(2)若tan ∠PDB ＝54，求这个二次函数的关系式．第26题图。

yxO yxO数学：《二次函数及其图像》同步练习（人教版九年级下）【课前热身】1．将抛物线y =-3x 2向上平移一个单位后，得到的抛物线解析式是___________. 2. 如图所示的抛物线是二次函数y =ax 2-3x +a 2-1的图象， 那么a 的值是______.3. 二次函数y =(x -1)2+2的最小值是( )A. -2B. 2C. -1D. 1 4. 二次函数y =2(x -5)2+3的图象的顶点坐标是( ) A.(5，3) B.(-5，3) C.(5，-3) D.(-5，-3)5. 二次函数y =ax 2+bx +c 的图象如图所示，则下列结论正确的是( ) A. a ＞0，b ＜0，c ＞0 B. a ＜0，b ＜0，c ＞0 C. a ＜0，b ＞0，c ＜0 D. a ＜0，b ＞0，c ＞0 【知识整理】 1. 解析式：(1)一般式：y =ax 2+bx +c (a ≠0)(2)顶点式：y =a (x -h )2+k (a ≠0)，其图象顶点坐标(h ，k ).(3)两根式：y =a (x -x 1)( x -x 2) (a ≠0)，其图象与x 轴的两交点分别为(x 1，0)，(x 2，0).注意：①一般式可通过配方法化为顶点式.②求二次函数解析式通常由图象上三个点的坐标，用待定系数法求得. 若已知抛物线的顶点和对称轴，可用顶点式；若已知抛物线与x 轴的两个交点，可用两根式；若已知三个非特殊点，通常用一般式. 2. 二次函数y =ax 2+bx +c (a ≠0)的图象和性质a ＞0a ＜0图 象开 口 对 称 轴 顶点坐标最值当x =_______时，y 有最 _____值为________.当x =_______时，y 有最_____值________.增减性在对称轴左侧 y 随x 的增大而______ y 随x 的增大而______ 在对称轴右侧y 随x 的增大而______y 随x 的增大而______3. 二次函数y =a (x -h )2+k (a ≠0)的对称轴是______________，顶点坐标是___________. 4. 二次函数y =ax 2+bx +c 用配方法可化成y =a (x -h )2+k 的形式，其中h =____，k =________. 5. 二次函数y =a (x -h )2+k 的图象和y =ax 2图象的关系.6. 二次函数y =ax 2+bx +c 图象与a ，b ，c 符号的关系.(1)a 决定抛物线开口方向：a ＞0时抛物线开口向上；a ＜0时抛物线开口向上； (2)a 、b 决定对称轴x =-2ba的位置：ab ＞0时对称轴在y 轴左侧；b =0时对称轴为y 轴； ab ＜0时对称轴在y 轴右侧.(3)c 决定抛物线与y 轴交点的位置：c ＞0时抛物线交y 轴于正半轴；c =0时抛物线过原点；c ＜0时抛物线交y 轴于负半轴. 【例题讲解】例1 已知二次函数y =x 2+4x .(1)用配方法把该函数化为y =a (x -h )2+k (其中a 、h 、k 都是 常数且a ≠0)形式，并求出函数图象的对称轴和顶点坐标； (2)求函数的图象与x 轴的交点坐标； (3)直接画出函数的图象.OyxBA例2 求满足下列条件的二次函数解析式.(1)一个二次函数的图象经过点(0，0)，(1，-3)，(2，-8).(2)抛物线与x 轴交于点(-2，0)和(1，0)，与y 轴交点的纵坐标是9. (3)抛物线y =ax 2+bx +c 图象的顶点为(-2，3)，且经过点(1，6).例3 如图，直线y =x +m 和抛物线y =x 2+bx +c 都经过点A(1，0)，B(3，2). (1)求m 的值和抛物线的解析式；(2)求不等式x 2+bx +c ＞x +m 的解集．(直接写出答案)【中考演练】1. 抛物线y ＝-x 2+1的开口向＿＿＿，对称轴是＿＿＿_＿. 2. 抛物线y =(x -2)2的顶点坐标是_________.3. 将抛物线y =2x 2先向左平移3个单位，再向下平移2个单位，最后所得的抛物线的解析式为_________________.4. 函数y =x 2+bx +3的图象经过点(-1，0)，则b =_________.5. 二次函数y =(x -1)2+2，当x =______时，y 有最小值.6. 函数y =3(x -1)2+3，当x ______时，函数值y 随x 的增大而增大.7. 将y =x 2-4x +3化成y =a (x -h )2+k 的形式，则y =________________. 8. 若点A(2，m )在函数y =x 2-1的图象上，则A 点的坐标是__________. 9. 抛物线y =2x 2+3x -4与y 轴的交点坐标是___________.10. 已知二次函数y =ax 2+bx +c 的图象如图所示：则这个二次函数的解析式是y =___________.11. 请写出一个开口向上，对称轴为直线x =2，且与y 轴的交点坐标为(0，3)的抛物线的解析式________________.xy O 1 1 2 -1DCBAoyxo yxoyxoy x12. 已知二次函数y =-x 2+2x +m 的部分图象如右图所示，则关于x 的一元二次方程-x 2+2x +m =0的解为_______________.13. 在圆的面积公式S=πr 2中，S 与r 的关系是( )A.一次函数关系B.正比例函数关系C.反比例函数关系D.二次函数关系 14. 已知函数22(2)my m x -=+是二次函数，则m 等于( )A.±2B.2C.-2D.±215. 苹果熟了，从树上落下所经过的路程s 与下落时间 t 满足 s ＝12gt 2(g =9.8)，则s 与t 的函数图象大致是( )A. B. C. D.16. 抛物线y =-x 2不具有的性质是( )A.开口向下B.对称轴是y 轴C.与y 轴不相交D.最高点是原点 17. 函数y =ax 2与y =ax +b (a ＞0，b ＞0)在同一坐标系中的大致图象是( )18. 已知函数y =x 2-2x -2的图象如下图所示，根据其中提供的信息， 可求得使y ≥1成立的x 的取值范围是( ) A ．-1≤x ≤3 B ．-3≤x ≤1 C ．x ≥-3 D ．x ≤-1或x ≥319. 已知二次函数y =ax 2-4x +3的图象经过点(-1，8). (1)求此二次函数的解析式；(2)根据(1)填写下表.在直角坐标系中描点，并画出函数的图象；s tOstO stO s t Ox 0 1 2 3 4y(3)根据图象回答：当函数值y＜0时，x的取值范围是什么？20. 已知二次函数y=(m-2)x2+(m+3)x+m+2的图象过点(0，5).(1)求m的值，并写出二次函数的解析式；(2)求出二次函数图象的顶点坐标，对称轴.21. 一次函数y=2x+3，与二次函数y=a(x-h)2+k的图象交于A(m，5)和B(3，n)两点，且当x=3时，抛物线取得最值为9.(1)求二次函数的表达式；(2)在同一坐标系中画出两个函数的图象；(3)从图象上观察，x为何值时，一次函数与二次函数的值都随x的增大而增大.(4)当x为何值时，一次函数值大于二次函数值.。