回归分析程序代码

#简单线性回归fit<-lm(weight~height,data=women) #r中自带的数据集womensummary(fit)fitted(fit) #可以看到回归的拟合值fit$residuals #可以看到残差值，最大的残差值在身高矮和身高高的地方出现plot(women$height,women$weight,xlab="Height(in inches)",ylab="Weight(in pounds)")abline(fit) #两行代码用来画回归拟合直线，abline()里面是串列，注意与lines区别#多项式回归fit2<-lm(weight~height+I(height^2),data=women)summary(fit2) #I(height^2)表示向预测等式加上一个身高的平方项plot(women$height,women$weight,xlab="Height(in inches)",ylab="Weight(in pounds)")lines(women$height,fitted(fit2)) #两行代码用来画回归拟合线,lines()里面要是个list，用自变量和拟合值来画线#car包中的scatterplot()函数可以提供散点图、线性拟合曲线和平滑曲线、箱线图library(car)scatterplot(weight~height,data=women,spread=F,lty.smooth=2,pch=19,main="。

",xlab="Height(inches)",ylab="Weight(lbs.)")#spread=F选项删除了残差正负均方差根，lty.smooth=2选项设置loess拟合曲线为虚线,pch=19设置点为实心圆#多元线性回归states<-as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")]) #lm函数需要一个数据框，这里先创建一个数据框cor(states) #多元分析中，第一步最好检查变量间的相关性fit<-lm(Murder~Population+Illiteracy+Income+Frost,data=states)summary(fit) #做多元线性回归#scatterplotMatrix函数默认在非对角区域画变量间的散点图并添加平滑曲线，对角区域画每个变量的密度图和轴须图library(car)scatterplotMatrix(states,spread=F,lty.smooth=2,pch=19,main=".")#有交互作用的多元线性回归fit<-lm(mpg~hp+wt+hp:wt,data=mtcars)summary(fit) #结果表示交互作用显著，就是说响应变量与其中一个预测变量的关系依赖于另外一个预测变量的水平#effects包中的effect()函数用图形展示交互项结果。

python实现线性回归的⽰例代码⽬录1线性回归1.1简单线性回归1.2多元线性回归1.3使⽤sklearn中的线性回归模型1线性回归1.1简单线性回归在简单线性回归中，通过调整a和b的参数值，来拟合从x到y的线性关系。

下图为进⾏拟合所需要优化的⽬标，也即是MES（Mean Squared Error)，只不过省略了平均的部分（除以m）。

对于简单线性回归，只有两个参数a和b，通过对MSE优化⽬标求极值（最⼩⼆乘法），即可求得最优a和b如下，所以在训练简单线性回归模型时，也只需要根据数据求解这两个参数值即可。

下⾯使⽤波⼠顿房价数据集中，索引为5的特征RM (average number of rooms per dwelling)来进⾏简单线性回归。

其中使⽤的评价指标为：# 以sklearn的形式对simple linear regression 算法进⾏封装import numpy as npimport sklearn.datasets as datasetsfrom sklearn.model_selection import train_test_splitimport matplotlib.pyplot as pltfrom sklearn.metrics import mean_squared_error,mean_absolute_errornp.random.seed(123)class SimpleLinearRegression():def __init__(self):"""initialize model parametersself.a_=Noneself.b_=Nonedef fit(self,x_train,y_train):training model parametersParameters----------x_train:train x ,shape:data [N,]y_train:train y ,shape:data [N,]assert (x_train.ndim==1 and y_train.ndim==1),\"""Simple Linear Regression model can only solve single feature training data"""assert len(x_train)==len(y_train),\"""the size of x_train must be equal to y_train"""x_mean=np.mean(x_train)y_mean=np.mean(y_train)self.a_=np.vdot((x_train-x_mean),(y_train-y_mean))/np.vdot((x_train-x_mean),(x_train-x_mean)) self.b_=y_mean-self.a_*x_meandef predict(self,input_x):make predictions based on a batch of datainput_x:shape->[N,]assert input_x.ndim==1 ,\"""Simple Linear Regression model can only solve single feature data"""return np.array([self.pred_(x) for x in input_x])def pred_(self,x):give a prediction based on single input xreturn self.a_*x+self.b_def __repr__(self):return "SimpleLinearRegressionModel"if __name__ == '__main__':boston_data = datasets.load_boston()x = boston_data['data'][:, 5] # total x data (506,)y = boston_data['target'] # total y data (506,)# keep data with target value less than 50.x = x[y < 50] # total x data (490,)y = y[y < 50] # total x data (490,)plt.scatter(x, y)plt.show()# train size:(343,) test size:(147,)x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)regs = SimpleLinearRegression()regs.fit(x_train, y_train)y_hat = regs.predict(x_test)rmse = np.sqrt(np.sum((y_hat - y_test) ** 2) / len(x_test))mse = mean_squared_error(y_test, y_hat)mae = mean_absolute_error(y_test, y_hat)# noticeR_squared_Error = 1 - mse / np.var(y_test)print('mean squared error:%.2f' % (mse))print('root mean squared error:%.2f' % (rmse))print('mean absolute error:%.2f' % (mae))print('R squared Error:%.2f' % (R_squared_Error))输出结果：mean squared error:26.74root mean squared error:5.17mean absolute error:3.85R squared Error:0.50数据的可视化：1.2 多元线性回归多元线性回归中，单个x的样本拥有了多个特征，也就是上图中带下标的x。

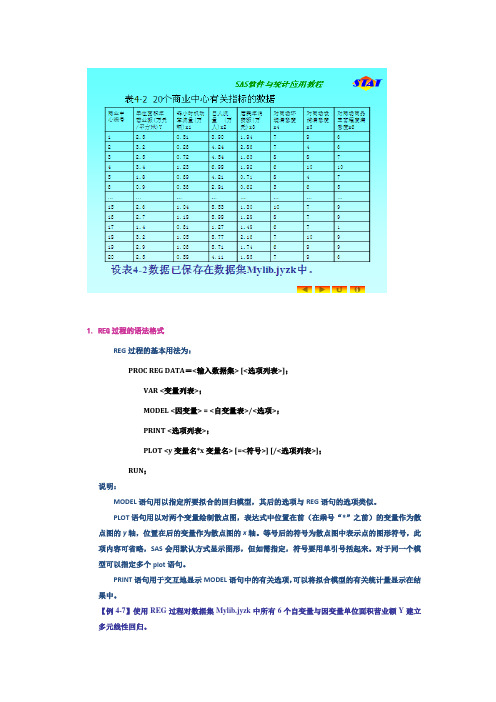
1. REG过程的语法格式REG过程的基本用法为：PROC REG DATA＝<输入数据集> [<选项列表>]；VAR <变量列表>；MODEL <因变量> = <自变量表>/<选项>；PRINT <选项列表>；PLOT <y变量名*x变量名> [=<符号>] [/<选项列表>]；RUN；说明：MODEL语句用以指定所要拟合的回归模型，其后的选项与REG语句的选项类似。

PLOT语句用以对两个变量绘制散点图，表达式中位置在前（在乘号“*”之前）的变量作为散点图的y轴，位置在后的变量作为散点图的x轴。

等号后的符号为散点图中表示点的图形符号，此项内容可省略，SAS会用默认方式显示图形，但如需指定，符号要用单引号括起来。

对于同一个模型可以指定多个plot语句。

PRINT语句用于交互地显示MODEL语句中的有关选项，可以将拟合模型的有关统计量显示在结果中。

【例4-7】使用REG过程对数据集Mylib.jyzk中所有6个自变量与因变量单位面积营业额Y建立多元线性回归。

调用如下的REG 过程就可以在输出窗口产生如图4-43所示的结果：procreg data = Mylib.jyzk; var y x1 – x6; model y = x1 – x6; run;逐步回归我们发现有些变量的作用不显著，所以使用REG 提供的自动选择最优自变量子集的选项。

在MODBL 语句中加上“SELECTION = 选择方法”的选项就可以自动挑选自变量，选择方法有NONE （全用，这是缺省），FORWARD （向前逐步引入法），BACKWARD （向后逐步剔除法），STEPWISE（逐步筛选法），MAXR （最大R 2增量法），MINR （最小R 2增量法），RSQUARE （R 2选择法），ADJRSQ （修正R 2选择法），CP （Mallows 的Cp 统计量法）。

利用SAS宏程序进行单因素Logistic回归分析在做单因素logistic回归时，如果有十几个自变量，每个自变量都运行一遍程序，然后把sas结果黏贴到word里再修改，最后合并生成一个汇总的数据，无疑是件很麻烦的事情，所以我编了一段程序，可以自动的汇总生成报表，省了很多事啊！欢迎大家共同交流宏程序如下：%macro log1(data,yy,xx,num); /*data=分析数据集，yy=应变量，xx=自变量，num=自变量个数%do i=1 %to &num;%let var_=%sysfunc(scan(&xx,&i,’ ‘));ods output ParameterEstimates=&var_.1 OddsRatios=&var_.2;proc logistic data=&data desc ;model &yy=&var_; run;data &var_.1(drop=i);set &var_.1;i=_n_;if i=1 then delete; run;data &var_ (drop=effect df);merge &var_.1 &var_.2;run;proc delete data=&var_.1 &var_.2;run;%end;data log1;set &xx;proc print noobs data=log1;proc delete data=log1 &xx;run;%mend;测试一下：%log1(factor,tw1,sex agegroup b4 b5 b6 b7 b10 b11 b12 b32a b32b b32c b32d,13);效果显示如下，（sas9.2自动生成html格式结果，stype选择journal）以上程序注意，logistic回归增加了desc选项，表示取2的概率。

proc import out= xt49 /*使用import过程导入数据并输出到数据集xt4.9*/datafile="E:\xt49.xls"dbms=excel2000 replace;getnames=yes; /*首行为变量名*/run;proc plot data=xt49;/*对xt49绘图*/plot y*x='*';/*以x为横坐标,y为纵坐标,以*为各点,画散点图*/ run;proc corr pearson data=xt49;/*对xt49运行相关分析过程*/var y x;/*计算y和x的Pearson相关系数*/run;proc reg data=xt49;/*对xt4.9运行回归分析过程*/model y=x;/*建立以y为因变量,以x为自变量的线性回归方程*/ model y=x/p r dw;/*建立以y为因变量,以x为自变量的线性回归方程，p是要求输出拟合值，r是要求输出残差值, dw是要求输出DW 检验统计量的值*/model y=x1-x4/vif；/*建立以y为因变量,以x1-x4为自变量的线性回归方程，vif是要求输出各自变量的VIF值*/output out=res p=yhat r=residual;/*输出拟合值和残差值至数据集res，以便绘制残差图*/run;-------------------------以下是绘制残差图的程序，data res_new;/*创建新数据集res_new*/set res;/*先把res数据集复制过来*/lag1residual=lag1(residual);/*lagn（n自定）函数可把一变量的各观测值移后n位；residual即t e,lag1residual即1t e-*/t=_n_;/*_n_是data步内读取观测值的计数器变量，从1开始，每读取一观测值自加1，因此变量t的观测值即为期数1,2,...,n*/ run;proc plot data=res_new;/*绘制残差图*/plot residual*lag1residual='*';/*以residual即残差值为纵坐标，以residual2即拟合值为横坐标*/plot residual*t='*';/*以residual即残差值为纵坐标，以t即拟合值为横坐标*/run;- ------------------以下是进行一阶差分后建立回归模型以及其自相关检验的程序data et49_new;/*创建新数据集ch4_new*/set xt49;/*先把ch4数据集复制过来*/difx=x-lag1(x);/*lagn（n自定）函数可把一变量的各观测值移后n 位；对x各观测值作一阶差分*/dify=y-lag1(y);/*lagn（n自定）函数可把一变量的各观测值移后n 位；对y各观测值作一阶差分*/run;proc reg;/*对ex4.9_new运行回归分析过程*/model dify=difx/p r dw;/*建立以y为因变量,以difx为自变量的线性回归方程，p是要求输出拟合值，r是要求输出残差值,dw是要求输出DW检验统计量的值*/output out=res p=yhat r=residual;/*输出拟合值和残差值至数据集res，以便绘制残差图*/run;data res_new;/*创建新数据集res_new*/set res;/*先把res数据集复制过来*/lag1residual=lag1(residual);/*lagn（n自定）函数可把一变量的各观测值移后n位；residual即,lag1residual即*/t=_n_;/*_n_是data步内读取观测值的计数器变量，从1开始，每读取一观测值自加1，因此变量t的观测值即为期数1,2,...,n*/run;proc plot data=res_new;/*绘制残差图*/plot residual*lag1residual='*';/*以residual即残差值为纵坐标，以residual2即拟合值为横坐标*/plot residual*t='*';/*以residual即残差值为纵坐标，以t即拟合值为横坐标*/run;_ _ _ _ _ _ _ _ _ 异常值的的识别假定有一数据集ch，因变量为y，自变量为x1-x2(或x)。

python代码实现回归分析--线性回归python代码实现回归分析--线性回归科技爱好者#概念篇:#⼀下是我⾃⼰结合课件理解的,如果理解的有问题,期望看到的⼈能够好⼼告诉我⼀下,我将感激不尽~#1.什么数据建模? 通过原有数据找到其中的规律,并总结成模型.#2.什么是模型概念? 通过规律总结的模型,来预测⾃变量的结果(因变量).#3.什么是回归分析? 是⽤来解释⾃变量和因变量之间关系的⼀种⽅法.#4.什么是线性回归? 回归分析的⼀种,评估⾃变量和因变量是⼀种线性关系的的⼀种⽅法.#5. 什么是⼀元线性回归? 就是⾃变量只有⼀个的线性回归(影响元素只有⼀种).#6. 什么是多元线性回归? 就是⾃变量是多个的线性回归(影响元素不⽌⼀种).#7. 什么是拟合? 回归分析的具体实现⽅式(构建出最能串联现实实际情况的算法公式)#8. 什么是模型参数? 就是能够解释⾃变量和因变量关系的参数.#代码表⽰篇:#⼀元线性回归程序:#1.基本⼯具导⼊.import numpy as np#调科学计算包中线性模块⾥的线性回归函数from sklearn.linear_model import LinearRegression#条⽤科学计算包中的⽅法选择模块⾥的⽤于切分测试集和训练集的函数.from sklearn.model_selection import train_test_split#2.建造数据#随机数种⼦,事先设置之后,就能固定值随机数.#PS:0可以理解成这组随机数的编号,只要在下边填写同样编号得到的数值是同⼀组随机数数值.np.random.seed(0)#从-10到10之间的100个等差数列(属于连续性数组)x = np.linspace(-10,10,100)#设置⼀个线性回归公式y = 0.85*x - 0.72#创建⼀组数量为100,均值为0,标准差为0.5的随机数组.e = np.random.normal(loc = 0,scale = 0.5,size = x.shape)#将变量y加上这个变量ey += e#将x转换为⼆维数组,因为fit⽅法要求x为⼆维结构.x= x.reshape(-1,1)lr = LinearRegression()#x:被划分的特征集,y:被划分的标签,test_size:样本的占⽐(如果是整数表⽰样本的数量),random_state:随机数种⼦编号X_train,X_test,y_train,y_test = train_test_split(x,y,test_size = 0.25,random_state=0)#拟合数据函数:(X_train,y_train)#拟合后可利⽤lr.coef和lr.intercept取出(w))权重和(b))截距.print('权重',lr.coef_)print('截距',lr.intercept_)#从训练集学习到了模型的参数(w与b),确定⽅程,就可以进⾏预测了.#定义⼀个预测函数y_hat = lr.predict(X_test)#⽐对⼀下预测的y值与实际y值print("实际值:",y_test.ravel()[:10])print("预测值:",y_hat[:10])import matplotlib as mplimport matplotlib.pyplot as plt#画布初始设定:mpl.rcParams[""] = "SimHei"mpl.rcParams["axes.unicode_minus"] =False#将训练集和测试集⽤散点形式表现plt.scatter(X_train,y_train,s = 15,label = '训练集') plt.scatter(X_test,y_test,s = 15,label = '测试集')#将预测结果⽤直线画出plt.plot(x,lr.predict(x),"r-")#显⽰说明plt.legend()#⽤图标表⽰出真实值与预测值plt.figure(figsize = (15,5))plt.plot(y_test,label = "真实值",color = "r",marker = "o") plt.plot(y_hat,label = "预测值",color = "g",marker = "o") plt.xlabel("测试集数据序号")plt.ylabel("数据值")plt.legend()#线性回归模型评估from sklearn.metrics import mean_squared_error,mean_absolute_error,r2_scoreprint("平均⽅误差(MSE):",mean_squared_error(y_test,y_hat))print("根均⽅误差( RMSE):",mean_absolute_error(y_test,y_hat))print("平均绝对值误差(MAE):",r2_score(y_test,y_hat))from sklearn.linear_model import LinearRegressionfrom sklearn.metrics import mean_absolute_errorfrom sklearn.model_selection import train_test_split#make_regression ⽤来⽣成样本数据,⽤于回归模型from sklearn.datasets import make_regression# n_sampless:⽣成样本个体的数量#n_features: 特征数量(x的数量)#bias:偏置值.#random_state :随机种⼦#noise:噪⾳#⽣成线性回归的样本数据# n_sampless:⽣成样本个体的数量#n_features: 特征数量(x的数量)#coef: 是否返回权重.ture 返回,false不返回#bias:偏置值.#random_state :随机种⼦X,y,coef = make_regression(n_samples=1000,n_features=2,coef=True,bias=5.5,random_state=0) X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.25,random_state=0)print("实际权重:",coef)lr = LinearRegression()(X_train,y_train)print("模型权重:",lr.coef_)print("截距:",lr.intercept_)y_hat = lr.predict(X_test)print("均⽅误差:",mean_absolute_error(y_test,y_hat))print("训练集R~2:",lr.score(X_train,y_train))print("训练集R~2:",lr.score(X_test,y_test))。

r语言逻辑回归代码R语言是一种用于统计分析和数据可视化的编程语言。

逻辑回归是R语言中常用的一种回归分析方法，用于建立分类模型。

下面我们将介绍逻辑回归在R语言中的代码实现和应用。

逻辑回归是一种广义线性模型，用于预测二分类或多分类的结果。

在逻辑回归中，我们需要使用一个或多个自变量来预测一个二分类或多分类的因变量。

逻辑回归的输出是一个概率值，表示某个样本属于某个类别的概率。

在R语言中，我们可以使用glm()函数进行逻辑回归的建模。

首先，我们需要准备数据集，并对数据进行预处理。

通常情况下，我们需要将数据集分为训练集和测试集，以便评估模型的性能。

接下来，我们可以使用glm()函数来建立逻辑回归模型。

该函数的基本语法如下：glm(formula, data, family)其中，formula表示模型的公式，data表示数据集，family表示模型的分布类型。

在逻辑回归中，我们通常使用二项分布（binomial）作为模型的分布类型。

在实际应用中，我们常常需要调整模型的参数以获得更好的性能。

例如，我们可以使用stepAIC()函数进行变量选择，以选择最佳的自变量组合。

此外，我们还可以使用cross-validation（交叉验证）来评估模型的性能，并选择最佳的模型。

完成模型建立后，我们可以使用predict()函数来对新的样本进行预测。

该函数的基本语法如下：predict(model, newdata, type)其中，model表示已建立的模型，newdata表示新的样本数据，type表示预测的类型（例如，类别或概率）。

在分析完成后，我们可以使用summary()函数来查看模型的摘要信息，包括模型的系数、标准误差、p值等统计指标。

此外，我们还可以使用confint()函数来计算模型系数的置信区间。

在实际应用中，逻辑回归可以用于许多领域，例如医学、金融、市场营销等。

在医学领域，逻辑回归可以用于预测疾病的风险因素，帮助医生进行疾病预防和治疗。

回归分析R语⾔代码9.1R中函数plot（）提供了散点图的绘制⽅法，其调⽤格式为：plot()函数是R中基本的画x-y两个变量的函数，其⽤法如下为：plot(x, y, ...)R中函数cor（）提供了相关系数的求解⽅法，其调⽤格式为：cor(x)中x是矩阵或数据框; 如果x和y为矩阵或者数据框，cor(x,y)可以计算x 和y的线性相关系数，或者相关矩阵R中函数cor.test（）提供了相关系数的求解⽅法，其调⽤格式为：cor.test(x, y, alternative = c(“two.sided”, “less”, “greater”), method = c("pearson", "kendall", "spearman"),conf.level = 0.95)其中x,y是供检验的样本；alternative指定是双侧检验还是单侧检验；method为检验的⽅法；conf.level为检验的置信⽔平。

在9.1案例中，R实现的代码如下：re=read.csv('E:/商务/a.csv',header=TRUE)plot(re)cor(re)cor.test(re[,1],re[,2]) #对re的第⼀列和第⼆列数据做相关性系数检验程序结果截图如下：将数据存储在命名为a的csv⽂件下，具体内容见下：re=read.csv('E:/商务/a.csv',header=TRUE)plot(re)cor(re)cor.test(re[,1],re[,2])9.2R中函数lm（）提供了R语⾔中经常⽤到的函数，⽤来拟合回归模型，其调⽤格式为：myfit<-lm(formula,data)formula指要拟合的模型形式，data是⼀个数据框，包含了⽤于拟合模型的数据。

在9.2案例中，R实现的代码如下：sol.lm<-lm(y~x,re)summary(sol.lm)程序结果截图如下：9.3R中函数lm（）提供了R语⾔中经常⽤到的函数，⽤来拟合回归模型，其调⽤格式为：myfit<-lm(formula,data)formula指要拟合的模型形式，data是⼀个数据框，包含了⽤于拟合模型的数据。

回归分析MATLAB 工具箱一、多元线性回归多元线性回归：p p x x y βββ+++=...110 1、确定回归系数的点估计值： 命令为：b=regress(Y , X ) ①b 表示⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=p b βββˆ...ˆˆ10②Y 表示⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n Y Y Y Y (2)1③X 表示⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=np n n p p x x x x x xx x x X ...1..................1 (12)12222111211 2、求回归系数的点估计和区间估计、并检验回归模型：命令为：[b, bint,r,rint,stats]=regress(Y ,X,alpha) ①bint 表示回归系数的区间估计. ②r 表示残差. ③rint 表示置信区间. ④stats 表示用于检验回归模型的统计量,有三个数值：相关系数r 2、F 值、与F 对应的概率p.说明：相关系数2r 越接近1,说明回归方程越显著；)1,(1-->-k n k F F α时拒绝0H ,F 越大,说明回归方程越显著；与F 对应的概率p α<时拒绝H 0,回归模型成立. ⑤alpha 表示显著性水平(缺省时为0.05) 3、画出残差及其置信区间. 命令为：rcoplot(r,rint) 例1.如下程序. 解：(1)输入数据.x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]'; X=[ones(16,1) x];Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]'; (2)回归分析及检验.[b,bint,r,rint,stats]=regress(Y ,X) b,bint,stats得结果：b = bint =-16.0730 -33.7071 1.5612 0.7194 0.6047 0.8340 stats =0.9282 180.9531 0.0000即7194.0ˆ,073.16ˆ10=-=ββ；0ˆβ的置信区间为[-33.7017,1.5612], 1ˆβ的置信区间为[0.6047,0.834]; r 2=0.9282, F=180.9531, p=0.0000,我们知道p<0.05就符合条件, 可知回归模型 y=-16.073+0.7194x 成立. (3)残差分析,作残差图. rcoplot(r,rint)从残差图可以看出,除第二个数据外,其余数据的残差离零点均较近,且残差的置信区间均包含零点,这说明回归模型 y=-16.073+0.7194x 能较好的符合原始数据,而第二个数据可视为异常点.(4)预测及作图.z=b(1)+b(2)*x plot(x,Y,'k+',x,z,'r')二、多项式回归 (一)一元多项式回归.1、一元多项式回归：1121...+-++++=m m m m a x a x a x a y(1)确定多项式系数的命令：[p,S]=polyfit(x,y,m)说明：x=(x 1,x 2,…,x n ),y=(y 1,y 2,…,y n )；p=(a 1,a 2,…,a m+1)是多项式y=a 1x m +a 2x m-1+…+a m x+a m+1的系数；S 是一个矩阵,用来估计预测误差. (2)一元多项式回归命令：polytool(x,y,m) 2、预测和预测误差估计.(1)Y=polyval(p,x)求polyfit 所得的回归多项式在x 处的预测值Y ；(2)[Y,DELTA]=polyconf(p,x,S,alpha)求polyfit 所得的回归多项式在x 处的预测值Y 及预测值的显著性为1-alpha 的置信区间Y±DELTA ；alpha 缺省时为0.5.例 1. 观测物体降落的距离s 与时间t 的关系,得到数据如下表,求s. (关于t 的回归方程2解法一：直接作二次多项式回归. t=1/30:1/30:14/30;s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48]; [p,S]=polyfit(t,s,2) 得回归模型为：1329.98896.652946.489ˆ2++=t t s解法二：化为多元线性回归. t=1/30:1/30:14/30;s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48]; T=[ones(14,1) t' (t.^2)'];[b,bint,r,rint,stats]=regress(s',T); b,stats得回归模型为：22946.4898896.651329.9ˆt t s ++=预测及作图： Y=polyconf(p,t,S) plot(t,s,'k+',t,Y,'r')(二)多元二项式回归多元二项式回归命令：rstool(x,y,’model’, alpha )说明：x 表示n ⨯m 矩阵；Y 表示n 维列向量；alpha ：显著性水平(缺省时为0.05)；model 表示由下列4个模型中选择1个(用字符串输入,缺省时为线性模型)：linear(线性)：m m x x y βββ+++= 110purequadratic(纯二次)：∑=++++=nj j jjm m x x x y 12110ββββinteraction(交叉)：∑≤≠≤++++=mk j k j jkm m x x x x y 1110ββββquadratic(完全二次)：∑≤≤++++=mk j k j jkm m x x x x y ,1110ββββ例1. 设某商品的需求量与消费者的平均收入、商品价格的统计数据如下,建立回归模型,预测平均收入为1000、价格为6时的商品需求量. 需求量 100 7580 70 50 65 90100 110 60 收入 1000 600 1200 500 300 400 13001100 1300 300解法一：选择纯二次模型,即2222211122110x x x x y βββββ++++=. 直接用多元二项式回归：x1=[1000 600 1200 500 300 400 1300 1100 1300 300]; x2=[5 7 6 6 8 7 5 4 3 9];y=[100 75 80 70 50 65 90 100 110 60]'; x=[x1' x2'];rstool(x,y,'purequadratic')在左边图形下方的方框中输入1000,右边图形下方的方框中输入6，则画面左边的“Predicted Y”下方的数据变为88.47981,即预测出平均收入为1000、价格为6时的商品需求量为88.4791. 在画面左下方的下拉式菜单中选”all”, 则beta 、rmse 和residuals 都传送到Matlab 工作区中. 在Matlab 工作区中输入命令：beta, rmse 得结果：beta =110.5313 0.1464 -26.5709 -0.0001 1.8475 rmse =4.5362故回归模型为：2221218475.10001.05709.261464.05313.110x x x x y +--+= 剩余标准差为4.5362, 说明此回归模型的显著性较好.解法二：将2222211122110x x x x y βββββ++++=化为多元线性回归： X=[ones(10,1) x1' x2' (x1.^2)' (x2.^2)']; [b,bint,r,rint,stats]=regress(y,X); b,stats结果为: b =110.5313 0.1464 -26.5709 -0.0001 1.8475 stats =0.9702 40.6656 0.0005三、非线性回归1、非线性回归：(1)确定回归系数的命令：[beta,r,J]=nlinfit(x,y,’model’, beta0)说明：beta 表示估计出的回归系数；r 表示残差；J 表示Jacobian 矩阵；x,y 表示输入数据x 、y 分别为矩阵和n 维列向量,对一元非线性回归,x 为n 维列向量；model 表示是事先用m-文件定义的非线性函数；beta0表示回归系数的初值. (2)非线性回归命令：nlintool(x,y,’model’, beta0,alpha) 2、预测和预测误差估计：[Y,DELTA]=nlpredci(’model’, x ,beta,r,J)表示nlinfit 或nlintool 所得的回归函数在x 处的预测值Y 及预测值的显著性为1-alpha 的置信区间Y±DELTA. 例1. 如下程序.解：(1)对将要拟合的非线性模型y=a x b e /,建立m-文件volum.m 如下：function yhat=volum(beta,x) yhat=beta(1)*exp(beta(2)./x); (2)输入数据： x=2:16;y=[6.42 8.20 9.58 9.5 9.7 10 9.93 9.99 10.49 10.59 10.60 10.80 10.60 10.90 10.76]; beta0=[8 2]'; (3)求回归系数：[beta,r ,J]=nlinfit(x',y','volum',beta0)； beta (4)运行结果：beta =11.6036 -1.0641 即得回归模型为：xey 10641.16036.11-=(5)预测及作图：[YY ,delta]=nlpredci('volum',x',beta,r ,J)； plot(x,y,'k+',x,YY,'r')四、逐步回归1、逐步回归的命令：stepwise(x,y,inmodel,alpha)说明：x 表示自变量数据,m n ⨯阶矩阵；y 表示因变量数据,1⨯n 阶矩阵；inmodel 表示矩阵的列数的指标,给出初始模型中包括的子集(缺省时设定为全部自变量)；alpha 表示显著性水平(缺省时为0.5).2、运行stepwise 命令时产生三个图形窗口：Stepwise Plot,Stepwise Table,Stepwise History. 在Stepwise Plot 窗口,显示出各项的回归系数及其置信区间.(1)Stepwise Table 窗口中列出了一个统计表,包括回归系数及其置信区间,以及模型的统计量剩余标准差(RMSE)、相关系数(R-square)、F 值、与F 对应的概率P.例1. 水泥凝固时放出的热量y 与水泥中4种化学成分x1、x2、x3、 x4有关,今测得一组数据如下,试用逐步回归法确定一个线性模型.解：(1)数据输入：x1=[7 1 11 11 7 11 3 1 2 21 1 11 10]';x2=[26 29 56 31 52 55 71 31 54 47 40 66 68]';x3=[6 15 8 8 6 9 17 22 18 4 23 9 8]';x4=[60 52 20 47 33 22 6 44 22 26 34 12 12]';y=[78.5 74.3 104.3 87.6 95.9 109.2 102.7 72.5 93.1 115.9 83.8 113.3 109.4]'; x=[x1 x2 x3 x4];(2)逐步回归.①先在初始模型中取全部自变量：stepwise(x,y)得图Stepwise Plot 和表Stepwise Table.图Stepwise Plot中四条直线都是虚线,说明模型的显著性不好.从表Stepwise Table中看出变量x3和x4的显著性最差.②在图Stepwise Plot中点击直线3和直线4,移去变量x3和x4.移去变量x3和x4后模型具有显著性虽然剩余标准差(RMSE)没有太大的变化,但是统计量F的值明显增大,因此新的回归模型更好.(3)对变量y和x1、x2作线性回归.X=[ones(13,1) x1 x2];b=regress(y,X)得结果：b =52.57731.46830.6623故最终模型为：y=52.5773+1.4683x1+0.6623x2。

用列表混凝土强度数据进行回归python步骤详细解答回归分析是统计学和数据分析中十分重要的一种分析方法。

它通常被用来研究两个或更多变量之间的关系。

在这篇文章中，我们将以列表混凝土强度数据为例，讲解如何进行回归分析。

第一步：导入数据和库在Python中，我们要使用pandas库来读取数据。

我们首先通过以下代码导入pandas、matplotlib库，然后读取数据并存储在一个名为df的数据框中。

```pythonimport pandas as pdimport matplotlib.pyplot as pltdf=pd.read_csv('concrete.csv')```第二步：数据预处理在我们进行回归分析之前，通常需要对数据进行预处理。

首先，让我们检查数据的一些基本信息。

我们可以使用以下代码来显示数据框的前五行和概要信息。

```pythonprint(df.head())print(df.describe())```在概要信息中，我们可以看到数据集有1030个样本，每个样本具有9个特征。

此外，我们还需要检查是否有缺失数据或异常数据。

在这个数据集中，我们没有缺失数据或异常数据。

第三步：数据分析在回归分析中，我们通常使用散点图来显示两个变量之间的关系。

我们可以使用以下代码来显示我们要研究的两个变量——混凝土强度(Concrete compressive strength)和水泥用量(Cement)之间的关系。

```pythonplt.scatter(df['Cement'],df['Concrete compressive strength'])plt.xlabel('Cement')plt.ylabel('Concrete compressive strength')plt.show()```通过散点图我们可以看到，混凝土强度和水泥用量之间存在着一定的正相关性。