近五年(含2017)新课标I卷全国高考文理科数学考点分布统计表

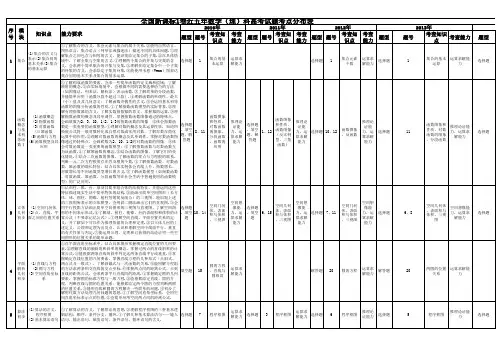
近5年高考全国卷各科高频考点分布图+2017年复习建议数学（文科）一、高频考点分析由以上柱形图可知，新课标I 卷高考文科数学近六年高频考点为：1. 函数与导数，立体几何，圆锥曲线，三角函数与解三角形，数列，年均占比14.45%，12.98%，10.13%，9.44%，6.78%；2. 统计，概率，不等式与线性规划，年均占比4-6%；集合与简易逻辑、复数、算法与框图，年均考查约5分左右，即一道选/填分值；3. 最后一道计算题为3选1，10分，可在圆、相似；参数方程、极坐标方程；解绝对值不等式、最值这三道大题中任选其一。

二、复习建议及应试技巧●试卷结构：1. 选择题12×5，最后2-3道较难；2. 填空题4×5，最后1-2道稍有难度；3. 解答题5×12+10。

●考试时间分布：共120分钟，选择题40分钟，解答题80分钟。

●复习建议：1. 研读大纲；2. 回归教材；3. 专题复习，归纳同类；4. 适当练习，重视典例。

语文语文科目课标Ⅰ卷与课标Ⅱ考查形式上和难度差别不大，考题内容选材上有所区别。

2017年考试大纲修订内容：更注重体现语文学科的基础性和综合性，优化考查内容，调整选考模块，全面考查语文能力和人文素养。

1．能力目标设计学科化，注重考查更高层级的思维能力，如鉴赏评价能力。

2．适度增加阅读量，考查信息时代和高校人才选拔要求的快速阅读能力和信息筛选处理能力。

3．现行考试大纲规定的2个选考模块分别为“文学类文本阅读”和“实用类文本阅读”，要求学生从两道选考题中选择1道作答。

修订后的考试大纲取消选考模式，将“文学类文本阅读”和“实用类文本阅读”均作为必考内容。

4．在“古诗文阅读”部分增加“了解并掌握常见的古代文化常识”的考查内容。

另外，需要注意的是，2011-2016年均是材料作文。

备考建议：1、今后的高考语文试题，势必会从新闻、科普文、学术论文、文学作品等材料中，选取更多生动鲜活的事例，意在引导考生将自身的发展与国家和民族的前途命运紧紧联系起来。

(1)卷全国高考文理科数学考点分布统计表近五年（含2017）新课标II2010-2017 卷高考理科数学考点分布统计表年新课标20172012 2015 2013 20102016 2011 2014 题次一元二求不等集合运算集合的运算（集合运算复数运算：不等式集（绝对值复数（集合的1 不等式有限集、并集式、除法、无理不等式合运算法、共轭合间关传统文化中的三角函（诱函数性复数平方复数相等复数（除法复数运算几何（单调性排列组合公式正弦和率问除法2乘分式、模的运乘法、共轭）运奇偶性公式逆用奇函数导数（切线复数的概念及等差数统计分函数及特称命题的算法（分式函数一复数运算 3 及其运抽绝对值环，算与简易逻比一次积的奇三角函数（独立重复试验双曲线古典概圆锥曲线圆锥曲线等差数列结合周运动、角几等车互斥事件和点到渐椭圆离（计数双曲线4度、画图，概式运心率公线的距理型思想向量数量积三角函函数的奇偶性双曲线数列等程序框图概率二曲线的标准逻 5 （单调性（定义范数分单调运算性倍角立体几何三视图二项式定理求二项分布的程序框图球体嵌三视图实际应用题球的表6三视功正方体锥体原立体积与体积计（双曲函数图算法（框图三视图空间几何体求数列等心率与平面向量的棱锥体的识别循环结构、程序框7线位置面何运数用了导计项求和系二项式三视图指数函由三角函数函数性质（圆锥曲线导数应用（两个方体与与对数像求单调递8函数、复合等轴双程序框积、特柱组合求切数的性区数线抛物积计项程序框三角函数二项式三角函数平移线性规三角（同角与算法程序框定积单调性数求参9 恒等变换求最的范圆锥曲线立体几何（函数性质抛物线与过焦抛物线抛物线向量与二项式定理韦判断函椭圆10 棱柱与球、点三角开式的系性弦长问定的表面积图像5/ 1（1）近五年新课标（含卷全国高考文理科数学考点分布统计表2017）1平面的截面面问题，分段函数（图立体几何面平行异面直三视图象变换含绝三角函球函数性质球体内指数与函数结ii 性质定理值对数运算（性质柱的表面所成的数形结三棱异面直函数图像所成的函数图三角函导数的综合递数列函数性质双曲线（中（反比的性（函数极用零点取数列新颖规12 三角关弦反函型点、单调范数向量的偶函数，求向量运算二项展随机模拟和向量运算量积及线性规13 向量模长运数量积积求参数标运线性规划二项式（与椭线性规划求最三角函四边形椭圆的顶点三视图（给理指定线的位数列：14最域视图写图形线性的标准方系关系三角函数双曲线与点到直线与圆（球内截函数奇等比数正态分布15 线性规划斜辅助角的距及其应求圆方程切求概性单调函数性质数列已平面图形折叠正余弦定理线性规解三角形（递推关对称性直线与解三角16 形结合思积、求角最大体的应求最项数列正弦定理解三角形项的解三角形与数列（递推等比数三角函数与解余弦定正弦定理数列通项等差数列系叠加、等比（列项正弦定理17 角放缩求余弦定理及三角余弦定错位相减义与通项公式和和求边面积公拆项消去垂直问立体几何立体几何空间垂直判证明面面垂直立几（统计与的证明线线垂四棱锥（线异面线面平行与性质分段体、垂直率系，求二面角18 空间向证明线线面角垂直线所成角的三棱锥二面角数分布余弦算的应5 / 2新课标1（卷全国高考文理科数学考点分布统计表含（1）近五年2017）非线性拟合；线概率与统立体几何：统计与概性回归方程求统计（随机抽计、独立重线性回归随机变服从正态分布模统计概率线线垂直率：利用回归方19样、独立性检法；型及数学期望量的分布证明二面方程（分布列）复试验概程进行预报预验率分布测解析几何直线与圆锥曲圆锥曲抛物线的切线椭圆（直线解析几何（椭圆）的位解析几轨迹方（圆、直线与抛物抛物线解析几何椭圆位置关关系（定（20弦长公式与函综合圆椭圆基本关系、等差位置关系探韦达定理，过法）、韦迹、导数列第一定义计算新问题点问题定导数：利用导数研导数及单线、求曲线的切线导数函数导数（应用（导数应用导数求利用导数求参新概念的理解数、二次、区间不数；不范围研究函数点、范围数不等函数单21分段函数的综合式分类式调性、最值零点问题不等式恒立求分类讨论点论求参分类讨论明取值范圆的切线判四点共圆直线与极坐标与参数与性质圆周（四点几何证几何证22圆、相几何证的位置圆、相似定理直角三系及证形射影定参数方程坐标系坐标系直角坐标方极坐标参数方程直线与圆的参数方程参数方程与极坐标互化程与直参数方数方程、求极坐标不等式证23坐标方直线与圆的求交点极坐标的互化求距置关应不等式不等式绝对值函数（分段函含绝对值不不等绝对值不等（图象，解绝的图像个绝绝对值式解法分段恒24等式个绝值不等式，对值不数一元二次值）、求等值求等式解形结合数的取式的数的范近五2017新课卷高考文科数学考点分布统计题20132014201520162017一元二次不集合运算不集合的运算（复数运算：分式求不等式集合的式、集合运算1式集合间关集、并集除法、交5/ 3近五年（含2017）新课标I卷全国高考文理科数学考点分布统计表（1）5/ 4近五年（含2017）新课标I卷全国高考文理科数学考点分布统计表（1）/ 5。

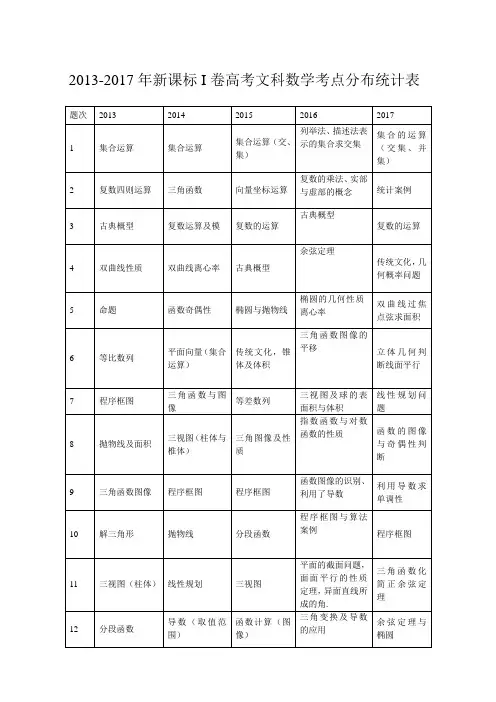
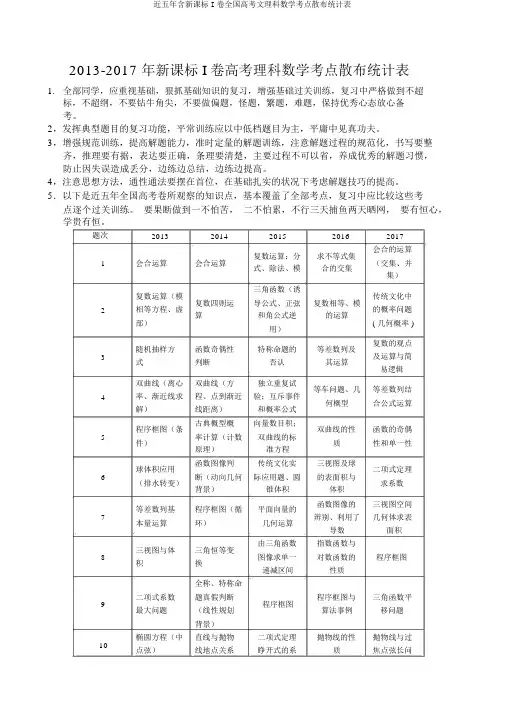
2013-2017 年新课标 I 卷高考理科数学考点散布统计表1.全部同学，应重视基础，狠抓基础知识的复习，增强基础过关训练，复习中严格做到不超标，不超纲，不要钻牛角尖，不要做偏题，怪题，繁题，难题，保持优秀心态放心备考。

2，发挥典型题目的复习功能，平常训练应以中低档题目为主，平庸中见真功夫。

3，增强规范训练，提高解题能力，准时定量的解题训练，注意解题过程的规范化，书写要整齐，推理要有据，表达要正确，条理要清楚，主要过程不可以省，养成优秀的解题习惯，防止因失误造成丢分，边练边总结，边练边提高。

4，注意思想方法，通性通法要摆在首位，在基础扎实的状况下考虑解题技巧的提高。

5．以下是近五年全国高考卷所观察的知识点，基本覆盖了全部考点，复习中应比较这些考点逐个过关训练。

要果断做到一不怕苦，二不怕累，不行三天捕鱼两天晒网，要有恒心，学贵有恒。

题次20132014201520162017复数运算：分求不等式集会合的运算1会合运算会合运算（交集、并式、除法、模合的交集集）复数运算（模三角函数（诱传统文化中复数四则运导公式、正弦复数相等、模2相等方程、虚的概率问题算和角公式逆的运算部）( 几何概率 )用）随机抽样方函数奇偶性特称命题的等差数列及复数的观点3及运算与简式判断否认其运算易逻辑双曲线（离心双曲线（方独立重复试等车问题、几等差数列结4率、渐近线求程、点到渐近验；互斥事件何概型合公式运算解）线距离）和概率公式程序框图（条古典概型概向量数目积；双曲线的性函数的奇偶5率计算（计数双曲线的标件）质性和单一性原理）准方程球体积应用函数图像判传统文化实三视图及球二项式定理6断（动向几何际应用题、圆的表面积与（排水转变）求系数背景）锥体积体积等差数列基程序框图（循平面向量的函数图像的三视图空间7辨别、利用了几何体求表本量运算环）几何运算导数面积三视图与体三角恒等变由三角函数指数函数与8图像求单一对数函数的程序框图积换递减区间性质全称、特称命9二项式系数题真假判断程序框图程序框图与三角函数平最大问题（线性规划算法事例移问题背景）10椭圆方程（中直线与抛物二项式定理抛物线的性抛物线与过点弦）线地点关系睁开式的系质焦点弦长问数题平面的截面含参不等式含参函数零三视图、球、问题，面面平指数与函数11恒建立（分段点散布（求解圆柱的表面行的性质定联合函数）参数范围）积理，异面直线所成的角数列判断（综三视图（求最导数的综合三角函数的数列新奇规12应用、零点、性质（零点、合三角形）长的棱）律取值范围单一性）向量数目积项的系数（两偶函数，求参向量的数目向量模长运13个二项式乘积及坐标运运算数，算积）算通项求解（退椭圆的极点、二项式定理线性规划求14逻辑推理圆的标准方一相减）指定项系数最优解程15三角函数最向量数目积线性规划、斜等比数列及双曲线与点值（夹角）率其应用到线的距离函数对称轴，解三角形（面正余弦定理；线性规划的平面图形折16数形联合思叠后最大概求最值积最值）应用想积数列前 n 项含参数列递和与第 n 项正弦定理、余17解三角形推（证明、判的关系；等差弦定理及三三角函数与断等差存在数列定义与角形面积公解三角形性问题）通项公式；拆式项消去法样本均值方空间垂直判垂直问题的证明面面垂证明及求二垂直证明与差、正态分定与性质；异直关系，求二18面角余弦值，线面角布、随机变量面直线所成面角的余弦空间向量的散布列希望角的计算；值应用独立事件概非线性拟合；垂直证明（等线性回归方概率与统计、听从正态分率计算、随机19腰）与求二面程求法；利用随机变量的布模型及数变量散布列角回归方程进散布列学希望希望行预告展望；抛物线的切直线与圆锥求轨迹方程直线与抛物曲线（椭圆）线；直线与抛圆锥曲线（定义法）与线地点关系、的地点关系，20物线地点关（圆、椭圆）最值问题、弦椭圆方程与弦长公式，韦系；探究新问综合问题长求解最值达定理，过定题；点问题导数意义及导数意义及利用导数研导数及其应利用导数求21应用，切线，应用（切线，究曲线的切用（零点、范参数范围研含参恒建立，单一性，不等线；对新观点围、不等式证究函数的零最值问题式证明，最的理解；分段明）点问题值）函数的零点；分类议论思想几何证明（角圆的切线判几何证明（边相等证明，四四点共圆、直定与性质；圆长相等，三角边形外接圆线与圆的位极坐标与参周角定理；直22性质，圆的性置关系及证数方程形外接圆半角三角形射径）质，等边三角明影定理形证明）极坐标方程参数方程与直角坐标方参数方程、极程与极坐标坐标方程与与参数方程一般方程互互化；直线与直角坐标方不等式证明23化，动点弦长互化，交点极圆的地点关程的互化及坐标最值系应用绝对值不等基本不等式含绝对值不等式解法；分分段函数的式求解，含参应用（求最段函数；一元图像，绝对值24值，存在性问恒建立范围二次不等式不等式的解求解，题）解法2013-2017 年新课标 I 卷高考文科数学考点散布统计表题次2013201420152016列举法、描绘法表1会合运算会合运算会合运算（交、示的会合求交集集）复数的乘法、实部2复数四则运算三角函数向量坐标运算与虚部的观点古典概型3古典概型复数运算及模复数的运算余弦定理4双曲线性质双曲线离心率古典概型椭圆的几何性质 -5命题函数奇偶性椭圆与抛物线离心率三角函数图像的平面向量（会合传统文化，锥平移6等比数列运算）体及体积2017会合的运算（交集、并集）统计事例复数的运算传统文化，几何概率问题双曲线过焦点弦求面积立体几何判断线面平行7程序框图三角函数与图等差数列像8抛物线及面积三视图（柱体与三角图像及性椎体）质9三角函数图像程序框图程序框图10解三角形抛物线分段函数11三视图（柱体）线性规划三视图12分段函数导数（取值范函数计算（图围）像）13平面向量古典概型等比数列14线性规划推理与论证导数几何意义，切线15球及截面分段函数线性规划16三角最值解三角形双曲线计算17等差数列及求等差数列及求解三角形（面和和积）18统计概率（均匀统计概率（数字立几垂直体积数茎叶图）特点及概率）和侧面积19立几（垂直，体立几（垂直及统计概率（回积）高）归方程）三视图及球的表线性规划问面积与体积题指数函数与对数函数的性质函数的图像与奇偶性判断函数图像的辨别、利用导数求利用了导数单一性程序框图与算法事例程序框图平面的截面问题，三角函数化面面平行的性质简正余弦定定理，异面直线所理成的角 .三角变换及导数余弦定理与的应用椭圆向量的数目积及向量的简单坐标运算计算三角变换利用导数求切线直线与圆订交，知利用正切值弦长，求面积求解余弦线性规划的应用三棱锥求外接球表面积等差数列与等比数列数列问题线面地点关系及立体几何面几何体体积面垂直、侧面积函数分析式、概率与统计数据办理及回归直线方程直线与抛物线函数导数 （切线20圆及其面积 直线与圆及极值）函数单一性，零点，导数应用解几（圆与椭圆函数与导数 函数与导数 （切21（零点与证 及弦长）线及取值范围）明）四点共圆、 直线与22几何证明几何证明平面几何证明圆的地点关系 及 证明直线与圆锥曲线（抛物线）的地点关系，弦长公式，韦达定理。

近五年全国卷数学考点分布全国新课标近五年全国卷数学考点分布全国新课标的文章应由本人根据自身实际情况书写，以下仅供参考，请大家根据自身实际情况撰写。

近五年全国卷数学考点分布全国新课标数学是一门基础学科，对于高考来说，数学也是必考科目之一。

在全国新课标卷中，数学的考点分布是比较稳定的，近五年的考点分布如下：一、代数代数是数学中的一个重要分支，也是高考数学中的必考内容。

在近五年的全国新课标卷中，代数的考点主要集中在以下几个方面：1、集合与逻辑用语。

主要考查集合的基本概念、集合的交并补运算以及充分必要条件的判断。

2、不等式。

主要考查不等式的性质、一元一次不等式（组）的解法以及含有绝对值的不等式的解法。

3、函数与方程。

主要考查函数的定义域、值域、解析式以及函数的性质，同时也考查了解方程的方法，例如换元法、待定系数法等。

4、数列。

主要考查数列的基本概念、通项公式以及前n项和公式的计算。

同时也考查了等差数列和等比数列的性质和计算方法。

二、几何几何是数学中的另一个重要分支，也是高考数学中的必考内容。

在近五年的全国新课标卷中，几何的考点主要集中在以下几个方面：1、平面几何。

主要考查三角形的面积、周长、内切圆半径等计算，四边形的基本性质和判定定理，圆的基本概念和性质，以及直线与圆、圆与圆的位置关系等。

2、立体几何。

主要考查空间几何体的基本概念、性质和计算方法，例如表面积、体积的计算，角度、距离的计算等。

3、解析几何。

主要考查直线、圆、椭圆、双曲线和抛物线的性质和计算方法，例如方程的求解、交点、切线、法线等。

三、概率与统计概率与统计是数学中的一个重要分支，也是高考数学中的必考内容。

在近五年的全国新课标卷中，概率与统计的考点主要集中在以下几个方面：1、概率。

主要考查古典概型和几何概型的概率计算方法，条件概率、相互独立事件概率的计算方法等。

2、统计。

主要考查数据的收集、整理、分析和描述方法，例如平均数、中位数、众数、方差等统计量的计算方法，直方图、折线图等统计图的绘制方法等。

近5年高考全国卷各科高频考点分布图+2017年复习建议数学（文科）一、高频考点分析由以上柱形图可知，新课标I 卷高考文科数学近六年高频考点为：1. 函数与导数，立体几何，圆锥曲线，三角函数与解三角形，数列，年均占比14.45%，12.98%，10.13%，9.44%，6.78%；2. 统计，概率，不等式与线性规划，年均占比4-6%；集合与简易逻辑、复数、算法与框图，年均考查约5分左右，即一道选/填分值；3. 最后一道计算题为3选1，10分，可在圆、相似；参数方程、极坐标方程；解绝对值不等式、最值这三道大题中任选其一。

二、复习建议及应试技巧●试卷结构：1. 选择题12×5，最后2-3道较难；2. 填空题4×5，最后1-2道稍有难度；3. 解答题5×12+10。

●考试时间分布：共120分钟，选择题40分钟，解答题80分钟。

●复习建议：1. 研读大纲；2. 回归教材；3. 专题复习，归纳同类；4. 适当练习，重视典例。

语文语文科目课标Ⅰ卷与课标Ⅱ考查形式上和难度差别不大，考题内容选材上有所区别。

2017年考试大纲修订内容：更注重体现语文学科的基础性和综合性，优化考查内容，调整选考模块，全面考查语文能力和人文素养。

1．能力目标设计学科化，注重考查更高层级的思维能力，如鉴赏评价能力。

2．适度增加阅读量，考查信息时代和高校人才选拔要求的快速阅读能力和信息筛选处理能力。

3．现行考试大纲规定的2个选考模块分别为“文学类文本阅读”和“实用类文本阅读”，要求学生从两道选考题中选择1道作答。

修订后的考试大纲取消选考模式，将“文学类文本阅读”和“实用类文本阅读”均作为必考内容。

4．在“古诗文阅读”部分增加“了解并掌握常见的古代文化常识”的考查内容。

另外，需要注意的是，2011-2016年均是材料作文。

备考建议：1、今后的高考语文试题，势必会从新闻、科普文、学术论文、文学作品等材料中，选取更多生动鲜活的事例，意在引导考生将自身的发展与国家和民族的前途命运紧紧联系起来。

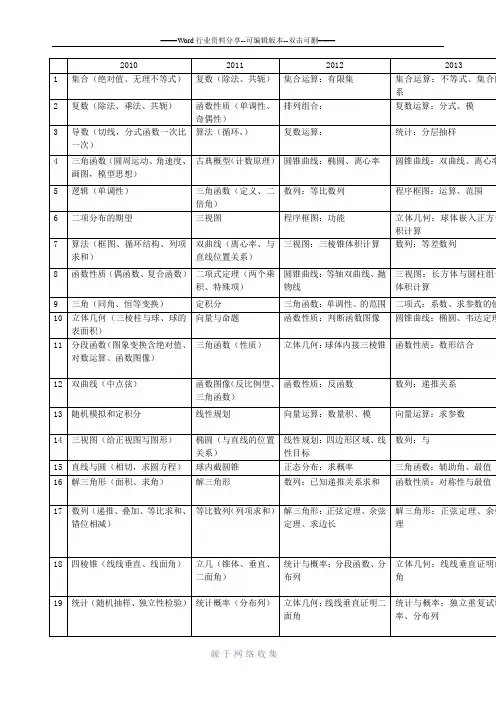
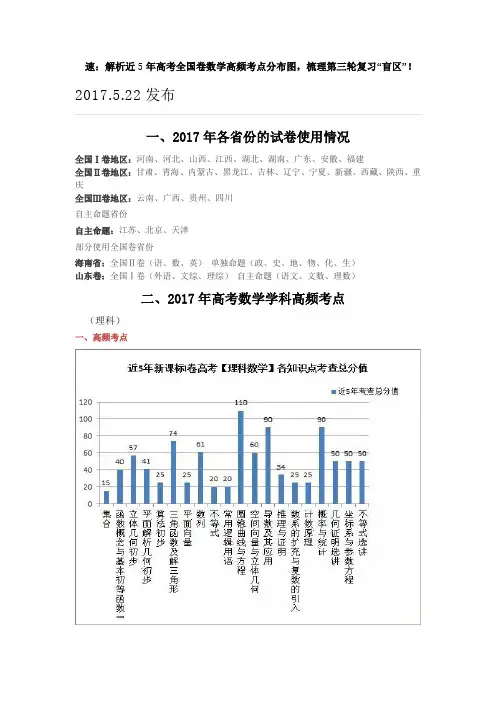
速：解析近5年高考全国卷数学高频考点分布图，梳理第三轮复习“盲区”！2017.5.22发布一、2017年各省份的试卷使用情况全国Ⅰ卷地区：河南、河北、山西、江西、湖北、湖南、广东、安徽、福建全国Ⅱ卷地区：甘肃、青海、内蒙古、黑龙江、吉林、辽宁、宁夏、新疆、西藏、陕西、重庆全国Ⅲ卷地区：云南、广西、贵州、四川自主命题省份自主命题：江苏、北京、天津部分使用全国卷省份海南省：全国Ⅱ卷（语、数、英）单独命题（政、史、地、物、化、生）山东卷：全国Ⅰ卷（外语、文综、理综）自主命题（语文、文数、理数）二、2017年高考数学学科高频考点（理科）一、高频考点由以上柱形图可以得出，新课标I卷高考理科数学近五年高频考点为：1. 圆锥曲线与方程，导数及其应用和概率与统计，三角函数与解三角形，数列，年均占比11.43%，9.36%，7.69%，6.34%；2. 立体几何初步/空间向量与立体几何，占比合计12%左右，也需同学们着重注意；3. 函数概念与基本初等函数Ⅰ/平面解析几何初步，推理与证明题，占比4%左右；其余知识点年均占分约为一道选/填题的分值5分；4. 最后一道计算题为2选1，共10分，可在2坐标系与参数方程、不等式这两道大题中任选其一。

二、三轮复习建议及应试技巧试卷结构与考试时间同文科数学。

●拿分技巧：1. 三角函数、数列、概率、立体几何、二选一题目难度不大，多拿分数；2. 圆锥曲线和导数难度相对较大，请拿到基本分后，再突破高难。

●三轮复习梳理重点：1. 补全易错题、薄弱知识点；2. 善于总结结论、方法；3. 多与同学交流做题经验与思路；4. 要进行有针对性的训练：①做往年的模拟题或真题，选填控制40分钟，进行强化训练；②优秀学生每天做1-2道圆锥曲线或者导数的大题，不用限制时间，做深入地分析。

（全国Ⅰ卷）20132014 2015 201620176 立体几何：球体嵌入正方体体积计算 实际应用题、圆锥体积 78三视图：长方体与圆柱组合，体积计算11三视图、球、圆柱的表面积12 三视图还原立体图 16 1718 立体几何：线线垂直证明线面角空间垂直判定与性质；异面直线所成角的计算；19 立体几何：线面垂直、二面角的求法【2013】6、如图，有一个水平放置的透明无盖的正方体容器，容器高8cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计容器的厚度，则球的体积为 ( )A 、500π3cm 3B 、866π3cm3C 、1372π3cm 3D 、2048π3cm 38、某几何体的三视图如图所示，则该几何体的体积为A .168π+B .88π+C .1616π+D .816π+ 18、（本小题满分12分）如图，三棱柱ABC-A 1B 1C 1中，CA=CB ，AB=A A 1，∠BA A 1=60°.（Ⅰ）证明AB ⊥A 1C;（Ⅱ）若平面ABC ⊥平面AA 1B 1B ，AB=CB=2，求直线A 1C 与平面BB 1C 1C 所成角的正弦值。

【2014】12.如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的个条棱中，最长的棱的长度为A .62B .42C .6D .419. (本小题满分12分)如图三棱柱111ABC A B C -中，侧面11BB C C 为菱形，1AB B C ⊥. (Ⅰ) 证明：1AC AB =；（Ⅱ）若1AC AB ⊥，o160CBB ∠=，AB=BC求二面角111A A B C --的余弦值.【2015】（6）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。

问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆为一个圆锥的四分之一)，米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为立方尺，圆周率约为3，估算出堆放斛的米约有斛 斛 斛 斛（11）圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体，该几何体三视图中的正视图和俯视图如图所示。

全国1卷2013 2014 2015 2016 20174 圆锥曲线：双曲线、离心率双曲线焦点到渐近线的距离5 向量数量积；双曲线的标准方程双曲线的性质910 圆锥曲线：椭圆、韦达定理抛物线焦点三角形抛物线的性质抛物线与过焦点弦长问题11121314 椭圆的顶点、圆的标准方程15 双曲线与点到线的距离161920 解析几何：轨迹方程（定义法）、韦达定理解析几何：椭圆抛物线的切线；直线与抛物线位置关系；探索新问题；圆锥曲线（圆、椭圆）综合问题直线与圆锥曲线（椭圆）的位置关系，弦长公式，韦达定理，过定点问题。

【2013Ⅰ卷】4、已知双曲线C：22221x ya b-=（0,0a b>>）的离心率为52，则C的渐近线方程为A.14y x=±B.13y x=±C.12y x=±D.y x=±【命题意图】本题主要考查双曲线的几何性质，是简单题.【解析】由题知，52 ca =，即54=22ca=222a ba+，∴22ba=14，∴ba=12±，∴C的渐近线方程为12y x=±，故选C.10、已知椭圆x 2a 2＋y 2b2＝1(a >b >0)的右焦点为F (3,0)，过点F 的直线交椭圆于A 、B 两点。

若AB 的中点坐标为(1，－1)，则E 的方程为 ( ) A 、x 245＋y 236＝1B 、x 236＋y 227＝1C 、x 227＋y 218＝1D 、x 218＋y 29＝1【命题意图】本题主要考查椭圆中点弦的问题，是中档题. 【解析】设1122(,),(,)A x y B x y ，则12x x +=2，12y y +=－2，2211221x y a b += ① 2222221x y a b+= ② ①－②得1212121222()()()()0x x x x y y y y a b+-+-+=， ∴AB k =1212y y x x --=212212()()b x x a y y +-+=22b a ，又AB k =0131+-=12，∴22b a =12，又9=2c =22a b -，解得2b =9，2a =18，∴椭圆方程为221189x y +=，故选D. (20)(本小题满分12分)已知圆M :22(1)1x y ++=,圆N :22(1)9x y -+=,动圆P 与M 外切并且与圆N 内切，圆心P 的轨迹为曲线 C. （Ⅰ）求C 的方程；（Ⅱ）l 是与圆P ,圆M 都相切的一条直线，l 与曲线C 交于A ，B 两点，当圆P 的半径最长时，求|AB|.【命题意图】【解析】由已知得圆M 的圆心为M （-1，0）,半径1r =1，圆N 的圆心为N (1,0),半径2r =3.设动圆P 的圆心为P （x ，y ），半径为R.（Ⅰ）∵圆P 与圆M 外切且与圆N 内切，∴|PM|+|PN|=12()()R r r R ++-=12r r +=4，由椭圆的定义可知，曲线C 是以M ，N 为左右焦点，场半轴长为2的椭圆(左顶点除外)，其方程为221(2)43x y x +=≠-. （Ⅱ）对于曲线C 上任意一点P （x ，y ），由于|PM|-|PN|=22R -≤2，∴R ≤2,当且仅当圆P 的圆心为（2，0）时，R=2.∴当圆P 的半径最长时，其方程为22(2)4x y -+=， 当l 的倾斜角为090时，则l 与y 轴重合，可得|AB|=当l 的倾斜角不为090时，由1r ≠R 知l 不平行x 轴，设l 与x 轴的交点为Q ，则||||QP QM =1Rr ，可求得Q（-4，0），∴设l ：(4)y k x =+，由l 于圆M 相切得2|3|11k k =+，解得24k =±. 当k =24时，将224y x =+代入221(2)43x y x +=≠-并整理得27880x x +-=，解得1,2x =4627-±，∴|AB|=2121||k x x +-=187.当k =－24时，由图形的对称性可知|AB|=187， 综上，|AB|=187或|AB|=23.【2014Ⅰ卷】4.已知F 是双曲线C ：223(0)x my m m -=>的一个焦点，则点F 到C 的一条渐近线的距离为A .3B .3C .3mD .3m【答案】：A【解析】：由C ：223(0)x my m m -=>，得22133x y m -=，233,33c m c m =+=+ 设()33,0Fm +，一条渐近线33y x m=，即0x m y -=，则点F 到C 的一条渐近线的距离331m d m+=+=3，选A. .10.已知抛物线C ：28y x =的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与C 的一个交点，若4FP FQ =，则||QF =A .72 B .52C .3D .2 【答案】：C【解析】：过Q 作Q M ⊥直线L 于M ，∵4FP FQ =∴34PQ PF =，又344QM PQ PF ==，∴3QM =，由抛物线定义知3QF QM ==选C20. (本小题满分12分) 已知点A （0，-2），椭圆E ：22221(0)x y a b a b+=>>的离心率为32，F 是椭圆的焦点，直线AF 的斜率为233，O 为坐标原点. (Ⅰ)求E 的方程；（Ⅱ）设过点A 的直线l 与E 相交于,P Q 两点，当OPQ ∆的面积最大时，求l 的方程. 【解析】：(Ⅰ) 设(),0F c ，由条件知2233c =，得3c = 又32c a =， 所以a=2，2221b a c =-= ,故E 的方程2214x y +=. ……….6分 （Ⅱ）依题意当l x ⊥轴不合题意，故设直线l ：2y kx =-，设()()1122,,,P x y Q x y将2y kx =-代入2214x y +=，得()221416120k x kx +-+=， 当216(43)0k ∆=->，即234k >时，21,22824314k k x k ±-=+ 从而2221241431k k PQ k x x +-=+-=又点O 到直线PQ 的距离21d k =+，所以∆OPQ 的面积214432OPQk S d PQ ∆-== ， 243k t -=，则0t >，244144OPQ t S t t t∆==≤++， 当且仅当2t =，7k =等号成立，且满足0∆>，所以当∆OPQ 的面积最大时，l 的方程为：72y x =- 或72y x =-. …………………………12分【2015Ⅰ卷】（5）已知M （00,x y ）是双曲线C ：2212x y -=上的一点，12,F F 是C 上的两个焦点，若120MF MF •<，则0y 的取值范围是( ) （A ）（-33，33） （B ）（-36，36） （C ）（223-，223） （D ）（233-，233）【答案】A【解析】由题知12(3,0),(3,0)F F -，220012x y -=，所以12MF MF •= 0000(3,)(3,)x y x y ---•-- =2220003310x y y +-=-<，解得03333y -<<，故选A. 【考点定位】双曲线的标准方程；向量数量积坐标表示；一元二次不等式解法.【名师点睛】本题考查利用向量数量积的坐标形式将12MF MF •表示为关于点M 坐标的函数，利用点M 在双曲线上，消去x 0，根据题意化为关于0y 的不等式，即可解出0y 的范围，是基础题，将12MF MF •表示为0y 的函数是解本题的关键.（14）一个圆经过椭圆221164x y +=的三个顶点，且圆心在x 轴的正半轴上，则该圆的标准方程为 . 【答案】22325()24x y -+=（20）（本小题满分12分）在直角坐标系xoy 中，曲线C ：y =24x 与直线y kx a =+(a ＞0)交与M ,N 两点，（Ⅰ）当k =0时，分别求C 在点M 和N 处的切线方程；（Ⅱ）y 轴上是否存在点P ，使得当k 变动时，总有∠OPM =∠OPN ？说明理由.【答案】（Ⅰ）0ax y a --=或0ax y a ++=（Ⅱ）存在【2016Ⅰ卷】（5）已知方程222213x y m n m n+=+-表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是 （A ）(–1,3) （B ）(–1,3) （C ）(0,3) （D ）(0,3) 【答案】A【解析】由题意知：双曲线的焦点在x 轴上，所以2234m n m n ++-=，解得21m =，因为方程22113x y n n -=+-表示双曲线，所以1030n n +>⎧⎨->⎩，解得13n n >-⎧⎨<⎩，所以n 的取值范围是()1,3-，故选A ． 【考点】双曲线的性质【名师点睛】双曲线知识一般作为客观题出现,主要考查双曲线的几何性质,属于基础题.注意双曲线的焦距是2c 而不是c ,这一点易出错.（10）以抛物线C 的顶点为圆心的圆交C 于A ，B 两点，交C 的准线于D ，E 两点.已知|AB |=42，|DE|=25，则C 的焦点到准线的距离为（A ）2 （B ）4 （C ）6 （D ）8 【答案】B 【解析】试题分析：如图，设抛物线方程为22y px =，圆的半径为r ,,AB DE 交x 轴于,C F 点，则22AC =，即A 点纵坐标为22，则A 点横坐标为4p ，即4OC p=，由勾股定理知2222DF OF DO r +==，2222AC OC AO r +==，即22224(5)()(22)()2p p+=+，解得4p =，即C 的焦点到准线的距离为4，故选B.【考点】抛物线的性质【名师点睛】本题主要考查抛物线的性质及运算,注意解析几何问题中最容易出现运算错误,所以解题时一定要注意运算的准确性与技巧性,基础题失分过多是相当一部分学生数学考不好的主要原因.（20）（本小题满分12分）设圆222150x y x ++-=的圆心为A ，直线l 过点B （1,0）且与x 轴不重合，l 交圆A 于C ，D 两点，过B 作AC 的平行线交AD 于点E .（I ）证明EA EB +为定值，并写出点E 的轨迹方程；（II ）设点E 的轨迹为曲线C 1，直线l 交C 1于M ,N 两点，过B 且与l 垂直的直线与圆A 交于P ,Q 两点，求四边形MPNQ 面积的取值范围.【答案】（I ）13422=+y x （0≠y ）；（II ）)38,12[ 【解析】试题分析：（I ）利用椭圆定义求方程；（II ）把面积表示为关于斜率k 的函数，再求最值。