算法与程序框图改j

一、算法1．算法的概念在数学上，现代意义上的“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成．注意：（1）算法可以理解为由基本运算及规定的运算顺序所构成的完整的解题步骤，或看成按要求设计好的有限的确切的计算序列，并且这样的步骤或序列能够解决一类问题．（2）通俗地讲，算法就是计算机解题的过程．在这个过程中，无论是形成解题思路还是编写程序，都是实施某种算法，前者是推理实现的算法，后者是操作实现的算法．（3）描述算法可以有不同的方式．可以用自然语言和数学语言加以叙述，也可以用算法语言给出精确的说明，或用框图直观的显示等．2．算法的特点（1）确定性：算法中的每一步应该是确定的并且能有效的执行且得到确定的结果，而不应当是模棱两可或者有歧义．（2）可行性：算法对于某一类问题的解决都必须是有效的，切实可行的，并且能重复使用．（3）有效性：一个算法的步骤序列是有限的，它应在有限步操作之后停止，而不是无限的．二、程序框图1．画程序框图的规则①使用标准的框图符号；②框图一般按从上到下、从左到右的方向画；③除判断框外，大多数框图符号只有一个进入点和一个退出点．判断框是具有超过一个退出点的唯一的符号；④一种判断是“是”与“不是”两分支的判断，而且有且仅有两个结果；另一种是多分支判断，有几种不同的结果；⑤在图形符号内描述的语言要非常简练、清楚．2．算法的基本逻辑结构及框图表示任何一种算法都可由顺序结构、条件结构和循环结构这三种基本逻辑结构组成．学习这部分时应注意：①循环结构中一定包含条件结构；②在循环结构中，通常都有一个起循环计数作用的变量，这个变量的取值一般都含在执行或终止循环体的条件中；③根据对条件的不同处理，循环结构又分为当型（ＷＨＩＬＥ型）和直到型（ＵＮＴＩＬ型）两种．当型循环在每次执行循环体前对控制循环的条件进行判断，当条件满足时执行循环体，不满足则停止；直到型循环在执行了一次循环体之后，对控制循环的条件进行判断，当条件不满足时执行循环体，满足则停止．3．三种基本逻辑结构的共同特点（1）只有一个入口．（2）只有一个出口，请注意一个菱形判断框有两个出口，而一个条件结构只有一个出口，不要将菱形框的出口和条件结构的出口混淆了．（3）结构内的每一部分都有机会被执行到．也就是说对每一个框来说，都应当有一条从入口到出口的路径通过它．（4）结构内不存在死循环，即无终止的循环．在程序设计中是不允许有死循环出现的．以上这些共同特点，也是检查一个程序框图或算法是否正确，合理的有效方法．。

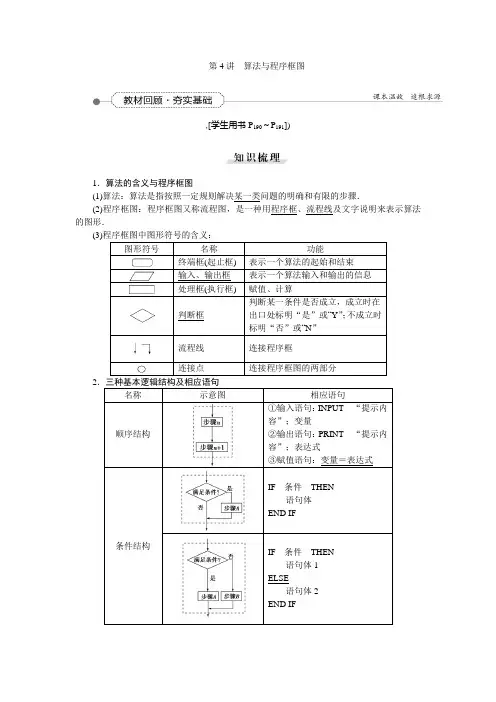
第4讲算法与程序框图,[学生用书P190～P191])1．算法的含义与程序框图(1)算法：算法是指按照一定规则解决某一类问题的明确和有限的步骤．(2)程序框图：程序框图又称流程图，是一种用程序框、流程线及文字说明来表示算法的图形．(3)2[做一做]1．在程序框图中，算法的一个步骤到另一个步骤的连接用( ) A ．连接点 B ．判断框 C ．流程线 D ．处理框解析：选C ．带有方向箭头的流程线将程序框连接起来． 2．(2015·福建福州模拟)执行如图所示的程序框图，若输入x ＝0．1，则输出的m 的值是( )A ．0B ．0．1C ．1D ．－1解析：选A ．当x ＝0．1时，m ＝lg 0．1＝－1，因为－1<0，执行m ＝m ＋1＝－1＋1＝0，将0赋给m ，输出的m 的值是0．1．辨明两个易误点(1)易混淆处理框与输入框，处理框主要是赋值、计算，而输入框只是表示一个算法输入的信息．(2)易忽视循环结构中必有条件结构，其作用是控制循环进程，避免进入“死循环”，是循环结构必不可少的一部分．2．识别三种结构的关系顺序结构是每个算法结构都含有的，而对于循环结构有重复性，条件结构具有选择性没有重复性，并且循环结构中必定包含一个条件结构，用于确定何时终止循环体，循环结构和条件结构都含有顺序结构．[做一做]3．(2014·高考北京卷)执行如图所示的程序框图，输出的S值为()A．1 B．3C．7 D．15解析：选C．程序框图运行如下：k＝0<3，S＝0＋20＝1，k＝1<3；S＝1＋21＝3，k＝2<3；S＝3＋22＝7，k＝3．输出S＝7．4．阅读如图所示的程序框图，若输出的y＝1，则输入的x的值可能是()A．±2和2 B．－2和2C．± 2 D．2解析：选C．由程序框图可知，当x>2时，log2x＝1⇒x＝2，舍去；当x≤2时，x2－1＝1，x＝±2．,[学生用书P 191～P 193])考点一__顺序结构与条件结构__________________(2013·高考课标全国卷Ⅰ)执行如图所示的程序框图，如果输入的t ∈[－1，3]，则输出的s 属于( )A ．[－3，4]B ．[－5，2]C ．[－4，3]D ．[－2，5][解析] 由程序框图得分段函数s ＝⎩⎪⎨⎪⎧3t ，t <1，4t －t 2，t ≥1.所以当－1≤t <1时，s ＝3t ∈[－3，3)；当1≤t ≤3时，s ＝4t －t 2＝－(t －2)2＋4，所以此时3≤s ≤4．综上函数的值域为[－3，4]，即输出的s 属于[－3，4]．[答案] A若本例的判断框中的条件改为“t ≥1？”，则输出的s 的范围是________．解析：由程序框图得分段函数s ＝⎩⎪⎨⎪⎧3t ，t ≥1，4t －t 2，t <1.所以当1≤t ≤3时，s ＝3t ∈[3，9]，当－1≤t <1时，s ＝4t －t 2＝－(t －2)2＋4，所以此时－5≤s <3．综上函数的值域为[－5，9]，即输出的s 属于[－5，9]．答案：[－5，9][规律方法] 应用顺序结构和条件结构的注意点 (1)顺序结构顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的．(2)条件结构利用条件结构解决算法问题时，重点是判断框，判断框内的条件不同，对应的下一图框中的内容和操作要相应地进行变化，故要重点分析判断框内的条件是否满足．1．(2015·辽宁省大连市高三模拟)执行如图所示的程序框图，若输入的x ∈[0，2π]，则输出y 的取值范围是( )A ．[0，1]B ．[－1，1]C ．[－22，1] D ．[－1，22] 解析：选C ．根据程序框中判断框内的条件，得知y 为sin x ，cos x 中的较大值．在同一个坐标系中画出y ＝sin x ，y ＝cos x 的图象，可知y 的取值范围为[－22，1]． 考点二__循环结构(高频考点)____________________循环结构是高考命题的一个热点问题，多以选择题、填空题的形式呈现，试题难度不大，多为容易题或中档题．高考对循环结构的考查主要有以下三个命题角度： (1)由框图求输出的结果； (2)完善程序框图；(3)由程序框图及输出结果，求输入的值．(1)(2014·高考重庆卷)执行如图所示的程序框图，若输出k 的值为6，则判断框内可填入的条件是( )A ．s >12B ．s >35C ．s >710D ．s >45(2)(2014·高考辽宁卷)执行如图所示的程序框图，若输入x ＝9，则输出y ＝________．(3)(2014·高考山东卷)执行如图所示的程序框图，若输入的x 的值为1，则输出的n 的值为________．[解析] (1)第一次执行循环：s ＝1×910＝910，k ＝8，s ＝910应满足条件；第二次执行循环：s ＝910×89＝810，k ＝7，s ＝810应满足条件，排除选项D ；第三次执行循环：s ＝810×78＝710，k ＝6，正是输出的结果，故这时程序不再满足条件，结束循环，而选项A 和B 都满足条件，故排除A 和B ，故选C ．(2)x ＝9时，y ＝93＋2＝5，|y －x |＝|5－9|＝4<1不成立；x ＝5，y ＝53＋2＝113，|y －x |＝⎪⎪⎪⎪113－5＝43<1不成立；x ＝113，y ＝119＋2＝299，|y －x |＝⎪⎪⎪⎪299－113＝49<1成立，输出y ＝299． (3)由x 2－4x ＋3≤0，解得1≤x ≤3．当x ＝1时，满足1≤x ≤3，所以x ＝1＋1＝2，n ＝0＋1＝1； 当x ＝2时，满足1≤x ≤3，所以x ＝2＋1＝3，n ＝1＋1＝2； 当x ＝3时，满足1≤x ≤3，所以x ＝3＋1＝4，n ＝2＋1＝3； 当x ＝4时，不满足1≤x ≤3，所以输出n ＝3． [答案] (1)C (2)299(3)3[规律方法] 利用循环结构表示算法的步骤： 利用循环结构表示算法，第一要先确定是利用当型循环结构，还是利用直到型循环结构；第二要选择准确的表示累计的变量；第三要注意在哪一步开始循环，满足什么条件不再执行循环体．2．(1)(2015·山西省四校联考)如图所示的程序框图的输出结果为( )A ．2 0142 015B ．12 015C ．2 0152 016D ．12 016(2)如图，在算法框图的判断框中，若输出S 的值为120，则判断框内可填入________．(3)(2015·沈阳市教学质量监测)有如图所示的程序框图，则该程序框图表示的算法的功能是( )A ．输出使1×2×4×…×n ≥2 015成立的最小整数nB ．输出使1×2×4×…×n ≥2 015成立的最大整数nC ．输出使1×2×4×…×n ≥2 015成立的最大整数n ＋2D ．输出使1×2×4×…×n ≥2 015成立的最小整数n ＋2解析：(1)本框图是对{1i （i ＋1）}的求和，所以S ＝11×2＋12×3＋…＋12 015×2 016＝1－12 016＝2 0152 016．(2)120＝1×2×3×4×5，所以当i ＝1，2，3，4，5时执行，判断框内可填入“i <6？”． (3)依题意与题中的程序框图可知，该程序框图表示的算法的功能是输出使1×2×4×…×n ≥2 015成立的最小整数n ＋2．答案：(1)C (2)i <6？ (3)D考点三__基本算法语句__________________(1)(2013·x 为60时，输出y 的值为( )A ．25B ．30C ．31D ．61(2)设计一个计算1×3×5×7×9×11×13的算法，下面给出了程序的一部分，则在①处不能填入的数是( )A ．13B ．13．5C ．14D ．14．5[解析] (1)该语句的分段函数y ＝⎩⎪⎨⎪⎧0.5x ，x ≤50，25＋0.6（x －50），x >50， 当x ＝60时，y ＝25＋0．6×(60－50)＝31． ∴输出y 的值为31．(2)若填13，当i ＝11＋2＝13时，不满足条件，终止循环，因此得到的是1×3×5×7×9×11的计算结果，故不能填13，但填的数字只要超过13且不超过15均可保证终止循环时，得到的是1×3×5×7×9×11×13的计算结果．[答案] (1)C (2)A[规律方法] 1．输入语句的要求(1)输入语句要求输入的值是具体的常量．(2)提示内容提示用户输入的是什么信息，必须加双引号，提示内容“原原本本”地在计算机屏幕上显示，提示内容与变量之间要用分号隔开．2．输出语句的要求(1)表达式是算法和程序要求输出的信息．(2)提示内容提示用户要输出的是什么信息，必须加双引号，提示内容和表达式要用分号分开．(3)输出语句可以一次完成输出多个表达式的功能，不同的表达式之间可用“，”分隔；输出语句还可以是“提示内容1”；表达式1，“提示内容2”；表达式2，“提示内容3”；表达式3，…的形式，例如，PRINT“a，b，c”；a，b，c；PRINT“a”；a，“b”；b，“c”；c．3．(1)．(2)．解析：(1)程序反映出的算法过程为i＝11⇒S＝11×1，i＝10；i＝10⇒S＝11×10，i＝9；i＝9⇒S＝11×10×9，i＝8；i＝8<9退出循环，执行“PRINT S”．故S＝990．(2)由程序可知，m为a，b中的较大值，故最后输出的m值为3．答案：(1)990(2)3,[学生用书P 194])交汇创新——算法与不等式的交汇(2014·高考四川卷)执行如图所示的程序框图，如果输入的x ，y ∈R ，那么输出的S 的最大值为( )A ．0B ．1C ．2D ．3[解析] 当条件x ≥0，y ≥0，x ＋y ≤1不成立时输出S 的值为1，当条件x ≥0，y ≥0，x ＋y ≤1成立时S ＝2x ＋y ，下面用线性规划的方法求此时S 的最大值．作出不等式组⎩⎪⎨⎪⎧x ≥0，y ≥0，x ＋y ≤1表示的平面区域如图中阴影部分所示，由图可知当直线S ＝2x ＋y 经过点M (1，0)时S 最大，其最大值为2×1＋0＝2，故输出S 的最大值为2．[答案] C[名师点评] 本题是算法与不等式的交汇，以算法为载体，考查了线性规划问题．在新课标中，算法成为高考的热点，算法经常与数列、函数、概率交汇出现．给出一个如图所示的程序框图，若要使输入的x 值与输出的y 值相等，则这样的x 值个数是( )A ．1B ．2C ．3D ．4解析：选C ．由程序框图得到如下分段函数：y ＝⎩⎪⎨⎪⎧x 2，x ≤2，2x －3，2<x ≤5，1x ，x >5.当x ≤2时，y ＝x 2＝x ，解得x 1＝0，x 2＝1； 当2<x ≤5时，y ＝2x －3＝x ，解得x ＝3； 当x >5时，y ＝1x ＝x ，解得x ＝±1(舍去)，故x 可为0，1，3．1．(2015·济南市模拟)若某程序框图如图所示，则该程序运行后输出的值是( )A ．2B ．3C ．4D ．5解析：选C ．逐次运行的结果是n ＝3，i ＝2；n ＝4，i ＝3；n ＝2，i ＝4．故输出的值是4．2．(2015·太原市模拟试题)如图是一算法的程序框图，若输出结果为S ＝720，则在判断框中应填入的条件是( )A ．k ≤6?B ．k ≤7?C ．k ≤8?D ．k ≤9?解析：选B ．第一次执行循环，得到S ＝10，k ＝9；第二次执行循环，得到S ＝90，k ＝8，第三次执行循环，得到S ＝720，k ＝7．此时满足条件，故选B ．3．(2014·高考课标全国卷Ⅰ)执行下面的程序框图，若输入的a ，b ，k 分别为1，2，3，则输出的M ＝( )A ．203B ．165C ．72D ．158解析：选D ．当n ＝1时，M ＝1＋12＝32，a ＝2，b ＝32；当n ＝2时，M ＝2＋23＝83，a ＝32，b ＝83；当n ＝3时，M ＝32＋38＝158，a ＝83，b ＝158；n ＝4时，终止循环．输出M ＝158．4．某程序框图如图所示，若该程序运行后输出的值是95，则( )A ．a ＝4B ．a ＝5C ．a ＝6D ．a ＝7解析：选A ．该程序框图的功能为计算1＋11×2＋12×3＋…＋1a （a ＋1）＝2－1a ＋1的值，由已知输出的值为95，可知当a ＝4时2－1a ＋1＝95．故选A ．5．已知实数x ∈[2，30]，执行如图所示的程序框图，则输出的x 不小于103的概率为( )A ．514B ．914C ．59D ．49解析：选B ．由程序框图可知，经过3次循环跳出，设输入的初始值为x ＝x 0，则输出的x ＝2[2(2x 0＋1)＋1]＋1≥103，∴8x 0≥96，即x 0≥12，故输出的x 不小于103的概率为P ＝30－1230－2＝1828＝914． 6．(2015·东北三校联考)已知某算法的程序框图如图所示，若输入x ＝7，y ＝6，则输出的有序数对为( )A ．(13，14)B ．(12，13)C ．(14，13)D ．(13，12)解析：选A ．执行程序框图得，n ＝1，x ＝6＋1＝7，y ＝8； n ＝2，x ＝y ＋1＝9，y ＝10； n ＝3，x ＝y ＋1＝11，y ＝12； n ＝4，x ＝y ＋1＝13，y ＝14；n ＝5，循环结束，输出(13，14)，故选A ． 7．(2015·合肥二检)执行如图所示的程序框图，输出的所有值之和是________．解析：列举几项，发现输出的x 开始为1，每次递增2，去掉x 是3的倍数的那些数，最后可得输出的所有值之和为1＋5＋7＋11＋13＋17＋19＝73．答案：738．关于函数f (x )＝⎩⎪⎨⎪⎧－x ，1<x ≤4，cos x ，－1≤x ≤1的程序框图如图，现输入区间[a ，b ]，则输出的区间是________．解析：由程序框图的第一个判断条件为f(x)>0，当f(x)＝cos x，x∈[－1，1]时满足，然后进入第二个判断框，需要解不等式f′(x)＝－sin x≤0，即0≤x≤1．故输出区间为[0，1]．答案：[0，1]9．(2015·海淀区第二学期调研)李强用流程图把早上上班前需要做的事情做了如下几种方案，则所用时间最少的是方案________．方案一：方案二：方案三：解析：方案一所用时间为8＋5＋13＋7＋15＋6＝54．方案二所用时间为8＋15＋7＝30．方案三所用时间为8＋13＋7＝28．所以所用时间最少的是方案三．答案：三10．(2015·长沙模拟)已知数列{a n}中，a1＝1，a n＋1＝2a n＋n－1，若利用如图所示的程序框图进行运算，则输出n的值为________．解析：由数列递推关系可得a n ＋1＋(n ＋1)＝2(a n ＋n )，故数列{a n ＋n }是首项为1＋1＝2，公比为2的等比数列，a n ＋n ＝2×2n －1＝2n ，a n ＝2n －n ，所以S n ＝(2＋22＋…＋2n )－(1＋2＋…＋n )＝2（1－2n ）1－2－n （n ＋1）2＝2n ＋1－2－n （n ＋1）2，当n ＝11时，S 11＝212－2－66＝4028>2 015，当n ＝10时，S 10＝211－2－55<2 015，结合程序框图可知输出的n ＝11．答案：111．(2015·大连模拟)在如图所示的程序框图中，输入A ＝192，B ＝22，则输出的结果是( )A ．0B ．2C ．4D ．6解析：选B ．输入后依次得到：C ＝16，A ＝22，B ＝16；C ＝6，A ＝16，B ＝6；C ＝4，A ＝6，B ＝4；C ＝2，A ＝4，B ＝2；C ＝0，A ＝2，B ＝0．故输出的结果为2．2．(2015·贵州省六校第一次联考)如图，x 1，x 2，x 3为某次考试三个评阅人对同一道题的独立评分，p 为该题的最终得分，当x 1＝6，x 2＝9，p ＝9．5时，x 3等于( )A．10 B．9C．8 D．7解析：选A．x1＝6，x2＝9，|x1－x2|＝3，|x3－6|<|x3－9|不成立，取x1＝x3⇒x3＋9＝9．5×2⇒x3＝10．3．(2015·成都模拟)已知某算法的程序框图如图所示，若将输出的(x，y)值依次记为(x1，y1)，(x2，y2)，…，(x n，y n)，…(1)若程序运行中输出的一个数组是(9，t)，求t的值；(2)程序结束时，共输出(x，y)的组数为多少？解：(1)由程序框图知，当x＝1时，y＝0，当x＝3时，y＝－2；当x＝9时，y＝－4，所以t＝－4．(2)当n＝1时，输出一对，当n＝3时，又输出一对，…，当n＝2 015时，输出最后一对，共输出(x，y)的组数为1 008．4．(2015·河南郑州市预测)每年的三月十二日，是中国的植树节．林管部门为保证树苗的质量，都会在植树前对树苗进行检测．现从甲、乙两种树苗中各抽测了10株树苗的高度，规定高于128厘米的树苗为“良种树苗”，测得高度如下(单位：厘米)：甲：137，121，131，120，129，119，132，123，125，133；乙：110，130，147，127，146，114，126，110，144，146．(1)根据抽测结果，画出甲、乙两种树苗高度的茎叶图，并根据你画出的茎叶图，对甲、乙两种树苗的高度作比较，写出对两种树苗高度的统计结论；(2)设抽测的10株甲种树苗高度平均值为x ，将这10株树苗的高度依次输入，按程序框图进行运算(如图)，问输出的S 大小为多少？并说明S 的统计学意义．解：(1)茎叶图如图所示：统计结论：①甲种树苗的平均高度小于乙种树苗的平均高度； ②甲种树苗比乙种树苗长得整齐；③甲种树苗高度的中位数为127，乙种树苗高度的中位数为128．5； ④甲种树苗的高度基本上是对称的，而且大多数集中在均值附近，乙种树苗的高度分布较为分散．(2)依题意，x －＝127，S ＝35．S 表示10株甲种树苗高度的方差，是描述树苗高度的离散程度的量． S 值越小，表示树苗长得越整齐，S 值越大，表示树苗长得越参差不齐．。

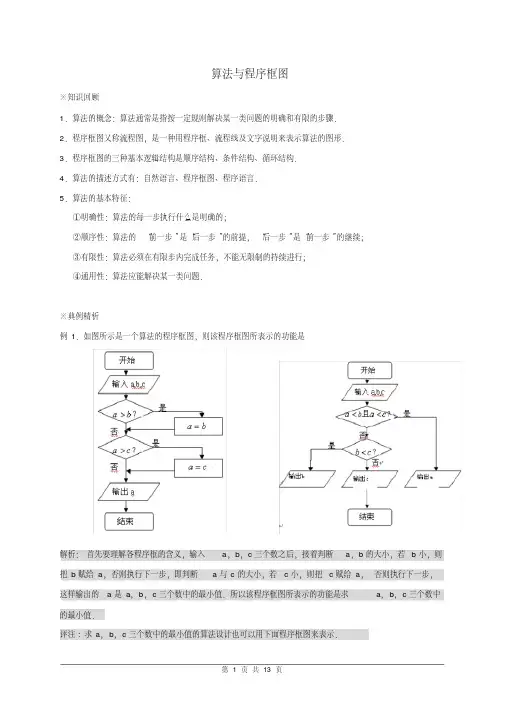
算法与程序框图知识图谱算法与程序框图知识精讲一．算法的概念1.算法的定义由基本运算及规定的运算顺序所构成的完整的解题步骤，或者看成按照一定规则，解决某一类问题的明确的和有限的步骤，称为算法．通常可以编成计算机程序，让计算机执行并解决问题．2.算法的特征：（1）有穷性：算法必须在执行有限步后结束，通常还理解为实际上能够容忍的合理限度；（2）确定性：算法的每一个步骤必须有确定的含义；（3）可行性：组成算法的每个步骤和操作必须是相当基本的，原则上都是能精确地执行的；（4）输入：有零个或多个输入；（5）输出：有一个或多个输出．二．算法的描述1．用自然语言；2．用数学语言；3．用算法语言（程序设计语言）；4．用程序框图（流程图）．三．程序框图的概念：用一些通用的图形符号构成的一张图来表示算法，称为程序框图（简称框图）．1.常用图形符号：图形符号名称符号表示的意义起、止框框图的开始或结束输入、输出框数据的输入或者结果的输出处理框赋值、执行计算语句、结果的传送判断框根据给定条件判断流程线流程进行的方向连结点连结另一页或另一部分的框图四．算法的三种基本逻辑结构：顺序结构、条件（分支）结构和循环结构．1.顺序结构：最简单的算法结构，语句与语句之间，框与框之间是按从上到下的顺序进行的．如下图，只有在执行完A 框指定的操作后，才能接着执行B 框指定的操作；2.条件（分支）结构：在一个算法中，用来处理需要根据条件是否成立有不同的流向的结构．常见的条件结构的程序框图有下面两种形式：否否是是BA A P PB A3.循环结构：从某处开始，按照一定的条件反复执行某些步骤的情况，就是循环结构，其中反复执行的步骤称为循环体．常见的循环结构的框图对应为：否是A P三点剖析一．注意事项：1.在画程序框图时，从开始框沿箭头必须能到达结束框，特别是条件分支结构应沿每条支路都能到达结束框，流程线必须加箭头表示顺序．2．对于循环结构有如下需要注意的情况：（1）循环结构非常适合计算机处理，因为计算机的运算速度非常快，执行成千上万次的重复计算，只不过是一瞬间的事，且能保证每次的结果都正确；（2）循环结构要有中止循环体的条件，不能无休止的运算下去，循环结构中一定包含条件结构，如i n ≤就是中止循环的条件；（3）循环结构的关键是，要理解“累加变量”和“用1i 代替i ”，S 是一个累加变量，i 是计数变量，每循环一次，S 和i 都要发生变化，这两步要重复计算若干次；（4）一种循环结构是先判断i n ≤是否成立，若是，执行循环体；若否，则中止循环，像这样，每次执行循环体前对控制循环条件进行判断，条件满足时执行循环体，不满足则停止，称为当型循环．除了当型循环外，常用的循环结构还有直到型循环．二．方法点拨1．画程序框图的规则：（1）使用标准的框图的符号；（2）框图一般按从上到下、从左到右的方向画；（3）除判断框外，大多数框图符号只有一个进入点和一个退出点．判断框是具有超过一个退出点的惟一符号；（4）一种判断框是“是”与“不是”两分支的判断，而且有且仅有两个结果；另一种是多分支判断，有几种不同的结果；（5）在图形符号内描述的语言要非常简练清楚．2．画程序框图要注意的几点：（1）起、止框是任何流程不可少的，表示程序的开始和结束；（2）输入、输出框可以用在算法中任何需要输入、输出的位置；（3）算法中间要处理数据或计算，可分别写在不同的处理框内；（4）当算法要求你对两个不同的结果进行判断时，要写在判断框内；（5）一个算法步骤到另一个算法步骤用流程线连结；（6）如果一个框图需要分开来画，要在断开处画上连结点，并标出连结的号码．程序框图例题1、下列说法正确的是（）A.算法就是某个问题的解题过程；B.算法执行后可以产生不同的结果；C.解决某一个具体问题算法不同结果不同；D.算法执行步骤的次数不可以为很大，否则无法实施．例题2、指出下列哪一个不是算法（）A.解方程260x -=的过程是移项和系数化为1B.从济南到温哥华需要先乘火车到北京，再从北京乘飞机到温哥华C.解方程2210x x +-=D.利用公式2πS r =，计算半径为3的圆的面积为2π3⨯例题3、下列语句中是算法的个数为（）①从济南到巴黎：先从济南坐火车到北京，再坐飞机到巴黎；②统筹法中“烧水泡茶”的故事；③测量某棵树的高度，判断其是否是大树；④已知三角形的一部分边长和角，借助正余弦定理求得剩余的边角，再利用三角形的面积公式求出该三角形的面积A.1B.2C.3D.4随练1、下面四种叙述能称为算法的是（）A.在家里一般是妈妈做饭B.做米饭要需要刷锅．添水．加热这些步骤C.在野外做饭叫野炊D.做饭必需要有米随练2、下列关于算法的说法正确的有（）①求解某一类问题的算法是唯一的；②算法必须在有限步操作之后停止；③算法的每一步操作必须是明确的，不能有歧义或模糊；④算法执行后产生确定的结果．A.1个B.2个C.3个D.4个随练3、早上从起床到出门需要洗脸刷牙（5min）．刷水壶（2min）．烧水（8min）．泡面（3min）．吃饭（10min）．听广播（8min）几个步骤，下列选项中最好的一种算法为（）A.s1洗脸刷牙s2刷水壶s3烧水s4泡面s5吃饭s6听广播B.s1刷水壶s2烧水的同时洗脸刷牙s3泡面s4吃饭s5听广播C.s1刷水壶s2烧水的同时洗脸刷牙s3泡面s4吃饭的同时听广播D.s1吃饭的同时听广播s2泡面s3烧水的同时洗脸刷牙s4刷水壶算法的三种逻辑结构和框图表示例题1、如果执行如图所示的程序框图，那么输出的a=（）A.2B.12 C.﹣1 D.以上都不正确例题2、如果执行如图所示的程序框图，那么输出的a=（）A.2B.12 C.﹣1 D.以上都不正确例题3、阅读右边的程序框图，运行相应的程序，输出的S的值是（）A.26B.40C.57D.无法确定随练1、如图是某算法的流程图，则执行该算法输出的结果是S=____．随练2、执行如图所示的程序框图，如果输入a=2，那么输出的a值为（）A.4B.16C.256D.log316随练3、执行如图所示的程序框图，则输出的k=（）A.4B.5C.6D.7拓展1、算法的有穷性是指（）A.算法最后包含输出B.算法的每个操作步骤都是可执行的C.算法的步骤必须有限D.以上都不正确2、下面对算法描述正确的一项是（）A.算法只能用自然语言来描述B.算法只能用图形方式来表示C.同一问题可以有不同的算法D.同一问题的算法不同，结果必然不同3、看下面的四段话，其中不是解决问题的算法的是（）A.从上海到北京旅游，先坐火车，再坐飞机抵达B.解一元一次方程的步骤是去分母．去括号．移项．合并同类项．系数化为1C.方程210x -=有两个实根D.求12345++++的值，先计算123+=，再由于336+=，6410+=，10515+=，4、根据如图程序框图，输出k 的值为（）A.3B.4C.5D.65、给出计算12+14+16+…+120的值的一个程序框图如图，其中判断框内应填入的条件是（）A.i ＞10B.i ＜10C.i ＞20D.i ＜206、如图所示的流程图表示一函数，记作y=f （x ），若x 0满足f （x 0）＜0，且f （f （x 0））=1，则x 0=____．。

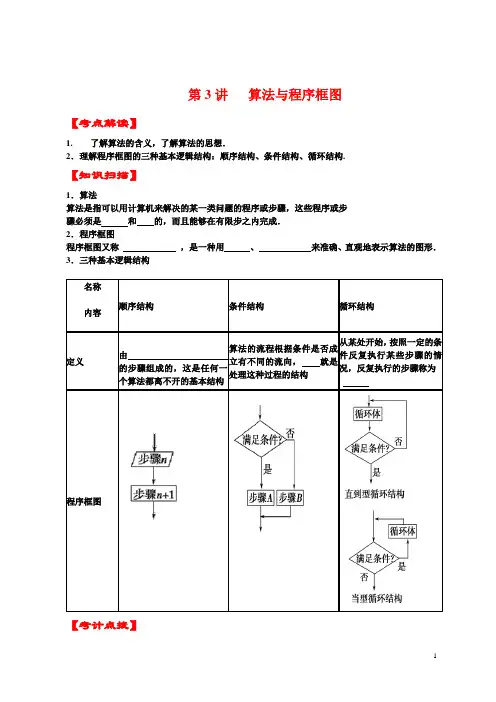
第3讲算法与程序框图【考点解读】1. 了解算法的含义，了解算法的思想．2．理解程序框图的三种基本逻辑结构：顺序结构、条件结构、循环结构.【知识扫描】1．算法算法是指可以用计算机来解决的某一类问题的程序或步骤，这些程序或步骤必须是和的，而且能够在有限步之内完成．2．程序框图程序框图又称，是一种用、来准确、直观地表示算法的图形．3．三种基本逻辑结构【考计点拨】牛刀小试：1．（2011高考北京卷）执行如图所示的程序框图，输出的s 值为 （A ）3- （B ）12- （C ）13（D ）2答案：D 2．（2011高考山东卷）执行右图所示的程序框图，输入l=2，m=3，n=5，则输出的y 的值是 . 【答案】68【解析】由输入l=2，m=3，n=5，计算得出y=278, 第一次得新的y=173;第二次得新的y=68<105,输出y.3．阅读下面的程序框图，则输出的S ＝()A ．14B ．20C ．30D ．55解析：选C.∵S 1＝0，i 1＝1；S 2＝1，i 2＝2；S 3＝5，i 3＝3；S 4＝14，i 4＝4；S 5＝30，i ＝5>4退出循环，∴输出结果为30.4. （2011高考辽宁卷）执行右面的程序框图，如果输入的n 是4，则输出的P 是(A) 8(B) 5 (C) 3 (D) 25．（2011高考陕西卷）右图中，1x ，2x ，3x 为某次考试三个评阅人对同一道题的独立评分，P 为该题的最终得分。

当1x =6，2x =9，p=8.5时，3x等于 （ ）(A)11 (B)10 (C)8 (D)7答案：C典题分析：考点：1.算法的含义，程序框图（1） 了解算法的含义和算法的思想.（2） 理解程序框图的三种基本逻辑结构：顺序，条件分支，循环. 2.基本语句理解几种基本算法语句——输入语句，输出语句，赋值语句，条件语句，循环语句的含义. 题型一算法的顺序结构 考点一 算法的循环结构例1.（2011高考湖南卷） 若执行如图3所示的框图，输入1231,2,3,2x x x x ====，则输出的数等于____________.答案：23考点二：算法的条件分支结构【例2】 函数y ＝，写出求该函数值的算法及程序框图． 解：算法如下： 第一步：输入x .第二步：如果x ＞0，则y =-2；如果x =0，则y =0；如果x ＜0，则y =2. 第三步：输出函数值y . 相应的程序框图如右图：变式2：“特快专递”是目前人们经常使用的异地邮寄信函或托运物品的一种快捷方式，某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算：()()()()⎩⎨⎧>⨯-+⨯≤=5085.05053.0505053.0ϖϖϖϖϖf解：算法如下：S1输入ω；S2如果ω≤50，那么f＝0.53ω；否则f＝50×0.53＋(ω－50)×0.85；S3输出f.程序框图为：【例3】画出计算12－22＋32－42＋…＋992－1002的值的程序框图．思维点拨：可以用循环结构来实现累加，设计一个累加变量，用S表示，设计一个计数变量，用I表示，另外还要对I进行奇偶数的判断，以决定是加还是减，因此还需要用到条件分支结构．解：程序框图如下图：变式3：画出求的值的程序框图．解：方法一：当型循环程序框图：方法二：直到型循环程序框图：规律总结：从近两年的高考试题来看，当型与直到型循环结构、条件分支结构是考查的热点，题型以选择题、填空题为主，分值5分左右，属容易题，主要考查算法基本结构以及读图、识图、利用框图解决简单算法问题的能力．预测2012年高考，循环结构与条件分支结构仍是考查的重点，但应同时注意算法的应。

1．程序框图(1)通常用一些通用图形符号构成一张图来表示算法．这种图称做程序框图(简称框图)．(2)基本的程序框图有起、止框、输入、输出框、处理框、判断框、流程线等图形符号和连接线构成．2．三种基本逻辑结构名称内容顺序结构条件分支结构循环结构定义最简单的算法结构，语句与语句之间，框与框之间按从上到下的顺序进行依据指定条件选择执行不同指令的控制结构根据指定条件决定是否重复执行一条或多条指令的控制结构程序框图3.基本算法语句(1)赋值语句①概念：用来表明赋给某一个变量一个具体的确定值的语句．②一般格式：变量名＝表达式．③作用：计算出赋值号右边表达式的值，把该值赋给赋值号左边的变量，使该变量的值等于表达式的值．(2)输入语句①概念：用来控制输入结构的语句．②一般格式：变量名＝input.③作用：把程序和初始数据分开．(3)输出语句①概念：用来控制把求解结果在屏幕上显示(或打印)的语句．②一般格式：print(%io(2)，表达式)．③作用：将结果在屏幕上输出．(4)条件语句①处理条件分支逻辑结构的算法语句．②条件语句的格式及框图．a．if语句最简单的格式及对应的框图b．if语句的一般格式及对应的框图(5)循环语句①算法中的循环结构是由循环语句来实现的．②循环语句的格式及框图．a．for语句b．while语句【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”) (1)算法只能解决一个问题，不能重复使用．(×)(2)程序框图中的图形符号可以由个人来确定．(×)(3)输入框只能紧接开始框，输出框只能紧接结束框．(×)(4)条件分支结构的出口有两个，但在执行时，只有一个出口是有效的．(√)(5)5＝x是赋值语句．(×)(6)输入语句可以同时给多个变量赋值．(√)1．已知一个算法：(1)m＝a.(2)如果b<m，则m＝b，输出m；否则执行第(3)步．(3)如果c<m，则m＝c，输出m.如果a＝3，b＝6，c＝2，那么执行这个算法的结果是()A．3 B．6C．2 D．m答案 C解析当a＝3，b＝6，c＝2时，依据算法设计，本算法是求a、b、c三个数的最小值，故输出m的值为2，故选C.2．(2015·陕西)根据如图所示的框图，当输入x为6时，输出的y等于()A．1 B．2C．5 D．10答案 D解析输入x＝6，程序运行情况如下：x＝6－3＝3＞0，x＝3－3＝0≥0，x＝0－3＝－3＜0，退出循环，执行y＝x2＋1＝(－3)2＋1＝10，输出y＝10.故选D.3．(2014·课标全国Ⅰ)执行下面的程序框图，若输入的a，b，k分别为1,2,3，则输出的M等于()A.203B.165C.72D.158答案 D解析 当n ＝1时，M ＝1＋12＝32，a ＝2，b ＝32；当n ＝2时，M ＝2＋23＝83，a ＝32，b ＝83；当n ＝3时，M ＝32＋38＝158，a ＝83，b ＝158；当n ＝4时，终止循环．输出M ＝158.4．(教材改编)程序：若输入a ＝10，则输出的结果是( ) A ．20 B ．10 C ．100 D ．200答案 C解析 程序所表示的函数表达式为y ＝⎩⎪⎨⎪⎧2a (a <10)a 2 (a ≥10)，∴当a ＝10时，y ＝102＝100.5．如图，是求实数x 的绝对值的算法程序框图，则判断框①中可填________________．答案 x >0(或x ≥0)解析 由于|x|＝⎩⎪⎨⎪⎧x ， x ≥0，－x ，x <0或|x |＝⎩⎪⎨⎪⎧x ，x >0，－x ，x ≤0，故根据所给的程序框图， 易知可填“x >0”或“x ≥0”.题型一 顺序结构与条件分支结构 命题点1 顺序结构例1 已知f (x )＝x 2－2x －3，求f (3)、f (－5)、f (5)，并计算f (3)＋f (－5)＋f (5)的值．设计出解决该问题的一个算法，并画出程序框图． 解 算法如下： 第一步，令x ＝3.第二步，把x ＝3代入y 1＝x 2－2x －3. 第三步，令x ＝－5.第四步，把x ＝－5代入y 2＝x 2－2x －3. 第五步，令x ＝5.第六步，把x ＝5代入y 3＝x 2－2x －3.第七步，把y 1，y 2，y 3的值代入y ＝y 1＋y 2＋y 3. 第八步，输出y 1，y 2，y 3，y 的值． 该算法对应的程序框图如图所示：命题点2 条件分支结构例2 执行如图所示的程序框图，如果输入的t ∈[－1,3]，则输出的s 属于( )A ．[－3,4]B ．[－5,2]C ．[－4,3]D ．[－2,5]答案 A解析 根据程序框图可以得到分段函数s ＝⎩⎪⎨⎪⎧3t ，t <1，4t －t 2，t ≥1，进而在函数的定义域[－1,3]内分段求出函数的值域．所以当－1≤t <1时，s ＝3t ∈[－3,3)；当1≤t ≤3时，s ＝4t －t 2＝－(t －2)2＋4，所以此时3≤s ≤4.综上可知，函数的值域为[－3,4]，即输出的s 属于[－3,4]． 引申探究若将本例中判断框的条件改为“t ≥1”，则输出的s 的范围是什么？解 根据程序框图可以得到，当－1≤t <1时，s ＝4t －t 2＝－(t －2)2＋4，此时－5≤s <3；当1≤t ≤3时，s ＝3t ∈[3,9]．综上可知，函数的值域为[－5,9]，即输出的s 属于[－5,9]． 思维升华 应用顺序结构与条件分支结构的注意点 (1)顺序结构顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的． (2)条件分支结构利用条件分支结构解决算法问题时，重点是判断框，判断框内的条件不同，对应的下一框中的内容和操作要相应地进行变化，故要重点分析判断框内的条件是否满足．(2014·四川)执行如图所示的程序框图，如果输入的x ，y ∈R ，那么输出的S 的最大值为( )A ．0B ．1C ．2D ．3答案 C解析 当条件x ≥0，y ≥0，x ＋y ≤1不成立时输出S 的值为1；当条件x ≥0，y ≥0，x ＋y ≤1成立时S ＝2x ＋y ，下面用线性规划的方法求此时S 的最大值．作出不等式组⎩⎪⎨⎪⎧x ≥0，y ≥0，x ＋y ≤1表示的平面区域如图中阴影部分，由图可知当直线S ＝2x ＋y 经过点M (1,0)时S最大，其最大值为2×1＋0＝2，故输出S 的最大值为2. 题型二 循环结构命题点1 由程序框图求输出结果例3 (2015·安徽)执行如图所示的程序框图，输出的n 为________．答案 4解析 结合程序框图逐一验证求解．执行第一次判断：|a －1.414|＝0.414>0.005，a ＝32，n ＝2；执行第二次判断：|a －1.414|＝0.086>0.005，a ＝75，n ＝3；执行第三次判断：|a －1.414|＝0.014>0.005，a ＝1712，n ＝4；执行第四次判断：|a －1.414|<0.005，输出n ＝4. 命题点2 完善程序框图例4 (2014·重庆)执行如图所示的程序框图，若输出k 的值为6，则判断框内可填入的条件是( )A ．s >12B ．s >35C ．s >710D ．s >45答案 C解析 第一次执行循环：s ＝1×910＝910，k ＝8，s ＝910应满足条件；第二次执行循环：s ＝910×89＝810，k ＝7，s ＝810应满足条件，排除选项D ；第三次执行循环：s ＝810×78＝710，k ＝6，正是输出的结果，故这时程序不再满足条件，结束循环，而选项A 和B 都满足条件，故排除A 和B ，故选C. 命题点3 辨析程序框图的功能例5 (2014·陕西)根据下面框图，对大于2的整数N ，输出的数列的通项公式是( )A ．a n ＝2nB ．a n ＝2(n －1)C．a n＝2n D．a n＝2n－1答案 C解析由程序框图可知第一次运行：i＝1，a1＝2，S＝2；第二次运行：i＝2，a2＝4，S＝4；第三次运行：i＝3，a3＝8，S＝8；第四次运行：i＝4，a4＝16，S＝16.故选C.思维升华与循环结构有关问题的常见类型及解题策略(1)已知程序框图，求输出的结果，可按程序框图的流程依次执行，最后得出结果．(2)完善程序框图问题，结合初始条件和输出结果，分析控制循环的变量应满足的条件或累加、累乘的变量的表达式．(3)对于辨析程序框图功能问题，可将程序执行几次，即可根据结果作出判断．(1)(2015·课标全国Ⅰ)执行如图所示的程序框图，如果输入的t＝0.01，则输出的n等于()A．5 B．6 C．7 D．8(2)(2014·课标全国Ⅱ)执行如图所示的程序框图，如果输入的x，t均为2，则输出的S等于()A．4 B．5 C．6 D．7答案 (1)C (2)D解析 (1)逐次运行程序，直至输出n .运行第一次：S ＝1－12＝12＝0.5，m ＝0.25，n ＝1，S >0.01；运行第二次：S ＝0.5－0.25＝0.25，m ＝0.125，n ＝2，S >0.01； 运行第三次：S ＝0.25－0.125＝0.125，m ＝0.062 5，n ＝3，S >0.01； 运行第四次：S ＝0.125－0.062 5＝0.062 5，m ＝0.031 25，n ＝4，S >0.01； 运行第五次：S ＝0.031 25，m ＝0.015 625，n ＝5，S >0.01； 运行第六次：S ＝0.015 625，m ＝0.007 812 5，n ＝6，S >0.01； 运行第七次：S ＝0.007 812 5，m ＝0.003 906 25，n ＝7，S <0.01. 输出n ＝7.故选C.(2)x ＝2，t ＝2，M ＝1，S ＝3，k ＝1. k ≤t ，M ＝11×2＝2，S ＝2＋3＝5，k ＝2；k ≤t ，M ＝22×2＝2，S ＝2＋5＝7，k ＝3；3>2，不满足条件，输出S ＝7. 题型三 基本算法语句例6 (1)下面程序输出的结果是________．(2)根据如图所示的程序，当输入a ，b 分别为2,3时，最后输出的m 的值为________．答案 (1)0 (2)3解析 (1)当s ＝5＋4＋3＋2＋1≥15时，停止循环，而此时，n ＝1－1＝0. (2)本程序的功能是求两个数中较大的一个数．思维升华 解决算法语句有三个步骤：首先通读全部语句，把它翻译成数学问题；其次领悟该语句的功能；最后根据语句的功能运行程序，解决问题．下面程序的作用是__________________．答案求－(3＋7＋11＋…＋199)的值解析这是for语句，循环变量为i，初值为3，步长为4，终值为199，先求S＝3＋7＋11＋…＋199，然后M＝－S＝－(3＋7＋11＋…＋199)．21．变量的含义理解不准致误典例执行如图所示的程序框图，输出的S值为()A．2 B．4 C．8 D．16易错分析(1)读不懂程序框图，把执行循环体的次数n误认为是变量k的值，没有注意到k的初始值为0.(2)对循环结构：①判断条件把握不准；②循环次数搞不清楚；③初始条件容易代错．解析当k＝0时，满足k<3，因此S＝1×20＝1；当k＝1时，满足k<3，则S＝1×21＝2；当k＝2时，满足k<3，则S＝2×22＝8；当k＝3时，不满足k<3，输出S＝8.答案 C温馨提醒在处理含有循环结构的算法问题时，关键是确定循环的次数，循环中有哪些变量，且每一次循环之后的变量S、k值都要被新的S、k值所替换．[方法与技巧]1．在设计一个算法的过程中要牢记它的五个特征：概括性、逻辑性、有穷性、不唯一性、普遍性．2．在画算法框图时首先要进行结构的选择．若所要解决的问题不需要分情况讨论，只用顺序结构就能解决；若所要解决的问题要分若干种情况讨论时，就必须引入条件结构；若所要解决的问题要进行许多重复的步骤，且这些步骤之间又有相同的规律时，就必须引入变量，应用循环结构． [失误与防范]1．注意起止框与处理框、判断框与循环框的不同．2．注意条件分支结构与循环结构的联系：对于循环结构有重复性，条件分支结构具有选择性没有重复性，并且循环结构中必定包含一个条件分支结构，用于确定何时终止循环体．3．循环语句有for 循环和while 循环两种，要区别两者的异同，主要解决需要反复执行的任务，用循环语句来编写程序．4．关于赋值语句，有以下几点需要注意：(1)赋值号左边只能是变量名字，而不是表达式，例如3＝m 是错误的．(2)赋值号左右不能对换，赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量，例如Y ＝x ，表示用x 的值替代变量Y 的原先的取值，不能改写为x ＝Y .因为后者表示用Y 的值替代变量x 的值． (3)在一个赋值语句中只能给一个变量赋值，不能出现多个“＝”．A 组 专项基础训练 (时间：25分钟)1．(2015·北京)执行如图所示的程序框图，输出的k 值为( )A ．3B ．4C ．5D ．6 答案 B解析 第一次循环：a ＝3×12＝32，k ＝1；第二次循环：a ＝32×12＝34，k ＝2；第三次循环：a ＝34×12＝38，k ＝3；第四次循环：a ＝38×12＝316<14，k ＝4.故输出k ＝4.2．(2015·课标全国Ⅱ)下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入的a ，b 分别为14,18，则输出的a 等于( )A ．0B ．2C ．4D ．14答案 B解析 由题知，若输入a ＝14，b ＝18，则第一次执行循环结构时，由a ＜b 知，a ＝14，b ＝b －a ＝18－14＝4； 第二次执行循环结构时，由a ＞b 知，a ＝a －b ＝14－4＝10，b ＝4； 第三次执行循环结构时，由a ＞b 知，a ＝a －b ＝10－4＝6，b ＝4； 第四次执行循环结构时，由a ＞b 知，a ＝a －b ＝6－4＝2，b ＝4； 第五次执行循环结构时，由a ＜b 知，a ＝2，b ＝b －a ＝4－2＝2； 第六次执行循环结构时，由a ＝b 知，输出a ＝2，结束． 故选B.3．执行如图所示的程序框图，则输出的k 的值是( )A ．3B ．4C ．5D ．6 答案 C解析 由题意，得k ＝1时，s ＝1；k ＝2时，s ＝1＋1＝2；k ＝3时，s ＝2＋4＝6；k ＝4时，s ＝6＋9＝15；k ＝5时，s ＝15＋16＝31>15，此时输出k 值为5.4．(2015·重庆)执行如图所示的程序框图，若输出k 的值为8，则判断框内可填入的条件是( )A ．s ≤34B ．s ≤56C ．s ≤1112D ．s ≤2524答案 C解析 由s ＝0，k ＝0满足条件，则k ＝2，s ＝12，满足条件；k ＝4，s ＝12＋14＝34，满足条件；k ＝6，s ＝34＋16＝1112，满足条件；k ＝8，s ＝1112＋18＝2524，不满足条件，输出k ＝8，所以应填“s ≤1112”． 5．(2015·天津)阅读右边的程序框图，运行相应的程序，则输出S 的值为( )A ．－10B ．6C ．14D ．18 答案 B解析 运行相应的程序，第一次循环：i ＝2，S ＝20－2＝18；第二次循环：i ＝4，S ＝18－4＝14；第三次循环：i ＝8，S ＝14－8＝6；8＞5，终止循环，输出S ＝6，故选B. 6．定义某种运算，a b 的运算原理如图所示．设S ＝1x ，x ∈[－2,2]，则输出的S 的最大值与最小值的差为( )A ．2B ．－1C ．4D ．3 答案 A解析 由题意可得，S (x )＝⎩⎪⎨⎪⎧|x |，－2≤x ≤1，1，1<x ≤2，∴S (x )max ＝2，S (x )min ＝0， ∴S (x )max －S (x )min ＝2.7．(2015·江苏改编)根据如图所示的语句，可知输出的结果S ＝________.答案 7解析 I ＝1，S ＝1；S ＝1＋2＝3，I ＝1＋3＝4＜8； S ＝3＋2＝5，I ＝4＋3＝7＜8； S ＝5＋2＝7，I ＝7＋3＝10＞8. 退出循环，故输出S ＝7.8．如图是一个程序框图，则输出的n 的值是________．答案 5解析 该程序框图共运行5次，各次2n 的值分别是2,4,8,16,32，所以输出的n 的值是5.9．(2015·山东)执行下边的程序框图，输出的T 的值为________.答案116解析 当n ＝1时，T ＝1＋⎠⎛01x 1dx ＝1＋⎪⎪12x 210＝1＋12＝32； 当n ＝2时，T ＝32＋⎠⎛01x 2dx ＝32＋⎪⎪13x 310＝32＋13＝116； 当n ＝3时，结束循环，输出T ＝116.10．关于函数f (x )＝⎩⎪⎨⎪⎧－x ，1<x ≤4，cos x ，－1≤x ≤1的程序框图如图所示，现输入区间[a ，b ]，则输出的区间是________．答案 [0,1]解析 由程序框图的第一个判断条件为f (x )>0，当f (x )＝cos x ，x ∈[－1,1]时满足．然后进入第二个判断框，需要解不等式f ′(x )＝－sin x ≤0，即0≤x ≤1.故输出区间为[0,1]．B 组 专项能力提升 (时间：25分钟)11．给出一个算法的程序框图(如图所示)，该程序框图的功能是( )A ．输出a ，b ，c 三数中的最大数B ．输出a ，b ，c 三数中的最小数C ．将a ，b ，c 按从小到大排列D ．将a ，b ，c 按从大到小排列 答案 B解析 先比较a ，b 的值，把较小的值赋值给a ；再比较a ，c 的值，把较小的值赋值给a ，输出a . 12．给出一个如图所示的程序框图，若要使输入的x 值与输出的y 值相等，则这样的x 值是________．答案 0,1,3解析 根据题意，本程序框图表示分段函数：y ＝⎩⎪⎨⎪⎧x 2，x ≤2，2x －3，2<x ≤5，1x ，x >5，由于输入的x 值与输出的y 值相等， 由x 2＝x 解得x ＝0或x ＝1，都满足x ≤2； 由x ＝2x －3解得x ＝3，也满足2<x ≤5； 由1x ＝x 解得x ＝±1，不在x >5内，舍去． 可见满足条件的x 共三个：0,1,3.13．下列是求一个函数的函数值的程序，在键盘上输入一个自变量x 的值，输出它的函数值．若执行的结果为3，则输入的x 值为__________． 答案 －3或414．对一个作直线运动的质点的运动过程观测了8次，第i 次观测得到的数据为a i ，具体如下表所示：i 1 2 3 4 5 6 7 8 a i4041434344464748在对上述统计数据的分析中，一部分计算见如图所示的程序框图(其中a 是这8个数据的平均数)，则输出的S 的值是________．答案 7解析 本题计算的是这8个数的方差，因为 a ＝40＋41＋43＋43＋44＋46＋47＋488＝44，所以S ＝(－4)2＋(－3)2＋(－1)2＋(－1)2＋02＋22＋32＋428＝7.15．如图(1)(2)所示，它们都表示的是输出所有立方小于1 000的正整数的程序框图，那么应分别补充的条件为：(1)____________；(2)______________．答案(1)n3<1 000(2)n3≥1 000解析第一个图中，n不能取10，否则会把立方等于1 000的正整数也输出了，所以应该填写n3<1 000；第二个图中当n≥10时，循环应该结束，所以填写n3≥1 000.16．(2014·湖北)设a是一个各位数字都不是0且没有重复数字的三位数．将组成a的3个数字按从小到大排成的三位数记为I(a)，按从大到小排成的三位数记为D(a)(例如a＝815，则I(a)＝158，D(a)＝851)．阅读如图所示的程序框图，运行相应的程序，任意输入一个a，输出的结果b＝________.答案495解析取a1＝815⇒b1＝851－158＝693≠815⇒a2＝693；由a2＝693⇒b2＝963－369＝594≠693⇒a3＝594；由a3＝594⇒b3＝954－459＝495≠594⇒a4＝495；由a4＝495⇒b4＝954－459＝495＝a4⇒b＝495.。