- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
区别
具有特殊形状的图形,
的位置关系,必须涉及
倍 速
只对( 一个 ) 图形而言; ( 两个 )图形; (2)对称轴(不一定) 只有一条 (2)只有(一条 )对称轴.
课
时
如果把轴对称图形沿对称轴 如果把两个成轴对称的图形
学
联系 分成两部分,那么这两个图形 拼在一起看成一个整体,那
练
就关于这条直线成轴对称. 么它就是一个轴对称图形.
经过线段中点并且垂直于这条线段的直线 叫做这条线段的垂直平分线,也叫中垂线。
2、线段垂直平分线有什么性质?
倍
线段垂直平分线上的点与这条线段的
速 课
两个端点的距离相等 。时学练源自你能画图说明吗?11
3.逆定理:与一条线段两个端点距离相等的点 都在线段的垂直平分线上。(完备性)
4.线段垂直平分线的集合定义:
8
练习:
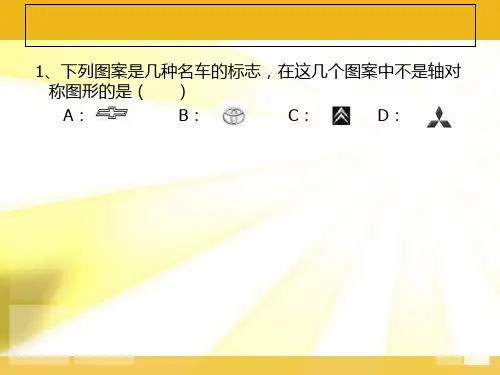
1、小明照镜子的时候,发现T恤上的英
文单词在镜子中呈现“
”的样子,
请你判断这个英文单词是( A )
A.
B.
倍 速
C.
D.
课
时
学
练
9
2、△ABC与△DEF关于直线L成轴
对称,则∠C是多少度?
L
A
D
650
65
倍
750
速
40
C
F
课 时
B
E
学
练
10
二.线段的垂直平分线
1、什么叫线段的垂直平分线?
倍
速
课 时
点(x, y)关于y轴对称的点的坐标为_(_-__x_,_y).
学
练
13
练习
1、完成下表. (抢答)
已知点
(2,-3)
(-1,2) (-6,-5) (0,-1.6) (4,0)
关于x轴的对称点
(2, 3) (-1,-2) (-6, 5) (0,1.6) (4,0)
关于y轴的对称点
(-2, -3) (1, 2) (6, -5) (0, -1.6) (-4,0)
归纳:先求出已知图形中的 特殊
-2
时
点(如多边形的顶点或端点)的对应
-3
学
点的坐标,描出并连接这些点,就可
-4
练
得到这个图形的轴对称图形.
15
思考:如图,分别作出点P,M,N关于直线
x=1的对称点, 你能发现它们坐标之间分别
· 有什么关系吗? P(-2,4)
y 5
4
x=1
· P’(4,4)
· M(-1,1)
第十三章 轴对称
1
一、知识梳理
(1)在现实世界中存在着大量的轴对称现象,你能举出一 些例子吗?成轴对称的图形有什么特点?
(2)在我们学过的几何图形中,有哪些是轴对称图形?它 们的对称轴与这个图形有怎样的位置关系?
(3)一个图形经过轴对称变换后,对应点所连线段与对称 轴有什么关系?如何作出一个图形的轴对称图形?
2、轴对称把一:个图形沿着某一条直线折叠,如果它能与另
一个图形完全重合,那么就说这两个图关于这条直线
倍
对称。这条直线叫做对称轴。折叠后重合的点是对应
速
点,叫做对称点.
课
时
学
练
6
知识回顾:
3、轴对称图形和轴对称的区别与联系
轴对称图形
轴对称
A
图形
A
A'
(1)
轴
对
B
称图
形
是
C
指
(一个
)
B
C
C'
B'
(1)轴对称是指(两个 )图形
轴对称的图形。
y
解:点A(-3,5),B(-4,1), C(-1,3),关于y轴对称 点的坐标分别为A’(3,5), B’(4,1),C’(1,3).依次连接 A’B’,B’C’,C’A’,就得到 △ABC关于y轴对称的
· A
5
·A’
· · c4 3 C’
·2
B
1
·B’
倍 速 课
△A’B’C’.
-4 -3 -2 -1-1O 1 2 3 4 5
4
体系构建
(2)等腰三角形与等边三角形之间有什么特殊的关 系?
生
活 中
轴对称
的
轴
对
称 等腰三角形
作轴对称图形的对称轴
画轴对称图形
关于坐标轴对称的 点的坐标的关系
等边三角形
5
知识回顾 一、轴对称图形
1、轴对称图形:把一个图形沿着一条直线折叠,如果直
线两旁的部分能够完全重合,那么这个图形就叫做轴 对称图形。这条直线就是它的对称轴。这时我们也说 这个图形关于这条直线(成轴)对称。
生
活 中
轴对称
的
轴
对
称 等腰三角形
作轴对称图形的对称轴
画轴对称图形
关于坐标轴对称的 点的坐标的关系
等边三角形
3
体系构建
(1)回顾本章的学习过程,说一说轴对称的性质在 本章中重要作用是如何体现的?
生
活 中
轴对称
的
轴
对
称 等腰三角形
作轴对称图形的对称轴
画轴对称图形
关于坐标轴对称的 点的坐标的关系
等边三角形
(4)在平面直角坐标系中,如果两个图形关于x 轴或y轴对 称,那么对应点的坐标有什么关系?请举例说明.
(5)利用等腰三角形的轴对称性,我们发现了它的哪些性 质?你能通过全等三角形加以证明吗?等边三角形作为特 殊的等腰三角形,有哪些特殊性质?
2
二、体系构建
整理一下本章所学的主要知识,你能发现它们之 间的联系吗?你能画出一个本章的知识结构图吗?
m
线段的垂直平分线可以看作是
A
与线段两个端点距离相等的所
倍 有点的集合。
速 课 时 学 练
C
D
B
12
三、用坐标表示轴对称小结:
在平面直角坐标系中,关于x轴对称的点 横坐标相等,纵坐标互为相反数.关于y轴 对称的点横坐标互为相反数,纵坐标相等.
点(x, y)关于x轴对称的点的坐标为_(_x_, -___y).
3 2
’
1
M’(3,1)
·
x
倍 速
· · -4
-3
-2
-1
0 -1
-2
12345
课
N(-3,-2)
N’(5,-2)
时
学
练
点(x, y)关于直线x=1对称的点的坐标为(2-x,16y)
如图,分别作出△ABC关于直线x=1(记为m) 和直线 y=-1(记为n)对称的图形,它们的对应点的坐标之 间分别有什么关系?
Ym
• 如图:
A(-4,5)
B(-1,3)
F(3,3)
D(6,5)
C(-4,1)
O
M(-4,-3)
E(6,1) xX
2、已知点P(2a+b,-3a)与点P’(8,b+2).
倍
速 课
若点p与点p’关于x轴对称,则a=__2___ b=___4____.
时
学 练
若点p与点p’关于y轴对称,则a=__6___ b=___-_2_0__.
14
例:已知△ABC的三个顶点的坐标分别为A
(-3,5),B(- 4,1),C(-1,3),作出△ABC关于y
7
4、轴对称的性质:
①关于某直线对称的两个图形是全等形。 ②如果两个图形关于某条直线对称,那么对称轴是任 何一对对应点所连线段的垂直平分线。 ③轴对称图形的对称轴,是任何一对对应点所连线段 的垂直平分线。 ④如果两个图形的对应点连线被同条直线垂直平分, 那么这两个图形关于这条直线对称。 倍 速 课 时 学 练