考点16 三角函数性质——2021年高考数学专题复习讲义

2021高考一轮复习 第十六讲 三角函数的图象与性质一、单选题（共12题；共24分）1.将函数 f(x)=sin2x 的图象向右平移 π6 个单位得到 g(x) ，下列关于 g(x) 的说法正确的是（ ） A. x =π12 是对称轴 B. 在 [0,π2] 上单调递增C. 在 [0,π3] 上最大值为1 D. 在 [−π3,0] 上最小值为 −1 【答案】 D【考点】正弦函数的单调性，函数y=Asin （ωx+φ）的图象变换2.已知函数 f(x)=sinωx +√3cosωx(ω>0) 的图象关于直线 x =π8 对称，则 ω 的最小值为（ ） A. 13 B. 23 C. 43 D. 83 【答案】 C【考点】正弦函数的奇偶性与对称性3.已知函数 y =sin(ωx +π3)(ω>0) 在区间 (−π6,π3) 上单调递增，则 ω 的取值范围是（ ）A. (0,12]B. [12,1]C. (13,23]D. [23,2] 【答案】 A【考点】正弦函数的单调性4.已知函数 f(x)=cos x2−√3sin x2 的图象为C ，为了得到关于原点对称的图象，只要把C 上所有的点（ ） A. 向左平移 π3 个单位 B. 向左平移 2π3个单位 C. 向右平移 π3 个单位 D. 向右平移 2π3个单位【答案】 A【考点】余弦函数的奇偶性与对称性，函数y=Asin （ωx+φ）的图象变换5.函数 f(x)=2sin (wx +φ)(w >0,x ∈R) 的部分图象如图所示，则该函数图象的一个对称中心是（ ）A. (π3,0)B. (−2π3,0) C. (−4π3,0) D. (4π3,0)【答案】 C【考点】正弦函数的奇偶性与对称性，由y=Asin （ωx+φ）的部分图象确定其解析式 6.下列函数中，周期为1的奇函数是( )A. y=1-2sin 2πxB. y=sin (2πx +π3) C. y=tan π2x D. y=sinπxcosπx【答案】 D【考点】二倍角的正弦公式，二倍角的余弦公式，正弦函数的奇偶性与对称性，正切函数的周期性 7.下列函数中，最小正周期为π的偶函数是（ ）A. y =sin2xB. y =cos x2 C. sin2x +cos2x D. y =1−tan 2x 1+tan 2x【答案】 D【考点】函数奇偶性的判断，二倍角的余弦公式，三角函数的周期性及其求法，同角三角函数间的基本关系8.已知函数 f(x)=√3sin(2x +φ)+cos(2x +φ) 为R 上的奇函数，且在 [π4,π2] 上单调递增，则 φ 的值可能是（ ） A. −2π3B. −π6C. π3D. 5π6 【答案】 D【考点】正弦函数的单调性9.函数 y =sin(2x +π4) 的最小正周期是（ ）A. πB. 2πC. π2 D. π4 【答案】 A【考点】三角函数的周期性及其求法10.函数 f(x)=cosx(1+√3tanx) 的最小正周期为（ ）A. 2πB. πC. 32π D. 12π 【答案】 A【考点】三角函数的周期性及其求法11.函数 y =cos 2x +sin x −1 的值域为（ ）A. (−∞,14] B. [0,14] C. [−2,14] D. [−2,0] 【答案】 C【考点】二次函数在闭区间上的最值，正弦函数的定义域和值域12.把函数 y =sin(x +π6) 图象上各点的横坐标伸长为原来的2倍，纵坐标不变，再将图象向右平移 π3 个单位，那么所得图象的一个对称中心为（ ）A. (π3,0) B. (π4,0) C. (π12,0) D. (0,0) 【答案】 D【考点】正弦函数的奇偶性与对称性，函数y=Asin （ωx+φ）的图象变换二、多选题（共2题；共6分）13.函数f（x）＝cos（2x +π6）的图象的一条对称轴方程为（）A. x =π6 B. x= 5π12C. x =11π12D. x= −2π3【答案】B,C【考点】余弦函数的奇偶性与对称性14.将函数f(x)=√3cos(2x+π3)−1的图象向左平移π3个单位长度，再向上平移1个单位长度，得到函数g(x)的图象，则下列关于函数g(x)的说法正确的是（）A. 最大值为√3，图象关于直线x=π12对称 B. 图象关于y轴对称C. 最小正周期为πD. 图象关于点(π4,0)对称【答案】B,C,D【考点】余弦函数的奇偶性与对称性，函数y=Asin（ωx+φ）的图象变换三、填空题（共3题；共4分）15.若函数f(x)=2sin(2x+φ)(0<φ<π2)的图象过点(0,√3)，则函数f(x)在[0,π]上的单调减区间是________．【答案】(π12,7π12)(或[π12,7π12])【考点】正弦函数的单调性16.函数f(x)=2sin(2x−π6)−m，若f(x)≤0在x∈[0,π2]上恒成立，则m的取值范围是________;若f(x)在x∈[0,π2]上有两个不同的解，则m的取值范围是________. 【答案】m≥2；1≤m＜2【考点】函数恒成立问题，正弦函数的图象，函数的零点与方程根的关系17.不等式sin2x−cos2x≥0的解集为________．【答案】[kπ+π4,kπ+3π4]，k∈Z【考点】二倍角的余弦公式，余弦函数的单调性四、解答题（共3题；共35分）18.已知函数f(x)=sinx−2√3cos2x2+√3（1）求f(π)的值；（2）求函数y=|f(x)|的单调递增区间.【答案】（1）解：化简得f(x)=sinx−√3cosx=2sin(x−π3)，所以f(π)=2sin2π3=√3（2）解：由于y=2|sin(x−π3)|，故kπ⩽x−π3⩽π2+kπ，k∈Z，解得函数y=|f(x)|的单调递增区间为[kπ+π3,kπ+5π6]，k∈Z【考点】两角和与差的正弦公式，二倍角的余弦公式，正弦函数的单调性19.已知函数f(x)=2√3cos2x+sin(π−2x)．（1）求函数f(x)的最小正周期．（2）求函数f(x)在[0,π2]上的单调区间．【答案】（1）解：∵f(x)=2√3cos2x+sin(π−2x)=√3(cos2x+1)+sin2x=sin2x+√3cos2x+√3=2sin(2x+π3)+√3，∴函数f(x)的最小正周期为2π2=π．（2）解：当x∈[0,π2]时，2x+π3∈[π3,4π3]，∴令π3≤2x+π3≤π2，得0≤x≤π12．令π2≤2x+π3≤4π3，得π12≤x≤π2．∴函数f(x)在[0,π2]上的单调增区间是[0,π12]，单调减区间是[π12,π2]．【考点】二倍角的余弦公式，三角函数的积化和差公式，正弦函数的单调性，正弦函数的周期性20.已知函数f(x)=sinxcosx+√32(cos2x−sin2x).（1）求f(π6)的值；（2）求f(x)的单调递增区间；（3）求f(x)的最大值.【答案】（1）解：由题意可得f(x)=sinxcosx+√32(cos2x−sin2x)=12sin2x+√32cos2x=sin(2x+π3)，所以f(π6)=sin(2×π6+π3)=sin2π3=√32；（2）解：由−π2+2kπ≤2x+π3≤π2+2kπ,k∈Z，解得−5π12+kπ≤x≤π12+kπ,k∈Z，所以f(x)的单调递增区间为[−5π12+kπ，π12+kπ](k∈Z)；)，（3）解：由（1）得f(x)=sin(2x+π3所以f(x)的最大值为1.【考点】三角函数中的恒等变换应用，正弦函数的单调性，三角函数的最值。

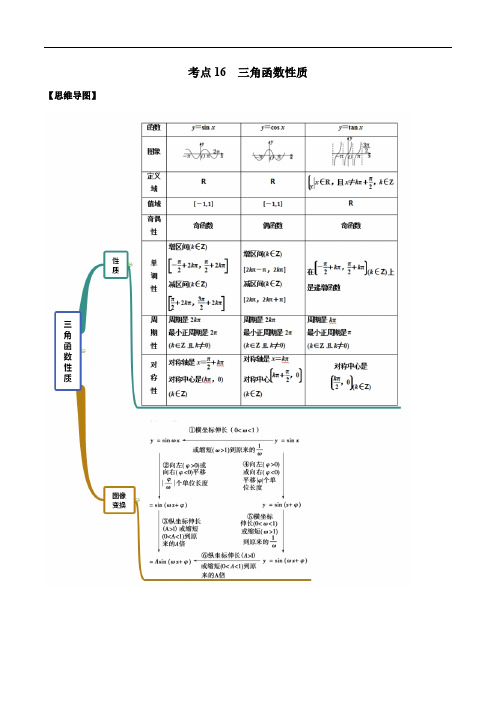
考点16 三角函数性质【思维导图】【常见考法】考点一：周期1．函数2()cos 3f x x π⎛⎫=+ ⎪⎝⎭的最小正周期为 。

2．函数tan y x ω=（其中0>ω）的最小正周期是2π，则ω= 。

3．在下列四个函数，①sin y x =②cos 2y x =③2sin 23y x π⎛⎫=- ⎪⎝⎭④2tan 10y x π⎛⎫=+⎪⎝⎭中，最小正周期为π的所有函数为 。

4．函数22cos sin 44y x x ππ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭的最小正周期为 。

5．给出四个函数（1）)cos sin y x xx x =+-；（2）44sin cos y x x =-；（3）sin y x =；（4）sin 2cos2y x x =+.其中最小正周期为π的函数个数为 。

6．已知函数()2tan 1tan xf x x=-，则函数()f x 的最小正周期为 。

考点二：定义域1．函数y =的定义域是 。

2．函数π3tan 24y x ⎛⎫=+ ⎪⎝⎭的定义域是 。

3．求函数 y =的定义域 。

4．函数()ln(sin cos )f x x x =-+的定义域为 。

考点三：单调性1．函数sin 4y x =-+⎪⎝⎭的一个单调递减区间是 。

A ．3,22ππ⎡⎤⎢⎥⎣⎦ B ．5,44ππ⎡⎤⎢⎥⎣⎦ C ．,22ππ⎡⎤-⎢⎥⎣⎦ D ．3,44ππ⎡⎤-⎢⎥⎣⎦2．函数sin 24y x π⎛⎫=- ⎪⎝⎭的单调递减区间为 。

3．函数y =的单调递增区间是 。

4．已知0>ω，函数()sin()4f x x πω=+在(,)2ππ上单调递减，则ω的取值范围是 。

5．若()cos f x x x =在[],a a -上是减函数,则实数a 的取值范围是 。

6．已知函数()2cos (0)3f x x πωω⎛⎫=-> ⎪⎝⎭在,32ππ⎡⎤-⎢⎥⎣⎦上单调递增，则ω的取值范围 。

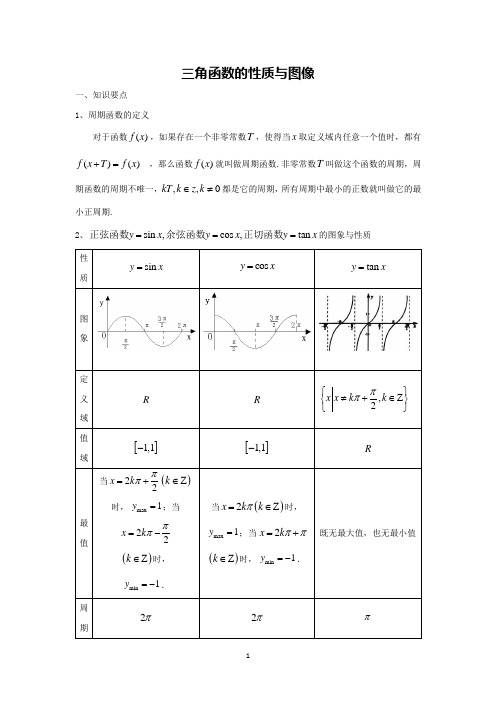
三角函数的性质与图像一、知识要点 1、周期函数的定义对于函数()f x ，如果存在一个非零常数T ，使得当x 取定义域内任意一个值时，都有()()f x T f x +=，那么函数()f x 就叫做周期函数.非零常数T 叫做这个函数的周期，周期函数的周期不唯一，,,0kT k z k ∈≠都是它的周期，所有周期中最小的正数就叫做它的最小正周期.2、sin ,cos ,tan y x y x y x ===正弦函数余弦函数正切函数的图象与性质3、复合函数的单调性设()y f u =，()u g x =[,]x a b ∈，[,]u m n ∈都是单调函数，则[()]y f g x =在[,]a b 上也是单调函数，其单调性由“同增异减”来确定，即“里外”函数增减性相同，复合函数为增函数，“里外”函数的增减性相反，复合函数为减函数.如下表：4、使用周期公式，必须先将解析式化为sin()y A x h ωϕ=++或cos()y A x h ωϕ=++的形式；正弦余弦函数的最小正周期是2T πϖ=，正切函数的最小正周期公式是T πϖ=；注意一定要注意加绝对值.5、sin()y A wx h φ=++（或cos()y A wx h φ=++）图象的作法有两种： （1）描点法（五点法），先列表，令0x ωϕ+=,2π, π, 32π,2π，求出对应的五个x 的值和五个y 值，再根据求出的对应的五个点的坐标描出五个点，再把五个点利用平滑的曲线连接起来，即得到sin()y A wx h φ=++在一个周期的图像，最后把这个周期的图像以周期为单位，向左右两边平移，则得到函数sin()y A wx h φ=++的图像.（2）图像变换法：一般先把函数sin y x =的图像通过左右平移得到函数sin()y x φ=+的图像，再把函数sin()y x φ=+的图像通过横坐标的伸缩变换得到函数sin()y wx φ=+，再把函数sin()y wx φ=+通过纵坐标的伸缩变换得到函数sin()y A x ωϕ=+的图像，最后把函数sin()y A x ωϕ=+的图像通过上下平移得到函数sin()y A wx h φ=++的图像. 6、三角函数图像的变换（平移变换和上下变换） 平移变换：左加右减，上加下减把函数()y f x =向左平移φ(0)φ>个单位，得到函数()y f x φ=+的图像 把函数()y f x =向右平移φ(0)φ>个单位，得到函数()y f x φ=-的图像 把函数()y f x =向上平移φ(0)φ>个单位，得到函数()y f x φ=+的图像 把函数()y f x =向下平移φ(0)φ>个单位，得到函数()y f x φ=-的图像 伸缩变换：①把函数()y f x =图象的纵坐标不变，横坐标伸长到原来的w 1倍得()y f x ω=(01)ω<< ②把函数()y f x =图象的纵坐标不变，横坐标缩短到原来的w1倍得()y f x ω=(1)ω>③把函数()y f x =图象的横坐标不变，纵坐标伸长到原来的ϖ倍得()y f x ω=(1)ω> ④把函数()y f x =图象的横坐标不变，纵坐标缩短到原来的ϖ倍得()y f x ω=(01)ω<< 7、用“五点法”作正余弦函数的图象要注意必须先将解析式化为sin()y A x h ωϕ=++或cos()y A x h ωϕ=++的形式.三角函数图像的变换的方式并不是唯一的，可以有多种变换方式.可以先左右平移，再伸缩，后上下.也可以先伸缩，再左右平移，后上下.但是三角函数图像的变换一般先选择左右平移，再进行其它变换.这样容易理解，计算也简单. 二、典型例题 【方法讲评】【例1】(10分，每一问5分)已知函数())cos()(0,0)f x x x πωφωφφω=+-+<<>为偶函数，且函数()y f x =图象的两相邻对称轴间的距离为.2π（Ⅰ）求()8πf 的值；（Ⅱ）将函数()y f x =的图象向右平移6π个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数()y g x =的图象，求()g x 的单调递减区间.【例2】(10分，每一问5分)已知函数()2sincos 442f x =． （Ⅰ）求函数()f x 的最小正周期及最值；（Ⅱ）令π()3g x f x ⎛⎫=+ ⎪⎝⎭，判断函数()g x 的奇偶性，并说明理由．【例3】(10分，每一问5分)已知函数x x f sin 2sin 2cos )(22+-=. （I ）求函数)(x f 的最小正周期；（II ）当)4,0(0π∈x 且524)(0=x f 时，求)6(0π+x f 的值. 【例4】(10分，每一问5分)已知函数()cos(2)2sin()sin()344f x x x x =-+-+（Ⅰ）求函数()f x 的最小正周期和图象的对称轴方程； （Ⅱ）求函数()f x 在区间[,]ππ-上的值域.【例5】（1）(5分)函数2()sin cos 2f x x x =+的最小正周期为 ．（2）(5分)已知(3sin ,cos )a x x =，(sin ,sin )b x x =，设函数23)(-⋅=b a x f .求函数()f x 的周期.【例6】（1）(5分)如果函数()cos 4f x x ωπ⎛⎫=+⎪⎝⎭()0ω>的相邻两个零点之间的距离为6π，则ω的值为（ ）A. 3 B. 6 C. 12 D. 24 （2）(5分)在函数①cos |2|y x =，②|cos |y x =，③cos(2)6y x π=+，④tan(2)4y x π=-中，最小正周期为π的所有函数为 .（请填序号）【例7】(5分)用五点法作出函数3sin(2)y x =+在一个周期的图像【例8】(1)(10分，每一问5分)已知函数22()sin cos 2cos f x x x x x =++,x R ∈.（I ）求函数()f x 的单调增区间；（Ⅱ）函数()f x 的图象可以由函数sin 2y x =（x R ∈)的图象经过怎样的变换得到？ （2）(5分)怎样将函数3sin(2)3y x π=-的图像变换得到函数3sin 2y x =的图像？三、巩固练习1.(5分)函数图象的对称中心是 .2.(5分)已知角φ的终边经过点(4,3)P -，函数()sin()f x wx w φ=+>（0)的图象的相邻两条对称轴之间的距离等于2π，则()4f π的值为（ ） A ．35 B ．45 C ．35- D ．45-3.(5分)已知函数()sin()2(0)3f x x πωω=++>的图象向右平移3π个单位后与原图象重合，则ω的最小值是（ ）A ．6B ．3C ．83 D ．434.(5分)要想得到函数sin 21y x =+的图象，只需将函数cos2y x =的图象( )A ．向左平移4π个单位长度，再向上平移1个单位长度 B ．向右平移4π个单位长度，再向上平移1个单位长度 C ．向左平移2π个单位长度，再向下平移1个单位长度 D ．向右平移2π个单位长度，再向下平移1个单位长度 5.(5分)已知曲线1:cos C y x =,22:sin(2)3C y x π=+，则下面结论正确的是( ) A ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移6π个单位长度，得到曲线2CB ．把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移12π个单位长度，得到曲线2CC ．把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移6π个单位长度，得到曲线2CD ．把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移12π⎪⎭⎫⎝⎛-⎪⎭⎫⎝⎛+=x x y 4cos 4sin 2ππ个单位长度，得到曲线2C6.(5分)函数()sin (0)f x x ωω=>的图象向左平移3π个单位长度，所得图象经过点2,03π⎛⎫⎪⎝⎭，则ω的最小值是( )A.32 B ．2 C ．1 D.127.(10分，每一问5分)已知函数2()2cos 23sin cos 1f x x x x =+-.（1）求()f x 的周期和单调递增区间；（2）说明()f x 的图象可由sin y x =的图象经过怎样变化得到. 自主提高8.设函数()sin()cos()(0,||)2f x x x πωϕωϕωϕ=+++><的最小正周期为π，且为偶函数，求函数的解析式.9.已知函数2π()sin 3sin sin 2f x x x x ωωω⎛⎫=++⎪⎝⎭（0ω>）的最小正周期为π． （Ⅰ）求ω的值；（Ⅱ）求函数()f x 在区间2π03⎡⎤⎢⎥⎣⎦，上的取值范围．10.设函数2()2sin cos cos 22f x x x x =+． （1）在给出的直角坐标系中画出函数()y f x =在区间[0,]π上的图象； （2）根据画出的图象写出函数()y f x =在[0,]π上的单调区间和最值．11.已知函数()3sin()cos()(0,0)f x x x πωφωφφω=+-+<<>为偶函数，且函数()y f x =图象的两相邻对称轴间的距离为.2π（Ⅰ）求()8f π的值；（Ⅱ）将函数()y f x =的图象向右平移6π个单位后，再将得到的图象上各点的横坐标舒畅长到原来的4倍，纵坐标不变，得到函数()y g x =的图象，求()g x 的单调递减区间.。

2021年高考数学三角函数专项知识点总结知识点总结2-1tan2A=(2tanA)/(1-tanA )(注：SinA 是sinA的平方 sin2(A) )三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asin)/2tan (α)=(1-cos(2α))/(1+cos(2α))推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos α1-cos2α=2sin α1+sinα=(sinα/2+cosα/2)=2sina(1-sin2a)+(1-2sin2a)sina=3sina-4sin3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos2a-1)cosa-2(1-sin2a)cosa=4cos3a-3cosasin3a=3sina-4sin3a=4sina(3/4-sin2a)=4sina[(√3/2)2-sin2a]=4sina(sin260°-sin2a)=4sina(sin60°+sina)(sin60°-sina)=4sina_2sin[(60+a)/2]cos[(60°-a)/2]_2sin[(60°-a)/2]cos[(60°-a)/2] =4sinasin(60°+a)sin(60°-a)cos3a=4cos3a-3cosa=4cosa(cos2a-3/4)=4cosa[cos2a-(√3/2)2]=4cosa(cos2a-cos230°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa_2cos[(a+30°)/2]cos[(a-30°)/2]_{-2sin[(a+30°)/2]sin[(a-30°)/ 2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin (a/2)=(1-cos(a))/2cos (a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))三角和sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·si nγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-si nα·cosβ·si nγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)两角和差cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)积化和差sinαsinβ = [cos(α-β)-cos(α+β)] /2cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-s in(α-β)]/2诱导公式sin(-α) = -sinαcos(-α) = cosαtan (—a)=-tanαsin(π/2-α) = cosαcos(π/2-α) = sinαsin(π/2+α) = cosαcos(π/2+α) = -sinαsin(π-α) = sinαcos(π-α) = -cosαsin(π+α) = -sinαcos(π+α) = -cosαα) +(cosα) =1(2)1+(tanα) =(secα)(3)1+(cotα) =(cscα)证明下面两式,只需将一式,左右同除(sinα) ,第二个除(cosα) 即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当_+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA) +(cosB) +(cosC) =1-2cosAcosBcosC(8)(sinA) +(sinB) +(sinC) =2+2cosAcosBcosC(9)sinα+sin(α+2π/n)+sin(α+2π_2/n)+sin(α+2π_3/n)+……+sin[α+2π_(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π_2/n)+cos(α+2π_3/n)+……+cos[α+2π_(n -1)/n]=0 以及sin (α)+sin (α-2π/3)+sin (α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0小编为大家提供的____年高考数学三角函数专项知识点总结最后祝考生们学习进步。

高中数学三角函数综合复习讲义1：产生背景：初中锐角三角函数定义：设a是一个任意大小的角，角的终边上任意一点P的坐标是（x,y），它于原点的距离是r（r>0），那么正弦: sinα=y/r余弦: cosα=x/r正切: tanα=y/x余切: cotα=x/y正割: secα=r/x余割: cscα=r/y都是a的函数，这六个函数统称为角a的三角函数。

2：找出结构：[函数]包括定义域，值域，对应法则。

本质:对于定义域内地任一x值在对应法则f(x)下都有值域中唯一的y和x对应，即y=f(x)3：分类：[角的大小]包括：正角三角函数，负角三角函数；[定义域]包括：【0，2π】，【0，2π】之外的[对应法则]包括：正弦: y= sinx余弦: y= cosx正切: y= tanx余切: y= cotx正割: y= secx余割: y= cscx[角的位置]包括:象限角的三角函数，坐标轴上的角的三角函数4：产生的条件：三角函数是在角的集合与实数集合之间建立的一种一一对应的关系。

5：研究概念的性质{特征、用途、作用、功能}基本三角函数的性质：同角的三角函数：倒数关系: 商的关系：平方关系： tanα ·cotα＝1 sinα ·cscα＝1 cosα ·secα＝1sinα/cosα＝tanα＝secα/cscα cosα/sinα＝cotα＝cscα/secαsin 2α＋cos 2α＝1 1＋tan 2α＝sec 2α 1＋cot 2α＝csc 2α诱导公式sin （－α）＝－sinα cos （－α）＝cosα tan （－α）＝－tanαcot （－α）＝－cotαsin （π/2－α）＝cos α cos （π/2－α）＝sin α tan （π/2－α）＝cot α cot （π/2－α）＝tan αsin （π/2＋α）＝cos αcos （π/2＋α）＝－sin α tan （π/2＋α）＝－cot α cot （π/2＋α）＝－tan α sin （π－α）＝sin α cos （π－α）＝－cos α tan （π－α）＝－tan α cot （π－α）＝－cot αsin （π＋α）＝－sin αcos （π＋α）＝－cos α tan （π＋α）＝tan α cot （π＋α）＝cot αsin （3π/2－α）＝－cos α cos （3π/2－α）＝－sin α tan （3π/2－α）＝cot α cot （3π/2－α）＝tan αsin （3π/2＋α）＝－cos α cos （3π/2＋α）＝sin α tan （3π/2＋α）＝－cot α cot （3π/2＋α）＝－tan α sin （2π－α）＝－sin α cos （2π－α）＝cos α tan （2π－α）＝－tan α cot （2π－α）＝－cot α sin （2k π＋α）＝sin αcos （2k π＋α）＝cos α tan （2k π＋α）＝tan α cot （2k π＋α）＝cot α(其中k∈Z)两角和与差的三角函数公式sin sin cos cos sin sin sin cos cos sin cos cos cos sin sin cos cos cos sin sin αβαβαβαβαβαβαβαβαβαβαβαβ（＋）＝＋（－）＝－（＋）＝－（－）＝＋ =1 ?tan tan tan tan tan αβαβαβ＋（＋）－1? ?tan tan tan tan tan αβαβαβ－（－）＝＋半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α＝2sinαcosαcos2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α2tanαtan2α＝—————1－tan2αsin3α＝3sinα－4sin3αcos3α＝4cos3α－3cosα3tanα－tan3αtan3α＝——————1－3tan2α万能公式2tan(α/2) 1－tan2(α/2) 2tan(α/2) cosα＝—————— sinα＝—————— tanα＝——————1＋tan2(α/2) 1＋tan2(α/2) 1－tan2(α/2) 三角函数的和差化积公式三角函数的积化和差公式sinα＋sinβ＝2sin2βα+cos2βα-sinα－sinβ＝2cos2βα+sin2βα-cosα＋cosβ＝2cos2βα+·cos2βα-cosα－cosβ＝－2sin2βα+·sin2βα-sinα ·cosβ＝21[sin（α＋β）＋sin（α－β）]cosα ·sinβ＝-21[sin（α＋β）－sin（α－β）]cosα ·cosβ＝21[cos（α＋β）＋cos（α－β）]sinα ·sinβ＝－21[cos（α＋β）－cos（α－β）]【三角形边角关系】1.正弦定理：在△ABC 中，∠A , ∠B , ∠C 的对边分別为 a , b , c ，则其中R 为外接圆半径。

（完整）高中数学专题系列三角函数讲义编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）高中数学专题系列三角函数讲义）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）高中数学专题系列三角函数讲义的全部内容。

§1.1。

1、任意角1、 正角、负角、零角、象限角的概念。

2、 与角α终边相同的角的集合：{}Z k k ∈+=,2παββ. §1。

1.2、弧度制1、 把长度等于半径长的弧所对的圆心角叫做1弧度的角。

2、 rl=α.3、弧长公式：R R n l απ==180.4、扇形面积公式：lR R n S 213602==π。

§1.2。

1、任意角的三角函数1、 设α是一个任意角，它的终边与单位圆交于点()y x P ,,那么:xyx y ===αααtan ,cos ,sin 2、设点(),A x y 为角α终边上任意一点，那么：（设r =sin y r α=，cos x r α=，tan y x α=,cot xyα=3、 αsin ，αcos ，αtan 在四个象限的符号和三角函数线的画法.正弦线:MP;余弦线正切线：AT5、 特殊角0°，30°45°，60°，90°，180°，270等的三角函数值。

§1.2.2、同角三角函数的基本关系式1、 平方关系：1cos sin 22=+αα 2、 商数关系：αααcos sin tan =。

3、 倒数关系：tan cot 1αα=§1.3、三角函数的诱导公式（概括为“奇变偶不变,符号看象限”Z k ∈）§1。

2021年新高考数学总复习讲义：三角函数的图像及性质知识讲解一、三角函数的图像和性质1.正弦函数图像和性质1）图像：2）定义域：R 3）值域：[11]，4）单调性： 5）奇偶性：奇函数 6）最小正周期：2 7）对称性：2.余弦函数图像和性质1）图像2）定义域：R 3）值域：[11]，xy -11-2π-π2ππo-3π23π2-π2π2xy -11-2π-π2ππo4）单调性：[22]x k k πππ，（k Z ）增函数 [22]x k k πππ，（kZ ）减函数5）奇偶性：偶函数 6）最小正周期：2π7）对称性：对称轴xk kZ π，；对称中心(0)2k k Zππ，，．3.正切函数图像和性质1）定义域：{|}2x xk k Z ππ，2）值域：R3）单调性：在()22k k ππππ，（k Z ）增函数．4）奇偶性：奇函数 5）最小正周期：π6）对称性：对称中心(0)2k k Zπ，，．二、三角函数的图像变换三角函数的几种变换：1）平移变换：函数sin()(0)yxϕϕ的图像可以看做将函数sin y x 的图像上的所有的点向左（当0ϕ时）或向右（当0ϕ时）平移ϕ个单位而得到．2）周期变换：函数sin()y xωϕ（0ω且1ω）的图像可以看做是把sin()yxϕ的图像上所有的点的横坐标缩短为（当1ω时）或伸长（当01ω时）到原来的1ω倍（纵坐标不变）而得到． 3）振幅变换：函数sin()yA xωϕ（0A 且1A ）的图像可以看做是将sin()yx ωϕ的图像上所有的点的纵坐标伸长（当1A 时）或缩短（当1A 时）到原来的A 倍（横坐标不变）而得到．经典例题一．选择题（共15小题）1．（2018•新课标Ⅲ）函数f（x）=tanx1+tan2x的最小正周期为（）A．π4B．π2C．πD．2π2．（2018•海南三模）函数f(x)=1+12sin2x的最小正周期与最小值分别为（）A．2π，12B．π，12C．2π，1D．π，13．（2018•福建模拟）将函数y=sin2x的图象上各点的横坐标伸长到原来的2倍，纵坐标不变，得到函数y=f（x）的图象，则（）A．y=f（x）的图象关于直线x=π8对称B．f（x）的最小正周期为π2C．y=f（x）的图象关于点(π2，0)对称D．f（x）在(−π3，π6)单调递增4．（2018•广西模拟）函数f(x)=cos(πx−π6)的图象的对称轴方程为（）A．x=k+23(k∈Z)B．x=k+13(k∈Z)C．x=k+16(k∈Z)D．x=k−13(k∈Z)5．（2018•宝鸡一模）函数f(x)=2sin(ωx+φ)(0＜ω＜12，|φ|＜π2)，若f(0)=−√3，且函数f（x）的图象关于直线x=−π12对称，则以下结论正确的是（）A．函数f（x）的最小正周期为π3B．函数f（x）的图象关于点(7π9，0)对称C．函数f（x）在区间(π4，11π24)上是增函数D．由y=2cos2x的图象向右平移5π12个单位长度可以得到函数f（x）的图象6．（2018•长沙一模）函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的图象中相邻对称轴的距离为π2，若角φ的终边经过点(3，√3)，则f(π4)的值为（）A．√32B．√3C．2D．2√37．（2018•永州三模）将函数f（x）=sin（2x+φ）（|φ|＜π2）的图象向左平移π6个单位后的图形关于原点对称，则函数f（x）在[0，π2]上的最小值为（）A．√32B．12C ．﹣12D ．﹣√328．（2018•全国三模）已知函数f(x)=2sin(ωx +φ)(ω＞0，0＜φ＜π2)，f （x 1）=2，f （x 2）=0，若|x 1﹣x 2|的最小值为12，且f(12)=1，则f （x ）的单调递增区间为（ ） A ．[−16+2k ，56+2k ]，k ∈ZB ．[−56+2k ，16+2k ]，k ∈ZC ．[−56+2kπ，16+2kπ]，k ∈ZD ．[16+2k ，76+2k ]，k ∈Z9．（2018•广州一模）已知函数f （x ）=sin （ωx +π6）（ω＞0）在区间[﹣π4，2π3]上单调递增，则ω的取值范围为（ ） A ．（0，83]B ．（0，12]C ．[12，83]D ．[38，2]10．（2018•珠海二模）若函数f （x ）=cos （2x +φ）在（0，π2）上单调递减，则φ的值可能是（ ） A ．2πB ．πC ．π2D ．﹣π211．（2018•全国）要得到y=cosx ，则要将y=sinx （ ） A ．向左平移π个单位 B ．向右平移π个单位C ．向左平移π2个单位D ．向右平移π2个单位12．（2018•榆林一模）已知曲线C 1：y =sinx ，C 2：y =cos(12x −5π6)，则下列说法正确的是（ ）A ．把C 1上各点横坐标伸长到原来的2倍，再把得到的曲线向右平移π3，得到曲线C 2B ．把C 1上各点横坐标伸长到原来的2倍，再把得到的曲线向右平移2π3，得到曲线C 2C ．把C 1向右平移π3，再把得到的曲线上各点横坐标缩短到原来的12，得到曲线C 2D ．把C 1向右平移π6，再把得到的曲线上各点横坐标缩短到原来的12，得到曲线C 213．（2018•凌源市模拟）将函数f （x ）=2√3cos 2x ﹣2sinxcosx ﹣√3的图象向左平移t （t ＞0）个单位，所得图象对应的函数为奇函数，则t 的最小值为（ ） A ．2π3B ．π3C ．π2D ．π614．（2018•四川模拟）若将函数y =sin2x +√3cos2x 的图象向左平移π6个单位长度，则平移后图象的对称轴方程为（ ）A ．x =kπ2−π12(k ∈Z) B ．x =kπ2+π2(k ∈Z)C ．x =kπ2(k ∈Z) D ．x =kπ2+π12(k ∈Z)15．（2018•河南模拟）已知点A(0，2√3)，B(π6，0)是函数f （x ）=4sin （ωx +φ）(0＜ω＜6，π2＜φ＜π)的图象上的两个点，若将函数f （x ）的图象向右平移π6个单位长度，得到函数g （x ）的图象，则函数g （x ）的图象的一条对称轴的方程为（ ） A ．x =π12 B ．x =π6 C ．x =π3D ．x =5π12二．填空题（共8小题）16．（2018•宝山区二模）函数 f （ x ）=2sin 4x cos 4x 的最小正周期为17．（2018•浦东新区三模）函数y=cos （2x +π4）的单调递减区间是 ．18．（2017•江苏模拟）若函数f （x ）=sin （ωx +π6），（ω＞0）最小正周期为π，则f （π3）的值为 ．19．（2017•上海一模）函数y=sin （ωx ﹣π3）（ω＞0）的最小正周期是π，则ω= ．20．（2018•江苏）已知函数y=sin（2x+φ）（﹣π2＜φ＜π2）的图象关于直线x=π3对称，则φ的值为．21．（2018•浙江模拟）已知函数f（x）=2sin（2x+π3）+1，则f（x）的最小正周期是，f（x）的最大值是.22．（2018•南通模拟）函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0≤φ＜2π）在R上的部分图象如图所示，则f（2018）的值为．23．（2017•江苏模拟）将函数y=5sin（2x+π4）的图象向左平移φ（0＜φ＜π2）个单位后，所得函数图象关于y轴对称，则φ=．三．解答题（共6小题）24．（2016•海淀区模拟）已知函数f（x）=2√2sinxcos（x+π4）．（Ⅲ）若在△ABC中，BC=2，AB=√2，求使f（A﹣π4）=0的角B．（Ⅲ）求f（x）在区间[π2，17π24]上的取值范围．25．（2018•海淀区二模）如图，已知函数f（x）=Asinx（ωx+φ）（A＞0，ω＞0，|φ|＜π）在一个周期内的图象经过B(π6，0)，C(2π3，0)，D(5π12，2)三点2（Ⅲ）写出A，ω，φ的值；（Ⅲ）若α∈(5π12，2π3)，且f（α）=1，求cos2α的值．26．（2018•朝阳区二模）已知函数f（x）=2sinx（sinx+cosx）﹣a的图象经过点（π2，1），a∈R．（1）求a的值，并求函数f（x）的单调递增区间；（2）若当x∈[0，π2]时，不等式f（x）≥m恒成立，求实数m的取值范围．27．（2017•北京）已知函数f（x）=√3cos（2x﹣π3）﹣2sinxcosx．（I）求f（x）的最小正周期；（II）求证：当x∈[﹣π4，π4]时，f（x）≥﹣12．28．（2018•玉溪模拟）已知函数f（x）=sin2x+√3sinx•cosx+2cos2x，x∈R （1）求函数f（x）的最小正周期和单调递减区间；（2）函数f（x）的图象可以由函数y=sin2x的图象经过怎样的变换得到？29．（2018•海淀区校级三模）若函数y=sin(ωx+φ)(ω＞0，|φ|＜π2)的部分图象如图所示．求：（Ⅲ）ω和φ；（Ⅲ）f（x）在区间(0，π3)上的取值范围．。