下载文档原格式
伺服阀频率响应计算方式
伺服阀是一种用于调节流体流量和压力的元件，通常应用于工业自动化控制系统中。
在实际应用中，伺服阀的频率响应是一个重要的参数，它表示了伺服阀能够对输入信号的变化做出快速、准确的响应能力。
本文将介绍伺服阀频率响应的计算方式。
1.频率响应的定义
在控制系统中，频率响应是指系统对不同频率的输入信号所表现出的输出特性。
频率响应通常通过系统的传递函数来描述，传递函数是输入输出关系的数学表示。
2.伺服阀的传递函数
伺服阀的传递函数描述了输入压力和输出流量之间的关系。
传递函数可以通过实验测量或者理论计算得到。
一般来说，伺服阀传递函数可以使用二阶系统来近似表示。
3.二阶系统的传递函数
二阶系统的传递函数一般形式为：H(s) = K / (s^2 + 2ξω_ns + ω_n^2)，其中K表示增益，ξ表示阻尼比，ω_n表示自然频率。
这里s 是一个复变量，表示复频域中的频率。
4.伺服阀的频率响应计算
伺服阀的频率响应可以通过传递函数来计算。
一般来说，有两种常用的方法：频域法和时域法。
(1)频域法
频域法通过在传递函数中将s替换为复频域上的频率值来计算频率响应。
可以使用频域分析工具，如波特图或者Nyquist图，来绘制伺服阀的频率响应曲线。
(2)时域法
时域法通过将传递函数表示成微分方程形式，然后使用微分方程的求解方法来计算频率响应。
这可以通过Laplace变换和逆Laplace变换来实现。
时域法更加适用于复杂的控制系统。
5.伺服阀频率响应的参数
6.频率响应的影响因素
总结：。
什么是频率响应频率响应是指信号经过系统或设备时，不同频率成分的增益或衰减程度。
它描述了系统对不同频率输入信号的响应能力，包括传输或处理信号时对频率的变化如何进行放大或减弱。
频率响应是衡量系统性能的重要参数之一，对于音频设备、通信系统、音响系统等具有重要的意义。
频率响应通常用图形的形式表示，其横轴表示频率，纵轴表示增益或衰减程度。
在图形上，我们可以看到不同频率点处的振幅变化情况，从而了解系统对不同频率信号的放大或衰减情况。
频率响应图形通常为连续曲线，能够直观地显示出系统对于不同频率信号的响应特性。
频率响应的单位通常以分贝（dB）为衡量标准。
分贝是一种相对单位，用于描述信号的增益或衰减程度。
在频率响应图形中，增益大于0dB表示信号被放大，而衰减则表示信号被减弱。
通过分析频率响应图形，我们可以了解系统在不同频率下对信号的处理能力，进而判断系统的性能优劣。
频率响应的主要特征有两个，分别是通频带和截止频率。
通频带是指系统能够传输或处理的频率范围，常用单位为赫兹（Hz）。
通频带可以告诉我们系统对于低频和高频信号的响应情况，对于音频系统来说，较宽的通频带可以提供更好的低频和高频音质表现。
而截止频率是指在该频率下系统的增益已经衰减到一定程度，无法再传输或处理信号。
截止频率通常是指-3dB的点，也就是系统响应下降3dB的频率点。
频率响应在音频系统设计和调试中有着重要的应用。
对于音响设备和扬声器，优秀的频率响应表现可以提供更加准确和平衡的音质体验。
在通信系统中，频率响应的平坦度能够决定信号传输质量和可靠性。
因此，在系统设计和选择设备时，频率响应是需要重点考虑的因素之一。
总结起来，频率响应是描述信号经过系统或设备后，不同频率成分的增益或衰减程度。
它能够直观地展示系统对于不同频率信号的响应特性，是衡量系统性能重要的参数之一。
在音频设备、通信系统等领域，频率响应的优劣直接关系到信号传输的质量和体验效果。
因此，了解和掌握频率响应的概念和特点，对于设计和选择合适的系统和设备都至关重要。
《模拟集成电路基础》课程研究性学习报告频率响应的波特图分析目录一.频率响应的基本概念 (2)1. 概念 (2)2. 研究频率响应的意义 (2)3. 幅频特性和相频特性 (2)4. 放大器产生截频的主要原因 (3)二．频率响应的分析方法 (3)1. 电路的传输函数 (3)2. 频率响应的波特图绘制 (4)（1）概念 (4)（2）图形特点 (4)（3）四种零、极点情况 (4)（4）具体步骤 (6)（5）举例 (7)三．单级放大电路频率响应 (7)1.共射放大电路的频率响应 (7)2.共基放大电路的频率响应 (9)四．多级放大电路频响 (10)1.共射一共基电路的频率响应 (10)（1）低频响应 (11)（2）高频响应 (12)2.共集一共基电路的频率响应 (13)3.共射—共集电路级联 (14)五．结束语 (14)一.频率响应的基本概念1.概念我们在讨论放大电路的增益时，往往只考虑到它的中频特性，却忽略了放大电路中电抗元件的影响，所求指标并没有涉及输入信号的频率。
但实际上，放大电路中总是含有电抗元件，因而，它的增益和相移都与频率有关。
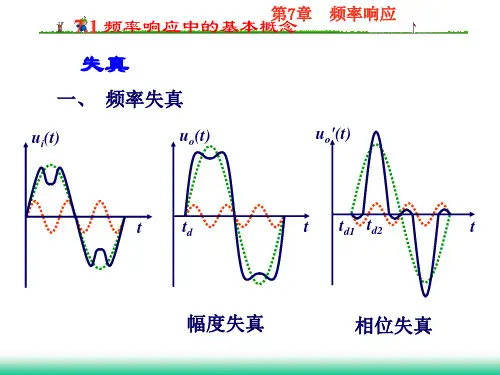
即它能正常工作的频率范围是有限的，一旦超出这个范围，输出信号将不能按原有增益放大，从而导致失真。
我们把增益和相移随频率的变化特性分别称为幅频特性和相频特性，统称为频率响应特性。
2.研究频率响应的意义通常研究的输入信号是以正弦信号为典型信号分析其放大情况的，实际的输入信号中有高频噪声，或者是一个非正弦周期信号。
例如输入信号i u 为方波，s U 为方波的幅度，T 是周期，0/2ωπ=T ，用傅里叶级数展开，得...)5sin 513sin 31(sin 22000++++=t t t U U u s s i ωωωπ 各次谐波单独作用时电压增益仍然是由交流通路求得，总的输出信号为各次谐波单独作用时产生的输出值的叠加。
但是交流通路和其线性化等效电路对低频、中频、高频是有差别的，这是因为放大电路中耦合电容、旁路电容和三极管结电容对不同频率的信号的复阻抗是不同的。
频率响应介绍_频率响应概念
频率响应是指将一个以恒电压输出的音频信号与系统相连接时，音箱产生的声压随频率的变化而发生增大或衰减、相位随频率而发生变化的现象，这种声压和相位与频率的相关联的变化关系称为频率响应。
也是指在振幅允许的范围内音响系统能够重放的频率范围，以及在此范围内信号的变化量称为频率响应，也叫频率特性。
在额定的频率范围内，输出电压幅度的最大值与最小值之比，以分贝数（dB）来表示其不均匀度。
频率响应在电能质量概念中通常是指系统或计量传感器的阻抗随频率的变化。
频率响应确定方法分析法基于物理机理的理论计算方法，只适用于系统结构组成易于确定的情况。
在系统的结构组成给定后，运用相应的物理定律，通过推导和计算即可定出系统的频率响应。
分析的正确程度取决于对系统结构了解的精确程度。
对于复杂系统，分析法的计算工作量很大。
实验法频率响应图册采用仪表直接量测的方法，可用于系统结构难以确定的情况。
常用的实验方式是以正弦信号作为试验信号，在所考察的频率范围内选择若干个频率值，分别测量各个频率下输入和稳态输出正弦信号的振幅和相角值。
输出与输入的振幅比值随频率的变化特性是幅频特性，输出与输入的相角差值随频率的变化特性是相频特性。
频率响应性能系统的过渡过程与频率响应有着确定的关系，可用数学方法来求出。
但是除一阶和二阶系统外，这样做常需要很多时间，而且在很多情况下实际意义不大。
常用的方法是根据频率响应的特征量来直接估计系统过渡过程的性能。
频率响应的主要特征量有：增益裕量和相角裕量、谐振峰值和谐振频率、带宽和截止频率。
增益裕量和相角裕量它可提供控制系统是否稳定和具有多大稳定裕量的信息。
谐振峰值Mr和谐振频率rMr和r规定为幅频特性|G（j）|的最大值和相应的频率值。
对于具有一对共轭复数主导极点（见根轨迹法）的高阶线性定常系统，当Mr值在（1.0～1.4）M0范围内时，可获得比较满意的过渡过程性能。
其中M0是=0时频率响应的幅值。
r的大小表征过渡过程的快速性：r值越大，系统在单位阶跃作用下输出响应的快速性越好。
带宽和截止频率截止频率c规定为幅频特性|G（j）|达到0.7M0并继续下降时的临界频率。
