小波变换与小波框架

Matlab中的小波变换与小波包分析方法详解引言近年来，小波变换在信号处理领域中得到了广泛的应用。

小波变换是一种能够捕捉信号时频特性的有效工具，可以用来分析、压缩和去噪各种类型的信号。

本文将详细介绍Matlab中的小波变换和小波包分析方法，以帮助读者更好地理解和应用这一强大的信号处理技术。

一、小波变换（Wavelet Transform）小波变换是一种将信号分解成不同尺度的基函数的技术。

与传统的傅里叶变换相比，小波变换具有更好的时频局部化特性。

Matlab中提供了丰富的小波分析工具箱，可以方便地进行小波变换的计算。

1.1 小波基函数小波基函数是小波变换的基础。

不同类型的小波基函数适用于不同类型的信号。

在Matlab中，我们可以使用多种小波基函数，如Daubechies小波、Haar小波和Morlet小波等。

1.2 小波分解小波分解是指将信号分解成多个尺度的小波系数。

通过小波分解，我们可以获取信号在不同尺度上的时频特性。

Matlab中提供了方便的小波分解函数，例如'dwt'和'wavedec'。

1.3 小波重构小波重构是指根据小波系数重新构建原始信号。

通过小波重构，我们可以恢复原始信号的时域特性。

在Matlab中，可以使用'idwt'和'waverec'函数进行小波重构。

二、小波包分析（Wavelet Packet Analysis）小波包分析是对小波变换的进一步扩展，它允许对信号进行更精细的分解和重构。

小波包分析提供了一种更灵活的信号分析方法，能够获得更详细的时频特性。

2.1 小波包分解小波包分解是指将信号分解成具有不同频带的小波包系数。

与小波分解相比，小波包分解提供了更高的分辨率和更详细的频谱信息。

在Matlab中，可以使用'wavedec'函数进行小波包分解。

2.2 小波包重构小波包重构是根据小波包系数重新构建原始信号。

其中，左上角的元素表示整个图像块的像素值的平均值，其余是该图像块的细节系数。 如果从矩阵中去掉表示图像的某些细节系数，事实证明重构的图像质量仍然可以接受。 具体做法是设置一个阈值，例如的细节系数δ≤5 就把它当作“0”看待，这样相比， Aδ 中“0”的数目增加了 18 个，也就是去掉了 18 个细节系数。这样做的好 处是可提高小波图像编码的效率。对矩阵进行逆变换，得到了重构的近似矩阵
7 50 42 31 39 18 10 63
57 16 24 33 25 48 56 1
使用灰度表示的图像如图 11.2 所示：
图 11.2 图像矩阵 A 的灰度图
一个图像块是一个二维的数据阵列， 可以先对阵列的每一行进行一维小波变换， 然后对 再行变换之后的阵列的每一列进行一维小波变换， 最后对经过变换之后的图像数据阵列进行 编码。 (1) 求均值与差值 利用一维的非规范化哈尔小波变换对图像矩阵的每一行进行变换， 即求均值与差值。 在 图像块矩阵 A 中，第一行的像素值为 R0: [64 2 3 61 60 6 7 57] 步骤 1：在 R0 行上取每一对像素的平均值，并将结果放到新一行 N0 的前 4 个位置， 其余的 4 个数是 R0 行每一对像素的差值的一半（细节系数） ： R0: [64 2 3 61 60 6 7 57] N0: [33 32 33 32 31 -29 27 -25] 步骤 2：对行 N0 的前 4 个数使用与第一步相同的方法，得到两个平均值和两个细节系 数，并放在新一行 N1 的前 4 个位置，其余的 4 个细节系数直接从行 N0 复制到 N1 的相应 位置上： N1: [32.5 32.5 0.5 0.5 31 -29 27 -25] 步骤 3：用与步骤 1 和 2 相同的方法，对剩余的一对平均值求平均值和差值， N2: [32.5 0 0.5 0.5 31 -29 27 -25] 3 0 0 1 V : V W W W2 其中，第一个元素是该行像素值的平均值，其余的是这行的细节系数。 (2) 计算图像矩阵 使用(1)中求均值和差值的方法，对矩阵的每一行进行计算，得到行变换后的矩阵：

小波分析理论及其应用胡安兴（武汉工业学院土木工程与建筑学院，交通091,学号090606119）摘要：小波分析的理论与方法是从Fourier分析的思想方法演变而来的。

就象Fourier 分析分为积分Fourier变换和Fourier级数一样，小波分析也分为(积分)小波变换和小波级数两部分，(积分)小波变换的主体是连续小波变换，多尺度小波变换和s－进小波变换；而小波级数的主体部分是关于小波框架的理论。

小波分析理论深刻，应用广泛，并且仍在迅速发展之中。

本文介绍了小波变换的来源及其发展，以及多分辨率分析的问题，小波分析在图像处理中有非常重要的应用。

关键词：小波分析；多分辨率；图像去噪The wavelet analysis theory and its applicationsHU An-xing(Wuhan institute of industrial, civil engineering and architecture institute, traffic civil 091 Student number: 090606119)Abstract:Wavelet analysis theory and method has evolved from the thinking method of Fourier analysis. As Fourier transform and Fourier series is divided into integral Fourier analysis, wavelet analysis is divided into (integral) two parts, the wavelet transform and wavelet series (integral) the body of the wavelet transform is a continuous wavelet transform and multi-scale wavelet transform and s - into the wavelet transform; And the main body of the wavelet series is about wavelet frame theory. Wavelet analysis theory, applications, and are still in rapid development. This paper introduces the source and development of wavelet transform, and multiresolution analysis, wavelet analysis has very important applications in image processing.Key words: Wavelet analysis; multi- resolution ratio; Image denoising1 引言1.1 问题的提出Fourier变换只能告诉我们信号尺度的范围，而无法给出信号的结构以及它蕴含的大小不同尺度的串级过程，即Fourier变换在时空域中没有任何分辨率。

小波包变换和小波变换小波包变换和小波变换是一种信号分析和处理的方法，它们可以将信号分解成不同尺度和频率的成分，并可以分析和处理这些成分。

下面将对小波包变换和小波变换进行解释。

1. 小波包变换：小波包变换是在小波变换的基础上发展而来的一种方法。

小波包变换将信号分解成多个子带，并对每个子带进行进一步的分解。

相比于小波变换，小波包变换提供了更高的频率分辨率和更细的频率划分。

小波包变换的核心思想是使用不同的小波基函数对信号进行分解。

通过选择不同的小波基函数，可以获得不同尺度和频率的信号成分。

小波包变换可以通过反复迭代的方式，不断将信号分解成更细的频率带，进一步提高频率分辨率。

在每一级分解中，信号被分解成低频和高频两部分，低频部分可以继续进行进一步的分解。

小波包变换的优势在于能够提供更详细的频域信息，可以更好地分析信号的特征和结构。

它在信号处理、图像处理等领域有着广泛的应用，例如信号去噪、特征提取等。

2. 小波变换：小波变换是一种将信号分解成不同频率成分的方法。

通过小波变换，我们可以将信号从时域转换到频域，同时可以分析信号的时间和频率特性。

小波变换的基本思想是使用小波基函数对信号进行分解。

小波基函数是一种具有局部性质的函数，它能够在时域和频域中同时提供较好的分辨率。

通过选择不同的小波基函数，可以获得不同频率范围内的信号成分。

小波变换通过对信号进行连续的分解和重构，可以分析信号的频域特性。

小波变换有多种变体，其中最常用的是离散小波变换（DWT）。

离散小波变换将信号分解成多个尺度和频率的子带，通过这些子带可以分析信号的不同频率成分。

离散小波变换具有高效性和局部性，可以在信号处理中广泛应用，例如信号去噪、压缩等。

总结：小波包变换是在小波变换的基础上发展的一种方法，它能够提供更高的频率分辨率和更细的频率划分。

小波包变换通过选择不同的小波基函数，将信号分解成多个子带，并对每个子带进行进一步的分解。

相比之下，小波变换是将信号分解成不同频率成分的方法，通过选择不同的小波基函数，可以获得不同频率范围内的信号成分。

为 f (t ) 的离散小波变换。
离散小波变换是尺度－位移平面的离散点上的函数，（这些点是 规则分布的），与连续小波变换比较少了许多点上的值。自然，会引 起以下的问题：
1） 离散小波变换Wf ( j, k ) 是否包含了函数 f (t ) 的全部信息？ 就是说，能否由Wf ( j, k ) 重构原函数 f (t ) ；
A 重构公式：
∑ f (t ) = 2
A + B j,k
f ,ψ j,k ψ j,k (t) + r
（4）
5
第 3 章 小波变换
其中是
r
=
2
ε +
ε
F
阶的，A 与 B 越接近，误差越小。
冗余表示
{ } 如
3.3
所述，一般情况下，小波框架
ψ j,k (t)
不是正交基，
j , k∈Z
( ) 它提供了对函数 f (t )的一种冗余表示，这种表示使得恢复信号 f t
An example of an R-function without a dual is easy to construct. Let φ be an orthogonal wavelet. Then define ψ(x)=φ(x)+zφ(2x) for some complex number z. It is straightforward to show that this ψ does not have a wavelet dual.
j,k
并记ψ j,k (t) 的对偶小波ψ j,k (t) = F −1ψ j,k (t) ，并取ψ j,k (t) 是
对ψ (t) 进行伸缩平移得到的， ψ j,k (t) = a0− j 2 ψ (a0− jt − k ) 。

正交小波的自对偶性：
当是正交小波时，我们有： ~ （自对偶性）
j ,k j ,k
证明：设是正交小波时， ~ 由f f , j ,k j ,k
j ,k
取f j0 , k 0 ~ j ,k , j ,k j ,k j ,k
0 0
b2 a2t *
t
小波变换的重构定理：
令是一个基小波，它定义了一个连续小波变换W ( f )(b, a ), 则：

－

da [W ( f )(b, a ) ( g )(b, a ) 2 db c f , g a －
__________ ______

对所有的f , g L2成立，并且对于f L2和f的连续点x R，有 1 f ( x) c

（振荡性）
对“容许性”条件的分析：
2.
为了“基小波” 能提供一个局部的时频窗口， 我们还得要求满足： ˆ ( ) L2 t (t ) L2 ,
连续小波变换的内积表示：
t b 用 b ,a (t ) a ( ), 则 a W ( f )(b, a ) f , b ,a
j 2
二进小波稳定性条件的另一种表述：
A f
2
Wj f



2
B f
2
f L2
定理：
令满足二进小波的稳定性条件，则满足： A ln 2
0
ˆ（）
2

2
d ,
ˆ（ ） d B ln 2 0
即：是一个基小波。
当A B时，有： ˆ（） C＝ d＝2A ln 2 －

小波变换的基本思想是将信号分 解成一系列的小波函数，每个小 波函数都有自己的频率和时间尺
度。
小波变换通过平移和缩放小波函 数，能够适应不同的频率和时间 尺度，从而实现对信号的精细分
析。
小波变换的特点
01
02
03
多尺度分析
小波变换能够同时分析信 号在不同频率和时间尺度 上的特性，提供更全面的 信号信息。
图像去噪
利用小波变换去除图像中的噪声，提高图像的清晰度和质 量。
在小波变换中，噪声通常表现为高频系数较大的值，通过 设置阈值去除这些高频系数，可以达到去噪的效果。去噪 后的图像能够更好地反映原始图像的特征和细节。
图像增强
ቤተ መጻሕፍቲ ባይዱ
利用小波变换增强图像的某些特征，突出显示或改善图像的某些部分。
通过调整小波变换后的系数，可以增强图像的边缘、纹理等特定特征。这种增强 方式能够突出显示图像中的重要信息，提高图像的可读性和识别效果。
在信号处理、图像处理、语音识别等 领域有广泛应用。
特点
能够同时分析信号的时域和频域特性 ，具有灵活的时频窗口和多分辨率分 析能力。
离散小波变换
定义
离散小波变换是对连续小波变换 的离散化，通过对小波函数的离 散化处理，实现对信号的近似和
细节分析。
特点
计算效率高，适合于数字信号处理 和计算机实现。
应用
在信号处理、图像处理、数据压缩等领域有广泛应用，如语音压缩、图像压缩 、数据挖掘等。
CHAPTER 04
小波变换在图像处理中的应用
图像压缩
利用小波变换对图像进行压缩，减少存储空间和传输带宽的 需求。
通过小波变换将图像分解为不同频率的子带，去除高频细节 ，保留低频信息，从而实现图像压缩。压缩后的图像可以通 过逆小波变换重新构造，保持图像质量的同时减小数据量。

在此添加您的文本16字
自适应压缩
在此添加您的文本16字
小波变换的自适应性质使得它在压缩过程中能够根据信号 的特性进行动态调整，进一步提高压缩效率。
信号去噪
有效去噪 多尺度分析 自适应去噪
小波变换能够检测到信号中的突变点，从而在去噪过程 中保留这些重要特征，同时去除噪声。
小波变换的多尺度分析能力使其在去噪过程中能够同时 考虑信号的全局和局部特性，实现更准确的去噪效果。
小波变换的算法优化
1 2
小波变换算法的分类
介绍不同类型的小波变换算法，如连续小波变换、 离散小波变换等。
算法优化策略
探讨如何优化小波变换算法，以提高计算效率和 精度。
3
算法实现技巧
介绍实现小波变换算法的技巧和注意事项。
小波变换在实际应用中的挑战与解决方案
01
小波变换在信号处理中的应用
介绍小波变换在信号处理领域的应用，如信号去噪、特征提取等。
小波变换ppt课件
• 小波变换概述 • 小波变换的基本原理 • 小波变换的算法实现 • 小波变换在信号处理中的应用 • 小波变换在图像处理中的应用 • 小波变换的未来发展与挑战
01
小波变换概述
小波变换的定义
01
小波变换是一种信号处理方法， 它通过将信号分解成小波函数的 叠加，实现了信号的多尺度分析 。
02
小波变换在图像处理中的应用
探讨小波变换在图像处理领域的应用，如图像压缩、图像增强等。
03
实际应用中的挑战与解决方案
分析小波变换在实际应用中面临的挑战，并提出相应的解决方案。
THANKS
感谢观看
离散小波变换具有多尺度、多方向和自适应的特点，能够提供信号或图像在不同尺 度上的细节信息，广泛应用于信号降噪、图像压缩和特征提取等领域。

17
小波尺度和信号频率的关系
大尺度 小尺度
信号的低频 信号的高频
18
1.6 离散小波变换（DWT）
在每个可能的缩放因子和平移参数下计算小波系 数，其计算量相当大，将产生惊人的数据量，而且有 许多数据是无用的。
如果缩放因子和平移参数都选择为2j（j>0且为
整数）的倍数， 即只选择部分缩放因子和平移参数 来进行计算， 就会使分析的数据量大大减少。
ECG signal 100.dat 1
0.8
0.6
0.4
Voltage / mV
0.2
0 28 1
1
1
1
1
1
1
8
-0.2
-0.4
-0.6
-0.8
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
Time / s
在实际工程应用中，通常所分析的信号具有非线性， 非平稳,并且奇异点较多的特点。含噪的一维信号模型 可表示为：
26
1.7 小波重构
H′ L′
H′
S L′
小波重构算法示意图
27
1.7 小波重构
(1) 重构近似信号与细节信号 由小波分解的近似系数和细节系数可以重构出原
始信号。 同样，可由近似系数和细节系数分别重构出信号
的近似值或细节值，这时只要近似系数或细节系数置 为零即可。
28
1.7 小波重构
H′ 0 约 500个 0
23
图 （a） 信号分解； (b) 小波分树； （c）小波分解树 24
1.6 离散小波变换（DWT）
在使用滤波器对真实的数字信号进行变换时， 得到的数据将是原始数据的两倍。

.语音增强算法研究p584.1小波理论4.1.1小波变换的定义4.1. 2小波去噪原理.4.2小波包变换语音增强方法4.2.1 小波包变换语音增强方法原理4 2. 2 Bark尺度小波包分解4.2.3闽值函数4.2.4 实验仿真4.3小波包变换和听觉掩蔽效应的语音增强方法4.3. 1小波包变换和听觉掩蔽效应的语音增强方法原理4.3. 2实验仿真第四章小波包语音增强算法小波(Wavelets)分析的起源可以追溯到20世纪初，在20世纪80年代后期开始形成一个新兴的数学分支。

小波变换是调和分析这一数学领域半个世纪以来的工作结晶，是傅里叶变换发展史上的里程碑式的进展，近些年来成为国外众多学者共同关注的热点。

它在傅里叶变换的基础上发展而来，但又有极大不同。

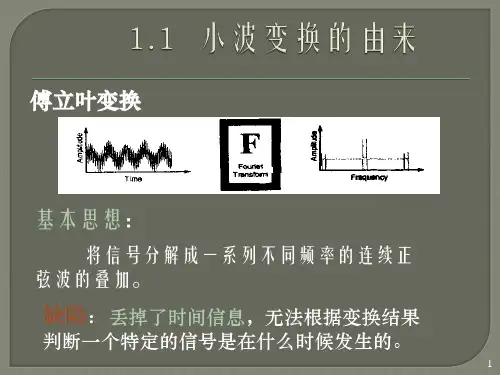
传统的信号处理方法是建立在傅立叶变换的基础上，而傅立叶分析使用的是一种全局的变换，要么完全在时域，要么完全在频域，因此无法表达信号的时频局域性质，而这种性质恰恰是非平稳信号(如语音信号)最根本和最关键的性质。

小波分析是建立在泛函分析、傅立叶分析、样条分析及调和分析基础上的新的分析处理工具它又称为多分辨分析，在时域和频域同时具有良好配局部化特性，常被誉为信号分析的“数学显微镜”。

小波变换在时频两域都具有表征信号局部特征的能力，它克服了短时傅立叶变换固定分辨率的缺点，在信号的高频部分，可以获得较好的时间分辨率，在信号的低频部分可以获得较高的频率分辨率，这就使指小波变换具有对信号的自适应性。

它能有效地从信号中提取信息，通过伸缩和平移等运算功能对信号进行多尺度细化分析。

小波分析是目前国际上公认的信号信息获取与处班领域的高新技术，是信号处理的前沿课题，其中小波去噪也是小波分析的主要应用之一，对语音增强的研究不可避免的要利用小波这一有效工具。

小波包变换理论是20世纪80年代中后期逐渐成熟并发展起来的，由于可同时进行时域和频域分析，具有时频局部化和变分辨特征，而且小波函数的选取也很灵活，因此在语音增强中得到了广泛的应用。

y ( n ) = ∑ x (m) h (m − Mn) ⇔
m
y ( n ) = ∑ x (m) h (n − Mm) ⇔
m
由上述预备知识和前面推导的 DWT 计算公式可以推出 DWT 的工程实现框 图，即离散小波变换的双通道多采样率滤波器组的实现结构图如下：
图 9 离散小波变换工程实现结构图 由以上分析可得一维信号的一级分解重建框图如下：
(18)
y ( n ) = C ⋅ x (n − k ) 即 Y ( z ) = C ⋅ z − kX (z )
从而可得 PR 条件如下：
(19)
° ( z) = 0 H ( z ) + G( − z ) G H (− z) ° −k −k ° ° H ( z ) H ( z ) + G( z )G( z ) = C1 ⋅ z = 2C ⋅ z
将条件(a)代入到条件(2)式中得：
(a)
(21)
− z l [G ( − z) H ( z ) − G ( z ) H (− z )] = C1 ⋅ z − k
M 抽取：每 M 个点中仅抽取一个值保留，因此信号的时域宽度会变为
原来的1 M 。 抽取操作的符号表示如下：
图 4 抽取符号图 上述插值操作的时频域的表达如下： 时域表达：
y ( n ) = x (Mn )
(4) (5)
1 2π −j 1 M −1 k M 复频域表达： Y ( z ) = ∑ X (w z ), w = e M M k =0
复频域表达： 频域表达：
(1)
Y ( z) = X ( zM ) Y (e jw ) = X ( e jMw )
(2) (3)
下面是当 M = 2 时，对信号 x ( n) 进行插值得 y ( n ) 的一个实例。

⼩波变换（wavelettransform）的通俗解释（⼀）⼩波变换⼩波，⼀个神奇的波，可长可短可胖可瘦（伸缩*移），当去学习⼩波的时候，第⼀个⾸先要做的就是回顾傅⽴叶变换（⼜回来了，唉），因为他们都是频率变换的⽅法，⽽傅⽴叶变换是最⼊门的，也是最先了解的，通过傅⽴叶变换，了解缺点，改进，慢慢的就成了⼩波变换。

主要的关键的⽅向是傅⽴叶变换、短时傅⽴叶变换，⼩波变换等，第⼆代⼩波的什么的就不说了，太多了没太多意义。

当然，其中会看到很多的名词，例如，内积，基，归⼀化正交，投影，Hilbert空间，多分辨率，⽗⼩波，母⼩波，这些不同的名词也是学习⼩波路上的标志牌，所以在刚学习⼩波变换的时候，看着三个⽅向和标志牌，可以顺利的⾛下去，当然路上的美景要⾃⼰去欣赏（这⾥的美景就是定义和推导了）。

因为内容太多，不是很重要的地⽅我都注释为（查定义）⼀堆⽂字的就是理论（可以⼤体⼀看不⽤⽴刻就懂），同时最下⾯也给了⼏个⽹址辅助学习。

⼀、基傅⽴叶变换和⼩波变换，都会听到分解和重构，其中这个就是根本，因为他们的变化都是将信号看成由若⼲个东西组成的，⽽且这些东西能够处理还原成⽐原来更好的信号。

那怎么分解呢？那就需要⼀个分解的量，也就是常说的基，基的了解可以类⽐向量，向量空间的⼀个向量可以分解在x，y⽅向，同时在各个⽅向定义单位向量e1、e2，这样任意⼀个向量都可以表⽰为a=xe1+ye2，这个是⼆维空间的基，⽽对于傅⽴叶变换的基是不同频率的正弦曲线，所以傅⽴叶变换是把信号波分解成不同频率的正弦波的叠加和，⽽对于⼩波变换就是把⼀个信号分解成⼀系列的⼩波，这⾥时候，也许就会问，⼩波变换的⼩波是什么啊，定义中就是告诉我们⼩波，因为这个⼩波实在是太多，⼀个是种类多，还有就是同⼀种⼩波还可以尺度变换，但是⼩波在整个时间范围的幅度*均值是0，具有有限的持续时间和突变的频率和振幅，可以是不规则，也可以是不对称,很明显正弦波就不是⼩波，什么的是呢，看下⾯⼏个图就是当有了基，以后有什么⽤呢?下⾯看⼀个傅⽴叶变换的实例：对于⼀个信号的表达式为x=sin(2*pi*t)+0.5*sin(2*pi*5*t);这⾥可以看到是他的基就是sin函数，频率是1和5，下⾯看看图形的表⽰，是不是感受了到了频域变换给⼈的⼀⽬了然。

[H,V,D] = detcoef2 ('all',C,S,N) returns the horizontal H, vertical V, and diagonal D detail coefficients at level N.
47
X = waverec2(C,S,'wname')
reconstructs the matrix X based on the multi-level wavelet decomposition structure [C,S]
10
幅度
频率
时间窗
时间
时域加窗分析
时间
时频平面划分示意图
11
窗口傅立叶变换
12
窗口傅立叶变换
另一个缺点是：无论怎样离散化，都不能 使Gabor变换成为一组正交基；
而傅立叶变换经离散化后可得到按正交函 数展开的傅立叶级数。
13
1909: Alfred Haar
Alfred Haar对在函数空间中寻找一个与傅立叶类似 的基非常感兴趣。1909年他发现并使用了小波， 后来被命名为哈尔小波(Haar wavelets)
C 0
Wf
(a,b)a,b(t)dbda2a
a,b(t)
1 (t b)
aa
28
小波系数的意义
Wf (a,b)表示信号与尺度为a小波的相关程 度。小波系数越大，二者越相似。
F() f(t)ejtdt
W f(a,b)f(t) a,b(t)dt
29
连续小波变换的简单步骤
选择尺度为a确定的小波，与信号开始的 一段比较；
A = appcoef2(C,S,'wname',N)

2mt n
（3.1）
4. 任意函数 f (t) 的离散小波变换为
WTf (m, n) R f (t) m,n (t)dt
（3.2）
DWT 与 CWT 不同，在尺度—位移相平面上，它对应一些如图 3.1 所示的
离散的点，因此称之为离散小波变换。将小波变换的连续相平面离散化，显然
引出两个问题：
低一半，即采样间隔可以增大一倍。因此，如果尺度m 0 时 的间隔为Ts ，则在
尺度为 2m 时，间隔可取2mTs 。此时 a, (t) 可表示为
1 2m
t
2m n 2m
Ts
1 2m
t 2m
n Ts
记作
m,
n
(t
);
m, n Z
为简化起见，往往把t 轴用Ts 归一化，这样上式就变为
m
m,n (t) 2 2
第三章 离散小波变换
3.1 尺度与位移的离散化方法
减小小波变换系数冗余度的做法是将小波基函数 a, (t)
1 t 的 a, 限
a a
定在一些离散点上取值。
1. 尺度离散化：一种最通常的离散方法就是将尺度按幂级数进行离散化，
即取 am a0m（ m 为整数，a0 1 ，一般取a0 2 ）。如果采用对数坐标，则尺度a 的 离散取值如图 3.1 所示。
（1）离散小波变换WT f (m, n) f (t), m,n (t) 是否完全表征函数 f (t) 的全部信 息，或者说，能否从函数的离散小波变换系数重建原函数 f (t) 。 （ 2 ） 是 否 任 意 函 数 f (t) 都 可 以 表 示 为 以 m,n (t) 为 基 本 单 元 的 加 权 和
3.2.2 离散小波变换的逆变换与重建核问题

小波变换与小波包变换的比较与适用场景分析引言：小波变换和小波包变换是信号处理中常用的两种变换方法，它们在不同的领域和场景中有着各自的优势和适用性。

本文将对小波变换和小波包变换进行比较与分析，探讨它们的特点、应用场景以及在实际问题中的应用。

一、小波变换的特点与应用小波变换是一种时频分析方法，可以将信号分解成不同频率的成分，并且可以在时间和频率上提供更好的局部化信息。

小波变换的主要特点包括：1. 局部性：小波变换能够在时间和频率上提供更好的局部化信息，对于非平稳信号的分析具有优势。

2. 多分辨率：小波变换可以通过选择不同的小波基函数来实现多分辨率分析，从而对信号的不同频率成分进行更细致的分析。

3. 时频分析：小波变换可以提供信号在时间和频率上的精确信息，对于瞬态信号的分析有较好的效果。

小波变换在实际应用中有着广泛的应用场景，例如：1. 信号处理：小波变换可以用于信号去噪、边缘检测、特征提取等方面，对于非平稳信号的处理效果较好。

2. 图像处理：小波变换可以用于图像压缩、图像增强、图像分割等方面，对于局部特征的提取和分析有较好的效果。

3. 生物医学工程：小波变换可以用于心电信号分析、脑电信号分析等方面，对于瞬态信号和非平稳信号的分析有较好的效果。

二、小波包变换的特点与应用小波包变换是在小波变换的基础上进行的改进，它能够提供更丰富的频率信息和更灵活的分析方式。

小波包变换的主要特点包括：1. 频率分解：小波包变换可以将信号进行更细致的频率分解，对于频率信息的提取和分析有较好的效果。

2. 灵活性：小波包变换可以通过选择不同的小波包基函数和分解层数来实现不同精度的分析，具有更高的灵活性和可调节性。

3. 能量集中：小波包变换可以将信号的能量集中在少数的小波包系数上，对于信号的重要信息提取有较好的效果。

小波包变换在实际应用中也有着广泛的应用场景，例如：1. 语音信号处理：小波包变换可以用于语音信号的分析和识别，对于频率特征的提取和分类有较好的效果。

小波变换教程小波变换教程一、序言欢迎来到这个小波变换的入门教程。

小波变换是一个相对较新的概念（大概十年的样子），但是有关于它的文章和书籍却不少。

这其中大部分都是由搞数学的人写给其他搞数学的人看的，不过，仍然有大部分搞数学的家伙不知道其他同行们讨论的是什么（我的一个数学教授就承认过）。

换言之，大多数介绍小波变换的文献对那些小波新手们来说用处不大（仅仅为个人观点）。

当我刚开始学习小波变换的时候，曾经为了弄明白这个神奇的领域到底说的是什么困扰了好多天，因为在这个领域的入门书籍少之又少。

为此我决定为那些小波新手们写这个入门级的教程。

我自己当然也是一个新手，也有很多理论性的细节没有弄清楚。

不过，考虑到其工程应用性，我觉得没有必要弄清楚所有的理论细节。

在这篇教程中，我将试图给出一些小波理论的基本原理。

我不会给出这些原理和相关公式的证明，因为我假定预期的读者在读这个教程时并不需要知道这些。

不过，感兴趣的读者可以直接去索引（所列的书籍）中获取更为深入的信息。

在这篇文档中，我假定你没有任何相关知识背景。

如果你有，请忽略以下的信息，因为都是一些很琐碎的东西。

如果你发现教程中有任何不一致或错误的信息，请联系我。

我将乐于看到关于教程的任何评论。

二、变换什么首先，我们为什么需要（对信号做）变换，到底什么是变换？原始信号中有一些信息是很难获取的，为了获得更多的信息，我们就需要对原始信号进行数学变换。

在接下来的教程中，我将时域内的信号视为原始信号，经过数学变换后的信号视为处理信号。

可用的变换有很多种，其中傅立叶变换可能是最受欢迎的一种。

实际中很多原始信号都是时域内的信号，也就是说不管信号是如何测得的，它总是一个以时间为变量的函数。

换言之，当我们画信号图的时候，横轴代表时间（独立变量），纵轴代表信号幅度（非独立变量）。

当我们画信号的时域图时，我们得到了信号的时幅表示。

对大多数信号处理应用来说，这种表示经常不是最好的表示。

在很多时候，大量特殊的信息是隐藏在信号的频率分量中的。

在时域，Shannon小波是无限次可微的，具有无穷阶消 失矩，不是紧支的，具有渐近衰减性但较缓慢；在频域， 是频率带限函数，具有好的局部化特性。
例 5.3 考虑线性样条函数
1 t 1, 2 t 0
(t) 1 1 t , 0 t 2
0,
其他
从几何上看， (t) 显然是一个基本小波
易知 (t) s(t) s(t 2)
t, 0 t 1 这里 s(t) 2 t, 1 t 2
0, 其他
是个帐篷函数
s()
s(t)eitdt
1teit dt
2 (2 t)eitdt
0
1
ei
i
1 ei
(i)2
ei
i
ei2 ei
(i)2
1 ei
i
2
ˆ () sˆ() e2i sˆ() (1 e2i )(1 ei )2 i
构成了子空间 S { f (t) L2(R) | fˆ() 0, }
的一个标准正交基
令S2m { f (t) L2(R) | fˆ() 0, 2m}，则 S2m
具有标准正交基
m
{2 2 (2mt
n)}
m
22
sin
2m
(t
n 2m
)
, m,n
Z.
2m
(t
n 2m
)
正交小波
且对任意
其中
cj,k
f (t) cj,k j,k (t)
j,k
正交小波级数分解
f (t), j,k (t) f (t) j,k (t)dt, j, k Z
称为 f 的小波系数
小波系数实质上是离散小波变换，前面所得的二进离 散小波与连续小波虽不会损失信息，但会产生冗余，而正 交小波则可以使变换后所产生的冗余消失。