各向异性屈服条件和流动理论

第十章各向异性材料的屈服条件和流动理论一 各向异性材料的初始屈服对于各向异性材料，其初始屈服条件需用下列一般形式的屈服函数来表示：12(,,,,,;,,......)0x y z xy yz zx n f c c c σσστττ= （1）式中12,,......n c c c 为与材料性质相关的参数。

取应力分量的二次齐次式作为屈服函数，从而将式（1）表示成2111213141516()ij x x y x z x yz x zx f K K K K K K σσσσσσστστσ=+++++2222324......yy z y yz K K K σσσστ++++233......zK σ++.........266xy K τ+const =（2）上式共包含21个独立系数。

现考虑正交异性材料，设材料性质对称于x 、y 、z 轴，显然，当坐标轴转至相反方向时（即旋转180°），例如，将x 、y 、z 坐标系转换到ξ、η、ζ坐标系，ξ=x 、η=y 、ζ= -z ，则屈服函数()ij f σ应该不变。

因为，对于ξ、η、ζ坐标系，应力分量为,x ξσσ=,y ησσ=,z ζσσ=,xy ξηττ= ,yz ηξττ= ,zx ζξττ=根据()ij f σ保持不变的条件，由（2）得14152425343546560K K K K K K K K ========同样的，如果取,x ξ=- ,y η= ,z ζ=以及,x ξ= ,y η=-,z ζ=则可进一步得到162636460K K K K ====可见，对于各向异性材料，（ 2）中的独立系数由21个减少至9个，从而该式可写成：222222112233445566()ij x y z yz zx xyf K K K K K K σσσστττ=+++++122313x y y z x z K K K σσσσσσ+++const=（3）如果屈服函数不受各向等压力（-p ）（球量）的影响，那么，我们可以用()x p σ-、()y p σ-、()z p σ-来代替方程（3）中的x σ、y σ、z σ，而等式仍然成立。

2-1.什么叫材料的本构关系？在上述的本构关系中，土的强度和应力-应变有什么联系？ 答：材料的本构关系是反映材料的力学性质的数学表达式，表现形式一般为应力-应变-强度-时间的关系，也成为本构定律，本构方程。

土的强度是土受力变形发展的一个阶段，即在微小的应力增量作用下，土单元会发生无限大或不可控制的应变增量，它实际上是土的本构关系的一个组成部分。

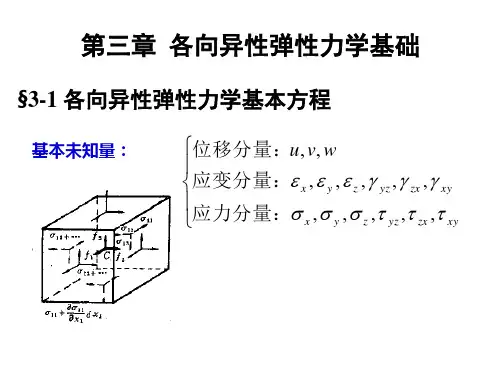
2-7什么是加工硬化？什么是加工软化？请绘出他们的典型的应力应变关系曲线。

答：加工硬化也称应变硬化，是指材料的应力随应变增加而增加，弹增加速率越来越慢，最后趋于稳定。

加工软化也称应变软化，指材料的应力在开始时随着应变增加而增加，达到一个峰值后，应力随应变增加而下降，最后也趋于稳定。

加工硬化与加工软化的应力应变关系曲线如右图。

2-8什么的是土的压硬性？什么是土的剪胀性？答：土的变形模量随着围压提高而提高的现象，称为土的压硬性。

土的剪胀性指土体在剪切时产生体积膨胀或收缩的特性。

2-9简述土的应力应变关系的特性及其影响因素。

答：土是岩石风化形成的碎散矿物颗粒的集合体，通常是固、液、气三相体。

其应力应变关系十分复杂，主要特性有非线性，弹塑性，剪胀性及各向异性。

主要的影响因素是应力水平，应力路径和应力历史。

2-10定性画出在高围压（MPa 303<σ）和低围压（KPa 1003=σ）下密砂三轴试验的v εεσσ--)(131-应力应变关系曲线。

答：如右图。

横坐标为1ε，竖坐标正半轴为)(31σσ-，竖坐标负半轴为v ε。

2-13粘土和砂土的各向异性是由于什么原因？什么是诱发各向异性？答：粘土和砂土的各向异性是由于其在沉积过程中，长宽比大于1的针、片、棒状颗粒在重力作用下倾向于长边沿水平方向排列而处于稳定的状态。

同时在随后的固结过程中，上覆土体重力产生的竖向应力与水平土压力大小不等，这种不等向固结也造成了土的各向异性。

诱发各向异性是指土颗粒受到一定的应力发生应变后，其空间位置将发生变化，从而造成土的空间结构的改变，这种结构的改变将影响土进一步加载的应力应变关系，并且使之不同于初始加载时的应力应变关系。

材料科学中的各向异性研究在材料科学中，人们经常遇到各向同性和各向异性的问题。

各向同性是指在各个方向上性质相同，各向异性则指在不同方向上物质性质存在差异。

各向异性多数情况下是由于内部结构因素引起的，如晶体结构、分子排列等。

因此，在材料科学中，研究各向异性对于材料性能的影响和适应各项需要的要求至关重要。

1. 各向异性研究在材料设计中的应用在研发材料时，对于材料的性能要求通常都是各向同性的，但在实际应用中，各向异性却十分常见。

例如，我们对于一种材料的强度、硬度等性能要求高，但若只从晶体结构角度出发，该材料的骨架只在某些方向上具有很强的性能，而在其他方向上则相对较弱。

这样就需要研究材料各向异性对于性能的影响，重新设计其中的晶体结构、分子排列来实现性能的提高，使材料能够满足真实需求。

2. 各向异性对材料力学性能影响的研究材料的力学性能，如弹性模量、泊松比、剪切模量等，均与其各向同性相关。

当材料出现各向异性时，力学性能也就会有变化。

例如，某些材料由于晶体结构的原因，在某个方向上的弹性模量可能远大于在另一个方向上的弹性模量，这就使得材料在受力时呈现出不同的变形模式，从而导致了材料不同的应力响应行为。

这样的影响在材料力学性能研究上显得尤为重要。

3. 各向异性对材料传输性质的影响各向异性对于材料的传输性质也有很大的影响。

例如，金属材料中存在着一些非球形的晶粒，在传热传电时会形成各向异性；木材由于其植物纤维的排列方式也表现出相应地各向异性特征。

而通过对各向异性的研究，我们可以更好地了解材料的传输性质，有助于我们制定更科学的实验方法和方案。

4. 各向异性在材料加工中的应用目前许多新型制备技术在利用各向异性进行材料加工方面有较高的应用价值。

比如在轧制工程中，利用物涌压加工原理使金属材料中的晶粒对处理气流产生阻挡，实现快速松弛并达到相应的分散、精炼目的；而在切削加工中，通过调整加工过程中的加工参数和工具的几何形状，实现材料高效率加工、精细切削和雷竭模拟效果等操作。

平面应变各向异性本构关系及在应力波传播模拟中的应用*黄霞,汤文辉,蒋邦海【摘要】摘要:为了研究平面应变条件下各向异性材料中应力波传播的特点,利用各向异性弹性H ooke 定律、Tsai-Hill 屈服准则、经典塑性流动理论,引入修正的物态方程计及高压下的体积压缩非线性,建立了平面应变条件下正交各向异性复合材料的弹塑性本构关系,并且分析了二维问题中材料变形引起的主轴旋转及客观应力率修正问题。

最后采用动态显式有限元方法自行编写程序模拟某种纤维增强复合材料碰撞过程中平面应力波的传播,模拟结果显示,在平面应变条件下应力波在该材料的传播过程中表现出明显的二维效应、各向异性特点及弹塑性特点。

【期刊名称】爆炸与冲击【年(卷),期】2010(030)004【总页数】7【关键词】关键词:固体力学;应力波传播;各向异性;平面应变;本构关系;有限元1 引言近年来,复合材料在国防领域得到了越来越广泛的应用,以高强度、高刚度、低密度等特点,已成为航空、航天等国防工业部门的一种重要工程材料。

在航空、航天等领域中,材料的外在环境非常复杂,可能面临高速撞击、射线辐射等动载荷环境,因此对复合材料动态响应特征的研究,对提高材料性能、加强航天器的安全性有着非常重要的作用。

在研究复合材料力学性能的过程中,必须考虑各向异性力学特征,它会对强度、应力波传播等带来影响,为了分析复合材料的各向异性响应特征,必须使用各向异性本构模型。

为了处理各向异性材料本构模型中容变和畸变的耦合效应,C.E.Anderson 等[1]、P.E.O'Donoghue 等[2]将各向异性条件下的静水压及应力偏量表达式进行了修正;另外,他们将物态方程引入到各向异性本构模型中,使得修改后的Grüneisen 物态方程既能反映高压下的体积压缩非线性,又能考虑低压下材料的各向异性强度性能。

各向异性强度准则是各向异性本构模型研究中的一个重要问题,从各向同性强度准则基础上发展起来的适用于复合材料的强度准则已有十几种[3],最常用的是T sai-Hill 屈服准则、Tsai-Wu 屈服准则等。

FASTAMP
专业钣金成形快速仿真软件FASTAMP 增量理论本构方程
FASTAMP 专业钣金成形快速仿真软件FASTAMP 专业钣金成形快速仿真软件
FASTAMP 专业钣金成形快速仿真软件全量形变理论本构方程
FASTAMP 专业钣金成形快速仿真软件
全量形变理论本构方程
⎦
⎣
090
FASTAMP 各向同性屈服准则
FASTAMP FASTAMP 专业钣金成形快速仿真软件FASTAMP 专业钣金成形快速仿真软件
FASTAMP 专业钣金成形快速仿真软件
材料的J2随动强化本构关系
K εσ=FASTAMP 专业钣金成形快速仿真软件
板料各向异性
FASTAMP 各向异性参数R 定义FASTAMP 各向异性系数ΔR
FASTAMP 专业钣金成形快速仿真软件FASTAMP 专业钣金成形快速仿真软件
FASTAMP 专业钣金成形快速仿真软件Barlat_Lian 屈服准则
FASTAMP 专业钣金成形快速仿真软件
Barlat 六参量正交各向异性屈服准则
6
FASTAMP 各种屈服准则比较
FASTAMP J2流动理论
FASTAMP 专业钣金成形快速仿真软件FASTAMP 专业钣金成形快速仿真软件
Barlat_Lian 屈服准则
FASTAMP 专业钣金成形快速仿真软件Barlat 六参量正交各向异性屈服准则
FASTAMP 专业钣金成形快速仿真软件。

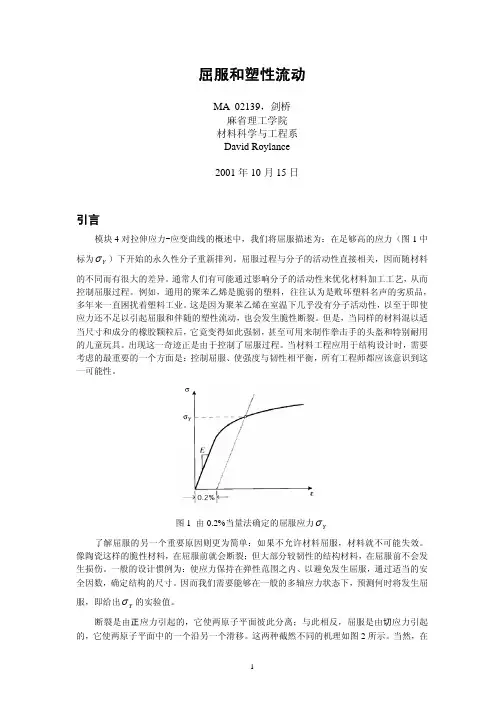
屈服和塑性流动MA02139，剑桥麻省理工学院材料科学与工程系David Roylance2001年10月15日引言模块4对拉伸应力-应变曲线的概述中，我们将屈服描述为：在足够高的应力（图1中σ）下开始的永久性分子重新排列。

屈服过程与分子的活动性直接相关，因而随材料标为Y的不同而有很大的差异。

通常人们有可能通过影响分子的活动性来优化材料加工工艺，从而控制屈服过程。

例如，通用的聚苯乙烯是脆弱的塑料，往往认为是败坏塑料名声的劣质品，多年来一直困扰着塑料工业。

这是因为聚苯乙烯在室温下几乎没有分子活动性，以至于即使应力还不足以引起屈服和伴随的塑性流动，也会发生脆性断裂。

但是，当同样的材料混以适当尺寸和成分的橡胶颗粒后，它竟变得如此强韧，甚至可用来制作拳击手的头盔和特别耐用的儿童玩具。

出现这一奇迹正是由于控制了屈服过程。

当材料工程应用于结构设计时，需要考虑的最重要的一个方面是：控制屈服、使强度与韧性相平衡，所有工程师都应该意识到这一可能性。

σ图1 由0.2%当量法确定的屈服应力Y了解屈服的另一个重要原因则更为简单：如果不允许材料屈服，材料就不可能失效。

像陶瓷这样的脆性材料，在屈服前就会断裂；但大部分较韧性的结构材料，在屈服前不会发生损伤。

一般的设计惯例为：使应力保持在弹性范围之内、以避免发生屈服，通过适当的安全因数，确定结构的尺寸。

因而我们需要能够在一般的多轴应力状态下，预测何时将发生屈σ的实验值。

服，即给出Y断裂是由正应力引起的，它使两原子平面彼此分离；与此相反，屈服是由切应力引起的，它使两原子平面中的一个沿另一个滑移。

这两种截然不同的机理如图2所示。

当然，在与屈服相关的滑移中，键必须被打破；但不同于断裂的是，它允许在新的位置重新形成键。

该过程能使材料产生实质性的改变，甚至导致最终的断裂（这就像反复前后弯折一根金属条使其断裂一样）。

“塑性”变形是屈服的基础，它本质上是一个粘性流动过程，并且遵循与流体十分相似的动力学定律。

万方数据　万方数据　万方数据　万方数据　万方数据各向异性屈服准则的发展及应用作者：史艳莉， 吴建军， SHI Yan-li， WU Jian-jun作者单位：西北工业大学,机电学院,陕西,西,安710072刊名：锻压技术英文刊名：FORGING & STAMPING TECHNOLOGY年，卷(期)：2006,31(1)被引用次数：9次1.俞汉清;陈金德金属塑性成形原理 19992.R 希尔;王仁塑性数学理论 19663.Hill R Theoretical plasticity of textured aggregates[外文期刊] 19794.Hill R Constitutive modeling of orthotropic plasticity in sheet metal[外文期刊] 1990(03)5.Hill R A user-friendly theory of orthotropic plasticity in sheet metal[外文期刊] 1993(01)6.Logan R W;Hosford W F Upper-bound anisotropic yield locus calculations assuming <111>-pencilgilde [外文期刊] 1980(07)7.Bralat F;Lian J Plastic behaviour and stretchability of sheet metals,Part Ⅰ A yield function for orthotropic sheet under plane stress conditions[外文期刊] 1989(01)8.Barlat F;Lege D J;Brem J C A six-component yield function for anisotropic materials 1991(07)9.Barlat F;Becker R C Yielding description for solution strengthened aluminum alloys sheets[外文期刊] 1997(04)10.Barlat F;Maeda Y;Chung K Yield function development for aluminum alloy sheets[外文期刊] 199711.Banabic D A new criterion for anisotropic sheet metals 199912.Banabic D;Balan T;Comsa S D Comments on a new anisotropic yield criterion[外文会议] 200013.Banabic D;Kuwabara T;Balan T An anisotropic yield criterion for sheet metals[外文期刊] 2004(0)14.Banabic D;Aretz H;Comsa D S An improved analytical description of orthotropy in metallic sheets [外文期刊] 2005(03)15.Gotoh M A theory of plastic anisotropy based on a yield function of fourth order (plane stress state) 197716.周维贤正交异性非二次屈服函数探讨 1989(07)17.Karafillis A;Boyce B C A general anisotropic yield criterion using bounds and a transformation weighting tensior[外文期刊] 199318.Banabic D Formability of Metallic Materials 200019.Banabic D;Mü ller W;K P O hlandt Experimental determination of yield loci for sheet metals 199820.吴向东不同加载路径下各向异性板料塑性变形行为的研究[学位论文] 200421.Pearce R Some aspects of anisotropic plasticity in sheet metals 1968(12)22.Woodthorpe J;Pearce R The anomalous behaviour of aluminum sheet under balanced biaxial tention[外文期刊] 1970(04)23.Lin S B;Ding J L Experimental study of the plastic yielding of rolled sheet metals with the cruciform plate specimen[外文期刊] 1995(05)24.Lege D J;Barlat F;Brem J C Characterization and modeling of the mechanical behavior and formability of a 2008-T4 sheet sample[外文期刊] 1989(07)25.Hayashida Y;Maeda Y FEM analysis of punch strengthening and cup drawing tests for aluminum,alloys using a planar anisotropic yield function 199526.Green D;Makinde A;Neale K W Experimental determination of yield surfaces and biaxial flow of 1145aluminum sheets 199827.Kuwabara T;VanBael A Measurement and analysis of yield locus of sheet aluminum alloy 6XXX 199928.倪向贵;吴恒安;王宇各向异性本构关系在板料成形数值模拟中的应用[期刊论文]-计算力学学报 2003(02)29.吴向东;万敏;周贤宾各向异性板料屈服轨迹的研究[期刊论文]-材料科学与工艺 2004(12)30.孙成智;陈关龙;林忠钦各向异性屈服准则对铝合金板成形预测精度的影响[期刊论文]-塑性工程学报 2004(03)31.Joao Pedro de Magalhaes Correia;Gérard Ferron Wrinkling Predictions in the deep-drawing process of anisotropic metal sheets[外文期刊] 2002(1-3)32.Kawaka M;Makinouchi A Plastic anisotropy in FEM analysis using degenerated solid element[外文期刊] 1996(1-4)33.沈启彧;卫原平;王玉国金属板料成形的一步有限元模拟方法[期刊论文]-上海交通大学学报 2000(10)34.刘腾喜;傅衣铭;丁皓江正交各向异性金属板料的成形极限[期刊论文]-固体力学学报 2000(02)35.中国仿真互动.利用ANSYS/LS DYNA仿真计算36.迅利科技有限公司ABAQUS公司介绍37.胡平板料冲压成形性模拟CAE软件系统KMAS1.张秀娟.刘彦奎.魏延刚.运新兵.韩锋.郑勇福.ZHANG Xiu-juan.LIU Yan-kui.WEI Yan-gang.YUN Xin-bing.HAN Feng.ZHENG Yong-fu各向异性铝合金板材本构关系及其有限元模拟[期刊论文]-大连交通大学学报2008,29(6)2.倪向贵.吴恒安.王宇.王秀喜各向异性本构关系在板料成形数值模拟中的应用[期刊论文]-计算力学学报2003,20(2)3.吴向东.万敏.周贤宾各向异性板料屈服轨迹的研究[会议论文]-20044.孙成智.陈关龙.林忠钦.赵亦希各向异性屈服准则对铝合金板成形预测精度的影响[期刊论文]-塑性工程学报2004,11(3)5.倪向贵.王宇.吴恒安.王秀喜.车玫.NI Xiang-gui.WANG Yu.WU Heng-an.WANG Xiu-xi.CHE Mei用于板料成形数值模拟的各向异性本构模型研究[期刊论文]-中国科学技术大学学报2000,30(6)1.柳玉起.徐丹.许江平改进的5参数Barlat-Lian屈服准则[期刊论文]-华中科技大学学报（自然科学版） 2008(1)2.邹修敏覆盖件的有限元和质量分析[期刊论文]-科技创业家 2012(14)3.潘秋红.董则防.黄瑶.王雷刚.万宝伟均匀化退火对纯铝铸轧-冷轧板各向异性的影响[期刊论文]-锻压技术2008(6)4.刘桂花.冯再新.贾青云.于晓东板料冲压成形过程中回弹预测及控制的研究进展[期刊论文]-热加工工艺2011(17)5.李玉强.王勇.董剑安.郭水军.须俊华.崔永生覆盖件冲压CAE分析材料模型的工程应用与发展[期刊论文]-模具技术 2009(4)6.蒋松.高锦张.贾俐俐板料多道次渐进成形下沉现象的模拟分析[期刊论文]-锻压技术 2010(2)7.沈黎萍.高锦张.蒋松.贾俐俐板料渐进成形半球形件的路径研究[期刊论文]-锻压技术 2010(6)8.曹瀚中.高锦张.肖士昌.贾俐俐渐进成形锥形件壁厚稳定区域影响因素的研究[期刊论文]-锻压技术 2012(6)9.徐梁.高锦张.贾俐俐.蒋松渐进成形直壁筒形件圆角缺陷的模拟分析[期刊论文]-锻压技术 2010(3)10.郭健.许模.宋丽娟.卢书强非均质花岗岩坝基典型地质缺陷处理研究[期刊论文]-人民黄河 2013(5)本文链接：/Periodical_dyjs200601031.aspx。

von mises 流动法则与二塑流全文共四篇示例，供读者参考第一篇示例：Von Mises 流动法则是一个在材料科学和力学领域广泛应用的原理，用于描述金属等材料在受到外力作用时的变形特性。

而二塑流则是一种基于Von Mises 流动法则的变形模型，用于描述金属在高应变速率条件下的流动行为。

Von Mises 流动法则最初由奥地利的工程师和数学家理查德·冯·米泽斯（Richard von Mises）在20世纪初提出。

该法则基于应力的平均值和剪切应力，而不考虑材料在不同方向上的强度差异。

根据Von Mises 流动法则，当材料达到一定应力水平时，就会开始发生塑性变形，这个应力水平被称为屈服应力。

Von Mises 流动法则可以用数学公式表示为：\[ \sigma_{eq} = \sqrt{\frac{3}{2} \left( \sigma_{1}-\sigma_{2} \right)^{2} + \left( \sigma_{2}-\sigma_{3} \right)^{2} +\left( \sigma_{3}-\sigma_{1} \right)^{2}} \]\( \sigma_{eq} \) 为等效应力，\( \sigma_{1} \)、\( \sigma_{2} \) 和\( \sigma_{3} \) 分别为材料在三个方向上的主应力。

基于Von Mises 流动法则，二塑流模型假设材料的屈服行为是由两个可变形的主应力平面决定的，这两个主应力平面在与主应力轴不平行的方向上发生滑移，从而导致材料的变形。

二塑流模型可以较好地描述金属在高速冲击或冲压等高变形速率条件下的行为，因为在这种情况下，应变速率较大，传统的Von Mises 流动法则可能无法准确描述材料的变形。

二塑流模型的数学表达形式可以表示为：\[ \dot{\epsilon} = A \cdot \sigma^{m} \cdot\overline{\dot{\epsilon}}^{k} \]Von Mises 流动法则和二塑流模型在工程设计和材料研究领域都具有重要的应用价值。

§7.3 Mises 流动理论（2J 流动理论）1．各向同性硬化1.4 屈服面的形状在应力偏张量空间中讨论屈服面的形状为球体，随着硬化参数()p Y Y ε=的变化屈服面为不断均匀膨胀的球体。

在一般应力空间中讨论屈服面的形状比较复杂，下边我们讨论在在主应力空间中初始屈服面的形状。

在主应力空间中，Mises 屈服条件(7.57)可以表示为()()()2222232Y σσσσσσ1231−+−+−=习题已经证明：塑性变形无体积变化（即0p ii ε=&）的充分必要条件为在屈服条件0),,,(1=n Y Y f L σ中与应力张量的第一不变量1()J σ无关，即对于任意参数a ，都有：11(,,,)(,,,)n n f a Y Y f Y Y +=σI σL L 。

这意味着如果σ在屈服面上，对于任意参数a ，a σ也在屈服面上。

所以在主应力空间()123,,σσσ中Mises 屈服条件为一个柱面。

柱面的中心线通过应力零点，方向为(1,1,1)，其方程为123σσσ==，通常称作等倾线。

通过应力零点与等倾线垂直的平面称作π平面，其方程为1230σσσ++=，三个主应力轴在该面上投影互相成120o 角。

根据上述分析，屈服面与π平面的交线为圆，圆的半径为Y ，见图7.11。

图7.11 π平面上的屈服条件所以在主应力空间中，Mises 屈服条件所表示的屈服面为以等倾线为中心线半径为Y 的圆柱面,随着硬化参数()p Y Y ε=的变化该圆柱面不断均匀向外膨胀。

2．混合硬化在初始状态为各向同性材料中，材料的拉伸曲线与压缩曲线形状相同。

拉伸屈服极限与压缩屈服极限的数值是相同的，记作s σ，见图7.12所示的单向拉伸（压缩）曲线的A 与A 点。

如果材料属于各向同性硬化，当拉伸到达屈服后的B 点（应力为B σ）时开始卸载并反向加压应力，在图7.12中表示应力与应变对应的点从B 沿一斜率为杨氏模量E 的直线BC 变化；当B σσ=−时出现反向屈服，这时材料的屈服限由初始值s σ增大至B σ，屈服面的大小由初始的2s σ增大为2B σ。