七年级下册数学知识树PPT课件
- 格式:ppt
- 大小:1.40 MB
- 文档页数:9

七年级下册数学知识点总结ppt PPT是现代演示文稿的主流形式,它为演示者提供了各种便利,能够成为演示者在公众场合展现自己的才华和技能的重要工具。
本文将为大家提供一份七年级下册数学知识点总结PPT的范本,希望能够给广大学生提供更好的学习体验。
第一部分:数学运算基础知识1.1 整数基础知识整数是数学中的基础概念之一。
它包括正整数、负整数和零。
在学习整数的过程中,我们需要掌握整数的加减乘除法规则,正确理解负数的概念,掌握约数和倍数的概念等基础知识。
1.2 小数基础知识小数是我们日常生活中经常遇到的一种数,我们需要掌握小数的定义、小数加减乘除法的计算方法,了解小数和分数的关系等基础知识。
1.3 分数基础知识分数是我们在小学学习数学时就开始接触的数学概念之一。
在七年级下册的数学学习中,我们需要深入理解分数的表示方法和意义,掌握分数的基本操作,理解分数的大小比较等知识。
第二部分:图形与几何图形2.1 平面图形平面图形是指所有的点都在一张平面上的图形。
常见的平面图形包括:三角形、四边形、多边形等,学习中需要了解各种平面图形的定义、性质、分类以及相关定理等。
2.2 空间图形空间图形是三维空间中的图形,用于描述真实物体的形状和结构。
学习中需要掌握空间图形的各种基本形状、表示方法、性质等知识,深入理解空间图形与平面图形的关系,以及掌握相关的计算技巧和方法。
第三部分:代数式与方程式3.1 代数式代数式是指由数、字母和运算符号组成的式子,它常常用来表示某种数学规律或者某种现实问题。
在学习代数式的过程中,我们需要掌握代数式的基本概念,包括如何读写代数式,如何进行代数式的简单运算,以及如何理解代数式的意义等。
3.2 方程式方程式是一种等式,它包含了一个或者多个未知量,并具有一定的数学意义。
在学习方程式的过程中,我们需要掌握方程式的各种基本形式,了解方程式的解法,掌握方程式的应用等知识。
第四部分:数据、概率与统计4.1 数据与统计数据和统计是我们日常生活中经常遇到的一种数学概念。



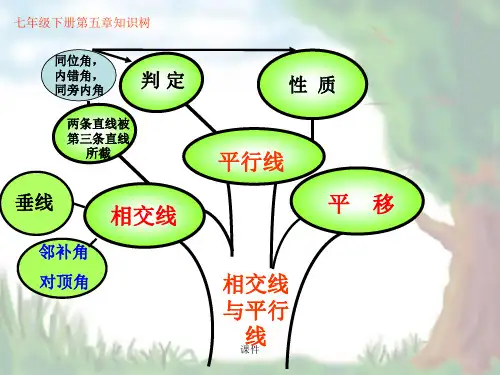
七年级下学期数学知识梳理第五章相交线与平行线一、知识结构图相交线相交线垂线同位角、内错角、同旁内角平行线平行线及其判定平行线的判定平行线的性质平行线的性质命题、定理平移二、知识定义邻补角:两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角。
对顶角:一个角的两边分别是另一个叫的两边的反向延长线,像这样的两个角互为对顶角。
垂线:两条直线相交成直角时,叫做互相垂直,其中一条叫做另一条的垂线。
平行线:在同一平面内,不相交的两条直线叫做平行线。
同位角、内错角、同旁内角:同位角:∠1与∠5像这样具有相同位置关系的一对角叫做同位角。
内错角:∠2与∠6像这样的一对角叫做内错角。
同旁内角:∠2与∠5像这样的一对角叫做同旁内角。
命题:判断一件事情的语句叫命题。
平移:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移平移变换,简称平移。
对应点:平移后得到的新图形中每一点,都是由原图形中的某一点移动后得到的,这样的两个点叫做对应点。
三、定理与性质对顶角的性质:对顶角相等。
垂线的性质:性质1:过一点有且只有一条直线与已知直线垂直。
性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
平行公理:经过直线外一点有且只有一条直线与已知直线平行。
平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
平行线的性质:性质1:两直线平行,同位角相等。
性质2:两直线平行,内错角相等。
性质3:两直线平行,同旁内角互补。
平行线的判定:判定1:同位角相等,两直线平行。
判定2:内错角相等,两直线平行。
判定3:同旁内角相等,两直线平行。
第六章平面直角坐标系一、知识结构图有序数对平面直角坐标系平面直角坐标系用坐标表示地理位置坐标方法的简单应用用坐标表示平移二、知识定义有序数对:有顺序的两个数a与b组成的数对叫做有序数对,记做(a,b)平面直角坐标系:在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系。



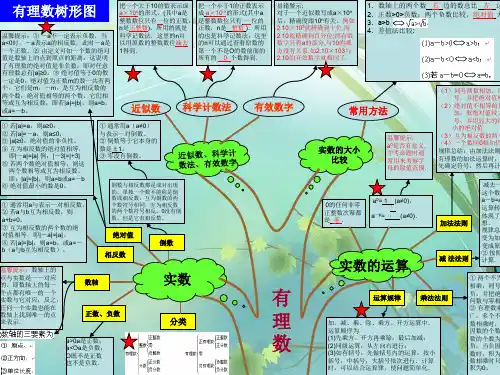
数学七年级下册第六章知识树在七年级下册的数学学习中,第六章是一个重要的知识板块。
这一章的内容涵盖了实数的相关知识,为我们打开了数学世界中更广阔、更深入的领域。
接下来,让我们一起构建这一章的知识树,清晰地梳理其中的要点。
首先,我们来了解一下实数的定义。
实数,简单来说,就是有理数和无理数的统称。
有理数包括整数和分数,比如-3、0、1/2 等等;而无理数则是无限不循环小数,像常见的圆周率π、根号 2 等。
有理数又可以进一步细分。
整数包括正整数、零和负整数;分数包括正分数和负分数。
整数和分数都可以表示为有限小数或无限循环小数。
无理数的出现,让我们对数字的认识不再局限于有限和循环。
无理数的特点就是无限不循环,比如根号 2 约等于 141421356,其小数位没有重复的规律。
接着,我们来探讨一下实数的运算。
在实数范围内,加、减、乘、除、乘方和开方等运算依然成立。
加法和减法遵循着“同号相加取同号,绝对值相加;异号相加取绝对值较大的符号,绝对值相减”的原则。
乘法运算中,两数相乘,同号得正,异号得负,并把绝对值相乘。
除法运算则是将除数化为倒数,与被除数相乘。
在实数的乘方运算中,正数的任何次幂都是正数,负数的奇次幂是负数,负数的偶次幂是正数。
开方运算则是乘方的逆运算。
对于正数,它有两个平方根,互为相反数;0 的平方根是 0;负数没有平方根。
对于一个非负数 a,它的算术平方根记为√a。
实数的大小比较也是一个重要的知识点。
我们可以通过数轴来直观地比较实数的大小。
数轴上右边的数总是大于左边的数。
另外,我们还可以将两个实数作差,判断差的正负来比较大小。
若差为正,则被减数大于减数;若差为零,则两数相等;若差为负,则被减数小于减数。
在实际应用中,实数的知识非常广泛。
比如在几何计算中,常常需要用到根号来计算边长和面积;在物理问题中,各种测量数据也常常是实数。
学习实数这一章,我们需要理解实数的概念,掌握实数的运算规则,能够熟练进行实数的计算和大小比较,并能将其应用到实际问题中。

数学14章知识树
数学这玩意儿,就像一座神秘的城堡,每一章都藏着不同的宝藏。
咱今天就来聊聊这第十四章,把它变成一棵知识树,让你轻轻松松搞明白!
你想想,知识树是不是就像一棵大树,有根、有枝、有叶?第十四章的基础知识就是那树根,深深扎在地里,为整棵树提供养分。
比如说那些基本的概念、定义,就像树根默默地支撑着一切。
要是没搞清楚这些,就像大树没了根,还能站得住吗?
再往上,那些重点公式和定理,就像是粗壮的树枝。
它们从树根延伸出来,把知识一点点展开。
你要是能熟练掌握这些公式定理,就如同树枝能稳稳地托住树叶,让知识的大树更加繁茂。
然后是各种例题和习题,这就像是树上的叶子。
一片一片,丰富多彩。
通过做这些例题习题,你能更好地理解和运用所学的知识。
这不就跟叶子通过光合作用为大树提供能量一样嘛!
说到解题方法,那可是这棵知识树上的花朵啊!美丽又实用。
掌握了巧妙的解题方法,就像花朵绽放出迷人的光彩,让你的数学学习之旅更加精彩。
咱们再想想,数学里的逻辑推理,像不像大树内部的脉络?它把各个部分连接起来,让知识流通,形成一个完整的体系。
还有那些易错点,就像是树上的小虫子。
你得小心,别让它们咬坏
了你的知识树。
要时刻警惕,把这些错误消灭在萌芽状态。
要是你能把第十四章的知识都这样梳理清楚,构建出一棵完整的知
识树,那数学对你来说还能难吗?你难道还会害怕考试?肯定不会啦!
所以,别再抱怨数学难,赶紧动手,种出属于你的第十四章知识树,让它在你的脑海里茁壮成长,为你的学习之路遮风挡雨!。
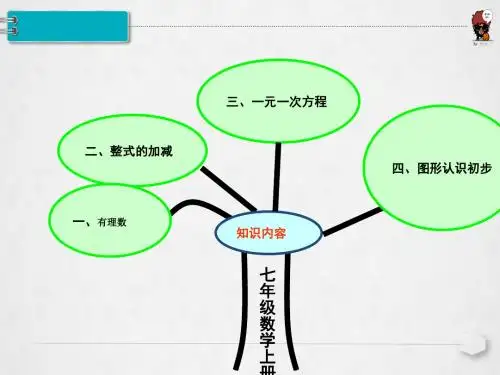
初一知识树数学《初一知识树之数学》初一的数学就像一棵知识树,每个知识点都是树上的一片叶子或者一根树枝,组合在一起就构成了一个充满趣味的知识体系。
先来说说有理数吧。
有理数就像是这棵树上最基础的树根部分。
我记得第一次上有理数这一课时,那感觉就像是进入了一个新的数字世界。
老师在黑板上写着正数、负数还有零,然后就开始讲它们之间的运算规则。
那时候,我心里就想:“嘿,这数字还能有正有负,就像生活中的收支一样呢。
”就像我自己有一次去买文具,带了10元钱,文具花了8元,我还剩下2元,这就是正数的概念。
可要是我本来欠别人5元,这就相当于 -5元,这个负数的概念一下子就变得很实在了。
有理数的四则运算就像是树根之间的交错联系,加法、减法、乘法、除法,每一种运算规则都像是树根的小分支,为整棵树提供养分。
再往上就是整式这根粗壮的树枝了。
单项式、多项式,刚开始学的时候真的有点晕乎。
单项式像个简单的小单元,比如3x,就一个数字和一个字母相乘。
多项式呢,就像是几个单项式组合起来的大家庭,像2x + 3y。
我对整式印象深刻是因为有一次做整式的化简题,那题目看起来乱乱的,就像一团缠在一起的毛线。
我费了好大的劲儿才慢慢把它理顺,把同类项合并起来。
这就好比把树上那些杂乱的小枝桠修剪整齐,让整式这根树枝看起来更利落。
方程就像是知识树上的花朵。
一元一次方程,设未知数、列方程、解方程,这个过程就像是花朵从含苞待放的花蕾到完全盛开。
我记得在做一道关于行程问题的一元一次方程题时,题目说小明和小红分别从两地相向而行,速度不同,问多久能相遇。
我就想象着他们在一条路上走着,然后根据路程= 速度×时间这个公式列出方程。
当最后算出答案的时候,就好像看到花朵绽放的那一刻,特别有成就感。
几何部分呢,就像是知识树的树叶。
那些三角形、四边形的知识,形状各异。
三角形的内角和是180度,这是个很神奇的存在。
我在课桌上用铅笔和直尺画三角形的时候,就想着怎么去验证这个内角和呢。