高中数列裂项相消公式

裂项相消法求和公式
裂项相消法是数学中常用的一种方法，用于简化求和式。

它通
常用于对称性比较明显的求和式，可以通过将求和式中的相邻项相减，从而简化问题。

裂项相消法常用于数学和物理中的求和问题，
下面我将从数学和物理两个方面来介绍裂项相消法的求和公式。

在数学中，裂项相消法可以用于简化一些复杂的求和式，特别
是在级数求和的过程中。

一个常见的裂项相消法求和公式是对称式
的求和。

比如，对于等差数列$a_1, a_2, a_3, ..., a_n$，我们可
以利用裂项相消法将求和式简化为$\frac{1}{2}(a_1+a_n)n$。

这个
公式的推导过程就是利用了裂项相消法，通过将数列的首尾项相加，次首尾项相加，依次类推，最终得到简化后的形式。

在物理中，裂项相消法同样有着重要的应用。

比如在物理中的
力学问题中，特别是涉及到质心的问题中，裂项相消法可以帮助简
化力矩的求和问题。

通过将作用在质点上的力分解成对称的部分，
然后利用裂项相消法简化力矩的表达式，从而简化了问题的求解过程。

总的来说，裂项相消法是一种非常有用的数学方法，它可以帮
助简化复杂的求和式，特别是对称性比较明显的求和式。

在数学和物理问题中都有着重要的应用。

通过合理运用裂项相消法，可以简化问题、加快计算速度，是数学和物理学习中的重要工具之一。

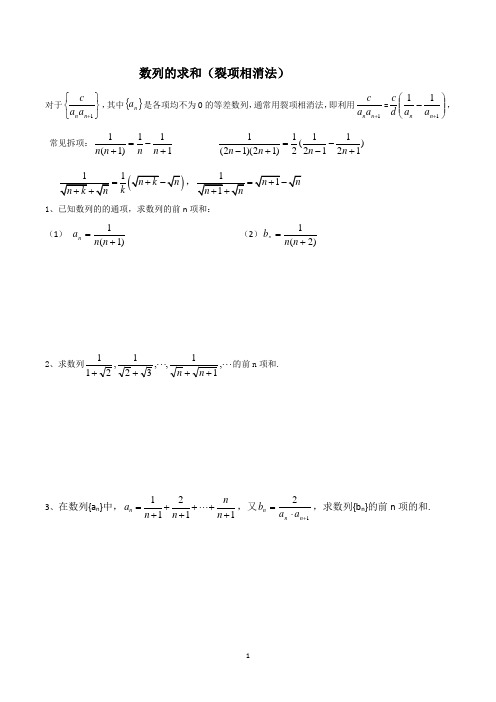
数列的求和（裂项相消法）对于⎭⎬⎫⎩⎨⎧+1n n a a c ，其中{}n a 是各项均不为0的等差数列，通常用裂项相消法，即利用1+n n a a c =⎪⎪⎭⎫⎝⎛-+111n n a a d c ， 常见拆项：111)1(1+-=+n n n n)121121(21)12)(12(1+--=+-n n n n1k==1、已知数列的的通项，求数列的前n 项和： （1） )1(1+=n n a n （2）)2(1+=n n b n2、求数列⋅⋅⋅++⋅⋅⋅++,11,,321,211n n 的前n 项和.3、在数列{a n }中，11211++⋅⋅⋅++++=n nn n a n ，又12+⋅=n n n a a b ，求数列{b n }的前n 项的和.4、等比数列{a n}的各项均为正数，且2a1+3a2=1，a32=9a2a6，（1）求数列{an}的通项公式；（2）设bn =log3a1+log3a2+…+log3an，求数列{}的前n项和．5、正项数列{an }满足﹣（2n﹣1）an﹣2n=0．（1）求数列{an }的通项公式an；（2）令bn=，求数列{bn}的前n项和Tn．6、已知等差数列{an }满足：a3=7，a5+a7=26．{an}的前n项和为Sn．（1）求an 及Sn；（2）令（n∈N*），求数列{bn}的前n项和Tn．7. 已知数列{}n a 的前n 项和为n S ，点),(n s n n 在直线21121+=x y 上，数列{}n b 满足0212=+-++n n n b b b ，()*N n ∈，113=b，且其前9项和为153.（1）求数列{}n a ，{}n b 的通项公式； （2）设)12)(112(3--=n n n b a c ，求数列{}n c 前n 项的和n T .8、已知等差数列{a n }的前n 项和S n 满足5,053-==S S (1)求{a n }的通项公式； (2)求数列21211n n a a -+⎧⎫⎨⎬⎩⎭的前n 项和．9、S n 为数列{a n }的前n 项和.已知a n >0，(Ⅰ)求{a n }的通项公式： (Ⅱ)设 ，求数列}的前n 项和10、已知公差不为零的等差数列{}n a 中，37a =，且1413,,a a a 成等比数列． （1）求数列{}n a 的通项公式； （2）令211n n b a =-（n N *∈），求数列{}n b 的前n 项和n S ．11、已知各项均为正数的等比数列{}n a 的首项12a =，n S 为其前n 项和，且312253S S S =+. （1）求数列{}n a 的通项公式； （2）设2log n n b a =，11n n n c b b +=，记数列{}n c 的前n 项和n T ，求4n Tn +的最大值.12. 已知数列{}n a 的前n 项和为n S ，且22n n S a =-，(1,2,3)n =⋅⋅⋅；数列{}n b 中，11,b = 点1(,)n n P b b +在直线20x y -+=上．（1）求数列{}n a 和{}n b 的通项公式； （2）设数列12n b +⎧⎫⎨⎬⎩⎭的前n 和为n S ，求12111nS S S +++；答案：1（1）1n n +（2）3111-)4212n n +++（21-；3、81n n +；4、（1）13n n a =（2）21n n S n =-+；5、（1）2n a n =（2）21n n T n =+（）;6、（1）2+1n a n =22n S n n =+（2）1n n T n =+4（）；7、（1）5;32n n a n b n =+=+（2）21n n T n =+；8、（1）2-n a n =（2）1-2n nT n=；9、（1）2+1n a n =（2）323)n n T n =+（10、（1）2+1n a n =（2）1)n n S n =+4（;11、、（1）2nn a =（2）1n n T n =+，最大值为19;12、（1）2nn a =；21n b n =-（2）21n nT n =+，。

高三数学数列不等式证明——裂项相消与放缩法总结一、裂项相消法通项特征：通项一般是分式，分母为偶数个因式相乘，且满足a是常数，a-=原分子分母大的因式分母小的因式2.解题思路类型①⎪⎭⎫⎝⎛+-=+knnkknn111)(1类型②()nknknkn-+=++11类型③⎪⎭⎫⎝⎛+--=-121121211412nnn类型④()()⎪⎭⎫⎝⎛++--=--121121114412nnnn nn类型⑤kkkk nnnnn+-+=++++112121)2)(2(2类型⑥kakakakaaannnnn+-+=++⎪⎭⎫⎝⎛-++1111))((11二、错位相减法错位相消法三种思维求法：以下三种思维，但还是建议练熟第一种。

如果第一种都掌握不了的学生，基本上也记不住第二和第三种方法。

1.思维结构结构图示如下2.公式型记忆：1(),n S=n+)q,,11n nn nC a n b q A B ca b AB C Bq q-=⋅++-==---则其前项和（其中A=3.可可裂项为如下11(),q1),[(1))](),((())k=pq-pp tb=pqnnn n nn n n na knb qa p n t q pn t q C C C pn t qtq t++=+≠=++-+=-=+⎧⎨+-⎩（则其中可通过方程组计算出、值：11=a()n=a[( )( )( )...( )]n=1 n=2 n=3 n=n-++++=⇑⇑⇑⇑原式分母小的因式分母大的因式前项和化简放缩模型——平方型与指数型证明下列不等式：1、、2、)(21......31211222*∈<++++Nnn3、)(471......31211222*∈<++++Nnn4、)(351......31211222*∈<++++Nnn)(21)12()12(1......751531311*∈<+⨯-++⨯+⨯+⨯NnnnnnS + + +...+n=1 n=2 n=3 n=nqS + + +...+q-=⇑⇑⇑⇑=①②①的基础上左右同时乘，即在①式中指数加1①②代入通项公式，等差数列当等比数列的系数在n-+k( )=+k( )=-S=--n得（1q)S①中的第一项指数函数相加②的最后一项①中的第一项等比求和公式②的最后一项化简两边同时除以（1q)即得平方型：分母是两项积可放缩到裂项相消模型指数型：可放缩为等比模型5、)(45)12(1......51311222*∈<-++++N n n6、),2(32121......121121121432*∈≥<-++-+-+-N n n n7、)(23231......231231231332211*∈<-++-+-+-N n nn8、)(342 (3232221211)432*+∈<-++-+-+-N n n n n一、单选题1．已知数列{}n a 的首项是11a =，前n 项和为n S ，且()1231n n S S n n N *+=++∈，设()2log 3n n c a =+，若存在常数k ，使不等式()()116n nc k n N n c *-≥∈+恒成立，则k 的取值范围为（ ） A ．1,9⎡⎫+∞⎪⎢⎣⎭B ．1,16⎡⎫+∞⎪⎢⎣⎭C ．1,25⎡⎫+∞⎪⎢⎣⎭D ．1,36⎡⎫+∞⎪⎢⎣⎭2．已知数列{}n a 的首项是11a =，前n 项和为n S ，且1231n n S S n +=++（*N n ∈），设()2log 3n n c a =+，若存在常数k ，使不等式()116n n c k n c -≥+（*N n ∈）恒成立，则k 的最小值为（ ）A ．19B ．116C ．125D ．136二、填空题3．已知数列{}n a 中，112a =，()1n n n n a a a +-=，*n ∈N ，数列11n n a a +⎧⎫⎨⎬⋅⎩⎭的前n 项和为n S .若对于任意的*n ∈N ，不等式n S t <恒成立，则实数t 的取值范围是________.4．已知首项为1的数列{}n a 的前n 项和为n S ，且()12n n nS n S +=+，数列2112n n n n a a a +++⎧⎫⎨⎬⎩⎭的前n 项和为n T ，若()110n n T λ++-⋅>，且λ∈Z ，则λ=___________.三、解答题5．已知数列{}n a 中11a =，)2n a n =≥.(1)求{}n a 的通项公式；(2)若21n n c a -=，数列1n c ⎧⎫⎨⎬⎩⎭的前n 项和为n T ，证明：21211n n n a T a +--<≤.6．已知数列{}n a 满足1222n n a a a a =-，*n N ∈．(1)证明：数列11n a ⎧⎫⎨⎬-⎩⎭是等差数列，并求数列{}n a 的通项公式；(2)记12n n T a a a =，*n N ∈，22212n n S T T T =++．证明：当*n N ∈时，11243n n S a +>-．7．已知函数()()3log 1(0)1x f x x x +=>+的图像上有一点列()()*,n n n P x y n N ∈，点n P 在x 轴上的射影是(),0n n Q x ，且(1322n n x x n -=+≥，且)*1,2n N x ∈=.(1)求证：{}1n x +是等比数列，并求数列{}n x 的通项公式；(2)对任意的正整数n ，当[]1,1m ∈-吋，不等式239181n y t mt <-+恒成立，求实数t 的取值范围；(3)设四边形11n n n n P Q Q P ++的面积是n T ，求证：1211132nT T nT +++<.8．已知正项数列{}n a 的首项11a =，前n 项和nS 满足)2n a n ≥. (1)求数列{}n a 的通项公式；(2)记数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为n T ，若对任意的*N n ∈，不等式24n T a a <-恒成立，求实数a 的取值范围.9．已知数列{}n a 满足11a =，且11n n a a n +-=+,n S 是1n a ⎧⎫⎨⎬⎩⎭的前n 项和.(1)求n S ；(2)若n T 为数列2n S n ⎧⎫⎪⎪⎛⎫⎨⎬ ⎪⎝⎭⎪⎪⎩⎭的前n 项和，求证：232n nT n >>+.10．已知数列{}n a 的前n 项和为n S ，11a =，22a =，且214n n n S S a ++=+． (1)求n a ；(2)求证：121112111n a a a +++<+++．11．已知数列{}n a 的前n 项和为n S ，13a =，24a =，()112322n n n S S S n +-+=-≥. (1)证明：数列{}2n a -是等比数列，并求数列{}n a 的通项公式；(2)记112n n n n b a a -+=，数列{}n b 的前n 项和为n T ，证明：11123n T≤<.12．证明：135212462n n -⨯⨯⨯⋯⨯13．已知数列{}n a 是等差数列，23a =，数列{}n b 是等比数列，18b =，公比3q >，且3q a =，2213b a a =.(1)求{}n a ，{}n b 的通项公式； (2)设24log n n n b c a =，n *∈N ，求证：1212nc c c ++⋅⋅⋅+<.14．已知各项为正的数列{}n a 满足：113a =，()*134N n n n a a n a +=∈+． (1)设0a >，若数列1log 1a n a ⎧⎫⎛⎫⎪⎪+⎨⎬ ⎪⎪⎪⎝⎭⎩⎭是公差为2的等差数列，求a 的值；(2)设数列1n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为n S ，证明4543n S n ≤<+．参考答案：1、 通项公式为： ()()⎪⎭⎫⎝⎛+--=+-=1211212112121n n n n a n2、通项公式为： ()⎪⎭⎫ ⎝⎛--=-<=≥n n n n n a n n 111111,22 3、通项公式为： ⎪⎭⎫ ⎝⎛+--=-<=≥111121111,222n n n n a n n 4、通项公式为： ⎪⎭⎫ ⎝⎛+--=-<==≥1211212144441,2222n n n n n a n n 5、通项公式为： ()⎪⎭⎫⎝⎛--=-<+-=-=≥n n n n n n n a n n 111414411441121,2222 6、通项公式为：()11111123121211221221121,2---++⋅=≤≤=-=-<-=≥n n n n n n n a a a n 7、通项公式为：11313231231--=⋅-<-=n n n n n n a 8、通项公式为：nn n n n nn n n n a n 2222,21<-+=-=≥+ 1．C 【详解】由1231n n S S n +=++，则当2n ≥时，得123(1)1n n S S n -=+-+， 两式相减得123n n a a +=+，变形可得：132(3)n n a a ++=+，又134a +=，122123116a a S S +==+⨯+=，所以25a =，2132(3)a a +=+， ∴数列{}3n a +是以4为首项、2为公比的等比数列，故113422n n n a -++=⨯=，所以2log (3)1n n c a n =+=+，所以2111116(16)(16)(1)17168172517n n c n n n c n n n n n n -===≤=++++++++， 当且仅当4n =时等号成立，故125k ≥.故选：C. 2．C 【详解】当2n ≥ 时，由1231n n S S n +=++可得-123-2n n S S n =+，两式相减得：123n n a a +=+ ，即132(3)n n a a ++=+，而134a +=，2121224,5a a S S a +==+=， 故2132(3)a a +=+ ，所以{3}n a + 是以134a +=为首项，2q为公比的等比数列，则11342,23n n n n a a -++=⨯=- ，故()122log 3log 21n n n c a n +=+==+，所以()111616(16)(1)17n n c n n c n n n n -==+++++，而16N ,8n n n*∈+≥ ，当且仅当4n = 时取等号， 故()11116162517n n c n c n n-=≤+++，当且仅当4n = 时取等号， 所以若存在常数k ，使不等式()116n n c k n c -≥+（*N n ∈）恒成立，则k 的最小值为125，故选：C 3．[)4,+∞【详解】由()1n n n n a a a +-=得11n n a n a n++=，则有 312412321234112321n n n n a a a a a n n a a a a a n n ----⨯⨯⨯⨯⨯=⨯⨯⨯⨯⨯--，化简得1n a n a =，即2n n a =， 所以1114114()1(1)122n n n n a a n n n n +===-+⋅++⨯， 所以111114(1)4(11)4223341111111n S n n n n n ---=-+-+-+++=-++<， 所以不等式n S t <恒成立，则有4t ≥.故答案为：[)4,+∞ 4．0【详解】由()12n n nS n S +=+，得()1()2n n n n S a n S ++=+， 即12n n na S +=，当1n =时，2122a S ==，21021a a -=；可知当2n ≥时，12n n na S +=，()112n n n a S --=， 两式相减整理，得101n na a n n，所以n a n ⎧⎫⎨⎬⎩⎭是以1为首项，0为公差的等差数列，所以1na n=，n a n =，所以()()21111211221221n n n n n n n a n a a n n n n ++++++==-⋅⋅+⋅⋅+，所以()12231111111()()()21222223221n n n T n n +=-+-+⋅⋅⋅+-⨯⨯⨯⨯⋅⋅+()111221n n +=-⋅+， ()110n n T λ++-⋅>等价于()()11111212n n n λ++-⋅>-⋅+；当n 是正奇数时，()111212n n λ+>-⋅+，因为()12111132122228n n +-≤-⨯=-⋅+，所以38λ>-； 当n 是正偶数时，()111221n n λ+<-⋅+，因为()1311111122122324n n +-≥-=⋅+⨯，所以1124λ<； 综上所述，λ的取值范围为311824λ-<<，则整数λ的值为0.故答案为：0. 5．(1)n a =证明见解析【解析】(1)将)2n a n =≥两边同时平方，整理得()22112n n a a n --=≥， 所以数列{}2n a 是首项为211a =，公差为1的等差数列，所以()2111n a n n =+-⨯=.由题知0n a >，所以n a(2)因为n a =21n n c a -==1n c =. 先证21n n T a -≤：当1n =时，11a =，11T =，满足21n n T a -≤； 当2n ≥时，1n c ==所以)(21112n n T n a -<++++-==.故21n n T a -≤得证.再证211n n T a+>-：因为1nc ==>=所以)(211211n n T n a +>++++==-.故不等式21211nn n a Ta +--<≤成立.【点睛】关键的点睛：本题考查等差数列的证明，以及放缩法证明不等式，本题的第二问的难点是对通项公式的放缩，放缩后，再进行裂项相消法求和，1n c==<=1n c ==>= 6．(1)证明见解析；()*12n n a n N n +=∈+(2)证明见解析 【解析】(1)当1n =时，1122a a =-，123a =，当2n ≥时，1222n n a a a a =-；121122n n a a a a --=- 相除得11(2)1n n n a a n a --=≥-，整理为：1111(2)111n n n n a n a a a -==-≥---，即1111(2)11n n n a a --=≥--， 11n a ⎧⎫∴⎨⎬-⎩⎭为等差数列，公差1d =，首项为1131a =-；所以()13121n n n a =+-=+-，整理为：()*12n n a n N n +=∈+，经检验，符合要求. (2)由（1）得：()*12n n a n N n +=∈+．1222n n T a a a n ==+， 2244114(2)(2)(3)23n T n n n n n ⎛⎫∴=>=- ⎪+++++⎝⎭，22212111112441342333n n S T T T n n n ⎛⎫⎛⎫∴=++>-++-=-- ⎪ ⎪+++⎝⎭⎝⎭，112224333n n n S a n ++∴>-=-+， 所以，当*n N ∈时，11243n n S a +>-．7．(1)证明见解析，31nn x =-(2)()(),22,∞∞--⋃+(3)证明见解析【解析】(1)因为2n ≥，且*1,32n n n N x x -∈=+，所以()1131n n x x -+=+，即1131n n x x -+=+（常数）； 因为113x +=，所以{}1n x +是首项为3，公比为3的等比数列，所以11333n n n x -+=⨯=，即31n n x =-；数列{}n x 的通项公式为31n n x =-.(2)由题可知()()3*log 10,1n n nn x y xn N x +=>∈+，由（1）可得3log 3033n n n n n y ==>，所以1113n ny n y n ++=<，即1n n y y +<，数列{}n y 为单调递减数列.所以n y 最大值为113y =；因为当[]1,1m ∈-吋，不等式239181n y t mt <-+恒成立，所以29180t mt ->恒成立.所以2291809180t t t t ⎧->⎨+>⎩，解得2t <-或2t >.所以t 的取值范围为()(),22,∞∞--⋃+.(3)四边形11n n n n P Q Q P ++的面积是()()114123n n n n n y y x x n T +++-+==.因为()()331134111n n n n n n ⎛⎫<=- ⎪+++⎝⎭，所以1211111111111313122233411n T T nT n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++<-+-+-++-=- ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦. 因为*n ∈N，所以13313311n n ⎛⎫-=-< ⎪++⎝⎭；所以121113.2nT T nT +++<8．(1)21n a n =-；(2)1a ≤-或2a ≥.【解析】(1)当2n ≥时，n a=∴1nn S S --=1=1=， 所以数列是首项为1，公差为1n ，又由n a 121n n n =+-=-（2n ≥），当1n =时，11a =也适合，所以21n a n =-. (2)∴()()()111111221212121n n a a n n n n +==--+-+，∴11111111111233521212212n T n n n ⎛⎫⎛⎫=-+-++-=-< ⎪ ⎪-++⎝⎭⎝⎭， 又∴对任意的*N n ∈，不等式24n T a a <-恒成立，，∴22a a ≤-，解得1a ≤-或2a ≥.即所求实数a 的范围是1a ≤-或2a ≥. 9．(1)21n nS n =+(2)证明见解析 【解析】(1)∴11n n a a n +-=+，∴212a a -=，323a a -=，…1n n a a n --= 由上述1n -个等式相加得12n a a n -=++，∴()1122n n n a a n +=+++=， ∴11121n a n n ⎛⎫=- ⎪+⎝⎭，11111122121223111n n S n n n n ⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪+++⎝⎭⎝⎭.(2)令()()22221441112n n S b n n n n n ⎛⎫⎛⎫⎛⎫===>⎪ ⎪ ⎪++++⎝⎭⎝⎭⎝⎭， ∴11111111244233412222n n T n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫>-+-++-=-= ⎪ ⎪ ⎪ ⎪⎢⎥++++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦， 又因为()22221411441111n n S b n n n n n n n ⎛⎫⎛⎫⎛⎫⎛⎫===<=- ⎪ ⎪ ⎪ ⎪++++⎝⎭⎝⎭⎝⎭⎝⎭，且11b =∴11111111414143323341211n T n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫<+-+-++-=+-=-< ⎪ ⎪ ⎪ ⎪⎢⎥+++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦，综上，232nn T n >>+，得证. 10．(1)()12n n a n -*=∈N (2)证明见解析【解析】(1)解：由214n n n S S a ++=+得24n n a a +=． 所以，当()21n k k *=-∈N 时，21214k k a a +-=，所以数列{}21k a -是首项为11a =，公比为4的等比数列， 故11211414k k k a a ---=⨯=⨯，即()211222122k k k a ----==． 当()2n k k *=∈N 时，则2224k k a a +=，所以，数列{}2k a 是首项为22a =，公比为4的等比数列，所以，1121224242k k k k a a ---=⨯=⨯=．所以()12n n a n -*=∈N ．(2)证明：由（1）知11111212n n n a --⎛⎫=< ⎪+⎝⎭，所以0121121111111111221111122221122nn n a a a -⎛⎫- ⎪⎛⎫⎛⎫⎛⎫⎛⎫⎝⎭+++<++++=<= ⎪ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭⎝⎭--.故原不等式成立.11．(1)证明见解析，122n n a -=+(2)证明见解析【解析】(1)解：当2n ≥时，由11232n n n S S S +-+=-可变形为()1122n n n n S S S S +--=--， 即122n n a a +=-，即()1222n n a a +-=-，所以()12222n n a n a +-=≥-，又因为13a =，24a =，可得1221,22a a -=-=，所以21222a a -=-，所以数列{}2n a -是以1为首项，2为公比的等比数列，所以122n n a --=，所以数列{}n a 的通项公式为122n n a -=+.(2)解：由122n n a -=+，可得()()11111221122222222n n n n nn n n n b a a ----+===-++++， 所以123n n T b b b b =+++⋅⋅⋅+1111111111134466102222322n n n-=-+-+-+⋅⋅⋅+-=-+++，因为1022n >+，所以1113223n -<+，即13n T <，又因为()11322n f n =-+，n *∈N 单调递增， 所以()()111212212n T b ≥==++，所以11123n T ≤<. 12．证明见解析 【详解】证明：212221n n n n -<+，∴135212452246235721n nn n -⨯⨯⨯⋯⨯<⨯⨯⨯⋯⨯+．213521135212421()()()24622462352121n n n n n n n --∴⨯⨯⨯⋯⨯<⨯⨯⨯⋯⨯⨯⨯⨯⋯⨯=++．∴135212462n n -⨯⨯⨯⋯⨯()f x x x -，x ∈当4π，∴cos cos 4x π>∴()10f x x '->()f x x x ∴-在上递增，()(0)0f x f ∴>=x x >，=∴综上：135212462n n -⨯⨯⨯⋯⨯< 13．(1)1n a n =+ ，212n n b +=(2)证明见解析【解析】(1)由题意，数列{}n a 是等差数列，23a =，数列{}n b 是等比数列，18b =，公比3q >， 设{}n a 的公差为d ，由()()23833q d q d d =+⎧⎪⎨=-⋅+⎪⎩可得()()()28333d d d +=-+，∴3d =-或1d =±，33q d =+>，∴1d =，∴4q =可得：()()223211n a a n d n n =+-=+-⨯=+, 11211842n n n n b b q --+==⨯=.(2)()()()()2124443log 2212221111n n n n c n n n n +++==<=++++ 且()()()3112n n n n +>++∴()()()()()21112112n c n n n n n n n <=-+++++∴()()()121111111122323341122n c c c n n n n ++⋅⋅⋅+<-+-+⋅⋅⋅+-<⨯⨯⨯⨯+++，故不等式得证. 14．(1)2(2)证明见解析 【解析】(1)因为()*134N n n n a a n a +=∈+，所以111141n n a a +⎛⎫+=+ ⎪⎝⎭等式两边同时取以a 为底的对数可得111log 1log 1log 4a a a n n a a +⎛⎫⎛⎫+=++⎪ ⎪⎝⎭⎝⎭，()*N n ∈又数列1log 1a n a ⎧⎫⎛⎫⎪⎪+⎨⎬ ⎪⎪⎪⎝⎭⎩⎭是公差为2的等差数列可知log 42a =，即2a =(2)由（1）可知数列11n a ⎧⎫+⎨⎬⎩⎭是公比为4的等比数列，可得11111414n n n a a -⎛⎫+=+= ⎪⎝⎭，可得数列{}n a 的通项公式为()*1N 14n n a n =∈- 记1n n n a b a +=可求得其通项公式为()1*4141N n n n b n +-=∈- 显然{}n b 为正项数列，因此()11*N 5n S S b n ≥==∈另一方面，构造数列{}n c 满足()*N 4n n c b n =-∈可得其通项公式为()*1N 34n n c n =∈- 注意到1113134414n n n n c ---⎛⎫=≤ ⎪⋅+-⎝⎭，记{}n c 的前n 项和为n T ，可得11441314n n T -≤<-， 而由于4n n c b =-，因此()*4N n n T S n n =-∈，从而443n S n <+，综上所述，4543n S n ≤<+.。

数列的裂项相消法
数列的裂项相消法是一种求和方法，适用于具有特定通项公式的数列。

该方法主要是通过将数列的每一项拆分成两个或多个部分，然后逐个部分进行相消，最终得到数列的和。

在裂项相消法中，首先要能裂项，即将通项an拆分成若干个部分；然后要把裂开的项给消掉，即在求和的过程中将它们相加或相减，以达到求和的目的。

裂项相消法可以应用于分母相乘型、根号型、对数型、指数型等多种形式的数列求和。

例如，对于形如an=1/n(n+1)的数列，可以通过裂项相消法求和。

具体来说，将每一项拆分成两个部分，即1/n和1/(n+1)，然后将它们相减得到1/n-1/(n+1)，再将所有项相加即可得到数列的和。

需要注意的是，裂项相消法虽然可以用于多种形式的数列求和，但在具体应用时需要针对不同的数列形式进行适当的调整。

同时，在应用该方法时也需要注意误差的把控，以避免因误差累积而影响最终结果的准确性。

裂项相消的解题思路如下：
1.分子拆分：将数列中的每一项分子拆分成两个因数的乘积，分
母保持不变。

例如，对于数列{1/(n(n+1))}，可以将每一项拆分为(1/n - 1/(n+1))，这样相邻两项的分子部分就可以相消。

2.分母拆分：将数列中的每一项分母拆分成两个因数的乘积，分
子保持不变。

例如，对于数列{n/(2n+1)(2n+3)}，可以将每一项拆分为(1/(2n+1) - 1/(2n+3))，这样相邻两项的分母部分就可以相消。

在应用裂项相消法时，需要注意以下几点：
1.找到合适的拆分方式，使得相邻两项能够相消。

2.正确处理剩余项，确保所有项都被考虑在内。

3.计算过程中要注意化简，避免出现复杂的计算过程。

常见裂项相消法公式一、等差型1.1a n a n +1=1d 1a n -1a n +1 1a n a n +2=12d 1a n -1a n +2 1a n a n +k=1kd 1a n -1a n +k 1n n +1=1n-1n +11+1n 2+1(n +1)2=[n (n +1)+1]2n 2(n +1)2=n (n +1)+1n (n +1)=1+1n -1n +11n n +k=1k 1n-1n +k 1n -1 n +1=121n -1-1n +1 12n -1 2n +1=1212n -1-12n +1 n22n +1 2n -1=2n242n +1 2n -1 =2n 2-1+142n +1 2n -1 =141+12n -1 2n +133n +1 3n +4=13n +1-13n +413n -2 3n +1=1313n -2-13n +1n n +1 =n (n +1)(n +2)-(n -1)n (n +1)3162n +1 2n +3 =2n +1 2n +3 2n +5 -2n -1 2n +1 2n +3 -1 n +12n +1 2n +3 =-1 n -2n 2-2n +12 --1 n +1-2n +1 2-2n +1 +12 二、根式型2.1n +k +n =1k n +k -n1n +1+n=n +1-nn +1+n n +1-n=n +1-n三、指数型3.a -1 ana n +b a n +1+b=1a n+b-1a n +1+b 4n4n -1 4n +1-1=1314n -1-14n +1-12×3n +13n -1 3n +1-1=313n -1-13n +1-1 2∙3n +13n +n 3n +1+n +1=13n +n -13n +1+n +12n +12n -1 2n +1-1=12n -1-12n +1-1四、对数型4.ba n +1a nlog =b a n +1log -b a n log 五、三角函数型5.1αcos βcos =1α-βsin αtan -βtan6.αtan βtan =1α-βtan αtan -βtan -1六、阶乘和组合数公式型7.n ×n !=n +1 !-n !8.n (n +1)!=1n !-1(n +1)!【解析】n (n +1)!=n +1-1(n +1)!=1n !-1(n +1)!试题(2022年全国高中数学联赛浙江赛区预赛)：已知数列a 1=1，a n =nn 2-1n ≥2 ，则nk =1a 1a 2⋯a k =21-1n +1 !.当n ≥2时，a n =n n 2-1=nn -1 n +1 ∴a 1a 2⋯a k =1×21×3×32×4×⋯×kk -1 k +1 =k !k -1 !k +1 !2=2k k +1 !=2k +1-1k +1 !=21k !-1k +1 !当n =1时，原式=21-12! =1当n ≥2时，原式=21-1n +1 !，综上所述，原式=21-1n +1 !9.n +2n !+n +1 !+n +2 !=1n +1 !-1n +2 !【解析】n +2n !+n +1 !+n +2 !=n +2n !1+n +1 +n +1 n +2 =n +2n !n 2+4n +4 =n +2n !n +22=1n !n +2 =n +1n +2 !=n +2 -1n +2 !=1n +1 !-1n +2 !10.C m -1n =C m n +1-C mn七、差比型a n 是等差数列，b n 是等比数列，设c n =a n ∙b n =kn +b ∙b 1q n -1=kb 1n +bb 1 q n -1因为kb 1n +bb 1是关于n 的一次式，于是，设c n =An +B q n -A n -1 +B q n -1=A q -1 n +q -1 B +A q n -1①由恒等式比较得A q -1 =kb 1q -1 B +A =bb 1，解得A =kb 1q -1，B =bq -b -kq -12②把A ，B 的值代入①各项相消即得“差比型数列”的前n 项和公式S n =c 1+c 2+c 3+⋯+c n =An +B q n -B ③其中A ，B 由②式确定.11.2018年浙江卷 b n +1-b n =4n -1 ⋅12n -1，即b n +1+16n +1 +122n +1=b n +16n +122n =b 1+16+122=15或者b n +1+8n +142n=b n +8n -1 +142n -1=b 1+141=1512.2020年浙江卷 b n 是等差数列：c n =b 1b 2b n b n +1=1+d d 1b n -1b n +1 =1+1d 1b n -1b n +1 13.2021年浙江卷 b n =(n -4)34n =3n -334 n -1-3n 34 n【解析】设b n =(n -4)34 n =a n -a n +1=A n -1 +B 34 n -1-An +B 34n=A n -1 +B 34 n -1×34×43-An +B 34n=43An -43A +43B -An -B 34 n =13An +13B -43A 34 n∴13A =113B -43A =-4A =3B =0∴b n =(n -4)34n =3n -3 34n -1-3n 34nS n =b 1+b 2+⋯+b n =a 1-a 2+a 2-a 3+⋯+a n -a n +1=a 1-a n +1=B -An +B 34 n =-3n 34n14.2n -1 -13n=12n +18-13n-12n -1 +18 -13n -1八、混合型15.1n n +1 n +2 =121n n +1 -1n +1 n +21n n 2-1=121n -1 n-1n n +116.2n +1n 2n +1 2=1n 2-1n +1 217.n ∙2nn +1 n +2 =2n +1n +2-2nn +118.3n -2 2n -1n n +2 =122n +2n +2-2n n19.n +2n n +1 2n -2=2n +1 -n n n +1 2n -2=1n ∙2n -3-1n +1 2n -220.n +2n n +1 2n=2n +1 -n n n +1 2n =1n ∙2n -1-1n +1 2n21.n +2n n +1 2n +1=2n +1 -n n n +1 2n +1=1n ∙2n -1n +1 2n +122.n 2+2n +2n n +1 2n +1=n +1 2+1n n +1 2n +1=12n +1+1n ∙2n -1n +1 ∙2n +1 23.n +42n +1∙n ∙n +1 ∙n +2 =1n +1∙n +42n +1∙n ∙n +2=12n∙n ∙n +1-12n +1∙n +1 ∙n +2 24.4n -n 22n=12n n 2-2n -1 2+2=n 22n -n -1 22n -1 +12n -125.-1 n ×4n2n -1 2n +1=-1 n×12n -1+12n +1 =-1 n 2n -1--1 n +12n +126.-1 n +1×4n +42n +1 2n +3=-1n +112n +1+12n +3=-1n +12n +1--1n +22n +327.-1 n +13n 8n -2 2n -1 2n +1=-1 n +13n 2n -1+3n +12n +1 =-1 n +13n +12n +1--1 n 3n 2n -128.3n +2n n +1 -2n +1=-1 n +11n ∙2n +1n +1 2n +1=1n +1 -2n +1-1n ∙-2 n29.3n +2-1 n -1n n +1 2n +1=-1 n -11n ∙2n +1n +1 2n +1=3n +2 -2n-1n -1n ∙2n -1 n n +1 2n +1=1-1 n -1n ∙2n -1-1 n n +1 2n +1。

差比数列求和裂项相消差比数列是一种数列,其中的每一项都是前两项的差或比。

差比数列的通项公式可以用来求出数列的前几项和。

差比数列求和裂项相消法是一种求差比数列和的方法,它通过将数列的前几项相加,并使用裂项公式求出数列的通项公式,然后使用通项公式求出数列的和。

举个例子,假设我们要求的是以2为公差的等差数列的前5项和。

我们可以将数列的前几项相加,得到：2 + 4 + 6 + 8 + 10 = 30然后使用裂项公式求出数列的通项公式,即：a + (n-1)d = 30其中a是数列的第一项,n是数列的项数,d是数列的公差。

在这个例子中,a=2,n=5,d=2。

将这些值代入公式中得到：2 + (5-1)2 = 30解得：2 + 8 = 3010 = 30显然,这个结果是不正确的,说明我们没有正确地求出数列的通项公式。

总之,差比数列求和裂项相消法是一种求差比数列和的方法,它通过将数列的前几项相加,并使用裂项公式求出数列的通项公式,然后使用通项公式求出数列的通项公式来求出数列的和。

差比数列的通项公式为：S = (a1 + an) * n / 2其中S是数列的和,a1是数列的第一项,an是数列的最后一项,n是数列的项数。

在这个例子中,a1=2,an=10,n=5。

将这些值代入公式中得到：S = (2 + 10) * 5 / 2S = 12 * 5 / 2S = 60 / 2S = 30这样我们就正确地求出了以2为公差的等差数列的前5项和。

总之,差比数列的通项公式是一种有效的求数列和的方法,它可以帮助我们快速求出数列的和,而无需手动求和。