2014广州越秀区初三数学一模试卷

2014学年第一学期学业水平调研测试九年级数学试卷答案二、填空题（本题共有6题，每小题3分，共18分）11．3 ；12．8 ；13．57°；14．4 ；15．x1＜x2＜x3；16．④．17．解：由x（x∴x∴x18．解：（1（2（319．∴又∴OC＝4，OD⊥AB，∴OD=，……………………7分在Rt△OBD中AD＝6，OD＝，∴OA=……………………10分（1）解法1：可画树状图如下：共6解法2（28分10分21．解：（1（2（3解：设该市7月份、8月份95号汽油月平均降价率为x，则8.45（1－x）2＝8.45－0.21－0.16 ，……………………6分化简得（1－x）2＝808 845，解得x≈1.9779或x≈0.0221 ，……………………10分∵x＜1，∴x≈0.0221＝2.21% ……………………11分答：该市7月份、8月份95号汽油月平均降价率约为2.21%．……………………12分23．解：（1（2……………………12分24．解：（1∴－4a＝－2 ，∴a＝12，……………………2分∴y＝12x2＋32x－2 ；……………………3分（2）如图所示：连接P A、PB、PC，因为点P在抛物线的对称轴上，∴PB＝P A，x p＝32-，……………………4分∴PB＋PC＝P A＋PC，∵当点P在直线AC上时P A＋PC的值最小，∴PB ＋PC ＝P A ＋PC ≥AC ， ……………………5分 由抛物线解析式y ＝12x 2＋32x －2得 A （－4，0），B （1，0） ， 又∵C （0，－2），∴AC 的解析式为y ＝－12x －2， ∵x p ＝－32， ∴yp ＝－54， ……………………7分∴当点P 的坐标为（－32，－54）时，PB ＋PC 的值最小；（3① ② ∴线段MN 可以看成由线段AC 平移得到， ∴y N －y A ＝y M －y C ， ∴y N ＝2 ， ∵y ＝12x 2＋32x －2 ， ∴12x 2＋32x －2＝2 ， 解得x ， ∴点N 有两种可能： N 2，2），如图2所示……………………12分N 3（32-，2），如图3所示……………………14分③ CM 为对角线时AM ∥CN ，易得点N 4（－3，－2）与点N 1重合，如图4所示，N1）．25．（1（2∵∴∴∴∴∠EBD ＝∠DBF ＝∠HBG ＝22.5°，………………5分 ∴∠EBG ＝67.5°， 又∵∠EGB ＝90°，∴∠BEG ＝22.5°＝∠HBG ， ………………6分∴»BG＝¼GH ； ……………………7分（3）如图3所示，将△BCF绕点B逆时针旋转90°到△BAP，过点B作BQ⊥EF，设圆O与CD相切于点M，连接OM，延长MO交AB于点N，在△BPE与△BFE中，BP＝BF，∠PBE＝∠EBF＝45°，BE＝BE，∴△BPE≌△BEF，∴∠AEB＝∠BEQ，①……………………8分PE＝EF，②……………………9分由①∠AEB＝∠BEQ可知，在△∠BAE∴△∴BQ由②C△EFD设AE∵O为又BE分又C△在Rt△∴EF∴S△1414。

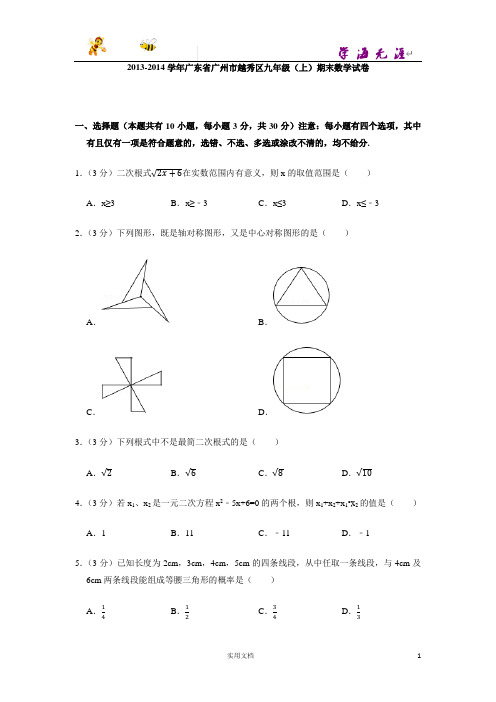
2013-2014学年广东省广州市越秀区九年级（上）期末数学试卷一、选择题（本题共有10小题，每小题3分，共30分）注意：每小题有四个选项，其中有且仅有一项是符合题意的，选错、不选、多选或涂改不清的，均不给分.1．（3分）二次根式√2x+6在实数范围内有意义，则x的取值范围是（）A．x≥3 B．x≥﹣3 C．x≤3 D．x≤﹣32．（3分）下列图形，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．3．（3分）下列根式中不是最简二次根式的是（）A．√2B．√6C．√8D．√104．（3分）若x1、x2是一元二次方程x2﹣5x+6=0的两个根，则x1+x2+x1•x2的值是（）A．1 B．11 C．﹣11 D．﹣15．（3分）已知长度为2cm，3cm，4cm，5cm的四条线段，从中任取一条线段，与4cm及6cm两条线段能组成等腰三角形的概率是（）A．14B．12C．34D．136．（3分）用配方法解方程x2﹣2x﹣5=0时，原方程应变形为（）A．（x+1）2=6 B．（x﹣1）2=6 C．（x+2）2=9 D．（x﹣2）2=97．（3分）在一个暗箱里放有a个除颜色外其它完全相同的球，这a个球中红球只有3个．每次将球搅拌均匀后，任意摸出一个球记下颜色再放回暗箱．通过大量重复摸球实验后发现，摸到红球的频率稳定在25%，那么可以推算出a大约是（）A．12 B．9 C．4 D．38．（3分）如图所示，⊙O1、⊙O2的圆心O1、O2在直线l上，⊙O1的半径为2，⊙O2的半径为3，O1O2=8，⊙O1以每秒1个单位的速度沿直线l向右平移运动，7秒后停止运动，此时⊙O1与⊙O2的位置关系是（）A．外切B．相交C．内切D．内含9．（3分）如图，已知扇形AOB的半径为6cm，圆心角的度数为120°，若将此扇形围成一个圆锥，则围成的圆锥的侧面积为（）A．4πcm2B．6πcm2C．9πcm2D．12πcm210．（3分）抛物线y=ax2+bx+c（a＞0）和直线y=mx+n（m≠0）相交于两点P（﹣1，2），Q （3，5），则不等式﹣ax2+mx+n＞bx+c的解集是（）A．x＜﹣1 B．x＞3 C．﹣1＜x＜3 D．x＜﹣1或x＞3二、填空题（本题共有6小题，每小题3分，共18分）11．（3分）已知|a+1|+√8−b=0，则a﹣b=．12．（3分）如图，⊙O的直径CD=10，弦AB=8，AB⊥CD，垂足为M，则DM的长为．13．（3分）如图，一个圆形转盘被分成八个扇形区域，上面分别标有数字1、2、3、4，转盘指针的位置固定，转动转盘后任其自由停止．转动转盘一次，当转盘停止转动时，记指针指向标有“3”所在区域的概率为P（3），指针标向标有“4”所在区域的概率为P（4），则P（3）P（4）（填“＞”、“=”或“＜”）14．（3分）某地区2012年农民人均收入为1万元，计划到2014年农民人均收入增加到1.2万元．设农民人均年收入的每年平均增长率为x，则可列方程．15．（3分）抛物线y=﹣2（x﹣1）2+5向左平移2个单位，再向下平移1个单位后得到的抛物线解析式是．16．（3分）如图，等边△ABC在直角坐标系xOy中，已知A（2，0），B（﹣2，0），点C 绕点A顺时针方向旋转120°得到点C1，点C1绕点B顺时针方向旋转120°得到C2，点C2绕点C顺时针方向旋转150°得到点C3，则点C3的坐标是．三.解答题（本大题有9小题，满分102分．解答题应写出必要的文字说明.演算步骤或证明过程）.；17．（9分）（1）计算√2(√2+1)−√8+√43（2）若a＞1，化简√(1−a)2−√a2．18．（9分）解方程：x（x+1）=3x+3．19．（10分）如图，AB是⊙O的直径，∠CAB=∠DAB．求证：AC=AD．20．（10分）在一个口袋中有5个球，其中2个是白球，其余为红球，这些球的形状、大小、质地等完全相同，在看不到球的条件下，从袋中随机地取出一个球．（1）求取出一个球是红的概率；（2）把这5个小球中的两个标号为1，其余分别标号为2，3，4，随机地取出一个小球后不放回，再随机地取出一个小球，求第二次取出小球标号大于第一次取出小球标号的概率．21．（12分）已知关于x的一元二次方程x2+2kx+k2﹣k=0有两个不相等的实数根．（1）求实数k的取值范围；（2）0可能是方程一个根吗？若是，求出它的另一个根；若不是，请说明理由．22．（12分）如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC=CD，∠ACD=120°．（1）求证：CD是⊙O的切线；（2）若⊙O的半径为2，求图中阴影部分的面积．23．（12分）如图，一架长2.5米的梯子AB斜靠在竖直的墙AC上，这时B到墙AC的距离为0.7米．（1）若梯子的顶端A沿墙AC下滑0.9米至A1处，求点B向外移动的距离BB1的长；（2）若梯子从顶端A处沿墙AC下滑的距离是点B向外移动的距离的一半，试求梯子沿墙AC下滑的距离是多少米？2013-2014学年广东省广州市越秀区九年级（上）期末数学试卷参考答案与试题解析一、选择题（本题共有10小题，每小题3分，共30分）注意：每小题有四个选项，其中有且仅有一项是符合题意的，选错、不选、多选或涂改不清的，均不给分.1．（3分）二次根式√2x+6在实数范围内有意义，则x的取值范围是（）A．x≥3 B．x≥﹣3 C．x≤3 D．x≤﹣3【解答】解：∵二次根式√2x+6在实数范围内有意义，∴2x+6≥0，解得x≥﹣3．故选：B．2．（3分）下列图形，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．【解答】解：A、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，也不是轴对称图形，故此选项错误；B、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项错误；C、此图形旋转180°后能与原图形重合，此图形是中心对称图形，不是轴对称图形，故此选项错误；D、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，也是轴对称图形，故此选项正确．故选：D．3．（3分）下列根式中不是最简二次根式的是（）A．√2B．√6C．√8D．√10【解答】解：各选项中只有选项C、√8=2√2，不是最简二次根式，故选：C．4．（3分）若x1、x2是一元二次方程x2﹣5x+6=0的两个根，则x1+x2+x1•x2的值是（）A．1 B．11 C．﹣11 D．﹣1【解答】解：根据题意得x1+x2=5，x1x2=6，所以x1+x2+x1•x2=5+6=11．故选：B．5．（3分）已知长度为2cm，3cm，4cm，5cm的四条线段，从中任取一条线段，与4cm及6cm两条线段能组成等腰三角形的概率是（）A．14B．12C．34D．13【解答】解：∵长度为2cm，3cm，4cm，5cm的四条线段，从中任取一条线段，共有4种等可能的结果，且与4cm及6cm两条线段能组成等腰三角形的有1种情况，∴与4cm及6cm两条线段能组成等腰三角形的概率是：14．故选：A．6．（3分）用配方法解方程x2﹣2x﹣5=0时，原方程应变形为（）A．（x+1）2=6 B．（x﹣1）2=6 C．（x+2）2=9 D．（x﹣2）2=9【解答】解：方程移项得：x2﹣2x=5，配方得：x2﹣2x+1=6，即（x﹣1）2=6．故选：B．7．（3分）在一个暗箱里放有a个除颜色外其它完全相同的球，这a个球中红球只有3个．每次将球搅拌均匀后，任意摸出一个球记下颜色再放回暗箱．通过大量重复摸球实验后发现，摸到红球的频率稳定在25%，那么可以推算出a大约是（）A．12 B．9 C．4 D．3【解答】解：∵摸到红球的频率稳定在25%，∴3=25%，a解得：a=12．故选：A．8．（3分）如图所示，⊙O1、⊙O2的圆心O1、O2在直线l上，⊙O1的半径为2，⊙O2的半径为3，O1O2=8，⊙O1以每秒1个单位的速度沿直线l向右平移运动，7秒后停止运动，此时⊙O1与⊙O2的位置关系是（）A．外切B．相交C．内切D．内含【解答】解：∵⊙O 1以每秒1个单位的速度沿直线l 向右平移运动，7秒后停止运动，O 1O 2=8， ∴运动后O 1O 2=8﹣7=1，∵⊙O 1的半径为2，⊙O 2的半径为3，∴半径差为：3﹣2=1，∴⊙O 1与⊙O 2的位置关系是：内切．故选：C ．9．（3分）如图，已知扇形AOB 的半径为6cm ，圆心角的度数为120°，若将此扇形围成一个圆锥，则围成的圆锥的侧面积为（ ）A ．4πcm 2B ．6πcm 2C ．9πcm 2D ．12πcm 2 【解答】解：圆锥的侧面积=120π×62360=12πcm 2，故选D ．10．（3分）抛物线y=ax 2+bx+c （a ＞0）和直线y=mx+n （m ≠0）相交于两点P （﹣1，2），Q（3，5），则不等式﹣ax 2+mx+n ＞bx+c 的解集是（ ）A ．x ＜﹣1B ．x ＞3C ．﹣1＜x ＜3D ．x ＜﹣1或x ＞3【解答】解：由不等式﹣ax 2+mx+n ＞bx+c 得mx+n ＞ax 2+bx+c ，∵两函数图象交点为P （﹣1，2），Q （3，5），a ＞0，∴不等式的解集是﹣1＜x ＜3．故选：C ．二、填空题（本题共有6小题，每小题3分，共18分）11．（3分）已知|a+1|+√8−b=0，则a﹣b=﹣9．【解答】解：∵|a+1|+√8−b=0，∴|a+1|=0，8﹣b=0，∴a=﹣1，b=8．则a﹣b=﹣1﹣8=﹣9．故答案为：﹣9．12．（3分）如图，⊙O的直径CD=10，弦AB=8，AB⊥CD，垂足为M，则DM的长为8．【解答】解：连接OA，∵AB⊥CD，AB=8，AB=4，∴根据垂径定理可知AM=12在Rt△OAM中，OM=√OA2−AM2=√52−42=3，∴DM=OD+OM=8．故答案为：8．13．（3分）如图，一个圆形转盘被分成八个扇形区域，上面分别标有数字1、2、3、4，转盘指针的位置固定，转动转盘后任其自由停止．转动转盘一次，当转盘停止转动时，记指针指向标有“3”所在区域的概率为P （3），指针标向标有“4”所在区域的概率为P （4），则P （3） ＞ P （4）（填“＞”、“=”或“＜”）【解答】解：∵一个圆形转盘被等分成八个扇形区域，“3”有三个区域，“4”有两个区域，∴P （3）=38，P （4）=28，所以P （3）＞P （4）． 故答案为：＞．14．（3分）某地区2012年农民人均收入为1万元，计划到2014年农民人均收入增加到1.2万元．设农民人均年收入的每年平均增长率为x ，则可列方程 （1+x ）2=1.2 ． 【解答】解：设人均年收入的平均增长率为x ，根据题意可列出方程为：（1+x ）2=1.2． 故答案为：（1+x ）2=1.2．15．（3分）抛物线y=﹣2（x ﹣1）2+5向左平移2个单位，再向下平移1个单位后得到的抛物线解析式是 y=﹣2（x+1）2+4 ．【解答】解：∵抛物线y=﹣2（x ﹣1）2+5的顶点坐标为（1，5）， ∴向左平移2个单位，再向下平移1个单位后， ∴1﹣2=﹣1，5﹣1=4，故平移后的抛物线的顶点坐标为（﹣1，4），∴所得抛物线解析式是y=﹣2（x+1）2+4．故答案为：y=﹣2（x+1）2+4．16．（3分）如图，等边△ABC在直角坐标系xOy中，已知A（2，0），B（﹣2，0），点C 绕点A顺时针方向旋转120°得到点C1，点C1绕点B顺时针方向旋转120°得到C2，点C2绕点C顺时针方向旋转150°得到点C3，则点C3的坐标是（0，12+2√3）．【解答】解：∵△ABC为等边三角形，∴CA=CB=AB=4，∠CAB=∠CBA=∠BCA=60°，∴∠BCO=30°，OC=√3OB=2√3，∵点C绕点A顺时针方向旋转120°得到点C1，∴点C1在BA的延长线上，且AC1=4，∵点C1绕点B顺时针方向旋转120°得到C2，∴点C2在CB的延长线上，且BC2=8，∵点C2绕点C顺时针方向旋转150°得到点C3，∴点C3在y轴的正半轴上，且CC3=12，∴点C3的坐标是（0，12+2√3）．故答案为（0，12+2√3）．三.解答题（本大题有9小题，满分102分．解答题应写出必要的文字说明.演算步骤或证明过程）.；17．（9分）（1）计算√2(√2+1)−√8+√43（2）若a＞1，化简√(1−a)2−√a2．√3【解答】解：（1）原式=2+√2﹣2√2+23√3．=2﹣√2+23（2）∵a＞1，∴√(1−a)2﹣√a2=|1﹣a|﹣|a|=a﹣1﹣a=﹣1．18．（9分）解方程：x（x+1）=3x+3．【解答】解：方程移项得：x（x+1）﹣3（x+1）=0，分解因式得：（x﹣3）（x+1）=0，可得x﹣3=0或x+1=0，解得：x1=3，x2=﹣1．19．（10分）如图，AB是⊙O的直径，∠CAB=∠DAB．求证：AC=AD．【解答】证明：如图，∵AB 是⊙O 的直径， ∴ACB̂=ADB ̂． 又∵∠CAB=∠DAB ， ∴BĈ=BD ̂， ∴ACB ̂﹣BC ̂=ADB ̂﹣BD ̂，即AC ̂=AD ̂， ∴AC=AD ．20．（10分）在一个口袋中有5个球，其中2个是白球，其余为红球，这些球的形状、大小、质地等完全相同，在看不到球的条件下，从袋中随机地取出一个球． （1）求取出一个球是红的概率；（2）把这5个小球中的两个标号为1，其余分别标号为2，3，4，随机地取出一个小球后不放回，再随机地取出一个小球，求第二次取出小球标号大于第一次取出小球标号的概率． 【解答】解：（1）∵在一个口袋中有5个球，其中2个是白球，其余为红球，∴取出一个球是红的概率为：5−25=35；（2）画树状图得：∵共有20种等可能的结果，第二次取出小球标号大于第一次取出小球标号的有9种情况，．∴第二次取出小球标号大于第一次取出小球标号的概率为：92021．（12分）已知关于x的一元二次方程x2+2kx+k2﹣k=0有两个不相等的实数根．（1）求实数k的取值范围；（2）0可能是方程一个根吗？若是，求出它的另一个根；若不是，请说明理由．【解答】解：（1）∵关于x的一元二次方程x2+2kx+k2﹣k=0有两个不相等的实数根，∴△=b2﹣4ac=（2k）2﹣4（k2﹣k）=4k＞0，∴k＞0，∴实数k的取值范围是k＞0．（2）把x=0代入方程得：k2﹣k=0，解得：k=0，k=1，∵k＞0，∴k=1，即0是方程的一个根，把k=1代入方程得：x2+2x=0，解得：x=0，x=﹣2， 即方程的另一个根为x=﹣2．22．（12分）如图，点D 在⊙O 的直径AB 的延长线上，点C 在⊙O 上，AC=CD ，∠ACD=120°． （1）求证：CD 是⊙O 的切线；（2）若⊙O 的半径为2，求图中阴影部分的面积．【解答】（1）证明：连接OC ． ∵AC=CD ，∠ACD=120°， ∴∠A=∠D=30°． ∵OA=OC ， ∴∠2=∠A=30°．∴∠OCD=180°﹣∠A ﹣∠D ﹣∠2=90°．即OC ⊥CD ， ∴CD 是⊙O 的切线．（2）解：∵∠A=30°， ∴∠1=2∠A=60°．∴S 扇形BOC =60π×22360=2π3．在Rt △OCD 中，∵ππππ=πππ60°，∴ππ=2√3．∴πππ△πππ=12ππ×ππ=12×2×2√3=2√3．∴图中阴影部分的面积为：2√3−2π3．23．（12分）如图，一架长2.5米的梯子AB斜靠在竖直的墙AC上，这时B到墙AC的距离为0.7米．（1）若梯子的顶端A沿墙AC下滑0.9米至A1处，求点B向外移动的距离BB1的长；（2）若梯子从顶端A处沿墙AC下滑的距离是点B向外移动的距离的一半，试求梯子沿墙AC下滑的距离是多少米？【解答】解：（1）∵AB=2.5m，BC=O.7m，∴AC=√2．52−0．72=2.4m∴A1C=AC﹣AA1=2.4﹣0.9=1.5m，∴B1C=√2．52−1．52=2m，∴BB1=B1C﹣BC=1.3（m）；（2）梯子从顶端A处沿墙AC下滑的距离是x，则点B向外移动的距离的一半为2x，由勾股定理得：（2.4﹣x）2+（0.7+2x）2=2.52，，解得：x=32答：梯子沿墙AC下滑的距离是3米．224．（14分）如图，AB是⊙O的直径，ππ=6√2，M是弧AB的中点，OC⊥OD，△COD 绕点O旋转与△AMB的两边分别交于E、F（点E、F与点A、B、M均不重合），与⊙O 分别交于P、Q两点．（1）求证：OE=OF；（2）连接PM、QM，试探究：在△COD绕点O旋转的过程中，∠PMQ是否为定值？若是，求出∠PMQ的大小；若不是，请说明理由；（3）连接EF，试探究：在△COD绕点O旋转的过程中，△EFM的周长是否存在最小值？若存在，求出其最小值；若不存在，请说明理由．【解答】（1）证明：∵AB是⊙O的直径，∴∠AMB=90°，∵M是弧AB的中点，∴弧MB=弧MA，∴MA=MB，∴△AMB 为等腰直角三角形，∴∠ABM=∠BAM=45°，∠OMA=45°，OM ⊥AB ，MB=√22AB=√22×6√2=6，∴∠MOE+∠BOE=90°， ∵∠COD=90°， ∴∠MOE+∠MOF=90°， ∴∠BOE=∠MOF ， 在△OBE 和△OMF 中， {ππ=ππππππ=ππππππππ=ππππ， ∴△OBE ≌△OMF （AAS ）， ∴OE=OF ；（2）解：∠PMQ 为定值．∵∠BMQ=12∠BOQ ，∠AMP=12∠AOP ， ∴∠BMQ+∠AMP=12（∠BOQ+∠AOP ）， ∵∠COD=90°， ∴∠BOQ+∠AOP=90°，∴∠BMQ+∠AMP=12×90°=45°，∴∠PMQ=∠BMQ+∠AMB+∠AMP=45°+90°=135°；（3）解：△EFM 的周长有最小值． ∵OE=OF ，∴△OEF 为等腰直角三角形，∴EF=√2OE ， ∵△OBE ≌△OMF ， ∴BE=MF ，∴△EFM 的周长=EF+MF+ME =EF+BE+ME =EF+MB =√2OE+6，当OE ⊥BM 时，OE 最小，此时OE=12BM=12×6=3，∴△EFM 的周长的最小值为3√2+6．25．（14分）平面直角坐标系xOy 中，抛物线y=ax 2﹣4ax+4a+c 与x 轴交于点A 、B ，与y 轴的正半轴交于点C ，点A 的坐标为（1，0），OB=OC ． （1）求此抛物线的解析式；（2）若点P 是线段BC 上的一个动点，过点P 作y 轴的平行线与抛物线在x 轴下方交于点Q ，试问线段PQ 的长度是否存在最大值？若存在，求出其最大值；若不存在，请说明理由；（3）若此抛物线的对称轴上的点M 满足∠AMC=45°，求点M 的坐标．【解答】解：（1）抛物线的对称轴为直线x=﹣−4π2π=2，∵点A （1，0），∴点B 的坐标为（3，0），∵点C 在y 轴的正半轴，OB=OC ，∴点C 的坐标为（0，3），∴{π−4π+4π+π=04π+π=3，解得{π=1π=−1，∴此抛物线的解析式y=x 2﹣4x+3；（2）设直线BC 的解析式为y=kx+b （k ≠0），则{3π+π=0π=3，解得{π=−1π=3，∴直线BC 的解析式为y=﹣x+3，∴PQ=（﹣x+3）﹣（x 2﹣4x+3）=﹣x 2+3x=﹣（x ﹣32）2+94，∵点Q 在x 轴下方，∴1＜x ＜3，又∵﹣1＜0，∴当x=32时，PQ 的长度有最大值94；（3）如图，设△ABC 的外接圆的圆心D ，则点D 在对称性直线x=2上，也在直线BC 的垂直平分线y=x 上， ∴点D 的坐标为（2，2），∴外接圆的半径为√(3−2)2+22=√5，∵OB=OC ，∴∠ABC=45°，∴∠AMC=45°时，点M 为⊙D 与对称轴的交点，点M 在点D 的下方时，M 1（2，2﹣√5），点M 在点D 的上方时，M 2（2，2+√5），综上所述，M （2，2﹣√5）或（2，2+√5）时，抛物线的对称轴上的点M 满足∠AMC=45°．。

2014学年越秀区第一学期学业水平调研测试九年级数学试卷注意：1．考试时间为120分钟．满分150分．2．试卷分为Ⅰ卷（选择题）与Ⅱ卷（非选择题）两部分．3．可以试用规定型号的计算器．4．所有试题答案必须写在答题卷相应的位置上，否则不给分．第Ⅰ卷 选择题（共30分）一、选择题（本题共有10小题，每小题3分，共30分）1．关于x 的方程()03212=-++mx x m 是一元二次方程，则m 的取值范围是（ ）．A ．任意实数B ．m ≠1C ．m ≠－1D ．m ＞－12．点P （4，－3）关于原点的对称点是（ ）．A ．（4，3）B ．（－3，4）C ．（－4，3）D ．（3，－4）3．抛物线1)2(212++=x y 的顶点坐标是（ ）． A ．（2，1） B ．（－2，1） C ．（2，－1） D ．（－2，－1）4．下列平面图形中，既是轴对称图形，又是中心对称图形的是（ ）．A ．B ．C ．D ．5．函数xy 31-=的图象与坐标轴的交点个数是（ ）． A ．0个 B ．1个 C ．2个 D ．3个6．下列说法正确的是（ ）．A.在同一年出生的367名学生中，至少有两人的生日是同一天．B.彩票中奖的机会是1%，那么买100张彩票一定会中奖．C.天气预报说明天下雨的概率是50%，所以明天一半的时间下雨．D.抛掷一枚图钉，钉尖着地和钉尖朝上的概率一样大．7．把抛物线22x y =先向左平移3个单位，再向上平移4个单位，所得抛物线的函数表达式是（ ）．A ．4)3(22++=x yB ．4)3(22-+=x yC ．4)3(22--=x yD ．4)3(22+-=x y8．用配方法解方程0522=--x x 时，原方程应变形为（ ）．A ．()612=+xB ．()612=-xC ．()922=+xD ．()922=-x9．如图1，AB 与⊙O 相切于点B ，OA =2，∠OAB =30°，弦BC ∥OA ，则劣弧BC 的弧长是（ ）．A ．2π B ．3π C ．4π D ．6π10．如图2所示是一个直角三角形的苗圃，由一个正方形花坛和两块直角三角形的草皮组成．如果两个直角三角形的两条斜边长分别为3米和6米，则草皮的总面积为（ ）平方米．A ．6B ．9C ．18D ．无法确定第Ⅱ卷 非选择题（共120分）二、填空题（本题共有6小题，每小题3分，共18分）11．若21,x x 是一元二次方程0132=--x x 的两个根，则21,x x 的值是__________．12．在一个不透明的布袋中装有2个白球和n 个黄球，它们除颜色不同外，其余均相同，若从中随机摸出一个球，摸到黄球的概率是54，则n =__________． 13．如图3，△COD 是△AOB 绕点O 顺时针方向旋转38°后所得的图形，点C 恰好在AB 上，∠AOD =90°，则∠B 的度数是__________．14．若圆锥的侧面面积是12πcm 2，它的底面半径为3cm ，则此圆锥的母线长是_________cm ． 15．若点)3,()2,()1,(321-x C x B x A 、、在双曲线xy 1-=上，则321x x x 、、的大小关系是__________（用“<”连接起来）．16．二次函数c bx ax y ++=2的图象如图4所示，则①abc ，②b 2－4ac ，③2a +b ，④a +b +c 这四个式子中，值为负数的是__________（填写编号）．图1 图 2图3三、解答题（本大题有9小题，满分102分．解答题应写出必要的文字说明．演算步骤或证明过程）．17．（本小题满分9分）解方程09102=++x x ．18．（本小题满分9分）如图5，在边长为1的正方形组成的网格中，△AOB 的顶点均在格点上，点A 、B 的坐标分别是A （3，2）、B （1，3）．△AOB 绕点O 逆时针旋转90°后得到△11OB A ．（1）画出旋转后的图形．（2）点A 1的坐标为___________．（3）求线段OB 在旋转过程中所扫过的图形面积（写过程）．19．（本小题满分10分）如图6，已知AB 是⊙O 的弦，点C 在线段AB 上，OC =AC =4，CB =8，求⊙O 的半径．20．（本小题满分10分）有红、白、蓝三种颜色的小球各一个，它们除颜色外没有任何区别．现将3个小球放入编号为①、②、③的三个盒子里，规定每个盒子放一个且只能放一个小球．（1）请用树状图或其它适当的形式列举出3个小球放入盒子的所有可能情况；（2）求红球恰好被放入②号盒子的概率．21．（本小题满分12分）二次函数)0(2≠++=a c bx ax y 的图象如图7所示，根据图象解答下列问题：（1）写出方程02=++c bx ax 的两个根；（2）写出不等式02>++c bx ax 的解集；（3）求y 的取值范围．22．（本小题满分12分）2014年以来，全国成品油价格经历了多次调整．已知某市2014年6月30日95号汽油每升价格为8.45元，7月份95号汽油每升下调0.21元，8月份95号汽油每升价格再下调0.16元．试问该市7月份、8月份95号汽油月平均降价率是多少？（结果精确到0.01%）图4图5 图6 图723．（本小题满分12分）如图8，已知一次函数)0(≠+=k b kx y 的图象与x 轴、y 轴分别交于A 、B 两点，且与反比例函数)0(≠=m xm y 的图象交于C 、D 两点，若OA =OB =1．（1）求一次函数的解析式； （2）若)(,)(2,21,1y x D y x C ，且321-=⋅x x ，求反比例函数的解析式．24．（本小题满分14分）如图9，抛物线a ax x y 43212-+=与x 轴交于A 、B 两点，与y 轴交于点C （0，－2）．（1）求该抛物线的解析式；（2）在抛物线的对称轴上有一动点P ，求PB +PC 的值最小时的点P 的坐标；（3）点M 为x 轴上一动点，在抛物线上是否存在一点N ，使以A 、C 、M 、N 四点为顶点构成的四边形为平行四边形？若存在，求出所有点N 的坐标；若不存在，请说明理由．25．（本小题满分14分）如图10，正方形ABCD 的边长为2，点E 在边AD 上（不与A 、D 重合），点F 在边CD 上，且∠EBF =45°．△ABE 的外接圆O 与BC 、BF 分别交于点G 、H ．（1）在图10中作圆O ，并标出点G 和点H ；（2）若EF ∥AC ，试说明弧BG 与弧GH 的大小关系，并说明理由；（3）如图11所示，若圆O 与CD 相切，试求△BEF 的面积．图8 图9图10 图11。

广州市越秀协作组2014届九年级下学期期中检测（一模）数学试题本试卷分选择题和非选择题两部分，共三大题25小题，共6页，满分150分,考试时间120分钟．可以使用规定型号的计算器。

注意事项：1.答卷前，考生务必用黑色字迹的钢笔或签字笔填写好自己的学校、班级、姓名、试室号、座位号、准考证号，再用2B 铅笔把准考证号对应的号码标号涂黑．2.选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号；不能答在试卷上．3.非选择题必须用黑色字迹的钢笔或签字笔作答，涉及作图的题目，用2B 铅笔画图．答案必须写在答题卡各题目指定区域内的相应位置上；如需要改动，先划掉原来的答案，然后再写上新的答案；改动的答案也不能超出指定的区域．不准使用铅笔、圆珠笔和涂改液．不按以上要求作答的答案无效．4.考生必须保持答题卡的整洁，考试结束后，将本试卷和答题卡一并交回．第一部分 选择题(共30分)一、选择题(本大题共10小题，每小题3分，满分30分.在每小题给出的四个选项中，只有一项是符合题目要求的) 1．4的平方根为（ * ）． A ．2B ．±2C ．4D ．±42. 对于样本数据1，2，3，2，2，以下判断：①平均数为5；②中位数为2；③众数为2；④极差为2．正确的有（ * ）． A ．1个B ．2个C ．3个D ．4个3.如图所示的几何体的主视图是（ * ）．4．如果代数式1x x有意义，那么x 的取值范围是（ * ）． A ．x ≥0B ．x ≠1C ．x ＞0D ．x ≥0且x ≠1A ．B ．C ．D ．第8题图BA ＇AB ＇O第6题图5. 已知一个圆锥的底面半径为3cm ，母线长为10cm ，则这个圆锥的侧面积为（ * ）． A ．30πcm 2B ．50πcm 2C ．60πcm 2D ．391πcm 26．如图，将△AOB 绕点O 按逆时针方向旋转45°后得到△A ＇OB ＇，若∠AOB=15°，则∠AOB ＇的度数是（ * ）． A ．25° B ．30° C ．35° D ．40°7．一次函数32-=x y 的大致图像为（ * ）．A ．B ． C． D ．8．如图，四个边长为1的小正方形拼成一个大正方形，A 、B 、O 是 小正方形顶点，⊙O 的半径为1，P 是⊙O 上的点，且位于右上方的小 正方形内，则∠APB 等于（ * ）．A ．30°B ．45°C ．60°D ．90°9．关于x 的二次函数2(1)2y x =--+，下列说法正确的是（ * ）．A ．图象的开口向上B ．图象与y 轴的交点坐标为（0，2）C ．当1x >时，y 随x 的增大而减小D ．图象的顶点坐标是（-1,2）10．如图，直角三角形纸片ABC 中，AB=3，AC=4，D 为斜边BC 中点，第1次将纸片折叠，使点A 与点D 重合，折痕与AD 交与点P 1；设P 1D 的中点为D 1，第2次将纸片折叠，使点A 与点D 1重合，折痕与AD 交于点P 2；设P 2D 1的中点为D 2，第3次将纸片折叠，使点A 与点D 2重合，折痕与AD 交于点P 3；…；如此类推，则AP 6的长为（ * ）．A ．512532⨯B ．69352⨯C ．614532⨯D ．711352⨯第10题图第13题图 C O DE F AB第二部分 非选择题(共120分)二、填空题(本大题共6小题，每小题3分，满分18分)11．点A （0,3）向右平移2个单位长度后所得的点A ’的坐标为 * ．12．已知空气的单位体积质量为0.00124克/厘米3，将0.00124用科学记数法表示为* ．13．如图，△ABC 与△DEF 是位似图形，相似比为2∶3，已知AB ＝4，则DE 的长为* ．14．化简：=+-+1112a a a * ． 15．如图，防水堤坝的轴截面是等腰梯形ABCD ，DA CB =，DC AB ∥，5=DA ，4=DC ，9=AB ，则斜坡DA 的坡角为 * __ 度．16．已知α ，β是关于x 的一元二次方程x 2+（2m +3）x +m 2=0的两个不相等的实数根，且满足βα11+=﹣1，则m 的值是 * ．三、解答题(本大题共9小题，满分102 分．解答应写出文字说明、证明过程或演算步骤) 17．（本小题满分9分）A B C D第15题图解方程：xx 332=-． 18．（本小题满分9分）如图，已知□ABCD .（1）作图：延长BC ，并在BC 的延长线上截取线段CE ，使得CE =BC （用尺规作图法，保留作图痕迹，不要求写作法）； （2）在（1）的条件下，连结AE ，交CD 于点F ， 求证:△AFD ≌ △EFC . 19．（本小题满分10分） 已知1=-b a 且2=ab ，求代数式32232ab b a b a +-的值．20．（本小题满分10分）小强对自己所在班级的48名学生平均每周参加课外活动的时间进行了调查，由调查结果绘制了频数分布直方图，根据图中信息回答下列问题： （1）求m 的值；（2）从参加课外活动时间在6～10小时的5名学生中随机选取2人，请你用列表或画树状图的方法，求其中至少有1人课外活动时间在8～10小时的概率．21．（本小题满分12分）为支持失学儿童，某中学计划用“义捐义卖”活动中筹集的部分资金用于购买A,B 两种型号的学习用品共1000件，已知A 型学习用品的单价为20元，B 型学习用品的单价为第18题图第20题图30元.（1）若购买这批学习用品用了26000元，则购买A,B 两种学习用品各多少件？ （2）若购买这批学习用品的钱不超过28000元，则最多能购买B 型学习用品多少件？ 22．（本小题满分12分）如图，在菱形ABCD 中，AB ＝23，∠BAD ＝60º，AC 交BD 于点O ，以点D 为圆心的⊙D 与边AB 相切于点E ． （1）求AC 的长；（2）求证：⊙D 与边BC 也相切．23．（本小题满分12分）如图，四边形ABCD 为正方形．点A 的坐标为（0，2），点B 的坐标为（0，﹣3），反比例函数xky =)0(≠k 的图象经过点C ． （1）求反比例函数的解析式；（2）若点P 是反比例函数图象上的一点，△P AD 的面积恰好等于正方形ABCD 的面积，求点P 的坐标．24．（本小题满分14分）如图1，在半径为2的扇形AOB 中，∠AOB =90°，点C 是 上的一个动点（不与点A 、B 重合）OD ⊥BC ，OE ⊥AC ，垂足分别为点D 、点E ．第23题图第22题图（1）当BC =1时，求线段OD 的长；（2）在点C 的运动过程中，△DOE 中是否存在长度保持不变的边或度数保持不变的角？如果存在，请指出并求其长度或度数（只求一种即可．．．．．．）；如果不存在，请说明理由； （3）作DF ⊥OE 于点F （如图2），当DF 2+EF 取得最大值时，求sin ∠BOD 的值．25．（本小题满分14分）如图，已知直线l ：2+-=x y 与y 轴交于点A ，抛物线k x y +-=2)1(经过点A ，其顶点为B ，另一抛物线h h x y -+-=2)(2（h >1）的顶点为D ，两抛物线相交于点C ， （1）求点B 的坐标，并判断点D 是否在直线l 上，请说明理由； （2）设交点C 的横坐标为m ．①请探究m 关于h 的函数关系式；②连结AC 、CD ，若∠ACD =90°，求m 的值．九年级数学参考答案与评分标准说明：（一）《答案》中各行右端所注分数表示正确作完该步应得的累加分数，全卷满分150分。

广州市越秀协作组2014届九年级下学期期中检测（一模）数学试题本试卷分选择题和非选择题两部分，共三大题25小题，共6页，满分150分,考试时间120分钟．可以使用规定型号的计算器。

注意事项：1.答卷前，考生务必用黑色字迹的钢笔或签字笔填写好自己的学校、班级、姓名、试室号、座位号、准考证号，再用2B 铅笔把准考证号对应的号码标号涂黑．2.选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号；不能答在试卷上．3.非选择题必须用黑色字迹的钢笔或签字笔作答，涉及作图的题目，用2B 铅笔画图．答案必须写在答题卡各题目指定区域内的相应位置上；如需要改动，先划掉原来的答案，然后再写上新的答案；改动的答案也不能超出指定的区域．不准使用铅笔、圆珠笔和涂改液．不按以上要求作答的答案无效．4.考生必须保持答题卡的整洁，考试结束后，将本试卷和答题卡一并交回．第一部分 选择题(共30分)一、选择题(本大题共10小题，每小题3分，满分30分.在每小题给出的四个选项中，只有一项是符合题目要求的) 1．4的平方根为（ * ）． A ．2B ．±2C ．4D ．±42. 对于样本数据1，2，3，2，2，以下判断：①平均数为5；②中位数为2；③众数为2；④极差为2．正确的有（ * ）． A ．1个B ．2个C ．3个D ．4个3.如图所示的几何体的主视图是（ * ）．4．如果代数式1x x有意义，那么x 的取值范围是（ * ）． A ． B ． C ． D ．第3题图A ．x ≥0B ．x ≠1C ．x ＞0D ．x ≥0且x ≠15. 已知一个圆锥的底面半径为3cm ，母线长为10cm ，则这个圆锥的侧面积为（ * ）． A ．30πcm 2B ．50πcm 2C ．60πcm 2D ．391πcm 26．如图，将△AOB 绕点O 按逆时针方向旋转45°后得到△A ＇OB ＇，若∠AOB=15°，则∠AOB ＇的度数是（ * ）． A ．25° B ．30° C ．35° D ．40°7．一次函数的大致图像为（ * ）．A ．B ．C ．D ．8．如图，四个边长为1的小正方形拼成一个大正方形，A 、B 、O 是 小正方形顶点，⊙O 的半径为1，P 是⊙O 上的点，且位于右上方的小 正方形内，则∠APB 等于（ * ）．A ．30°B ．45°C ．60°D ．90°9．关于x 的二次函数2(1)2y x =--+，下列说法正确的是（ * ）． A ．图象的开口向上 B ．图象与y 轴的交点坐标为（0，2）C ．当1x >时，y 随x 的增大而减小D ．图象的顶点坐标是（-1,2）10．如图，直角三角形纸片ABC 中，AB=3，AC=4，D 为斜边BC 中点，第1次将纸片折叠，使点A 与点D 重合，折痕与AD 交与点P 1；设P 1D 的中点为D 1，32-=x y o yxo y x yxooy x BAOP第8题图BA ＇AB ＇O第6题图第10题图第2次将纸片折叠，使点A 与点D 1重合，折痕与AD 交于点P 2；设P 2D 1的中点为D 2，第3次将纸片折叠，使点A 与点D 2重合，折痕与AD 交于点P 3；…；如此类推，则AP 6的长为（ * ）．A ．512532⨯B ．69352⨯C ．614532⨯D ．711352⨯第二部分 非选择题(共120分)二、填空题(本大题共6小题，每小题3分，满分18分)11．点A （0,3）向右平移2个单位长度后所得的点A ’的坐标为 * ．12．已知空气的单位体积质量为0.00124克/厘米3，将0.00124用科学记数法表示为 * ． 13．如图，△ABC 与△DEF 是位似图形，相似比为2∶3，已知AB ＝4，则DE 的长为 * ．14．化简：=+-+1112a a a * ． 15．如图，防水堤坝的轴截面是等腰梯形ABCD ，DA CB =，DC AB ∥，5=DA ，4=DC ，9=AB ，则斜坡DA 的坡角为 * __ 度．16．已知α ，β是关于x 的一元二次方程x 2+（2m +3）x +m 2=0的两个不相等的实数根，且满足βα11+=﹣1，则m 的值是 * ．三、解答题(本大题共9小题，满分102 分．解答应写出文字说明、证明过程或演算步骤) 17．（本小题满分9分） 解方程：． 18．（本小题满分9分）如图，已知□ABCD .（1）作图：延长BC ，并在BC 的延长线上截取线段CE ，使得CE =BC （用尺规作图法，保留作图痕迹，不要求写作法）； （2）在（1）的条件下，连结AE ，交CD 于点F ， 求证:△AFD ≌ △EFC . 19．（本小题满分10分） 已知1=-b a 且2=ab ，求代数式32232ab b a b a +-的值． 20．（本小题满分10分）小强对自己所在班级的48名学生平均每周参加课外活动的时间进行了调查，由调查结果绘制了频数分布直方图，根据图中信息回答下列问题：xx 332=-第18题图 第13题图C O DE F ABA B CD第15题图（1）求m 的值；（2）从参加课外活动时间在6～10小时的5名学生中随机选取2人，请你用列表或画树状图的方法，求其中至少有1人课外活动时间在8～10小时的概率． 21．（本小题满分12分）为支持失学儿童，某中学计划用“义捐义卖”活动中筹集的部分资金用于购买A,B 两种型号的学习用品共1000件，已知A 型学习用品的单价为20元，B 型学习用品的单价为30元.（1）若购买这批学习用品用了26000元，则购买A,B 两种学习用品各多少件？ （2）若购买这批学习用品的钱不超过28000元，则最多能购买B 型学习用品多少件？22．（本小题满分12分）如图，在菱形ABCD 中，AB ＝23，∠BAD ＝60º，AC 交BD 于点O ，以点D 为圆心的⊙D 与边AB 相切于点E ． （1）求AC 的长；（2）求证：⊙D 与边BC 也相切．23．（本小题满分12分）如图，四边形ABCD 为正方形．点A 的坐标为（0，2），点B 的坐标为（0，﹣3），反比例函数xky =)0(≠k 的图象经过点C ． 第20题图 第22题图（1）求反比例函数的解析式；（2）若点P 是反比例函数图象上的一点，△P AD 的面积恰好等于正方形ABCD 的面积，求点P 的坐标．24．（本小题满分14分）如图1，在半径为2的扇形AOB 中，∠AOB =90°，点C 是 上的一个动点（不与点A 、B 重合）OD ⊥BC ，OE ⊥AC ，垂足分别为点D 、点E ． （1）当BC =1时，求线段OD 的长；（2）在点C 的运动过程中，△DOE 中是否存在长度保持不变的边或度数保持不变的角？如果存在，请指出并求其长度或度数（只求一种即可．．．．．．）；如果不存在，请说明理由；（3）作DF ⊥OE 于点F （如图2），当DF 2+EF 取得最大值时，求sin ∠BOD 的值．25．（本小题满分14分）如图，已知直线l ：2+-=x y 与y 轴交于点A ，抛物线k x y +-=2)1(经过点A ，其顶点为B ，另一抛物线h h x y -+-=2)(2（h >1）的顶点为D ，两抛物线相交于点C ，第24题图1第24题图2第23题图（1）求点B 的坐标，并判断点D 是否在直线l 上，请说明理由； （2）设交点C 的横坐标为m ．①请探究m 关于h 的函数关系式；②连结AC 、CD ，若∠ACD =90°，求m 的值．九年级数学参考答案与评分标准说明：（一）《答案》中各行右端所注分数表示正确作完该步应得的累加分数，全卷满分150分。

2014-2015学年广州市第三中学九年级一模数学试卷2014-2015学年广州市第三中学九年级一模数学试卷一、选择题（每小题3分，共30分）1、4的平方根是（）A.2B.2± C.2 D.2±2、下列各式计算结果正确的是（）A.233aaa=+ B.1)1(22-=-aa C.)0(122≠=-aaaD.226)3(aa=3、将点A（2,1）向左平移2个单位长度得到点1A，则点1A关于x轴的对称点2A的坐标是（）A.（0,1） B.（0，—1） C.（—1,0）D.（2,1）4、如图，AB∥CD，0075,35=∠=∠CA，则E∠的度数是（）A.35°B.40°C.45°D.75°第4题图第7题图第8题图5、函数121--=xxy有意义，则x的取值范围是（ ）A.21>x B.21≥x C.121≠≥x x 且 D.21>x 1≠x 且 6、若),1(),,2(),3(321y C y B y A --，三点都在函数xy 1-=的图像上，则321,,y y y 的大小关系是（ ）A.321y y y >> B.312y y y >> C.213y y y >>D.123y y y>>7、一直圆锥的地面半径为6cm ，侧面积为60π2cm ，设圆锥的母线与高的夹角为θ（如图所示），则θcos 的值为（ ） A.43 B.53C.54D.658、如图，数轴上A 、B 两点分别对应实数b a 、，则下列结论正确的是（ ） A.0>+b a B.0>ab C.0>-b aD.0>-b a9、如图，边长为2的正方形ABCD 中，P 是CD 的中点，连接AP 并延长，交BC 的延长线于点F ，10、11、填空题（本大题共6小题，每小题3分，满分18分）11、广州某慈善机构全年共募集善款5250000元，将5250000用科学记数法表示为________.12、方程xx 527=+的解是_______.13、一个多边形内角和比外角和的3倍多0180，则它的边数是_____.14、如右图，这是一个长方体的主视图和俯视图，由图示数据（单位：cm ）可以得到该长方体的体积是________3cm .第14题图 第15题图15、如图，在梯形ABCD 中，AB ∥CD ，BCD ABC ∠∠和的平分线交于AD 的中点E ，已知AB=4，CD=6，53=CB BE ，则BEC ∆的面积为_______. 16、已知等边三角形ABC 的高为4，在这个三角形所在的平面内有一点P ，若P 到AB 的距离是1，点P 到AC 的距离是2，则点P 到BC 的最小距离与最大距离的和是________.三、解答题（本大题共9小题，满分102分，解答应写出文字说明、证明过程或演算步骤） 17、（本小题满分9分）先化简代数式：aaa a a -÷-)1(，然后选一个合适的a 值，代入求值.18、（本小题满分9分）已知：如图，ABC ∆中，AB=AC ，矩形BCDE 的边DE 分别与AB 、AC 交于点F 、G.求证：EF=DG.19、（本小题满分10分）已知关于x 的一元二次方程0622=--k x x （k为常数）.（1）求证：方程有两个不相等的实数根； （2）设21,x x 为方程的两个实数根，且14221=+x x，试求方程的两个实数根和k 的值.20、（本小题满分10分）某公司组织部分员工到一博览会的A、B、C、D、E五个展馆参观，公司所购门票种类、数量绘制成的条形和扇形统计图如图所示：请根据统计图回答下列问题：（1）求出门票的总数量，C所占圆心角度的度数，并将条形统计图和扇形统计图在图中补充完整；（2）若A馆门票仅剩一张，而员工小明和小华都想要，他们决定采用抽扑克牌的方法来确定，规则是：“将同一副牌中正面分别标有数字1，2，3，4的四张牌洗匀后，背面朝上放置在桌面上，每人随机抽一次且一次只抽一张；一人抽后记下数字，将牌放回洗匀背面朝上放置在桌面上，再由另一人抽.若小明抽得的数字比小华抽得的数字大，门票给小明，否则给小华.”请用画树状图或列表的方法计算出小明和小华获得门票的概率，并说明这个规则对双方是否公平.21、（本小题满分12分）如图，在平面直角坐标系中，矩形OABC的一边OA在x轴上且B（4，点Q.（1）若P为BC边的中点，求双曲线的函数表达式及点Q的坐标；（2求k的取值范围；（3）连接PQ，AC，当PQ存在时，PQ∥AC是否总成立；若成立请证明，若不成立请说明理由.22、（本小题满分12分）某服装店用6000元购进A 、B 两种服装，按标价售出后可获得毛利润3800元（毛利润=售价—进价），这两种服装的进价、标价如表所示：A 型 B型进价（元/件） 60 100 标价（元/件） 100 160（1）求这两种服装各购进的件数；（2）如果A中服装按标价的8折出售，B中服装按标价的7折出售，那么这批服装全部售完后，服装店比按标价出售少收入多少元？23、（本小题满分12分）如图，AB是⊙O的直径，D为⊙O上一点，AT平分BAD交⊙O于点T. （1）动手操作：利用尺规作过T作AD的垂线，并标出与AD延长线的交点C（保留作图痕迹，不写作法）；（2）综合应用：在你所作的图中，①求证：CT为⊙O的切线；②若⊙O 的半径为2，3=CT ，求AD 的长和ABTADTS S∆∆的值.24、（本小题满分14分）如图，在平面直角坐标系xoy 中，一次函数m x y +=45的图像与x 轴交于A（—1,0），与y 轴交于点C ，以直线2=x 为对称轴的抛物线)0(21≠++=a c bx axy C ：经过A 、C 两点，并与x 轴正半轴交于点B.（1）求m 的值及抛物线)0(21≠++=a c bx ax y C ：的函数表达式； （2）设点D （0，1225），若F 是抛物线)0(21≠++=a c bx ax y C ：对称轴上使得ADF ∆的周长取得最小值的点，过F 任意作一条与y 轴不平行的直线交抛物线1C 于),(),,(222111y x My x M 两点，试探究FM FM 2111+是否为定值？请说明理由. （3）将抛物线1C 作适当平移，得到抛物线1,)(41222>--=h h x y C ：，若当x y m x -≥≤<21时，恒成立，求m 的最大值.25、（本小题满分14分）如图1，在平行四边形ABCD 中，AH ⊥DC ，垂足为H ，21774===AH AD AB ，，,现有两个动点E ，F 同时从点A 出发，分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC 方向匀速运动，点E 、F 在运动过程中，以EF 为边作等边EFG ∆，使EFG ∆与ABC ∆在射线AC 的同侧，当点E 运动到点C 时，E 、F 两点同时停止运动，设运动时间为t 秒. （1）求线段AC 的长；（2）在整个运动过程中，设等边EFG ∆与ABC ∆重叠部分的面积为S ，请直接写出S 与t 之间的函数关系式，并写出相应的自变量t 的取值范围； （3）当等边EFG ∆的顶点E 到达C 时，如图2，将EFG ∆绕着点C 旋转一个角度)3600(00<<αα，在旋转过程中，点E 与点C 重合，F 的对应点为F '，G 的对应点为G '，设直线G F ''与射线DC 、射线AC 分别相交于M 、N 两点，试问：是否存在点M 、N ，使得CMN ∆是以MCN ∠为底角的等腰三角形？若存在，请求出CM 的长度；若不存在，请说明理由.。

2014-2015学年广州市第三中学九年级一模数学试卷一、选择题（每小题3分，共30分）1、4的平方根是（ ）A.2 B.2± C.2 D.2±2、下列各式计算结果正确的是（ ）A.233aa a =+ B.1)1(22-=-a a C.)0(122≠=-a aa D.226)3(a a = 3、将点A （2,1）向左平移2个单位长度得到点1A ，则点1A 关于x 轴的对称点2A 的坐标是（ ）A.（0,1）B.（0，—1）C.（—1,0）D.（2,1）4、如图，AB ∥CD ，0075,35=∠=∠C A ，则E ∠的度数是（ ）A.35°B.40°C.45°D.75°第4题图 第7题图 第8题图5、函数121--=x x y 有意义，则x 的取值范围是（ ）A.21>xB.21≥xC.121≠≥x x 且 D.21>x 1≠x 且6、若),1(),,2(),3(321y C y B y A --，三点都在函数xy 1-=的图像上，则321,,y y y 的大小关系是（ ）A.321y y y >> B.312y y y >> C.213y y y >> D.123y y y >>7、一直圆锥的地面半径为6cm ，侧面积为60π2cm ，设圆锥的母线与高的夹角为θ（如图所示），则θcos 的值为（ ）A.43 B.53 C.54D.658、如图，数轴上A 、B 两点分别对应实数b a 、，则下列结论正确的是（ ）A.0>+b aB.0>abC.0>-b aD.0>-b a9、如图，边长为2的正方形ABCD 中，P 是CD 的中点，连接AP 并延长，交BC 的延长线于点F ，作CPF ∆的外接圆⊙O 于点E ，连接EF ，则EF 的长为（ ）A.554B.553C.23 D.3510、已知：如图，在090=∠=∠∆∆DAE BACADE ABC 中，，,AB=AC,AD=AE,点C ，D ，E三点在同一条直线上，连接BD ，BE.一下四个结论：①BD=CE=BC ；②BD ⊥CE ；③045=∠+∠DBC ACE ；④)(2222AB AD BE +=，其中结论正确的个数是（ ）A.1B.2C.3D.4第9题图 第10题图二、填空题（本大题共6小题，每小题3分，满分18分）11、广州某慈善机构全年共募集善款5250000元，将5250000用科学记数法表示为________.12、方程xx 527=+的解是_______.13、一个多边形内角和比外角和的3倍多0180，则它的边数是_____.14、如右图，这是一个长方体的主视图和俯视图，由图示数据（单位：cm ）可以得到该长方体的体积是________3cm .第14题图 第15题图15、如图，在梯形ABCD 中，AB ∥CD ，BCD ABC ∠∠和的平分线交于AD 的中点E ，已知AB=4，CD=6，53=CB BE ，则BEC ∆的面积为_______.16、已知等边三角形ABC 的高为4，在这个三角形所在的平面内有一点P ，若P 到AB的距离是1，点P 到AC 的距离是2，则点P 到BC 的最小距离与最大距离的和是________.三、解答题（本大题共9小题，满分102分，解答应写出文字说明、证明过程或演算步骤）17、（本小题满分9分）先化简代数式：a aa a a -÷-)1(，然后选一个合适的a 值，代入求值.18、（本小题满分9分）已知：如图，ABC ∆中，AB=AC ，矩形BCDE 的边DE 分别与AB 、AC 交于点F 、G.求证：EF=DG.19、（本小题满分10分）已知关于x 的一元二次方程0622=--k x x （k 为常数）.（1）求证：方程有两个不相等的实数根；（2）设21,x x 为方程的两个实数根，且14221=+x x ，试求方程的两个实数根和k 的值.20、（本小题满分10分）某公司组织部分员工到一博览会的A 、B 、C 、D 、E 五个展馆参观，公司所购门票种类、数量绘制成的条形和扇形统计图如图所示： 请根据统计图回答下列问题：（1）求出门票的总数量，C所占圆心角度的度数，并将条形统计图和扇形统计图在图中补充完整；（2）若A 馆门票仅剩一张，而员工小明和小华都想要，他们决定采用抽扑克牌的方法来确定，规则是：“将同一副牌中正面分别标有数字1，2，3，4的四张牌洗匀后，背面朝上放置在桌面上，每人随机抽一次且一次只抽一张；一人抽后记下数字，将牌放回洗匀背面朝上放置在桌面上，再由另一人抽.若小明抽得的数字比小华抽得的数字大，门票给小明，否则给小华.”请用画树状图或列表的方法计算出小明和小华获得门票的概率，并说明这个规则对双方是否公平.21、（本小题满分12分）如图，在平面直角坐标系中，矩形OABC 的一边OA 在x 轴上且B （4，3），双曲线xky =（0>x ）交BC 于点P ，交AB 于点Q. （1）若P 为BC 边的中点，求双曲线的函数表达式及点Q 的坐标；（2）若双曲线xky =（0>x ）和线段BC 有公共点，求k 的取值范围； （3）连接PQ ，AC ，当PQ 存在时，PQ ∥AC 是否总成立；若成立请证明，若不成立请说明理由.22、（本小题满分12分）某服装店用6000元购进A 、B 两种服装，按标价售出后可获得毛利润3800元（毛利润=售价—进价），这两种服装的进价、标价如表所示： （1）求这两种服装各购进的件数；（2）如果A 中服装按标价的8折出售，B 中服装按标价的7折出售，那么这批服装全部售完后，服装店比按标价出售少收入多少元？23、（本小题满分12分）如图，AB 是⊙O 的直径，D 为⊙O 上一点，AT 平分BAD ∠交⊙O 于点T.（1）动手操作：利用尺规作过T 作AD 的垂线，并标出与AD 延长线的交点C （保留作图痕迹，不写作法）；（2）综合应用：在你所作的图中，①求证：CT 为⊙O 的切线；②若⊙O 的半径为2，3=CT ，求AD 的长和ABTADTS S ∆∆的值. 24、（本小题满分14分）如图，在平面直角坐标系xoy 中，一次函数m x y +=45的图像与x 轴交于A （—1,0），与y 轴交于点C ，以直线2=x 为对称轴的抛物线)0(21≠++=a c bx ax y C ：经过A 、C 两点，并与x 轴正半轴交于点B.（1）求m 的值及抛物线)0(21≠++=a c bx axy C ：的函数表达式；A 型B 型进价（元/件）60100标价（元/件）100160（2）设点D （0，1225），若F 是抛物线)0(21≠++=a c bx ax y C ：对称轴上使得ADF ∆的周长取得最小值的点，过F 任意作一条与y 轴不平行的直线交抛物线1C 于),(),,(222111y x M y x M 两点，试探究FM F M 2111+是否为定值？请说明理由. （3）将抛物线1C 作适当平移，得到抛物线1,)(41222>--=h h x y C ：，若当x y m x -≥≤<21时，恒成立，求m 的最大值.25、（本小题满分14分）如图1，在平行四边形ABCD 中，AH ⊥DC ，垂足为H ，21774===AH AD AB ，，,现有两个动点E ，F 同时从点A 出发，分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC 方向匀速运动，点E 、F 在运动过程中，以EF 为边作等边EFG ∆，使EFG ∆与ABC ∆在射线AC 的同侧，当点E 运动到点C 时，E 、F 两点同时停止运动，设运动时间为t 秒.（1）求线段AC 的长；（2）在整个运动过程中，设等边EFG ∆与ABC ∆重叠部分的面积为S，请直接写出S 与t 之间的函数关系式，并写出相应的自变量t 的取值范围；（3）当等边EFG ∆的顶点E 到达C 时，如图2，将EFG ∆绕着点C 旋转一个角度)3600(00<<αα，在旋转过程中，点E 与点C 重合，F 的对应点为F '，G 的对应点为G '，设直线G F ''与射线DC 、射线AC 分别相交于M 、N 两点，试问：是否存在点M 、N ，使得CMN ∆是以MCN ∠为底角的等腰三角形？若存在，请求出CM 的长度；若不存在，请说明理由.2020-2-8。

2013学年下学期初三一模测试数学科测试试题（四中）第Ⅰ卷（30分）一、选择题（每题3分，共30分）1.16的算术平方根是（）A.±2B.2C. ± 2D. 22.下列运算正确的是（）A.3x-2x=1B.－2x2=－12x2C.(－a)2a3=a6D. (－a2)3=－a53.下列图形中，既是中心对称图形又是周对称图形的是（）A.等边三角形B.菱形C. 等腰三角形D. 平行四边形4.实数a、b在数轴上的位置如图所示，那么化简|b－a|－b2的结果是（）A.2b－aB. a－2bC. aD.－a5.如图，点A、B、C是⊙O上的三点，∠BAC=30°，BC=1，则⊙O的半径为（）A.1.5B.2C. 12D. 16.袋中有同样大小的4个小球，其中3个红色，1个白色，从袋中任意地同时摸出两个球，这两个球颜色相同的概率是（）A. 12B.13C.23D.147抛物线y=x2-2x+2的顶点坐标是（）A.（1,1）B.（-1,1）C.（-1,2）D.（1,2）8.二次函数（a≠0）的图形不经过第三象限，则一次函数y=ax+b的图像不经过第（）象限A.一B.二C. 三D. 四9.在如图所示的扇形中，∠AOC=90°，面积为4πcm2，用这个扇形围成一个圆锥的侧面，这个圆锥底面半径为（）A.1cmB.2cmC.4cmD. 15 cm第5题第9题第10题10.如图⊙O1和⊙O2内切于A，⊙O1的半径为3，⊙O2的半径为2，点P为⊙O1上的任一点（与点A不重合），直线PA交⊙O2于点C，PB切⊙O2于点B，则BPPC的值为（）A. 2B. 3C. 32D.62b 0 aOAC B第Ⅱ卷（120分）二、填空题（本题有6个小题，每小题3分，共18分）11.若1x代数式在实数范围内有意义，则x 的取值范围是 。

12.若2x 2-6x -1=0，则3x 2-9x = 。

13.不等式组的整数解能使一元二次方程x 2+2x +k =0没有实数解的概率为 。

2014-2015学年广东省广州市越秀区九年级（上）期末数学试卷一、选择题：每小题 3分，共30分.6. （3分）（2007?兰州）下列说法正确的是（ ）A. 在同一年出生的 367名学生中，至少有两人的生日是同一天B. 彩票中奖的机会是 1%,买100张一定会中奖C. 天气预报说每天下雨的概率是50%,所以明天将有一半的时间在下雨D. 抛一枚图钉钉尖着地和钉尖朝上的概率一样大2精英教育中小学个性化教育品牌1. ) A .任D ・2. （P (3）关)A . ((-4, D. (3. （31 =(x 2 + 1的)A . (2D .2).4. （3分）（2014秋？安顺期末）下列图形屮既是轴对称图形，乂是中心对称图形的是（5. （3分）（2014秋？越秀区期末）函数 y=- 丄乔］图象与坐标轴的交点个数是（A. 0个B 彳、C ・2个。

.3个AH7. （3分）（2014秋？越秀区期末）把抛物线 y 二2x 先向左平移3个单位，再向上平移 4个单位，所得抛物线的函 数表达式为（ ）2 2 2 2A. y=2 （x+3） +4B. y=2 （x+3）- 4 C ・ y=2 （x - 3） - 4 D ・ y=2 （x - 3）+48. A. (3分) (x+1)（2013?呼伦贝尔）用配方法解方程 2 2B. (x - 1) =6 9. （3 分） 兀长是专 （2014秋？越秀区期末）如兀 ）亏 兀 兀 ~6 A.B. C. D.2-2x - 5=0时，原方程应变形为（ x2 2C. (x+2) =9BC则劣弧D. (x - 2) =910. （3分）（2014秋？越秀区期末）如图所示是一个直角三角形的苗圃，由一个正方形花坛和两块直角三角形的 草皮组成.如果两个直角三角形的两条斜边长分别为3米和6米，则草皮的总面积为（）平方米.二、填空题：每小题3分，共18分.211. 3分）（2014秋？萝岗区期末）若X1, X2是一元二次方程 x - 3x- 1= 0的两个根，则X1+X2的值是 12. （3分）（2014?江阴市二模）在一个不透明的布袋中装有4个白球和n 个黄球，它们除颜色不同外，其余均相4同，若从中随机摸出一个球，摸到黄球的概率是g,则n 二 --------------- ・13. （3分）（2014秋？越秀区期末）如图， ACOD 是厶AOB 绕点O 顺时针方向旋转 38。

绝密★启用并考试结束前 试卷类型：A2014年天河省实中考一模考试数学试题第I 卷（选择题 共30分）一、选择题（本大题共10小题，每小题3分，满分30分，在每小题给出的四个选项中，只有一项是符合题目要求的） 1.=--)3(2（ ▲ ）A.5-B.1-C.1D.5 2.一个图形的主视图与俯视图如右图所示，则此图形可能是（ ▲ ）A.三棱锥B.三棱柱C.圆锥D.圆柱3.已知)3,1(A ，将线段OA 绕原点O 旋转︒60后得到'OA ，则'OA 的长度是（ ▲ ）A.10B.3C.22D.1 4.已知b a 、互为相反数，则下列说法中正确的是（ ▲ ）A.1=abB.1)1(2=++b a C.1=+b a D.02=+b a5.如图所示，ABC RT ∆中，BC AB ⊥，︒=∠30C ，3=BC ，则=BD （ ▲ ）A.1B.2C.3D.2第2题 第5题 第6题6.如图所示，C B A O 、、、在数轴上对应的数分别是c b a 、、、0， 则下列说法正确的是（ ▲ ）A.0<abcB.0>++c b aC.0)(>-c a bD.0)(<-b a c 7.给出定义：12+-=⊗b a b a ，则关于03≥⊗x x ，下列说法正确的是（ ▲ ）A.满足条件的最大整数x 是1-B.满足条件的最小整数x 是0C.满足条件的x 的取值范围是51-≤xD.满足条件的x 的取值范围是51≥x 8.二次函数122-+=x ax y 的顶点坐标在x 轴下方，则a 的取值范围是（ ▲ ）9.如图，在边长为2的正方形中，E 是CD 的中点，且CDCEBF AF =217， 则四边形EBFD 的周长是（ ▲ ） A.1757++ B.252177++ C.21727+ D.2710.给出计算符号“* ”，使符号“* ”满足：32631=*，61212=*，921053=*，121634=*，1511265=*， ，则=++*-*1415022014201320132014（ ▲ ）A.2013B.2013-C.2014D.2014-第II 卷（非选择题 共120分）二．填空题（本大题共6小题，每小题3分，满分18分）11.截止至2013年底，广州某银行信用卡发卡量达到9260000张，比当年初增长%8.20，其中9260000用科学计数法表示为 ▲ 。