常用坐标计算及公路路线坐标计算

铁路公路曲线防样坐标计算方法一、随着我国公路铁路的大力建设，对坐标放样的要求精度越来越高，以及通过一种快速的捷径来达到一次性对整个路基、桥梁的中线编辑公式，准确较快的计算出中心坐标，使得坐标放样在我们的施工中带来更大的方便。

1、首先熟悉测量知识圆曲线基本公式及概念。

偏角法测设圆曲线1-1知道了圆曲线的测设里程，即测设的曲线长Li ，即可进行计算，其计算公式如下：πα0180∙=R L i i2iiαδ=i i R c δsin 2= （1-1）式中，i δ，i c 为曲线测设曲线点i 的偏角与弦长。

切线支距法测设圆曲线ZYi i R x αsin ∙= )c o s 1(i i R y α-∙= π180∙=R L a i i（1-2）1-2式中i L 为曲线上点i 至ZY （或YZ ）的曲线长。

2、缓和曲线的基本公式及概念。

缓和曲线是直线与圆曲线之间的一种过渡曲线，它与直线分界处半径为∞，与圆曲线相接处半径与圆曲线半径R 相等，缓和曲线上任一点的曲率半径ρ与该点到曲线起点的长度成反比。

如下图中，存在公式： ρ∝l1 或Cl =ρ （2-1）公式中C 是一个常数，称缓和曲线半径变更率。

当0l l =时，R =ρ 所以C l R =∙0，C l =ρ，是缓和曲线的必要条件，实用中能满足这一条件的曲线可称为缓和曲线，如辐射螺旋线、三次抛物线等，我国缓和曲线均采用辐射螺旋线。

1-33、缓和曲线方程式：按照C l =ρ为必要条件导出的缓和曲线方程为：∙∙∙∙++-=∙∙∙∙∙++-=5113734925422403366345640Cl C l C l y Cl C l l x （3-1） 根据测设精度的要求，实际应用中可将高次项舍去，并顾及到C Rl =0，则上式变为32025640Rl l y l R l l x =-=（3-2）式中，x ，y 为缓和曲线上任一点的直角坐标，坐标原点为直缓点（ZH ）或缓直（HZ ），通过该点的缓和曲线切线为x 轴。

公路道路上有关P 点的坐标计算：在公路施工过程中，需要进行放样的点位，不外乎两种情况：一种是该点位于公路中心线上，即公路中桩，另一类则是点位在中线以外，位于某个中桩的横断方向上。

这样无论哪种情况，需要放样的点的桩号首先是已知的。

以下就这两种情况，对公路点位放样计算进行一下阐述，讲述一下坐标计算方法。

一：P 点位于直线段上，各桩坐标计算： 1、 P 点在直线上各中桩坐标计算当需要放样的P 点位于直线上时，有两种情况：位于YZ 到ZY 或者HZ 到ZH 之间， 或者位于公路QZ 和ZH （ZY ）之间，其计算方法相同，公式如下：[公式（1）]X p =X 0+l cosA i-1,i Y p =Y 0+l sin A i-1,I式中， （X 0 ,Y 0） 为该段直线的起点（可以是YZ ，HZ 或QZ ）坐标 l 为要求计算的P 点与该直线段起点的桩号差（距离）。

2、 P 点位于横断面上，其所对应的中桩位于直线上时：X p =X z +Dcos （A i-1,i ±90） Y p =Y z +Dsin （A i-1,i ±90）式中， （X z ，Y z ）为P 点对应的中桩的坐标 P 点位于左幅时，取“—”反之取“+” D 为P 点到直线上的法线距离二、P 点位于单圆曲线上，各桩坐标计算：1、当需要放样的P 点位于单圆曲线上，其中桩坐标计算如下：[公式（2）]式中， （X 0，Y 0）为ZY 点坐标，R 为圆曲线半径 l 为P 点与ZY 点的桩号差（弧长） 当路线左转时，取“—”，反之取“+”2、P 点位于横断面上，其所对应的中桩位于单圆曲线上时：式中，第一个“”号，路线左转取“—”，右转取“+”第二个“”号，P 点位于左幅时，取“—”，反之取“+”三、P 点位于带缓和曲线的圆曲线上，各桩坐标计算：当P 点位于带缓和曲线的圆曲线时，分为以下三种情况： 第一种情况，ZH 到HY 段，中桩和边桩计算： 1、ZH 到HY 段，中桩坐标计算：[公式（3）]式中，c = l -(X 0，Y O )为ZH 点坐标l 为P 点与ZH 点桩号差，L s 为缓和曲线长 当路线左转时，取“—”，反之取“+”2、ZH 到HY 段，P 点对应的中桩位于带缓和曲线的圆曲线上：式中，（Xz ，Yz ）为P 点对应的中桩坐标l 为P 点对应的中桩与ZH 点桩号差，Ls 为缓和曲线长 第一个“”号，路线左转取“—”，右转取“+” 第二个“”号，P 点位于左幅时，取“—”，反之取“+” 第二种情况，HY 到YH 段，中桩和边桩计算：1、HY 到YH 段，中桩坐标计算：[公式（4）]式中，(X 0，Y O )为HY 点坐标l 为P 点与HY 点桩号差，Ls 为缓和曲线长 当路线左转时，取“—”，反之取“+”2、HY 到YH 段，P 点对应的中桩位于带缓和曲线的圆曲线上：式中，（Xz ，Yz ）为HY 点坐标l 为P 点对应的中桩与HY 点桩号差，Ls 为缓和曲线长 前两个“”号，路线左转取“”，右转取“” 第三个“”号，P 点位于左幅时，取“—”，反之取“+”第三种情况，YH 到HZ 段，中桩和边桩计算： 1、YH 到HZ 段，中桩坐标计算：[公式（5）]c = l -(X 0，Y O )为HZ 点坐标l 为HZ 点与P 点桩号差，L s 为缓和曲线长 当路线左转时，取“+”，反之取“—”2、YH 到HZ 段，P 点对应的中桩位于带缓和曲线的圆曲线上：式中，（Xz ，Yz ）为P 点对应中桩坐标l 为HZ 点桩号与P 点对应的中桩桩号差，Ls 为缓和曲线长 第一个“”号，路线左转取“+”，右转取“—” 第二个“”号，P 点位于左幅时，取“—”，反之取“+”四、复曲线上各点的坐标计算：1、 当复曲线中间不设缓和曲线时，采用以下方法进行计算：对于第一缓和曲线、第一段圆曲线以及第二缓和曲线，分别用公式（3）、公式（4）和公式（5）计算；对于第二段圆曲线，用公式（2）计算，计算时将公式（2）中的换成，l 1，L s1分别为第一圆曲线和第一缓和曲线长度，左转取“—”，右转取“+”。

一个excle模板的制作在当今社会，eｘcle的使用已经是越来越来频繁了,几乎涉及所有的行业,路桥施工也不例外。

我在某路桥公司曾经负责过某项目部的测量工作。

大家都知道，测量最主要的就是计算了,如坐标、高程、横坡度等。

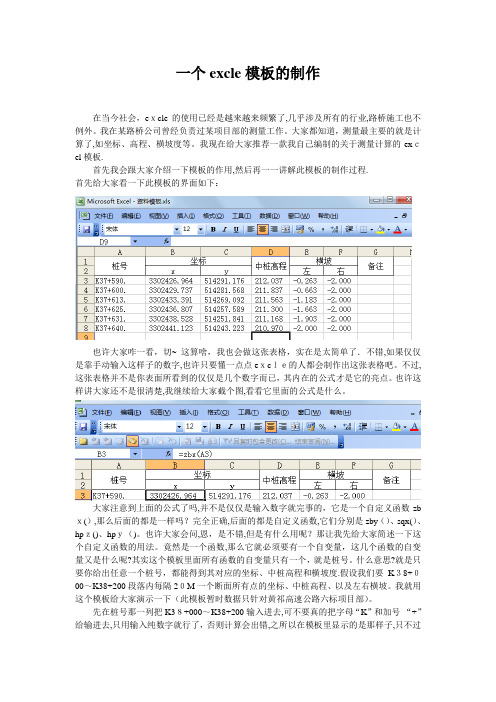
我现在给大家推荐一款我自己编制的关于测量计算的exｃel模板.首先我会跟大家介绍一下模板的作用,然后再一一讲解此模板的制作过程.首先给大家看一下此模板的界面如下：也许大家咋一看，切~ 这算啥，我也会做这张表格，实在是太简单了．不错,如果仅仅是靠手动输入这样子的数字,也许只要懂一点点eｘcｌｅ的人都会制作出这张表格吧。

不过,这张表格并不是你表面所看到的仅仅是几个数字而已，其内在的公式才是它的亮点。

也许这样讲大家还不是很清楚,我继续给大家截个图,看看它里面的公式是什么。

大家注意到上面的公式了吗,并不是仅仅是输入数字就完事的，它是一个自定义函数zb ｘ(）,那么后面的都是一样吗？完全正确,后面的都是自定义函数,它们分别是zby（）、sqx(）、hpｚ()、hpｙ（)。

也许大家会问,恩，是不错,但是有什么用呢？那让我先给大家简述一下这个自定义函数的用法。

竟然是一个函数,那么它就必须要有一个自变量，这几个函数的自变量又是什么呢?其实这个模板里面所有函数的自变量只有一个，就是桩号。

什么意思?就是只要你给出任意一个桩号，都能得到其对应的坐标、中桩高程和横坡度.假设我们要K３8+０00～K38+200段落内每隔2０M一个断面所有点的坐标、中桩高程、以及左右横坡。

我就用这个模板给大家演示一下（此模板暂时数据只针对黄祁高速公路六标项目部）。

先在桩号那一列把K3８+000～K38+200输入进去,可不要真的把字母“K”和加号“+”给输进去,只用输入纯数字就行了，否则计算会出错,之所以在模板里显示的是那样子,只不过是自定义的单元格式而已。

第二步剩下的仅仅就是拖动公式了，后面的都是公式,所以可以一起拖下来，先选定后面的所有单元格,然后向下直接拖动至最后,那么你需要的数据就全部出来了。

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：。

公路测量坐标计算公式引言公路测量是一项基础工作，用于确定公路建设或维护所需的各个节点坐标。

在公路工程领域，测量坐标计算公式是至关重要的工具，用于测算和确定公路各个位置的坐标信息。

本文将介绍公路测量坐标计算公式的原理和应用。

坐标系统在公路测量中，使用的坐标系统通常是平面直角坐标系。

这个坐标系统由X轴和Y轴组成，其中X轴表示东西方向，Y轴表示南北方向。

公路测量中，测量标准一般会规定一个起始点作为基准点，所有的测量点都以该基准点为原点建立坐标。

公路测量坐标计算公式坐标计算原理坐标计算公式的原理是通过已知的测量数据和几何关系，推导出待求点的坐标。

常用的坐标计算方法包括三角测量法、坐标转换法和横断面测量法等。

三角测量法三角测量法是基于三角形几何学原理的坐标计算方法。

它通过测量已知点与待求点之间的夹角和距离，利用三角函数关系计算出待求点的坐标。

三角测量法适用于平面内的测量，并具有较高的精度。

坐标转换法坐标转换法是将已知点的坐标转换到待求点坐标的计算方法。

它利用已知点和待求点在同一坐标系统中的相对位置关系，通过坐标转换公式计算待求点的坐标。

坐标转换法适用于已知点坐标较为准确的情况。

横断面测量法横断面测量法适用于公路等线性工程的坐标计算。

它通过测量已知点的高程和于待求点的高程差，利用高程差和水平距离之间的关系计算待求点的坐标。

横断面测量法适用于公路中断面的测量和计算。

应用示例公路测量坐标计算公式在实际工程中具有广泛的应用。

下面以一个简单的示例来说明其应用过程：假设有一段公路，已知起点的坐标为（0,0），终点的坐标为（1000,0）。

现在需要测算该公路上距离起点100米处的坐标。

根据三角测量法，可以通过测量起点和待求点之间的夹角和距离来计算待求点的坐标。

假设测量得到的夹角为45度，距离为100米。

根据三角函数的性质，可以计算出待求点的坐标为（100,100）。

总结公路测量坐标计算公式是公路工程中不可或缺的工具。

通过三角测量法、坐标转换法和横断面测量法等方法，可以准确计算公路上各个位置的坐标信息。

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知：①缓和曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当计算第二缓和曲线上的点坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ，yZ为点HZ的坐标切线角计算公式：二、圆曲线上的点坐标计算已知：①圆曲线上任一点离ZH点的长度：l②圆曲线的半径：R③缓和曲线的长度：l0④转向角系数：K(1或－1)⑤过ZH点的切线方位角：α⑥点ZH的坐标：xZ，yZ计算过程：说明：当曲线为左转向时，K=1，为右转向时，K=-1，公式中n的取值如下：当只知道HZ点的坐标时，则：l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ，yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明：l——任意点到起点的曲线长度（或缓曲上任意点到缓曲起点的长度）l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知：①第一坡度：i1(上坡为“＋”，下坡为“－”)②第二坡度：i2(上坡为“＋”，下坡为“－”)③变坡点桩号：SZ④变坡点高程：HZ⑤竖曲线的切线长度：T⑥待求点桩号：S计算过程：五、超高缓和过渡段的横坡计算已知：如图，第一横坡：i1第二横坡：i2过渡段长度：L待求处离第二横坡点（过渡段终点）的距离：x 求：待求处的横坡：i解：d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知：①待求点桩号：K②曲线起点桩号：K0③曲线终点桩号：K1④曲线起点坐标：x0，y0⑤曲线起点切线方位角：α0⑥曲线起点处曲率：P0(左转为“－”，右转为“＋”)⑦曲线终点处曲率：P1(左转为“－”，右转为“＋”)求：①线路匝道上点的坐标：x,y②待求点的切线方位角：αT计算过程：注：sgn(x)函数是取符号函数，当x<0时sgn(x)=-1，当x>0时sgn(x)=1，当x=0时sgn(x)=0。

智璟安卓工程计算系统公路路线坐标计算说明书一、计算原理1、公路路线坐标计算是用线元法方式进行坐标、方位角（均指中桩切线方位角）的计算的，其中缓和曲线是用复化辛普森公式进行计算的。

线元法计算方式通用性强，不用区分直线、圆曲线、缓和曲线的组合方式，计算对象为每一个独立的线元，而非组合线型。

计算方式为通过逐个计算每个线元的终点坐标、方位角来计算整条路线上任意一点的坐标和方位角。

2、公路路线坐标计算所指的线元仅为直线、圆曲线和缓和曲线（回旋线）这三种，要求两线元交接点的曲率半径和方位角相同，即前一线元终点的曲率半径、方位角等于后一线元起点的曲率半径、方位角；如果两线元交接点的曲率半径不同，需要采用加入虚线元的方式进行处理，但仍需保证两线元交接点的方位角相同。

3、计算前先要建立整条路线的基本数据及线元终点桩号、终点曲率半径的数据库，计算时选择路线文件后只要输入所在路线上的任何一个桩号，即可进行此桩号坐标和方位角的计算。

4、建立路线数据库可以在程序界面提示下逐个手工输入数据，也可以通过外部TXT 文本文件导入数据，毕竟用电脑在TXT文件中输入数据更快、更方便。

5、由于计算任意桩号的坐标、方位角都是从整条路线的起点坐标、方位角开始逐个线元计算出来的，因此为了减少累积误差，均采用较高的计算精度，在利用辛普森公式迭代计算时，曲线分段数（迭代次数）均给予了偏高的取值，保证每次计算X、Y坐标同时精确到0.000001；同时角度（8位小数）、半径（6位小数）数据均要求较高的输入精度。

由于计算方式、计算精度、数据输入精度（角度、半径）的不同，计算结果可能与设计给出的结果存在微小的偏差，属正常现象。

6、程序未提供断链处理功能，如果整条路线有断链情况，请从断链处分段建立不同的路线文件。

7、程序只适合于一般手机竖屏显示状态下的正常使用。

二、功能介绍1、对整条路线上任意桩号的中桩、正交边桩、斜交边桩的坐标进行计算，包括中桩切线方位角。

ZY 里程=JD 里程-T ； YZ 里程=ZY 里程+L ；公路工程常用公式一、三角函数公式：1）、在直角三角形 ABC 中，如果/ C=90°,Z A ,Z B ,Z C 所对的边分别为a , b , c ,那么®锐角之间的关系为/ A+Z B=90°O 边角之间的关系为（4）其他有关公式公路测量常用公式:|'1 LU◎S = R0EC —— 1] 外距： 2（1 ）主点里程的计算①三边之间的关系为肚'+沪三F（勾股定理）sin A =—csmB =— ccosB =—Ctail A =-□tanB =— a c ot A = 一a acotB =—h= —ab 面积公式：2-Ckc 2 （hc 为c 边上的高）2）、正弦公式，即为正弦定理在一个三角形中，各边和它所对角的 等。

正弦的比相（2R 在同一个三角形中是恒量，是此三角形外接圆的半径的两倍）这一定理对于任意三角形ABC,都有貝卩 a/sinA=b/sinB=c/sinC=2R(1)a/sinA=b/sinB=c/sinC=2RR 为三角形外接圆半径正弦定理的变形公式⑴ a=2RsinA, b=2RsinB, c=2RsinC;3）任意三角形余弦公式： a 2=b 2+c 2-2bc （cosA ） 二、弧长公式：n n r/180;扇形面积公式：n n r 2/360(2) sinA : sinB ; sinC = a : b : c;2 2 2;cosA=(b +c -a )/2bc一、圆曲线：曲线要素的计算 若已知：转角a 及半径R ，则:切线长: ；曲线长:QZ里程=YZ里程-L/2 ；JD里程=QZ里程+D/2 （用于校核）（1）切线角公式P上丄比Q——缓和曲线长所对应的中心角。

（2 ）缓和曲线角公式（3）缓和曲线的参数方程（4）圆曲线终点的坐标k ISO"枣血――缓和曲线全长J所对应的中心角亦称缓和曲线角。