本科毕业设计中期检查报告范本

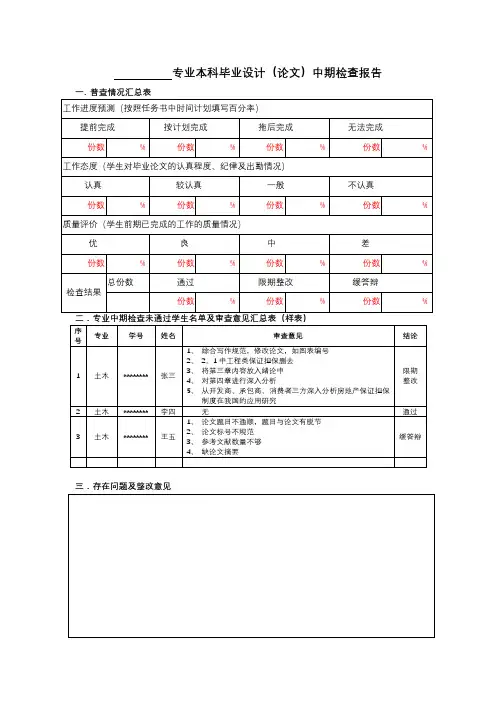
（中期检查报告规范）
毕业设计（论文）中期检查报告（二号宋体字加粗居中）
题目：（四号宋体字）
专业：（四号宋体字）
学生：（四号宋体字）
指导教师：（四号宋体字）
＊＊＊＊＊学院（四号宋体字居中）
二00 年月日（四号宋体字居中）
一、毕业设计（论文）进度安排（四号宋体字）
内容（小四号宋体，行距1.25）
二、开题或第一次阶段检查以后完成的工作（四号宋体字）
内容（小四号宋体，行距1.25）
三、存在问题及解决措施（四号宋体字）
内容（小四号宋体，行距1.25）
四、后期工作计划（四号宋体字）
内容（小四号宋体，行距1.25）
打印规格：A4纸，左右页边距各2cm，上下页边距各2.5cm。

本科毕业设计中期报告尊敬的评委，同学们：大家好！我是XX学院计算机系XX班的XX，今天非常荣幸地站在这里，向大家汇报我本科毕业设计的中期进展情况。

首先，我选题的背景和意义。

随着互联网的普及和信息技术的飞速发展，人们对于数据处理和数据安全的需求越来越高。

同时，随着大数据的兴起，对于数据的存储和处理能力也提出了更高的要求。

因此，我选择了“基于云计算的大数据管理系统的设计与实现”作为我的毕业设计课题。

其次，我完成了本课题的相关调研工作。

我通过查阅大量的文献资料和网络资源，了解了大数据管理系统的基本概念、关键技术和研究现状。

并且，我还分析了目前已有的大数据管理系统存在的问题和不足之处。

通过调研，我得出结论，云计算技术在大数据管理系统中具有重要的作用，可以提高数据的处理效率和安全性。

因此，我确定了本课题的主要目标，就是设计一个基于云计算的大数据管理系统，并实现相关的功能和特性。

接下来，我进行了系统的设计。

根据调研结果，我确定了系统的总体架构和模块划分。

我将系统分为数据采集、数据存储、数据处理和数据分析四个模块，在每个模块中又分别设计了若干子模块和功能。

同时，我还考虑了系统的扩展性和可靠性问题，使得系统在面对大量数据和高并发操作时仍能稳定运行。

在设计过程中，我遇到了一些困难和问题。

例如，如何选择合适的云计算平台和工具，如何设计高效的数据存储和处理算法等。

但是通过不断的学习和实践，我逐渐解决了这些问题。

最后，我进行了一些初步的实验和测试。

我使用了一个开源的大数据集进行了数据采集和存储的实验，并对测试结果进行了分析和比较。

实验结果表明，我设计的系统能够稳定、高效地处理大规模的数据，并提供快速的数据查询和分析功能。

目前，我已经完成了本课题的大部分设计和实验工作。

下一步，我将继续进行系统的完善和优化，并进行更多的实验和测试，以验证系统的性能和可靠性。

同时，我还将撰写毕业论文，对整个项目进行总结和分析。

在此，我衷心感谢我的指导教师和同学们对我毕业设计工作的支持和鼓励。

上海电机学院
本科生毕业设计（论文）中期检查报告
按照工作计划的安排，完成英文科技资料的翻译，积极准备并完成开题答辩和开题报告，通过到图书馆借阅相关的书籍、期刊；上网查阅相关的资料文献和学术论文等；并向相关人士和指导老师请教和了解相关知识。

因此，对毕业设计中所涉及的理论知识以及它们的应用有所了解和掌握，从若干个设计方案中获得最优化设计方案，对毕业设计系统的总体方案进行了最充分的论证。

并且到当地化工厂进行实地考察，了解了在现今化工厂中所用到的废液处理系统，并确定了其发展方向和所要求的精度范围。

在收集大量的资料后，开始对毕业设计（论文）系统进行整体方案设计（重要是硬件系统的设计），现正在进行硬件部分的部分单元电路设计。

目前已经完成了翻译外文资料、系统硬件原理方框图设计、单片机（AT89C51）、A/D（ADC0809）、D/A（DAC0832）、键盘/显示接口电路、传感变送电路等的设计。

基于以上各个部分的设计及连接，此系统的硬件组成基本完善，但还存在一些问题。

河北联合大学本科毕业设计（论文）中期检查报告题目：10KV线路微机自动化装置设计学院：电气工程学院专业：电气工程及其自动化班级：09 电气 2 班姓名：李卓学号：200901050206指导教师：屈滨2013年4月10日微机保护的算法采用傅氏变换算法导数式算法是针对理想正弦信号进行计算，由于故障时的电流、电压波形畸变很大，此时不能把他们假设为单一频率的正弦函数，而应该假设它们是包含各种分量的周期函数，这时就要采用傅氏变换算法。

傅氏变换算法来自于傅里叶级数，以电流为例，即一个周期性函数I （t ）可用傅里叶级数展开为各次谐波的正弦项和余弦项之和，即：∑∞=+=011]sin cos [)(nns ne t I t n I t i ωω （1.1）式（1.1）中，n 为自然数，n=0,1,2……表示谐波分量次数。

于是电流)(t i 中的基波分量可表示为：t I t I t i e s 11111cos sin )(ωω+= （1.2）)(t i 还可以表示为一般表达式：)sin(2)(111αω+=t I t i （1.3）式（1.3）中，1I 为基波有效值；1α为t=0时基波分量初相角。

将)sin(11αω+t 用和角公式展开，再与式（1.2）比较，可以得到：111cos 2αI I S =（1.4） 111sin 2αI I C =（1.5）从式（1.4）和式（1.5）可以看出，只要求出基波的正弦幅值S I 1和余弦幅值C I 1，就很容易救得基波的有效值和初相角1α。

根据傅氏级数的逆变换原理可求的和：⎰=Ts tdt t i TI 011sin )(2ω （1.6）⎰=Tc tdt t i TI 011cos )(2ω （1.7）在用微机计算s I 1和c I 1时，通常都是采用有限离散方法算得，即将用各采样点数值代入，通过梯形法就和来代替积分法。

考虑到N k T t N /2,1πω==∆时式（1.6）和式（1.7）可表示为⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛=∑-=1112sin 21N k k sN k i N I π （1.8） ⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫⎝⎛+=∑-=11012cos 1N k k k ci N ki i N I π （1.9） 式中，N 为一周采样点数；k i 为弟k 次采样值；0i 、n i 分别为k=0和N 时的采样值。

★毕业设计中期汇报_共10篇范文一:毕业设计中期汇报中期汇报表１、开题以来所做的具体工作和取得的进展和成果自开题以来，我所做的工作主要是完成小型生物膜反应器的设计,并补充前期设计方面没有考虑全面的问题.所取得的进展和成果:1。

收集资料,阅读文献了解课题背景，研究内容和主要目的；收集与生物膜反应器有关的资料,阅读相应的文献；了解相关的法律法规２.实地调研，制定生物膜反应器设计方案（确定工艺流程）３.撰写与生物膜反应器有关的读书报告4.已完成部分构筑物的计算（粗格栅、细格栅和调节池）２、下一步的主要研究任务，具体设想和安排1．完成生物膜反应器系统的其他构筑物的设计２．完成设备及构筑物的绘图３、存在的具体问题１．对选取的生物膜反应器不够熟悉2.已设计好的构筑物，偶尔会出现问题,仍需校核范文二:毕业设计中期汇报表2021届本科生毕业（设计)中期汇报表填表日期：2021年专姓业名建筑环境与设备工程王宇学院月日工程学院杨忠国指导教师（设计）题目**市某住宅楼地板辐射采暖毕业设计1、初步完成了毕业设计的初期的负荷计算,进行了地热盘管的初步方案确定。

２、负荷计算中,地板辐射采暖不考虑高度附加，计算地面负荷是乘以０.95的附加系数,冷风渗透耗热量采用换气次数法设计,冷风侵入耗热量采用外门开启附加计算。

3、负荷计算后还需乘以1。

2的家俱遮挡系数。

毕业（设计)前期工作小结4、绘制图纸时，盘管距墙面的距离应为200mm，地热盘管间距应为300mm。

５、本设计选用分户调节的方案，所以**户盘管在方案确定中尽量每房间一个环路，如果该房间较大,可以一个房间多个环路。

6、楼梯间采用散热器采暖，散热器选择钢制柱式散热器GＺ－２-20-1．0.7、散热器片数采用等温降法算得。

８、散热器布置在前5层.9、由于本设计是多层住宅楼工程，采用下供下回式采暖系统。

1０、本设计供回水系统采用同程式。

11、本设计完全按照最新规范设计,达到规范的**点要求.指导教师意见指导教师签名:范文三：毕业设计中期检查汇报提纲航海学院毕业设计(）中期检查汇报提纲题目水下ＲOV设计与仿真专业名称班级自动化03030９01高小斌刘卫学生姓名指导教师(.)研究背景和意义(选题、选题依据、理论价值或工程应用前景):一、研究背景：自上世纪90年代以来,水下机器人(ROV）在海洋科学考察和军事领域得到了非常应用。

毕业设计论文工作中期检查自查报告一、工作目标回顾在进行毕业设计论文工作的中期检查自查报告之前，回顾工作目标非常重要。

本次毕业设计的目标是研究企业的生产流程，并进行改进优化，以提高生产效率和降低成本。

具体而言，工作目标包括以下几个方面：1.调研企业现有生产流程：了解企业目前的生产流程、设备使用情况以及生产效率等相关数据。

2.分析现有问题：通过对企业生产流程的调研和数据分析，识别出当前生产流程中存在的问题和瓶颈。

3.提出改进方案：基于问题的分析，提出相应的生产流程改进方案，并进行模拟和评估，以验证改进方案的可行性和效果。

4.实施改进方案：在验证改进方案的可行性之后，将改进方案实施到企业的生产流程中，并进行效果跟踪和评估。

二、工作进展情况1.调研企业现有生产流程：通过与企业相关部门的沟通和访谈，成功获取了企业的生产流程和设备使用情况等相关数据。

2.分析现有问题：在对企业的生产流程进行详细调研和分析的基础上，成功地识别了生产流程中存在的一些问题和瓶颈，如生产线设计不合理、设备维护不及时等。

3.提出改进方案：基于对现有问题的认识和理解，提出了一系列的生产流程改进方案，包括调整生产线布局、优化设备维护计划等。

并基于模拟和评估的方法，对这些改进方案进行了验证和评估。

4.实施改进方案：在验证改进方案可行性的基础上，成功地将一部分改进方案实施到企业的生产流程中，包括对生产线布局的调整和设备维护计划的优化。

并对实施后的改进方案进行了效果跟踪和评估。

三、存在的问题和困难在工作过程中，也遇到了一些问题和困难，主要包括以下几个方面：1.数据获取困难：由于涉及的数据涉及到企业的内部情况，因此在获取部分数据时遇到了困难，需要与企业相关部门进行沟通和协调。

2.实施改进方案困难：由于企业的生产流程改变涉及到多个部门和人员的协作，因此在改进方案的实施过程中遇到了一定的困难，需要耐心和沟通来解决。

3.模拟和评估的复杂度：对改进方案进行模拟和评估是确保其可行性和效果的重要手段，但由于存在复杂的多变量和不确定性，模拟和评估的过程较为复杂，需要借助相关工具和方法的支持。

2024年毕业设计检讨书尊敬的评审老师、亲爱的班主任、亲爱的同学们：大家好！我是XXX，是XXX专业的一名学生。

今天，我要向大家汇报一下我本次毕业设计的进展以及自我检讨。

首先，我想回顾一下我本次毕业设计的主题和目标。

我选择的题目是XXX，并且希望通过本次设计，能够完成XXX。

于是，我进行了一系列的文献调研和实地调查，对相关理论和技术进行了研究和学习。

在初期的规划中，我制定了详细的计划和时间表，并且与指导老师进行了充分的讨论和交流，确保了毕业设计工作的顺利进行。

然而，在实际的实施过程中，我遇到了一些困难和挑战。

首先，我对于XXX方面的知识和技术了解不够深入，导致在实际操作中遇到了一些问题。

其次，时间的安排和管理上也存在一些不足，导致进度拖延，工作效率不高。

最后，我在撰写论文和制作展示文稿的过程中，存在表达不清晰、组织不合理等问题，影响了我对于毕业设计成果的阐述和展示。

针对以上问题，我深刻反思了自己的不足，并且采取了一些措施进行改进。

首先，我加强了对于相关知识和技术的学习，通过查阅大量的文献资料和参与讨论，我逐渐提高了对于XXX的理解和运用能力。

同时，我也积极寻求老师和同学的帮助和建议，通过与大家的讨论和交流，我对于毕业设计的方向和思路有了更加清晰的认识。

其次，我合理规划了时间，并制定了详细的计划和任务，通过将任务细化和分解，我能够更好地掌控进度，提高自己的工作效率。

最后，我认真研读了相关学术论文和毕业设计报告，并结合自己的实践经验进行反思和总结，改进了论文和文稿的写作方式和组织结构，提高了表达的准确性和清晰度。

通过这次毕业设计，我收获了很多。

首先，我在实际应用中深入了解了XXX，并且对于其中的一些关键技术和方法有了更加深刻的认识。

其次，我学到了如何进行有效的团队协作和沟通，通过与同学们的讨论和交流，我认识到了团队的力量和合作的重要性。

最后，我明白了毕业设计除了要求我们的专业知识和技术水平，更需要我们具备一种主动学习、解决问题的能力和良好的沟通能力。

毕业设计中期报告毕业设计中期报告1根据教务处《关于做好20xx届本科学生毕业设计(论文)中期检查的通知》文件精神，教科学院认真组织了自查工作。

现将自查情况汇报如下：一、学院领导高度重视学院领导和毕业论文领导小组成员在毕业论文领导小组工作会议上认真学习了《通知》精神，做了专门讨论和研究，决定成立由学院督导委员会成员为组成的毕业论文中期检查专家组，具体负责本次毕业论文中期检查工作，制定了工作步骤、方式和要求，安排好各自任务。

二、计划周密我院依据学校的检查通知，参照通知要求的检查内容和方式，制定了周密详细的工作计划。

分两个阶段进行检查。

第一阶段是自查阶段，学院教学管理科、指导教师和学生自我检查论文中期工作情况，并且做好学院检查的准备。

第二阶段是学院检查阶段，对学院的管理资料、指导教师的《中期检查表》和部分学生的论文资料进行全面检查。

在全面检查的基础上，分别召开指导教师和学生座谈会，听取他们对学校、学院在毕业论文工作的规章制度、保障措施等方面的意见和建议，以进一步规范管理和提高毕业论文的质量。

三、检查工作认真细致在自查阶段，学院各方面都能够认真仔细，圆满按时保质保量地完成工作。

3月26日下午，我院督导委员会成员按照计划安排，分别进行了资料检查、教师代表座谈会和学生代表座谈会。

(一)毕业论文中期资料检查按照教务处《通知》要求，我院决定对于学院的相关文件资料和指导教师的《中期检查表》进行全面检查，学生论文资料抽查不少于总数的1/4，每班随机抽取10名学生的资料，检查论文工作的完成情况。

具体检查情况如下：1.管理方面：学院毕业设计(论文)工作管理文件，包括文件、通知等资料完整、规范、有序。

毕业论文工作计划制定详细具体，符合学校的要求，切合学生的学习情况，整个论文工作执行基本按照计划安排的时间点推进，目前论文工作已经完成计划的80%多。

学院制定的《毕业论文实施细则》符合学院学科专业特点与要求，符合学校的’毕业论文工作要求，对于毕业论文工作的各个方面工作要求细致而明晰，一目了然。

《毕业设计中期报告》毕业设计中期报告（一）：20XX届毕业论文(设计)中期检查报告第一部分总体状况我校2007届毕业论文(设计)中期检查于4月15-19日进行。

此次，中期检查分为两个部分进行：学院自查和专家检查。

在学院开展为期一周的自查后，学校30多名督导专家分别到各学院抽查学生的毕业论文(设计)，并就毕业论文(设计)工作进行学生问卷调查。

此次，督导专家从六个方面检查了八十多个专业三百多名学生的毕业论文(设计)前期开展的工作。

从专家上报的检查状况和学生的问卷调查来看，督导专家对我校各学院的毕业论文(设计)前期工作，学生的毕业论文(设计)的进度、论文前期各环节的质量，以及指导教师的指导等方面基本上是满意的，总体状况与质量比较好。

各学院领导都比较重视本科毕业论文(设计)工作，都能根据学校要求，根据学院的具体状况，及时部署毕业论文(设计)工作，能够认真开展各个环节的工作;绝大部分指导教师工作认真负责，给予学生以悉心的指导和帮忙。

但是，透过检查也发现一些问题。

比如，有些学院接教务处通知后，并没有对本学院毕业论文(设计)工作进行统一安排;教务处文件、通知都要求在第七学期末就要开始进入新一届毕业论文(设计)工作，可有些学院毕业论文(设计)工作仍然开始的过晚，学生反映时间太紧;透过专家检查和学生座谈发现，还有一些学院仍然没有统一对学生进行过毕业论文(设计)的写作培训，学生不知怎样写论文，不会写论文，感到无从下手，对毕业论文(设计)写作方法、格式等也都不很了解;有些指导教师由于自己工作忙等原因，对指导的学生指导、关心不够;指导学生时间太少。

学生方面由于考研、考公务员、找工作等大多集中在三、四月份，对毕业论文(设计)干扰和影响很大，情绪浮躁，有部分学生对毕业论文(设计)不够认真和重视，时间上也不能够保证等问题。

老师和学生反映最突出的问题是图书资料缺乏且陈旧过时;实验设备不足;指导不够;事先对所选课题缺乏了解。

学院没有对学生进行毕业论文(设计)写作培训。