下载文档原格式
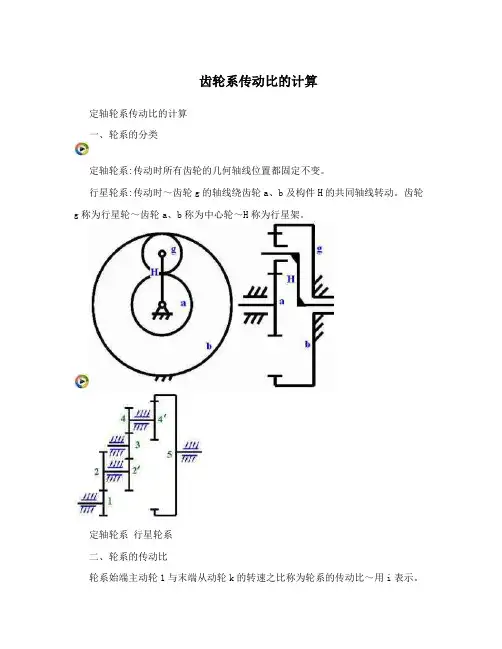
齿轮系传动比的计算定轴轮系传动比的计算一、轮系的分类定轴轮系:传动时所有齿轮的几何轴线位置都固定不变。
行星轮系:传动时～齿轮g的轴线绕齿轮a、b及构件H的共同轴线转动。
齿轮g称为行星轮～齿轮a、b称为中心轮～H称为行星架。
定轴轮系行星轮系二、轮系的传动比轮系始端主动轮1与末端从动轮k的转速之比称为轮系的传动比～用i表示。
,n11i,,1k,nkk传动比的计算包括大小和方向两个方面。
三、一对齿轮传动比的计算1、大小的计算,一对齿轮传动比等于主动齿轮的角速度与从动齿轮角速度的比值～亦等于两齿轮齿数的反比。
1,nz112i,,,12,nz2212、方向的判断,,正负号法: 1式中正负号表示两轮的转向相同或相反～仅适用于圆柱齿轮传动,平面齿轮传动,。
2,画箭头法:外啮合时方向相反,反向箭头,～内啮合时方向相同,同向箭头,。
锥齿轮同时指向节点或同时背离节点。
蜗杆传动的转向也只能用画箭头法来表示。
外啮合内啮合锥齿轮蜗杆传动四、定轴轮系传动比的计算1、大小的计算,图示轮系中～齿轮1为主动轮～齿轮5为末端从动轮～下面讨论定轴轮系传动比的计算方法。
2m 这个公式计算出的仅是定轴轮系传动比的大小～方向则可采用,,1,法或画箭头法慈范ā?/span>2、方向的判断,m 1,,,1,法:只适用于圆柱齿轮所组成的定轴轮系。
m表示外啮合齿轮的对数。
2,画箭头法:先画出主动轮的转向箭头～根据一对齿轮传动转向的箭头表示法～依次画出各轮的转向。
它是确定定轴轮系从动轮转向的普遍适用的方法。
3、定轴轮系传动比的计算通式,上述结论可适用于任何轮系。
设轮,为始端主动轮～轮k为末端从动轮～则轮系传动比大小的计算公式为:n从动轮齿数连乘积1i,,1kn主动轮齿数连乘积k对于转向的判断有两种情况:1,当齿轮都是圆柱齿轮且各轴线平行时～从动轮的转向不是相同就是相反～m此时可采用,,1,法。
n从动轮齿数连乘积m1,,,i(1)1kn主动轮齿数连乘积k32,若轮系中有圆锥齿轮传动或蜗杆蜗轮传动时～则可采用画箭头法。
齿轮齿条传动力计算公式
齿轮齿条传动力计算公式主要包括传动比和转动惯量两个部分。
传动比是指齿轮和齿条之间的速比，公式为：传动比 = 齿轮有效齿数/齿条齿数。
有了传动比，我们就可以根据齿轮和齿条的不同尺寸来计算出输出轴和输入轴之间的速比，即：输出轴转速/输入轴转速 = 传动比。
转动惯量是指齿轮和齿条组件的惯性，公式如下：转动惯量 = 齿轮转动惯量 + 齿条转动惯量。
以上信息仅供参考，如有需要，建议咨询机械设计工程师或查阅机械设计类书籍。
1.传动比=从动轮齿数/主动轮齿数=主动轮转速/从动轮转速i=z2/z1=n1/n2。
2.低速齿轮直接影响减速器的尺寸和重量，降低低速齿轮的传动比意味着降低低速齿轮和包含低速齿轮的机体的尺寸和重量。
3.增大高速齿轮的传动比，即增大高速齿轮的尺寸，减小了高速齿轮和低速齿轮的尺寸差，有利于所有齿轮同时油浴润滑。
4.同时，高速小齿轮尺寸减小后，高速小齿轮和后齿轮的圆周速度降低，有利于降低噪声和振动，提高传动稳定性。
5.所以在满足强度的情况下，最终传动比小是合理的。
6.扩展信息:注:齿轮加工的工艺性能是指不同的材料能满足不同的加工工艺要求。
7.齿轮的常见制造形式有铸造、锻造、切削和热处理。
8.不同的工艺性能直接影响齿轮材料的选择。
9.2.铸造齿轮内部组织差，强度低，成本低，可应用于一般工况。
10.锻造齿轮内部组织严密，强度高，但成本高，可在苛刻的工作条件下应用。
11,3.另外，塑料、球墨铸铁、灰铸铁、铸钢的切削工艺性能较好，但强度不够高，淬透性差，机械性能一般，只能在一般工况下使用。
12.合金钢如调质钢、淬火钢、渗碳淬火钢和氮化钢具有良好的淬透性和高强度。
行星齿轮传动比8个公式
1.齿轮比计算公式：
齿轮比=-(R+2)/(R+1)，其中R为行星轮的齿数。
2.行星轮直径公式：
行星轮的直径可以通过行星轮齿数来计算。
行星轮直径=齿数*模数。
3.太阳轮直径公式：
太阳轮的直径可以通过太阳轮齿数来计算。
太阳轮直径=齿数*模数。
4.行星轮轮齿厚度公式：
行星轮的轮齿厚度可以通过行星轮直径和模数来计算。
行星轮轮齿厚度=2*模数。
5.太阳轮轮齿厚度公式：
太阳轮的轮齿厚度可以通过太阳轮直径和模数来计算。
太阳轮轮齿厚度=2*模数。
6.行星齿轮传动的速度比公式：
速度比=齿数A/齿数B，其中齿数A为太阳轮齿数，齿数B为行星轮齿数。
7.行星齿轮传动的扭矩比公式：
扭矩比=(半径A/半径B)^2，其中半径A为太阳轮半径，半径B为行星轮半径。
8.行星齿轮传动的传动效率公式：
传动效率=输出功率/输入功率。
综上所述，行星齿轮传动的8个常用公式分别是齿轮比计算公式、行星轮直径公式、太阳轮直径公式、行星轮轮齿厚度公式、太阳轮轮齿厚度公式、行星齿轮传动的速度比公式、行星齿轮传动的扭矩比公式和行星齿轮传动的传动效率公式。
这些公式帮助工程师在设计和计算行星齿轮传动时能够准确地确定齿轮比、轮齿尺寸和传动性能等参数，从而提高传动系统的可靠性和效率。
传动比公式是：传动比=主动轮转速除以从动轮转速的值=其分度圆直径比值的倒数。
具体含义如下：
1. 在机械传动系统中，其始端主动轮与末端从动轮的角速度或转速的比值，被称为传动比。
2. 传动比(i)=主动轮转速(n1)与从动轮转速(n2)的比值=齿轮分度圆直径的反比=从动齿轮齿数(Z2)与主动齿轮齿数(Z1)的比值。
即i=n1/n2=D2/D1 i=n1/n2=z2/z1。
3. 对于多级齿轮传动，每两轴之间的传动比按照上面的公式计算。
从第一轴到第n轴的总传动比等于各级传动比之积。
4. 传动比是机构中两转动构件角速度的比值，也称速比。
构件a和构件b的传动比为i=ωa/ωb=na/nb，式中ωa和ωb分别为构件a和b的角速度（弧度/秒）；na和nb分别为构件a和b的转速（转/分）。
当式中的角速度为瞬时值时，则求得的传动比为瞬时传动比。
当式中的角速度为平均值时，则求得的传动比为平均传动比。
理论上对于大多数渐开线齿廓正确的齿轮传动，瞬时传动比是不变的；对于链传动和摩擦轮传动，瞬时传动比是变化的。
对于啮合传动，传动比可用a和b轮的齿数Za和Zb表示，i=Zb/Za；对于摩擦传动，传动比可用a和b轮的直径Da和Db表示，i=Db/Da。
希望以上信息对您有所帮助，如果您还有其他问题，欢迎告诉我。
齿轮系传动比的计算齿轮系统是一种常用的传动装置，通过两个或多个齿轮之间的啮合来实现不同轴的旋转传动。
传动比是指输入轴和输出轴的转速之比，通常用于计算齿轮传动的输出速度以及扭矩的增减。
计算齿轮传动比涉及到齿数和模数的计算，下面将详细介绍齿轮传动比的计算公式和步骤。
1.齿数的计算：齿数是齿轮的一个重要参数，可以用来计算齿轮传动比。
如果已知输入轴齿轮的齿数为N1，输出轴齿轮的齿数为N2，那么传动比K为：K=N2/N12.模数的计算：模数是齿轮的另一个重要参数，用来描述齿轮的齿大小和齿距之间的关系。
模数可以通过以下公式计算：m=D/(Z+2)其中，m为模数，D为齿轮的分度圆直径，Z为齿数。
3.传动比的计算：已知输入轴齿轮的齿数为N1，输出轴齿轮的齿数为N2，齿轮的模数分别为m1和m2，则传动比K为：K=N2/N1=(m2/m1)*(D1/D2)在实际计算中，可以根据已知的参数来计算模数，然后使用模数来计算齿轮的分度圆直径，最后计算出传动比。
齿轮的模数、齿数和分度圆直径的计算公式如下：D=m*(Z+2)m=K*m1N=(π*D)/m其中，D为分度圆直径，m为模数，Z为齿数，N为轮齿数。
除了传动比的计算，齿轮系统在实际应用中还需要考虑一些其他因素，如轴间距的确定、齿轮啮合角等。
这些因素都会对齿轮传动比的计算和实际传动效果产生影响。
总结：齿轮传动比的计算涉及到齿数和模数的计算，传动比可以通过已知的齿数和模数来计算。
同时，在实际应用中还需要考虑一些其他因素的影响，如轴间距和齿轮啮合角。
这些因素的综合作用使得齿轮传动比的计算变得更加复杂，在实际应用中需要综合考虑多个因素来确定传动比。
三级齿轮组的传动比计算
三级齿轮组是由三个齿轮组成的传动系统，其中每个齿轮都与相邻的齿轮啮合。
传动比是指传动系统中输出轴（输出齿轮）转速与输入轴（输入齿轮）转速之间的比值。
在三级齿轮组中，传动比可以通过下面的公式来计算：
传动比=(输出齿轮的齿数/输入齿轮的齿数)*(输出齿轮的齿数/输入齿轮的齿数)*(输出齿轮的齿数/输入齿轮的齿数)
换句话说，传动比等于每一级齿轮的传动比相乘。
举个例子，假设三级齿轮组的齿轮参数如下：
输入齿轮（第一级）：齿数为N1，转速为S1
中间齿轮（第二级）：齿数为N2，转速为S2
输出齿轮（第三级）：齿数为N3，转速为S3
传动比=(N2/N1)*(N3/N2)*(S3/S1)
在实际计算中，要注意单位的一致性，确保输入和输出的齿数和转速单位相同，一般都使用齿数或转速的数量级，如齿数个、转速转/分等。
三级齿轮组的传动比计算较为复杂，但这个公式可以帮助你计算三级齿轮组的整体传动比。
根据具体的齿轮参数，可以轻松计算出传动比，并根据需要进行进一步的设计和分析。
齿 轮 系 传 动 比 计 算 C1 齿轮系的分类在复杂的现代机械中，为了满足各种不同的需要，常常采用一系列齿轮组成的传动系统。
这种由一系列相互啮合的齿轮（蜗杆、蜗轮）组成的传动系统即齿轮系。
下面主要讨论齿轮系的常见类型、不同类型齿轮系传动比的计算方法。
齿轮系可以分为两种基本类型：定轴齿轮系和行星齿轮系。
一、定轴齿轮系在传动时所有齿轮的回转轴线固定不变齿轮系，称为定轴齿轮系。
定轴齿轮系是最基本的齿轮系，应用很广。
如下图所示。
二、行星齿轮系若有一个或一个以上的齿轮除绕自身轴线自转外，其轴线又绕另一个轴线转动的轮系称为行星齿轮系，如下图所示。
1. 行星轮——轴线活动的齿轮.2. 系杆 (行星架、转臂) H .3. 中心轮 —与系杆同轴线、与行星轮相啮合、轴线固定的齿轮4. 主轴线 —系杆和中心轮所在轴线.5. 基本构件—主轴线上直接承受载荷的构件.行星齿轮系中，既绕自身轴线自转又绕另一固定轴线（轴线O1）公转的齿轮2形象的称为行星轮。
支承行星轮作自转并带动行星轮作公转的构件H 称为行星架。
轴线固定的齿轮1、3则称为中心轮或太阳轮。
因此行星齿轮系是由中心轮、行星架和行星轮三种基本构件组成。
显然，行星齿轮系中行星架与两中心轮的几何轴线（O1-O3-OH ）必须重合。
否则无法运动。
根据结构复杂程度不同，行星齿轮系可分为以下三类：（1）单级行星齿轮系： 它是由一级行星齿轮传动机构构成的轮系。
一个行星架及和其上的行星轮及与之啮合的中心轮组成。
（2）多级行星齿轮系：它是由两级或两级以上同类单级行星齿轮传动机构构成的轮系。
（3）组合行星齿轮系：它是由一级或多级以上行星齿轮系与定轴齿轮系组成的轮系。
行星齿轮系 根据自由度的不同。
可分为两类： 1450rpm 53.7rpm1 2 H 3 1 2 3 4 H 51 2 H 3（1） 自由度为2 的称差动齿轮系。
（2） 自由度为1 的称单级行星齿轮系。
按中心轮的个数不同又分为：2K —H 型行星齿轮系；3K 型行星齿轮系；K —H —V 型行星齿轮系。
2 定轴齿轮系传动比的计算一、齿轮系的传动比齿轮系传动比即齿轮系中首轮与末轮角速度或转速之比。
进行齿轮系传动比计算时除计算传动比大小外，一般还要确定首、末轮转向关系。
确定齿轮系的传动比包含以下两方面：(1) 计算传动比I 的大小；(2) 确定输出轴(轮)的转向.二、定轴齿轮系传动比的计算公式1、一对齿轮的传动比：传动比大小:i 12=ω1/ω2 =Z 2/Z 1转向 外啮合转向相反 取“-”号内啮合转向相同 取“+”号对于圆柱齿轮传动，从动轮与主动轮的转向关系可直接在传动比公式中表示即：i 12=±z 2/z 1其中"+"号表示主从动轮转向相同，用于内啮合；"－"号表示主从动轮转向相反，用于外啮合；对于圆锥齿轮传动和蜗杆传动，由于主从动轮运动不在同一平面内，因此不能用"±"号法确定，圆锥齿轮传动、蜗杆传动和齿轮齿条传动只能用画箭头法确定。
对于齿轮齿条传动，若ω1表示齿轮1角速度，d1表示齿轮1分度圆直径，v2表示齿条的移动速度，存在以下关系：V 2=d 1ω1/2对于一个轮系：如图所示为一个简单的定轴齿轮系。
运动和动力是由轴经Ⅱ轴传动Ⅲ轴。
Ⅰ轴和Ⅲ轴的转速比，亦即首轮和末轮的转速比即为定轴齿轮系的传动比：齿轮系总传动比应为各齿轮传动比的连乘积，从Ⅰ轴到Ⅱ轴和从Ⅱ轴到轴Ⅲ传动比分别为：i 12=n1/n2=-Z 2/Z 1; i 34=n 2/n 3=-Z 4/Z 3314234123234131421Z Z Z Z Z Z Z Z n n n n i i i =-⨯-=⨯=⨯=定轴齿轮系传动比，在数值上等于组成该定轴齿轮系的各对啮合齿轮传动的连乘积，也等于首末轮之间各对啮合齿轮中所有从动轮齿数的连乘积与所有主动轮齿数的连乘积之比。
设定轴齿轮系首轮为1轮、末轮为K 轮，定轴齿轮系传动比公式为：i =n1/nk=各对齿轮传动比的连乘积i 1k=(-1)M 所有从动轮齿数的连乘积/所有主动轮齿数的连乘积式中："1"表示首轮，"K"表示末轮，m 表示轮系中外啮合齿轮的对数。
当m 为奇数时传动比为负，表示首末轮转向相反；当m 为偶数时传动比为负，表示首末轮转向相同。
注意：中介轮(惰轮)不影响传动比的大小,但改变了从动轮的转向。
例题8-1 如图所示齿轮系，蜗杆的头数z1=1，右旋；蜗轮的齿 数z2=26。
一对圆锥齿轮z3=20，z4=21。
一对圆柱齿 轮z5=21，z6=28。
若蜗杆为主动轮，其转速n1=1500r/min ，试求齿轮6的转速n6的大小和转向。
解 ：根据定轴齿轮系传动比公式：4.36212012821265316426116=⨯⨯⨯⨯===z z z z z z n n i 转向如图中箭头所示。
例题8-2 如图所示定轴齿轮系，已知z1=20，z2=30，z'2=20，z3=60，z'3=20，z4=20，z5=30，n1=100r/min 。
逆时针方向转动。
求末轮的转速和转向。
解：根据定轴齿轮系传动比公式，并考虑1到5间有3对外啮合，故末轮5的转速8.1475.61001515-=-==i n n (r/min) 负号表示末轮5的转向与1首轮相反，顺时针转动。
3 行星齿轮系传动比的计算一、 单级行星齿轮系传动比的计算对于行星轮系，其传动比的计算，肯定不能直接用定轴齿轮系传动比的计算公式来计算，这是因为行星轮的轴线在转动。
为了利用定轴齿轮系传动比的计算公式，间接计算行星齿轮系的传动比，必须采用转化机构法。
即假设给整个齿轮系加上一个与行星架H 的转速大小相等，转向相反的附加转速“—n H ”。
根据相对性原理，此时整个行星轮系中各构件间的相对运动关系不变。
但这时行星轮架转速为零。
即原来运动的行星轮架转化为静止。
这样原来的行星齿轮系就转化为一个假象的定轴轮系。
这个假象的定轴轮系称原行星轮系的转化机构。
对于这个转化机构的传动比，则可以按定轴齿轮系传动比的计算公式进行计算。
从而也可以间接求出行星齿轮系传动比。
转化轮系：给整个机构加上－n H 使行星架静止不动n H ＝0，各构件之间相对运动关系不变，这个转换轮系是个假想的定轴轮系。
行星轮系的组成太阳轮：齿轮1、3行星轮：齿轮2行星架：构件H行星轮系的传动比计算构件 原转速 相对转速中心轮1 n 1 n 1＝n 1－n H行星轮2 n 2 n 2＝n 2－n H中心轮3 n 3 n 3＝n 3－n H行星架H n H n H ＝n H －n H ＝0转化轮系为定轴轮系13313113z z n n n n n n i H H H H H -=--==“－”在转化轮系中齿轮1、3转向相反。
一般公式：/3/21532351)1(Z Z Z Z Z Z n n i -==所有主动轮齿数乘积至从所有从动轮齿数乘积至从K G K G n n n n n n i m H K H G H KH G H GK )1(-=--== 式中：m 为齿轮G 至K 转之间外啮合的次数。
(1)主动轮G ，从动轮K ，按顺序排队主从关系。
(2)公式只用于齿轮G 、K 和行星架H 的轴线在一条直线上的场合。
(3)n G 、n K 、n H 三个量中需给定两个；并且需假定某一转向为正相反方向用负值代入计算。
例8—3：如图所示的行星轮系中已知电机转速n 1=300r/min （顺时针转动）当z 1＝17，z 3 =85，求当n 3=0和n 3=120r/min （顺时针转动）时的n H 。
解：例8—4.行星齿轮系如图所示， 已知各齿轮的齿数分别为：Z 1 = 15，Z 2 = 25， Z 2’ = 20Z 3 = 60， n 1=200 rpm ， n 3=50 rpm ，且转向图示。
求：系杆的转速n H 的大小和转向？解:根据相对转动原理可知：例题8-5行星齿轮系如图所示， 已知各齿轮的齿数分别为：且齿数Z a = Z b ；转速n a 、n H 也知道。
求：B 轮的转速n b=?解: 根据相对转动原理可列出方程:min/5051785120300min/50517853001331r n n n r n n n z z n n n n H H H H H H H H -=-=-=---=-=-=---=--'21323113z z z z n n n n i H H H⋅⋅-=--=2015602550200⨯⨯-=---H H n n rpmn H 33.8-= a bc H a bc H 1-=-=--=ab H b H a H ab z z n n n n i H b a n n n 2=+a H b n n n -=2Hc Ha H ac n n n n i --=二、多级行星齿轮系传动比的计算多级行星齿轮系传动比是建立在各单级行星齿轮传动比基础上的。
其具体方法是：把整个齿轮系分解为几个单级行星齿轮系，然后分别列出各单级行星齿轮系转化机构的传动比计算式，最后再根据相应的关系联立求解。
划分单级行星齿轮系的方法是：（1）找出行星轮和相应的系杆（行星轮的支架）；（2）找出和行星齿轮相啮合的太阳轮（3）由行星轮、太阳轮、系杆和机架组成的就是单级行星齿轮系。
（4）列出各自独立的转化机构的传动比方程，进行求解。
在多级行星齿轮系中，划分出一个单级行星齿轮系后，其余部分可按上述方法继续划分，直至划分完毕为之。
三、组合行星齿轮系传动比的计算在实际应用中，有的轮系既包含定轴轮系又包含行星齿轮系。
则形成组合轮系。
计算混合轮系传动比一般步骤如下：1、区别轮系中的定轴轮系部分和行星齿轮系部分。
2、分别列出定轴轮系部分和行星齿轮系部分的传动比公式，并代入已知数据。
3、找出定轴轮系部分与行星齿轮系部分之间的运动关系，并联立求解即可求出组合轮系中两轮之间的传动比。
如图所示的组合行星齿轮系分解为由由齿轮Z1、Z2组成的定轴轮系1-2由齿轮Z2/、Z3、Z4组成的行星轮系2´-3-4-H组成例题8—7如图所示的扬机机构中已知各齿轮的齿数为：Z1=24, Z2=48, Z2/=30, Z3=90, Z3/=20, Z4=40,Z5=100。
求传动比i1H。
若电动机的转速n1=1450r/min，其卷筒的转速n H为多少。
解：首先把齿轮系进行分解；（1）定轴轮系3’-4-5（2）行星轮系1-2-2’-3-H由定轴轮系可得：由行星轮系可得：补充方程'355'3zz-=ωω3'3ωω=5ωω=H其余联立方程求解即可。
