当前位置：文档之家 › 大学物理第十一章光学第4节 劈尖 牛顿环

大学物理第十一章光学第4节 劈尖 牛顿环

  • 格式：ppt
  • 大小：969.50 KB
  • 文档页数：27

下载文档原格式

  / 27

合集下载

牛顿环和劈尖干——实验报告

牛顿环和劈尖干——实验报告

牛顿环和劈尖干涉【实验目的】1. 学习用牛顿环测量透镜的曲率半径和劈尖的厚度。

2. 熟练使用读数显微镜。

【实验仪器】移测显微镜，钠光灯，牛顿环仪和劈尖装置。

【实验原理】测量透镜曲率半径的公式为：224()m nd dRm nλ-=-【实验内容】一、用牛顿环测量透镜的曲率半径1．调节牛顿环仪，使牛顿环的中心处于牛顿环仪的中心。

（为什么？）2. 将牛顿环仪置于显微镜平台上，调节半反射镜使钠黄光充满整个视场。

此时显微镜中的视场由暗变亮。

（一定能调出条纹吗？）3. 调节显微镜，直至看清十字叉丝和清晰的干涉条纹。

（注意：调节显微镜物镜镜筒时，只能由下向上调节。

为什么？）4. 观察条纹的分布特征。

察看各级条纹的粗细是否一致，条纹间隔是否一样，并做出解释。

观察牛顿环中心是亮斑还是暗斑，若为亮斑，如何解释？5. 测量暗环的直径。

转动移测显微镜读数鼓轮，同时在目镜中观察，使十字刻线由牛顿环中央缓慢向一侧移动然后退回第30环，自30环开始单方向移动十字刻线，每移动一环即记下相应的读数直到第25环，然后再从同侧第15环开始记数直到第10环；穿过中心暗斑，从另一侧第10环开始依次记数到第15环，然后从第25环记数直至第30环。

并将所测数据记入数据表格中。

（为什么测量暗环的直径，而不是测量亮环的直径？）6. 观察透射光束形成的牛顿环。

7. 观察白光产生的牛顿环（选做）二、利用劈尖测量薄片厚度（表格自拟）利用牛顿环测透镜的曲率半径【思考与讨论】1、用移测显微镜测量牛顿环直径时，若测量的不是干涉环直径，而是干涉环的同一直线上的弦长，对实验是否有影响？为什么？2、透射光能否形成牛顿环？它和反射光形成的牛顿环有什么区别？。

4等厚干涉劈尖牛顿环

4等厚干涉劈尖牛顿环

r 2ndk 2n 2R 2 2
2 k
nr R 2
2 k
k
( k 1,2) 加强
(2k 1)
2 k

2
( k 0,1,2) 减弱
2.牛顿环半径 明环由
nr k R 2
rk ( k 1 / 2)R / n
§4.等厚干涉、劈尖、牛顿环 / 三、牛顿环
e

2n

n
相邻两明纹的间距与相应厚度差e 间存在如下关系
l sin e
在角很小时，有

2n


2n l
例12－13 用波长λ=500nm (1nm =10－9 m）的单色光垂直照射 在由两块玻璃板（一端刚好接触成为劈棱）构成的空气劈尖上， 劈尖角 =2×10－2rad ，如果劈尖内充满折射率为 n= 1.40的 液体，求从劈棱数起第五个明条纹在充入液体前后移动的距离。 解：设第五个明纹处膜厚为 e， 则有 2 n e + λ ／2 = 5 λ 设该处至劈棱的距离为L，则有近似关系 e =L ， 由上两式得 2nL = 9λ／2 ， L= 9λ／4 n 充入液体前第五个明纹位置 L1= 9λ／4 充入液体后第五个明纹位置 L2= 9λ／4 n 充入液体前后第五个明纹移动的距离 L=L1 - L2＝9λ(1 – 1／n )／4 = 1.61 mm
l

2n sin


2n
hk
Pk
当平玻璃慢慢向上平移，干涉条纹向棱边方向平移，明纹 或暗纹之间的距离是相同的
答案[c]
例12－12 用波长为的单色光垂直照射折射率为n的劈尖薄膜 形成等厚干涉条纹，若测得相邻明条纹的间距为，则劈尖角＝ －－－－－。 解：相邻两明纹之间的厚度差为

大学物理第十一章光学第4节 劈尖 牛顿环

大学物理第十一章光学第4节 劈尖 牛顿环

例 1 波长为680 nm的平行光照射到L=12 cm长的两块玻璃片上，两玻璃片的一边相互 接触 ，另一边被厚度Ｄ=0.048 mm的纸片隔开. 试问在这12 cm长度内会呈现多少条暗条纹 ? 解
2d

2 k 0,1,2,
( 2k 1)

2
第 十一章 光学
7
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
n2
SiO2
e
Si
eN
第 十一章 光学

2n1
9
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
(3)检验光学元件表面的平整度
e
b e b 2
'
b b'
1 3 2 6
第 十一章 光学
10
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
(4)测细丝的直径
讨论
n

(1)棱边处
D
d 0
n / 2
L
n1
Δ 为暗纹. 2 1
b
劈尖干涉
d
(k ) （明纹） 2 2n
k 2n （暗纹）
第 十一章 光学
2
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
b
n1 n
(2)相邻明纹（暗纹）间 的厚度差
n

d i 1 d i
第 十一章 光学
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
讨 明环半径 论 暗环半径
1 r (k ) R (k 1,2,3,) 2 r kR (k 0,1,2,)

2009-2010第21次课 等厚干涉 劈尖、牛顿环

2009-2010第21次课 等厚干涉 劈尖、牛顿环

2n
6
b
θ
3.相邻条纹间距 相邻条纹间距
dk
θ
dk+1
∆d
∆d λ b= = Q θ 很小， sin θ ≈ θ sin θ 2n sin θ
7
b=
λ
2n sin θ
λ ≈ 2nθ
λ
θ=
λ
2nb
θ
n
8
4.空气劈尖 空气劈尖
n
b
n1 n1
d
∆ = 2d +
λ
2
kλ , k = 1,2,L ∆= λ
2 k
dk
r dk = 2R
2 k
22
λ = 2n r + λ ∆ = 2ndk +
2 k
2
2R
2
r dk = 2R
( k = 1,2L) 加强
2 k
r λ = + = R 2
2 k
kλ
(2k + 1)
λ
2
( k = 0,1,2L) 减弱
r λ + = kλ R 2
2 k
牛顿环半径： 牛顿环半径： 明环由
•测量未知单色平行光的波长、测透镜曲率半径 测量未知单色平行光的波长、 测量未知单色平行光的波长
用读数显微镜测量第 k 级和第 m 级暗环 半径 rk、rm
rk = kRλ rm = mRλ
2 k
r − r = mRλ − kRλ
2 m
(r − r ) λ= (m − k ) R
2 m 2 k
(D − D ) λ= 4(m − k ) R
例2
解
Q
θ=
λ
2nb

大学物理11-4 薄膜干涉(2)汇总

大学物理11-4 薄膜干涉(2)汇总

例 11-8 干涉膨胀仪如图所示,
干涉膨胀仪
一个石英圆柱环B放在平台上，
其热膨胀系数极小，可忽略不计。l
环上放一块平破璃板P，并在环
内放置一上表面磨成稍微倾斜的 柱形待测样品R，石英环和样品
l0
B
的上端面已事先精确磨平，于是
R的上表面与P的下表面之间形
成楔形空气膜，用波长为 的
单色光垂直照明，即可在垂直方 向上看到彼此平行等距的等厚条
dk
2n
n
2
b
n1 n
sin n 2
b
3）条纹间距（明纹或暗纹）
b 2n
tan D L
D n L L
2b 2nb
L
n n / 2 D
n1
b
劈尖干涉
11 - 4 薄膜干涉（2）
4 ）干涉条纹的移动
每一条 纹对应劈尖 内的一个厚 度，当此厚 度位置改变 时，对应的 条纹随之移 动.
2
所以对于厚度均匀的平面薄膜来说，光程差是随光线的倾
角（入射角）的改变而改变，倾角相同，光程差相同，干
涉条纹的级数也相同。
11 - 4 薄膜干涉（2）
第十一章 波动光学
1 劈 尖干涉
n
T
L
n1
n1
d
S
劈尖角
M
2nd
D
2
n n1
k, k 1,2, 明纹
b
(2k 1) , k 0,1, 暗纹
B
膨胀值为 l N
2
根据热膨胀系数的定义
l
l0T
得样品的热膨胀系数
l N
l0T 2l0T
11 - 4 薄膜干涉（2） 劈尖干涉的应用

东北大学大学物理总结课件

东北大学大学物理总结课件

3.会分析缝宽及波长对衍射条纹分布的影响。
4
11-8 圆孔衍射 光学仪器的分辨本领
1.了解夫琅和费圆孔衍射、艾里斑、瑞利判据、衍射对
光学仪器分辨本领的影响；
2.理解最小分辨角、光学仪器的分辨本领；
3.能够根据已知条件计算出光学仪器所能分辨的最小距
离。
11－9 衍射光栅
1.理解光栅、光栅常数、光栅衍射、缺级等概念；
17
5.理解可逆过程与不可逆过程的概念，能够使用公式：
dS dQ T
2 dQ
S2 S1 1 T
（对可逆过程）
计算基本的可逆与不可逆过程前后熵变。
6.理解玻尔兹曼关系式：
S k lnW
7.理解熵与热力学第二定律的统计意义。
8.了解信息熵。
18
CV
d e dT
V
iR 2
15
8.掌握p-V图中绝热线与等温线的区别及其形成的原因。
9.循环过程:
(1)掌握循环过程的特征;
(2)掌握正循环与热机(包括热机效率公式)间的关系;
(3)掌握逆循环与制冷机(包括制冷系数公式)间的关系。
10.掌握与理想气体循环过程有关的计算:
主要包括：吸热、作功、内能变化和效率、制冷系
明确作功和吸热是与过程有关的物理量。
4.热力学第一定律：掌握热力学第一定律的内容及其数
学表述： Q W E dQ dW d E
14
5.理解内能的概念: 明确内能是状态的单值函数，其增量只与始末状态
有关，而与系统所经历的具体过程无关的结论。 6.热力学第一定律的应用： (1)掌握理想气体等容、等温、等压和绝热过程的特征， 过程方程(其中绝热过程的过程方程要求会推导); (2)掌握上述过程中气体吸热、作功和内能变化的计算。 7.掌握理想气体热容量的计算方法和迈耶公式，能使用 能量均分定理计算各种刚性分子理想气体的热容量。

11-4劈尖 牛顿环

11-4劈尖 牛顿环
2 2 2 1 2
λ
2
i=0
n =1
类 似 劈 d 尖
光程差
∆ = 2nd +
λ
2
∆ = 2d +
λ
2
16
光程差
λ = ∆ = 2d +
2
kλ (k = 1,2,⋯)
(2k +1)
明纹
λ
2
(k = 0,1,⋯) 暗纹
R r d
d相同，则光程差 ∆ 相同
d = 0， = λ / 2 , k = 0(暗） ∆
dk = k
明纹
λ
2n 2
k = 0,1,2,⋯
明纹
24
dk = k
λ
2n 2
k = 0,1,2,⋯
k = 0,
明纹
n2 = 1.2 λ = 600nm
油膜边缘
d0 = 0 零级明纹
k = 1, d 1 = 250 nm 一级明
k = 2 , d 2 = 500 nm 二级明
k = 3, d 3 = 750 nm 三级明
设: n =1
=(2k+1λ/2 k级暗 )
d :↑ (λ / 2)，∆ :由k级↑ (k +1)
(o) : d = 0, ∆ = λ / 2，k = （暗） 0
(o) : d = 0 ↑ λ / 2
∆ = 3λ / 2
k = （暗） 1
条纹向左移动
10劈尖Biblioteka 涉的应用(1)干涉膨胀仪∆l
l0
11
波长为680 nm的平行光照射到 的平行光照射到L=12cm 例 1 波长为 的平行光照射到 长的两块玻璃片上， 长的两块玻璃片上，两玻璃片的一边相互接触 ， 另一边被厚度Ｄ 的纸片隔开. 另一边被厚度Ｄ=0.048mm的纸片隔开 试问在这 的纸片隔开 12cm长度内会呈现多少条暗条纹 ? k = ? 长度内会呈现多少条暗 长度内会呈现多少条 解 ∆ = 2d +

劈尖-牛顿环知识

劈尖-牛顿环知识

nn21 G
dk k 2n2
k 0,1,2,
第 十一章 光学
21
物理学
第五版
hr
oR
11-4 劈尖 牛顿环
油膜边缘 k 0, d0 0
k 1, d1 250 nm
k 2, d2 500 nm
d k 3, d3 750 nm
k 4, d4 1000 nm
由于 h 8.0102 nm 故 可观察到四条明纹 .
b
第 十一章 光学
4
物理学
第五版
11-4 劈尖 牛顿环
b
L
n1 n
n
n / 2 D
n1
(3)条纹间距
b 2n
D n L L
2b 2nb
b
劈尖干涉
第 十一章 光学
5
物理学
第五版
11-4 劈尖 牛顿环
(4 )干涉条纹的移动
第 十一章 光学
6
物理学
第五版
11-4 劈尖 牛顿环
例 1 波长为680 nm的平行光照射到 L=12 cm长的两块玻璃片上，两玻璃片的一 边相互接触 ，另一边被厚度Ｄ=0.048 mm的 纸片隔开. 试问在这12 cm长度内会呈现多 少条暗条纹 ？
解 2d (2k 1)
2
2
k 0,1,2,
第 十一章 光学
7
物理学
第五版
2d (2k 1)
2
2
2D
2
(2km
1)
2
km
2D
141.2
共有142条暗纹
11-4 劈尖 牛顿环
k 0,1,2,
第 十一章 光学
8
物理学
第五版

普通物理学劈尖牛顿环优秀课件

普通物理学劈尖牛顿环优秀课件

3）将牛顿环置于 n1的液体中，条纹如何变？
4）应用例子:可以用来测 量光波波长，用于检测透镜质 量，曲率半径等。
工件 标准件
测量透镜的曲率半径
R
rk2 kR
r
rk2 m(km )R
R
r2 km
rk2
m
2r
例2：用氦氖激光器发出的波长为633nm的单色光做
牛顿环实验，测得第个 k 暗环的半径为5.63mm , 第 k+5 暗环的半径为7.96mm，求平凸透镜的曲率半径R。
Rd d20
r 2dR ()R
r (k1)R 明环半径
2
2
r kR 暗环半径
讨 论
明环半径
r (k1)R (k1,2,3, )
2
暗环半径 r kR (k0,1,2, )
1）从反射光中观测，中心点是暗点还是亮点？ 从透射光中观测，中心点是暗点还是亮点？（互补）
2）属于等厚干涉，条纹间距不等，为什么？
普通物理学劈尖牛顿 环
b
L
b
n1 n
n n / 2 D
n1
讨论
（1）劈尖 d 0
为暗纹. 2
(k 1) （明纹）
d 2 2n
劈尖干涉
k 2n （暗纹）
（2）相邻明纹（暗纹）间的厚度差
dk1dk
n
2n 2
b
DL n 2
b
（3）条纹间距（明纹或暗纹）
L
n1 n
n n / 2 D
如果 M 2 平移 d
的距离，则非线性增长 条纹不等间距。
3）条纹的动态变化分析（ n,, 变化时）。
4 ）半波损失需具体问题具体分析。
n n

大学物理第5版课件 第11章 光学

大学物理第5版课件 第11章 光学

1
M1 n1 n2
M2 n1
L 2
iD
3
A C

B
E
45
P
d
第十一章 光学
35
物理学
第五版
Δ32

n2
( AB

BC)

n1 AD


2
AB BC d cos γ
AD ACsin i
n2 n1
L
2
P
2d tan sini
1
iD 3
M1 n1 n2
A
C
d
M2 n1
B
C
d
M2 n1
B
E
45
注意：透射光和反 射光干涉具有互补 性 ，符合能量守恒 定律.
第十一章 光学
38
物理学
第五版
当光线垂直入射时 i 0
当 n2 n1 时
Δr

2dn2


2
当 n3 n2 n1 时
Δr 2dn2
第十一章 光学
n1 n2 n1
n1 n2
n3
39
物理学
第五版
四 了解衍射对光学仪器分辨率的影响.
五 了解 x 射线的衍射现象和布拉格公式 的物理意义.
第十一章 光学
7
物理学
第五版
光的偏振
11-0 教学基本要求
一 理解自然光与偏振光的区别.
二 理解布儒斯特定律和马吕斯定律.
三 了解双折射现象.
四 了解线偏振光的获得方法和检验 方法.
第十一章 光学
8
物理学
第五版
第十一章 光学

113-4薄膜干涉劈尖牛顿环

113-4薄膜干涉劈尖牛顿环

条纹面间距
：
l
2n
l
k
k1 e
Chapter 11. 光学
作者：杨茂§田11. 3 -4薄膜干涉 劈尖 牛顿环
P. 21 / 36 .
利用劈尖干涉测量小物体尺寸 :
设 小物体高度为 h ，干涉
明纹 (或暗纹) 总数为 N：
N
int(
h e
)
1
o
e l sin l
条纹面间距
：
l
2n
o l e
2e
n22 n12 sin2 i
2
若：n2 = mid{ n1 ，n3 }
1
n1
i A
n2
2
3
D
iB
e
( n2
ACB
n1 AD )
2
n3
C
ACB 2e cos , AD AB sini 2e tg sini
Chapter 11. 光学
作者：杨茂§田11. 3 -4薄膜干涉 劈尖 牛顿环
l
2n
变密，向底边移动！
P. 24 / 36 .
上移时： 不变 l 不变
e k
疏密不密，向底边移动！
Chapter 11. 光学
2、牛顿环
作者：杨茂§田11. 3 -4薄膜干涉 劈尖 牛顿环
P. 25 / 36 .
o点处密接触，即 o 点 e = 0
2e
2
r 2 R2 (R e)2 2 Re e2
P. 15 / 36 .
Chapter 11. 光学
作者：杨茂§田11. 3 -4薄膜干涉 劈尖 牛顿环
P. 16 / 36 .
1、劈尖
设 垂直入射，空气劈尖 : i 0

等厚干涉牛顿环劈尖实验报告

等厚干涉牛顿环劈尖实验报告
继续转动鼓轮， 使十字叉线向右跨过圆环中心， 使竖直叉丝依次与第6级到第15级的暗环的右内侧相切， 顺次
记录读数。
同一级暗环的左右位置两次读数之差为暗环的直径。
2. 用劈尖测量薄片的厚度(或细丝直径)
(1) 将牛顿环器件换成劈尖器件， 重新进行方位与角度调整， 直至可见清晰的平行干涉条
纹， 且条纹与搭接线平行; 干涉条纹与竖直叉丝平行。
(2) 在劈尖中部条纹清晰处， 测出每隔10条暗纹的距离l， 测量5次。 (3) 测出两玻璃搭接线到薄片的有效距离L， 测量5次。
* 注意， 测量时， 为了避免螺距的空程误差， 读数显微镜的测微鼓轮在每一次测量过程中只能单方向旋转， 中途不能反转。
数据记录与处理: 牛顿环第一次测量直径
第二次测量直径
rk?2Rdk?kR?， k?0,1,2...,暗环
由以上公式课件， rk与dk成二次幂的关系， 故牛顿环之间并不是等距的， 且为了避免背光因素干扰， 一般
选取暗环作为观测对象。
而在实际中由于压力形变等原因， 凸透镜与平板玻璃的接触不是一个理想的点而是一个圆面; 另外镜面沾染回程会导致环中心成为一个光斑， 这些都致使干涉环的级数和半径无法准确测量。 而使用差值法消去附加的光程差， 用测量暗环的直径来代替半径， 都可以减少以上类型的误差出现。 由上可得:
3(用劈尖干涉法测定细丝直径或微小厚度。
[实验仪器]
牛顿环仪，移测显微镜、钠灯、劈尖等。
[实验内容]
1(用牛顿环测量平凸透镜表面的曲率半径
(1)按图11-2安放实验仪器
(2)调节牛顿环仪边框上三个螺旋，使在牛顿环仪中心出现一组同心干
涉环。将牛顿环仪放在显微镜的平台上，调节45?玻璃板，以便获得最大的照度。

大学物理B2_第11章_2

大学物理B2_第11章_2

2 垂直入射的光程差： 2dn2 2
2014年10月15日星期三
2dn2 cos

13
第十一章 光学2
2. 干涉条纹特点： 明暗相间等间距的条纹。 相同的厚度是同一条干涉条纹 3.明暗条纹位置 （1）明纹极大：
n
n1 n1
dk
2 （2）暗纹极小： 2d k n (2k 1) k 0,1,2,3... 暗纹 2 2 明纹 4. 条纹的膜厚度差 明纹之间 d d k 1 d k
15
第十一章 光学2
劈尖可测微小的厚度
b
n1 n
n

D
D tan L

D


2
2nb
L
n1

2nb
L
b
干涉条纹的移动
2014年10月15日星期三
16
第十一章 光学2
6. 劈尖干涉应用举例
1）干涉膨胀仪
2）测膜厚
n0
n2
l
n2 n1 n0
l0
si
n1
si o 2
d
b
明纹
暗纹
明暗纹之间的膜厚度差
5.明、暗条纹间距
d dk明 dk暗 4n
d d b tan sin
dk
d
d k 1
说明：对斜面上的间距与平面上的间距 视同相等。
因为 很小，以后在应用中对斜面或平面不加区分。
b 2 n
d
2014年10月15日星期三
2n 2 1.5 5 105 h 2nh ] [250] 250 暗条纹间距 ][ N [ ] [ 6 0.6 10 d N N 1 有251暗条纹。 明条纹有多少？ N明 250 解二： 2d k n (2k 1) 2 2 k 250 k 0,1,2,3... N 251

大学物理B2_第11章_4

大学物理B2_第11章_4
(2) 可分为波带数 当k=2，N=5； 当k=3，N=7
2014年10月15日星期三
13
第十一章 光学4
例2.在单缝夫琅禾费衍射实验中，垂直入射的光有两种波长， 1=400nm，2=760nm。已知单缝宽度b=1.0×10-2cm，透镜焦距
f=50cm。求两种光第二级衍射明纹中心之间的距离。 解：由明纹极大 b sin (2k 1) k2 2 5 52 sin 1.9 10 2 很小 2b 2b 5f 3 x ( ) 4 . 5 10 m x x x 2 1 2 1 sin tan 2b f 例3.设有一单色光斜射到宽度为b的单缝上， 求各级暗纹的衍射角。 解： AD BC b(sin sin )
暗纹极小的线位置
当 较大时，如 >3 时， sin tan sin k x f tan f sin 2 b 1 sin f x ( 2k 1) 2. 次明纹极大位置： b sin (2k 1) b 2 2 当 sin tan 一定要分别计算 2014年10月15日星期三
光栅的总缝数为N。通过每一狭缝向不同方向发射的光通过 透镜聚集在屏幕上不同的位置， 2.光栅衍射条纹的特点 光栅衍射是衍射和干涉的综合结果。或者说，光栅衍射条纹 21 是由缝间干涉花样受到单缝衍射的限制而产生的。 2014年10月15日星期三
第十一章 光学4
(1) =0的平行光会聚于O点，形成中央明纹，两侧出现一系列明 暗相间的条纹；
2014年10月15日星期三
k 1,2,3... k arcsin( sin ) b
k
14
第十一章 光学4 11-7 圆孔衍射 光学仪器的分辩本领

11-04劈尖 牛顿环 (2)

11-04劈尖 牛顿环 (2)


在劈尖棱处为零级暗条纹； 条纹宽度为b= /(2n)， 越小，条纹越疏； 相邻明纹或（暗纹）所对应的膜厚之差为 /(2n) ；
思考：1.如果劈尖不是空气而是介质，n ≠1，结论如何？ 2.如果劈尖角变大(或变小),条纹如何变化？ 3.如果劈尖上板向上(下)移动,条纹怎样变化？
§11-4 劈尖 牛顿环
k 2n （暗纹）
§11-4 劈尖 牛顿环
2）相邻明纹（暗纹）间的厚度差
d i 1 d i

2n

n
2
b
b
n1 n
D L
b 2 n
n 2

L
n
n / 2
D
3）条纹间距和最大厚度D
n1
D L 2nb
b
劈尖干涉
§11-4 劈尖 牛顿环
结论：

当平行光垂直照射空气劈尖时，干涉条纹为平行于 劈尖棱的明暗相间的等距直条纹；
2
5R r
R r
2 k 5
r
2 k

2
r
5
2 k
(7.96mm) (5.63mm) 10.0m 5 633nm
§11-4 劈尖 牛顿环
例3 利用牛顿环的干涉条纹，可以测定凹曲面的曲率半径。 在透镜磨制工艺中常用的一种检测方法是：将已知半径的 平凸面镜的凸面放在待测的凹面上（如图），在两镜面之 间形成空气薄层，可观察到环状的干涉条纹。 试证明第 k个暗环中心的半径rk与 凹面半径R2、凸面半径R1及光波波 长λ之间的关系式为
同心园环，内稀外密， 级次从中心到边缘越来 越低。 若膜厚e增加，则环纹向 边缘移动；若膜厚e减少， 则环纹向中心移动
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第 十一章 光学
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
讨 明环半径 论 暗环半径
1 r (k ) R (k 1,2,3,) 2 r kR (k 0,1,2,)
(1)从反射光中观测，中心点是暗点还 是亮点？从透射光中观测，中心点是暗点 还是亮点？ (2)属于等厚干涉，条纹间距不等，为 什么？
第 十一章 光学
24
物理学
第五版
牛顿环 11-4 11-4 劈尖 劈尖 牛顿环
h
r
o
R
讨论
d 油滴展开时，条纹间
距变大，条纹数减少
R2 r 2 [ R (h d )]2
r 2R(h d )
2
r2 R 2( h d )
第 十一章 光学
25
物理学
第五版
牛顿环 11-4 11-4 劈尖 劈尖 牛顿环
等厚干涉总结
(1)干涉条纹为光程差相同的点的轨迹，即膜的厚度 相等的点的轨迹. 牛顿环 劈尖
R
d
r
d
k 1 d

2n
26
第 十一章 光学
(2)厚度线性增长条纹等间距（劈尖条纹等宽平行）， 厚度非线性增长条纹不等间距（牛顿环条纹中心稀疏 边缘密集的圆环中心条纹比边缘的宽）. (3)条纹的动态变化分析（ n, , 变化时） i)向上平移时，条纹左移； d变化 /2，条纹移动b。 向下平移时，条纹右移。 ii) 变大条纹密集； 变小条纹稀疏。 (4)半波损失需具体问题具体分析.
2 k 2 k m
R
r
D 4kR
D
2 k 2 k mபைடு நூலகம்
4(k m)R
2 2 Dk D m k R 4m
2r D
第 十一章 光学
21
物理学
第五版
牛顿环 11-4 11-4 劈尖 劈尖 牛顿环
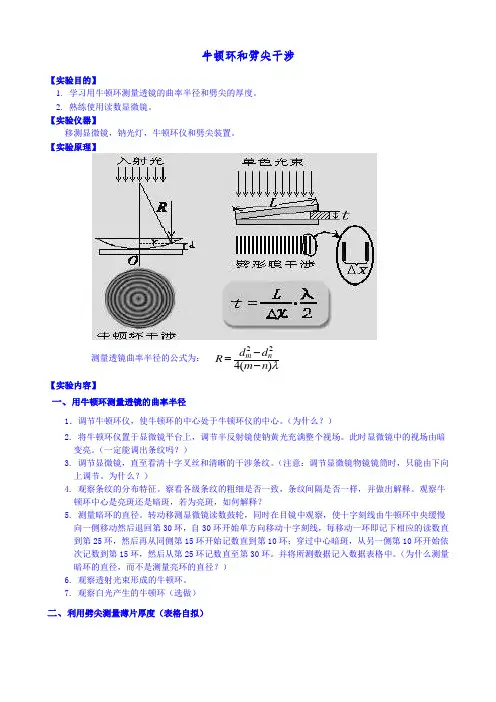
例2 如图所示为测量油膜折射率的实验装 置，在平面玻璃片G上放一油滴，并展开成圆 形油膜，在波长 600 nm 的单色光垂直入射 下，从反射光中可观察 到油膜所形成的干涉条 L 纹．已知玻璃的折射率 S 为 n1 1.50 ，油膜的折 射率 n2 1.20 ，问：当 n 2 h n1 G 油膜中心最高点与玻璃
空气 n 1
n1 n1
L
n
d
L d 2n b
b
第 十一章 光学
11
物理学
第五版
牛顿环 11-4 11-4 劈尖 劈尖 牛顿环
二
牛顿环
由一块平板玻璃和一平凸透镜组成
d
第 十一章 光学
12
物理学
第五版
牛顿环 11-4 11-4 劈尖 劈尖 牛顿环
牛顿环实验装置
显微镜 T L S M 半透 半反镜
n2
SiO2
e
Si
eN
第 十一章 光学

2n1
9
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
(3)检验光学元件表面的平整度
e
b e b 2
'
b b'
1 3 2 6
第 十一章 光学
10
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
(4)测细丝的直径
R
r
d
牛顿环干涉图样
第 十一章 光学
13
物理学
第五版
牛顿环 11-4 11-4 劈尖 劈尖 牛顿环
牛顿环照片
第 十一章 光学
14
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
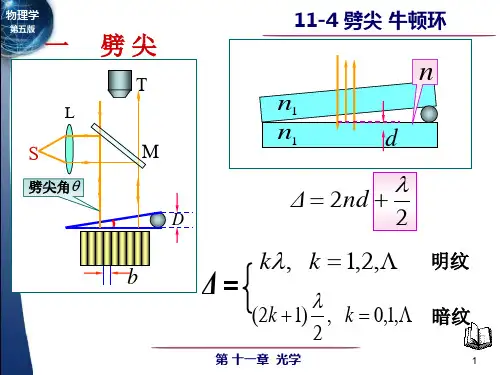
光程差
Δ 2d

2
明纹
R r d
Δ
k (k 1,2,)
1 (k ) (k 0,1,) 暗纹 2
第 十一章 光学
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
2 2 2 2
r R ( R d ) 2dR d
R d d 0
2
R r d
r 2dR ( Δ ) R 2 1 r (k ) R 明环半径 2 暗环半径 r kR
(3)属于等厚干涉，但是条纹间距不等。
牛顿环应用
rk kR
实用的观测公式:
rk m (k m)R
r
2 k m
r mR
2 k
▲测透镜球面半径R: 已知 , 测出m, rk+m, rk, 可得R ▲测 :已知R, 测出m, rk+m, rk, 可得
▲检测透镜球表面质量
r kR ( k 0,1,2,)
(1) 牛顿环是同心圆环,条纹从里向外逐渐变密,中心干 涉级次最低。 (2)中心接触点: d=0, '=/2 是暗纹;
R r rk 1 rk ( k 1) R kR ( k 1) k (4)将牛顿环置于n>1的液体中，条纹如何变？ 1 明环半径 r ( k ) R 2 n Δ 2nd 条纹半径 2 暗环半径 r kR n
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
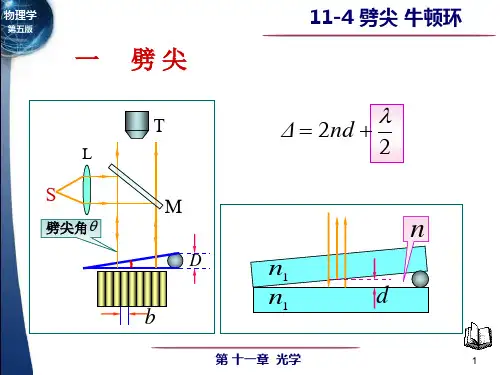
一
L
劈尖
T
n
n1 n1
S
劈尖角
M
D
d
Δ 2nd

2
明纹
b
Δ
k, k 1,2,
(2k 1) , k 0,1, 暗纹 2
1
第 十一章 光学
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
b
n1 n
讨论
n

(1)棱边处
D
d 0
n / 2
L
n1
Δ 为暗纹. 2 1
b
劈尖干涉
d
(k ) （明纹） 2 2n
k 2n （暗纹）
第 十一章 光学
2
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
b
n1 n
(2)相邻明纹（暗纹）间 的厚度差
n

d i 1 d i
第 十一章 光学
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
(3)将牛顿环置于 n 1 的液体中，条 纹如何变？ (4)应用例子:可以用来测量光波波长， 用于检测透镜质量，曲率半径等.
工 件 标 准 件
第 十一章 光学
讨 论
明环半径 暗环半径
1 r (k ) R ( k 1,2,3,) 2
n n
n1 n3
n2
n1 n2 n3

2n

n
2
n / 2
L
D
(3)条纹间距
n1
n 2 D L 且 b
b 2n
n D L L 2b 2nb
b
劈尖干涉
第 十一章 光学
3
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
(4 )干涉条纹的移动
a.两板夹角减小
时条纹间距变长。
b.上玻璃板竖直 向上移动时，条 纹左移；上玻璃 板竖直向下移动 时，条纹右移。
若条纹如图,说明待测透镜球B 表面不规则, 曲率半径有误差

标准验规 待测透镜 暗纹
2d

2 k=0,1,2,...喑纹
2 d k 2 一圈暗条纹表示球面有/2误差。
( 2k 1)

物理学
第五版
牛顿环 11-4 11-4 劈尖 劈尖 牛顿环 测量透镜的曲率半径
r kR r (k m)R
2d 2D
km

2 2
(2k 1)

2 2
k 0,1,2,

(2k m 1)
141 .1

2D

共有142条暗纹
第 十一章 光学
8
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
劈尖干涉的应用
(1)干涉膨胀仪
l N
(2)测膜厚
n1

2
l
l0
第 十一章 光学
4
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
劈尖 等厚干涉条纹 第 十一章 光学
不规则表面
5
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
白光入射
肥皂膜的等厚干涉条纹
单色光入射
第 十一章 光学
6
物理学
第五版
11-4 劈尖 牛顿环 11-4 劈尖 牛顿环
第 十一章 光学
22
物理学
第五版
牛顿环 11-4 11-4 劈尖 劈尖 牛顿环
片的上表面相距 h 8.0 10 nm 时，干涉条 纹是如何分布的？可看到几条明纹？明纹所 在处的油膜厚度为多少 ?
2
解 条纹为同心圆
L S
dk k
h
Δ 2n2dk k
明纹
n2 n1 G
2n2 k 0,1,2,
例 1 波长为680 nm的平行光照射到L=12 cm长的两块玻璃片上，两玻璃片的一边相互 接触 ，另一边被厚度Ｄ=0.048 mm的纸片隔开. 试问在这12 cm长度内会呈现多少条暗条纹 ? 解
2d

2 k 0,1,2,
( 2k 1)

2
第 十一章 光学