第1讲_基础知识
- 格式:pdf
- 大小:1.70 MB
- 文档页数:22

第1讲 方程的基本知识一、学习目标1.知识目标:理解方程的概念、什么是方程的解,学习等式的基本性质、方程的变形规则,学会移项;2.能力目标:会根据等式的性质对方程进行基本的变形,会正确的进行移项;3.情感目标:在学习方程基本知识的活动中获取成功的体验,激发学生学习数学的热情,建立自信心。
二、教学过程(一)课前测评(5分钟)1、下列各式:①7x-3=3x+5;②4x-7;③2²+3=7;④2x<5;⑤x+2y=3.其中是方程的有( ) A.2个 B.2个 C.3个 D.4个2、下列根据等式的性质变形不正确的是( ) A. 由x+2=y+2,得到x=y B.由2a-3=b-3,得到2a=b B. 由cx=cy,得到x=y D.由x=y,得到1122+=+c yc x 3、已知关于x 的方程3x-a-6=0的解是x=3,则a 的值为( ) A.1 B.-1 C.3 D.-34、已知a 、b 互为相反数,且ab ≠0,则方程ax+3b=0的解为 。
5、规定:★为一种新运算,对任意的有理数a,b ,有a ★b=52b a -,若2★x=53,则x= . 6、解下列方程:(1)x+5=-1; (2)-2x=6-3x; (2)231=x ; (4)-8x=4.(二)知识点拨1、方程的概念:含有 的 叫做方程.2、判断某数是否为方程的解:使方程左右两边相等的 是方程的解.3、等式的基本性质:①等式的两边都加上(或都减去)同一个数或同一个 ,结果仍然是等式。
即如果a=b,那么a ±c=b ±c;②等式两边都乘以(或除以)同一个数(除数 ),做得结果仍是 。
即如果a=b ,那么ac= ;如果a=b,那么=ca(c ≠0)。
4、方程的变形规则:①方程的两边都加上(或都减去)同一个数或同一个 ,方程的解 .②方程的两边都乘以(或都除以)同一个 的数,方程的解 。
5、理解移项的概念:将方程中的某些项 后,从方程的一边 另一边,这样的变形叫做移项。

第一节计算机的发展与应用复习目的:1、了解计算机的发展分类2、掌握计算机的工作原理、应用、病毒、操作系统3、要求对知识能熟练掌握之处,对重点内容能达到理解应用复习重点:1、计算机的工作原理2、计算机的发展、分类、应用3、计算机的病毒4、操作系统复习难点:计算机的性能指标的理解和应用高考指南:这部分主要题型是用于单选题,多选主要在病毒和操作系统。
计算机专业词汇测试也在这一章节复习过程及内容:一、计算机的工作原理1、概念:计算机是一种能接收和存储信息,并按照存储在其内部的程序对输入的信息进行加工、处理,然后把处理结果输出的高度自动化电子设备。
2、计算机工作原理也称冯.诺会依曼原理(称存储程序原理)[典型题型分析]1、世界上第一台电子计算机是()年,由美国科学家()发明的,其代号为ENIAC。
A、1945B、1946C、1947D、1948E、图灵F、福雷斯特G、莫奇里H、冯.诺依曼2.简述冯诺依曼原理的基本思想?(2004年高考题)二、计算机的发展按电子计算机所采用的元器件将其划分为四代(具体见P2页表1-1),从第四代的大、超大规模集成电路的出现进入微机时代(具体见P2页表1-2)[典型题型分析]1、第二代电子计算机的主要元件器件是()A、电子管B、晶体管C、小规模集成电路D、大规模集成电路相对应的第一代、第三代、第四代的电子元件必须记下。
2、微型计算机的分代是根据()划分的。
A、体积B、速度C、微处理器D、内存三、计算机的特点○1处理速度快:用MIPS(每秒执行多少百万条指令)来衡量○2计算精度高:用二进制码数来决定○3记忆能力强○4可靠的逻辑判断能力○5可靠性高,通用性强[典型题型分析]1、下列数据都表示为计算机处理数据的位数,()的精度最高A、16位B、32位C、64位D、128位2、下列哪些是属于计算机的特点的是()(多选)A、处理速度快B、可靠性高,通用性强C、连续性D、计算精度高F、信息管理四、计算机的性能指标○1主频:是指计算机CPU在单位时间内输出的脉冲数,定了计算机的运行速度,单位为MHZ。

第1讲化学实验基础知识和技能【考纲解读】1.了解化学实验室常用仪器的主要用途和使用方法。
2.掌握化学实验的基本操作,能识别药品安全使用标识。
3.了解实验室一般事故的预防和处理方法。
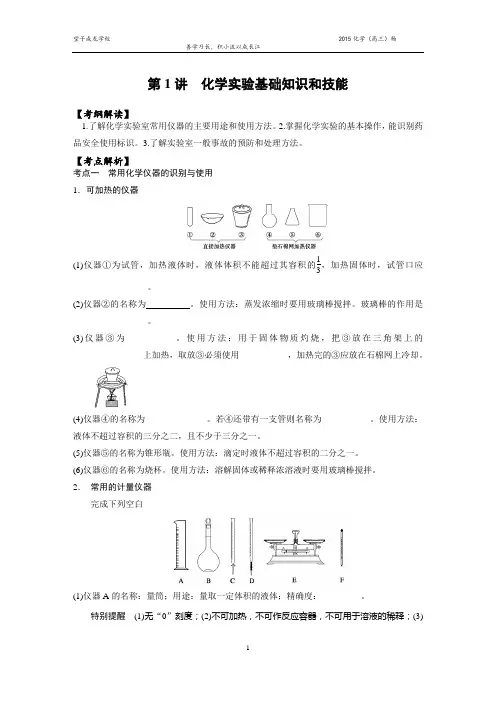
【考点解析】考点一常用化学仪器的识别与使用1.可加热的仪器(1)仪器①为试管,加热液体时,液体体积不能超过其容积的13,加热固体时,试管口应_________________。
(2)仪器②的名称为__________。
使用方法:蒸发浓缩时要用玻璃棒搅拌。
玻璃棒的作用是_________________。
(3)仪器③为___________。
使用方法:用于固体物质灼烧,把③放在三角架上的________________上加热,取放③必须使用___________,加热完的③应放在石棉网上冷却。
(4)仪器④的名称为______________。
若④还带有一支管则名称为___________。
使用方法:液体不超过容积的三分之二,且不少于三分之一。
(5)仪器⑤的名称为锥形瓶。
使用方法:滴定时液体不超过容积的二分之一。
(6)仪器⑥的名称为烧杯。
使用方法:溶解固体或稀释浓溶液时要用玻璃棒搅拌。
2.常用的计量仪器完成下列空白(1)仪器A的名称:量筒;用途:量取一定体积的液体;精确度:_________。
特别提醒 (1)无“0”刻度;(2)不可加热,不可作反应容器,不可用于溶液的稀释;(3)选取量筒的规则是“大而近”,思考:量取5.6 mL NaOH 溶液应选取的量筒的量程是( ) A. 5 mL B. 50 mL C. 10 mL D. 5.6 mL(2)仪器B 的名称:_________;用途:配制一定物质的量浓度的溶液;该仪器能长时间贮存溶液吗?_________。
(3)仪器C 的名称:_________。
①使用前需“查漏”;②“0”刻度在上方;③不可盛装碱性溶液;④精确度:_________。
(4)仪器D 的名称:_________。



质量管理体系基础知识第一讲:质量管理体系基础知识一、质量管理的基础术语一)产品的概念1.产品的定义:活动或过程的结果。
产品可包括硬件产品、软件产品或它们的组合;产品可以是有形的(如组件或流程性材料),也可以是无形的(如知识或概念)或是它们的组合;产品可以预期的(如提供给顾客)或非预期的(如污染、损坏或不愿有的结果)。
2.产品划分为四种类型:硬件、流程性材料、软件和服务。
1)硬件:不连续的具有特定形状的产品。
如:制造零件、元件、组件、装配产品、机械、建筑物。
2)流程性材料:将原料转化成某一预定状态的产品。
如:液体、气体、线体。
3)软件:通过支持媒体表达的信息所构成的一种智力创作。
如:信息、程序、规则、信息。
4)服务:为满足顾客的需要,供方和顾客之间在接触时的活动以及供方内部活动所产生的结果。
如:旅游、交通、金融、医疗、教育、咨询、公共事业等。
任何一个组织提供的产品,通常有两种或两种以上产品组成。
二)过程的概念1.过程定义:将输入转化为输出的一组彼此相关的资源和活动。
资源可包括人员、资金、设施、设备技术和方法。
所有工作是通过过程来完成的。
2.过程的特征:1)任何过程都有输入和输出,输入是实施过程的基础和依据,输出是完成过程的结果,即有行或无形的产品。
如:产品设计,输入是市场需求的信息或特定的顾客的要求,输出是图样、规范、样品。
2)完成过程必须投入适当的资源和活动。
如:为了进行产品设计需要配备能胜任该项设计的人员和必要的设施、资金等;为了控制设计过程的质量,需要开展的活动可包括编制设计计划,进行设计评审和验证,进行样品试制和鉴定,控制设计的更改等。
3)过程本身是价值增加的转换,价值的增加来源于投入过程中的资源和活动的结合所产生的结果。
4)为确保过程的质量,对输入过程的信息、要求和输出的产品(有形或无形)以及在过程中的适当阶段应进行必要的检查、评审、验证。
三)过程网络及其质量体系的关系1.每个组织的存在都是为了实现价值的增值,例如:从接受顾客的合同要求开始,经过组织内部的一系列过程,直到向顾客提供满意的产品。




平面及其基本性质知识点1 平面的概念平面是没有厚薄的,可以无限延伸,这是平面最基本的属性常见的桌面,黑板面,平静的水面等都是平面的局部形象指出: 平面的两个特征:①无限延展②平的(没有厚度)。
平面的表示:一般用一个希腊字母α、β、γ……来表示,还可用平行四边形对角顶点的字母来表示。
平面的画法:在立体几何中,通常画平行四边形来表示平面。
一个平面,通常画成水平放置,通常把平行四边形的锐角画成45 ,横边画成邻边的2倍长。
两个相交平面:画两个相交平面时,若一个平面的一部分被另一个平面遮住,应把被遮住部分的线段画成虚线或不画。
集合中“∈”的符号只能用于点与直线,点与平面的关系,“⊂”和“ ”的符号只能用于直线与直线、直线与平面、平面与平面的关系,虽然借用于集合符号,但在读法上仍用几何语言。
知识点2 公理1 如果一条直线的两点在一个平面内,那么这条直线上的所有点都在这个平面内指出:符号语言:,,,A l B l A B l ααα∈∈∈∈⇒⊂.知识点3 公理2如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线指出:符号语言:P ∈α,且P ∈β⇒α∩β=l ,且P ∈l .知识点4 公理3 经过不在同一条直线上的三点,有且只有一个平面指出:符号语言:,, ,,,,A B C A B C A B C ααβ⎫⎪∈⇒⎬⎪∈⎭不共线与β重合推论1 一条直线和直线外的一点确定一个平面.(证明见课本)指出:推论1的符号语言:A a ∉⇒有且只有一个平面α,使得A α∈,l α⊂推论2 两条相交直线确定一个平面推论3 两条平行直线有且只有一个平面三、典例解析例1 用符号语言表示下列图形中点、直线、平面之间的位置关系.例2 求证:两两相交而不通过同一点的四条直线必在同一平面内。
例3 正方体ABCD-A 1B 1C 1D 1中,对角线A 1C∩平面BDC 1=O ,AC 、BC 交于点M ,求证:点C 1、O 、M 共线.例4 已知平面α、β、γ两两相交于三条直线l 1、l 2、l 3,且l 1、l 2、l 3不平行.求证:l 1、l 2、l 3相交于一点.基础练习:一、选择题:1.下面给出四个命题: ①一个平面长4m, 宽2m; ②2个平面重叠在一起比一个平面厚; ③一个平面的面积是25m 2; ④一条直线的长度比一个平面的长度大, 其中正确命题的个数是( )A. 0B.1C.2D.32.若点N 在直线a 上,直线a 又在平面α内,则点N ,直线a 与平面α之间的关系可记作( ) A、N α∈∈a B、N α⊂∈a C、N α⊂⊂a D、N α∈⊂a3.A,B,C表示不同的点,a, 表示不同的直线,βα,表示不同的平面,下列推理错误的是( ) A.A ααα⊂⇒∈∈∈∈ B B A ,;,B.βαβαβα⋂⇒∈∈∈∈B B A A ,;,=ABC.αα∉⇒∈⊄A A ,D.A,B,C α∈,A,B,C β∈且A ,B ,C 不共线α⇒与β重合4. 空间不共线的四点,可以确定平面的个数为( )A.0 B.1 C.1或4 D. 无法确定5. 空间 四点A ,B ,C ,D 共面但不共线,则下面结论成立的是( )A. 四点中必有三点共线 B. 四点中必有三点不共线C. AB ,BC ,CD ,DA 四条直线中总有两条平行D. 直线AB 与CD 必相交6. 空间不重合的三个平面可以把空间分成( )A. 4或6或7个部分B. 4或6或7或8个部分C. 4或7或8个部分D. 6或7或8个部分7.下列说法正确的是( )①一条直线上有一个点在平面内, 则这条直线上所有的点在这平面内; ②一条直线上有两点在一个平面内, 则这条直线在这个平面内; ③若线段AB α⊂, 则线段AB 延长线上的任何一点一点必在平面α内; ④一条射线上有两点在一个平面内, 则这条射线上所有的点都在这个平面内.A. ①②③B. ②③④C. ③④D. ②③8.空间三条直线交于同一点,它们确定平面的个数为n ,则n 的可能取值为( )A. 1B.1或3C. 1或2或3D.1或 4二、填空题:9.水平放置的平面用平行四边形表示时,通常把横边画成邻边的___________倍.10.设平面α与平面β交于直线 , A αα∈∈B ,, 且直线AB C =⋂ ,则直线AB β⋂=_____________.11.设平面α与平面β交于直线 , 直线α⊂a , 直线β⊂b ,M b a =⋂, 则M_______ .12.直线AB 、AD α⊂,直线CB 、CD β⊂,点E ∈AB ,点F ∈BC ,点G ∈CD ,点H ∈DA ,若直线HE ⋂直线FG=M ,则点M 必在直线___________上.三、解答题:13.判断下列说法是否正确?并说明理由.(1)平行四边形是一个平面; (2)任何一个平面图形都是一个平面;(3)空间图形中先画的线是实线,后画的线是虚线.14.如图,E、F、G、H分别是空间四边形AB、BC、CD、DA上的点,且EH与FG交于点O. 求证:B、D、O三点共线.15.证明梯形是平面图形。
热控仪表知识培训周亚明第一讲基础知识第一章、测量1. 仪表主要由传感器、变换器、显示装置、传输通道四部分,其中传感器是仪表的关键环节。
2. 测量过程有三要素:一是测量单位、二是测量方法、三是测量工具。
3. 按参数种类不同,热工仪表可为温度、压力、流量、料位、成分分析及机械量等仪表。
4. 根据分类的依据不同,测量方法有直接测量与间接测量、接触测量与非接触测量、静态测量与动态测量。
*.什么叫绝对误差,相对误差?绝对误差是指示值与实际值的代数差,即绝对误差=测量值—真值相对误差是绝对误差与实际值之比的百分数相对误差=p x 100%第二章、检测第一节、温度检测:1. 温度:温度(temperature )是表示物体冷热程度的物理量,微观上来讲是物体分子热运动的剧烈程度。
温度只能通过物体随温度变化的某些特性来间接测量,而用来量度物体温度数值的标尺叫温标。
它规定了温度的读数起点(零点)和测量温度的基本单位。
目前国际上用得较多的温标有华氏温标(°F)、摄氏温标(°C)、热力学温标(K)和国际实用温标。
从分子运动论观点看,温度是物体分子平均平动动能的标志。
温度是大量分子热运动的集体表现,含有统计意义。
对于个别分子来说,温度是没有意义的。
温度测量:分为接触式和非接触式两类。
接触式测温法接触式测温法的特点是测温元件直接与被测对象接触,两者之间进行充分的热交换,最后达到热平衡,这时感温元件的某一物理参数的量值就代表了被测对象的温度值。
这种方法优点是直观可靠,缺点是感温元件影响被测温度场的分布,接触不良等都会带来测量误差,另外温度太高和腐蚀性介质对感温元件的性能和寿命会产生不利影响。
接触式仪表主要有:膨胀式温度计、压力式温度计、热电偶、热电阻及半导体二极管温度计。
非接触式测温法非接触式测温法的特点是感温元件不与被测对象相接触,而是通过辐射进行热交换,故可以避免接触式测温法的缺点,具有较高的测温上限。
第一章 概率论基础知识概率论是随机过程的基础,在传统的概率论中,限于各种原因,往往借助于直观理解来说明一些基本概念,这对于简单随机现象似乎无懈可击,但对于一些复杂随机现象就难以令人信服了.随着随机数学理论的不断完善,随机过程越来越成为现代概率论的一个重要分支和发展方向. 为了更好地学习随机过程,我们必须对基础概率论的理论有一个比较深入和全面的了解.本章就是在此基础上系统介绍概率论基础知识,包括概率空间、随机变量及其分布、数学期望的若干性质、特征函数和母函数、随机变量列的收敛性及其相互关系、条件数学期望等.1.1 概率空间概率论是研究随机现象统计规律的一门数学分科,由于随机现象的普遍性,使得概率论具有极其广泛的应用.随机试验是概率论的基本概念之一,随机试验所有可能结果组成的集合称为这个试验的样本空间,记为Ω.Ω中的元素ω称为样本点,Ω中的子集A 称为随机事件,样本空间Ω也称为必然事件,空集Φ称为不可能事件.定义 1.1 设Ω是一个集合,F 是Ω的某些子集组成的集合簇(collection )(或称集类),如果 (1)Ω∈F ;(2)若A ∈F ,则\A A =Ω∈F ;(取余集封闭) (3)若n A ∈F ,1,2,n = ,则1n n A ∞=∈ F ;(可列并封闭)则称F 为σ-代数(sigma algebra -)(B orel 域或事件域(field of events )),(,ΩF )称为可测空间(m easurable space ).由定义可以得到 (4)Φ∈F ;(5)若,A B ∈F ,则\A B ∈F ;(取差集封闭)(6)n A ∈F ,1,2,n = ,则1ni i A = ,1ni i A = ,1i i A ∞= ∈F (有限交,有限并,可列交封闭)定义1.2 设(,ΩF )为可测空间,()P ⋅是定义在F 上的实值函数,如果 (1)任意A ∈F ,0()1P A ≤≤;(非负性) (2)()1P Ω=;(正规性)(3)对两两互不相容事件12,,A A (当i j ≠时,i j A A =Φ ),有11()i ii i P A P A ∞∞==⎛⎫=⎪⎝⎭∑ (可列可加性). 则称P 是(,Ω F)上的概率(p r o b a b i l i ),(,ΩF ,P )称为概率空间(probability space ),()P A 为事件A 的概率. 由定义知(4),A B ∈F ,A B ⊂,则(\)()()P B A P B P A =- (可减性)一事件列{,1}n A n ≥称为单调增列,若1,1n n A A n +⊂≥;称为单调减列,若1,n n A A +⊃1n ≥. 显然,如果{,1}n A n ≥为单调增列,则1lim n in i A A∞→∞==;如果{,1}n A n ≥为单调减列,则1lim n in i A A∞→∞==.(5)(概率的连续性)若{,1}n A n ≥是递增或递减的事件列,则lim ()(lim )n n n n P A P A →∞→∞=定义1.3 设(,ΩF ,P )为概率空间,B ∈F ,且()0P B >,如果对任意A ∈F ,记()(|)()P AB P A B P B =则称(|)P A B 为事件B 发生条件下事件A 发生的条件概率(conditional probability ). 由条件概率的定义可得到: (1)乘法公式 设,A B ∈F ,则()()(|)P AB P B P A B =一般地,若i A ∈F ,1,2,,i n = ,且121()0n P A A A -> ,则121121312121()()(|)(|)(|)n n n P A A A P A P A A P A A A P A A A A --=(2) 全概率公式 设(,ΩF ,P )是概率空间,A ∈F ,i B ∈F ,1,2,,i n =()i j B B i j =Φ≠,且1,()0,ni i i B P B ==Ω> ,则1()()(|)niii P A P B P A B ==∑(3) (Bayes 公式)设(,ΩF ,P )是概率空间,A ∈F ,i B ∈F ,1,2,,i n =()i j B B i j =Φ≠,且1,()0,()0ni i i B P B P A ==Ω>> ,则1()(|)(|)()(|)i i i niii P B P A B P B A P B P A B ==∑一般地,若12,,,n A A A ∈ F ,有11()()nni ii i P A P A ===∏ , 则称F 为独立事件簇.1.2 随机变量及其分布随机变量是概率论的主要研究对象之一,随机变量的统计规律用分布函数来描述. 定义 1.4 设(,ΩF ,P )为概率空间,()X X ω=是定义在Ω上的实值函数,如果对于任意实数x ,有()1(,]Xx --∞={}:()X x ωω≤∈F ,则称()X ω为F上的随机变量(random variable ),简记为..r v X .随机变量实质上是(,ΩF )到(,R B ()R )上的可测映射(函数),记1(){()|X XB B σ-=∈B ()R }⊂F ,称()X σ为随机变量X 所生成的σ域.称{}()1()():()((,])(,]F x P X x P X xP X x P Xx ωω-=≤=≤=∈-∞=-∞为随机变量X 的分布函数(distribution function )(简记.d f ).由定义,分布函数有如下性质:(1)()F x 为不降函数:即当12x x <时,有12()()F x F x ≤; (2)()lim ()0,x F F x →-∞-∞==()lim ()1x F F x →+∞+∞==;(3)()F x 是右连续的,即()()F x F x ο+=可以证明,定义在R 上的实值函数()F x ,若满足上述三个性质,必能作为某个概率空间(,ΩF ,P )上某个随机变量的分布函数.推广到多维情形,类似可得到定义 1.5 设(,ΩF ,P )为概率空间,()12()(),(),,()n X X X X X ωωωω== 是定义在Ω上的n 维空间n R 中取值的向量实值函数.对于任意12(,,,)n n x x x x R =∈ ,有{}1122:(),(),,()n n X x X x X x ωωωω≤≤⋅⋅⋅≤∈F ,则称()X X ω=为n 维随机变量,称12()(,,,)n F x F x x x P =⋅⋅⋅={}1122:(),(),,()n n X x X x X x ωωωω≤≤⋅⋅⋅≤为()12()(),(),,()n X X X X X ωωωω==⋅⋅⋅的联合分布函数.随机变量有两种类型:离散型随机变量和连续型随机变量,离散型随机变量的概率分布用概率分布列来描述:(),1,2,k k p P X x k === ,其分布函数为()k k x xF x p ≤=∑;连续型随机变量的概率分布用概率密度函数()f x 来描述,其分布函数为()()x F x f t dt -∞=⎰.类似地可定义n 维随机变量12(,,,)n X X X X = 的联合分布列和联合分布函数如下: 对于离散型随机变量12(,,,)n X X X X = ,联合分布列为()121122,,,n x x x n n p P X x X x X x ====其中,i i i x I I ∈为离散集,1,2,,i = n ,X 的联合分布函数为: 1,12,,121,2,,(,,,)(,,,)n i i nn x x n x y i n F y y y p y y y R ≤==⋅⋅⋅∈∑对于连续型随机变量12(,,,)n X X X X = ,如果存在n R 上的非负函数12(,,,)n f x x x ,对于任意12(,,,)nn y y y R ∈ ,有12(,,,)n X X X X = 的联合分布函数12121212(,,,)...(,,,)n y y y n n n F y y y f x x x dx dx dx -∞-∞-∞⋅⋅⋅=⋅⋅⋅⋅⋅⋅⎰⎰⎰12(,,,)n f x x x 为X 的联合密度函数.1.3 数学期望及其性质设()X X =⋅是定义在概率空间(,ΩF ,P )上的.r v ,如果||X dP Ω<∞⎰,就称.r v .X的数学期望(expectation )或均值存在(或称.r v .X 是可积的),记为E X ,有下列定义:EX XdP Ω=⎰利用积分变换,也可写成()EX xdF x +∞-∞=⎰.设()g x 是1R 上的B orel 可测函数,如果.r v .()g X 的数学期望存在,即|()|E g X <∞,由积分变换可知()()()()Eg X g X dP g x dF x +∞Ω-∞==⎰⎰设k 是正整数,若.r v .k X 的数学期望存在,就称它的k 阶原点矩(k th -moment aboutthe origin ),记为k α,即()kkk EXx dF x α+∞-∞==⎰设k 是正整数,若.r v .||k X 的数学期望存在,就称它的k 阶绝对原点矩(k th - absolute m o m e n tabout the origin ),记为k β,即 ||||()kkk E X x dF x β+∞-∞==⎰类似地,X 的k 阶中心矩(k th - central moment )k μ和k 阶绝对中心矩(k th -absolutely central moment )k υ分别定义为1()()()kkk E X EX x dF x μα+∞-∞=-=-⎰1||||()kkk E X EX x dF x να+∞-∞=-=-⎰我们称二阶中心矩为方差(variance ),记为V a r X 或D X ,显然有22221VarX μναα===-关于数学期望,容易验证下列的性质:(1)若.r v .X ,Y 的期望E X 和E Y 存在,则对任意实数,αβ,()E X Y αβ+也存在,且()E X Y EX EY αβαβ+=+(2)设A ∈F ,用A I 表示集A 的示性函数,若E X 存在,则()A E XI 也存在,且()A AE XI XdP =⎰(3)若{}k A 是Ω的一个划分,即()i j A A i j =Φ≠ ,且i iA Ω= ,则iA i EX XdP XdP Ω==∑⎰⎰关于矩的存在性,有如下的必要条件和充分条件定理1.1 设对.r v X 存在0p >,使||pE X <∞,则有lim (||)0px x P X x →∞≥=定理1.2 设对.r v X 0(.)a s ≥,它的.d f 为()F x ,那么E X <∞的充要条件是(1())F x dx ∞-<∞⎰此时EX =(1())F x dx ∞-⎰推论1.1 ||E X <∞的充要条件是0()F x dx -∞⎰与0(1())F x dx +∞-⎰均有限,这时有EX =(1())F x dx ∞-⎰()F x dx -∞-⎰推论 1.2 对于0,||pp E X <<∞<∞的充要条件是11(||)p n P X n ∞=≥<∞∑,也等价于11(||)p n nP X n ∞-=≥<∞∑1.4 特征函数和母函数特征函数是研究随机变量分布又一个很重要的工具,用特征函数求分布律比直接求分布律容易得多,而且特征函数有良好的分析性质.定义 1.6 设X 是n 维随机变量(随机向量),分布函数为()F x ,称()F x 的Fourier Stieltjes -变换()()(),itXitxg t E ee dF x t ∞-∞==-∞<<∞⎰为X 的特征函数(characteristic function ).简记.c f从本质上看,特征函数是实变量t 的复值函数,随机变量的特征函数一定是存在的. 当X 是离散型随机变量,分布列(),1,2,k k p P X x k === ,则1()kitx k k g t ep ∞==∑当X 是连续型随机变量,概率密度函数为()f x ,则()(),itxg t ef x dx t ∞-∞=-∞<<∞⎰从定义,我们能够看出特征函数有如下性质: (1)(0)1;g =(2)(有界性)|()|1;g t ≤ (3)(共轭对称性)()();g t g t -=(4)(非负定性)对于任意正整数n 及任意实数12,,,n t t t 和复数12,,,n z z z ,有,1()0nk l k l k l g t t z z =-≥∑(5)(连续性)()g t 为n R 上一致连续函数;(6)有限多个独立随机变量和的特征函数等于各自特征函数的乘积,即随机变量12,,,n X X X 相互独立,12n X X X X =+++ 的特征函数为:12()()()()n g t g t g t g t =其中()i g t 为随机变量i X 的特征函数;(7)(特征函数与矩的关系)若随机变量X 的n 阶矩n EX 存在,则X 的特征函数()g t 可微分n 次,且当k n ≤时,有()(0)k k k g i EX =;(8)随机变量的分布函数由其特征函数唯一确定.定理1.3 (B ocher 定理) n R 上函数()g t 是某个随机变量特征函数当且仅当()g t 连续非负定且(0)1g =.定理1.4 (逆转公式) 设()F x 是随机变量X 的分布函数,相应的特征函数为()g t 若12,x x 为()F x 的连续点,则12211()()lim()2itx itx TT Tee F x F x g t dt itπ--→∞---=-⎰很显然,具有相同特征函数的两个分布函数是恒等的.由此还可推出一个事实:一个随机变量是对称的,当且仅当它的特征函数是实的. 事实上,由X 的对称性知X 和X -有相同的分布函数,根据定义()()()itX itXg t E e E eg t g t -===-=,也就是说()g t 是实的;反之,从()()()itX itXg t Ee g t g t Ee -===-=知X 和X -有相同的特征函数,因此,它们的分布函数相等,这说明X 是对称的.例1.1 设X 服从(,)B n p ,求X 的特征函数()g t 及2,,EX EX D X解 X 的分布列为{},1,0,1,2,,k k n kn P X k C p q q p k n -===-=()()()n nitxk k n kk it k n kit nnnk k g t eC p qCpe qpe q --=====+∑∑因此 0(0)()|itt d E X ig ipe qnp dt='=-=-+=22222202()(0)()()|it t d EXi g i pe q npq n p dt=''=-=-+=+故 22()D X EX EX npq =-= 例1.2 设~(0,1)X N ,求X 的特征函数()g t解 22()itx xg t edx ∞--∞=由于2222||||itx xxixe xe--=221||xx edx ∞--∞<∞⎰,可对上式两边求导,得2222()()itx xitx xg t ixedx e de∞∞---∞-∞'==-⎰2222()x x itx itx edx tg t ∞∞---∞-∞=--=-于是得到微分方程 ()()g t t g t '+=. 这是变量可分离型方程,有()()dg t tdt g t =-两边积分得 2l n ()2g t tc=-+,得方程的通解为 22()tcg t e -+=.由于(0)1g =,因此,0c =.于是X 的特征函数为22()tg t e -=例1.3 设,X Y 相互独立,~(,),~(,)X B n p Y m p ,证明:~(,)X Y n m p ++ 证明 ,X Y 的特征函数分别为()(),()(),1itnitmX Y g t q pe g t q pe q p =+=+=-X Y +的特征函数为()()()(),1it n mX Y X Y g t g t g t q pe q p ++==+=-即X Y +的特征函数是服从参数为,n m p +二项分布的特征函数,由唯一性定理~(,)X Y n m p ++附表一给出了常用分布的均值、方差和特征函数.在研究只取非负整数值的随机变量时,以母函数代替特征函数比较方便.定义1.7 设随机变量X 的分布列为(),0,1,2,k p P X k k === 其中01k k p ∞==∑,称()()kk k k P s E s p s ∞===∑为X 的母函数(或称概率生成函数)(p r o b a b i l i t y generating function ).母函数具有下列性质:(1)非负整数值随机变量的分布列由其母函数唯一确定; (2)(1)1P =,()P s 在||1s ≤绝对且一致收敛;(3)若随机变量X 的l 阶矩存在,则可以用母函数在1s =的导数值来表示,特别地, 有2(1),(1)(1)EX P EXP P ''''==+;(4)独立随机变量之和的母函数等于母函数的积.证明 (1)01(),0,1,2,nkkkk k k k k k n P s p s p s p s n ∞∞===+==+=∑∑∑两边对s 求n 阶导数,得到()1()!(1)(1)n k nn k k n Ps n p k k k n p s∞-=+=+--+∑令0s =,则()(0)!n n p n p =,因此()(0),0,1,!n n pp n n ==(3)由0()kk k P s p s ∞==∑,得到11()k kk P s kps∞-='=∑,令1s ↑,得到1(1)kk EX kpP ∞='==∑,类似可得到 2(1)(1)E X PP '''=+ 例1.4 从装有号码为1,2,3,4,5,6的小球的袋中,有放回地抽取5个球,求所得号码总和为15的概率.解 令i X 为第i 次取得的小球的号码,且i X 相互独立,125X X X X =+++ 为所取的球的号码的总和.i X 的母函数为261()()6i P s s s s =+++X 的母函数为 5265655551()()(1)(1)66s P s s s s s s -=+++=--所求概率为()P s 展开式的15s 的系数,因此,5651{15}6P X ==1.5 随机变量列的收敛性定义 1.8设{},;1n X X n ≥概率空间(,ΩF ,P )上随机变量,如果存在集A ∈F ,()0P A =,当cA ω∈时,有lim ()()n n X X ωω→∞=,则称n X 几乎处处收敛(convergencealm ost everywhere )到X ,简称n X ..a s 收敛到X ,记为n X X → ..a s下面我们给出..a s 收敛的一个判别准则.定理1.5 n X X → ..a s 的充分必要条件是任一ε>0,有lim (||)0m n m n P X X ε∞→∞=⎧⎫-≥=⎨⎬⎩⎭下面给出定理1.3的一个应用.例1.5 设{}n X 是..r v 列,且11()()2n n n P X n P X n +===-=,1111122n n n P X P X n n ⎧⎫⎧⎫⎛⎫===-=-⎨⎬⎨⎬ ⎪⎩⎭⎩⎭⎝⎭对于给定的ε>0,考虑1n ε>,有 1(||)0,2m mm nm n P X n ε∞∞==⎧⎫≥≤→→∞⎨⎬⎩⎭∑,因此 0n X →,..a s定义1.9 设{},;1n X X n ≥概率空间(,ΩF ,P )上随机变量,如果对任一0ε>,{}lim ||0n n P X X ε→∞-≥=则称n X 依概率收敛(convergence in probability )到X ,简记Pn X X −−→. 由定义,n X 依概率收敛到X ,那么极限随机变量X ..a s 是唯一的.定义 1.10 设{},;1n X X n ≥概率空间(,ΩF ,P )上随机变量,若||rn E X (0r >)存在,且lim ||0rn n E X X →∞-=,则称 n X r 阶平均收敛(convergence in mean oforder r )到X ,特别地,当2r =时,称为均方收敛.定义1.11 设{},;1n X X n ≥概率空间(,ΩF ,P )上随机变量,其分布函数序列()n F x 满足lim ()()n n F x F x →∞=在每个()F x 连续点处成立,则称n X 依分布收敛(convergence indistribution )到X .简记dn X X −−→.这里()F x 为X 的分布函数.下面我们不加证明地给出几种收敛之间的关系.a sPn n X X X X −−→⇒−−→dn X X ⇒−−→⇓..k a s n X X −−→且11(||)2kn kk P X X ∞=-≥<∞∑⇑,r rn n X X X X '−−→⇒−−→ 0r r '<< 1.6 条件数学期望设,X Y 是离散型随机变量,对一切使{}0P Y y =>的y ,定义给定Y y =时,X 的条件概率为 {,}{|}{}P X x Y y P X x Y y P Y y ======;给定Y y =时,X 的条件分布函数为(|){|}F x y P X x Y y =≤=; 给定Y y =时,X 的条件期望为(|)(|){|}xE X Y y xdF x y xP Xx Y y =====∑⎰设,X Y 是连续型随机变量,其联合密度函数为(,)f x y ,对一切使()0Y f y ≥,给定Y y =时,X 的条件密度函数为(,)(|)()Y f x y f x y f y =;给定Y y =时,X 的条件分布函数(|){|}F x y P X x Y y =≤==(|)xf x y dx ⎰; 给定Y y =时,X 的条件期望定义为 (|)(|)(|)E X Y y x d F x y x f x y d x===⎰⎰由定义可以看出,条件概率具有无条件概率的所有性质.(|)E X Y y =是y 的函数,y 是Y 的一个可能值,若在Y 已知的条件下,全面考察X 的均值,需要用Y 替代y ,(|)E X Y y =是Y 的函数,显然,它也是随机变量,称为X 在Y 条件下的条件期望(conditional expectation ).条件期望在概率论、数理统计和随机过程中是一个十分重要的概念,下面我们列举以下性质:设,,X Y Z 为随机变量,()g x 在R 上连续,且,,,[()]EX EY EZ E g Y Z ⋅都存在. (1) 当X 和Y 相互独立时,(|)E X Y EX =; (2) [(|)]EX E E X Y =;(3) [()|]()(|)E g Y X Y g Y E X Y ⋅=; (4) (|)E c Y c =,c 为常数;(5) (线性可加性)[()|](|)(|)E aX bY Z aE X Z bE Y Z +=+ (,a b 为常数); (6) 若0,X ≥则(|)0,..E X Y a s ≥ 下面只对(2)和(3)证明:证明 (2)离散型情况.设(,)X Y 的联合分布列为{,},,1,2,i j ij P X x Y y p i j ====则 [(|)](|){}jj j y E E X Y E XY y P Y y ===∑{|}{}ji i i j j y x x P X x Y y P Y y ⎡⎤====⎢⎥⎣⎦∑∑ {,}{}ji ii i j i y x x x P X x Y y P Xx EX ⎡⎤======⎢⎥⎣⎦∑∑∑由此可见,E X 是给定j Y y =时X 条件期望的一个加权平均值,每一项(|)j E X Y y =所加的权数是作为条件事件的概率,称(|){}jj j y EX E XY y P Y y ===∑为全期望公式.连续型情形:设(,)X Y 的联合密度函数为(,)f x y ,则[](|)(|)()(|)()Y Y E E X Y E X Y y f y dy xf x y dx f y dy ∞∞∞-∞-∞-∞⎡⎤===⎢⎥⎣⎦⎰⎰⎰(,)(,)x f x y d x d yx f x y dy d x∞∞∞∞-∞-∞-∞-∞⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰⎰⎰()X xf x dx EX ∞-∞==⎰(|)()Y EX E X Y y f y dy ∞-∞==⎰也称为全期望公式.全期望公式表明:条件期望的期望是无条件期望. (3)只需证明对任意使[]()|E g Y X Y y ⋅=存在的y 都有[]()|()(|)E g y X Y y g y E X Y y ⋅===因为[|](|)E X Y y xdF x y ∞-∞==⎰,因此,当y 固定时,[]()|()(|)()(|)E g y X Y y g y xdF x y g y xdF x y ∞∞-∞-∞⋅===⎰⎰()[|]g y E X Y y ==例1.6 设在某一天走进商店的人数是期望为1000的随机变量,又设这些顾客在该商店所花钱数都为期望为100元的相互独立的随机变量,并设一个顾客花钱数和进入该商店的总人数独立,问在给定的一天内,顾客们在该商店所花钱数的期望是多少?解 设N 表示这天进入该商店的总人数,i X 表示第i 个顾客所花的钱数,则N 个顾客所花的总数为1Ni i X =∑.由于 11|N N i i i i E X E E X N ==⎡⎤⎡⎤⎛⎫=⎢⎥ ⎪⎢⎥⎣⎦⎝⎭⎣⎦∑∑而 1111||N n n i i i i i i E X N n E X N n E X nEX ===⎡⎤⎡⎤⎡⎤=====⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦∑∑∑因此 11|,N i i E X N N E X =⎡⎤=⎢⎥⎣⎦∑[]111N i i E X E N E X E N E X =⎡⎤=⋅=⎢⎥⎣⎦∑由题设 11000,100EN EX == 于是11000100100000Ni i X ==⨯=∑即该天顾客花费在该商店的钱数的期望为100000元.。