三角函数式的化简和证明
- 格式:doc
- 大小:137.50 KB
- 文档页数:2

顺德大良总校 顺德大良一分校 顺德大良北区分校 顺德大良新桂分校 顺德容桂分校 顺德容桂体育路分校 顺德龙江分校 顺德北滘分校 顺德乐从分校 顺德勒流分校 南海桂城分校 南海黄岐分校 南海大沥分校 禅城丽雅苑分校 禅城金澜分校 一、 基础知识:1、诱导公式sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosatgA=tanA =aacos sin2、 两角和与差的三角函数公式:⑴ sin()_____________________αβ±=; ⑵ cos()____________________αβ±= ; ⑶ tan()_____________αβ±= 3、二倍角公式;⑴ cos 2__________α= __________= __________= ⑵sin 2__________θ= ⑶tan 2____________θ= 4、公式的变形应用:⑴ 降次公式:2cos _______α=, 2sin _________α=;22cos _______α=, 22sin _________α=;sin cos _______θθ=⑵ 升幂公式:1cos 2______;α-= 1cos 2_______α+= ⑶ 常用变形公式:13sin _______22x x += ; sin cos _______x x +=;31cos _______22x x -=; sin cos _______x x -=; tan tan __________________αβ+=⑷ 常见的角的变换:2α=(α+β)+( );α=2βα++______; α=(α+β)- =(α-β)+2βα+=(α-2β)-( ); ()(_____)4x π-+=2π5、和差化积sina+sinb=2sin2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2ba - cosa+cosb = 2cos 2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+6、积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb =21[sin(a+b)-sin(a-b)]7、主要方法与思路:⑴.分析思路上,主要有三看: 、 、 ; ⑵.主要方法上:函数名称的变换( 、 )、角的变换( )、1的变换等方面;二.两角和与差的三角函数(1)公式不但要会正用,还要会逆用. 例6 计算:.(2)公式的变形应用要熟悉.熟记:tan α+tan β=tan(α+β)(1-tan α·tan β),它体现了两个角正切的和与积的关系.分析(1)中涉及80°与70°的正切和与积,(2)中涉及α+β与α的正切差与积,所以都用正切和角公式的变形公式.(3)角的变换要能灵活应用,如α=(α+β)-β,β=α-(α-β),2α=(α+β)+(α-β)等.分析因为β=(α+β)-α,所以求cosβ用余弦两个角差的公式.分析因为2β=(α+β)-(α-β),所以例10已知3sinβ=sin(2α+β),则tan(α+β)=2tanα.证明将已知变形:3sin(α+β-α)=sin(α+β+α) 3sin(α+β)cosα-3cos(α+β)sinα=sin(α+β)cosα+cos(α+β)sinα.等式两边同时除以cos(α+β)·cosα,即得tan(α+β)=2tanα.4.倍角公式,半角公式(2)使用二倍角的正弦、余弦公式时,公式的选择要准确.如已知sinα,cosα,tanα求cos2α时,应分别选择cos2α=1-(3)余弦的二倍角公式的变形——升幂公式、降幂公式必须熟练掌握.要明确,降幂法是三角变换中非常重要的变形方法.对sin3α,cos3α的公式应记住.(4)使用正弦、余弦的半角公式时,要注意公式中符号的确定方法.正在使用无理表达式时,须要确定符号;在使用两个有理表达式时,无须确定符号,这是与选用无理表达式最大的区别,因此在化简、证明题中,例11求值:(4)先把sin10°·sin50°·sin70°化成余弦,得cos20°·cos40°·cos80°,由于20°,40°,80°顺序为2倍的关系,联想到正弦的2倍角公式,分析使用1±cosα的升幂公式,便于开方.(2)5sin2θ-3sinθ·cosθ+2cos2θ.分析由已知得tanθ=-4.(2)原式可以加一个分母sin2θ+cos2θ,这样分子、分母同时除以cos2还可以这样研究:将sin2θ、cos2θ降幂,使用万能公式.原式=5·5.和差化积、积化和差公式这两组公式现在不要求记忆,但要会使用.(1)要明确,这两组公式是解决正、余弦的加、减、乘的运算关系式.(3)对下列关系式要熟记:例14将下列各式化积:(1)1-sin2α-cos2α;(2)sin5x·sin4x-sin3x·sin2x-sin8x·sinx;分析对(1),题中有1±cosα时,通常都用升幂公式.对(2)、(3),先将乘积化和差,再和差化积.例15求值:(1)cos2A+cos2(60°+A)+cos2(60°-A);(1)分析可以用余弦的两角和、差公式展开计算;若先降幂,再化积更简单.(1)cos(α-β);(2)sin(α+β)-2cos(α+β).解(1)将已知的两式平方相加,得(2)将已知的两式化积并相除,得评述对sinα±sinβ=a,cosα±cosβ=b这样两个式子通常的用法是,如(1),两式平方相加;如(2),两式化积并相除.这两种用法要掌握.。
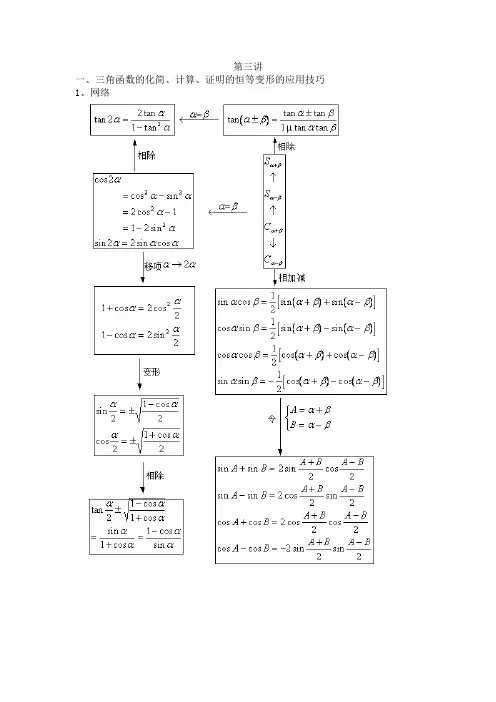
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结(1)变换函数名对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通过同一和化归以有利于问题的解决或发现解题途径。
【例1】已知θ同时满足和,且a、b 均不为0,求a、b的关系。
练习:已知sin(α+β)=,cos(α-β)=,求的值。
2)变换角的形式对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/2可看作α/4的倍角;(45°+α)可看成(90°+2α)的半角等等。
【例2】求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值。
练习已知,求的值【例3】已知sinα=Asin(α+β)(其中cosβ≠A),试证明:tan(α+β)=提示:sin[(α+β)-β]=Asin (α+β)(3)以式代值利用特殊角的三角函数值以及含有1的三角公式,将原式中的1或其他特殊值用式子代换,往往有助于问题得到简便地解决。
这其中以“1”的变换为最常见且最灵活。
“1”可以看作是sin2x+cos2x, sec2x-tan2x, csc2x -cot2x,tanxcotx, secxcosx, tan45°等,根据解题的需要,适时地将“1”作某种变形,常能获得较理想的解题方法。
【例4】化简:(4)和积互化积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化的特殊情形。
这往往用到倍、半角公式。

三角函数的化简公式三角函数是数学中常见的一类函数,主要包括正弦函数、余弦函数、正切函数等。
在数学的计算和分析中,经常需要对三角函数进行化简和简化,以便更方便地进行运算和推导。
本文将介绍三角函数的一些常见的化简公式。
1. 正弦函数的化简公式正弦函数是三角函数中最常见的函数之一,其常用的化简公式包括:(1)正弦函数的和差化简公式:sin(x ± y) = sin(x)cos(y) ± cos(x)sin(y)(2)正弦函数的倍角化简公式:sin(2x) = 2sin(x)cos(x)(3)正弦函数的平方化简公式:sin^2(x) = (1 - cos(2x))/2(4)正弦函数的和差的平方化简公式:sin^2(x ± y) = (1 - cos(2x ± 2y))/22. 余弦函数的化简公式余弦函数也是三角函数中常用的函数之一,其常用的化简公式包括:(1)余弦函数的和差化简公式:cos(x ± y) = cos(x)cos(y) ∓ sin(x)sin(y)(2)余弦函数的倍角化简公式:cos(2x) = cos^2(x) - sin^2(x)(3)余弦函数的平方化简公式:cos^2(x) = (1 + cos(2x))/2(4)余弦函数的和差的平方化简公式:cos^2(x ± y) = (1 + cos(2x ± 2y))/23. 正切函数的化简公式正切函数是三角函数中与正弦函数和余弦函数密切相关的函数,其常用的化简公式包括:(1)正切函数的和差化简公式:tan(x ± y) = (tan(x) ± tan(y))/(1 ∓ tan(x)tan(y))(2)正切函数的倍角化简公式:tan(2x) = (2tan(x))/(1 - tan^2(x))(3)正切函数的平方化简公式:tan^2(x) = (1 - cos(2x))/(1 + cos(2x))(4)正切函数的和差的平方化简公式:tan^2(x ± y) = ((1 - tan(x)tan(y))/(1 + tan(x)tan(y)))^2综上所述,三角函数的化简公式包括了正弦函数、余弦函数和正切函数的常见变换和简化形式。

数学部分•知识结构与拓展高一使用2021年6月解:原式=化简三甬函懿述的\f3sin12°—3cos12°2sin12°cos12°(2cos212°—1)2^3sin(12°—60°)4V3o當用冇法■廖庆伟三角函数式的化简的常用方法有:直用公式,变用公式,化切为弦,异名化同名,异角化同角,高次化低次等。
下面举例分析,供大家学习与参考。
一、直用公式例1设函数/(rc)=sin 兀7C—sin48°评注:先化切为弦,再利用倍角公式进行转化,最后逆用两角差的正弦公式即可求值。
四、异名化同名例4已知tan0=2,则sin20+sin Ceos0—2cos2^._h亠sin20+sin^cos0一2cos'。
解:原式sin2+cos2tan20+tan Q—2_4+2—2_4tar?e十1=4+1=T°评注:先把分母用sir?。
+cos2。
代换,再把分子、分母同除以cos20即得结果。
五、异角化同角例5函数(乞)=cos(2z+詈)+sin2gTT2cos2—+1,则/X h)的最小正周期为的最大值为解:因为函数/(rc)=sin于工一解:因为jf(;r)=cos2^ccos——sin2h•-|-cos晋:r=sin7T7T,故函数/(工)sin令+—c;s2j*_欝鈕,所以函数的最小正周期为丁=弐=8。
T评注:直接利用差角公式、二倍角的余弦公式即可得到结果。
二、变用公式例2当函数夕=sin工—</3"cos h(0W 鼻V2tc)取得最大值时,jc____o解:由》=sin jc一43cos h2(cos守sin工一sin专cos町—2sin h—訂,可知当'7Tsin=1时,此函数取得最大值。
又0W h V2jt,所以rr=警o评注:三角函数公式既可正用,也可变用,变用公式是三角恒等变换的难点。

三角函数的化简、求值与证明(3)主化锐:当已知角是90 到360内的角时,可利用180,270,360ααα--- 的诱导公式把这个角的三角函数值化为0 到90 内的角.二. 两角和与差的三角函数公式1. 两角和与差的正弦公式:()sin αβ±=______________.变形式:()()sin sin αβαβ++-=_______()();sin sin αβαβ+--=_______;2.两角和与差的余弦公式:()cos αβ±=__________________变形式:()()cos cos αβαβ++-=_____________;()()cos cos αβαβ+--=__________;3.两角和与差的正切公式:()tan αβ±=___________())2k k Z παβαβπ+≠+∈(、、.变形式:tan tan αβ±=_________________.【例1】计算:2(sincos )tan()643πππ++-=【例2】已知tan α=sin()cos()()sin()sin()n n n n n αααα+π-π∈+π+-πZ 的值.【例3】函数()cos()sin(),22xx f x x =-+π-∈R . (1)求()f x 的最小正周期有最大值; (2)求)(x f 在[0,)π上的减区间.【例4】若[0,2α∈π]sin co s αα=+,则α的取值范围是( ) A.(0,)2π B.(,)2ππ C.(,)23ππ D.(,2)23ππ【例5】已知关于x 的方程221)0x x m -++=的两根为s i nc o s θθ、,其中(0,2)θπ∈.(1)求m 的值;(2)求sin cos 1cot 1tan θθθθ+--的值.【例6】已知02x π-<<,1sin cos 5x x +=. (1)求sin cos x x -的值;(2)求sin 22cos21tan x x x++的值.针对性训练1、已知θ是第三象限角,且4459sin cos θθ+=,那么2sin θ等于 ( ) A、3 B、3- C 、23 D 、23- 2、函数22y sin x x =- ( ) A 、2π B 、π C 、3π D 、4π3、tan70cos10201)- 等于 ( ) A 、1 B 、2 C 、-1 D 、-24、已知46sin (4)4m m mαα-=≠-,则实数m 的取值范围是______。

三角函数的化简与证明三角函数是数学中的重要概念之一,它在解析几何、物理学、工程学等领域中有广泛应用。
在使用三角函数时,我们经常面临的一个问题就是如何将复杂的三角函数化简为简单形式,或者证明两个三角函数之间的等式。
本文将探讨三角函数的化简和证明方法。
一、三角函数的化简1. 三角恒等式三角恒等式是三角函数化简的基础。
它是一种等式关系,使得两个或多个三角函数能够互相转化。
下面是一些常见的三角恒等式:- 余弦函数的平方加正弦函数的平方等于1:$cos^2θ + sin^2θ = 1$- 2倍角公式:$cos(2θ) = cos^2θ - sin^2θ$- 倍角公式:$sin(2θ) = 2sinθcosθ$- 三角和差公式等通过运用这些恒等式,我们可以将复杂的三角函数化简为简单的形式,便于计算和理解。
2. 其他化简方法除了三角恒等式,还有一些其他的化简方法。
例如,使用欧拉公式,将三角函数转化为复指数函数进行化简。
这个方法可以将三角函数的复杂计算转化为简单的指数函数计算,能够提高计算效率。
在实际问题中,我们还可以利用对称性、周期性等性质进行化简。
这需要根据具体问题进行分析和推导,找到合适的化简方法。
二、三角函数的证明1. 等式的证明证明三角函数之间的等式是数学中的重要问题。
通过证明三角函数之间的等式,可以建立它们之间的联系,拓宽我们对三角函数的理解。
在证明三角函数等式时,我们可以运用三角恒等式、代数运算、数学归纳法等方法。
具体的证明过程需要根据问题的要求和条件进行推导。
2. 不等式的证明除了等式的证明,我们还经常需要证明三角函数之间的不等式。
三角函数的不等式证明在数学分析和优化等领域中有广泛应用。
在证明三角函数不等式时,我们可以使用极限、导数、积分和数学归纳法等方法。
通过分析三角函数的性质和变化趋势,找到合适的不等式证明方法。
需要注意的是,在证明过程中,要严谨而准确地推导,避免出现漏洞和错误,确保证明的有效性和可靠性。



三角函数的化简与展开公式的推导三角函数是高中数学中的重要内容之一,它们在各个数学分支中都有广泛应用。
而化简与展开公式的推导对于解题和简化计算过程有着重要的作用。
本文将介绍三角函数的化简与展开公式的推导,并讨论其应用。
一、正弦函数的化简与展开公式推导1. 两倍角公式:正弦函数的化简与展开公式之一是两倍角公式,其推导如下:根据三角函数的定义可知,sin2θ = sin(θ+θ) = sinθcosθ + cosθsinθ化简得到:sin2θ = 2sinθcosθ2. 半角公式:正弦函数的化简与展开公式之二是半角公式,其推导如下:根据三角函数的定义可知,sin^2(θ/2) + cos^2(θ/2) = 1利用三角函数的化简公式sin2θ = 2sinθcosθ,有:sin^2(θ/2) = (1 - cosθ)/2cos^2(θ/2) = (1 + cosθ)/23. 和差化积公式:正弦函数的化简与展开公式之三是和差化积公式,其推导如下:根据三角函数的定义可知,sin(α±β) = sinαcosβ ± cosαsinβ化简得到:sin(α±β) = sinαcosβ ± cosαsinβ二、余弦函数的化简与展开公式推导1. 两倍角公式:余弦函数的化简与展开公式之一是两倍角公式,其推导如下:根据三角函数的定义可知,cos2θ = cos^2θ - sin^2θ化简得到:cos2θ = 1 - 2sin^2θ2. 半角公式:余弦函数的化简与展开公式之二是半角公式,其推导如下:根据三角函数的定义可知,sin^2(θ/2) + cos^2(θ/2) = 1利用三角函数的化简公式cos2θ = 1 - 2sin^2θ,有:cos^2(θ/2) = (1 + cosθ)/2sin^2(θ/2) = (1 - cosθ)/23. 和差化积公式:余弦函数的化简与展开公式之三是和差化积公式,其推导如下:根据三角函数的定义可知,cos(α±β) = cosαcosβ - sinαsinβ化简得到:cos(α±β) = cosαcosβ - sinαsinβ三、正切函数的化简与展开公式推导1. 两倍角公式:正切函数的化简与展开公式之一是两倍角公式,其推导如下:根据三角函数的定义可知,tan2θ = (2tanθ)/(1 - tan^2θ)化简得到:tan2θ = (2tanθ)/(1 - tan^2θ)2. 半角公式:正切函数的化简与展开公式之二是半角公式,其推导如下:根据三角函数的定义可知,tan(θ/2) = ±√((1 - cosθ)/(1 + cosθ))利用三角函数的化简公式sin^2(θ/2) = (1 - cosθ)/2和cos^2(θ/2) = (1 + cosθ)/2,有:tan(θ/2) = sin(θ/2)/cos(θ/2) = ±√((1 - cosθ)/(1 + cosθ))3. 和差化积公式:正切函数的化简与展开公式之三是和差化积公式,其推导如下:根据三角函数的定义可知,tan(α±β) = (tanα ± tanβ)/(1 ∓ tanαtanβ)化简得到:tan(α±β) = (tanα ± tanβ)/(1 ∓ tanαtanβ)通过以上推导和化简公式,我们可以在解题和计算过程中更加方便地使用三角函数。

三角恒等式的化简与应用三角函数是高等数学中重要的概念之一,在数学和物理等学科中都有广泛的应用。
在解三角方程以及计算三角函数的值时,经常需要运用三角恒等式来进行化简和转化。
本文将探讨三角恒等式的化简方法,并介绍一些常见的应用场景。
一、三角恒等式的化简方法1. 倍角恒等式倍角恒等式是三角函数中常用的一种恒等式,可将一个角的函数值转化为其两倍角的函数值。
以下是常用的倍角恒等式:sin(2θ) = 2sinθcosθcos(2θ) = cos²θ - sin²θtan(2θ) = 2tanθ / (1 - tan²θ)根据这些倍角恒等式,我们可以将复杂的三角函数表达式转化为简化形式,从而更方便地进行计算。
2. 三角和差恒等式三角和差恒等式能够将两个角的函数和差转化为函数乘积或商的形式。
以下是常见的三角和差恒等式:sin(α ± β) = sinαcosβ ± cosαsinβcos(α ± β) = cosαcosβ ∓ sinαsinβtan(α ± β) = (tanα ± tanβ) / (1 ∓ tanαtanβ)通过利用这些三角和差恒等式,我们可以将复杂的三角函数表达式化简为较简单的形式,以便进行计算。
3. 三角平方恒等式三角平方恒等式能够将三角函数的平方转化为其他三角函数的形式。
以下是常见的三角平方恒等式:1 - cos²θ = sin²θ1 - sin²θ = cos²θtan²θ + 1 = sec²θcot²θ + 1 = csc²θ通过运用这些三角平方恒等式,我们可以将复杂的三角函数表达式中的平方项转化为其他函数,从而简化计算步骤。
二、三角恒等式的应用场景1. 解三角方程在解三角方程时,我们常常需要通过转化和化简三角函数的表达式来得到等价的方程形式。

A B C B【例4] 在中,若sin2_2 +sin2y +sin2y =cos2_2 ,tan—• tan —=-.2 2 3B 满足关系式:V3 (tan a • t^n B +a) +tan a =0,则tan B 二c- f(1+a)D- T(1~a) A. V3 (1+a) B. V3 (1 —爲)三角函数的化简1、三角函数式的化简:(1)常用方法:①直接应用公式进行降次、消项;②切割化弦,异名化同名,异角化同角;③三角公式的逆用等。
(2)化简要求:①能求出值的应求出值;②使三角函数种数尽量少;③使项数尽量少;④尽量使分母不含三角函数;⑤尽量使被开方数不含三角函数2、三角函数的求值类型有三类:(1)给角求值:一般所给出的角都是非特殊角,要观察所给角与特殊角间的关系,利用三角变换消去非特殊角,转化为求特殊角的三角函数值问题;(2)给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如& =(© + "丿—0,2Q =(Q +"丿+ (©-0丿等,把所求角用含己知角的式子表示,求解时要注意角的范围的讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。
3、三角等式的证明:(1)三角恒等式的证题思路是根据等式两端的特征,通过三角恒等变换,应用化繁为简、左右同一等方法,使等式两端的化“异”为“同”;(2)三角条件等式的证题思路是通过观察, 发现已知条件和待证等式间的关系,采用代入法、消参法或分析法进行证明。
一、化简[例求值.2sin2(P + cosl0o + tan20。
sin 10°esc 40° + cot 80°2 cos 40° + cosl 0°(1 + tan60°tanl 0°) Jl + cosl0°【例2】(三兄弟)已知s 阮普,"罟,求畔翥卫的值【变式】(05天津)已知sin (&) =晋,COS 2*£,【例3](最值辅助角)已知函数A^)=2asin 2T —273 asinxcosA+a+b —1,(弘b 为常数,a<0),它的定 义域为[0,兰],值域为[ — 3,1],试求禺b 的值。
1.三角恒等变换的两原则(1)化繁为简:变复角为单角,变不同角为同角,化非同名函数为同名函数,化高次为低次,化多项式为单项式,化无理式为有理式。
(2)消除异差:消除已知与未知、条件与结论、左端与右端以及各项的次数、角、函数名称、结构式等方面的差异。
2.三角函数式的化简 (1)化简要求①三角函数名称尽量少;②次数尽量低;③能求值的尽量求值; ④尽量使分母不含三角函数;⑤使被开方数不含三角函数. (2)化简思路对于和式,基本思路是降次、消项和逆用公式;对于三角分式,基本思路是分子与分母约分或逆用公式;对于二次根式,注意二倍角公式的逆用,另外,还可以用切割化弦、变量代换、角度归一等方法 (3)化简的方法弦切互化,异名化同名,异角化同角,降幂或升幂,和差化积,积化和差等。
3.三角恒等式的证明 (1)证明三角恒等式的方法观察等式两边的差异(角、函数、运算的差异),从解决某一差异入手(同时消除其他差异),确定从该等式的哪些证明(也可两边同时化简),当从解决差异方面不易入手时,可采用转换命题法或用分析法等。
(2)证明三角条件等式的方法首先观察条件与结论的差异,从解决这一差异入手,确定从结论开始.通过变换,将已知表达式代入得出结论,或通过变换已知条件得出结论,如果这两种方法都证不出来,可采用分析法;如果已知条件含参数,可采用消去参数法;如果已知条件是连比的式子,可采用换元法等。
1. 三角函数的化简、计算、证明的恒等变形的基本思路是:一角二名三结构。
即首先观察角与角之间的关系,注意角的一些常用变式,角的变换是三角函数变换的核心!第二看函数名称之间的关系,通常“切化弦”;第三观察代数式的结构特点。
基本的技巧有:(1)巧变角(已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换. 如()()ααββαββ=+-=-+,2()()ααβαβ=++-,2()()αβαβα=+--,22αβαβ++=⋅,()()222αββααβ+=---等),如 (1)已知2tan()5αβ+=,1tan()44πβ-=,那么tan()4πα+的值是_____ (答:322);(2)已知02πβαπ<<<<,且129cos()βα-=-,223sin()αβ-=,求cos()αβ+的值(答:490729); (3)已知,αβ为锐角,sin ,cos x y αβ==,3cos()5αβ+=-,则y 与x 的函数关系为______(答:43(1)55y x x =<<)(2)三角函数名互化(切化弦),如 (1)求值sin 50(13tan10)+(答:1);(2)已知sin cos 21,tan()1cos 23αααβα=-=--,求tan(2)βα-的值(答:18)(3)公式变形使用(tan tan αβ±()()tan 1tan tan αβαβ=±。
三角函数化简的方法技巧三角函数是数学中常见的函数,它们在许多领域中都有广泛的应用。
化简三角函数是数学中的重要技巧,它可以简化复杂的表达式,使计算更加简单和直观。
以下是一些常用的三角函数化简方法和技巧。
1. 基本公式使用三角函数的基本公式是化简的基础。
例如,正弦函数的基本公式是:$$\sin^2\theta + \cos^2\theta = 1$$这个公式可以用来化简包含正弦函数的表达式。
根据需要,还可以使用余弦函数、正切函数和余切函数的基本公式。
2. 和差化积公式和差化积公式是一种常见的化简方法。
对于两个角度$\alpha$ 和 $\beta$,我们有以下的和差化积公式:$$\sin(\alpha \pm \beta) = \sin\alpha \cos\beta \pm \cos\alpha\sin\beta$$$$\cos(\alpha \pm \beta) = \cos\alpha \cos\beta \mp \sin\alpha\sin\beta$$这些公式可以用来化简包含和差角的三角函数表达式,并将它们转化为乘积形式。
3. 二倍角公式二倍角公式是化简三角函数的另一种常用方法。
对于角度$\theta$,我们有以下的二倍角公式:$$\sin2\theta = 2\sin\theta\cos\theta$$$$\cos2\theta = \cos^2\theta - \sin^2\theta$$这些公式可以用来将包含二倍角的三角函数表达式转化为简单的乘积形式。
4. 三倍角公式类似于二倍角公式,三倍角公式也是化简三角函数的方法之一。
对于角度 $\theta$,我们有以下的三倍角公式:$$\sin3\theta = 3\sin\theta - 4\sin^3\theta$$$$\cos3\theta = 4\cos^3\theta - 3\cos\theta$$这些公式可以用来将包含三倍角的三角函数表达式转化为简单的表达形式。
三角函数的求值与化简一 三角函数式的化简与证明 1.两角和与差的三角函数公式 sin(α+β)=sin αcos β+cos αsin β(S α+β) sin(α-β)=sin αcos β-cos αsin β.(S α-β) cos(α+β)=cos αcos β-sin αsin β;(C α+β) cos(α-β)=cos αcos β+sin αsin β.(C α-β) tan (α+β)=tan α+tan β1-tan αtan β;(T α+β)tan (α-β)=tan α-tan β1+tan α·tan β(T α-β)2.二倍角公式sin 2α=2sin αcos α;(S 2α)cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α;(C 2α) tan 2α=2tan α1-tan 2α.(T 2α)3.公式的变形与应用(1)两角和与差的正切公式的变形 tan α+tan β=tan (α+β)/(1-tan αtan β); tan α-tan β=tan (α-β)/(1+tan αtan β). (2)升幂公式1+cos α=2cos 2α2;1-cos α=2sin 2α2.(3)降幂公式 sin 2α=1-cos 2α2;cos 2α=1+cos 2α2. (4)其他常用变形sin 2α=2sin αcos αsin 2α+cos 2α=2tan α1+tan 2α; cos 2α=cos 2α-sin 2αcos 2α+sin 2α=1-tan 2α1+tan 2α;1±sin α=⎝⎛⎭⎫sin α2±cos α22; tan α2=sin α1+cos α=1-cos αsin α.5.角的拆分与组合 (1)已知角表示未知角例如,2α=(α+β)+(α-β),2β=(α+β)-(α-β), α=(α+β)-β=(α-β)+β, α=⎝⎛⎭⎫π4+α-π4=⎝⎛⎭⎫α-π3+π3. 例1化简:sin 2αsin 2β+cos 2αcos 2β-12cos 2αcos 2β=________.即时训练1化简:sin(θ+75°)+cos(θ+45°)-3cos(θ+15°)=________.例24cos 50°-tan 40°=( ) A.2B.2+32C.3D.22-1 (2)已知cos ⎝⎛⎭⎫α-β2=-513,sin ⎝⎛⎭⎫α2-β=45且0<β<π2<α<π,则sin(α+β)的值为________.即时训练2.(1)已知α为锐角,且sin α(1+3tan 10°)=1,则α的值为________. (2)已知α,β∈(0,π),且tan (α-β)=12,tan β=-17,求2α-β的值.。
简单的三角恒等变换——化简与证明
学习目标:能正确地运用三角函数的有关公式进行三角函数式的求值,化简与恒等式的证明. 学习重点:三角函数的有关公式的灵活应用和一些简单的变性技巧.
学习过程
一、知识清单
1.证明了cos()a b -= ®cos()a b += ®cos()2p a -= ,cos()2
p a += ®sin()a b += sin()a b -= ®tan()a b += ,tan()a b -= 2. cos (+)a b = ®cos 2a = = = sin()a b += ®sin 2a = tan()a b += ®tan 2a =
3.倍角的相对性
sin a = ,cos a = ,tan a =
4.要掌握这些公式的推导和联系,用时注意公式的“正用”,“逆用”和“变用”.
如:降幂扩角公式 2sin a = ;2
cos a = ; 1cos a += ;1cos a -= ;
1sin a += ;1sin a -= .
5. 划一公式:sin cos a x b x += (其中tan f = ,f 所在象限由 确定).
二、范例解析
题型一 三角函数式的化简和证明
1.三角函数式的化简要求:
通过对三角函数式的恒等变形使最后所得到的结果中:
①所含函数和角的名称或种类最少;②各项的次数尽可能地低;③出现的项数最少; ④一般应使分母和根号不含三角函数式;⑤对能求出具体数值的,要求出值.
2.三角变换的三项基本原则:
(1)角的变换:划同角(角的拆分,配角和凑角,1的变换);
(2)函数名称的变换:划同名(正切划弦);
(3)幂指数的变换:划同次(升幂、降幂公式,同角公式).
例1化简下列各式 ; ②1sin 2cos 21sin 2cos 2a a a a
+-=++ ; ③2sin 2cos 1cos 2a a a
-=+ ; ④222cos 12tan()sin ()44
a p p a a -=-+ ; 例2 证明下列各式(从左到右或从右到左或左右开攻中间会师,一般化繁为简)
①22tan 2sin 1tan 2a a a =+ ②2
2
1tan 2cos 1tan 2a a a -=+
③sin 1cos tan
21cos sin a a a a a -==+ ④[]1sin cos sin()sin()2a b a b a b =++-
⑤sin sin 2sin
cos 22
q f q f q f +-+=.
三、课下练习: 课本142P 2 ; 143P A 组 1, 2, 3, 4;B 组 1; 146P 8;147P 5.。