第四章《图形认识初步》综合测试题.doc11111

第四章综合能力检测卷时间:60分钟满分:100分一、选择题(每题3分,共30分)1.下列图形中,与其他三个不同类的是( )A B C D2.如图,下列说法正确的是( )A.图中共有5条线段B.直线AB与直线AC是同一条直线C.射线AB与射线BA是同一条射线D.点O在直线AC上3.如图,四个图形是由四个立体图形展开得到的,相应的立体图形依次是( )A.正方体、圆柱、三棱柱、圆锥B.正方体、圆锥、三棱柱、圆柱C.正方体、圆柱、三棱锥、圆锥D.正方体、圆柱、四棱柱、圆锥4.根据下列线段的长度,能判断A,B,C三点不在同一条直线上的是( ) A.AB=8,BC=19,AC=27 B.AB=10,BC=9,AC=18.9C.AB=21,BC=11,AC=10D.AB=7.5,BC=14,AC=6.55.如图,点C是线段AB上一点,点M是AC的中点,点N是BC 的中点,如果MC比NC长2 cm,那么AC比BC长( )A.1 cmB.2 cmC.4 cmD.6 cm6.如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列关于这个几何体的说法正确的是( )A.从正面看得到的平面图形的面积为5B.从左面看得到的平面图形的面积为3C.从上面看得到的平面图形的面积为3D.从三个方向看得到的平面图形的面积都是47.黑板上有四个不同的点A,B,C,D,过其中任意两个点画直线,可以画出直线的条数为( ) A.1或2 B.1,4或6C.1,3,4或6D.1,2,4或68.已知∠α的余角是23°17'38″,∠β的补角是113°17'38″,那么∠α和∠β的大小关系是( )A.∠α>∠βB.∠α=∠βC.∠α<∠βD.不能确定9.下列时刻,时针与分针的夹角为直角的是( )分A.3时30分 B.9时30分 C.8时55分 D.3时3601110.如图,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )A.点AB.点BC.A,B之间D.B,C之间二、填空题(每题3分,共18分)11.如图,在我国“西气东输”的工程中,从A城市往B城市架设管道,有三条路线可供选择,在不考虑其他因素的情况下,架设管道的最短路线是,依据是.第11题图第12题图第13题图12.如图,O为直线AB上一点,已知∠1=40°,OD平分∠BOC,则∠AOD= .13.如图,点A,O,B在同一条直线上,射线OD平分∠BOC,射线OE在∠AOC的内部,且∠DOE=90°,写出图中所有互为余角的角: .14.一个角的余角的3倍比它的补角小10°,则这个角的度数为.15.如图,线段AB表示一根对折以后的绳子,现从P处把绳子剪断,剪断后的各段绳子中最长的一段为10 cm,若AP=1PB,2则这条绳子的原长为cm.第15题图第16题图16.如图,平面内∠AOB=∠COD=90°,∠COE=∠BOE,OF平分∠AOD,给出以下结论:①∠AOE=∠DOE;②∠AOD+∠COB=180°;③∠COB-∠AOD=90°;④∠COE+∠BOF=180°.其中正确的是.(填序号)三、解答题(共52分)17.(6分)计算:(1)19°24'+76°26″-24°2'16″;(2)29°11'×3-106°32'÷4.AC,D,E 18.(8分)如图,已知C为线段AB上一点,AC=12,CB=23分别为AC,AB的中点,求DE的长.19.(8分)如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.(1)试确定射线OC的方向;(2)求∠COD的度数;(3)若射线OE平分∠COD,求∠AOE的度数.20.(8分)如图,OB,OC,OD是三条射线,OB平分∠AOC,且∠AOE 是平角,由这些条件能否得到结论∠BOD=90°?若能,请说明理由;若不能,请你补充一个条件,并说明你的理由.21.(10分)如图,M是线段AB上一定点,点C从点M出发以1 cm/s的速度沿线段MA向左运动,同时点D从点B出发,以3 cm/s的速度沿线段BA向左运动.(点C在线段AM上,点D在线段BM上)(1)若AB=10 cm,点C,D运动了2 s,则AC+MD= ;(2)若点C,D运动时,总有MD=3AC,则AM= AB;(3)在(2)的条件下,N是直线AB上一点,且AN-BN=MN,求MN的AB 值.22.(12分)已知O是AB上一点,∠COE=90°,OF平分∠AOE.(1)如图1,当点C,E,F在直线AB的同侧时,若∠AOC=40°,求∠BOE和∠COF的度数;(2)在(1)的条件下,∠BOE和∠COF有什么数量关系?请直接写出结论,不必说明理由;(3)如图2,当点C,E,F分别在直线AB的两侧时,若∠AOC=β,则(2)中∠BOE和∠COF的数量关系是否仍然成立?请说明理由.第四章综合能力检测卷题号 1 2 3 4 5 6 7 8 9 10 答案 C B A B C B B B D A 11.①两点之间,线段最短12.110°13.∠1与∠3,∠1与∠4,∠2与∠3,∠2与∠4 14.50°15.15或30 16.①②④17. (1)71°22'10″.(2)60°55'.18. 4.19. (1)北偏东70°.(2)70°.(3)90°.20. 不能,需要添加条件:OD平分∠COE.21. (1)2 cm(2)14(3)1或1.222. (1)25°.(2)∠BOE=2∠COF.。

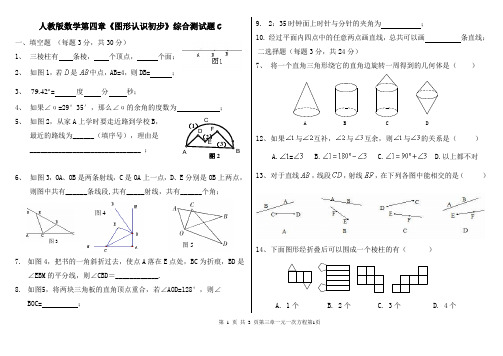
第 1 页 共 3人教版数学第四章《图形认识初步》综合测试题C一、填空题 （每题3分，共30分）1、 三棱柱有 条棱， 个顶点， 个面；2、 如图1，若是中点，AB=4，则DB= ；3、42.79= 度 分 秒；4、 如果∠α=29°35′，那么∠α的余角的度数为 ；5、 如图2，从家A 上学时要走近路到学校B ，最近的路线为______（填序号），理由是 _______________________________ ；6、 如图3，OA 、OB 是两条射线，C 是OA 上一点，D 、E 分别是OB 上两点，则图中共有______条线段,共有_____射线，共有______个角；7. 如图4，把书的一角斜折过去，使点A 落在E 点处，BC 为折痕，BD 是∠EBM 的平分线，则∠CBD ＝____________.8. 如图5，将两块三角板的直角顶点重合，若∠AOD=128°，则∠BOC= ；9. 2：35时钟面上时针与分针的夹角为 ；10. 经过平面内四点中的任意两点画直线，总共可以画 条直线； 互补，与互余，则与 C.13、 对于直线，线段，射线，在下列各图中能相交的是（ ）B图2图3图5图415、已知M是线段AB的中点，那么，①AB=2AM；②BM=12AB；③AM=BM；④AM+BM=AB。

上面四个式子中，正确的有（）A．1个 B．2个 C．3个 D．4个16、在海上，灯塔位于一艘船的北偏东40度方向，那么这艘船位于这个灯塔的（）方向A.南偏西50度B.南偏西40度C.北偏东50度D.北偏东40度17、如右图，AB、CD交于点O，∠AOE=90°，若∠AOC：∠COE=5：4，则∠AOD等于（）A．120° B．130°C．140° D．150°18、图中(1)-(4)各图都是正方体的表面展开图，若将他们折成正方体，各面图案均在正方体外面，则其中两个正方体各面图案完全一样，他们是（）A. (1)(2)B.（2）（3）C.（3）（4）D.（2）（4）三、作图题（各7分，共21分）19、已知、求作线段AB使AB=2a－b（不写作法，保留作图痕迹）20、按照要求，在图中画出表示下列方向的射线：(1)南偏东300 (2)北偏西600 (3)西南方向四、解答题（8+8+9分，共25分）21、若一个角的补角等于它的余角的4倍，求这个角的度数。

⎧⎨⎩⎧⎨⎩第四章 图形的初步认识知识点及评价测试题一、立体图形与平面图形立体图形：棱柱、棱锥、圆柱、圆锥、球等。

1、几何图形 平面图形：三角形、四边形、圆等。

主（正）视图---------从正面看 2、几何体的三视图 侧（左、右）视图-----从左（右）边看俯视图---------------从上面看（1）会判断简单物体（直棱柱、圆柱、圆锥、球）的三视图。

（2）能根据三视图描述基本几何体或实物原型。

3、立体图形的平面展开图（1）同一个立体图形按不同的方式展开，得到的平现图形不一样的。

（2）了解直棱柱、圆柱、圆锥、的平面展开图，能根据展开图判断和制作立体模型。

4、点、线、面、体（1）几何图形的组成点：线和线相交的地方是点，它是几何图形最基本的图形。

线：面和面相交的地方是线，分为直线和曲线。

面：包围着体的是面，分为平面和曲面。

体：几何体也简称体。

（2）点动成线，线动成面，面动成体。

二、直线、射线、线段（一）.直线、射线、线段的区别与联系： 基本概念（二）.直线、线段性质：经过两点有一条直线，并且只有一条直线；或者说两点确定一条直线；1、线段的性质 两点的所有连线中，线段最短。

简单地：两点之间，线段最短。

2.画线段的方法（1）度量法（2）用尺规作图法3、线段的大小比较方法（1）度量法（2）叠合法4、点与直线的位置关系二、角（一）.角的意义：1、角：由公共端点的两条射线所组成的图形叫做角。

2、角的表示法（四种）：3、角的度量单位及换算4、角的分类有公共端点的两条射线组成的图形叫做角，公共端点是角的顶点，这两条射线是角的两条边，角也可以看做由一条射线绕着它的端点旋转而形成的图。

注意：表示角时，一定要对照几何图形，注意不能漏掉角的符号，切记用三个大写字母表示一个角时，顶点字母一定要写在中间；同一顶点处有多个角时，切不可用顶点字母来表示。

（二）.角的度量：1°=60′ 1′=60″1直角=90° 1平角=180 ° 1周角=360°（三）.角的大小的比较：（1）叠合法，使两个角的顶点及一边重合，另一边在重合边的同旁进行比较；（2）度量法。

第4章 图形认识初步综合测试（时间90分钟，满分100分）一、填空题.（每小题3分，共30分） 1. 植树时只要先定两个树坑的位置，？就能确定一行树所在的位置，其根据是 ______________2. 已知线段 AB=9厘米，在直线 AB 上画线段BC,使它等于3厘米，则线段 AC= __________ .3. 若/ AOB=40，/ BOC=60，则/ AOC== __________4. ______________________________________ 53° 40' 30"X 2-75 ° 57' 28〃+ 2= .5. __________________________________________________________________________ 已知线段AB=3厘米，延长AB 到C,使BC=2AB 若D 为AB 中点，则线段DC?勺长为 ____________ 6. 8 ° 44' 24〃用度表示为 _______ , 110. 32。

用度、分、秒表示为 ___________7.如图1是一套三角尺组成的图形， 则/ AFD=(3) (4)1 1 1 9.将线段AB 延长到C ,使BC A AB,延长BC 到D,使CD — BC,延长CD 到 E ,使DE — CD333若AE=?80厘米，则AB= ________ .10•在圆柱的展开图中，圆柱的侧面展开图为 __________ , ?棱柱的侧面展开图为 ________ ，圆锥的侧面展开图为 _________ . 二、选择题.（每小题3分，共30分） 11.下列说法正确的是（ ）.A .直线的一半是射线;B.直线上两点间的部分叫做线段；C .线段AB 的长度就是 A, B 两点间的距离；D .若点P 使PA=AB 则P 是AB 的中点. 12 .钟表在5点半时，它的时针和分针所成的锐角是（ ）.A . 15°B . 70°C . 75°D . 90°13 .从点A 看B 的方向是北偏东35°，那么从B 到A 的方向是（）. A .南偏东55 ° B .南偏西55° C .南偏东35° D .南偏西35° 14 .图2是一正方体展开图，则“有志者”三面的对面分别是（ ）.A .事竟成B .事成竟C .成竟事 C .竟成事 15 .图3中的三棱柱的三视图是（）.A .三个三角形 B.两个长方形和一个三角形C .三个长方形有r 瓦 S8.Z a 与/ 3互补，若/ a =4737'，则/ 3 = ________⑴ (2)D .两个长方形，且长方形内有一条连结对边的点的线段和一个三角形18.线段AB=5厘米，BC=4厘米，那么A, C 两点的距离是（）.A . 1厘米B . 9厘米C . 1厘米或9厘米 D.以上结果都不对419 .已知一个角的余角的补角是这个角补角的 ，则这个角的角的余角度数是（？）.5A . 90°B . 80°C . 30°D . 10 °20 .轮船从A 地出发向北偏东 70°方向行驶了 4海里到达B 地，又从B 地出发向南偏西20。

企方舟教育中坷叭■导专业导歸第四章《图形的初步认识》综合测试题班级_________ 姓名_______________ 得分___________（时间：90分钟满分：100分）一、轻松入门选一选，（每小题2分，共20分）1•下列说法：①若一个物体的三视图都是圆，则这个物体是球；②圆柱的侧面展开图的形状是长方形；③圆柱由3个面组成，其中2个是曲面，1个是平面；④直角三角形绕着它的一条直角边旋转一周所得的立体图形是棱锥•其中不正确的个数是（）A. 1个B.2个C.3个D.4个2•下列说法：① 延长射线OA；②线段AB与线段BA是同一条线段；③ 在所有连结两点的线A. 1个B.2个C.3个D.4个3•若点C在直线AB上，且AC=13, BC=8,则A、B两点间的距离是A. 5B.21C.5 或21D.无法确定中，直线最短；④ 两点之间的线段，叫做两点之间的距离•其中正确的个数是4 •已知ZA是它的补角的4倍，则ZA等于A. 36°B.72°C. 90°D.144°5•甲看乙的方向是北偏东30°,则乙看甲的方向是A.南偏东60°B.南偏西30°C.南偏东30°D.南偏西60 6•若和z2互余，z 1与z3互补，则z 2与z3的关系是A. z3=90°+z2B. Z3=90°- Z2C. z3=180°+z2D. Z3=180°- Z27 •下列判断正确的是A. 两个锐角的和一定是钝角B. 平角是一条直线C. 有公共点的两条射线所组成的图形叫做角D. 角的和、差、倍、分的度数等于它们的度数的和、差、倍、分金方舟教育8•如图1,下列说法错误的是9•若 zA=33.33： Z B=33°33/，"=33・5 ,A. ZA= ZBB.ZA>ZBC.ZB>ZC11.甲从O 点向北偏东30°走200米，到达A 处，乙从O 点向北偏西30°走200米到达B 处,A. Z3和ZC 是同位角B. Z1和Z3是内错角C. ZA 和ZB 是同旁内角D.Z3和ZA 是内错角D.ZA + ZB>2ZC10•如图2所示, O已知 Z AOC =ZBOC = 90 , ZBOE 二ZCQFI,则图中互为余角的角共有A. 2对B.3对C.4对D. 5对二、快乐晋级填一填 （每小题3分，共24分） D则B点在A的方向・12•在直线I上顺次取A、B、C三点，使AB = 4cm, BC=5cm.若O是线段AC的中点，则13•若一=3胛/'则" ；钟表4点40分时，时针与分针的夹角是14•如图3所示，已知AC丄CB, CD丄AB,则图中共有个直角；线段C 至I] AB 的距离；线段AD的长度表示点的距离・线段OB的长是15.如图4, 已知AB || CD, Z G-Z EBF,则图中与Z DCG相等的角有16.如图5, C是ZAOB的边OA上一点，D、E是OB上两点，则图中共有条线段, 条射线, 个小于平角的角・/D = 140°, 17•如图6所示，一辆汽车在公路上行驶，Z AOB =40°, Z CO企方舟教育可看出是______ 和 ____ ；ZCOF的补角从图中可看出是_______ 和 _____E19. （6分）图8是个正方体的展开图，若此正方体相对而上的数互为相反数，求 a （b c）的值.18•如图7,已知直线AB、CD、EF 相交于0,且ZA0D = 90°,则ZEOD的余角从图中三、形成能力解一解（共56分）试，把拼成的四边形分别画在图③、图④的虚线框内・图7ABF B DG 图420062008 2007 a20. （6分）如图9,用剪刀将形状加图① 所奈的矩形前片\B6D-沼直线'CM 两部分厂長中M为AD的中点.用这两部分纸片可拼成一些新图形，如图②中的ABCE就是拼成的一个图形・用这两部分纸片除了可拼成图② 中的ABCE夕卜，还可拼成一些四边形•请你试一EMDA M21. （7分）一只蚂蚁从O点出发，如图10所示，沿北偏东60°的方向行了2.5厘米，碰到障碍物（记为点B）,又沿西北方向行了3厘米（此时位置记为C点）.（1）请画出蚂蚁爬行的路线；图9(2)计算ZOBC的度数・西东O南图1022. （7分）已知Z AOB = 70°, ZBOC是ZAOB的补角，画出图形并求出Z AOC的大小.23. （9分）已知线段AC和BC在一条直线上，若AC = 8cm, BC=3cm.求线段AC和BC 的中点间的距离・24. （9 分）如图"所示，ZABC 二ZACB, BD 平分ZABC , CE 平分ZACB , ZDBF=ZF. CE 与DF平行吗？请说明理由・B C F图1125. （12分）如图12,田径运动会上一名服务的同学要往返于百米起跑点A、终点记时处B（A、B位于东西方向）及检录处C,他在A处看C点位于北偏东60°方向上，在B处看C 点位于西北方向（即北偏西45°）上.（1）检录处C的位置；（2）现限定只用刻度尺作为工具，如果想知道这位同学在检录处C与百米起跑点A之间往返一次要走多少米（不考虑其它因素），请说出你的办法（不要求作具体的计算）・企方舟教育第四章《图形的初步认识》综合测试题参考答案、1. B ； 2. A ； 3. C ； 4. D ； 5. B ； 6. A ； 7. D ； 8.D ； 9. C ； 10. C. 12.0.5cm ； 13.91°3/' 400。

第四章《图形认识初步》综合复习检测卷(四)一、选择题（每小题3分，共30分）1.下列关于棱柱的说法：①棱柱的所有面都是平面；②棱柱的所有棱长都相等；③棱柱的所以侧面都是长方形或正方形；④棱柱的侧面个数与底面边数相等；⑤棱柱的上、下底面形状、大小相等其中正确的有 （ ）.（A ）2个 （B ）3个 （C ）4个 （D ）5个2．下列图形中是正方体的表面展开图的是 （ ）.(A) (B) (C) (D)3.如图1，点C 是线段AB 的中点，点D 线段BC 的中点，下列等式不正确的是（ ）.（A ）CD=AC-DB （B ）CD=AD-BC （C ）CD=21AB-BD （D ）CD=31AB图14.一个物体的从正面、左面、上面三个方向看是下面三个图形，则该物体形状的名称为 （ ）(A) 圆柱 (B) 棱柱(C) 圆锥 (D) 球 正面 左面 上面5．下列判断正确的是 （ ）． 图2（A ）平角是一条直线 （B ）凡是直角都相等（C ）两个锐角的和一定是锐角 （D ）角的大小与两条边的长短有关6．如图3，∠AOB ＝∠COD ＝90°，那么∠AOC=∠BOD ，这是根据 （ ）.(A)直角都相等 (B) 同角的余角相等(C)同角的补角相等 (D)互为余角的两个角相等图37. 点M 、O 、N 顺次在同一直线上，射线0C 、0D 在直线MN 同侧，且∠MOC=64°，∠DON=46°，北则∠MOC 的平分线与∠DON 的平分线夹角的度数是 （ ）.（A ）85° （B ）105° （C ）125° （D ）145°8. 某测绘装置上一枚指针原来指向南偏西50°（如图4）， 把这枚指针按逆时针方向旋转41周，则结果指针的指向 （ ）． （A ）南偏东50º （B ）西偏北50º（C ）南偏东40º （D ）南偏东45° 图49．如图5，每个长方体的六个面上分别写着1～6这六个数，并且任意两个相对的面上所写的两个数之和所写的两个数之和都等于7，靠在一起的长方体中，相连接两个面的数字之和等于8，图中打“？”的面上所写的数字是 （ ）.（A ）3 （B ）5 （C ）2 （D ）110．计算180°-48°39′40″-67°41′35″的值是 （ ）. 图5（A ）63°38′45″ （B ）58°39′40″ （C ）64°39′40″ （D ）63°78′65″二、填空题（每小题2分，共20分）11．如图6所示的图形绕虚线旋转一周,所围成的几何体是_____.图6 图7 12.如图7是一个正方体纸盒的展开图,在其中的四个正方形内有数字1、2、3和-3，要在其余正方形内分别填上-1、-2，使得按虚线折成正方体后，相对面上的两个数互为相反数，则A 处应填_____.13.植树时,只要定出_______个树坑的位置,就能确定同一行树坑所在直线,根据是_______.14.如图8是三个几何体的展开图,请写出这三个立体图形_________ __________ ________图815.某工程队在修筑高速公路时,有时需要将弯曲的道路改直,以缩短路程,这样作的理论依据是________.16.如图9,点C是∠AOB的边OA上一点,D、E是OB上两点，则图中共有_____条线段,_____条射线,_____个小于平角的角.图9 图1017.如果一个角的补角是150°,那么这个角的余角是________.18.乘火车从A站出发,沿途经过3个车站可到达B站,那么在A、B两站之间共有____种不同的票价.19.如图10,将一副三角板叠放在一起,使直角的定顶点重合于点0,则∠AOC+∠DOB=_____.20.在直线l上取A、B、C三点，使得AB=4cm，BC=3cm，如果0是线段AC的中点，则线段OB的长度为_________.三、解答题(1-6每小题6分,7-8分每小题7分)21．观察图11中的几何体，画出从正面、左面、上面三个方向看，得到的平面图形。

《图形认识初步》综合练习 2. 以下四个图中 ,能用∠ 1、∠ AOB、∠ O三种方法表示同一个的是一、填空题（）1．圆柱的侧面睁开图是；2．要在墙上固定一根木条,起码要个钉子,依据的原理是3．已知∠与∠互余, 且∠40o,则∠为.4．如图, 若是中点 ,是中点 ,若,,_________。

5 ．小明每日下午 5:30 回家 ,这时分针与时针所成的角的度数为___________。

6．⑴° ；⑵ 0.5°=______′=______″7．不在同向来线上的四点最多能确立条直线。

8．一个角的补角等于它的余角的 3 倍, 则这个角的度数为.二、选择题1．关于直线,线段,射线,在以下各图中能订交的是（）3．如图 ,∠1＝15 ,∠AOC=90点B、O、D在同向来线上 ,则的度数为（）A 75°B 15°C 105°D 165°4．将以下图形绕直线l 旋转一周 , 能够获得右图所示的立体图形的是 ()5．以下图中 , 是正方体的睁开图是 ()A B C D三、作图题：依据以下要求绘图：（1）连结线段 AB ；（2）画射线 OA, 射线 OB；（ 3）在线段 AB 上取一点 C, 在射线 OA 上取一点 D（点 C、D 不与点 A 重合） , 画直··A B线 CD, 使直线 CD 与射线 OB 交于点 E。

四、计算题·O(1)76 35 69 65(2)180 23 17 57五、解答题1. 如图 ,D 是 AB的中点 , E 是 BC的中点 ,BE= 1AC=2cm, 求线段 DE的长5A CD BE 有个角 ,求画n条射线所得的角的个．数。

．4．（1）以以下图 ,已知点 C 在线段 AB 上,且 AC 6cm ,BC 4cm ,点M，N 分别是 AC ,BC的中点 , 求线段MN的的长度．（2）在（ 1）中,假如AC acm,BC bcm,其余条件不变,你能猜出MN的长度吗？请你用一句简短的话表述你发现的规律．（3）关于（ 1）题 , 假如我们这样表达它：“已知线段AC6cm ,2. 如图 , 点 A、O、E 在同向来线上 , ∠AOB=4 0°, ∠EOD=28° , ODBC 4cm ,点 C 在直线 AB 上,点M，N分别是AC，BC的中点,求 MN均分∠ COE,求∠ COB 的度数B C的长度．”结果会有变化吗？假如有 , 求出结果．DA O E3．以以下图 , 在已知角内画射线 , 画 1 条射线 , 图中共有个角；画 2 条射线 , 图中共有个角；画3条射线,图中共的延伸线上时 ,MN1cm．参照答案一、填空题：1．矩形或长方形2．两；两点确立一条直线3． 50°4． 15． 15°6．23.5 30 18007．68．45°二、选择题：1．Ｂ2．D3．Ｃ 4 ．Ｃ5．B三、作图题：略四、计算题(1) 146°40′(2) 156°42′3〞五、解答题1.5cm2.∠COB=84°3. 3 6 10 1 (n+2)(n+1)24．（1）5cm；（2）a b,直线上相邻两线段中点间的距离为两线段长度和的一半；2（3）有变化 ,当点C在线段AB上时,MN5cm；当点C在AB或BA。