《计算方法》第四章 插值方法共90页文档

《 计 算 方 法 》
4
3
xi 4 yi 2
9 16 3 4
2
0
4
7
9
16
第4章 插值法
应用背景
造函数表：三角函数、对数 预测：鸡蛋价格、城市用水量
《 计 算 方 法 》
数控加工：造船、飞机机翼骨架、服装 样片、模具加工、刀具 计算机辅助设计：潜水艇、汽车造型
服装样片
第4章 插值法
实际问题中，f (x)多样，复杂，通常只能观测到一些离散 数据；或者f (x)过于复杂而难以运算。这时我们要用近似函数 φ(x)来逼近f (x)。
《 计 算 方 法 》
φ (x)= y0
第4章 插值法
§2 线性插值与二次插值
2.1 线性插值
线性插值是代数多项式插值的最简单的形式。假设
《 计 算 方 法 》
给定了函数f (x)在两个互异点x0，x1的值,即
x x0值）
y y0 x0
y1
x1
x
第4章 插值法
现要用一线性函数
满足插值条件：
y( xi ) = yi , i = 0,1, 2
22
第4章 插值法 例：已知函数 y=f (x)的观测数据为
x
《 计 算 方 法 》
1 0
2 -5
3 -6
4 3
y
试求拉格朗日插值多项式。
第4章 插值法
《 计 算 方 法 》
( x 2)( x 3)( x 4) 解 ：p3 ( x ) = 0 (1 2)(1 3)(1 4) ( x 1)( x 3)( x 4) ( 5) (2 1)(2 3)(2 4) ( x 1)( x 2)( x 4) ( 6) (3 1)(3 2)(3 4) ( x 1)( x 2)( x 3) 3 (4 1)(4 2)(4 3) = x3 4 x2 3

n
( x xi ) i 0 ( x j xi )
i j
j 0,1,2 ,, n
n+1次多项式
令 n1 ( x) ( x x0 )( x x1 )( x xn )
则 n1 ( x j ) ( x j x0 )( x j x1 )( x j x j 1 )( x j x j 1 )( x j xn )
x0
x1
x2
x
x3
x4
Lagrange插值多项式
假定已知区间 xk , xk 1 端点处的函数值yk f ( xk ), yk 1 f ( xk 1 )
为了求得便于使用的简单的插值多项式P(x), 我们先讨论n=1的情形
要求线性插值多项式L1(x), ( xk 1 ) yk 1
L1(x)的几何意义就是通过这两点的直线；
yk 1 yk L1 ( x) yk ( x xk )(点斜式） xk 1 xk xk 1 x x xk L1 ( x) yk yk 1 (两点式） xk 1 xk xk 1 xk
xk 1 x x xk L1 ( x) yk yk 1 (两点式） xk 1 xk xk 1 xk
在例1中,如果只给出两个节点169和225,也可以作插值 多项式,即1次Lagrange插值多项式,有两个插值基函数, 这种插值方法称为Lagrange线性插值,也可以在n+1个 节点中取相邻的两个节点作线性插值
例2. 用Lagrange 线性插值多项式求例1中的f (175).
解: 由于插值点x 175在x1 169与x2 225之间
解: 设x0 144, x1 169, x2 225 y0 12, y1 13, y2 15

代数插值
代数插值
当f(x)是次数不超过n的多项式时,给定n+1个节点,其n次插值多项式就是f(x)本身.
代数插值几何意义
拉格朗日插值 逐次线性插值 牛顿插值 等距节点插值 反插值 埃尔米特插值 分段插值法 三次样条插值
拉格朗日插值 线性插值
格朗日插值 抛物线插值
基函数之和为1.
拉格朗日插值 n次插值
当插值点x∈(a,b)时称为内插，否则称为外插。
内插的精度高于外插的精度。
拉格朗日插值余项
余项 设函数f(x)在包含节点x0 , x1 ,…, xn的区间[a,b]上有n+1阶导数，则
拉格朗日插值
活动14
写出3次拉格朗日插值多项式及余项
拉格朗日插值
拉格朗日插值
作业5
已知函数表
应用拉格朗日插值公式计算f(1.300)的近似值.
数值计算方法
苏 强
江苏师范大学连云港校区
数学与信息工程学院 E-mail: 412707233@
数值计算方法 第四章 插值与曲线拟合
没有明显的解析表达式
使用不便的解析表达式
简单函数代替
插值问题
插值问题
代数插值 插值函数
被插值函数 插值节点
插值区间
三角多项式插值 有理函数插值
代数插值
抛物线插值
三点插值
拉格朗日插值 抛物线插值
抛物线插值
三点插值
拉格朗日插值 抛物线插值
拉格朗日插值 n次插值
称为关于节点
的n次插值基函数.
拉格朗日插值n次插值
基函数的个数等于节点数.
n+1个节点的基函数是n次代数多项式 基函数和每一个节点都有关。节点确定，基函数就唯一的确定。 基函数和被插值函数无关

米插值基函数。
计算方法
第四章 函 数 插 值
下面利用拉格朗日插值基函数li(x)(i=0，1，…，n)来构
造ai(x)和βi(x)。
因关于节点x0，x1，…，xn的拉格朗日基函数li(x)满足：
(j≠i, j=0, 1, …，n) 且l2i(x)是2n次多项式，由条件(4.25)式，可设ai(x)为
计算方法
第四章 函 数 插 值
定理4.4 满足插值条件(4.24)式的埃尔米插值多项式是
唯一的。 证明 设H2n+1(x)和 H 2n1 x 都是满足条件(4.24)式的埃 尔米插值多项式，令
x H2n1 x H2n1 x
则每个节点xi(i=0，1，…，n)均为φ(x)的二重根，即φ(x)有 2n+2个根，但φ(x)是个不高于2n+1次的多项式，所以φ(x)≡0，
米(Hermit)插值，它是代数插值问题的推广。
.5.1 一般情形的埃尔米插值问题
已知函数y=f(x)在区间［a, b］上n+1个互异节点x0，
x1，…，xn处的函数值为yi=f(xi)(i=0, 1, 2, …，n)，导数值为 f′(xi)(注意：函数值个数与导数值个数相同)，现要求做一个 次数不超过2n+1次的多项式H2n+1(x)，使其满足下述2n+2个 插值条件:
2 2
2
2
计算方法 例1.
第四章 函 数 插 值
已知f ( x)在节点1， 2处的函数值为 f (1) 2 , f ( 2 ) 3 f ( x)在节点1， 2处的导数值为 f (1) 0 , f ( 2 ) 1
求f ( x)的两点三次插值多项式 , 及f ( x)在x 1.5,1.7处的函数值 .

目前二十四页\总数八十九页\编于九点
➢ Lagrange插值法的插值余项
设节点 ax0x1 xnb，且 f 满足条件 f Cn[a,b],
f (n1)在[a , b]内存在 , 截断误差(或插值余项):
f(n 1)( ) R n(x)f(x)L n(x)(n1 )! n 1(x)
,
(a,b)
l2 ( x)
(x (x2
x 0 )( x x1 ) x 0 )( x 2 x1 )
抛物线基函数
于是
L 2(x)
(x (x0
x1)(x x1)(x0
xx 2) 2)y0
(x (x1
x0)(x x0)(x1
xx22 ))y1
(x (x2
x0)(x x0)(x2
xx 1) 1)y2
2
li(x)yi
目前九页\总数八十九页\编于九点
插值的几何意义
从几何上看，插值就是求一条曲线 y P(x) 使其通过给定的 n 个 1点 (，x i , y i ) (i0,1, ,n) 并且与已知曲线 y 有f (一x)定的近似度。
x
y = f (x) •
y = p(x)
(xi, yi)
曲线 P ( x)
§4.0 引言
➢ 许多数据都是用表格法给出的(如观测和实验而得到的函数数据 表格)，可是，从一个只提供离散的函数值去进行理论分析和 进行设计，是极不方便的, 甚至是不可能的。因此需要设法去 寻找与已知函数值相符，并且形式简单的插值函数(或近似函 数)。
➢ 另外一种情况是，函数表达式完全给定，但其形式不适宜计算机 使用，因为计算机只能执行算术和逻辑操作，因此涉及连续变 量问题的计算都需要经过离散化以后才能进行。如数值积分 方法、数值微分方法、差分方程以及有限元法等，都必须直

=f (x) 在给定互异的自变量值x0, x1, x2上对 应的函数值为y0, y1, y2，二次插值就是构造一个二次 多项式
P2 ( x) a0 a1 x a2 x 2
使之满足
P2 ( xi ) yi , i 0, 1, 2
计算机科学与工程系 19

令
lk ( x ) ( x x0 )( x x1 ) ( x xk 1 )( x xk 1 ) ( x xn ) ( x x j )
j 0 j k n
计算机科学与工程系 27
4.2.3 拉格朗日插值多项式

由lk (xk) = 1，得：
1 ( xk x0 )( xk x1 ) ( xk xk 1 )( xk xk 1 ) ( xk xn )
计算机科学与工程系 25
10
11
4.2.3 拉格朗日插值多项式

插值公式

设连续函数y = f（x）在[a, b]上给定n + 1个不同结 点： x0, x1, …, xn 分别取函数值 y0, y1, …, yn 其中 yi = f (xi) i = 0, 1, 2,…, n 构造一个次数不超过n的插值多项式
因此
( x x0 )( x x2 ) ( x x1 )( x x2 ) P2 ( x ) y0 y1 ( x0 x1 )( x0 x2 ) ( x1 x0 )( x1 x2 ) ( x x0 )( x x1 ) y2 ( x2 x0 )( x2 x1 )

因此有
lk ( x ) ( x x0 )( x x1 ) ( x xk 1 )( x xk 1 ) ( x xn ) ( xk x0 )( xk x1 ) ( xk xk 1 )( xk xk 1 ) ( xk xn )

两点
多项式插值就是直线
， 经过这两点的
称给定
为线性插值多项式。称
为关于点
的线性插值基函数，其在节点处满足：
6
4.2.1 线性插值与二次插值 假定插值节点为 ， ， ，要求二次插值多项式
几何上
是通过三点
可以用基函数的方法求的表源自式，是二次函数，的抛物线.
7
4.2.2 拉格朗日插值多项式
求n+1个次数 满足
且次数不超过n 的多项式，其所给出形式的系数为
称
为牛顿（Newton）均差插值多项式.
系数 就是均差表4-1中主对角线上的各阶均差， 它比拉格朗日插值计算量省，且便于程序设计.
25
4.3.2 Newton均差插值多项式 （*）为插值余项，由插值多项式惟一性知，它与
拉格朗日插值多项式的余项应该是等价的. 事实上，利用均差与导数关系式就可以证明这一点. 但（3.7）更有一般性，它在 是由离散点（给3.出7）的
式求 x 的近似值。
解 (1) 选取节点x=2,3,4
xf 一 二 三
kk
(x k)
阶 均
阶 均
阶 均
31
32
4.4 分段低次插值
4.4.1 Runge现象 在次数 增加时逼近 的精度是否也增加?
问题：根据区间 上给出的节点做出的插值多项式
事实上，对于有些函数，插值多项式次数很高时会在某些区 间内产生较大的误差。例如著名的Runge现象。
分段插值的基本思想是将插值区间划分为若干个小区 间, 然后在每个小区间上做满足一定条件的低阶插值.
35
4.4.2 分段低次插值
例如分段线性插值。 所谓分段线性插值就是通过插值点用折线段连接起来

1)
Rn ( x ) K ( x) ( x - xi )
i 0
n
考察 j ( t ) Rn ( t ) - K ( x ) ( t - x i )
i0
n
j(t)有 n+2 个不同的根 x0 …
f (n ( x ) - L(nn

1)
xn x， j ( n1) ( x ) 0, x (a, b)
x - x0 y x1 - x 0 1
l ( x) y
i 0 i
1
i
l0(x)
l1(x)
n1
希望找到li(x)，i = 0, …, n 使得 li(xj)=ij ；然后令
Pn ( x )
l (x) y
i0 i
n
i
，则显然有Pn(xi) = yi 。
每个 li 有 n 个根 x0 … xi-1， xi+1 … xn li ( x) Ci ( x - x j )
插值法 比较古老, 常用的方法。 当未知函数 y = f(x) 非常复杂时，在一系列节 点 x0 … xn 处测得函数值： y0 = f(x0) … yn = f(xn) 由此构造一个简单易算的近似函数 P(x) f(x)， 满足条件P(xi) = f(xi) (i = 0, … n)，称P(x) 为f(x) 的插值函数。 最常用的插值函数是多项式
项式是唯一存在的。 证明：
i 0, ... , n 的 n 阶插值多
若除了Ln(x) 外还有另一 n 阶多项式 Pn(x) 满足 Pn(xi) = yi 。 考察 Qn ( x) Pn ( x) - Ln ( x) , 则 Qn 的阶数 n 而 Qn 有 n + 1 个不同的根 x0 … xn

4 插值插值在科学计算和工程技术中有广泛应用。

例如由实验得到一系列点x0, x1,…, x n及对应的值y0, y1,…, y n，要构造函数y = f (x)，使y i=f(x i)，这就是简单的插值问题。

插值核心问题是：插值函数的构造、插值函数的存在性、唯一性以及误差分析等。

图4.1 插值在CAD中的应用4.1 代数插值图4.2 插值一个基本的插值问题就是构造函数)(x f y =的近似表达式。

常用方法是构造n 次多项式)(x P n ，使i i n y x P =)(，n i ,,1,0 =。

作为)(x f 的近似表达式，称)(x P n 为)(x f 的插值函数，n x x x ,,,10 为插值节点。

以代数多项式作为工具来构造插值的方法叫做代数插值，代数插值的优点是基于多项式求值方便且连续可导的特性。

设n x x x <<< 10为插值节点，令n x b x a ==,0，称],[b a 为插值区间。

设插值多项式为：n n n x a x a x a a x P ++++= 2210)(，由插值条件n i y x P i i ,,1,0,)( ==，得到如下线性代数方程组：n i y a x a x a i n n i i 2,1,0,110==+++⋅该线性方程组的系数行列式为∏≤<≤-==ni j jin nn nn nx x x x x x x x x x x D 0212110200)(111，D 为范得蒙行(Vandermonde)列式。

由于对于任何满足n i j ≤<≤0的j i ,，都有j i x x ≠，所以0≠D ，即该线性方程组有唯一解，故)(x P n 由n a a a ,,,10 唯一确定。

4.2 拉格朗日插值图4.3 线性插值与抛物线插值已知)(x f y =在给定节点10,x x 上的值为10,y y 。

线性插值就是构造一次多项式b ax x P +=)(1，使它满足条件001)(y x P =，111)(y x P =。

P( x) an x an1 x
n
n1
a1 x a0
满足
P( xi ) f ( xi )
(i 0,1,2,, n)
计 则称P(x)为f(x)的n次插值多项式。这种插值法通常 算 称为代数插值法。其几何意义如下图所示 方 法 课 件 y=p(x)
y=f(x)
2016/12/27
算 l0 ( x0 ) 1, l0 ( x1 ) 0 , l0 ( x2 ) 0 方 法 这个问题容易求解。由上式的后两个条件知 : 课 件 x1 , x 2 是 l0 ( x) 的两个零点。于是
1 再由另一条件 l0 ( x0 ) 1 确定系数 c ( x0 x1 )(x0 x2 ) ( x x1 )(x x2 ) 从而导出 l0 ( x) ( x0 x1 )(jkhh x0 x 2 ) 2016/12/27 14
直接由插值条件决定，
y
计 即 a0 , a1 , a 2 满足下面 y0 算 的代数方程组： 方 O x0 法 课 2 a a x a x 0 1 0 2 0 y0 件 该三元一
y=L2(x) y1 x1 y1 x2 y=f(x) x
2 a a x a x 0 1 1 2 1 y1 2 a a x a x 2 2 y2 0 1 2
(i=0,1,2,…,n )
的便于使用的插值多项式P(x),先考察几种简单情形,
线性插值是代数插值的最简单形式。假设给定了函数 近似地代替f(x)。选
x1 的值， f(x)在两个互异的点 x0 ， y0 f ( x0 ), y1 f ( x1 )
,现要求用线性函数 p( x) ax b 择参数a和b, 使 p( xi ) f ( xi )(i 0,1) P(x) 为f(x)的线性插值函数 2016/12/27 jkhh 。

定理2 设f(x)在a, b有n+1阶导数， x0, x1,…, xn 为 a, b上n+1个互异的节点, p(x)为满足 p(xi) = f(xi) (i=1,2, …, n) 的n 次插值多项式，那么对于任何x a, b有
插值余项
f ( n 1) ( ) R( x) f ( x) p ( x) ( x) (n 1)!
P( x) l0 ( x) y0 l1 ( x) y1 l n ( x) y n
l k ( x)( k 0,1,, n)
P( x)
l
k 0
n
k
( x) y k
（2.8）
是次数不超过n次的多项式 , 称形如（2.8）式的插 值多项式为n次拉格朗日插值多项式。并记为
Ln (x)
li (x)
xi
l k ( x0 ) 0,, l k ( xk 1 ) 0, l k ( xk ) 1, l k ( xk 1 ) 0,, l k ( xn ) 0
即
1 (i k ) l k ( xi ) ki 0 (i k )
由条件
l k ( xi )( 0 )知,i k
在插值区间a, b上用插值多项式p(x)近似代替f(x), 除了在插值节点xi上没有误差外， 在其它点上一般是存在误差的。
y=f(x)
y=p(x)
a x0 x1
b xixi+1 xn-1 xn
若记 R (x) = f(x) - p(x) 则 R(x) 就是用 p(x) 近似代替 f(x) 时的截断误差, 或称 插值余项我们可根据后面的定理来估计它的大小。
f[x1,x2]- f[x0,x1]

§4.2.2 插值多项式的构造
现在考虑一般情况。已知节点 (xi, yi), i=0,1,…,n, x0<x1<…<xn, 则
Ln ( x ) yi li ( x )
i 0 n
( x x0 )...( x xi 1 )( x xi 1 )...( x xn ) yi i 0 ( xi x0 )...( xi xi 1 )( xi xi 1 )...( xi xn )
计算方法 (力学系本科生)
第四章 插值方法
(interpolation methods)
第四章插值方法
§4.1 问题的提出
§4.1 问题的提出
实际背景 • 实验和观察得到的一些离散数据点 ( xi , yi ), yi f ( xi ), i 0,1, 2,..., n, 需要 用这些离散数据点给出简单的函数表达 式 ( x)来近似原来函数 f ( x) 。
§4.2.2 插值多项式的构造
一般情形的拉格朗日插值多项式
设离散数据为(xk,δik), k=0,1,2,…,n, i 是固 定的非零整数 0 i n ,且 x0 x1 ... , n x δik是Kronecher记号
1, i k ik 0, i k
( n 1)
成立。
§4.2.3 拉格朗日插值余项
罗尔(Rolle)定理：若f(x)在[a,b]上连续,在 (a,b)上可导, 且f(a)=f(b), 则存在 (a, b) 满足 f ( ) 0 。
§4.2.3 拉格朗日插值余项
证明：∵ Rn(xi)=f(xi)-Ln(xi)=0, i=0,1,…,n
证明：由插值条件知
c x c x

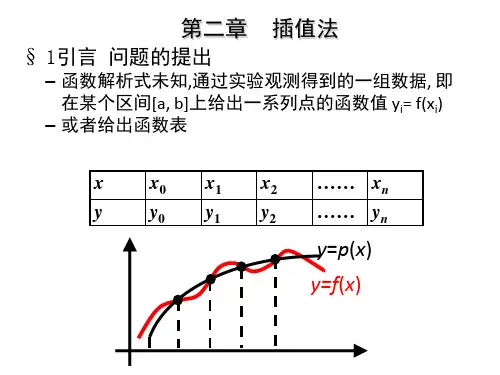
第四章函数插值§1 引言§2 Lagrange插值法§3 Newton插值法§4 等距节点插值§5 Hermite插值§6 分段插值§7 三次样条插值西北工业大学理学院欧阳洁1§1 引言问题提出仅有采样值，但需要知道非采样点处的函数值。

解决上述问题的一种思路：对用数据表给出的未知函数，建立一个便于计算的近似函数作为表达式。

函数插值法是建立近似函数表达式的一种基本方法。

西北工业大学理学院欧阳洁2西北工业大学理学院欧阳洁4二插值多项式的存在唯一性⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡)()()()(111210210212110200n n n n n n n n x f x f x f x f a a a a x x x x x x x x x M M L L L L L L L L 当节点互异, 系数矩阵非奇异, 故得到：{}ni i x 0=定理满足插值条件的不超过n 次的插值多项式存在唯一。

n n xa x a x a a x ++++=L 2210)(ϕ设求多项式函数ϕ(x )，满足，等价于确定多项式ϕ(x )的系数，使得满足n i x f x i i ,,1,0),()(L ==ϕ⎪⎩⎪⎨⎧=++++==++++=)()()()(2210002020100n n n n n n nn n x f x a x a x a a x x f x a x a x a a x L L L L L ϕϕ即西北工业大学理学院欧阳洁18§3 Newton 插值法Lagrange 插值公式的特点：1+n M 当未知，无法估计误差。

当增加插值节点时，在实际计算中不方便(当需要增加插值节点时, 拉格朗日插值基函数都要随之发生变化)。

形式对称；0⇐A )()(00x l x f A A +⇐)()(11x l x f A A +⇐)()(x l x f A A n n +⇐LL 通常用于理论分析；∑==ni i i n x l x f x L 0)()()(Hermite插值多项式的构造给定m+1个插值条件，构造次数不超过m次的插值多项式。