光学思考题和习题解答第三章
- 格式:doc
- 大小:130.50 KB
- 文档页数:4


第一章 几何光学基本定律1. 已知真空中的光速c =3810⨯m/s ,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s, 当光在冕牌玻璃中,n=1.51时,v=1.99 m/s, 当光在火石玻璃中,n =1.65时,v=1.82 m/s , 当光在加拿大树胶中,n=1.526时,v=1.97 m/s ,当光在金刚石中,n=2.417时,v=1.24 m/s 。
2. 一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:,所以x=300mm即屏到针孔的初始距离为300mm 。
3. 一厚度为200mm 的平行平板玻璃(设n =1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形的纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片的最小直径应为多少?2211sin sin I n I n = 66666.01sin 22==n I745356.066666.01cos 22=-=I1mm I 1=90︒n 1 n 2200mmL I 2 x88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ,包层的折射率为2n ,光纤所在介质的折射率为0n ,求光纤的数值孔径(即10sin I n ,其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有: n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n 0 .5. 一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上,求其会聚点的位置。

第一章 光的干涉1、波长为nm 500的绿光投射在间距d 为cm 022.0的双缝上,在距离cm 180处的光屏上形成干涉条纹,求两个亮条纹之间的距离.若改用波长为nm 700的红光投射到此双缝上,两个亮条纹之间的距离又为多少?算出这两种光第2级亮纹位置的距离.解:由条纹间距公式λd r y y y j j 01=-=∆+ 得cm 328.0818.0146.1cm146.1573.02cm818.0409.02cm573.010700022.0180cm 409.010500022.018021222202221022172027101=-=-=∆=⨯===⨯===⨯⨯==∆=⨯⨯==∆--y y y drj y d rj y d r y d r y j λλλλ2.在杨氏实验装置中,光源波长为nm 640,两狭缝间距为mm 4.0,光屏离狭缝的距离为cm 50.试求:(1)光屏上第1亮条纹和中央亮条纹之间的距离;(2)若p 点离中央亮条纹为mm 1.0,问两束光在p 点的相位差是多少?(3)求p 点的光强度和中央点的强度之比.解:(1)由公式λd r y 0=∆ 得λd r y 0=∆ =cm 100.8104.64.05025--⨯=⨯⨯(2)由课本第20页图1-2的几何关系可知52100.01sin tan 0.040.810cm 50y r r d d dr θθ--≈≈===⨯521522()0.8106.4104r r πππϕλ--∆=-=⨯⨯=⨯(3) 由公式2222121212cos 4cos 2I A A A A A ϕϕ∆=++∆= 得8536.042224cos 18cos 0cos 421cos 2cos42cos 422202212212020=+=+==︒⋅=∆∆==πππϕϕA A A A I I pp3.把折射率为1.5的玻璃片插入杨氏实验的一束光路中,光屏上原来第5级亮条纹所在的位置为中央亮条纹,试求插入的玻璃片的厚度.已知光波长为6×10-7m .解:未加玻璃片时,1S 、2S 到P 点的光程差,由公式2rϕπλ∆∆=可知为 Δr =215252r r λπλπ-=⨯⨯=现在1S 发出的光束途中插入玻璃片时,P 点的光程差为()210022r r h nh λλϕππ'--+=∆=⨯=⎡⎤⎣⎦所以玻璃片的厚度为421510610cm 10.5r r h n λλ--====⨯-4. 波长为500nm 的单色平行光射在间距为0.2mm 的双狭缝上.通过其中一个缝的能量为另一个的2倍,在离狭缝50cm 的光屏上形成干涉图样.求干涉条纹间距和条纹的可见度.解:6050050010 1.250.2r y d λ-∆==⨯⨯=m m122I I = 22122A A =12A A =7. 试求能产生红光(λ=700nm)的二级反射干涉条纹的肥皂膜厚度.已知肥皂膜折射率为1.33,且平行光与发向成30°角入射.解:根据题意222(210)2710nmd n j d λ-=+∴===8. 透镜表面通常镀一层如MgF 2(n=1.38)一类的透明物质薄膜,目的是利用干涉来降低玻璃表面的反射.为了使透镜在可见光谱的中心波长(550nm )处产生极小的反射,则镀层必须有多厚? 解:可以认为光是沿垂直方向入射的。

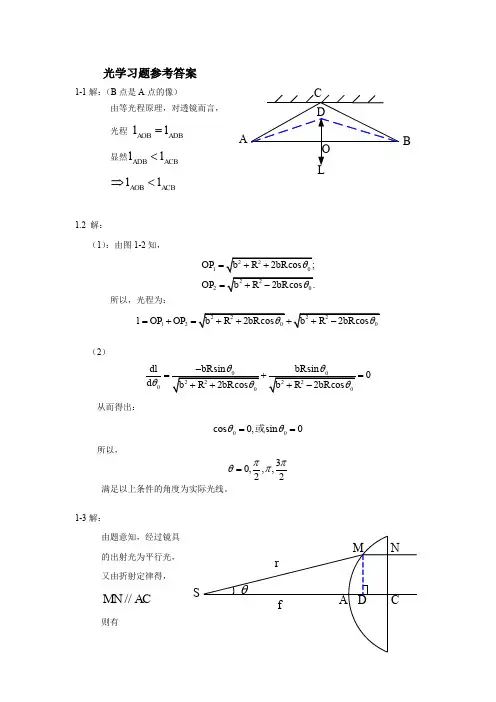
1. 证:设两个均匀介质的分界面是平面,它们的折射率为n 1和n 2。
光线通过第一介质中指定的A 点后到达同一介质中指定的B 点。
为了确定实际光线的路径,通过A,B 两点作平面垂直于界面,O O ′是他们的交线,则实际 光线在界面上的反射点C 就可由费马原理来确定(如右图)。
(1) 反正法:如果有一点C ′位于线外,则对应于C ′,必可在O O ′线上找到它的垂足C ′′.由于C A ′>C A ′′,B C ′>B C ′′,故光谱B C A ′总是大于光程B C A ′′而非极小值,这就违背了费马原理,故入射面和反射面在同一平面内得证。
(2) 在图中建立坐oxy 标系,则指定点A,B 的坐标分别为(y x 11,)和(yx 22,),未知点C 的坐标为(0,x )。
C 点在B A ′′,之间是,光程必小于C 点在B A ′′以外的相应光程,即x xx 21<<,于是光程ACB 为:x x n y x x n CB n AC n ACB n 21121221111)()(+−++−=+=根据费马原理,它应取极小值,即:()()()()()(12222211212111−′=+−−−+−−=AC C A n y x x x x n y x x x x n ACB n dx dQ i i 11=′,∴0)(1=ACB n dx d取的是极值,符合费马原理。
故问题得证。
2.(1)证:如图所示,有位于主光轴上的一个物点S 发出的光束经薄透镜折射后成一个明亮的实象点S ′。
由于球面AC 是由S 点发出的光波的一个波面,而球面DB 是会聚于S ′的球面波的一个波面,固而SB SC =, B S D S ′=′.又Q光程FD EF n CE CEFD ++=,而光程AB n AB =。
根据费马原理,它们都应该取极值或恒定值,这些连续分布的实际光线,在近轴条件下其光程都取极大值或极小值是不可能的,唯一的可能性是取恒定值,即它们的光程却相等。

第一章3、一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm 。
4、一厚度为200mm 的平行平板玻璃(设n =1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形的纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片的最小直径应为多少?8、.芯的折2n ,10sin I n ,其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2(1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0.16、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
如果在凸面镀反射膜,其会聚点应在何处?如果在凹面镀反射膜,则反射光束在玻璃中的会聚点又在何处?反射光束经前表面折射后,会聚点又在何处?说明各会聚点的虚实。
解:该题可以应用单个折射面的高斯公式来解决,设凸面为第一面,凹面为第二面。
(1)首先考虑光束射入玻璃球第一面时的状态,使用高斯公式:会聚点位于第二面后15mm 处。
(2)将第一面镀膜,就相当于凸面镜像位于第一面的右侧,只是延长线的交点,因此是虚像。
还可以用β正负判断:(3)光线经过第一面折射:, 虚像第二面镀膜,则:得到:(4)在经过第一面折射物像相反为虚像。
18、一直径为400mm,折射率为1.5的玻璃球中有两个小气泡,一个位于球心,另一个位于1/2半径处。
沿两气泡连线方向在球两边观察,问看到的气泡在何处?如果在水中观察,看到的气泡又在何处?解:设一个气泡在中心处,另一个在第二面和中心之间。


光学思考题和习题解答第三章第三章思考题部分暂时略去4、⼲涉条纹产⽣在⼀定的空间内,称为定域深度;因此⽤⽬镜看到地是属于定域深度范围的⼲涉条纹。
5、(1)等厚⼲涉条纹的定义就是指薄膜表⾯沿等厚线分布的⼲涉条纹,光程差等于i nh L cos 2=?,可见只有当光线近似垂直⼊射时,光程差只与厚度有关,从⽽⼲涉强度也近似地仅与⾼度有关,这时的⼲涉条纹是沿等厚线分布的等厚条纹。
但实际上光程差还与倾⾓有关,从⽽等光程的轨迹与⾼度和折射⾓都有关,条纹必然偏离等厚线。
因此⼀般说来,薄膜表⾯的⼲涉条纹并不是等厚条纹。
等厚条纹只是⼀种在特定实验条件下出现的现象。
6、对于单⾊点光源⽽⾔,由于相⼲长度⽐较长,1、2或者3、4两个界⾯的反射光是可以⼲涉形成⼲涉条纹的。
实际上,通常的光源是⾯光源,不同点光源产⽣的⼲涉条纹错位从⽽影响衬⽐度,若两个界⾯的厚度⼤,错位⽐较明显,因⽽衬⽐度差;有两个界⾯的厚度⼩,错位才⼩,因⽽衬⽐度才⽐较⼤。
7、根据空间相⼲性的要求,为提⾼条纹的衬⽐度,应限制光源的宽度。
点光源照明时,衬⽐度最⾼。
但⽤⾁眼直接观察薄膜表⾯的⼲涉条纹时,由于眼睛瞳孔对光束截⾯的限制,只能接收来⾃扩展光源上⼀部分点光源的反射线,从⽽限制了光源的有效宽度。
因此,决定视场中条纹衬⽐度的不是扩展光源的实际宽度,⽽是被瞳孔所限制的有效宽度。
只有进⼊瞳孔的反射光的⼲涉条纹才能被眼睛看到。
透过真孔⽐较容易看到⼲涉条纹,原因在于真孔进⼀步限制扩展光源的有效宽度,从⽽提⾼了观察区域的衬⽐度。
8、窗玻璃表⾯是扩展光源产⽣的⼲涉条纹的⾮相⼲叠加。
由于不同点光源产⽣的⼲涉条纹产⽣错位,折射⾓不同的两个点光源在上下表⾯同⼀点产⽣光程差,两个光程差的差异等于i i nh L d sin 2)(=?δ,这个差异与厚度有关,厚度越⼤,⼲涉条纹错位造成的条纹衬⽐度下降越严重;⼤到⼀定程度时,⼲涉条纹看不见。
11、出现⼤约三个亮纹,相邻亮纹的⾼度差为半个波长,故厚度差约为22λ?。


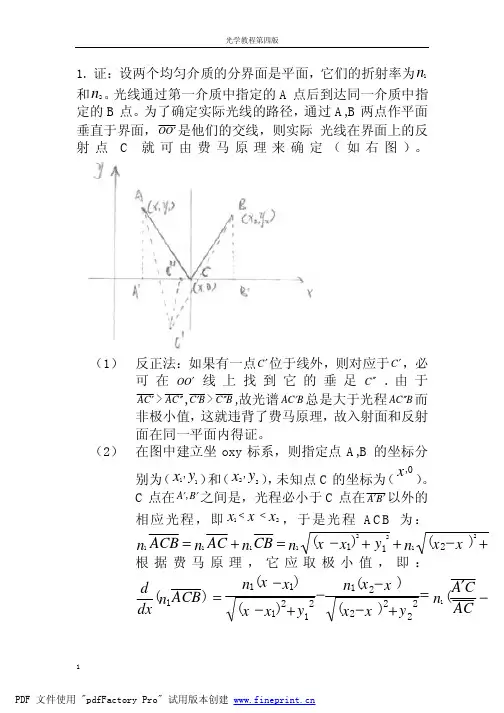
3.1 证明反射定律符合费马原理。
证明:设两个均匀介质的分界面是平面,它们的折射率为n 1和n 2。
光线通过第一介质中指定的A 点后到达同一介质中指定的B 点。
为了确定实际光线的路径,通过A,B 两点作平面垂直于界面,'OO 是它们的交线,则实际光线在界面上的反射点C 就可由费马原理来确定,如下图所示。
(1)反证法:如果有一点'C 位于线外,则对应于'C ,必可在'OO 线上找到它的垂足''C .由于''AC 'AC >,''BC 'BC >,故光线B AC'总是大于光程B ''AC 而非极小值,这就违背了费马原理,故入射面和反射面在同一平面内得证。
(2)在图中建立坐XOY 坐标系,则指定点A,B 的坐标分别为(x1,y1)和(x2,y2),未知点C 的坐标为(x ,0)。
C 点是在'A 、'B 之间的,光程必小于C 点在''B A 以外的相应光程,即21v x x <<,于是光程ACB 为y x x n y x x n CB n AC n ACB n 2211221221111)()(+-++-=+=根据费马原理,它应取极小值,即0)(1=n dxd0)sin (sin )()()()()()(21112222211212111=-='-'=+---+--=i i n B C C A n y x x x x n y x x x x n ACB n dx d 所以当11'i i =,取的是极值,符合费马原理。
3.2 根据费马原理可以导出在近轴条件下,从物点发出并会聚倒像点的所有光线的光程都相等。
由此导出薄透镜的物象公式。
解:略3.3 眼睛E 和物体PQ 之间有一块折射率为1.5的玻璃平板(见题3.3图),平板的厚度d 为30cm 。
《应用光学基础》思考题部分参考解答《应用光学基础》思考题参考答案第一章几何光学的基本定律和成像概念1-1 (1)光的直线传播定律:例子:影子的形成。
应用:射击瞄准。
实验证明:小孔成像。
(2)光的独立传播定律:例子:两束手电灯光照到一起。
应用:舞台灯光照明;无影灯。
实验证明:两束光(或两条光线)相交。
(3)光的反射定律:例子:照镜子;水面上的景物倒影。
应用:制镜;汽车上的倒车镜;光纤通讯。
实验证明:平面镜成像;球面反射镜成像。
(4)光的折射定律:例子:插入水中的筷子出现弯折且变短;水池中的鱼看起来要比实际的位置浅。
应用:放大镜;照相机;望远镜等实验证明:光的全反射;透镜成像;用三棱镜作光的色散。
1-2 否。
这是因为光线在棱镜斜面上的入射角I2 = 45°,小于此时的临界角I m= 62.46°。
1-3小孔离物体有90cm远。
1-4此并不矛盾,这是因为光在弯曲的光学纤维中是按光的全反射现象传播的,而在光的全反射现象中,光在光学纤维内部仍按光的直线传播定律传播。
第二章平面成像2-1 略。
2-2 以35°的入射角入射。
2-3 二面镜的夹角为60°。
2-4 双平面镜夹角88.88°。
2-5 平面镜的倾斜角度为0.1°。
2-6 实际水深为4/3 m。
2-7 平板应正、反转过0.25rad的角度。
2-8 (1)I = 55.59°;(2)δm = 51.18°。
2-9 光楔的最大折射角应为2°4′4〞。
2-10 略。
第三章球面成像3-1 该棒长l′= 80mm。
3-2l = -4.55 mm,D = 4.27 mm。
3-3最后会聚点在玻璃球后面l2′= 15 mm (或离球心45 mm的右侧)处。
3-4l2′=7.5cm。
3-5l2′= -105.96 mm(即位于第一面前97.96mm处),y′= 14.04mm。
3-6n = 1.5,r = 7.5 mm(或r = -7.5 mm)。
《光学教程》(姚启钧)课后习题解答(总47页)-本页仅作为预览文档封面,使用时请删除本页-《光学教程》(姚启钧)习题解答第一章 光的干涉1、波长为500nm 的绿光投射在间距d 为0.022cm 的双缝上,在距离180cm 处的光屏上形成干涉条纹,求两个亮条纹之间的距离。
若改用波长为700nm 的红光投射到此双缝上,两个亮纹之间的距离为多少算出这两种光第2级亮纹位置的距离。
解:1500nm λ= 7011180500100.4090.022r y cm d λ-∆==⨯⨯= 改用2700nm λ= 7022180700100.5730.022r y cm d λ-∆==⨯⨯= 两种光第二级亮纹位置的距离为: 21220.328y y y cm ∆=∆-∆=2、在杨氏实验装置中,光源波长为640nm ,两狭缝间距为0.4mm ,光屏离狭缝的距离为50cm ,试求:⑴光屏上第1亮条纹和中央亮纹之间的距离;⑵若P 点离中央亮纹为0.1mm 问两束光在P 点的相位差是多少⑶求P 点的光强度和中央点的强度之比。
解:⑴ 7050640100.080.04r y cm d λ-∆==⨯⨯= ⑵由光程差公式210sin yr r d dr δθ=-== 0224y dr πππϕδλλ∆==⋅= ⑶中央点强度:204I A =P 点光强为:221cos 4I A π⎛⎫=+ ⎪⎝⎭012(10.8542I I =+=3、把折射率为1.5的玻璃片插入杨氏实验的一束光路中,光屏上原来第5级亮条纹所在的位置变为中央亮条纹,试求插入的玻璃片的厚度。
已知光波长为7610m -⨯ 解: 1.5n =,设玻璃片的厚度为d由玻璃片引起的附加光程差为:()1n d δ'=- ()15n d λ-= ()7645561061061010.5d m cm n λ---==⨯⨯=⨯=⨯-4、波长为500nm 的单色平行光射在间距为0.2mm 的双缝上。
第三章
思考题部分暂时略去
4、干涉条纹产生在一定的空间内,称为定域深度;因此用目镜看到地是属于定域深度范围的干涉条纹。
5、(1)等厚干涉条纹的定义就是指薄膜表面沿等厚线分布的干涉条纹,光程差等于
i nh L cos 2=∆,可见只有当光线近似垂直入射时,光程差只与厚度有关,从而干涉强度也近似地仅与高度有关,这时的干涉条纹是沿等厚线分布的等厚条纹。
但实际上光程差还与倾角有关,从而等光程的轨迹与高度和折射角都有关,条纹必然偏离等厚线。
因此一般说来,薄膜表面的干涉条纹并不是等厚条纹。
等厚条纹只是一种在特定实验条件下出现的现象。
6、对于单色点光源而言,由于相干长度比较长,1、2或者3、4两个界面的反射光是可以干涉形成干涉条纹的。
实际上,通常的光源是面光源,不同点光源产生的干涉条纹错位从而影响衬比度,若两个界面的厚度大,错位比较明显,因而衬比度差;有两个界面的厚度小,错位才小,因而衬比度才比较大。
7、根据空间相干性的要求,为提高条纹的衬比度,应限制光源的宽度。
点光源照明时,衬比度最高。
但用肉眼直接观察薄膜表面的干涉条纹时,由于眼睛瞳孔对光束截面的限制,只能接收来自扩展光源上一部分点光源的反射线,从而限制了光源的有效宽度。
因此,决定视场中条纹衬比度的不是扩展光源的实际宽度,而是被瞳孔所限制的有效宽度。
只有进入瞳孔的反射光的干涉条纹才能被眼睛看到。
透过真孔比较容易看到干涉条纹,原因在于真孔进一步限制扩展光源的有效宽度,从而提高了观察区域的衬比度。
8、窗玻璃表面是扩展光源产生的干涉条纹的非相干叠加。
由于不同点光源产生的干涉条纹产生错位,折射角不同的两个点光源在上下表面同一点产生光程差,两个光程差的差异等于i i nh L d sin 2)(=∆δ,这个差异与厚度有关,厚度越大,干涉条纹错位造成的条纹衬比度下降越严重;大到一定程度时,干涉条纹看不见。
11、出现大约三个亮纹,相邻亮纹的高度差为半个波长,故厚度差约为22λ⨯。
13、薄膜表面的光程差为i nh L cos 2=∆,相位差为i nh cos 22λπ
ϕ=∆,厚度、折射角和
波长不同,相位差不同。
不同波长产生不同颜色的干涉条纹。
22、F-P 干涉仪的可分辨最小波长间隔为R
R k -=∆1πλλ,由干涉级别、反射率决定。
自由光谱范围就是相邻级别不同波长条纹不重叠的光谱范围。
不同波长λλλλ∆+=', 的两束光入射到F-P 干涉仪上,则它们在不同角度产生同心圆形的干涉条纹,对于同一级别,波长长的干涉圆环的直径小于波长短的,但当波长的间隔达到一定程度时,将发生不同波长在在相同位置产生干涉条纹的现象,即满足')1(cos 2λλ-==k k i nh k ,这时自由波长范围为'1111'λλλλλλλk
k k k =-=--=-=∆。
考虑小角度的情况:由于小角度时h h h k k nh i nh k 22',/2,2cos 22λλλλλλ≈=
∆=∴=≈。
厚度大,自由光谱范围小
部分习题解答与思路
8、解:
(1)虚线所在的三角形区域为叠加区;
(2)设s 到1s 的光程为1g ;s 到2s 由于成像,1g ,2g 交点处,分别经过1L 和2L 的两条光线的光程差为零
,叠加后为极大强度;其他在虚线上的叠加点的光程差为22)2/(2r d -,其中r 为叠加
点到光轴的距离;若满足 2,1,0,)2/(222==-k k r d k
λ,将出现上述亮度的周期性出现;呈现同心的半圆环状分布; 2,1,0,)2/()2/(22=-=k k d r k λ
(3) 1s 和2s 的距离d 可以分别通过求两个像点的位置差而获得;
9、解:(1)上移;(2)利用公式0λN l nl =-可以获得折射率;
10、解法与第9题类似;
11、解:应用公式,00λd
R b ≤
,可以获得双缝间隔d ;
24、解:应用公式,2/0λN d =∆,可以算得;
25、解:应用公式,;2,2/211λλλλλ=+∆=N 可以算得两个波长;
26、解:应用公式,2/0λN d =∆,可以算得;
27、解:精度为20/0λ;一次测量长度量程为λλ∆=∆2/2max L ;
28、解:(1);1,;2=∆===∆t N N
d t νλυ可以求得;;2λνυ= (2)Hz 50;2==νλ
νυ,可以求得速度;
(3)两个波长对应的频率分别为2211/2,/2λυνλυν==;拍频为21ννν-=∆
29、解:依据非单色谱线宽度公式:R
R k k -=∆1πλλ。
k 的值可以通过公式0,2cos 2≈=≈k k i k nh i nh λ求得;已经知道95.0=R
30、解:已经知道,500,0.1nm cm h ==λ依据公式k k k i nh λ=cos 2,不同的入射角对应不同的亮纹级次,所以分别对中央亮环和第十级亮环,有
中央亮环:λk nh i nh k ==2cos 2;(1)
第十级亮环:λ10cos 2k i nh k =;(2)
两式相减,得到1010,10)()cos 1(2k k k k i nh k >=-=- λλ,通过该式子可以求得k i ,它的两倍就是角直径。
31、解:
(1) 依据公式0,2cos 2==≈k k i k nh i nh λ,可以求得中心亮环的级次k ;
(2) 依据公式某一级的半角宽度公式98.0;180/,1sin 2==-=∆R i R R i nh i k k k ππλ
;
(3) 依据色分辨本领公式R R k k -=∆1πλλ可以求得;根据公式 R
R k k -=∆1πλλ,其中k 为中心亮环的级次,因为中心亮纹的k 级次最高,可以求得可分辨的最小波长间隔,k 满足)(0,2cos 2中心亮纹===k k i k nh i nh λ。
(4) 依据频率间隔nh
c 2=∆ν,然后用可见光的频率范围Hz 1414105.7~104⨯⨯,用频率间隔除以ν∆,可以计算谱线条数。
(5) 依据纵模间隔公式nh
c 2=∆ν,h 的改变将引起ν∆产生一个微小变化,对该式子两边求微分,得h
h nh c δνδ2)(=∆;
32、解:
(1) 依据公式0,2cos 2==≈k k i k nh i nh λ,可以求得,/2k nh =λ但波长必须满足
,760/2380<=<k nh λ可以求得合适的k ,再计算可能的波长值;
(2) 依据公式R
R k k -=∆1πλλ可以求得相应的每个波长值可分辨的最小波长间隔;。