下载文档原格式
12东南大学考试卷（A）Array课程名称工程矩阵理论考试学期08-09-2 得分
适用范围工科硕士研究生考试形式闭卷考试时间长度150分钟
1．地子空间地一组基是；
2．若线性空间地线性变换在基下地矩阵是,则在基下地矩阵是；
3．如果矩阵满足,并且地秩为,则行列式；
4．若矩阵,则矩阵函数地行列式；
5．若是维单位列向量,是正定地,则参数满足条件.
二．（12%）设矩阵.讨论地可能地Jordan标准形.并问：当参数满足什么条件时,矩阵与是相似地.
三．（20%）记,上地变换定义为：对,.
1．证明：是上地线性变换；
2．求在地基下地矩阵；
3．求地特征值及相应地特征子空间地基；
4．问：是否存在地基,使得在这组基下地矩阵是对角阵？如存在,试给出这样地一组基及相应地对角阵；如不存在,请说明理由.
四．（10%）设.试将表示成关于地次数不超过2地多项式.
五．（8%）求地广义逆矩阵.
六．（15%）假设是有限维欧氏空间,是单位向量,上地线性变换定义如下：对任意,.
1.证明：是上地正交变换.
2.在中定义内积：对,.于是,成为欧氏空间.分别求中向量及地长度,并求正实数及单
位向量,使得如上地正交变换将变成.
七．证明题（20%）
1.假设是矩阵,分别是、酉矩阵.证明：.
2.假设是正规矩阵.若地特征值地模都等于1,证明：是酉矩阵.
3.假设是Hermite矩阵,其中,是地子矩阵,并且都是方阵.若是正定地.证明关于行列
式地不等式：.。
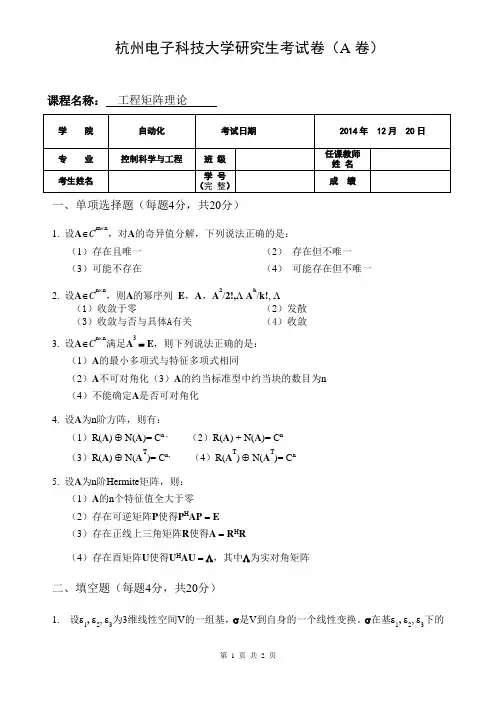
杭州电子科技大学研究生考试卷（A卷）课程名称：工程矩阵理论学院自动化考试日期2014年 12月 20日专业控制科学与工程班级任课教师姓名考生姓名学号（完整）成绩一、单项选择题（每题4分，共20分）1. 设AÎC m´n，对A的奇异值分解，下列说法正确的是：（1）存在且唯一（2）存在但不唯一（3）可能不存在（4）可能存在但不唯一2. 设AÎC n´n，则A的幂序列E，A，A2/2!, A k/k!, （1）收敛于零（2）发散（3）收敛与否与具体）收敛与否与具体A A有关（4）收敛3. 设AÎC n´n满足A3=E，则下列说法正确的是：（1）A的最小多项式与特征多项式相同（2）A不可对角化（3）A的约当标准型中约当块的数目为n（4）不能确定A是否可对角化4. 设A为n阶方阵，则有：（1）R(A) Å N(A)= C n , （2）R(A) + N(A)= C n（3）R(A) Å N(A T)= C n, （4）R(A T) Å N(A T)= C n5. 设A为n阶Hermite矩阵，则：（1）A的n个特征值全大于零（2）存在可逆矩阵P使得P H AP=E（3）存在正线上三角矩阵R使得A=R H R（4）存在酉矩阵U使得U H AU=L，其中L为实对角矩阵二、填空题（每题4分，共20分）1. 设e1, e2, e3为3维线性空间V的一组基，s是V到自身的一个线性变换。
s在基e1, e2, e3下的第1 页共2 页第 2 页 共 2 页 矩阵为úúúûùêêêëé333231232221131211a a a a a a a a a ，则s 在基e 3, 2e 2, 3e 1下的矩阵为。
2. 设方阵A 满足A 2 = 3A, 则sin (3A ) = 。
实用标准文案精彩文档东南大学考试卷（A卷）姓名学号班级课程名称数学建模与实验考试学期 09-10-2 得分适用专业各专业考试形式闭卷考试时间长度120分钟实用标准文案精彩文档一．填空题：（每题2分，共10分）1. 阻滞增长模型0.5(10.001)(0)100dx x x dtx ⎧=-⎪⎨⎪=⎩的解为 。
2. 用Matlab 做常微分方程数学实验，常用的命令有 。
3. 整数m 关于模12可逆的充要条件是： 。
4. 根据Malthus 模型,如果自然增长率为2%，则人口数量增长为初值3倍所需时间为(假设初值为正) 。
5. 请补充判断矩阵缺失的元素13192A ⎛⎫⎪=⎪ ⎪⎝⎭。
二．选择题：（每题2分，共10分）1. 在下列Leslie 矩阵中，不能保证模最大特征值唯一的是 ( )A. 0230.20000.40⎛⎫ ⎪ ⎪ ⎪⎝⎭；B. 1.1 1.230.20000.40⎛⎫ ⎪ ⎪ ⎪⎝⎭；C. 0030.20000.40⎛⎫ ⎪⎪ ⎪⎝⎭； D.以上都不对2. 判断矩阵能通过一致性检验的标准是 （ )A. 0.1CR <B. 0.1CI <C. 0.1CR >D.0.01CR < 3. 模28倒数表中可能出现的数是 ( )A. 12B.5C.14D.74. 线性最小二乘法得到的函数不可能为 （ ）A.线性函数B. 对数函数C. 样条函数D. 指数函数5. 关于泛函极值问题，下面的描述正确的有 （ ） A.泛函()J x 在x *处取极值的充要条件是泛函变分()0J x δ*=； B. 泛函()J x 在x *处取极值的充分条件是泛函变分()0J x δ*=； C. 泛函()J x 在x *处取极值的必要条件是泛函变分()0J x δ*=；D. A,B,C 均正确三．判断题（每题2分，共10分） 1. Hill 密码体系中，任意一个可逆矩阵都可以作为加密矩阵。
（ ） 2. 拟合函数不要求通过样本数据点。
杭州电子科技大学研究生考试卷（A卷）课程名称：工程矩阵理论一、单项选择题（每题4分，共20分）1. 设A∈C m⨯n，对A的奇异值分解，下列说法正确的是：（1）存在且唯一（2）存在但不唯一（3）可能不存在（4）可能存在但不唯一2. 设A∈C n⨯n，则A的幂序列E，A，A2/2!, A k/k!,（1）收敛于零（2）发散（3）收敛与否与具体A有关（4）收敛3. 设A∈C n⨯n满足A3= E，则下列说法正确的是：（1）A的最小多项式与特征多项式相同（2）A不可对角化（3）A的约当标准型中约当块的数目为n（4）不能确定A是否可对角化4. 设A为n阶方阵，则有：（1）R(A) ⊕ N(A)= C n , （2）R(A) + N(A)= C n（3）R(A) ⊕ N(A T)= C n, （4）R(A T) ⊕ N(A T)= C n5. 设A为n阶Hermite矩阵，则：（1）A的n个特征值全大于零（2）存在可逆矩阵P使得P H AP=E（3）存在正线上三角矩阵R使得A=R H R（4）存在酉矩阵U使得U H AU=Λ，其中Λ为实对角矩阵二、填空题（每题4分，共20分）1. 设ε1, ε2, ε3为3维线性空间V的一组基，σ是V到自身的一个线性变换。
σ在基ε1, ε2, ε3下的矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡333231232221131211a a a a a a a a a ，则σ在基ε3, 2ε2, 3ε1下的矩阵为。
2. 设方阵A 满足A 2= 3A, 则sin (3A ) = 。
3.矩阵A = diag 21312,,0203⎛⎫⎡⎤⎡⎤ ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭，则A 的最小多项式为 。
4. 设X = (x 1, x 2, , x n )T 为变向量，α = (a 1, a 2, , a n )T 为常向量，H = (h ij )n ⨯n 为常矩阵，则：，()=HX X XT D D。
5. 设A ∈C n ⨯n 为Hermite 矩阵，X ∈C n ，A 的n 个特征值为λ1，λ2， ，λn ，满足λ1 ≤ λ2 ≤ ≤ λn ，则： XX AXX H X H 0max ≠ =。
东 南 大 学 考 试 卷（A 卷）课程名称 数学建模与数学实验 考试学期09-10-3得分适用专业 理工各专业考试形式 开卷闭卷半开卷 考试时间长度 120分钟（可带计算器）注：以下各题只需计算到小数点后两位。
一 填空与选择（每题3分，共30分） 1 已知113,(mod19)02A A -⎡⎤==⎢⎥⎣⎦则 。
2 已知一组(1,1),(2,1),(3,2)-观测数据，则其分段线性插值多项式为 。
3 根据一组等距节点的观测数据分析知其2阶差分波动最小，则其最合适的拟合多项式阶数是 。
4 已知微分方程'()0.005(1/10000)(0)2000x t x x x =-⎧⎨=⎩，则其变化率最大时间为 。
5考虑V olterra 模型'0.050.001'0.10.0001x x xyy x xy=-⎧⎨=-+⎩， 则,x y 的周期平均值为x y ⎛⎫⎪ ⎪⎝⎭= 6 已知非线性差分方程 21(2)n n n x bx x +=-的正平衡点稳定 （b>0），则参数b 的取值范围为 。
7 记123()((),(),())a k a k a k a k =考虑马氏链0.40.30.3(1)()0.40.40.2(0)(0.3.0.4.0.3)0.30.20.5a k a k a ⎡⎤⎢⎥+==⎢⎥⎢⎥⎣⎦，，其正平衡点为 。
自觉 遵 守 考 场 纪 律 如 考 试 作 弊 此 答 卷 无 效8 轮渡船上甲板总面积为A 。
它能运载小轿车，每辆小轿车所占甲板面积为C ，能运载卡车，每辆卡车所占甲板面积为 L 。
每辆小轿车要付渡船费p 元；每辆卡车要付q 元。
调度想知道在渡船上运载多少辆小轿车(x) 和多少辆卡车(y)才能获取最大的利润？ 下列哪一个选项给出利润函数及需满足的约束条件？ （ ）A. yq xp +，满足 A xL yC ≤+B. yq xp +，满足 A yL xC ≤+C. ))((q p y x ++， 满足A yL xC ≤+D. ))((q p y x ++ ，满足A L C y x ≤++))((9 下面哪一个选项最接近小轿车从静止开始起步的的速度变化模型？ （ ）A t e --1B 2)1(t -C2t t - D 1t e -+10 模型检验是建模过程中的必要步骤，以下哪一个选项不是常见的模型检验过程。
一. （10％）求22×C
的子空间12,V V 的交空间12V V ∩及和空间12V V +的基和维数，其中，V x ∈⎬． 12,y ⎧⎫⎨⎬⎩⎭
|,|,C V x ⎛⎞⎞=∈⎜⎟⎟⎝⎠⎠x
y x y x y y x ⎧⎛=⎨⎜−−⎝⎩y C ⎫⎭二. （10%）欧氏空间3[]R x 中的内积定义为：对3(),()[]x x R x ϕψ∀∈，
)1
1(),()()(x x ϕψ−<>∫x ϕψ=x dx 。
令1α=，x β=，2x η=， (,)W L αβ=。
求η在W 中的正投影，即求0W η∈，使得
0min W ξηηη∈ξ−=−． 三. （20%）在22×矩阵空间22C ×上定义线性变换f 如下：对任意矩阵22X C ×∈，
⎟，其中，a 为234a a a a ⎜()f X ⎛⎞=⎝⎠
X 的迹()tr X 。
1. 求f 在22C ×的基11122122,,,E E E E 下的矩阵M ；
2. 分别求f 的值域()R f 及核子空间()K f 的基及维数；
3. 求f 的特征值及相应的特征子空间的基；
4. 问：是否存在22C ×的基，使得f 在这组基下的矩阵为对角阵？为什么？
四. （10%）根据参数,a b 不同的值，讨论矩阵b ⎟⎟的Jordan 标准形，并求矩阵100的秩。
1702001a A ⎛⎞⎜=⎜⎜⎟⎝⎠
()A I −五. （14%）假设矩阵． 101002101A ⎛⎞⎜⎟=⎜⎟⎜⎟⎝⎠
1. 求A 的广义逆矩阵A +
；
2. 求一个次数不超过2的多项式()f λ，使得()At f A Ae =．
六. （10%）假设f 是n 维酉空间V 上的线性变换，若对任意,V αβ∈，有())((),)(,f f αβα=β。
1. 证明：在V 的标准正交基下，f 的矩阵为Hermite 矩阵；
2. 证明：存在V 的一组标准正交基，使得f 的矩阵为对角阵。
七. （8%）假设s n ×矩阵A 的秩为r
，证明22F A A A ≤≤。
八. （8%）假设A +是s n A C ×∈的广义逆矩阵，证明：，其中，分别表示矩阵A 的核空间和A ()()n C K A R A +
=⊕(),(K A R A )++的值域．
九. （12%）假设,A B 都n 阶Hermite 矩阵．
1. 如果A 是正定的，证明：存在可逆矩阵C ，使得,都是对角阵；
H H C AC C BC 2. 如果,A B 都是半正定的，并且A 的秩()1r A n =−，证明：存在可逆矩阵C ，
使得,都是对角阵。
H H C C BC C A。
