主成分分析及matlab实现..

§10.利用Matlab 编程实现主成分分析1.概述Matlab 语言是当今国际上科学界 (尤其是自动控制领域) 最具影响力、也是最有活力的软件。

它起源于矩阵运算，并已经发展成一种高度集成的计算机语言。

它提供了强大的科学运算、灵活的程序设计流程、高质量的图形可视化与界面设计、与其他程序和语言的便捷接口的功能。

Matlab 语言在各国高校与研究单位起着重大的作用。

主成分分析是把原来多个变量划为少数几个综合指标的一种统计分析方法，从数学角度来看，这是一种降维处理技术。

1.1主成分分析计算步骤 ① 计算相关系数矩阵 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=pp p p p p r r r r r r r r r R 212222111211 （1） 在（3.5.3）式中，r ij （i ，j=1，2，…，p ）为原变量的xi 与xj 之间的相关系数，其计算公式为 ∑∑∑===----=n k n k j kj i ki n k j kj i ki ij x x x x x x x x r 11221)()())(( （2） 因为R 是实对称矩阵（即r ij =r ji ），所以只需计算上三角元素或下三角元素即可。

② 计算特征值与特征向量首先解特征方程0=-R I λ，通常用雅可比法（Jacobi ）求出特征值),,2,1(p i i =λ，并使其按大小顺序排列，即0,21≥≥≥≥pλλλ ；然后分别求出对应于特征值i λ的特征向量),,2,1(p i e i =。

这里要求i e =1，即112=∑=p j ij e ，其中ij e 表示向量i e 的第j 个分量。

③ 计算主成分贡献率及累计贡献率 主成分i z 的贡献率为),,2,1(1p i p k k i =∑=λλ 累计贡献率为 ),,2,1(11p i pk k i k k =∑∑==λλ一般取累计贡献率达85—95%的特征值m λλλ,,,21 所对应的第一、第二，…，第m （m ≤p ）个主成分。

主成分分析类型：一种处理高维数据的方法。

降维思想：在实际问题的研究中，往往会涉及众多有关的变量。

但是，变量太多不但会增加计算的复杂性，而且也会给合理地分析问题和解释问题带来困难。

一般说来，虽然每个变量都提供了一定的信息，但其重要性有所不同，而在很多情况下，变量间有一定的相关性，从而使得这些变量所提供的信息在一定程度上有所重叠。

因而人们希望对这些变量加以“改造”，用为数极少的互补相关的新变量来反映原变量所提供的绝大部分信息，通过对新变量的分析达到解决问题的目的。

一、总体主成分1.1 定义设 X 1，X 2，…，X p 为某实际问题所涉及的 p 个随机变量。

记 X=(X 1，X 2，…,Xp)T ，其协方差矩阵为()[(())(())],T ij p p E X E X X E X σ⨯∑==--它是一个 p 阶非负定矩阵。

设1111112212221122221122Tp p Tp pT pp p p pp p Y l X l X l X l X Y l X l X l X l X Y l X l X l X l X⎧==+++⎪==+++⎪⎨⎪⎪==+++⎩ （1） 则有()(),1,2,...,,(,)(,),1,2,...,.T T i i i i TT T i j ijij Var Y Var l X l l i p Cov Y Y Cov l X l X l l j p ==∑===∑= （2）第 i 个主成分： 一般地，在约束条件1T i i l l =及(,)0,1,2,..., 1.T i k i k Cov Y Y l l k i =∑==-下，求 l i 使 Var(Y i )达到最大，由此 l i 所确定的T i i Y l X =称为 X 1，X 2，…，X p 的第 i 个主成分。

1.2 总体主成分的计算设 ∑是12(,,...,)T p X X X X =的协方差矩阵，∑的特征值及相应的正交单位化特征向量分别为120p λλλ≥≥≥≥及12,,...,,p e e e则 X 的第 i 个主成分为1122,1,2,...,,T i i i i ip p Y e X e X e X e X i p ==+++= （3）此时(),1,2,...,,(,)0,.Ti i i i Ti k i k Var Y e e i p Cov Y Y e e i k λ⎧=∑==⎪⎨=∑=≠⎪⎩ 1.3 总体主成分的性质1.3.1 主成分的协方差矩阵及总方差记 12(,,...,)T p Y Y Y Y = 为主成分向量，则 Y=P T X ，其中12(,,...,)p P e e e =，且12()()(,,...,),T T p Cov Y Cov P X P P Diag λλλ==∑=Λ=由此得主成分的总方差为111()()()()(),p ppTTiii i i i Var Y tr P P tr PP tr Var X λ=====∑=∑=∑=∑∑∑即主成分分析是把 p 个原始变量 X 1，X 2，…，X p 的总方差1()pii Var X =∑分解成 p 个互不相关变量 Y 1，Y 2，…，Y p 的方差之和，即1()pii Var Y =∑而 ()k k Var Y λ=。

MATLAB主成分分析法统计与数学模型分析实验中心《MATLAB数据分析方法》实验报告(4)排名的结果是否合理？为什么？程序：clc,clearA=load('hiyan4_1.t某t');[m,n]=ize(A);%根据指标的属性将原始数据统一趋势化,其中资产负债率为成本型，转换成，效益型。

A1=(A(:,1)-min(A(:,1)))./(ma某(A(:,1))-min(A(:,1)));A2=(A(:,2)-min(A(:,2)))./(ma某(A(:,2))-min(A(:,2)));A3=(ma某(A(:,3))-A(:,3))./(ma某(A(:,3))-min(A(:,3)));A4=(A(:,4)-min(A(:,4)))./(ma某(A(:,4))-min(A(:,4)));A5=(A(:,5)-min(A(:,5)))./(ma某(A(:,5))-min(A(:,5)));A6=(A(:,6)-min(A(:,6)))./(ma某(A(:,6))-min(A(:,6)));A=[A1,A2,A3,A4,A5,A6];%利用相关系数矩阵进行主成分分析R=corrcoef(A);%在指标中无明显的共线关系[v,d]=eig(R);%计算特征值与特征向量%输出结果显示，最大特征值对应的不是正向量，所以不能用第一主成分进行排名%利用协方差矩阵进行主成分分析R1=cov(A);[v1,d1]=eig(R1);%输出结果显示，最大特征值对应的不是正向量，所以不能用第一主成分进行排名%利用R矩阵进行主成分分析fori=1:nforj=1:nR2(i,j)=2某dot(A(:,i),A(:,j))./[um(A(:,i).^2)+um(A(:,j).^2)];endend[v2,d2]= eig(R2);w=um(d2)/um(um(d2));%输出结果显示，最大特征值对应的是正向量，且其贡献率为71.68%,所以能用第一主成分进行排名F=[A-one(m,1)某mean(A)]某d(:,6);%计算主成分第一主成分得分[F1,I1]=ort(F,'decend');%给出各市名次的序号[F2,I2]=ort(I1);%给出各市排名plot(1:m,F,'某');%主成分得分图结果分析：(1)统一趋势化见程序中矩阵A(2)利用协方差和相关系数，最大特征值对应的不是正向量，所以均不能用第一主成分进行排名(3)构造的实对称矩阵，最大特征值对应的是正向量，且其贡献率为71.68%,所以能用第一主成分进行排名，排名结果为：实验结果分析北京天津河北山西内蒙古辽宁吉林黑龙江上海江苏166112717153014135浙江安徽福建江西山东河南湖北湖南广东广西4237191020211292海南重庆四川贵州云南西藏陕西甘肃青海宁夏129182583124262822新疆3(4)排名结果不合理，因为从第一主成分得分图可以看出，指标的属性并没有明显的区别：10.5-0.5-1-1.5-25101520253035建议利用总贡献率达到90%以上后运用加权得分的结果，再进行排名得出结果。

Matlab 编程示例.程序结构及函数作用在软件Matlab 中实现主成分分析可以采取两种方式实现：一是通过编程来实现；二是直接调用Matlab 种自带程序实现。

下面主要主要介绍利用Matlab 的矩阵计算功能编程实现主成分分析。

1程序结构主函数子函数2函数作用Cwstd.m ——用总和标准化法标准化矩阵Cwfac.m ——计算相关系数矩阵；计算特征值和特征向量；对主成分进行排序；计算各特征值贡献率；挑选主成分（累计贡献率大于85%），输出主成分个数；计算主成分载荷Cwscore.m ——计算各主成分得分、综合得分并排序Cwprint.m ——读入数据文件；调用以上三个函数并输出结果3.源程序3.1 cwstd.m 总和标准化法标准化矩阵%cwstd.m,用总和标准化法标准化矩阵function std=cwstd(vector)cwsum=sum(vector,1); %对列求和[a,b]=size(vector); %矩阵大小,a 为行数,b 为列数for i=1:afor j=1:bCwprint.m Cwstd.m Cwfac.m Cwscore.mstd(i,j)= vector(i,j)/cwsum(j);endend3.2 cwfac.m计算相关系数矩阵%cwfac.mfunction result=cwfac(vector);fprintf('相关系数矩阵:\n')std=CORRCOEF(vector) %计算相关系数矩阵fprintf('特征向量(vec)及特征值(val)：\n')[vec,val]=eig(std) %求特征值(val)及特征向量(vec)newval=diag(val) ;[y,i]=sort(newval) ; %对特征根进行排序，y为排序结果，i为索引fprintf('特征根排序：\n')for z=1:length(y)newy(z)=y(length(y)+1-z);endfprintf('%g\n',newy)rate=y/sum(y);fprintf('\n贡献率：\n')newrate=newy/sum(newy)sumrate=0;newi=[];for k=length(y):-1:1sumrate=sumrate+rate(k);newi(length(y)+1-k)=i(k);if sumrate>0.85 break;endend %记下累积贡献率大85%的特征值的序号放入newi中fprintf('主成分数：%g\n\n',length(newi));fprintf('主成分载荷：\n')for p=1:length(newi)for q=1:length(y)result(q,p)=sqrt(newval(newi(p)))*vec(q,newi(p));endend %计算载荷disp(result)3.3 cwscore.m%cwscore.m,计算得分function score=cwscore(vector1,vector2);sco=vector1*vector2;csum=sum(sco,2);[newcsum,i]=sort(-1*csum);[newi,j]=sort(i);fprintf('计算得分：\n')score=[sco,csum,j]%得分矩阵：sco为各主成分得分；csum为综合得分；j为排序结果3.4 cwprint.m%cwprint.mfunction print=cwprint(filename,a,b);%filename为文本文件文件名，a为矩阵行数(样本数)，b为矩阵列数(变量指标数)fid=fopen(filename,'r')vector=fscanf(fid,'%g',[a b]);fprintf('标准化结果如下：\n')v1=cwstd(vector)result=cwfac(v1);cwscore(v1,result);4.程序测试例题4.1原始数据中国大陆35个大城市某年的10项社会经济统计指标数据见下表。

主成分分析法(PCA)在实际问题中.我们经常会遇到研究多个变量的问题.而且在多数情况下.多个变量之间常常存在一定的相关性。

由于变量个数较多再加上变量之间的相关性.势必增加了分析问题的复杂性。

如何从多个变量中综合为少数几个代表性变量.既能够代表原始变量的绝大多数信息.又互不相关.并且在新的综合变量基础上.可以进一步的统计分析.这时就需要进行主成分分析。

I. 主成分分析法(PCA)模型（一）主成分分析的基本思想主成分分析是采取一种数学降维的方法.找出几个综合变量来代替原来众多的变量.使这些综合变量能尽可能地代表原来变量的信息量.而且彼此之间互不相关。

这种将把多个变量化为少数几个互相无关的综合变量的统计分析方法就叫做主成分分析或主分量分析。

主成分分析所要做的就是设法将原来众多具有一定相关性的变量.重新组合为一组新的相互无关的综合变量来代替原来变量。

通常.数学上的处理方法就是将原来的变量做线性组合.作为新的综合变量.但是这种组合如果不加以限制.则可以有很多.应该如何选择呢？如果将选取的第一个线性组合即第一个综合变量记为1F .自然希望它尽可能多地反映原来变量的信息.这里“信息”用方差来测量.即希望)(1F Var 越大.表示1F 包含的信息越多。

因此在所有的线性组合中所选取的1F 应该是方差最大的.故称1F 为第一主成分。

如果第一主成分不足以代表原来p 个变量的信息.再考虑选取2F 即第二个线性组合.为了有效地反映原来信息.1F 已有的信息就不需要再出现在2F 中.用数学语言表达就是要求0),(21 F F Cov .称2F 为第二主成分.依此类推可以构造出第三、四……第p 个主成分。

（二）主成分分析的数学模型 对于一个样本资料.观测p 个变量p x x x ,,21.n 个样品的数据资料阵为：⎪⎪⎪⎪⎪⎭⎫⎝⎛=np n n p p x x x x x x x x x X 212222111211()p x x x ,,21=其中：p j x x x x nj j j j ,2,1,21=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=主成分分析就是将p 个观测变量综合成为p 个新的变量（综合变量）.即⎪⎪⎩⎪⎪⎨⎧+++=+++=+++=ppp p p p pp p p x a x a x a F x a x a x a F x a x a x a F 22112222121212121111 简写为：p jp j j j x x x F ααα+++= 2211p j ,,2,1 =要求模型满足以下条件：①j i F F ,互不相关（j i ≠.p j i ,,2,1, =） ②1F 的方差大于2F 的方差大于3F 的方差.依次类推 ③.,2,1122221p k a a a kp k k ==+++于是.称1F 为第一主成分.2F 为第二主成分.依此类推.有第p 个主成分。

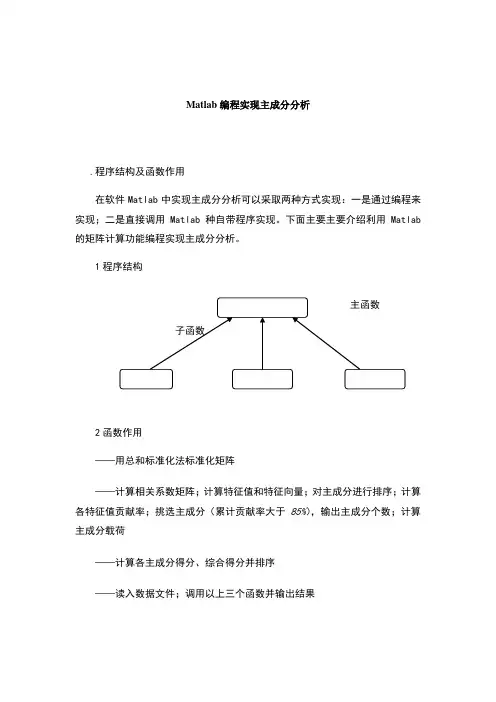
Matlab编程实现主成分分析.程序结构及函数作用在软件Matlab中实现主成分分析可以采取两种方式实现：一是通过编程来实现；二是直接调用Matlab种自带程序实现。

下面主要主要介绍利用Matlab 的矩阵计算功能编程实现主成分分析。

1程序结构2函数作用——用总和标准化法标准化矩阵——计算相关系数矩阵；计算特征值和特征向量；对主成分进行排序；计算各特征值贡献率；挑选主成分（累计贡献率大于85%），输出主成分个数；计算主成分载荷——计算各主成分得分、综合得分并排序——读入数据文件；调用以上三个函数并输出结果3.源程序总和标准化法标准化矩阵%,用总和标准化法标准化矩阵function std=cwstd(vector)cwsum=sum(vector,1); %对列求和[a,b]=size(vector); %矩阵大小,a为行数,b为列数for i=1:afor j=1:bstd(i,j)= vector(i,j)/cwsum(j);endend计算相关系数矩阵%function result=cwfac(vector);fprintf('相关系数矩阵:\n')std=CORRCOEF(vector) %计算相关系数矩阵fprintf('特征向量(vec)及特征值(val)：\n')[vec,val]=eig(std) %求特征值(val)及特征向量(vec)newval=diag(val) ;[y,i]=sort(newval) ; %对特征根进行排序，y为排序结果，i为索引fprintf('特征根排序：\n')for z=1:length(y)newy(z)=y(length(y)+1-z);endfprintf('%g\n',newy)rate=y/sum(y);fprintf('\n贡献率：\n')newrate=newy/sum(newy)sumrate=0;newi=[];for k=length(y):-1:1sumrate=sumrate+rate(k);newi(length(y)+1-k)=i(k);if sumrate> break;endend %记下累积贡献率大85%的特征值的序号放入newi中fprintf('主成分数：%g\n\n',length(newi));fprintf('主成分载荷：\n')for p=1:length(newi)for q=1:length(y)result(q,p)=sqrt(newval(newi(p)))*vec(q,newi(p));endend %计算载荷disp(result)%,计算得分function score=cwscore(vector1,vector2);sco=vector1*vector2;csum=sum(sco,2);[newcsum,i]=sort(-1*csum);[newi,j]=sort(i);fprintf('计算得分：\n')score=[sco,csum,j]%得分矩阵：sco为各主成分得分；csum为综合得分；j为排序结果%function print=cwprint(filename,a,b);%filename为文本文件文件名，a为矩阵行数(样本数)，b为矩阵列数(变量指标数)fid=fopen(filename,'r')vector=fscanf(fid,'%g',[a b]);fprintf('标准化结果如下：\n')v1=cwstd(vector)result=cwfac(v1);cwscore(v1,result);4.程序测试例题原始数据中国大陆35个大城市某年的10项社会经济统计指标数据见下表。

主成分分析法例子与matlab 中的应运可联系我邮箱 ******************1.概述主成分分析也称主分量分析，旨在利用降维的思想，把多指标转化为少数几个综合指标。

在实证问题研究中，为了全面、系统地分析问题，我们必须考虑众多影响因素。

这些涉及的因素一般称为指标，在多元统计分析中也称为变量。

因为每个变量都在不同程度上反映了所研究问题的某些信息，并且指标之间彼此有一定的相关性，因而所得的统计数据反映的信息在一定程度上有重叠。

在用统计方法研究多变量问题时，变量太 多会增加计算量和增加分析问题的复杂性，人们希望在进行定量分析的过程中，涉及的变量较少，得到的信息量较多。

1.1主成分分析计算步骤① 计算相关系数矩阵⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=pp p p p p r r r r r r r r r R 212222111211 （1）在（3.5.3）式中，r ij （i ，j=1，2，…，p ）为原变量的xi 与xj 之间的相关系数，其计算公式为∑∑∑===----=nk nk j kji kink j kj i kiij x xx xx x x xr 11221)()())(( （2）因为R 是实对称矩阵（即r ij =r ji ），所以只需计算上三角元素或下三角元素即可。

② 计算特征值与特征向量首先解特征方程0=-R I λ，通常用雅可比法（Jacobi ）求出特征值),,2,1(p i i =λ，并使其按大小顺序排列，即0,21≥≥≥≥pλλλ ；然后分别求出对应于特征值i λ的特征向量),,2,1(p i e i =。

这里要求i e =1，即112=∑=pj ij e ，其中ij e 表示向量i e 的第j 个分量。

③ 计算主成分贡献率及累计贡献率 主成分i z 的贡献率为),,2,1(1p i pk ki=∑=λλ累计贡献率为),,2,1(11p i pk kik k=∑∑==λλ一般取累计贡献率达85—95%的特征值m λλλ,,,21 所对应的第一、第二，…，第m （m ≤p ）个主成分。

§9. 利用Matlab 和SPSS 实现主成分分析1.直接调用Matlab 软件实现在软件Matlab 中实现主成分分析可以采取两种方式实现：一是通过编程来实现；二是直接调用Matlab 中自带程序实现。

通过直接调用Matlab 中的程序可以实现主成分分析：)(]2,var ,,[X princomp t iance score pc =式中：X 为输入数据矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nm n n m m x x x x x x x x x X 212222111211（一般要求n>m ）输出变量：①pc 主分量f i 的系数，也叫因子系数；注意：pc T pc=单位阵②score 是主分量下的得分值；得分矩阵与数据矩阵X 的阶数是一致的； ③variance 是score 对应列的方差向量，即A 的特征值；容易计算方差所占的百分比percent-v = 100*variance/sum(variance); ④t2表示检验的t2-统计量（方差分析要用） 计算过程中应用到计算模型:ξ+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡m T p x x x A f f f 2121 (要求p<m )例：表1为某地区农业生态经济系统各区域单元相关指标数据，运用主成分分析方法可以用更少的指标信息较为精确地描述该地区农业生态经济的发展状况。

表1 某农业生态经济系统各区域单元的有关数据样本序号 x 1：人口密度(人/km 2) x 2：人均耕地面积(ha) x 3：森林覆盖率(%) x 4：农民人均纯收入(元/人) x 5：人均粮食产量 (kg/人) x 6：经济作物占农作物播面比例(％)x 7：耕地占土地面积比率(％) x 8：果园与林地面积之比(％) x 9：灌溉田占耕地面积之比(％)1 363.912 0.352 16.101 192.11 295.34 26.724 18.492 2.231 26.262 2 141.503 1.684 24.301 1 752.35 452.26 32.314 14.464 1.455 27.066 3 100.695 1.067 65.601 1 181.54 270.12 18.266 0.162 7.474 12.489 4 143.739 1.336 33.205 1 436.12 354.26 17.486 11.805 1.892 17.534 5 131.412 1.623 16.607 1 405.09 586.59 40.683 14.401 0.303 22.932 6 68.337 2.032 76.204 1 540.29 216.39 8.128 4.065 0.011 4.861 7 95.416 0.801 71.106 926.35 291.52 8.135 4.063 0.012 4.862 8 62.901 1.652 73.307 1 501.24 225.25 18.352 2.645 0.034 3.2019 86.624 0.841 68.904 897.36 196.37 16.861 5.176 0.055 6.167 10 91.394 0.812 66.502 911.24 226.51 18.279 5.643 0.076 4.477 11 76.912 0.858 50.302 103.52 217.09 19.793 4.881 0.001 6.165 12 51.274 1.041 64.609 968.33 181.38 4.005 4.066 0.015 5.402 13 68.831 0.836 62.804 957.14 194.04 9.110 4.484 0.002 5.790 14 77.301 0.623 60.102 824.37 188.09 19.409 5.721 5.055 8.413 15 76.948 1.022 68.001 1 255.42 211.55 11.102 3.133 0.010 3.425 16 99.265 0.654 60.702 1 251.03 220.91 4.383 4.615 0.011 5.593 17 118.505 0.661 63.304 1 246.47 242.16 10.706 6.053 0.154 8.701 18 141.473 0.737 54.206 814.21 193.46 11.419 6.442 0.012 12.945 19 137.761 0.598 55.901 1 124.05 228.44 9.521 7.881 0.069 12.654 20 117.612 1.245 54.503 805.67 175.23 18.106 5.789 0.048 8.461 21122.7810.731 49.102 1 313.11 236.29 26.724 7.162 0.092 10.078对于上述例子，Matlab 进行主成分分析，可以得到如下结果。

§10.利用Matlab 编程实现主成分分析1.概述Matlab 语言是当今国际上科学界 <尤其是自动控制领域> 最具影响力、也是最有活力的软件。

它起源于矩阵运算,并已经发展成一种高度集成的计算机语言。

它提供了强大的科学运算、灵活的程序设计流程、高质量的图形可视化与界面设计、与其他程序和语言的便捷接口的功能。

Matlab 语言在各国高校与研究单位起着重大的作用。

主成分分析是把原来多个变量划为少数几个综合指标的一种统计分析方法,从数学角度来看,这是一种降维处理技术。

1.1主成分分析计算步骤① 计算相关系数矩阵⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=pp p p p p r r r r r r r r r R 212222111211〔1在〔,r ij 〔i,j=1,2,…,p 为原变量的xi 与xj 之间的相关系数,其计算公式为∑∑∑===----=n k nk j kj i ki nk j kj i kiij x x x x x x x xr 11221)()())(( 〔2因为R 是实对称矩阵〔即r ij =r ji ,所以只需计算上三角元素或下三角元素即可。

② 计算特征值与特征向量首先解特征方程0=-R I λ,通常用雅可比法〔Jacobi 求出特征值),,2,1(p i i =λ,并使其按大小顺序排列,即0,21≥≥≥≥pλλλ ；然后分别求出对应于特征值i λ的特征向量),,2,1(p i e i =。

这里要求i e =1,即112=∑=pj ij e ,其中ije 表示向量i e 的第j 个分量。

③ 计算主成分贡献率及累计贡献率 主成分i z 的贡献率为 累计贡献率为一般取累计贡献率达85—95%的特征值m λλλ,,,21 所对应的第一、第二,…,第m 〔m ≤p 个主成分。

④ 计算主成分载荷 其计算公式为),,2,1,(),(p j i e x z p l ij i j i ij ===λ 〔3得到各主成分的载荷以后,还可以按照〔,得到各主成分的得分⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nm n n m m z z z z z z z z z Z 212222111211〔42.程序结构及函数作用在软件Matlab 中实现主成分分析可以采取两种方式实现：一是通过编程来实现；二是直接调用Matlab 种自带程序实现。

§10.利用Matlab 编程实现主成分分析1.概述Matlab 语言是当今国际上科学界 (尤其是自动控制领域) 最具影响力、也是最有活力的软件。

它起源于矩阵运算，并已经发展成一种高度集成的计算机语言。

它提供了强大的科学运算、灵活的程序设计流程、高质量的图形可视化与界面设计、与其他程序和语言的便捷接口的功能。

Matlab 语言在各国高校与研究单位起着重大的作用。

主成分分析是把原来多个变量划为少数几个综合指标的一种统计分析方法，从数学角度来看，这是一种降维处理技术。

1.1主成分分析计算步骤① 计算相关系数矩阵⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=pp p p p p r r r r r r r r r R 212222111211 （1）在（3.5.3）式中，r ij （i ，j=1，2，…，p ）为原变量的xi 与xj 之间的相关系数，其计算公式为∑∑∑===----=n k n k j kj i ki n k j kj i ki ij x x x x x x x x r 11221)()())(( （2）因为R 是实对称矩阵（即r ij =r ji ），所以只需计算上三角元素或下三角元素即可。

② 计算特征值与特征向量首先解特征方程0=-R I λ，通常用雅可比法（Jacobi ）求出特征值),,2,1(p i i =λ，并使其按大小顺序排列，即0,21≥≥≥≥p λλλ ；然后分别求出对应于特征值i λ的特征向量),,2,1(p i e i =。

这里要求ie =1，即112=∑=p j ij e ，其中ij e 表示向量i e 的第j 个分量。

③ 计算主成分贡献率及累计贡献率主成分i z 的贡献率为),,2,1(1p i p k ki=∑=λλ 累计贡献率为),,2,1(11p i p k k i k k =∑∑==λλ一般取累计贡献率达85—95%的特征值m λλλ,,,21 所对应的第一、第二，…，第m （m ≤p ）个主成分。