下载文档原格式
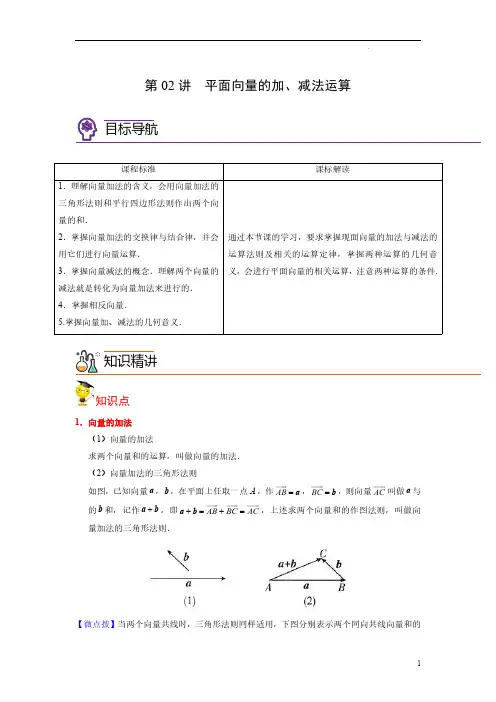
第02讲平面向量的加、减法运算目标导航课程标准课标解读1．理解向量加法的含义，会用向量加法的三角形法则和平行四边形法则作出两个向量的和．2．掌握向量加法的交换律与结合律，并会用它们进行向量运算．3．掌握向量减法的概念．理解两个向量的减法就是转化为向量加法来进行的．4．掌握相反向量．5.掌握向量加、减法的几何意义．通过本节课的学习，要求掌握现面向量的加法与减法的运算法则及相关的运算定律，掌握两种运算的几何意义，会进行平面向量的相关运算，注意两种运算的条件.知识精讲知识点1．向量的加法（1）向量的加法求两个向量和的运算，叫做向量的加法．（2）向量加法的三角形法则如图，已知向量a ，b ，在平面上任取一点A ，作AB = a ，BC = b ，则向量AC叫做a 与的b 和，记作+a b ，即AB BC AC +=+=a b ，上述求两个向量和的作图法则，叫做向量加法的三角形法则．【微点拨】当两个向量共线时，三角形法则同样适用，下图分别表示两个同向共线向量和的情形，及两个异向共线向量和的情形．（3）向量加法的平行四边形法则如图，已知两个不共线的向量a 和b ，作OA = a ，OB =b ，则O 、A 、B 三点不共线，以OA 、OB 为邻边作平行四边形OACB ，则对角线上的向量OC OA OB =+，此种作法称为向量加法的平行四边形法则．【微点拨】若n 个向量顺次首尾相接，则由起始向量的起点指向末向量的终点的向量就是它们的和，即1112233411n n n n n A A A A A A A A A A A A +-+=+++⋅⋅⋅+，如图．（4）和向量的模与原向量之间的关系一般地，我们有+≤+a b a b ．当a 与b 共线且同向时，+=+a b a b ；当a 与b 共线且异向时，+=-a b a b ；当a 与b 不共线时，+<+a b a b ．（5）向量加法的运算律交换律：+=+a b b a ；结合律：()()++=++a b c a b c ．注意：①当a 、b 至少有一个为零向量时，交换律和结合律仍成立；②当a 、b 共线时，交换律和结合律也成立．（6）向量求和的多边形法则由两个向加法的定义可知，两个向量的和仍是一个向量，这样我们就能把三个、四个或任意多个向量相加，现以四个向量为例，如图，已知向量a ，b ，c ，d ，在平面上任选一点O ，作OA = a ，AB = b ，BC = c ，CD = d ，则OD OA AB BC CD =+++=+++a b c d ．已知n 个向量，依次把这n 个向量首尾相连，以第一个向量的起点为起点、第n 个向量的终点为终点的向量叫做这n 个向量的和向量．这个法则叫做向量求和的多边形法则．（7）向量加法的实际应用向量的加法在三角形、四边形等平面几何知识，物理知识中都有着广泛的应用，在解决向量与平面几何知识相结合的题目时，要注意数形结合，这也体现了向量作为一种工具在几何学、物理学等知识领域的应用．2．向量的减法（1）相反向量我们把与向量a 长度相等、方向相反的向量，叫做a 的相反向量，记作-a ．规定零向量的相反向量仍为零向量，且①()--=a a ；②()()0+-=-+=a a a a ；若a ，b 互为相反向量，则=-a b ，=-b a ，0+=a b ．（2）向量减法的定义向量a 加上向量b 的相反向量，叫做a 与b 的差，即()-=+-a b a b ，求两个向量差的运算，叫做向量的减法，向量的减法实质上也是向量的加法．3．向量减法的几何意义（1）非零共线向量a ，b 的差-a b ；①若a ，b 反向，则-a b 与a 同向，且-=+a b a b ．②若a ，b 同向，（ⅰ）若>a b ，则-a b 与a 同向，且-=-a b a b ；（ⅱ）若<a b ，则-a b 与a 反向，且-=-a b b a ；（ⅲ）若=a b ，则0-=a b ．其几何意义分别如图（1）（2）（3）（4）．（2）非零不共线向量a ，b 的差-a b ：①如图，在平面内任取一点O ，作OA = a ，OB = b ，则向量BA为所求，即BA OA OB =-=-a b ．即把两个向量的起点放在一起，则两个向量的差是以减向量的终点为起点、被减向量的终点为终点的向量．②如图，在平面内任取一点O ，作OA = a ，OB =b ，分别以OA ，OB 为边作平行四边形OACB ，连接BA ，则BA BC CA =+=-a b ，这种作差向量的方法实质上是利用向量减法的定义．4．向量减法的三角形法则和平行四边形法则-a b 从“相反向量”这个角度有两种作法：三角形法则和平行四边形法则．减法的三角形法则的作法：在平面内取一点O ，作OA = a ，OB = b ，则BA =-a b ，即-a b 可以表示从向量b 的终点指向向量a 的终点的向量（注意：差向量的“箭头”指向被减向量）．具体作法如图（1）（a ，b 不共线）和图（2）、（3）（a ，b 共线）所示．减法的平行四边形法则的作法：当a ，b 不共线时．如图（1），在平面内任取一点O ，作OA = a ，OB =-b ，则由向量加法的平行四边形法则可得()OC =+-=- a b a b ，这是向量减法的平行四边形法则．若a ，b 同向共线，如图（2）所示；若a ，b 异向共线．如图（3）所示．5．向量的加法和减法的运算问题关于向量的加法和减法运算问题，一种解法就是依据三角形法则通过作图来解决，另一种解法就是通过表示向量的有向线段的字母符号运算来解决．具体地说，在一个用有向线段表示向量的运算式子中，将式子中的“−”改为“＋”只需把表示向量的两个字母的顺序颠倒一下即可．如“AB - ”改为“BA +”．解用几个基本向量表示某向量问题的基本技巧是，第一步：观察各向量位置；第二步：寻找（或作）相应的平行四边形或三角形：第三步：运用法则找关系；第四步：化简结果．【微点拨】向量减法运算是加法的逆运算．在理解相反向量的基础上，结合向量的加法运算掌握向量的减法运算．【即学即练1】在△ABC 中，BC = a ，CA = b ，则AB等于（）A ．+a bB ．--a bC ．-a bD ．-b a【答案】B【解析】AB CB CA =- =–BC CA -=--a b ，故选B ．【即学即练2】如图，在矩形ABCD 中，AO OB AD ++=（）A ．ABB ．ACC ．ADD ．BD【答案】B【解析】在矩形ABCD 中，AD BC = ，则AO OB AD AO ++= +OB +BC AC =，故选B ．【名师点睛】（1）向量加法的多边形法则：n 个向量经过平移，顺次使前一个向量的终点与后一个向量的起点重合，组成组向量折线，这n 个向量的和等于折线起点到终点的向量．这个法则叫做向量加法的多边形法则．多边形法则实质就是三角形法则的连续应用．（2）|a +b |≤|a |+|b |．【即学即练3】向量()()AB MB BO BC OM ++++ 化简后等于（）A ．BCB ．ABC ．ACD ．AM【答案】C【解析】()()AB MB BO BC OM AB ++++= +BO +OM +MB +BC AO = +OM +MB +BC =AM+MB +BC AB = +BC AC =．故选C ．【名师点睛】（1）首先观察各向量字母的排列顺序，再进行恰当的组合，利用向量加法法则求解．（2）此类问题应根据三角形法则或平行四边形形法则，观察是否具备应用法则的条件，若不具备，应改变条件，以便使用法则求解．【即学即练4】在△ABC 中，BC = a ，CA = b ，则AB等于（）A ．+a bB ．--a bC ．-a bD ．-b a【答案】B【解析】AB CB CA =- =–BC CA -=--a b ，故选B ．【即学即练5】下列四式不能化简为PQ的是（）A ．()AB PA BQ ++B．()()AB PC BA QC ++- C ．QC CQ QP+- D ．PA AB BQ+- 【答案】D 【分析】由向量加减法法则计算各选项，即可得结论．【详解A 项中，()()AB PA BQ AB BQ AP AQ AP PQ ++=+-=-=；B 项中，()()()()AB PC BA QC AB AB PC CQ PQ ++-=-++= ；C 项中，QC CQ QP QP PQ +-=-=；D 项中，PA AB BQ PB BQ PQ +-=-≠.故选：D.【即学即练6】已知非零向量a 与b方向相反，则下列等式中成立的是（）A ．a b a b -=-B ．a b a b+=- C ．a b a b+=- D ．a b a b+=+ 【答案】C 【分析】根据方向相反的两个向量的和或差的运算逐一判断.【详解】A.a b -可能等于零，大于零，小于零，0a b a b -=+> ，A 不成立B.a b a b +=-r r r r ，a b a b -=+，B 不成立C.a b a b -=+，C 成立D.a b a b a b +=-≠+，D 不成立.故选：C.【即学即练7】在平行四边形ABCD 中，BC CD BA -+等于（）A ．BCB ．DAC ．ABD ．AC【答案】A【解析】∵在平行四边形ABCD 中，DC 与BA 是一对相反向量，∴DC BA =-，∴–BC CD BA BC -+= BA +BA BC =，故选A ．【名师点睛】注意向量几何意义的应用，利用数形结合的思想解题．能力拓展考法011．向量加法运算及其几何意义（1）平行四边形法则的应用前提：两个向量是从同一点出发的不共线向量．三角形法则应用的前提：两个向量“首尾相接”．（2）当两个向量不共线时，三角形法则和平行四边形法则实质是一样的．三角形法则作出的图形是平行四边形法则作出图形的一半．但当两个向量共线时，平行四边形法则便不再适用．（3）向量加法的三角形法则和平行四边形法则是向量加法的几何意义．【典例1】如图，在正六边形ABCDEF 中，BA CD FB ++等于（）A ．0B ．BEC ．AD D ．CF【答案】A 【分析】根据相等向量和向量加法运算直接计算即可.【详解】CD AF = ，∴0BA CD FB BA AF FB ++==++ .故选：A.考法022．向量加法的运算律（1）向量的加法与实数加法类似，都满足交换律和结合律．（2）由于向量的加法满足交换律与结合律，因此多个向量的加法运算就可按照任意的次序与任意组合来进行．例如，（a +b ）+（c +d ）=（b +d ）+（a +c ），a +b +c +d +e =[d +（a +c ）]+（b +e ）．【典例2】化简下列各式：①AB BC CA ++ ；②()AB MB BO OM +++uu u r uuu r uu u r uuu r ；③OA OC BO CO +++；④AB CA BD DC +++．其中结果为0 的个数是（）A ．1B ．2C ．3D ．4【答案】B 【分析】根据向量的加减运算法则计算，逐一判断①②③④的正确性，即可得正确答案.【详解】对于①：0AB BC CA AC CA ++=+=，对于②：()AB MB BO OM AB BO OM MB AM MB AB +++=+++=+=uu u r uuu r uu u r uuu r uu u r uu u r uuu r uuu r uuu r uuu r uu u r，对于③：()()0OA OC BO CO BO OA CO OC BA BA +++=+++=+=，对于④：()()0AB CA BD DC AB BD DC CA AD DA +++=+++=+= ，所以结果为0的个数是2，故选：B考法033．向量的減法运算及其几何意义（1）向量减法的实质是向量加法的逆运算．利用相反向量的定义可以把减法化为加法．在用三角形法则作向量减法时，只要记住“连接两向量的终点，箭头指向被减向量”即可．（2）以向量AB =a ，A 6=b 为邻边作平行四边形ABCD ，则两条对角线的向量为AC =a +b ，BD =b –a ，DB =a –b ，这一结论在以后应用非常广泛，应该牢记并加强理解．【典例3】已知85AB AC == ，，则BC的取值范围是__________．【答案】[3，13]【解析】∵–BC AC AB = ，∴BC =|–AC AB|，∴AB AC - ≤BC ≤AB AC + ，即3≤BC≤13．故答案为：[3，13]．【名师点睛】本题考查的知识点是两向量的和或差的模的最值，两向量反向，差的模有最大值，两向量反向，差的模有最小值是解答本题的关键．|a –b |、|a |–|b |、|a |+|b |三者的大小关系（1）当向量a 与b 共线时，当两非零向量a 与b 同向时，|a –b |=|a |–|b |<|a |+|b |；当两非零向量a 与b 反向时，|a –b |=|a |+|b |>|a |–|b |；当a 与b 中至少有一个为零向量时，|a –b |=|a |–|b |=|a |+|b |．（2）当两非零向量a 与b 不共线时，如在△ABC 中，AC =a ，AB =b ，则BC =AC –AB =a –b ，根据三角形中任意两边之差总小于第三边，任意两边之和总大于第三边，可得||a |–|b ||<|a –b |<|a |+|b |．综合可知，对任意的向量a 与b 都有||a |–|b ||≤|a –b |≤|a |+|b |．只当a 与b 同向或a 与b 中至少有一个为零向量时||a |–|b ||≤|a –b |中的等号成立；当a 与b 反向或a 与b 中至少有一个为零向量时|a –b |≤|a |+|b |中的等号成立．考法044．向量加、减法的综合应用向量的几何意义及加、减法运算常用来解决平面几何问题，解题时要将所给向量式中各向量进行移项或重新组合，并灵活运用相反向量，把向量相等、平行、模的关系进行转化．【典例4】化简（1）()()AB CD AC BD --- （2）OA OD AD -+ ；（3）AB DA + ＋BD BC CA --．【答案】（1）0 ；（2）0 ；（3）AB.【分析】（1）方法一：将CD - 转化为DC，将AC - 转化为CA ，利用向量的加法法则，即可求得答案.方法二：利用向量的减法法则，化简整理，即可得答案.（2）利用向量的减法法则，化简整理，即可得答案.（3）根据向量的线性运算法则，即可求得答案.【详解】（1）方法一(统一成加法)：()()AB CD AC BD AB AC CD BD ---=--+AB BD DC CA AD DA =+++=+= 方法二(利用OA OB BA -=uu r uu u r uu r)：()()AB CD AC BD AB CD AC BD ---=--+ 0AB AC CD BD CB CD BD DB BD =--+=-+=+= （2）0OA OD AD DA AD -+=+=uu r uuu r uuu r uu u r uuu r r ．（3）AB DA BD BC CA AB DA AC BD BC ++--=+++- AB DC CD AB=++= 【典例5】如图，M 、N 在线段BC 上，且BM CN =，试探求AB AC + 与AM AN +的关系，并证明之.【答案】相等，证明见解析【分析】求AB AC + 与AM AN +的关系为相等，利用向量加法的三角形法则即可证明.【详解】A A M C ANB A =++ 证明：由向量加法三角形法则知：,AB AM MB AC AN NC =+=+，所以AB AC AM MB AN NC +=+++ ，因为BM CN =，所以MB NC =- ，所以AB AC AM MB AN NC AM AN NC NC AM AN +=+++=++-=+ 【点睛】本题主要考查了向量的加法法则，相反向量，属于中档题.【典例6】如图所示，已知在矩形ABCD 中，3AD = ，8AB = .设,,AB a BC b BD c ===，求a b c -- .【答案】87a b c --=r r r【分析】延长直线AB ,使得直线AB 上一点B '满足AB BB '=,同理,延长直线AD ,使得直线AD 上一点D ¢满足AD DD '=,画出图形,则''a b c D B --=,进而求解即可【详解】延长直线AB ,使得直线AB 上一点B '满足AB BB '=,同理,延长直线AD ,使得直线AD 上一点D ¢满足AD DD '=,如图所示,则'b c BD += ,()'''''a b c a b c a BD BB BD D B --=-+=-=-=,则()()22''2432887a b c D B --==⨯+⨯=【点睛】本题考查向量的加法,减法在几何中的应用,考查向量的模.分层提分题组A 基础过关练1．向量AB CB BD BE DC ++++化简后等于（）A ．A EB ．AC C ．ADD ．AB【答案】A 【分析】根据向量的线性运算求解即可.【详解】由AB CB BD BE DC AC CB BE AE →→++++=++= ,故选：A2.如图，向量AB a =，AC b = ，CD c = ，则向量BD 可以表示为（）A ．a b c ++B ．a b c-+ C ．b a c-+D ．b a c-- 【答案】C 【分析】利用向量加法和减法的三角形法则计算即可.【详解】AD AB AC CD AB BD b a c=-=-+-=+ 故选：C.3..设D 为∆ABC 中BC 边上的中点，且O 为AD 边上靠近点A 的三等分点，则（）A.5166BO AB AC=-+B.1162BO AB AC=-C.5166BO AB AC=- D.1162BO AB AC=-+【答案】A【解析】本题考点是平面向量的加减法运算法则，由题意可知在三角形BAO 中：()11513666BO AO AB AD AB AB AC AB AB AC =-=-=+-=-+，故选A.4.设D ，E ，F 分别为△ABC 的三边BC ，CA ，AB 的中点，则EB FC +=()．A ．ADB ．12ADC ．BCD ．12BC【答案】A【解析】本题的考点是平面向量的加法、减法法则，线段中点的性质，考查转化能力，用向量法表示三角形中线的性质要引起重视，由题意可知D ，E ，F 分别是BC ，CA ，AB 的中点，所以有以下结论：()()1122EB FC BA BC CA CB+=-+-+()()1112222BA CA AB AC AD AD =-+=+==，故选A.5.已知点G 是三角形ABC 所在平面内一点，满足0GA GB GC ++=，则G 点是三角形ABC的（）A ．垂心B ．内心C ．外心D ．重心【答案】D 【分析】由题易得GA GB CG +=，以GA 、GB 为邻边作平行四边形GADB ，连接GD ，交AB 于点O ，进而可得CG GD =，进而可得13GO CO = ，所以CG 所在的直线CO 是AB 边上的中线，同理可证AG 所在的直线是BC 边上的中线，BG 所在的直线是AC 边上的中线，最后得出答案即可.【详解】因为0GA GB GC ++= ，所以GA GB GC CG +=-= ，以GA ､GB 为邻边作平行四边形GADB ，连接GD ，交AB 于点O ，如图所示：则CG GD =，所以13GO CO = ，点O 是AB 边的中点，所以CG 所在的直线CO 是AB 边上的中线，同理可证AG 所在的直线是BC 边上的中线，BG 所在的直线是AC 边上的中线，所以G 点是三角形ABC 的重心.故选：D .6.如图，D ，E ，F 分别为ABC 的边AB ，BC ，CA 的中点，则（）A ．0AD BE CF ++= B ．0++= BD CF DF C ．0++= AD CE CF D ．0++= BD BE FC 【答案】A 【分析】根据平面向量的线性运算法则计算可得；【详解】解：D Q ，E ，F 分别是ABC 的边AB ，BC ，CA 的中点，∴12AD AB = ，12BE BC = ，12CF CA =，则1111()02222AD BE CF CA AB CA CA AB CA ++=++=++=，故A 正确；()1111122222BD CF DF BA CA BA CA BA BC BC ++=++=++=，故B 错误；()1111122222AD CE CF AB CB CA CA AB CB CB ++=++=++=，故C 错误；()1111122222BD BE FC BA BC AC BA AC BC BC ++=++=++=，故D 错误；故选：A ．7.在ABC 中，点P 满足2AP AB AC =-，则（）A ．点P 不在直线BC 上B ．点P 在CB 的延长线上C ．点P 在线段BC 上D ．点P 在BC 的延长线上【答案】B 【分析】由已知条件可得BP CB = ，从而可得BP 与CB共线，进而可得结论【详解】因为2AP AB AC =-，得AP AB AB AC =-- ，所以BP CB = ，所以,,B P C 三点共线，且点P 在CB 的延长线上，故选：B8.五角星是指有五只尖角､并以五条直线画成的星星图形，有许多国家的国旗设计都包含五角星，如中华人民共和国国旗.如图在正五角星中，每个角的角尖为36°，则下列说法正确的是（）A ．0CH ID += B ．AB FE∥ C ．2AF FG HG+= D ．AF AB AJ=+ 【答案】D 【分析】利用相反向量可判断A ；利用向量共线可判断B ，利用向量的加法可判断C 、D.【详解】A ，由图可知CH 与ID 相交，所以CH 与ID不是相反向量，故A 错误；B ，AB 与DE 共线，所以DE 与FE 不共线，所以AB 与FE不共线，故B 错误；C ，2AF FG AG HG +=≠，故C 错误；D ，连接,BF JF ，由五角星的性质可得ABJF 为平行四边形，根据平行四边形法则可得AF AB AJ =+，故D 正确.故选：D9.已知A ，B ，C 为三个不共线的点，P 为△ABC 所在平面内一点，若PA PB PC AB +=+，则下列结论正确的是（）A ．点P 在△ABC 内部B ．点P 在△ABC 外部C ．点P 在直线AB 上D ．点P 在直线AC 上【答案】D 【分析】由向量的运算可得CA AP =，进而可得解.【详解】∵PA PB PC AB +=+ ，∴PB PC AB PA -=- ，∴CB AB AP CB AB AP =+-= ，，即CA AP = .故点P 在边AC 所在的直线上.故选：D.10.平面上有三点A ，B ，C ，设m AB BC =+ ，n AB BC =-，若,m n 的长度恰好相等，则有（）A ．A ，B ，C 三点必在同一条直线上B ． ABC 必为等腰三角形，且∠B 为顶角C ． ABC 必为直角三角形，且∠B=90°D ． ABC 必为等腰直角三角形【答案】C【分析】根据,m n 的长度相等，由|AC |=|BD|得到ABCD 是矩形判断.【详解】如图：因为,m n的长度相等，所以|AB BC + |=|AB BC - |，即|AC |=|BD |，所以ABCD 是矩形，故 ABC 是直角三角形，且∠B=90°.故选：C11.在平行四边形ABCD 中，设M 为线段BC 的中点，N 为线段AB 上靠近A 的三等分点，AB a = ，AD b = ，则向量NM =（）A ．1132a b+B ．2132a b+C ．1132a b-D ．2132a b-【答案】B【分析】根据题意作出图形，将AM 用a 、b的表达式加以表示，再利用平面向量的减法法则可得出结果.【详解】解：由题意作出图形：在平行四边形ABCD 中， M 为BC 的中点，则12AM AB BM a b =+=+又 N 为线段AB 上靠近A 的三等分点，则1133AN AB ==11212332NM AM AN a b a a b∴=-=+-=+故选：B12.若O 是平面上的定点，A ，B ，C 是平面上不共线的三点，且满足()OP OC CB CAλ=++（R λ∈），则P 点的轨迹一定过ABC 的（）A ．外心B ．内心C ．重心D ．垂心【答案】C【分析】由()OP OC CB CA λ=++ （R λ∈），得到()CP CB CA λ=+ ，再根据CB CA +经过在ABC 的重心判断.【详解】因为()OP OC CB CA λ=++（R λ∈），所以()CP CB CA λ=+，所以CB CA +在ABC 的边AB 上的中线所在直线上，则()CB CA λ+ 在ABC 的中线所在直线上，所以P 点的轨迹一定过ABC 的重心，故选：C13.下列命题中正确的是（）A ．如果非零向量a 与b 的方向相同或相反，那么a b + 的方向必与a ，b之一的方向相同B ．在ABC 中，必有0AB BC CA ++=C ．若0AB BC CA ++=，则A ，B ，C 为一个三角形的三个顶点D ．若a ，b均为非零向量，则||a b + 与||||a b + 一定相等【答案】B 【分析】根据向量的线性运算法则，逐一分析各个选项，即可得答案.【详解】对于A ：当a 与b 为相反向量时，0a b +=，方向任意，故A 错误；对于B ：在ABC 中，0AB BC CA ++=，故B 正确；对于C ：当A 、B 、C 三点共线时，满足0AB BC CA ++=，但不能构成三角形，故C 错误；对于D ：若a ，b 均为非零向量，则a b a b +≤+ ，当且仅当a 与b同向时等号成立，故D错误.故选：B14.如右图，D ，E ，P 分别是ABC 的边AB ，BC ，CA 的中点，则（）A ．0AD BE CF ++= B ．0BD CF DF -+=uu u r uu u r uuu r r C ．0AD CE CF +-=uuu r uur uu u r r D ．0BD BE FC --= 【答案】A 【分析】根据向量加法和减法的运算法则结合图像逐一运算即可得出答案.【详解】解：0AD BE CF DB BE ED DE ED ++=++=+=，故A 正确；BD CF DF BD FC DF BC -+=++=，故B 错误；AD CE CF AD FE AD DB AB +-=+=+=，故C 错误；2BD BE FC ED FC ED DE ED --=-=-=，故D 错误.故选：A.15.如图，在ABC 中，3BC BD →→=，23AE AD →→=，则CE →=（）A ．4599AB AC→→+B ．4799AB AC→→-C ．4133AB AC→→-D ．4799AB AC→→-+【答案】B 【分析】利用向量定义，22()33CE AE AC AD AC AB BD AC →→→→→→→→=-=-=+-，最后化简为,AB AC →→来表示向量即可.【详解】22()33CE AE AC AD AC AB BD AC→→→→→→→→=-=-=+-2122()()3339AB BC AC AB AC AB AC →→→→→→→=+-=+--4799AB AC →→=-故选：B题组B 能力提升练1.在等腰梯形ABCD 中，//AB DC ，2AB DC =，E 为BC 的中点，则（）A ．3142AE AB AD→→→=+B ．3122AE AB AD→→→=+C ．1142AE AB AD →→→=+D ．3144AE AB AD →→→=+【答案】A 【分析】作出示意图，利用数形结合，在梯形ABCD 中，利用三角形法则即可求解.【详解】如图所示：在三角形ABE 中，12AE AB BE AB BC→→→→→=+=+12AB BA AD DC →→→→⎛⎫=+++ ⎪⎝⎭1122AB AB AD AB →→→→⎛⎫=+-++ ⎪⎝⎭1122AB AB AD →→→⎛⎫ ⎪=+-+ ⎪⎝⎭3142AB AD →→=+.故选：A.2.已知O 是三角形ABC 内部的一点，230OA OB OC ++=，则OAC 的面积与OAB 的面积之比是（）A ．32B ．23C ．2D ．1【答案】B 【分析】取D 、E 分别是BC 、AC 中点，根据向量的加法运算以及向量共线可得2OE OD =，再由三角形的相似比即可求解.【详解】如下图所示，D 、E 分别是BC 、AC 中点，由230OA OB OC ++=得()2OA OC OB OC +=-+ 即2OE OD =- ，所以2OE OD =，由COE AOE S S = ，COD BOD S S =△△，设1AOC S S = ，2BOC S S = ，则12COE AOE S S S ==，22COD BOD SS S == ，由三角形相似比可得1212122322AOB S S S S S +=++ ，解得12AOB S S S += ，因为:2:1AOE BOD S S = ，所以12:2:1S S =，即122S S =，所以112AOB S S S += ，所以123AOB S S = ，即OAC 的面积与OAB 的面积之比是23故选：B.3.已知平面向量a ，b ，c满足222a c a b b c ==-=-= ，则b 的取值范围为（）A ．[]1,3B ．7⎡⎣C ．[]2,3D ．7⎡⎣【答案】C 【分析】由复数的几何意义画出简图，数形结合可得结果.【详解】令a OA =，由2a = 知点A 在以O 为圆心，2为半径的圆上；令2a OD =，由2a = 知点D 在以O 为圆心，4为半径的圆上；令c OC =，由2c = 知点C 在以O 为圆心，2为半径的圆上；令b OB =，由22a b -= 知点B 在以D 为圆心，2为半径的圆上，由1b c -= 知点B 也在以C为圆心，1为半径的圆上，所以点B 在以O 为圆心，内径为2，外径为3的圆环上，如图阴影部分，从而[]2,3b ∈.故选：C.4.在平行四边形ABCD 中，设CB a = ，CD b =，E 为AD 的靠近D 的三等分点，CE 与BD交于F ，则AF =（）A ．3144a b--B ．3144a b-+C ．1344a b--D ．1344a b-【答案】A 【分析】找到AD 、BC 上的三等分点，则////AK GH EC ，结合图形易得4DBDF =，由AF AD DF =+ 即可知正确选项.【详解】如图，在AD 上取G 点，使得AG GE ED ==，在BC 上由左到右取K ，H ，使得BK KH HC ==，连接AK ，GH ，则////AK GH EC ，∵//DE BC 且13DE BC =，∴由相似比可知：4DBDF =，∴()131444AF AD DF a a b a b =+=-+-=-- .故选：A5.在ABC 中，D 、E 、F 分别是边BC 、CA 、AB 的中点，AD 、BE 、CF 交于点G ，则：①1122EF CA BC =- ；②1122BE AB BC =-+ ；③AD BE FC += ；④0GA GB GC ++= ．上述结论中，正确的是（）A ．①②B ．②③C ．②③④D ．①③④【答案】C 【分析】作出图形，利用平面向量的加法法则可判断①②③④的正误.【详解】如下图所示：对于①，F 、E 分别为AB 、AC 的中点，111222FE BC CA BC ∴=≠-，①错误；对于②，以BA 、BC 为邻边作平行四边形ABCO ，由平面向量加法的平行四边形法则可得2BE BO BA BC AB BC ==+=-+，1122BE AB BC ∴=-+，②正确；对于③，由②同理可得2AD AB AC =+uuu r uu u r uuu r，1122AD AB AC ∴=+ ，同理可得1122CF CA CB =+ ，()102AD BE CF AB AC BA BC CA CB ∴++=+++++=，AD BE CF FC ∴+=-=，③正确；对于④，易知点G 为ABC 的重心，所以，23GA AD =- ，23GB BE =- ，23GC CF =-，因此，()203GA GB GC AD BE CF ++=-++=，④正确.故选：C.【点睛】本题考查平面向量加法运算的相关判断，考查平面向量加法法则的应用，考查计算能力，属于中等题.6.八卦是中国文化中的哲学概念，如图1是八卦模型图，其平面图形记为图2中的正八边形ABCDEFGH ，其中1OA =，则给出下列结论：①0BF HF HD -+= ；②2OA OC OF +=- ；③AE FC GE AB +-=．其中正确的结论为（）A ．①②B ．①③C ．②③D ．①②③【答案】C 【分析】根据平面向量的线性运算逐项进行化简计算，由此确定出正确选项.【详解】对于①：因为BF HF HD BF FH HD BH HD BD -+=++=+=，故①错误；对于②：因为3602908AOC ︒∠=⨯=︒，则以,OA OC 为邻边的平行四边形为正方形，又因为OB 平分AOC ∠，所以22OA OC +=-，故②正确；对于③：因为AE FC GE AE FC G EG A FC +-=++=+ ，且FC GB =，所以AE FC GE AG GB AB +-=+=，故③正确，故选：C.【点睛】关键点点睛：解答本题的关键利用合适的转化对向量的减法运算进行化简，由此验证关于向量的等式是否正确.7.ABC 中，AD DC =，点M 在BD 上，且满足37AM AB t AC =+ ，则实数t 的值为（）A ．67B ．47C ．27D ．59【答案】C 【分析】由题意，可设DM k DB =，结合条件整理可得11(1)22AM AC DM k AC k AB =+=-+ ，得到关于k 与t 的方程组，解出t 即可．【详解】如图，因为AD DC =，所以12AD AC= 则12AM AD DM AC DM =+=+ ，因为M 在BD 上，不妨设1()()2DM k DB k AB AD k AB AC ==-=- ，则1111()(1)2222AM AC DM AC k AB AC k AC k AB =+=+-=-+ ，因为37AM AB t AC =+，所以371(1)2⎧⎪⎪⎨⎪⎩=-=⎪k k t ，解得27t =，故选：C【点睛】本题主要考查了平面向量的线性运算的应用及平面向量基本定理的应用，意在考查学生对这些知识的理解掌握水平．8.（多选题）下列各式结果为零向量的有（）A ．AB CA BC→→→++B ．AB AC BD CD+++ C ．OA OD AD-+ D ．NQ QP MN MP++- 【答案】ACD 【分析】根据平面向量的线性运算逐个求解即可【详解】对A ，0AB CA BC CA AB BC CB BC ++=++=+=，故A 正确；对B ，()()2AB AC BD CD AB BD AC CD AD AD AD +++=+++=+=，故B 错误；对C ，0OA OD AD DA AD -+=+=，故C 正确；对D ，0NQ QP MN MP NP PN ++-=+=，故D 正确；故选：ACD 【点睛】本题主要考查了平面向量的线性运算9.（多选题）在平行四边形ABCD 中，点E ，F 分别是边BC 和DC 的中点，P 是DE 与BF 的交点，则有（）A ．12AE AB AD=+uu u r uu u r uuu rB ．1122AF AB AD=+ C ．2233AP AB AD=+ D ．1122CP CD CB=+【答案】AC 【分析】对A ，B ，由向量的加法法则即可判断；对C ，D ，由向量的加法法则以及三角形重心的性质即可判断.【详解】解：如图所示：对A ，12AE AB BE AB BC =+=+，又BC AD = ，即12AE AB AD =+uu u r uu u r uuu r，故A 正确；对B ，1122AF AD DC AB AD =+=+，故B 错误；对C ，设O 为AC 与BD 的交点，由题意可得：P 是CBD 的重心，故2CP PO = ，222333AP AO OP AC AB AD =+==+，故C 正确；对D ，221111332233CP CO CB CD CB CD ⎛⎫==⨯+=+ ⎪⎝⎭，故D 错误.故选：AC.10.（多选题）设P 是OAB 内部（不含边界）的一点，以下可能成立的是（）A ．2155OP OA OB =+B ．2455OP OA OB =+C ．2155OP OA AB=+ D ．2455OP OA AB=+【答案】AC 【分析】作出图示，根据向量的平行四边形法则逐项进行判断即可.【详解】对于A ：如下图所示，可知P 在OAB 内部，故成立；对于B ：如下图所示，可知P 在OAB 外部，故不成立；对于C ：因为21211115555555OP OA AB OA AO OB OA OB =+=++=+，如下图所示，可知P 在OAB 内部，故成立；对于D ：因为24244245555555OP OA AB OA AO OB OA OB =+=++=-+ ，如下图所示，可知P 在OAB 外部，故不成立；故选：AC.【点睛】关键点点睛：解答本题的关键是采用图示结合向量的平行四边形法则进行说明，其中CD 选项中的向量关系式要根据AB AO OB =+进行化简.11.（多选题）设点D 是ABC 所在平面内一点，则下列说法正确的有（）A ．若()12AD AB AC =+，则点D 是边BC 的中点B ．若()13AD AB AC =+，则点D 是ABC 的重心C ．若2AD AB AC =-，则点D 在边BC 的延长线上D ．若AD xAB y AC =+ ，且12x y +=，则BCD △是ABC 面积的一半【答案】ABD 【分析】对A ，根据中点的性质即可判断；对B ，根据重心的性质即可判断；对C ，根据向量的运算得到BD CB =，即可判断；对D ，根据三点共线的性质即可求解.【详解】解：对A ，()12AD AB AC =+，即11112222AD AB AC AD -=-，即BD DC = ，即点D 是边BC 的中点，故A 正确；对B ，设BC 的中点为M ，()1122333AD AB AC AM AM =+=⨯= ，即点D 是ABC 的重心，故B 正确；对C ，2AD AB AC =-，即AD AB AB AC -=- ，即BD CB = ，即点D 在边CB 的延长线上，故C 错误；对D ，AD xAB y AC =+，且12x y +=，故222AD xAB y AC =+，且221x y +=，设2AM AD =，则22AM xAB y AC =+，且221x y +=，故,,M B C 三点共线，且2AM AD =，即BCD △是ABC 面积的一半，故D 正确.故选：ABD.12.对于菱形ABCD ，给出下列各式，其中结论正确的为（）A ．AB BC =B ．AB BC = C ．AB CD AD BC-=+D ．AD CD CD CB+=- 【答案】BCD 【分析】由向量的加法减法法则及菱形的几何性质即可求解.【详解】菱形中向量AB 与BC的方向是不同的，但它们的模是相等的，所以B 结论正确，A 结论错误；因为2AB CD AB DC AB -=+= ，2AD BC BC +=，且AB BC = ，所以AB CD AD BC -=+ ，即C 结论正确；因为AD CD BC CD BD +=+= ，||||CD CB CD BC BD -=+=，所以D 结论正确.故选：BCD【点睛】本题主要考查了向量加法、减法的运算，菱形的性质，属于中档题.13.．四边形ABCD 中，若BD BC BA =+，则四边形ABCD 的形状为_____.【答案】平行四边形【分析】由平面向量的加法法则直接可得答案【详解】解：因为四边形ABCD 中，BD BC BA =+，所以BC CD BC BA +=+ ，所以CD BA = ，所以CD BA = ，且CD ‖BA ，所以四边形ABCD 为平行四边形，故答案为：平行四边形。
