2015年陕西省中考数学总复习考点跟踪突破：第9讲 不等式与不等式组

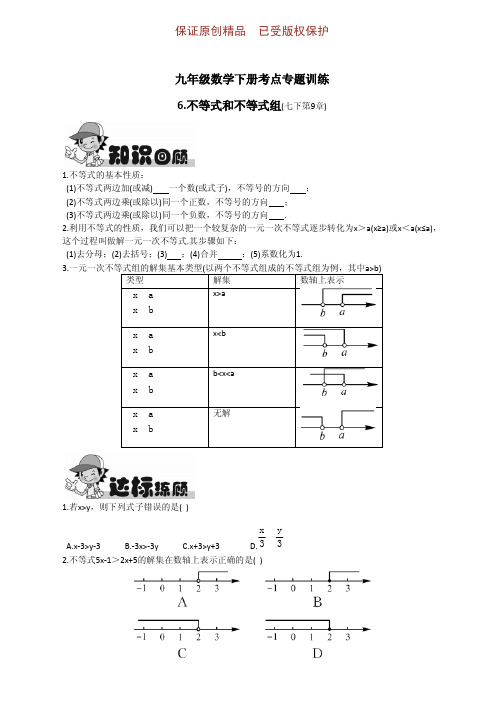
不等式和不等式组1.不等式的基本性质：(1)不等式两边加(或减) 一个数(或式子)，不等号的方向 ；(2)不等式两边乘(或除以)同一个正数，不等号的方向 ；(3)不等式两边乘(或除以)同一个负数，不等号的方向 .2.利用不等式的性质，我们可以把一个较复杂的一元一次不等式逐步转化为x ＞a(x ≥a)或x ＜a(x ≤a)，这个过程叫做解一元一次不等式.其步骤如下：(1)去分母；(2)去括号；(3) ；(4)合并 ；(5)系数化为1.3.a>b)1.若x>y ，则下列式子错误的是( )A.x-3>y-3B.-3x>-3yC.x+3>y+3D.3y 3x > 2.不等式5x-1＞2x+5的解集在数轴上表示正确的是( )3.设“▲”、“●”、“■”分别表示三种不同的物体，现用天平秤两次，情况如图所示，那么▲、●、■这三种物体按质量从大到小排列应为( )A.■、●、▲B.▲、■、●C.■、▲、●D.●、▲、■4.不等式组⎩⎨⎧-7>1-2≥-x x ,12的解集在数轴上表示正确的是( )5.不等式组⎪⎩⎪⎨⎧≥+>+2332-,1-x 1)3(x x 的整数解是( ) A.-1，0，1 B.0，1 C.-2，0，1 D.-1，16.我省从2014年起在公众场所实行“禁烟”，为配合“禁烟”行动，某校组织开展了“吸烟有害健康”的知识竞赛，共有20道题.答对一题记10分，答错(或不答)一题记-5分.小明参加本次竞赛得分要超100分，他至少要答对 道题.7.解下列不等式或不等式组：(1)3(x-1)＞2x+2； (2)x-2≥21(x+1)；(3)⎩⎨⎧0<1->+;x 12x x ， (4)⎩⎨⎧<4-+≤+3x.3x 1)2(x x ，8.解不等式组⎪⎩⎪⎨⎧<+-2+≤+,12312)3(x 52x x x ，把不等式组的解集在数轴上表示出来，并写出不等式组的非负整数解.参考答案知识回顾1.(1)同 不变(2)不变(3)改变2.移项同类项达标练习1.B2.A3.C4.D5.A6.147.(1)x＞5.(2)x≥5.(3)-1＜x＜1.(4)-2＜x≤1.8.由①得x≥-1.由②得x＜3.不等式组的解集为：-1≤x＜3.在数轴上表示为：不等式组的非负整数解为2，1，0.。

中考数学不等式与不等式组的知识点分析第1篇：中考数学不等式与不等式组的知识点分析一、目标与要求1、感受生活中存在着大量的不等关系，了解不等式和一元一次不等式的意义，通过解决简单的实际问题，使学生自发地寻找不等式的解，会把不等式的解集正确地表示到数轴上;2、经历由具体实例建立不等模型的过程，经历探究不等式解与解集的不同意义的过程，渗透数形结合思想;3、通过对不等式、不等式解与解集的探究，引导学生在*思考的基础上积极参与对数学问题的讨论，培养他们的合作交流意识;让学生充分体会到生活中处处有数学，并能将它们应用到生活的各个领域。

二、重点理解并掌握不等式的*质;正确运用不等式的*质;建立方程解决实际问题，会解"ax+b=cx+d"类型的一元一次方程;寻找实际问题中的不等关系，建立数学模型;一元一次不等式组的解集和解法。

三、难点一元一次不等式组解集的理解;弄清列不等式解决实际问题的思想方法，用去括号法解一元一次不等式;正确理解不等式、不等式解与解集的意义，把不等式的解集正确地表示到数轴上。

小编导语：每一门功课都有它自身的规律，有它自身的特点，数学当然也不例外。

下面是有关中考数学考试知识点分析:矩形的内容，供你学习参考!1、矩形的概念有一个角是直角的平行四边形叫做矩形。

2、矩形的*质(1)具有平行四边形的一切*质(2)矩形的四个角都是直角(3)矩形的对角线相等(4)矩形未完，继续阅读 >第2篇：中考数学不等式与不等式组点分析小编导语：每一门功课都有它自身的规律，有它自身的特点，数学当然也不例外。

下面是有关中考数学考试知识点分析:不等式与不等式组的内容，供你学习参考!一、目标与要求1、感受生活中存在着大量的不等关系，了解不等式和一元一次不等式的意义，通过解决简单的实际问题，使学生自发地寻找不等式的解，会把不等式的解集正确地表示到数轴上;2、经历由具体实例建立不等模型的过程，经历探究不等式解与解集的不同意义的过程，渗透数形结合思想;3、通过对不等式、不等式解与解集的探究，引导学生在*思考的基础上积极参与对数学问题的讨论，培养他们的合作交流意识;让学生充分体会到生活中处处有数学，并能将它们应用到生活的各个领域。

陕西初中毕业考试数学中考考点一、数与式（一）、实数（1）了解平方根、算术平方根、立方根的概念，会用根号表示数的平方根和立方根。

（2）会用平方运算求百以内正整数的平方根，用立方运算求百以内整数的立方根。

（3）了解近似数的概念，并在解决实际问题中，能对计算结果按要求取近似数。

（4）二次根式的概念及加、减、乘、除运算法则，并用它们进行有关实数的四则运算。

（5）理解有理数的意义，在数轴上表示实数，并比较实数的大小。

（6）借助数轴理解相反数和绝对值的意义，并会求任一实数的相反数和绝对值。

（7）实数的加、减、乘、除、乘方、开方及简单运算。

（8）实数的运算律。

（9）能用有理数估计一个无理数的大致范围。

（二）、整式和分式（1）会用科学计数法表示数。

（2）整式的概念，进行简单的整式加、减运算，及整式乘法运算。

（3）分式的概念，利用分式的性质进行约分和通分，简单的分式加、减、乘、除运算。

（4）用代数式表示简单问题中的数量关系。

（5）推导乘法公式, .（6）提公因式法、公式法进行分解因式。

二、方程与方程组（一）、方程与方程组（1）根据实际问题的实际意义，列出方程或方程组并求解，并有意识地检验结果的合理性。

（2）会解一元一次方程、简单的二元一次方程组，可化为一元一次方程的分式方程。

（3）用配方法、因式分解法、公式法解简单的数字系数的一元二次方程。

（二）、不等式与不等式组（1）会解简单的一元一次不等式，并在数轴上表示出解集；会解由两个一元一次不等式组成的不等式组，并会用数轴确定解集。

（2）不等式性质的应用。

三、函数（一）、函数（1）常量、变量的意义（2）确定简单整式、分式以及简单实际问题中函数的自变量取值范围，求函数值。

（3）结合图象对简单实际问题中的函数关系进行分析。

（二）、一次函数（1）根据已知条件确定一次函数表达式。

（2）会画一次函数的图象。

（3）正比例函数概念、图象及解析式。

（4）利用一次函数的图象求一元一次方程、二元一次方程组的解。

七年级数学下册第九章不等式与不等式组笔记重点大全单选题1、已知关于x 的不等式组{−2x −3≥1x 4−1≥a−12无实数解，则a 的取值范围是（ ） A ．a ≥−52B ．a ≥−2C ．a >−52D ．a >−2 答案：D分析：首先解出两个不等式，根据题目该不等式组无实数解，那么两个解集没有公共部分，列出关于a 的不等式，即可求解．解：解不等式−2x −3≥1得，x ≤−2，解不等式x 4−1≥a−12得， x ≥2a +2，∵该不等式组无实数解，∴2a +2>−2，解得：a >−2，故选：D ．小提示：本题考查了不等式的解法和不等式组解集的确定，解题关键是熟练掌握不等式解集的确定，即“大大取大，小小取小，大小小大中间找，大大小小无解了”．2、不等式x −2≤3+x 3的非负整数解有（ ）A ．3个B ．4个C ．5个D ．无数个答案：C分析：求出不等式的解集，再根据非负整数解的条件求出特殊解．解：去分母得：3(x －2)≤x ＋3，去括号，得3 x -6≤x +3，移项、合并同类项，得2x ≤9，系数化为1，得x≤4.5，则满足不等式的“非负整数解”为：0，1，2，3，4，共5个，故选：C．小提示：本题考查解不等式，解题的关键是理解题中的“非负整数”．3、整数a使得关于x的不等式组{6−2x>02(x+a)≥x+3至少有4个整数解，且关于y的方程1﹣3（y﹣2）＝a有非负整数解，则满足条件的整数a的个数是（）A．6个B．5个C．3个D．2个答案：A分析：解不等式组中两个不等式得出3−2a≤x<3，结合其整数解的情况可得a≥2，再解方程得y=7−a3，由其解为非负数得出a≤7，最后根据方程的解必须为非负整数可得a的取值情况．解：解不等式6−2x>0，得：x<3，解不等式2(x+a)≥x+3，得：x≥3−2a，∵不等式组至少有4个整数解，∴3−2a≤−1，解得a≥2，解关于y的方程1−3(y−2)=a得y=7−a3，∵方程有非负整数解，∴7−a3≥0，则a≤7，所以2≤a≤7，其中能使7−a3为非负整数的有2，3，4，5，6，7，共6个，故选：A．小提示：本题主要考查一元一次不等式组的整数解，解题的关键在于正确解得不等式组或不等式的解集，然后再根据题目中对于解集的限制得到下一步所需要的条件，再根据得到的条件进而求得不等式组的整数解．4、已知x=m+15，y=5−2m，若m>−3，则x与y的关系为（）A ．x =yB ．x >yC ．x <yD ．不能确定答案：B分析：根据题意，直接利用作差法进行计算，得x −y =3m +10，比较3m +10与0的大小，即可得到答案． 解：∵x −y =m +15−(5−2m)=3m +10，∵m >−3，∴3m >−9．∴3m +10>1>0．∴x >y ．故选：B ．小提示：本题考查了有理数的比较大小，以及代数式的变形和不等式的解法，难度适中．解题的关键是熟练掌握作差法比较大小．5、若a 、b 是有理数，则下列说法中正确的是（ ）A ．若a >b 则a 2>b 2B ．若a 2>b 2则a >bC ．若|a|>|b|则a 2>b 2D ．若a ≠b 则a 2≠b 2答案：C分析：利用举反例的方法判断A,B,D, 利用不等式的性质判断C, 从而可得答案.解：当a =1,b =−8时满足a >b ，但a 2＜b 2，故A 不符合题意；当a =−4,b =2时满足a 2>b 2，但a ＜b ，故B 不符合题意；由|a|>|b|，利用不等式的性质可得a 2>b 2，故C 符合题意；当a =1,b =−1时满足a ≠b ，但a 2=b 2，故D 不符合题意；故选：C.小提示：本题考查的是不等式的基本性质，掌握“利用举反例的方法判断某说法是错误的”是解题的关键.6、若关于x 的方程3m(x ＋1)＋5＝m(3x －1)－5x 的解是负数，则m 的取值范围是( )A ．m ＞－54B ．m ＜－54C ．m ＞54D ．m ＜54解：去括号得，3mx+3m+5=3m−mx−5x，移项得，3mx+mx+5x=3m−3m−5，合并同类项得,(4m+5)x=−5，，系数化为1,得x=−54m+5∵方程3m(x+1)+1=m(3−x)−5x的解是负数，∴−5<0，4m+5∴4m+5>0，.解得m>−54故选A.小提示：先解方程，再根据解为负数，求得m的取值范围即可．7、设“●”“▲”“■”表示三种不同的物体，现用天平称了两次，情况如图所示，那么这三种物体的质量按从大到小的顺序排列应为( )A．■●▲B．●▲■C．■▲●D．▲■●答案：C依图①得：2■=■+▲，即■=▲，依图②得到●+●+●=▲+ ●，即●+●=▲，故有：■＞▲＞●．故选：C．点睛：本题考查一元一次不等式组的应用，将现实生活中的事件与数学知识联系起来，读懂题列出不等式关系式即可求解．=1的解是负数，则m的取值范围是（）8、已知关于x的分式方程m−2x+1A．m≤3B．m≤3且m≠2C．m＜3D．m＜3且m≠2答案：D分析：解方程得到方程的解，再根据解为负数得到关于m的不等式结合分式的分母不为零，即可求得m的取m−2=1，x+1解得：x=m﹣3，∵关于x的分式方程m−2=1的解是负数，x+1∴m﹣3＜0，解得：m＜3，当x=m﹣3=﹣1时，方程无解，则m≠2，故m的取值范围是：m＜3且m≠2，故选D．小提示：本题考查了分式方程的解，熟练掌握分式方程的解法以及分式方程的分母不为零是解题关键．9、下列数值“－2，0，1，2，4”中是不等式x+2≥4的解的有（）个．A．4B．3C．2D．1答案：C分析：求出不等式的解集再进行判断即可．解：解x+2≥4，得x≥2在－2，0，1，2，4中符合条件的有2和4共2个，故选：C小提示：本题考查了不等式的解集．解答此题关键是根据不等式的解集与各选项相比较看是否相符．的解集为x<3，那么m的取值范围是（）10、关于x的不等式组{3x−1>4(x−1)x<mA．m≥3B．m>3C．m<3D．m=3答案：A分析：先解出第一个不等式的解集，再由不等式组的解集为x<3，即可求解．解：{3x−1>4(x−1)①x<m②，解不等式①得：x<3，∵不等式组的解集为x<3，∴m≥3．故选：A小提示：本题主要考查了解一元一次不等式组，熟练掌握解不等式组解集的口诀：同大取大，同小取小大小小大中间找，大大小小找不到（无解）是解题的关键．填空题11、关于x的不等式组{2x+1>3a−x>1的解集为1＜x＜3，则a的值为____．答案：4解不等式2x+1＞3可得：x＞1，解不等式a-x＞1，可得：x＜a-1，然后根据不等式组的解集为：1＜x＜3，可知a-1=3，解得a=4.所以答案是：4.小提示：此题主要考查了不等式组的解，解题关键是根据不等式组的解集和求出不等式的解集的特点，求解即可.12、已知关于x的不等式2x−a>−3的解集如图所示则a的值为____________．答案：1分析：求出不等式的解集并与图示作比较，可以求得a的值．解：解2x−a>−3可得x>a−32，又由图示可知x>−1，两相比较可得a−3=−1，解得：2a=1．故答案为1．小提示：本题考查不等式的解集，熟练掌握不等式解集在数轴上的表示方法是解题关键．13、若(m−2)x2m−1−1>5是关于x的一元一次不等式，则m的值为______________．答案：1分析：根据一元一次不等式的定义可得：2m−1=1且m−2≠0，求解即可．解：根据一元一次不等式的定义可得：2m−1=1且m−2≠0解得m=1故答案为1小提示：此题考查了一元一次不等式的定义，解题的关键是掌握一元一次不等式的概念．14、某学校为落实“五项管理”工作，促进学生健康和全面发展，丰富学生的体育活动，准备从体育用品商店购买一些排球、足球和篮球，排球和足球的单价相同，买一个足球需要50元，买一个篮球需要80元．根据实际需要，该学校从体育用品商店一次性购买了三种球共100个，且购买三种球的总费用不超过6000元，则这所中学最多可购买篮球________个．答案：33分析：购买足球和篮球的总费用不超过6000元，列式求得解集后得到相应整数解，从而求解．解：设该中学购买篮球m个，根据题意得出：80m+50（100-m）≤6000，解得：m≤331，3∵m是整数，∴m≤33（m的最大整数解是33）．所以答案是：33．小提示：此题主要考查了一元一次不等式的应用；得到相应总费用的不等式是解决本题的关键．15、不等式组{2x−6<3x ﹐x+25−x−14 ⩾ 0的解集为________．答案：－6＜x≤13分析：根据不等式组分别求出x的取值，然后画出数轴，数轴上相交的点的集合就是该不等式的解集．若没有交集，则不等式无解．{2x−6<3x ﹐x+25−x−14 ⩾ 0，解得{x>−6x≤13在坐标轴上表示为：∴不等式组的解集为﹣6＜x≤13所以答案是：﹣6＜x≤13．小提示：本题考查了一元一次不等式组的解题问题，熟练掌握其解法及表示方法是解题的关键．解答题16、解下列不等式：（1）|x+2|−3>0（2）|3x−52|+5<7答案：（1）x<−5或x>1；（2）13<x<3分析：根据绝对值的意义，分类讨论，再解一元一次不等式不等式即可．（1）|x+2|−3>0当x≥−2时，则x+2−3>0，解得x>1，∴x>1，当x<−2时，则−x−2−3>0，解得x<−5，∴x<−5，综上，x<−5或x>1；（2）|3x−52|+5<7当3x−52≥0，即x ≥53时，3x−52+5<7，解得x <3，∴53≤x <3，当x <53时，则−3x−52+5<7，解得x >13， ∴13<x <53， 综上，13<x <3．小提示：本题考查了解一元一次不等式，根据绝对值的意义，分类讨论是解题的关键．17、（1）已知关于x 的不等式①x +a ＞7的解都能使不等式②x−2a 5＞1﹣a 成立，求a 的取值范围．（2）若关于x 、y 的二元一次方程组{2x +y =−3m +2x +2y =4的解满足x +y ＞﹣32，求出满足条件的m 的所有正整数值．答案：（1）a≥﹣1；（2）1，2，3分析：（1）分别取出求出不等式①②的解集，再根据题意得到7﹣a ≥5﹣3a ，最后解不等式即可求出a 的取值范围．（2）两个方程相加，即可得出关于m 的不等式，求出m 的范围，即可得出答案．解：（1）解不等式①x +a ＞7得：x ＞7﹣a解不等式②x−2a 5＞1﹣a 得：x ＞5﹣3a根据题意得，7﹣a ≥5﹣3a解得：a ≥﹣1．（2）{2x +y =−3m +2①x +2y =4②①+②得：3x +3y ＝﹣3m +6∴x +y ＝﹣m +2∵关于x 、y 的二元一次方程组{2x +y =−3m +2x +2y =4的解满足x +y ＞﹣32 ∴﹣m +2＞﹣32∴m ＜72∴满足条件的m 的所有正整数值是1，2，3．小提示：本题考查的是解一元一次不等式与一元一次不等式组，正确理解不等式组的解集是解此题的关键．18、某学校准备购买若干台A 型电脑和B 型打印机．如果购买1台A 型电脑，2台B 型打印机，一共需要花费5900元；如果购买2台A 型电脑，2台B 型打印机，一共需要花费9400元．（1）求每台A 型电脑和每台B 型打印机的价格分别是多少元？（2）如果学校购买A 型电脑和B 型打印机的预算费用不超过20000元，并且购买B 型打印机的台数要比购买A 型电脑的台数多1台，那么该学校至多能购买多少台B 型打印机？答案：（1）每台A 型3500元，每台B 型1200元；（2）5台．分析：（1）设每台A 型电脑的价格为x 元，每台B 型打印机的价格为y 元，根据“1台A型电脑的钱数+2台B 型打印机的钱数=5900，2台A 型电脑的钱数+2台B 型打印机的钱数=9400”列出二元一次方程组，解之可得，（2）设学校购买a 台B 型打印机，则购买A 型电脑为（a - 1）台，根据“（a -1）台A 型电脑的钱数+a 台B 型打印机的钱数≤20000”列出不等式，解之可得．解：（1）设每台A 型电脑的价格为x 元，每台B 型打印机的价格为y 元，根据题意，得：{x +2y =59002x +2y =9400， 解得：{x =3500y =1200， 答：每台A 型电脑的价格为3500元，每台B 型打印机的价格为1200元；（2）设学校购买a 台B 型打印机，则购买A 型电脑为（a ﹣1）台，根据题意，得：3500（a ﹣1）+1200a ≤20000，解得：a ≤5，答：该学校至多能购买5台B 型打印机．小提示：本题考查了一元一次不等式与二元一次方程组的应用，解题的关键是熟练的掌握一元一次不等式与二元一次方程组的应用．。

人教版初中数学第九章不等式与不等式组知识点编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（人教版初中数学第九章不等式与不等式组知识点）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为人教版初中数学第九章不等式与不等式组知识点的全部内容。

第九章 不等式与不等式组9.1 不等式9。

1。

1 不等式及其解集1．不等式：用符号“>"“〈”表示大小关系的式子，叫做不等式。

2．不等式的解集：对于一个含有未知数的不等式,它的所有解的集合叫做这个不等式的解的集合,简称这个不等式的解集。

3．解不等式:求不等式的解集的过程,叫做解不等式.例1．用不等式表示“7与m 的4倍的和是正数“就是 ．【答案】． 例2．“x 与y 的和大于1"用不等式表示为 ．【答案】x+y ＞1例3．用不等式表示x 与5的差不小于4： ．【答案】． 例4．把不等式≥在数轴上表示出来，正确的是（ ）【答案】C9。

1。

2 不等式的基本性质1．不等式两边都加上（或减去）同一个数或同一个整式，不等号的方向不变。

2．不等式两边都乘以（或除以)同一个正数，不等号的方向不变.3．不等式两边都乘以（或除以)同一个负数，不等号的方向改变。

例1．如果a ＞b,那么下列结论一定正确的是（ ）A ．a ﹣3＜b ﹣3B ．3﹣a ＜3﹣bC ．ac 2＞bc 2D ．a 2＞b 2解：∵a ＞b ，∴﹣a ＜﹣b ，∴3﹣a ＜3﹣b ；例2．如果a ＜b ，那么下列不等式成立的是( ）A ．－3a ＞－3bB ．a －3＞b －3C 。

D ．a －b ＞0 解：根据不等式的基本性质1可得,选项B 、D 错误；根据不等式的基本性质12可得,选项C740m +>45≥-x x1-1133a b >错误；根据不等式的基本性质3可得，选项A 正确。