解一元一次方程(讲义)(含答案)
- 格式:doc
- 大小:192.00 KB
- 文档页数:6

一元一次方程复习讲义1.方程的有关概念2.等式的基本性质3.解一元一次方程的基本步骤:4.应用一元一次方程解决实际问题的一般步骤(1)审 (2)找 (3)设 (4)列 (5)解 (6)验 (7)答1.下列方程是一元一次方程的有哪些? x+2y=9 x 2-3x=111=x x x 3121=- 2x=1 3x –5 3+7=10 x 2+x=12、解下列方程:⑴ 103.02.017.07.0=--x x ⑵16110312=+-+x x⑶03433221=-+++++x x x ⑷2362132432⎪⎭⎫ ⎝⎛+--=+--x x x x x(5)|5x 一2|=33、8=x 是方程a x x 2433+=- 的解,又是方程 ()[]b x b x x x +=⎥⎦⎤⎢⎣⎡---913131的解,求 b4、小张在解方程1523=-x a (x 为未知数)时,误将 - 2x 看成 2x 得到的解为3=x ,请你求出原来方程的解5、已知关于x 的方程 ()()x n x m 121232+=-+无穷多解,求m 、n1、(本题7分)按要求完成下面题目:323221+-=--x x x解:去分母,得424136+-=+-x x x ……① 即 8213+-=+-x x ……②移项,得 1823-=+-x x ……③合并同类项,得 7=-x ……④∴ 7-=x ……⑤上述解方程的过程中,是否有错误?答:__________;如果有错误,则错在__________步。
如果上述解方程有错误,请你给出正确的解题过程:2、(本题7分)请阅读下列材料:让我们来规定一种运算:bcad dc ba -=,例如:5432=2×5-3×4=10-12=-2. 按照这种运算的规定,若2121x x-=23,试用方程的知识求x 的值。
3、检修一处住宅区的自来水管,甲单独完成需要14天,乙单独完成需18天,丙单独完成需要12天。

第三章 一元一次方程(韩老师)本章知识网络结构图3.1一元一次方程的概念和性质【本讲主要内容】1. 等式与方程表示相等关系的式子叫做等式。
含有未知数的等式叫做方程。
可见方程必须具备两个条件:一是必须含有未知数,二是必须是一个等式。
2. 等式的性质等式的性质1:等式两边加(减)同一个数(式子)。
结果仍相等。
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
应用等式的性质对等式进行变形时,必须注意“同”字。
要对等式进行变形,就要保证等式两边始终相等,也就是说,运用等式的性质时,等式两边必须同时进行变形。
3. 一元一次方程的概念我们把含有一个未知数,并且未知数的指数都是1的方程叫做一元一次方程。
一元一次方程的最简形式是b ax =(≠a 0)。
方程中的未知数叫做“元”,一个方程中有几个未知数,就称这个方程为几元方程。
方程中含未知数的项的最高次数叫做方程的次数,这一点和多项式的次数有类似的地方。
例如27x 3-=-是一元一次方程,4y 4y 2y 2-=+是一元二次方程,0y x 3=-是二元一次方程,6y 4x 32-=+是二元二次方程。
4. 方程的解与解方程方程是一个有待研究的等式,即研究这个等式中的未知数取什么值时等式才成立。
解方程就是确定使方程中等号左右两边相等的未知数的值,我们把这样的未知数的值叫做方程的解。
这样的值可能有一个或多个,也可能没有,所以方程可能有一个解、多个解,也可能无解。
如方程3x-5=4x+3只有一个解x=-8。
方程2x-7=5x-(3x+7)有无数个解,而方程2x-3=2x+2无解。
求方程的解或判定方程无解的过程叫做解方程。
利用等式的性质,对方程进行一系列的变形,就可以求出方程的解。
5. 思想方法(本单元常用到的数学思想方法小结)⑴建模思想:通过对实际问题中的数量关系的分析,抽象成数学模型,建立一元一次方程的思想.⑵方程思想:用方程解决实际问题的思想就是方程思想.⑶化归思想:解一元一次方程的过程,实质上就是利用去分母、去括号、移项、合并同类项、未知数的系数化为1等各种同解变形,不断地用新的更简单的方程来代替原来的方程,最后逐步把方程转化为x=a 的形式. 体现了化“未知”为“已知”的化归思想.⑷数形结合思想:在列方程解决问题时,借助于线段示意图和图表等来分析数量关系,使问题中的数量关系很直观地展示出来,体现了数形结合的优越性.⑸分类思想:在解含字母系数的方程和含绝对值符号的方程过程中往往需要分类讨论,在解有关方案设计的实际问题的过程中往往也要注意分类思想在过程中的运用.【典型例题】例1. 已知方程2x m -3+3x=5是一元一次方程,则m= .解析:由一元一次方程的定义可知m -3=1,解得m=4.或m -3=0,解得m=3所以m=4或m=3警示:很多同学做到这种题型时就想到指数是1,从而写成m=1,这里一定要注意x 的指数是(m -3).例2. 已知2x =-是方程ax 2-(2a -3)x+5=0的解,求a 的值.解析:∵x=-2是方程ax 2-(2a -3)x+5=0的解∴将x=-2代入方程,得 a·(-2)2-(2a -3)·(-2)+5=0化简,得 4a+4a -6+5=0∴ a=81 点拨:要想解决这道题目,应该从方程的解的定义入手,方程的解就是使方程左右两边值相等的未知数的值,这样把x=-2代入方程,然后再解关于a 的一元一次方程就可以例3.已知a 、b 为定值,无论k 为何值,关于x 的一元一次方程26bk x 3a kx 3=--+的解总是1,试求a 、b 的值。

1x3x基础训练内容提要考法.利用特殊解求字母的值2. 解下列方程:(1)2(x﹣2)﹣3(4x﹣1)=9(1﹣x); (2)2.3.解下列方程:(1)1 (2)31.[单选题] 解方程3时,去分母正确的是( )A.2(2x﹣1)﹣10x﹣1=3 B.2(2x﹣1)﹣10x+1=3 C.2(2x﹣1)﹣10x﹣1=12 D.2(2x﹣1)﹣10x+1=122.[单选题]把方程0.5的分母化为整数,正确的是( )A . 0.5 B . 0.5 C . 0.5 D .0.53.解方程:(1)7x+2(3x﹣3)=29 (2)(3)例题基础训练1.若方程3(x+1)=2+x的解与关于x的方程2(x+3)的解互为倒数,求k的值.2.小明在解方程1,方程两边都乘以各分母的最小公倍数去分母时,漏乘了不含分母的项﹣1,得到方程的解是x=3,请你帮助小明求出m的值和原方程正确的解.3. 已知:方程(m+2)x﹣m=0①是关于x的一元一次方程.(1)求m的值;(2)若上述方程①的解与关于x的方程x3x②的解互为相反数,求a的值.|m|﹣11.(2020·越秀区)已知关于x的方程2(x﹣1)﹣6=0与的解互为相反数,则a=.2.小明解方程1时,由于粗心大意,在去分母时,方程左边的1没有乘以10,由此得到方程的解为x=﹣1,试求a的值,并正确地求出原方程的解.内容提要考法.方程的解的讨论例题3.小明的练习册上有一道方程题,其中一个数字被墨汁污染了,成为1,他翻看了书后的答案,知道了这个方程的解是4,于是他把被污染了的数字求出来了,请你把小明的计算过程写出来.1.[单选题]有下列结论:①若a+b+c =0,则abc≠0;②若a (x ﹣1)=b (x ﹣1)有唯一的解,则a≠b ;③若b =2a ,则关于x 的方程ax+b =0(a≠0)的解为x;④若a+b+c =1,且a≠0,则x =1一定是方程ax+b+c =1的解;其中结论正确的个数有( )A .4个 B .3个 C .2个 D .1个2.[单选题]若关于x 的方程有无数解,则3m+n 的值为( )A .﹣1 B .1 C .2 D .以上答案都不对3. 解关于x 的方程:a (x ﹣1)=2(x+2)基础训练内容提要考法.新定义运算例题基础训练1.[单选题]如果关于x 的方程(a﹣3)x=2019有解那么实数a的取值范围是()A.a<3B.a=3C.a>3D.a≠32.[单选题] 已知关于x的方程•a(x﹣6)无解,则a的值是( )A.1 B.﹣1 C.±1 D.a≠13.[单选题]已知方程2x+k=6的解为正整数,则k所能取的正整数值为( )A.1 B.2 或 3 C.3 D.2 或 41.[单选题]对任意四个有理数a,b,c,d定义新运算:,已知18,则x=( )A.﹣1 B.2 C.3 D.42. 用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab﹣2ab+b.如:2☆(﹣3)=2×(﹣3)﹣2×2×(﹣3)+(﹣3)=27(1)求(﹣4)☆7的值;(2)若(1﹣3x)☆(﹣4)=32,求x的值.221. 用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab﹣2ab+a.如:1☆3=1×3﹣2×1×3+1=4.(1)求(﹣2)☆5的值;22模块二含绝对值的一元一次方程内容提要最简绝对值方程(2)若☆3=8,求a 的值;(3)若m =4☆x ,n =(1﹣2x )☆3(其中x 为有理数),试比较大小m n (用不等号填空).2. 设x 、y 是任意两个有理数,规定x 与y 之间的一种运算“⊕”为:若对任意有理数x 、y ,运算“⊕”满足x ⊕y =y ⊕x ,则称此运算具有交换律.x ⊕y (1)试求1⊕(﹣1)的值;(2)试判断该运算“⊕”是否具有交换律,说明你的理由;(3)若2⊕x =0,求x 的值.3. 我们规定,若关于x 的一元一次方程ax =b 的解为x =b ﹣a ,则称该方程为“奇异方程”.例如:2x =4的解为x =2=4﹣2,则该方程2x =4是“奇异方程”.请根据上述规定解答下列问题:(Ⅰ)判断方程5x =﹣8 (回答“是”或“不是”)“奇异方程”;(Ⅱ)若a =3,有符合要求的“奇异方程”吗?若有,求b 的值;若没有,请说明理由.(Ⅲ)若关于x 的一元一次方程2x =mn+m 和﹣2x =mn+n 都是“奇异方程”,求代数式﹣2(m+11)+4n+3[(mn+m )﹣m] 的值.2例题基础训练1.(1)解方程:|3x+1|﹣5=0.(2)若方程|x﹣1|=m﹣1有解,则m应满足的条件是 .2.解方程: |x﹣2|=|﹣3|.3.解方程:|3x﹣2|=x 4.解方程:3+|2x﹣1|=x1.[单选题] 方程|2x+1|=5的解是( )A.2 B.﹣3 C.±2 D.2或﹣3 内容提要考法.含多个绝对值的方程例题2.[单选题]若关于x的方程a﹣|x|=0有两个解,b﹣|x|=0只有一个解,c﹣|x|=0无解,则a、b、c的关系是( )A.a<b<c B.a<c<b C.b<c<a D.c<b<a 3.方程|5x+6|=6x﹣5的解是 . 4.解方程:(1)|3x﹣2|﹣4=0.(2)当b为何值时,关于x的方程|x﹣2|=b+1,(1)无解;(2)只有一个解;(3)有两个解. 1.解方程:|x﹣2|+|x﹣1|=5.2.解方程|x﹣4|+|x+3|=7.基础训练3.解方程:|2x+1|=|x ﹣3| 4.解绝对值方程:|x ﹣1|﹣|x ﹣2|=x ﹣3. 1.(1)解方程:|2x+3|=8.(2)解方程:|2x+3|﹣|x ﹣1|=1.2.解方程:|x ﹣2|+|x+3|=6 3.解方程:|x ﹣3|﹣3|x+2|=x ﹣9.内容提要考法.含多重绝对值的方程例题4.解方程:|2x ﹣3|=|1﹣3x| 5.解方程:3|x ﹣1|﹣|x+1|=2|x ﹣2|.1. 解方程:||x|﹣4|=52.求方程|x ﹣|2x+1||=3的不同的解的个数.3.设a ,b 为有理数,且|a|>0,方程||x ﹣a|﹣b|=5,恰好有两个不相等的根,求b 的取值范围.基础训练模块三含参数的一元一次方程内容提要考法1.解含字母系数的方程例题1. 解方程:|x ﹣|3x+1||=4. 2.求关于x 的方程||x ﹣2|﹣1|﹣a =0(0<a <1)的所有解的和. 3.设a 、b 为实数,且a≠0,方程||x+a|+2b|=4,恰有三个不相等的解,求b 的值.4.已知关于x 的方程||x ﹣200|﹣250|=a 有三个解,求a 的值.1.解关于x 的方程:2(x ﹣1)=3m ﹣1. 2.已知关于x 的方程5m+3x =1+x 的解比关于x 的方程2x+m =3m 的解大2,求7m ﹣1的值.2基础训练内容提要考法2.方程的整数解3.已知关于x的方程m4的解是关于x 的方程的解的2倍,求m的值.1.解关于x的方程:5m+12x2.[单选题] 若关于x的方程2x+a=3与x+2a=7的解相同,则a的值为( )A . B . C . D.3.若关于x的方程x+m﹣3=0和2m=2x﹣1的解的和为4,求m的值. 4.当k为何值时,关于x的方程3(2x﹣1)=k+2x的解与关于x的方程8﹣k=2(x+1)的解互为相反数.例题基础训练1.[单选题] 已知关于x 的方程x﹣a=3x﹣14,若a为正整数时,方程的解也为正整数,则a的最大值是( )A.12 B.13 C.14 D.152.[单选题]已知关于x方程x1的解是非正整数,则符合条件的所有整数a的和是( )A.﹣4 B.﹣3 C.2 D.33.[单选题]若关于x的方程(k﹣2020)x﹣2019=7﹣2020(x+1)的解是整数,则整数k的取值个数是( )A.6 B.8 C.9 D.101. 已知关于x的方程kx=9﹣x的解为自然数,求整数k的值.2.已知k位非负整数,且关于x的方程3(x﹣3)=kx的解为正整数,求k的所有可能取值.3.若关于x的方程mx=2﹣x的解为整数,且m为负整数,求代数式5m﹣[m﹣(6m﹣5m)﹣2(m﹣3m)]的值. 2222内容提要考法3.含参数的一元一次方程的讨论例题基础训练4.已知a 为整数,关于x 的一元一次方程的解也为整数,求所有满足条件的数a 的和.1. 已知kx ﹣m =(2k ﹣1)x+4是关于x 的一元一次方程,当k ,m 为何值时:(1)方程只有一个解;(2)方程无解;(3)方程有无数个解.2.已知关于x 的方程m (x ﹣1)=5x ﹣2有唯一解,求m 的值. 1.已知关于x 的方程2kx+m =x+4.当k 、m 为何值时:(1)方程有唯一解;模块四自定义新一元一次方程内容提要自定义新一元一次方程例题(2)方程有无数个解;(3)方程无解.2. 当a取何值时,关于x的方程6(ax﹣2)﹣(x+1)=4(x)(1)有唯一解;(2)没有解. 3.已知方程(x+1)+1ax有无数个解,求a、b的值. 4.已知关于x的方程a(3x﹣2)+b(2x﹣3)=8x﹣7.(1)若b=1,a≠2时,求方程的解;(2)当a,b满足什么条件时,方程有无数个解?5.若关于x的一元一次方程(5a+3b)x+ax+b=0有唯一解,则x= .21. 定义:对于一个有理数x,我们把[x]称作x的对称数.若x≥0,则[x]=x﹣2;若x<0,则[x]=x+2.例:[1]=1﹣2=﹣1,[﹣2]=﹣2+2=0.(1)求[],[﹣1]的值;(2)已知有理数a>0,b<0,且满足[a]=[b],试求代数式(b﹣a)﹣2a+2b的值;(3)解方程:[2x]+[x+1]=1.32.我们称使方程成立的一对数x ,y 为“相伴数对”,记为(x .y ).(1)若(4,y )是“相伴数对”,求y 的值;(2)若(a ,b )是“相伴数对”,请用含b 的代数式表示a ;(3)若(m ,n )是“相伴数对”,求代数式m n ﹣[4m ﹣2(3n ﹣1)]的值.3.已知f (x )是关于字母x 的多项式f (x )=a x +a x +……+a x +a x+c (其中a ,a ,…,a 是各项的系数,c 是常数项);我们规定f (x )的伴随多项式是g (x ),且g (x )=na x +(n ﹣1)a x +……+2a x+a .如f (x )=4x ﹣3x +5x ﹣8,则它的伴随多项式g (x )=3×4x ﹣2×3x+1×5=12x ﹣6x+5请根据上面的材料,完成下列问题:(1)已知f (x )=x ,则它的伴随多项式g (x )= ;(2)已知f (x )=3x ﹣2(7x ﹣1),则它的伴随多项式g (x )= ;若g (x )=10,求x 的值.(3)已知二次多项式f (x )=(a ﹣3)x ﹣8x+7,并且它的伴随多项式是g (x ),若关于x 的方程g (x )=﹣2x 有正整数解,求a 的整数值.1n 2n ﹣1n ﹣12n 12n 1n ﹣12n ﹣2n ﹣1n 32222224.若x 是关于x 的方程ax+b =0(a≠0)的解,y 是关于y 的方程cy+d =0(c≠0)的解,且x ,y 是满足|x ﹣y |≤1,则称方程ax+b =0(a≠0)与方程cy+d =0(c≠0)的解接近.例如:方程4x+2x ﹣6=0的解是x =1,方程3y ﹣y =3的解是y =1.5,因为x ﹣y =0.5<1,方程4x+2x ﹣6=0与方程3y ﹣y =3的解接近.(1)请直接判断方程3x ﹣3+4(x ﹣1)=0与方程﹣2y ﹣y =3的解是否接近;(2)若关于x 的方程3x ﹣3+4(x ﹣1)=0与关于y 的方程y =2k+1的解接近,请你求出k 的最大值和0000000000自主评价自主探究自主探究题目最小值;(3)请判断关于x的方程x﹣m=2x﹣5与关于y的方程y+7×2018﹣1=4036y+2018m的解是否接近,并说明理由. 1.[单选题]若方程2x+1=﹣2与关于x的方程1﹣2(x﹣a)=2的解相同,则a的值是()A.1B.﹣1C.﹣2D.2.[单选题]关于x的方程﹣4+ax=3x+b有无数个解,则a、b的值分别是( )A.﹣3;4 B.0;0 C.3;﹣4 D.3;43.[单选题]当a取什么范围时,关于x的方程|x﹣4|+2|x﹣2|+|x﹣1|+|x|=a总有解( )A.a≥4.5 B.a≥5 C.a≥5.5 D .a≥64.解方程:(1)4x﹣3=12﹣x;(2)+1=.5.已知方程5x﹣3=2x与方程4x=6的解互为相反数,求(1k)的值.56.已知关于x的方程ax+6=5x﹣b有无数个解,试求a+b的值.27.(2019·花都区)已知两个方程3x+2=﹣4与3y﹣3=2m﹣1的解x、y互为相反数,求m的值.8. 解关于x的方程:a(x﹣5)=x+19. 一般的,数a的绝对值|a|表示数a对应的点与原点的距离.同理,绝对值|a﹣b|表示数轴上数a对应的点与数b对应的点的距离.例如:|3﹣0|指在数轴上表示数3的点与原点的距离,所以3的绝对值是3,即|3﹣0|=|3|=3.|6﹣2|指数轴上表示6的点和表示2的点的距离,所以数轴上表示6的点和表示2的点的距离是4,即|6﹣2|=4.结合数轴与绝对值的知识,求含绝对值的方程的整数解.10.已知关于x的方程的解是正整数,求正整数a的值.参考答案模块一解一元一次方程例题1.解:(1)移项得:x﹣4x=27+9,合并同类项得:﹣3x=36,系数化为1得:x=﹣12,(2)方程两边同时乘以2得:2﹣3x=6x+5,移项得:﹣3x﹣6x=5﹣2,合并同类项得:﹣9x=3,系数化为1得:x,解析:2.解:(1)去括号得:2x﹣4﹣12x+3=9﹣9x,移项得:2x﹣12x+9x=9+4﹣3,合并同类项得:﹣x=10,系数化为1得:x=﹣10,(2)去分母得:2(2x﹣1)﹣(5x+2)=3(1﹣2x)﹣12,去括号得:4x﹣2﹣5x﹣2=3﹣6x﹣12,移项得:4x﹣5x+6x=3﹣12+2+2,合并同类项得:5x=﹣5,系数化为1得:x=﹣1.解析:3.解:(1)方程整理得: 1,去分母得:50x﹣10﹣37x﹣100=20,移项合并得:13x=130,解得:x=10.(2)方程整理得: 3,即5y﹣10﹣2y﹣2=3,移项合并得:3y=15,解得:y=5.解析:基础训练基础训练题目1.C解析:2.C解析:3.解:(1)去括号得:7x+6x﹣6=29,移项合并得:13x=35,解得:x ;(2)去分母得:3(x ﹣2)﹣2(2x ﹣1)=12,去括号得:3x ﹣6﹣4x+2=12,解得:x =﹣16;(3)方程整理得: 1,去分母得:30x ﹣7(17﹣20x )=21,去括号得:30x ﹣119+140x =21,移项合并得:170x =140,解得:x.解析:例题1.解:解3(x+1)=2+x ,得x,∵两方程的解互为倒数,∴将x =﹣2代入2(x+3)得2,解得k =0.解析:2.解:根据题意,x =3是方程4(2x ﹣1)=3(x+m )﹣1的解,将x =3代入得4×(2×3﹣1)=3(3+m )﹣1,解得m =4,所以原方程为1,解方程得x.解析:3.解:(1)∵方程(m+2)x ﹣m =0①是关于x 的一元一次方程,∴|m|﹣1=1,且m+2≠0,解得m =2.(2)当m =2时,原方程变形为4x ﹣2=0,解得x,∵方程①的解与关于x 的方程x3x ②的解互为相反数,∴方程②的解为x.方程x 3x 去分母得:6x+2(6x ﹣a )=a ﹣18x 去括号得:6x+12x ﹣2a =a ﹣18x ,移项、合并同类项得:3a =36x ,∴a =12x =12×()=﹣6.解析:基础训练基础训练题目|m|﹣11.﹣.解析:解:解方程2(x﹣1)﹣6=0得:x=4,解方程得:x=3a﹣3,∵两个方程的解互为相反数,∴4+(3a﹣3)=0,解得:a=﹣,故答案为:﹣.2.解:按方程左边的1没有乘以10,去分母得:2(2x﹣6)+1=5(x+a),把x=﹣1代入得:2×(﹣8)+1=﹣5+5a,解得:a=﹣2,把a=﹣2代入原方程,得1,去分母得:2(2x﹣6)+10=5(x﹣2),去括号得:4x﹣12+10=5x﹣10,移项合并得:﹣x=﹣8,解得:x=8,答:a的值是﹣2,原方程的解为x=8.解析:3.解:设被墨汁污染的数字为y,原方程可整理得:1,把x=4代入得:1,解得:y=﹣12,即被污染了的数字为﹣12.解析:例题1.C解析:解:①错误,当a=0,b=1,c=﹣1时,a+b+c=0+1﹣1=0,但是abc=0;②正确,方程整理得:(a﹣b)x=a﹣b,由方程有唯一解,得到a﹣b≠0,即a≠b,此时解为x=1;③错误,由a≠0,b=2a,方程解得:x2;④正确,把x=1,a+b+c=1代入方程左边得:a+b+c=1,右边=1,故若a+b+c=1,且a≠0,则x=1一定是方程ax+b+c=1的解,故选:C.2.A解析:解:mx x,移项得:mx+x,合并同类项得:(m+1)x,∵该方程有无数解,∴,解得:,把m=﹣1,n=2代入3m+n得:原式=﹣3+2=﹣1,故选:A.3.解:a(x﹣1)=2(x+2),ax﹣a=2x+4,ax﹣2x=4+a,(a﹣2)x=4+a,当a﹣2≠0时,x,当a﹣2=0时,方程无解.解析:基础训练基础训练题目1.D解析:解:∵关于x的方程(a﹣3)x=2019有解,∴a﹣3≠0,即a≠3,故选:D.2.A解析:解:去分母得:2ax=3x﹣(x﹣6),去括号得:2ax=2x+6移项,合并得,x,因为无解;所以a﹣1=0,即a=1.故选:A.3.D解析:解:2x+k=6,移项得:2x=6﹣k,系数化为1得:x,∵方程2x+k=6的解为正整数,∴6﹣k为2的正整数倍,6﹣k=2,6﹣k=4,6﹣k=6,6﹣k=8…,解得:k=4,k=2,k=0,k=﹣2…,故选:D.例题1.C解析:解:∵,∴2x+4x=18,即:x=3,故选:C.2.解:(1)根据题意得:(﹣4)☆7=(﹣4)×7﹣2×(﹣4)×7+7=﹣133,(2)根据题意得:(1﹣3x)☆(﹣4)=(1﹣3x)×(﹣4)﹣2×(1﹣3x)×(﹣4)+(﹣4)=32,整理得:16(1﹣3x)+8(1﹣3x)﹣4=32,解得:x.解析:基础训练基础训练题目1.解:(1)(﹣2)☆5=(﹣2)×5﹣2×(﹣2)×5+(﹣2)=﹣50+20﹣2=﹣32;(2)☆3=8,3﹣238,9(a+1)﹣6(a+1)+a+1=16,9a+9﹣6a﹣6+a+1=16,4a=12,a=3;(3)∵m=4☆x=4•x﹣2×4x+4=4x﹣8x+4,n=(1﹣2x)☆3=(1﹣2x)•3﹣2(1﹣2x)•3+1﹣2x=﹣8x+4,2222222m ﹣n =4x ≥0,∴m≥n ,故答案为:≥.解析:2.解:(1)1⊕(﹣1)=2×1+3×(﹣1)﹣7=2﹣3﹣7=﹣8答:1⊕(﹣1)的值为﹣8.(2)该运算具有交换律理由:分三种情况当x >y 时,x ⊕y =2x+3y ﹣7,y ⊕x =3y+2x ﹣7,此时x ⊕y =y ⊕x当x =y 时,x ⊕y =2x+3y ﹣7,y ⊕x =2y+3x ﹣7,此时x ⊕y =y ⊕x当x <y 时,x ⊕y =3x+2y ﹣7,y ⊕x =2y+3x ﹣7,此时x ⊕y =y ⊕x所以该运算“⊕”具有交换律(3)当x≤2时,2⊕x =0,2×2+3x ﹣7=0解得x =1当x >2时,2⊕x =03×2+2x ﹣7=0解得x (舍去)答:x 的值为1.解析:3.解:(Ⅰ):∵5x =﹣8,∴x ,∵﹣8﹣5=﹣13,,∴5x =﹣8不是奇异方程;故答案为:不是;(Ⅱ)∵a =3,∴x =b ﹣3,∴,∴,即b 时有符合要求的“奇异方程”;(Ⅲ)且由题可知:mn+m =4,mn+n,两式相减得,m ﹣n ,∴﹣2(m+11)+4n+3[(mn+m )﹣m] 22=﹣5(m ﹣n )﹣22+3(mn+m)(mn+n ),,.解析:模块二含绝对值的一元一次方程例题1.解:(1)原方程化为|3x+1|=5,当3x+1≥0时,方程可化为3x+1=5,解得:x ,当3x+1≤0时,方程可化为3x+1=﹣5,解得:x =﹣2,所以原方程的解是x 或x =﹣2,(2)∵方程|x ﹣1|=m ﹣1有解,∴m ﹣1≥0,解得:m≥1,解析:2.解:∵|x ﹣2|=3,∴x ﹣2=3或x ﹣2=﹣3,∴x =10或x =﹣2.解析:3.解:(1)|3x ﹣2|=x ,∴3x ﹣2=x 或3x ﹣2=﹣x ,∴x =1或x;解析:4.解:当x时,原方程等价于3+1﹣2x =x ,解得x (不符合题意要舍去),当x 时,原方程等价于3+2x ﹣1=x ,解得x =﹣2(不符合题意要舍去)综上所述,原方程无解.解析:基础训练基础训练题目1.D解析:解:根据题意,原方程可化为:2x+1=5或2x+1=﹣5,解得x =2或x =﹣3,故选:D .2.D22解析:解:∵关于x的方程a﹣|x|=0有两个解,∴a>0,∵b﹣|x|=0只有一个解,∴b=0,∵c﹣|x|=0无解,∴c<0,则a、b、c的关系是c<b<a.故选:D.3.x=11解析:解:∵|5x+6|=6x﹣5,∴5x+6=±(6x﹣5),解得,x=11或(舍去).故答案为:x=11.4.解:①当3x﹣2≥0时,原方程可化为:3x﹣2=4,解得x=2;当3x﹣2<0时,原方程可化为:3x﹣2=﹣4,解得x.所以原方程的解是x=2或x;②∵|x﹣2|≥0,∴当b+1<0,即b<﹣1时,方程无解;当b+1=0,即b=﹣1时,方程只有一个解;当b+1>0,即b>﹣1时,方程有两个解解析:例题1.|x﹣2|+|x﹣1|=5,①当x﹣2≥0,即x≥2时,原方程可化为x﹣2+x﹣1=5,它的解是x=4;②当x﹣1≤0,即x≤1时,原方程可化为2﹣x+1﹣x=5,它的解是x=﹣1;③当1<x<2时,原方程可化为2﹣x+x﹣1=5,此时方程无解;∴原方程的解为x=4和﹣1.解析:2.解:(1)当x<﹣3时,原方程可化为:﹣(x﹣4)﹣(x+3)=7解得:x=﹣3,与题意不符,故舍去.(2)当﹣3≤x≤4时,原方程可化为:﹣(x﹣4)+x+3=7即7=7所以﹣3≤x≤4(3)当x>4时,原方程可化为x﹣4+x+3=7,x=4与题意不符,故舍去.故原方程的解是﹣3≤x≤4.解析:3.解:当x时,原方程等价于﹣1﹣2x=3﹣x,解得x=﹣4;当x<3时,原方程等价于1+2x=3﹣x,解得x;当x≥3时,原方程等价于1+2x=x﹣3,解得x=﹣4(不符合题意要舍去),综上所述:x=﹣4或x;解析:4.解:当x<1时,原方程等价于1﹣x﹣(2﹣x)=x﹣3.解得x=2(不符合范围,舍);当1≤x<2时,原方程等价于x﹣1﹣(2﹣x)=x﹣3.解得x=0(不符合范围,舍);当x≥2时,原方程等价于x﹣1﹣(x﹣2)=x﹣3.解得x=4,综上所述:x=4.解析:基础训练基础训练题目1.解:(1)当x时,原方程等价于2x+3=﹣8,解得x;当x时,原方程等价于2x+3=8,解得x;综上所述,方程|2x+3|=8的解为x或x.(2)当x时,原方程等价于﹣x﹣4=1,解得x=﹣5;当x<1时,原方程等价于3x+2=1,解得x;当x≥1时,原方程等价于x+4=1,解得x=﹣3,(不符合题意,舍);综上所述,方程:|2x+3|﹣|x﹣1|=1的解为x=﹣5或x.解析:2.当x≥2时,|x﹣2|+|x+3|=2x+1=6,∴x=2.5;当﹣3<x<2时,|x﹣2|+|x+3|=2﹣x+x+3=5,不成立;当x≤﹣3时,|x﹣2|+|x+3|=﹣2x﹣1=6,∴x=﹣3.5;综上所述,|x﹣2|+|x+3|=6的解有两个:x=2.5或-3.5解析:3.解:①当x<﹣2时,原方程等价于3﹣x+3(x+2)=x﹣9,解得x=﹣18,符合x<﹣2,②当﹣2≤x<3,时,原方程等价于价于3﹣x﹣3(x+2)=x﹣9,解得x,符合﹣2≤x<3,③当x≥3时,原方程等价于x﹣3﹣3(x+2)=x﹣9,解得x=0,不符合x≥3,∴原方程的解为:x=﹣18,x.解析:4.解:根据题意得:2x﹣3=1﹣3x或2x﹣3=3x﹣1,解得:x或x=﹣2,即原方程的解为:x,x=﹣2,解析:5.解:当x<﹣1时,得:﹣3(x﹣1)+(x+1)=﹣2(x﹣2)解得:恒成立,∴x<﹣1当﹣1≤x≤1时得:﹣3(x﹣1)﹣(x+1)=﹣2(x﹣2)解得x=﹣1当1<x≤2时得:3(x﹣1)﹣(x+1)=﹣2(x﹣2)解得x=2当x>2时得:3(x﹣1)﹣(x+1)=2(x﹣2)解得:恒成立,则x>2.综上所述:x≤﹣1或x≥2.解析:例题1.解:||x|﹣4|=5,∴|x|﹣4=5或|x|﹣4=﹣5,∴|x|=9或|x|=﹣1(舍去),∴x=9或x=﹣9;解析:2.解:|x﹣|2x+1||=3,当x时,原方程化为|x|=3,无解;当x时,原方程化为:|1+x|=3,解得:x=2或x=﹣4(舍去).当x时,原方程可化为:|x+(2x+1)|=3,12即|3x+1|=3,∴3x+1=±3,解得:x(舍去)或x.综上可得方程的解只有x=2或x两个解.解析:3.解:∵方程||x﹣a|﹣b|=5有两个不相等的解,∴方程|x﹣a|﹣b=±5,即|x﹣a|=b±5,(1)当b=﹣5时,即|x﹣a|=0或|x﹣a|=﹣10①|x﹣a|=0时,方程有一个解;②|x﹣a|=﹣10,此时方程无解.所以当b=﹣5时,方程只有一个解;(2)当﹣5<b<5时,即b+5>0,b﹣5<0①b+5>0时,方程有两个不相等解,②b﹣5<0时,方程无解.所以当﹣5<b<5时,方程有两个不相等解;(3)当b=5时,即|x﹣a|=0或|x﹣a|=10①|x﹣a|=0时,方程有一个解;②|x﹣a|=10,此时方程有两个不相等解.所以当b=5时,方程有三个解;(4)当b>5时,即b±5>0①b+5>0时,方程有两个不相等解,②b﹣5>0时,方程有两个不相等解.所以当b>5时,方程有四个不相等解.故答案为:﹣5<b<5.解析:基础训练基础训练题目1.解:原方程式化为x﹣|3x+1|=4或x﹣|3x+1|=﹣4(1)当3x+1>0时,即x,由x﹣|3x+1|=4得x﹣3x﹣1=4∴x与x不相符,故舍去由x﹣|3x+1|=﹣4得x﹣3x﹣1=﹣4∴x(2)当3x+1<0时,即x,由x ﹣|3x+1|=4得x+3x+1=4∴x 与x 不相符,故舍去由x ﹣|3x+1|=﹣4得x+3x+1=﹣4∴x 故原方程的解是x 或x 解析:2.解:由原方程得||x ﹣2|﹣1|=a ,∴|x ﹣2|﹣1=±a ,∵0<a <1,∴|x ﹣2|=1±a ,即x ﹣2=±(1±a ),∴x =2±(1±a ),从而x =3+a ,x =3﹣a ,x =1+a ,x =1﹣a ,∴x +x +x +x =8,即原方程所有解的和为8.解析:3.解:∵方程||x+a|+2b|=4,∴|x+a|=4﹣2b 或﹣4﹣2b ,∵有三个不相等的解,∴4﹣2b 与﹣4﹣2b ,其中一个为0,则得3个解,如果都不是零,则得4个解,故b =2或﹣2.经检验,b =2不合题意舍弃,∴b =﹣2故答案为﹣2.解析:4.解:根据题意得:a≥0,|x ﹣200|﹣250=±a ,|x ﹣200|=250±a ,x ﹣200=±(250±a ),x =200±(250±a ),所以x =450+a ,x =﹣50﹣a ,x =450﹣a ,x =﹣50+a ,则有两个相等,12341234显然450+a=﹣50+a,﹣50﹣a=450﹣a不成立,若450+a=﹣50﹣a,解得:a=﹣250,(舍去),若450+a=450﹣a,解得:a=0,x=450,x=﹣50,(舍去),若﹣50+a=﹣50﹣a,解得:a=0,x=450,x=﹣50,(舍去),若450﹣a=﹣50+a,解得:a=250,x=700,x=﹣300,x=200,(符合题意),故答案为:a=250.解析:模块三含参数的一元一次方程例题1.解:2x﹣2=3m﹣1 2x=3m+1解析:2.解:解方程5m+3x=1+x得x,解方程2x+m=3m得x=m,由题意知m=2,解得:m,则7m﹣1=7×()﹣1=711.解析:3.解:解方程m4得:x=12﹣3m ,解方程1得:x=6﹣m,根据题意得:222(6﹣m)=12﹣3m,解得:m=0.解析:基础训练基础训练题目1.解:去分母:10m+24x=2x+1 22x=1-10m解析:2.B解析:3.解:方程x+m﹣3=0的解为x=3﹣m,方程2m=2x﹣1解为:x(2m+1),根据题意得:3﹣m(2m+1)=4,去分母得:9﹣3m+4m+2=12,移项合并得:m=1解析:4.解:方程3(2x﹣1)=k+2x,解得:x,方程8﹣k=2(x+1),解得:x,根据题意得: 0,解得:k=15.解析:例题1.B解析:解:方程移项合并得: x=a﹣14,去分母得:﹣x=2a﹣28,解得:x=28﹣2a,∵方程的解x是正整数,∴28﹣2a>0,∴a<14则a的最大值为13,故选:B.2.A解析:解:x1,6x﹣(4﹣ax)=2(x+a)﹣66x﹣4+ax=2x+2a﹣66x+ax﹣2x=2a﹣6+4(a+4)x=2a﹣2x,∵方程的解是非正整数,∴0,解得:﹣4<a≤1,当a=﹣3时,x=﹣8;当a=﹣2时,x=﹣3;当a=﹣1时,x(舍去);当a=0时,x(舍去);当a=1时,x=0;则符合条件的所有整数a的和是﹣3﹣2+1=﹣4.故选:A.3.B解析:解:方程整理得:kx﹣2020x﹣2019=7﹣2020x﹣2020,移项合并得:kx=6,解得:x,由x为整数,得到k=±1,±2,±3,±6,共8个,故选:B.基础训练基础训练题目1.解:移项,得kx+x=9,合并,得(k+1)x=9,当k+1≠0时,x∵关于x的方程的解为自然数,∴9能被k+1整除.∴k+1=1、3、9,即k=0、2、8时,关于x的方程的解为自然数.解析:2.解:方程去括号得:3x﹣9=kx,移项合并得:(3﹣k)x=9,解得:x ,由x 为正整数,得到k =2,0解析:3.解:解方程mx =2﹣x 得:x ,∵关于x 的方程mx =2﹣x 的解为整数,且m 为负整数,∴1+m =±2或±1,解得:m =1或﹣3或0或﹣2,其中m =1和m =0舍去(不是负整数),即m =﹣3或﹣2;5m ﹣[m ﹣(6m ﹣5m )﹣2(m ﹣3m )]=5m ﹣[m ﹣6m+5m ﹣2m +6m]=5m ﹣m +6m ﹣5m +2m ﹣6m=m ,当m =﹣2时,原式=(﹣2)=4;当m =﹣3时,原式=(﹣3)=9,所以代数式5m ﹣[m ﹣(6m ﹣5m )﹣2(m ﹣3m )]的值是4或9.解析:4.解:∵,∴(6﹣a )x =6,∵关于x的一元一次方程的解为整数,∴x 为整数,∴6﹣a =±1或±2或±3或±6,又∵a 为整数,∴a =5或7或4或8或3或9或0或12,∴所有满足条件的数a 的和为:5+7+4+8+3+9+0+12=48.解析:例题1.解:化简kx ﹣m =(2k ﹣1)x+4得(k ﹣1)x =﹣m ﹣4,(1)当k≠1时方程只有一个解,即x.(2)当k =1,m≠﹣4时方程无解.(3)当k =1,m =﹣4时方程有无数个解.解析:2.解:方程去括号得:mx ﹣m =5x ﹣2,移项合并得:(m ﹣5)x =m ﹣2,由方程有唯一解,得到m ﹣5≠0,解得:m≠5.2222222222222222222解析:基础训练基础训练题目1.解:方程移项合并得:(2k﹣1)x=4﹣m,(1)由方程有唯一解,得到2k﹣1≠0,即k;(2)由方程有无数个解,得到2k﹣1=0,4﹣m=0,解得:k,m=4;(3)由方程无解,得到2k﹣1=0,4﹣m≠0,解得:k,m≠4.解析:2.解:6(ax﹣2)﹣(x+1)=4(x),去括号得6ax﹣12﹣x﹣1=2+4x,移项、合并同类项得(6a﹣5)x=15.(1)当6a﹣5≠0,即a时,方程有唯一解.(2)当6a﹣5=0,即a时,方程没有解.解析:3.解:原方程即x1ax,移项,得: x ax1,合并同类项,得:()x,当0,且0时,方程有无数个解.则b=﹣2,a.解析:4.解:(1)b=1,代入原式得:a(3x﹣2)+2x﹣3=8x﹣7,去括号得:3ax﹣2a+2x﹣3=8x﹣7,移项合并同类项得:(3a﹣6)x=2a﹣4,(a≠2)化系数为1得:x.(2)a(3x﹣2)+b(2x﹣3)=8x﹣7,去括号得:3ax﹣2a+2bx﹣3b=8x﹣7,移项合并同类项得:(3a+2b﹣8)x=2a+3b﹣7,∴当3a+2b﹣8=0,2a+3b﹣7=0时,x有无数个解,解得:b=1,a=2.故a=2,b=1时,方程有无数个解.解析:5.解析:解:∵(5a+3b )x +ax+b =0是一元一次方程,∴5a+3b =0,∵方程(5a+3b )x +ax+b =0有唯一解,∴a≠0,x,∴ba ,∴x .故答案是:.模块四自定义新一元一次方程例题1.解:(1)[] 2,[﹣1]=﹣1+2=1;(2)a >0,b <0,[a]=[b],即a ﹣2=b+2,解得:a ﹣b =4,故(b ﹣a )﹣2a+2b =(b ﹣a )﹣2(a ﹣b )=(﹣4)﹣8=﹣72;(3)当x≥0时,方程为:2x ﹣2+x+1﹣2=1,解得:x ;当﹣1<x<0时,方程为:2x+2+x+1﹣2=1,解得:x =0(舍弃);当x≤﹣1时,方程为:2x+2+x+1+2=1,解得:x;故方程的解为:x.解析:2.解:(1)∵(4,y )是“相伴数对”,∴解得y =﹣9;(2)∵(a ,b )是“相伴数对”,∴解得a b ;(3)∵(m ,n )是“相伴数对”,∴由(2)得,mn ,∴原式=﹣3mn ﹣2=﹣3×(n )n ﹣2=﹣2.解析:3.解:(1)由题意得:g (x )=2x ;故答案为:2x ;(2)由题意得:g (x )=6x ﹣14,22333由g(x)=10,得6x﹣14=10,解得:x=4;故答案为:6x﹣14;(3)由题意得:g(x)=2(a﹣3)x﹣8=(2a﹣6)x﹣8,由g(x)=﹣2x,得(2a﹣6)x﹣8=﹣2x,化简整理得:(a﹣2)x=4,∵方程有正整数解,∴a﹣2≠0,可得x,∵a为整数,∴a﹣2=1或2或4,∴a=3或4或6,又∵f(x)是二次多项式,∴a﹣3≠0,可得a≠3,综上可知,a=4或6.解析:4.解:(1)解方程3x﹣3+4(x﹣1)=0得,x=1,解方程﹣2y﹣y=3得,y=﹣1,∵1﹣(﹣1)=2>1,∴方程3x﹣3+4(x﹣1)=0与方程﹣2y﹣y=3的解不接近;(2)关于x的方程3x﹣3+4(x﹣1)=0的解为x=1,关于y的方程y=2k+1的解为y=3k+2,∵关于x的方程3x﹣3+4(x﹣1)=0与关于y的方程y=2k+1的解接近,∴|1﹣(3k+2)|≤1,解得k≤0或k,即k≤0,∴k的最大值是0,最小值;(3)解方程x﹣m=2x﹣5得,x解方程y+7×2018﹣1=4036y+2018m得,y∵1∴方程x﹣m=2x﹣5与方程y+7×2018﹣1=4036y+2018m的解接近.解析:自主探究自主探究题目1.B解析:解:解2x+1=﹣2,得x.把x代入1﹣2(x﹣a)=2,得1﹣2(a)=2.解得a=﹣1,故选:B.2.C解析:解:方程移项合并得:(a﹣3)x=b+4,由方程有无数个解,得到a﹣3=0,b+4=0,解得:a=3,b=﹣4,故选:C.3.B解析:解:令y=|x﹣4|+2|x﹣2|+|x﹣1|+|x|,当x≥4时,y=5x﹣9≥11,当2<x<4时,y=3x﹣1,∴5<y<11;当1≤x≤2时,y=﹣x+7,∴5≤y≤6;当0<x<1时,y=﹣3x+9,∴6<y<9;当x≤0时,y=﹣5x+9,∴y≥9;综上所述,y≥5,∴a≥5时等式恒有解.故选:B.4.(1) x=3;(2) x=1.解析:解:(1)移项得:4x+x=12+3,合并得:5x=15,解得:x=3;(2)去分母得:3(1﹣x)+12=4(2x+1),去括号得:3﹣3x+12=8x+4,移项得:﹣3x﹣8x=4﹣3﹣12,合并得:﹣11x=﹣11,解得:x=1.5.解:解方程5x﹣3=2x,可得:x=1,∵5x﹣3=2x与方程4x=6的解互为相反数,∴方程4x=6的解是x=﹣1,∴,解得k,∴(1k)=(1)=﹣1.解析:556.解:由方程ax+6=5x﹣b有无数个解,得到a=5,b=﹣6,则原式=25﹣6=19.解析:7.解:方程3x+2=﹣4,解得:x=﹣2,因为x、y互为相反数,所以y=2,把y=2代入第二个方程得:6﹣3=2m﹣1,解得:m=2.解析:8.解:去括号得:ax﹣5a=x+1,移项得:ax﹣x=1+5a,合并得:(a﹣1)x=1+5a,当a﹣1≠0时,x,当a﹣1=0时,方程无实数解,∴当a≠1时,方程的根是x;当a=1时,方程没有实数根.解析:9.解:方程的解是数轴上到与到的所有点的集合,∴x,则该方程的整数解为x=﹣1或x=0;解析:10.解:去分母,得:ax+10=7x﹣3,移项、合并同类项,得:(a﹣7)x=﹣13,系数化成1得:x,∵x是正整数,∴a﹣7=﹣1或﹣13,∴a=6或﹣6.又∵a是正整数.∴a=6.解析:。

一元一次方程一、等式及其性质1、等式用等号表示相等关系的式子叫等式。
如:m+n=n+m,x+2x=3,3×3+1=5×2,3x+1=5y,等等。
注意:等式中一定含有等号。
2、等式的性质等式性质1 等式两边加上(或减去)同一个数(或式子),结果仍相等。
a=b ,那么a ±c=b ±c等式性质2 等式两边乘以同一个数,或除以同一个不为0的数,结果仍相等。
a=b ,那么ac=bc ;如果a=b ,那么a /c=b /c (c ≠0)。
注意:①等式两边除以一个数时,这个数必须不为0;②对等式变形必须同时进行,且是同一个数或式。
思考:回答下列问题:(1)从a+b=b+c ,能否能到a=c ,为什么?(2) 从a-b=b-c ,能否能到a=c ,为什么?(3) 从ab=bc ,能否能到a=c ,为什么?(4) 从a/b=c/b ,能否能到a=c ,为什么?(5)从xy=1,能否能到x=1/y ,为什么?二、解一元一次方程的步骤:①去分母; ⇐(没有分母的项不要漏乘;去掉分数线,同时要把分子加上括号) ②去括号; ⇐(当括号外面是负号,去掉括号后,要注意变号)③移项; ⇐(移项要注意变号)④合并同类项; ⇐(如果方程中有同类项,一定要合并同类项)⑤系数化为1; ⇐(记得每一项都要除系数) 例:解一元一次方程3122133---=+x x x三、一元一次方程解的实际应用1、列方程解应用题的步骤(1)审:明确已知什么,求什么及基本关系。
找出能表示题目全部含义的相等关系(2)设:设未知数。
可直接设,也可间接设,要尽量使列出的方程简单。
①直接设未知数:题目求什么就设什么。
②间接设未知数:设的未知数不是题目直接求的量。
③设辅助未知数:所设未知数仅作为题目中量与量之间关系的桥梁,它在解方程的过程中会自然消去(3)列:根据等量关系列方程。
(4)解:解方程(5)验:检验方程的解和解是否符合实际问题。

一元一次方程专题详解专题03 一元一次方程专题详解 (1)3.1从算式到方程 (2)知识框架 (2)一、基础知识点 (2)知识点1 方程和一元一次方程的概念 (2)知识点2 方程的解与解方程 (3)知识点3 等式的性质 (4)二、典型题型 (5)题型1 依题意列方程 (5)题型2 运用等式的性质解方程 (6)三、难点题型 (7)题型1 利用定义求待定字母的值 (7)3.2解一元一次方程-合并同类项和移项 (8)知识框架 (8)一、基础知识点 (8)知识点1 合并同类项解一元一次方程 (8)知识点2 移项解一元一次方程 (9)二、典型题型 (10)题型1 一元一次方程的简单应用 (10)3.3解一元一次方程-去括号与去分母 (11)知识框架 (11)一、基础知识点 (11)知识点1 去括号 (11)知识点2 去分母 (12)二、典型题型 (13)题型1 去括号技巧 (13)题型2 转化变形解方程 (15)题型3 解分子分母中含有小数系数的方程 (16)三、难点题型 (18)题型1 待定系数法 (18)题型2 同解问题 (18)题型3 含参数的一元一次方程 (19)题型4 利用解的情况求参数的值 (20)题型5 整体考虑 (21)3.4实际问题与一元一次方程 (21)一、基础知识点 (21)知识点1 列方程解应用题的合理性 (21)知识点2 建立书写模型常见的数量关系 (22)知识点3 分析数量关系的常用方法 (23)二、典型例题 (24)3.1从算式到方程知识框架一、基础知识点知识点1 方程和一元一次方程的概念1) 方程:含有未知数的等式。
例:3x=5y+2;100x=200;3x 2+2y=3等2)一元一次方程:只含有一个未知数(元,隐含未知数系数不为0),未知数的次数是1(次),等号两边都是整式(整式:未知数的积,而非商)的方程。
如何判断一元一次方程:①整式方程;②只含有一个未知数,且未知数 的系数不为0;③未知数的次数为1. 例:3112=+x ;3112=+x ;3m-2n=5;3m=5;6x 2-12=0 例1.下列各式中,那些是等式?那些是方程?①3x-6;②3-5=-2;③x+2y=8;④x+2≠3;⑤x-x1=2; ⑥y=10;⑦3y 2+2y=0;⑧3a<-5a ;⑨3x 2+2x-1=0;⑩213m m y =-+ 【答案】是方程的有:③、⑤、⑥、⑦、⑨、⑩方程需满足2个条件:1)含有未知数;2)是等式。

浙江版2019-2020学年度七年级数学上册第5章一元一次方程 5.1 一元一次方程【知识清单】 一、一元一次方程:1.方程:含有未知数的等式叫做方程.2.方程的解:使方程左右两边的值都相等的未知数的值叫做方程的解3.一元一次方程:只含有一个未知数,未知数的次数是1,这样的方程叫做一元一次方程. 二、方程的判定方法归纳:1.判断一个式子是不是方程必须看两点:一是等式,二是含有未知数,二者缺一不可;2.判定一个方程是不是一元一次方程,要看方程是否只含一个未知数并且未知数的指数都是1,而且是整式方程. 【经典例题】例题1、下列方程中,是一元一次方程的是( )A .x 2-2x =1B .-5x =0C .3x +2y =5D .x =x1【考点】一元一次方程的定义.【分析】根据一元一次方程的定义判断即可.【解答】A 、方程的次数是2次,即不是一元一次方程,故本选项错误;B 、是一元一次方程,故本选项正确;C 、含有两个未知数,即不是一元一次方程,故本选项错误;D 、不是整式方程,即不是一元一次方程,故本选项错误; 故选B .【点评】本题考查了对一元一次方程的定义的应用,熟练掌握一元一次方程的定义是解决问题的关键.例题2、如果方程(m -2)1-m x+26=0是关于x 的一元一次方程,那么m 的取值是______.【考点】一元一次方程的定义.【分析】只含有一个未知数(元),并且未知数的指数是1(次)的方程叫做一元一次方程,高于一次的项系数是0.据此可得出关于m 的方程,继而可求出m 的值. 【解答】由一元一次方程的定义,得⎩⎨⎧=-≠-1102m m ,解得m =-2.故填:-2.【点评】本题主要考查了一元一次方程的定义,只含有一个未知数,未知数的指数是1,一次项系数不是0,这是这类题目考查的重点.【夯实基础】1.下列方程中,是一元一次方程的是( )A .2x =3y B.y 1+1=0 C .2x 2+3x =2 D. )2(31-x =1 2.下列说法正确的是( )A .x =-2是方程2x +5=0的解B .y =0是方程0.5(5-2y )=2.5的解C .方程3x -4=)3(31-x )的解是x =3D .方程43-x =2的解是x =383.一件高于成本50%标价的上衣,按8折销售仍可获利40元.设这件上衣的成本价为x 元,根据题意,下面所列方程正确的是( )A .x (1+50%)×0.8-x =30B . ( x +50%)×0.8-x =30C .x (1+50%)×0.8=30-xD .( x +50%)×0.8=30-x 4.关于|x -2|=2的说法正确的是 ( )A .不是方程B .是方程其解为0C .是方程其解为4D .是方程其解为0或45.若关于x 的方程(3k -2)x 2- (3k +2)x +5=0是一元一次方程,则k 的值为 .6.如图,两边都放着物体的天平处于平衡状态,用等式表示天平两边所放物体的质量关系为__ __________.7.下列不是方程的是__________.(填序号)① 1+2=3; ② 2x +1; ③ 2m +15=3; ④ x 2-6=0; ⑤ 3x +2y =9; ⑥ 3a +9>15.8.已知关于x 的方程5a -2x =9的解为x =3,求代数式(-a )2-2a +1的值.9.有甲、乙两支同样长的蜡烛,甲蜡烛可使用12 h ,乙蜡烛可使用10 h .两蜡烛同时点燃,几小时后乙蜡烛的长度是甲蜡烛长度的三分之一?(列出方程,不必求解)【提优特训】10.若5x -6与2x -8是一个正数两个平方根,则可列方程来表示为( )A .5x -6=2x -8B .5x -6+2x -8=0C .5x +6+2x +8=0D .5x +6+2x -8=0 11.若方程(3a -2)x 2+bx +c =0是关于x 的一元一次方程,则字母系数a ,b ,c 的值满足( )A .a =32,b =0,c 为任意数 B .a ≠32,b ≠0,c =0 C .a =32,b ≠0,c 为任意数 D .a =32,b ≠0,c ≠0 12.下列方程中,解为x =-2的方程是( )A .21x +3=x B . x -2=0 C .2x =4 D .321)63(31-=-x x 13.已知单项式-ma 3b m -1与单项式4a 3b 2是同类项,则关于m 的方程一定正确的是( )A .-m +4=0B .-m -4=0C .m -1+2=0D . m -1=2 14.已知53-m x-1=m 是关于x 的一元一次方程,则这个方程的解 .15.对于有理数a ,b ,c ,d ,规定一种运算bc ad dbc a -=,如43525342⨯-⨯==-2. 若32331=----x x ,则所得到的方程为 .16.根据下列条件列出方程. 1.设某数为x : (1)某数的65与-5的和是6; (2)某数的5倍等于该数的2倍与18的差; (3)某数减少20%后比该数的60%小5; (4)比某数的3倍大6的数是12”用方程表示为.2.(1)某长方形的周长是64,长与宽之比为5∶3,则长和宽各是多少?设长方形的长为5x . (2)爸爸今年38岁,比儿子年龄的3倍少4岁,则小明今年几岁?设小明今年x 岁.17.已知关于x 的方程ax 2+x b -3-2=0是一元一次方程,试求x a +b 的值.18.数学课上老师出示了四张卡片,上面分别写着不同的代数式,要求同学们解决下面的问题:用等号将这四张卡片的任意两张卡片上的数或式子连接起来,就会得到等式或方程. (1)你一共能写出几个等式?(2)在这些等式中,有几个一元一次方程?请写出这几个一元一次方程.19.汽车的油箱内储油40kg,已知工作时的耗油以及油箱内的剩油量的关系如表所示工作时间t(h) 耗油量p(kg) 剩油量m(kg)1 2.5 40-2.5=37.52 5 40-5=353 7.5 40-7.5=32.54 10 40-10=30………(1)写出工作10h后,油箱内的剩油量;(2)写出工作t h后,油箱内的剩油量为7.5kg,请你列出关于t的方程(不解方程).20.如图用火柴棒搭正方形,用n表示所搭正方形的个数,从而计算火柴棒的根数,当n=1,所需火柴棒为4根,当n=2,所需火柴棒为7根,当n=3,所需火柴棒为10根,…,请问:(1)第5个图形中火柴棒有多少根?(2)第n个图形中火柴棒有多少根?(3)若有一个图形由781根火柴棒组成,那么这个图形由几个正方形组成?【中考链接】21.(2018•临安)(3分)中央电视台2套“开心辞典”栏目中,有一期的题目如图所示,两个天平都平衡,则三个球体的重量等于()个正方体的重量.A.2 B.3 C.4 D.522.(2018•临沂)任何一个无限循环小数都可以写成分数的形式,应该怎样写呢?我们以无限循环小数7.0 为例进行说明:设7.0 =x ,由7.0 =0.7777…可知,l0x =7.7777…,所以l0x -x =7,解方程,得x =97,于是.得7.0 =97.将63.0 写成分数的形式是 .参考答案1、D2、B3、A4、D5、326、x+4=107、①②⑥ 10、B 11、C 12、D 13、D 14、-1或3 15、-(x -2)+3(3-x )=3 21、D 22、114 8.已知关于x 的方程5a -2x =9的解为x =3,求代数式(-a )2-2a +1的值. 解:∵方程5a -2x =9的解为x =3,∴5a -2×3=9, ∴a =3.∴(-a )2-2a +1 =(-3)2-2×3+1=4.9.有甲、乙两支同样长的蜡烛,甲蜡烛可使用12 h ,乙蜡烛可使用10 h .两蜡烛同时点燃,几小时后乙蜡烛的长度是甲蜡烛长度的三分之一?(列出方程,不必求解) 解:设x 小时后乙蜡烛的长度是甲蜡烛长度的一半,则1-101x =31(1-121x ). 16.根据下列条件列出方程. 1.设某数为x : (1)某数的65与-5的和是6; (2)某数的5倍等于该数的2倍与18的差; (3)某数减少20%后比该数的60%小5; (4)比某数的3倍大6的数是12”用方程表示为.2.(1)某长方形的周长是64,长与宽之比为5∶3,则长和宽各是多少?设长方形的长为5x . (2)爸爸今年38岁,比儿子年龄的3倍少4岁,则小明今年几岁?设小明今年x 岁. 16.解:1.(1)65x -5=6; (2) 5x =2x -18;(3) (1-20%)x =60%x -5; (4) 3x +6=12;2.解:(1)由长方形的长为3x ,得宽为2x ,则2(5x +3x )=64.(2)根据题意,得3x -4=38.17.已知关于x 的方程ax 2+x b -3-2=0是一元一次方程,试求x a +b 的值. 解:∵ax 2+x b-3-2=0是关于x 的一元一次方程,∴a =0,b -3=1, ∴a =0,b =4, ∴x -2=0, ∴x =2. ∴x a +b =24=16.18.数学课上老师出示了四张卡片,上面分别写着不同的代数式,要求同学们解决下面的问题:用等号将这四张卡片的任意两张卡片上的数或式子连接起来,就会得到等式或方程. (1)你一共能写出几个等式?(2)在这些等式中,有几个一元一次方程?请写出这几个一元一次方程. 18. 解:(1)6个.(2)有3个一元一次方程,它们分别是5x -3=-6,6261-=-x ,5x -3=261-x . 19.汽车的油箱内储油40kg ,已知工作时的耗油以及油箱内的剩油量的关系如表所示工作时间t (h) 耗油量p (kg) 剩油量m (kg) 1 2.5 40-2.5=37.5 2 5 40-5=35 3 7.5 40-7.5=32.5 4 10 40-10=30 ………(1)写出工作10h 后,油箱内的剩油量;(2)写出工作t h 后,油箱内的剩油量为7.5kg ,请你列出关于t 的方程(不解方程). 解: (1)40-10×2.5=15;工作10h 后,油箱内的剩油量为15 kg ; (2)根据题意,得40-2.5t =7.5.20.如图用火柴棒搭正方形,用n 表示所搭正方形的个数,从而计算火柴棒的根数,当n =1,所需火柴棒为4根,当n =2, 所需火柴棒为7根,当n =3, 所需火柴棒为10根,…,请问:(1)第5个图形中火柴棒有多少根?(2)第n个图形中火柴棒有多少根?(3)若有一个图形由781根火柴棒组成,那么这个图形由几个正方形组成?解:根据图形特点和题意可得:第1个图形n=1,火柴棒为3×1+1=4根,第2个图形n=2,火柴棒为3×2+1=7根,第3个图形n=3,火柴棒为3×3+1=10根,…(1)第5个图形中火柴棒有3×5+1=16根,(2)第n个图形中火柴棒有3×n+1=(3n+1)根,(3)3n+1=781,解得n=260,答:这个图形由260个正方形组成.。

教师讲义〔4〕期数:存入的时间叫期数.〔5〕利率:每个期数内的利息与本金的比叫利率.2.储蓄中的常用公式:〔1〕每个期数内:〔2〕利息=本金〔3〕利息=本金〔4〕本息和=本金+利息四、典型例题及同步练习〔一〕、行程问题【例1】小华和小玲同时从相距700米的两地相对走来,小华每分钟走60米,小玲每分钟走80米.几分钟后两人相遇?分析:先画线段图:假设x分钟后两人相遇,此时小华走了_________米,小玲走了_________米,两人一共走了_________米.找出等量关系,小华和小玲相遇时_________+_________=_________写解题过程:同步练习1假设A、B两地相距480千米,一列慢车从A地开出,每小时走60千米,一列快车从B地开出,每小时走65千米.两车同时开出,相向而行,过几小时后两车相遇?分析:先画线段图:写解题过程:需要〔〕A、3小时B、3小时C、4小时D、4小时3、学校到县城有28千米,除公共汽车以外,还需步行一段路程,公共汽车的速度为36千米/时,步行的速度为4千米/时,全程共需1小时,那么步行所用时间是〔〕A、小时B、小时C、小时D、小时4、一个图书馆对图书进行防火保险,如果每年的保险费是图书价值的0.4%,参加保险6年,一共交付保险费7.8万元,那么图书馆的图书价值〔〕A、300万元B、305万元C、320万元D、325万元5、某企业为节约用水,自建污水净水站,3月份净化污水3000吨,4月份净化污水3300吨,那么这个月净化污水的量的增长百分率为〔〕A、7%B、8%C、9%D、10%6、小明同学存入300元的活期储蓄,存满3个月时取出,共得本息和301.35元〔不计利息税〕,那么此活期储蓄的月利率是〔〕A、1.6‰B、1.5‰C、1.8‰D、1.7‰二、填空题〔共5小题,每题5分,总分值25分〕1、A,B两地间的路程为450千米,一列慢车从A地出发,每小时行驶60千米,一列快车从B地出发,每小时行驶90千米.假设两车同时开出,相向而行,_________小时相遇;假设慢车先开1小时,快车在同地同向开出,快车经过了_________小时可追上慢车.2、某行军纵队以7千米/时的速度行进,队尾的通讯员以11千米/时的速度赶到队伍前送一封信,送交后又立即返回队尾,共用13.2分钟,那么这支队伍的长度为_________千米.3、假设一艘轮船在静水中的速度是7千米/时,水流速度是2千米/时,那么这艘船逆流而上的速度是_________千米/时,顺流而下的速度是_________千米/时.4、环形跑道400米,小明跑步每秒行9米,爸爸骑车每秒行16米,两人同时同地反向而行,经过_________秒两人相遇.5、在一段复线铁道上,两辆火车迎头驶头,A列车车速为20米/秒,B列车车速为25米/秒,假设A列车全长200米,B列车全长160米,两列车错车的时间为_________秒.6、妈妈用10 000元钱为小彬存了6年期的教育储蓄,6年后能取得11 728元,这种储蓄的年利率为_________%.7、某人将一笔钱按定期2年存入银行,年利率为2.25%〔不计复利〕,到期支取扣除20%利息税,实得利息72元,5、从甲地到乙地,公共汽车原需行驶7个小时,开通高速公路后,车速平均每小时增加了20千米,只需5个小时即可到达,求甲、乙两地的路程?6、甲、乙两人骑自行车同时从相距80千米的两地出发,相向而行,2小时后相遇,甲每小时比乙多走2.4千米,求甲、乙每人每小时走多少千米?7、甲、乙二人从相距91千米的A、B两地相向而行,甲先出发1小时,二人在乙出发4小时后相遇,而甲每小时比乙快2千米,求甲、乙二人的速度?附答案典型例题及同步练习〔一〕【例1】解:小华走的路程为60x米,小玲走的路程为80x米,两人一共走了700米,60x+80x=700,解得x=5.答:5分钟后两人相遇.故答案为60x;80x;700;60x;80x;700.同步练习1解:设经过x小时相遇,根据题意可得〔60+65〕x=480,解得:x=3.84〔小时〕.答:两车需要3.84小时相遇.同步练习2解:设货车的速度为x千米/小时,根据题意可作出如下方程及图示:80×4+x×4=600,解得:x=70〔千米/小时〕.答:货车每小时行70千米.【例2】解:〔1〕设爸爸追上小明用了x 分钟,根据题意可得线段图〔红线代表爸爸,黑线代表小明〕:得方程:80×5+80x=180x ,解得:x=4.答:爸爸追上小明用了4分钟.各空依次填:180x 、400、80x 、400+80x=180x .〔2〕爸爸追上小明用了4分钟,爸爸和小时走了180×4=720〔米〕,此时离学校还有1000﹣720=280米.同步练习1解:设小明x 秒钟追上小兵,7x=6×〔4+x 〕,解得x=24.答:小明24秒钟追上小兵.同步练习2解:设x 秒后小明能追上小华,7x ﹣5x=20,解得x=10.答:10秒后小明能追上小华.同步练习3解:设经过x 小时摩托车可以追赶上自行车,根据题意得:60x -20x =80 解得x =2所以经过2小时摩托车可以追赶上自行车。

第三章一元一次方程复习讲义知识点1.等式:用“=”号连接而成的式子叫等式.2.等式的性质:等式性质1:等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式;等式性质2:等式两边都乘以(或除以)同一个不为零的数,所得结果仍是等式.例1(1)怎样从等式x-5=y-5得到等式x=y?(2)怎样从等式3+x=1得到等式x=-2?(3)怎样从等式4x=12得到等式x=3?例2利用等式的性质解下列方程:(1)x+7=26(2)-5x=203.方程:只含有一个未知数,未知数的次数是1,等号两边都是整式,这样的方程叫做一元一次方程.4.方程的解:使等式左右两边相等的未知数的值叫方程的解;注意:“方程的解就能代入”!5.移项:改变符号后,把方程的项从一边移到另一边叫移项.移项的依据是等式性质1. 6.一元一次方程:只含有一个未知数,并且未知数的次数是1,并且含未知数项的系数不是零的整式方程是一元一次方程.7.一元一次方程的标准形式:ax+b=0(x是未知数,a、匕是已知数,且aW0).8.一元一次方程解法的一般步骤:化简方程分数基本性质去分母同乘(不漏乘)最简公分母去括号先去小括号,再去中括号,最后去大括号.依据是去括号法则和乘法分配律,注意符号变化移项把含有未知数的项移到一边,常数项移到另一边.“过桥变号”,依据是等式性质一合并同类项将未知数的系数相加,常数项相加.依据是乘法分配律合并后注意符号系数化为1在方程的两边除以未知数的系数.依据是等式性质二.例1解下列方程[1]用合并同类项的方法解一元一次方程(1)2x-£%=6-8;(2)7x—2.5x+3x-1.5x=-15x4—6x3.[2]用移项的方法解一元一次方程(1)7-2x=3-4x(2)4x+10=6x[3]利用去括号解一元一次方程去括号法则:去掉“+()”,括号内各项的符号不变.去掉“-()”,括号内各项的符号改变.用三个字母a、b、c表示去括号前后的变化规律:a+(b+c)=a+b+ca-(b+c)=a—b—c(1)2x-(x+10)=5x+2(x—1)(2)3x—7(x—1)=3—2(x+3)[4]利用去分母解一元一次方程(总结:像上面这样的方程中有些系数是分数,如果能化去分母,把系数化为整数,则可以使解方程中的计算更方便些.)2x+2x+7x+x=33(2)3x+x-1=3-2x-1(1)^要点归纳1.去分母时,应在方程的左右两边乘以分母的最小公倍数;2.去分母的依据是等式性质2,去分母时不能漏乘没有分母的项;3.去分母与去括号这两步分开写,不要跳步,防止忘记变号.10.列一元一次方程解应用题:(1)读题分析法:多用于“和,差,倍,分问题”仔细读题,找出表示相等关系的关键字,例如:“大,小,多,少,是,共,合,为,完成,增加,减少,配套”,利用这些关键字列出文字等式,并且据题意设出 未知数,最后利用题目中的量与量的关系填入代数式,得到方程.(2)画图分析法:…………多用于“行程问题”利用图形分析数学问题是数形结合思想在数学中的体现,仔细读题,依照题意画出有关图形,使图形各部分具有特定的含义,通过图形找相等关系是解决问题的关键,从而取得列方程的依据,最后利用量与量之间的关系(可把未知数看做已知量),填入有关的代数式是获得方程的基础.11.列方程(组)的应用题的一般步骤:审:审清题意,分清题中的已知量、未知量.设:设未知数,设其中某个未知量为x.列:根据题意寻找等量关系列方程.解:解方程.验:检验方程的解是否符合题意.答:写出答案(包括单位).[注意]审题是基础,找等量关系是关键.11.解实际应用题:知识点1:市场经,^、打折销售问题(1)商品利润=商品售价一商品成本价(3)商品销售额=商品销售价X 商品销售量(4)商品的销售利润=(销售价一成本价)X 销售量例1一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?变式1.某琴行同时卖出两台钢琴,每台售价为960元.其中一台盈利20%,另一台亏损20%.这次琴行是盈利还是亏损,或是不盈不亏?例2一件服装先将进价提高25%出售,后进行促销活动,又按标价的8折出售,此时售价为60元.请问商家是盈是亏,还是不盈不亏?例3.某商品的进价是1000元,售价是1500元,由于销售情况不好,商店决定降价出 售,但又要保证利润率不低于5%,那么商店最多可打几折出售此商品?(2) 商品利润率= 商品利润 商品成本价X 100%例4.某商场国庆节搞促销活动,购物不超过200元不给优惠,超过200元但不超过500元的优惠10%,超过500元,其中500元按9折优惠,超过的部分按8折优惠。

一元一次方程的基础解法一、课堂目标1.掌握移项、去分母、去括号的依据,会用移项和合并同类项、去括号、去分母等手段解一元一次方程.2.掌握解一元一次方程的一般步骤,能熟练准确的解方程.二、知识引入前面我们学过等式的性质:等式性质——如果,那么.等式性质——如果,那么;如果(),那么.也能用等式的性质解简单的一元一次方程,例如,①解方程;②解方程.三、知识讲解1. 解方程——移项、合并同类项解方程解:两边加,得这个过程也可以看成把原方程左端的常数项移动到方程右端、得,此时这项在等号右端变成符号( →);像上面这样把等式一边某一项变号后移到另一边叫做移项,所以我们可以用移项这个手段来解形如的一元一次方程.【注意】移项要变号.解方程解:两边减 ,得这个过程也可以看成把原方程左端的未知数项 移动到方程右端、得 ,此时这项在等号右端变成符号( →).再比如,解方程 ,观察到这个方程两边都有含未知数项和常数项,因此【总结】解形如 的一元一次方程的一般步骤为:移项→合并同类项→系数化.经典例题11.已知关于的方程的解是,那么.思路梳理知识点:1、2、3、A. B.C.D.2.方程移项后,正确的是( ).思路梳理知识点:1、2、3、题目练习1A. B. C.D.1.对方程合并同类项正确的是().(1)(2)(3)(4)2.给下列各方程移项:: .:.: .:.A. B. C. D.3.若,则的值是().经典例题2解关于的方程:.思路梳理知识点:1、2、3、 题目练习21.解方程:.2.解方程:.(1)3.解方程:.4.当 时,代数式与的值互为相反数.2. 解方程——去括号接下来看这个方程.观察发现这个方程多了带括号的成分,因此【总结】解带括号的一元一次方程的一般步骤:去括号→移项→合并同类项→系数化.经典例题3阅读下列解方程的过程,回答问题:,去括号,得: ①,移项,得: ②,合并同类项,得: ③,系数化为, 得: ④,上述过程中,第 步计算出现错误,其错误原因是 ,第②步的数学依据是.思路梳理知识点:1、2、3、题目练习3A.由 得B.由 得C.由得 D.由得1.下列方程去括号正确的是().。
一元一次方程例题讲解及答案.doc去括号,得12 兀+ 66-25 + 10x30. 移项、合并同类项,得22 兀=-11.解这个方程,得例3列方程求下列问题的解:in = -6 —元一次方程课标要求:1?解一元一次方程及其解的意义.2.理解方程变形的基木原理,能在解方程屮正确应用.3.掌握一元一次方程中移项、系数化为1等基本步骤,会解一元一次方程,并会对方程的解进行检验.4.能根据具体情境中的数量关系,列出方程,解决简单的实际问题.中招考点一元一次方程概念及解法,一元一次方程的应用,能利用一元一次方程解决生活屮的实际问题.典型例题例1解方程生巴一土空=1.6(2X4-11)-5(5-2X)=1X 30.系数化为1,得说明:注意在解方程过程中正确进行有理数及整式的运算,步骤不宜过于简单. 例2已知兀=-2是关于兀的方程2(x-m) = 8x-4m的解,求加的值.分析:本题已知方程的解,要求方程中待确定的字母系数,可以像解数字系数的方程一样, 先求出方程的解,再进行比较;也可以根据方程的解的定义:能使方程两边代数式的值相等的未知数的取值叫做方程的解,将工=-2代入原方程,转化为关于加的方程求解.解1解关于兀的方稈:lx-Im = 8x-4m .因为已知方程的解是兀=-2,所以巴=-2,即m=-63解2因为x = -2是方程的解,所以2(-2-m) = 8(-2) 一4/n .解:去分母,强化训练1.选择题(1)下列方程变形正确的是(Y — 1A?由 -- =0得x-l = 55r — 1C.由---- =1 得X -1 = 55 ).YB.由一一1 = 0得x-l = 05D?由兰一1 = 1得兀一5 = 1(1)甲乙两车分别从相距360千米的两地相向开出,己知甲车速度是60千米/小时.乙车速度是40千米/小时.若甲车先开1小时,问乙车开出多少时间后两车相遇?(2)小陈和老师一起整理了一篇教学材料,准备打印成稿.按篇幅估计老师单独打字需4个小时,小陈单独打字需6个小时,后来小陈先打了一个小时后,老师开始一起打.问还需多少小时完成?分析:方程是刻画现实世界数量之间相等关系的一个重要数学模型,通过对实际问题中数量关系的分析,列出相关的代数式,进而建立方程,可以把复杂的实际问题转化为纯数学问题来解决.这一过程的关键是要透过纷繁多变的问题的表象,抓住数量关系的实质,抽象为数学问题.因此,常有面目迥异的情形,在学习屮我们不能机械地记忆、套用某些题型而忽略了问题的本质.像上述两个问题,不论是甲、乙两车还是师、生两人,主要的等量关系都是两个对象所完成数量的和等于总量,而其中一个对象所完成的数量又分为两部分;前一小时的和后來的.请同学们注意强化训练第8题两个问题中数量关系和解法的比较. 解:(1)设乙车开出兀小时后两车相遇,根据题意,得60(1 + 兀)+ 40x = 360 ?解这个方程得经检验,符合题意.答乙车开出3小吋两车相遇.(2)设老师开始打字后还需兀小时完成,扣+兀)+*=1.解这个方程得答老师开始打字后还需要2个小时完成.D.(2)下列方程后所列出的解不正确的是().x 2 ----- 1—23(2) 0.7x +1.37 = 1.5x-0.23;(3) x-3(20-x) = 3x-7(9-x);(4)2x-ll + 4x5(5)A.7B. ±7 C ?3 D ?7 或 3(4) 一种书包经两次降价10%,现在售价Q 元,则原售价为( )元.A. 81%? C ?80%aD.-^81% 80%2 .填空题(1) 若关于兀的方程、x = 5-k 的解是x = -3 ,则比= __________________ .3 (2) 当兀= ___________ 时,代数式2x4-3与6-4兀的值相等. 3. 解下列方程:(1) 3x-2 = -5(x-2);4.当x = -2时,代数式x 2+bx-2的值是12,求当x = 2时,这个代数式的值.5. 初一 (4)班课外乒乓球组买了两副乒乓球板,若每人付9元,则多了 5元,后来组长收了每人8元,自己多付了 2元,问两副乒乓球板价值多少?3y+ 6856(6)6 ?请你编制-道关于兀的方程,形如一咛冷使它的解在】到2之间.7.已y = ax3 +bx-8,当x = 3时,y = 5 .求当兀=一3日寸,y的值.8.应用方程解下列问题:(1)某车间原计划每周装配36台机床,预计若干周完成任务,在装配了三分之一后,改进操作技术,功效提高了一倍,结果提前一周半完成任务?求这次任务需装配的机床总台数.(2)某人有急事,预定搭乘一辆小货车从A地赶住B地,实际上他乘小货车行了三分路后改乘出租车,车速提高了一倍,结果提前一个半小时到达.己知小货车的车速是36千米 /小时,求两地间的路程.一元一次方程参考答案13 11.(1) C (2) C (3) D (4) B2. (1) 6 (2) 一3?(1) x = - (2) x = 2(3) x = -2 2 27(4) x = —(5) y = 2(6) j = -6 4. -8 (提示:先求得方=一5 ) 5?两副乒乓球拍2价值58元6?略(提示:本题解答不唯一,任収符合条件的一个根,如x = -,代入原方程,2即能得到一个对应的加的值)7. -21 (提示:将已知条件代入后可求得27a + 36 = 13,当兀=一3 时,j =-27a-3^-8 =-(27a+ 3*)-8 = -13-8 = -21 )2 28. (1)装配机床总台数162台(提示:设共装配机床x台,根据题意,3—二一--;或72 36 2设共装配机床3兀台,根据题意,得竺二—72 36 2(2)两地间的路程为162千米(提示:与第(1)题具有相同的等量关系和方程)解:(1)由②得代入①,得解得代入③,得所以方程组的解是(2)①+(§)x6,得即代入①,得x = 7 -3y.3(7-3J)-4J =-5.y = 2.x = 1.x = l,y = 2.32 兀= 16,1x =—,2J = -l第6部分二元一次方程组课标要求1.了解二元一次方程组及其解的概念,会将二元一次方程化为用含一个未知数的代数式表示另一个未知数的形式,会检验未知数的一组对应值是否为二元一次方程的解.2.了解二元一次方程组、方程组的解、解方程组等基本概念,掌握用消元法解方程组的基本思想;通过“消元”,转化为一元一次方程.3.会灵活应用代入消元法和加减消元法解二元一次方程组.4.能应用二元一次方程组解决简单的实际问题.中招考点二元一次方程概念及解法,代入法和加减法解方程组,用含一个未知数的代数式表示另一个未知数,会检验未知数的一组对应值是否为二元一次方程的解,能应用二元一次方程组解决简单的实际问题.典型例题例1解下列方程组:j3x-4J = -5, ①小严①(1)—(2) 5 1 _x+ 3j = 7; ②5x + —y = 2.②2分析:要结合方程组中方程的系数特征,合理选择消元的方法?通常方程中系数比较简单,尤其当一个未知数系数的绝对值是1时,可选用代入消元法,一般常采用加减消元法.Y =—所以方程组的解是2'y=~1 2例2已知关于工、y的方程组戶[尸& 与[x-2y = 5y有相同的解,求(l-2m)x + 2y = \-n ?[兀兀 + 丿=m + 1.“2、兀值?分析:这里两个方程组屮都有待定系数,但并未知道具体的解,不能应用方程解的定义,代入后转化为关于加、H的方程来解.注意到两个方程组中都有一个方程的系数是已知的.且根据方程组的解的定义,本题“相同的解”也就是方程组!2x_3j=8,的解,因此,这个解可[x-2y = 5.y* — 1 f 1 — 2"? — 4 _ 1 —U以先予求出:~ :这时再将它代入另两个方程组,得几 ~ '[y = -2. [n-2 = m + 1.解这个方程组,得m = -l,7i = 2.例3某公园的学生门票价格如下:1 初一甲、乙两个班共104人,若分别购票,需1240元.两个班合起来购票,能否节约一些?或己知甲班人数稍多一些,请求出两班各有多少人?2若不知道两班学生总数及各班人数的多少,你能求出各班人数吗?分析本题具有较大的开放性?在第(1)个问题中,首先应根据题意,判断各班人数的大致范围:两班共104人,则至少有一个班级人数50,但总票价1240元不是11的倍数,说明另一个班级人数不超过50.根据这些信息,可以着手应用列方程组求解.在第二个问题中,减弱了条件,两班学生的总数也是未知数.比较上述分析,共同之处是两班人数不可能是同一范围内的数(因为1240不是13、11、9的倍数),不同之处是少了一个方程.则应该用到求二元一次方程的整数解的知识,同吋还应根据实际情况,选取合适的解.解(1)设初一甲班学生兀人,初一乙班学生y人,根据题意,两班票价总数1240不是13 或11的倍数,所以甲班人数大于50,乙班人数小于50.可得方程组x + y = 104,llx + 13j = 1240?1240-13兀n = 112—兀 +8-2x11= 112—兀 +2(4-兀)H(1)3兀一丿=2,5x + 4y = 1.3x + 5y = 42.(4)j5/n +7" = 26,[4,72 + 6〃= 18. 解这个方程组,得经检验,符合题意.y = 4&答:初一甲班学生56人,初一乙班学生48人.(2)设两个班级人数分别为兀人和y人,根据实际情况,其屮兀、J 的值是不超过100的正整数,且X <卩根据题意,得方程13x + llj = 124 0?将方程变形为含X的代数式表示”得所以4-x是11的倍数,依次取工=4,15,26,37,48.求出对应的y = l 0& 95,82,69,56.根据实际情况,我们选取甲、乙两班人数分别为37人、69人、69人、37人、48人、56人或56人、48人四种比较合理的解答.强化训练1?填空题(1)已知4兀+ 5y —20 = 0 ,用含工的代数式表示只得___________________________当y = _4 时,X= ______________________________ .(2)己知x = 3』=一2是关于兀、丿的方程2兀一加丿+ 2加一2 = 0的解,贝【J:m= _______ .(3)己知|2x +J-3|+(X-3J +2)2 =0 ,贝ij x-y= ___________________(4)己知关于的方程组:%二亠的解’与y相等’则" ------------------------------------2.解下列方程组:(2) x3-t 丄、,十门.e 小「2兀一y = 2a + b 3.已知关于兀、丿的万程组彳 .[x^2y = a-b.的解是{二求…的值.4.已知当x = l 吋,代数式ax + b 的值等于2;当x = 2吋,代数式ax+ b 的值是1.求当x = 5 时,这个代数式的值.5?甲、乙两件商品成本共400元,甲商品按30%的利润定价,乙商品按20%的利润定价.后应顾客的要求,两种商品都按定价的90%出售,商店仍获利55?4元.求两种商品的成本各是多少?6. 求方程4x + 3y = 31的正整数解.7. 探索用适当的方法解下列方程组:(1)8. 某校课外阅读小组同学每人订甲、乙两份杂志,甲杂志是月刊,每月一期定价2?2元:乙杂志是双月刊,两个月一期定价2?6元.每位同学都是一份杂志订半年,另一份杂志订全年. 经统计,甲杂志订费858元,乙杂志订费429元,求这个阅读小组的人数.J17x + 23j = 57, [23兀+ 17y = 63;x + y-z = 5, (3) ? 2x + 3j+ z = 10,x-2y-z = 20.第6部分二元一次方程组1. (1) 丁=20一4兀]05 (2) -1 (3) 0 (4) 4 2. (1)9x ——,17 (2)7 y = ?17口⑶y = 6.X =29 7 = -!(4)m = 15.n = —7.3a = 2° 4. -2 5?甲商品成本260元,乙商品成本140元b = -5.商品成本兀元,乙商品成本J元,根据题意得方程组x + j = 400,x(l + 30%) x 90% + y (1 + 20%) x 90% = 400 + 55.4 6.x2 =4,兀1 =y=9; J2=5;l j3=l.(提示:I — x先将方程化为y = 10-x + —;或先确定y是1与9之间的奇数)37. (1) X =29J = 1(提示:将两式分别相减和相加,得x-y = t)x+j=3?(2) x = l,1y = -2(3)35X~T,j = -5, 8?这个阅读小组有40人(提示:设订甲种杂志全年的学5 Z_3'生兀人,订乙种杂志全年的学生y人,列方程组2.2x12兀+ 2?2x6y = 85& 曰解得<〔2.6x3 兀+ 2?6x6y = 429.x = 25,)y = 15.。
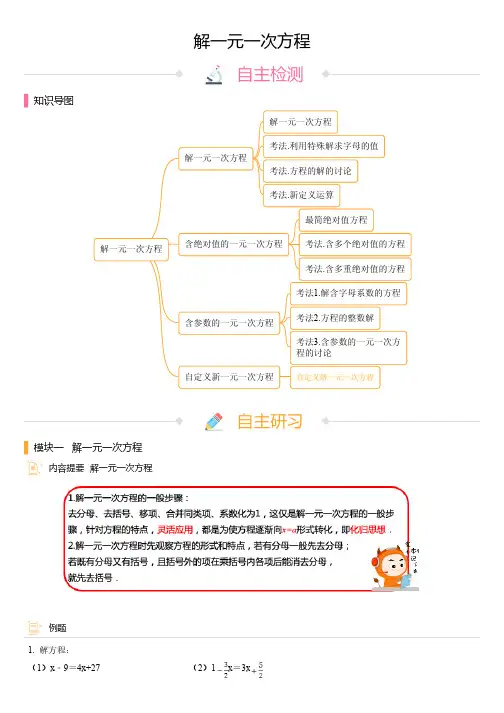
专题06 一元一次方程【专题目录】技巧1:巧用一元一次方程求字母系数的值技巧2:特殊一元一次方程的解法技巧【题型】一、一元一次方程概念【题型】二、一元一次方程的解法【题型】三、一元一次方程应用之配套问题和工程问题【题型】四、一元一次方程应用之销售盈亏问题【题型】五、一元一次方程应用之比赛积分问题【考纲要求】1、了解等式、方程、一元一次方程的概念,掌握等式的基本性质.2、掌握一元一次方程的标准形式,熟练掌握一元一次方程的解法.3、会列方程(组)解决实际问题.【考点总结】一、一元一次方程【注意】一元一次方程的特征1.只含有一个未知数x2.未知数x的次数都是13.等式两边都是整式,分母中不含未知数。
2.解一元一次方程的一般步骤:(1)去分母;(2)去括号; (3)移项; (4)合并同类项; (5)未知数的系数化为1. 【技巧归纳】技巧1:巧用一元一次方程求字母系数的值【类型】一、利用一元一次方程的定义求字母系数的值1.已知方程(m -2)x |m|-1+16=0是关于x 的一元一次方程,求m 的值及方程的解. 2.已知方程(3a +2b)x 2+ax +b =0是关于x 的一元一次方程,求方程的解.3.已知(m 2-1)x 2-(m +1)x +8=0是关于x 的一元一次方程,求式子199(m +x)(x -2m)+9m +17的值.【类型】一、利用方程的解求字母系数的值 题型1:利用方程的解的定义求字母系数的值4.关于x 的方程a(x -a)+b(x +b)=0有无穷多个解,则( )A .a +b =0B .a -b =0C .ab =0D .ab =05.关于x 的方程(2a +b)x -1=0无解,则ab 是( )A .正数B .非正数C .负数D .非负数6.已知关于x 的方程9x -3=kx +14有整数解,那么满足条件的整数k =__________. 7.已知x =12是方程6(2x +m)=3m +2的解,求关于y 的方程my +2=m(1-2y)的解.8.当m 取什么整数时,关于x 的方程12mx -53=12⎝⎛⎭⎫x -43的解是正整数? 题型2:利用两个方程同解或解具有已知倍数关系确定字母系数的值9.如果方程x -43-8=-x +22的解与关于x 的方程2ax -(3a +5)=5x +12a +20的解相同,确定字母a 的值.题型3:利用方程的错解确定字母系数的值10.小马虎解方程2x -13=x +a2-1,去分母时,方程右边的-1忘记乘6,其他步骤都正确,这时方程的解为x =2,试求a 的值,并正确解方程. 参考答案1.解:由题意,得⎩⎪⎨⎪⎧|m|-1=1,m -2≠0,所以m =-2.将m =-2代入原方程,得-4x +16=0,解得x =4.2.解:由题意,得⎩⎪⎨⎪⎧3a +2b =0,a≠0,所以3a =-2b ,即a =-23b.当3a +2b =0时,原方程可化为ax +b =0,则x =-ba .将a =-23b 代入方程的解中,得x =-b a =32.3.解:由题意,得⎩⎪⎨⎪⎧m 2-1=0,m +1≠0,所以m =1.当m =1时,原方程可化为-2x +8=0,解得x =4.当m =1,x =4时,199(m +x)(x -2m)+9m +17=199×5×2+9×1+17=2 016. 4.A 5.B 6.8,-8,10或267.解:将x =12代入方程6(2x +m)=3m +2,得6⎝⎛⎭⎫2×12+m =3m +2,解得m =-43. 将m =-43代入方程my +2=m(1-2y),得-43y +2=-43(1-2y),解得y =56.点拨:已知一元一次方程的解,确定关于某一个未知数的方程中另外一个字母的值,只需把未知数的值(方程的解)代入原方程,即可得出含另一个字母的方程,通过求解确定另一个字母的值,从而进行关于其他字母的计算.8.解:原方程可化为12mx -53=12x -23,所以12(m -1)x =1,所以(m -1)x =2.因为x 必须为正整数且m 为整数,故m -1=1或2.当m -1=1,即m =2时,x =2; 当m -1=2,即m =3时,x =1.所以当m =2或3时,方程的解为正整数. 9.解:x -43-8=-x +22,去分母,得2(x -4)-48=-3(x +2).去括号、移项、合并同类项,得5x =50.系数化为1,得x =10.把x =10代入方程2ax -(3a +5)=5x +12a +20, 得2a×10-(3a +5)=5×10+12a +20, 去括号、移项,得20a -3a -12a =5+50+20. 合并同类项,得5a =75,系数化为1,得a =15. 10.解:由题意得4x -2=3x +3a -1,移项、合并同类项,得x =3a +1. 因为x =2,所以2=3a +1,则a =13.当a =13时,原方程为2x -13=x +132-1,解得x =-3.技巧2:特殊一元一次方程的解法技巧【类型】一、分子、分母含小数的一元一次方程 题型1:巧化分母为11.解方程:4x -1.60.5-3x -5.40.2=1.8-x0.1.2.解方程:2x +10.25-x -20.5=-10.题型2:巧化同分母3.解方程:x 0.6-0.16-0.5x0.06=1.题型3:巧约分去分母4.解方程:4-6x 0.01-6.5=0.02-2x0.02-7.5.【类型】二、分子、分母为整数的一元一次方程 题型1:巧用拆分法5.解方程:x -12-2x -36=6-x3.6.解方程:x 2+x 6+x 12+x20=1.题型2:巧用对消法7.解方程:x 3+x -25=337-6-3x15.题型3:巧通分8.解方程:x +37-x +25=x +16-x +44.【类型】三、含括号的一元一次方程 题型1:利用倒数关系去括号9.解方程:32⎣⎡⎦⎤23⎝⎛⎭⎫x 4-1-2-x =2. 题型2:整体合并去括号10.解方程:x -13⎣⎡⎦⎤x -13(x -9)=19(x -9). 题型3:整体合并去分母11.解方程:13(x -5)=3-23(x -5).题型4:不去括号反而添括号12.解方程:12⎣⎡⎦⎤x -12(x -1)=23(x -1). 题型5:由外向内去括号13.解方程:13⎣⎡⎦⎤14⎝⎛⎭⎫13x -1-6+2=0. 题型6:由内向外去括号14.解方程:2⎣⎡⎦⎤43x -⎝⎛⎭⎫23x -12=34x. 参考答案1.解:去分母,得2(4x -1.6)-5(3x -5.4)=10(1.8-x).去括号、移项、合并同类项,得3x =-5.8. 系数化为1,得x =-2915.点拨:本题将各分数分母化为整数1,从而巧妙地去掉了分母,给解题带来了方便 . 2.解:去分母、去括号,得8x +4-2x +4=-10.移项、合并同类项,得6x =-18. 系数化为1,得x =-3.点拨:由0.25×4=1,0.5×2=1,可巧妙地将分母化为整数1. 3.解:化为同分母,得0.1x 0.06-0.16-0.5x 0.06=0.060.06.去分母,得0.1x -0.16+0.5x =0.06. 解得x =1130.4.解:原方程可化为4-6x 0.01+1=0.01-x0.01.去分母,得4-6x +0.01=0.01-x. 解得x =45.点拨:本题将第二个分数通过约分处理后,使两个分数的分母相同,便于去分母.5.解:拆项,得x 2-12-x 3+12=2-x3.移项、合并同类项,得x2=2.系数化为1,得x =4.点拨:方程通过拆项处理后,便于合并同类项,使复杂方程简单化. 6.解:拆项,得⎝⎛⎭⎫x -x 2+⎝⎛⎭⎫x 2-x 3+⎝⎛⎭⎫x 3-x 4+⎝⎛⎭⎫x 4-x5=1. 整理得x -x 5=1.解得x =54.点拨:因为x 2=x -x 2,x 6=x 2-x 3,x 12=x 3-x 4,x 20=x 4-x5,所以把方程的左边每一项拆项分解后再合并就很简便 .7.解:原方程可化为x 3+x -25=247+x -25,即x 3=247.所以x =727. 点拨:此题不要急于去分母,通过观察发现-6-3x 15=x -25,两边消去这一项可避免去分母运算.8.解:方程两边分别通分后相加,得5(x +3)-7(x +2)35=2(x +1)-3(x +4)12.化简,得-2x +135=-x -1012.解得x =-36211.点拨:本题若直接去分母,则两边应同乘各分母的最小公倍数420,运算量大容易出错,但是把方程左右两边分别通分后再去分母,会给解方程带来方便. 9.解:去括号,得x4-1-3-x =2.移项、合并同类项,得-34x =6.系数化为1,得x =-8.点拨:观察方程特点,由于32与23互为倒数,因此让32乘以括号内的每一项,则可先去中括号,同时又去小括号,非常简便.10.解:原方程可化为x -13x +19(x -9)-19(x -9)=0.合并同类项,得23x =0.系数化为1,得x =0.11.解:移项,得13(x -5)+23(x -5)=3.合并同类项,得x -5=3.解得x =8.点拨:本题将x -5看成一个整体,通过移项、合并同类项进行解答,这样避免了去分母,给解题带来简便.12.解:原方程可化为12[(x -1)+1-12(x -1)]=23(x -1).去中括号,得12(x -1)+12-14(x -1)=23(x -1).移项、合并同类项,得-512(x -1)=-12.解得x =115.13.解:去中括号,得112⎝⎛⎭⎫13x -1-2+2=0.[来源:学科网] 去小括号,得136x -112=0.移项,得136x =112.系数化为1,得x =3.14.解:去小括号,得2[43x -23x +12]=34x.去中括号,得43x +1=34x.移项,合并同类项,得712x =-1.系数化为1,得x =-127.【题型讲解】【题型】一、一元一次方程概念例1、关于x 的一元一次方程224a x m -+=的解为1x =,则a m +的值为( ) A .9 B .8C .5D .4【详解】解:因为关于x 的一元一次方程2x a -2+m=4的解为x=1, 可得:a -2=1,2+m=4, 解得:a=3,m=2, 所以a+m=3+2=5, 故选:C .【题型】二、一元一次方程的解法例2、解一元一次方程11(1)123x x +=-时,去分母正确的是( )A .3(1)12x x +=-B .2(1)13x x +=-C .2(1)63x x +=-D .3(1)62x x +=-【答案】D【分析】根据等式的基本性质将方程两边都乘以6可得答案. 【详解】解:方程两边都乘以6,得:3(x +1)=6﹣2x ,故选:D . 例3、解方程:221123x x x ---=-【答案】27x =【分析】去分母、去括号、移项、合并同类项、系数化为1,依此即可求解. 【详解】解:221123x x x ---=-()()6326221x x x --=--636642x x x -+=-+ 634662x x x -+=-+ 72x =27x =【题型】三、一元一次方程应用之配套问题和工程问题例4、某车间有22名工人,每人每天可生产1200个螺钉或2000个螺母,1个螺钉需配2个螺母,为使生产的螺钉和螺母刚好配套,若设x 名工人生产螺钉,依题意列方程为( ) A .1200x =2000(22﹣x ) B .1200x =2×2000(22﹣x ) C .1200(22﹣x )=2000x D .2×1200x =2000(22﹣x )【答案】D【分析】首先根据题目中已经设出每天安排x 个工人生产螺钉,则(22-x )个工人生产螺母,由1个螺钉需要配2个螺母①可知螺母的个数是螺钉个数的2倍①从而得出等量关系,就可以列出方程. 【详解】解:设每天安排x 个工人生产螺钉,则(22-x )个工人生产螺母,利用一个螺钉配两个螺母.由题意得:2×1200x=2000①22-x ),即2×1200x=2000①22-x①①故选D① 【题型】四、一元一次方程应用之销售盈亏问题例5、随着传统节日“端午节”临近,某超市决定开展“欢度端午,回馈顾客”的活动,将进价为120元一盒的某品牌粽子按标价的8折出售,仍可获利20%,则该超市该品牌粽子的标价为__元.( )A .180B .170C .160D .150【答案】A【分析】设该超市该品牌粽子的标价为x 元,则售价为80%x 元,根据等量关系:利润=售价﹣进价列出方程,解出即可.【详解】解:设该超市该品牌粽子的标价为x 元,则售价为80%x 元, 由题意得:80%x ﹣120=20%×120, 解得:x =180.即该超市该品牌粽子的标价为180元. 故选:A .【题型】五、一元一次方程应用之比赛积分问题例6、一张试卷有25道选择题,做对一题得4分,做错一题得-1分,某同学做完了25道题,共得70分,那么他做对的题数是( ) A .17道 B .18道C .19道D .20道【答案】C【分析】设作对了x 道,则错了(25-x )道,根据题意列出方程进行求解. 【详解】设作对了x 道,则错了(25-x )道,依题意得4x -(25-x)=70,解得x=19 故选C.一元一次方程(达标训练)一、单选题1.(2020·浙江·模拟预测)下列各式:①253-+=;①235=3x x x -+;①211x +=;①21=x;①23x +;①4x =.其中是一元一次方程的有( ) A .1个 B .2个C .3个D .4个【答案】B【分析】根据一元一次方程的定义逐个判断即可 【详解】解:①不含未知数,故错 ①未知数的最高次数为2,故错①含一个未知数,次数为1,是等式且两边均为整式,故对 ①左边不是整式,故错 ①不是等式,故错①含一个未知数,次数为1,是等式且两边均为整式,故对故选:B【点睛】本题考查了一元一次方程的定义,熟练掌握并理解一元一次方程的定义是解本题的关键2.(2022·浙江温州·三模)解方程2233522x x x x x --+=--,以下去分母正确的是( )A .22335x x x ---=B .22335x x x --+=C .()223352x x x x ---=-D .()223352x x x x --+=-【答案】D【分析】利用等式的性质在分式方程两边分别乘()2x - 即可.【详解】A ,()223352,x x x x +--=-故此选项不符合题意. B ,()223352,x x x x +--=-故此选项不符合题意. C ,()223352,x x x x +--=-故此选项不符合题意. D ,()223352,x x x x +--=-故此选项符合题意.故选:D .【点睛】本题主要考查了解分式方程去分母,根据等式的性质在分式方程两边分别乘以分母的最简公分母,熟练掌握等式的性质是解此题的关键.3.(2022·重庆沙坪坝·一模)若关于x 的方程25x a +=的解是2x =,则a 的值为( ) A .9- B .9 C .1- D .1【答案】D【分析】把2x =代入方程计算即可求出a 的值. 【详解】解:把2x =代入方程得:45a +=, 解得1a =. 故选:D .【点睛】本题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值. 4.(2022·河北石家庄·二模)1x =是下列哪个方程的解( ) A .65x =- B .2233+=+x xC .21133x x x x -=-- D .2x x =【答案】D【分析】把x =1代入各选项进行验算即可得解. 【详解】解:A 、5−1=4≠6,故本选项错误; B 、2124⨯+=,3136⨯+=,4≠6,故本选项错误; C 、当x =1时,x -1=0即分式的分母为0,故本选项错误;D 、211=,故本选项正确. 故选:D .【点睛】本题考查了方程的解的概念,使方程的左右两边相等的未知数的值是方程的解. 5.(2022·广东·佛山市南海外国语学校三模)我国古代的《洛书》中记载了最早的三阶幻方—九宫图.在如图所示的幻方中,每一横行、每一竖列以及两条对角线上的数字之和都相等,则m 的值是( )A .5B .3C .1-D .2-【答案】A【分析】根据幻方中,每一横行、每一竖列以及两条对角线上的数字之和都相等列出方程,即可求解. 【详解】解:设幻方正中间的数字为a , 依题意得:124a m a ++=++, 解得:5m =. 故选A .【点睛】此题考查了一元一次方程的应用,正确理解题意是解题的关键.二、填空题6.(2022·四川达州·二模)方程2x -3=5的解为________. 【答案】x =4【分析】根据解一元一次方程的解法求解即可得. 【详解】解:2x -3=5, 移项得2x =8, 系数化为1得:x =4, 故答案为:x =4.【点睛】题目主要考查解一元一次方程,熟练掌握方法是解题关键.7.(2022·四川广元·二模)已知:A ,B 在数轴上对应的数分别用a ,b 表示,且2(4)|12|0a b ++-=.若点C 点在数轴上且满足3AC BC =,则C 点对应的数为________. 【答案】8或20##20或8【分析】先根据非负数的性质求出a ,b 的值,分C 点在线段AB 上和线段AB 的延长线上两种情况讨论,即可求解.【详解】解:①2(4)|12|0a b ++-= ①a +4=0,b −12=0 解得:a =−4,b =12①A 表示的数是−4,B 表示的数是12 设数轴上点C 表示的数为c ①AC =3BC ①|c +4|=3|c −12| 当点C 在线段AB 上时 则c +4=3(12−c ) 解得:c =8当点C 在AB 的延长线上时 则c +4=3(c −12) 解得:c =20综上可知:C 对应的数为8或20.【点睛】本题考查了非负数的性质,方程的解法,数轴两点之间的距离,运用分类讨论思想方程思想和数形结合思想是解本题的关键.三、解答题8.(2022·四川广元·一模)解方程:2(1)13x x x --=-. 【答案】12x =-【分析】先去括号,再移项,合并同类项,最后把未知数的系数化“1”,从而可得答案. 【详解】解:去括号,得2213x x x -+=-. 移项及合并同类项,得21x =-. 系数化为1,得12x =-.【点睛】本题考查的是一元一次方程的解法,掌握“解一元一次方程的步骤”是解本题的关键. 9.(2022·湖南·长沙市长郡双语实验中学二模)“小口罩,大温暖”,为有效防控疫情,缓解基层防疫物资短缺问题,2020年2月10日,福山区首批4万只口罩免费派发.烟台市政府紧急调拨的这批民用口罩包括A ,B 两种不同款型,其中A 型口罩单价100元,B 型口罩单价80元.(1)先进行试点发放,某社区环卫工人共收到A ,B 两种款型的口罩100盒,总价值共计9200元,求免费发放给该社区环卫工人的A 型口罩和B 型口罩各多少盒?(2)我区某街道办事处决定将此项公益活动在其整个街道社区全面铺开,按照试点发放中A,B两种款型的数量比共发放2000盒.若该社区人口平均每500人发放A型口罩m盒,B型口罩(328m-)盒.求该街道社区人口总数.【答案】(1)免费发放给该社区环卫工人的A型口罩60盒,B型口罩40盒(2)该街道社区人口总数为50000人【分析】(1)设免费发放给该社区环卫工人的A型口罩x盒,B型口罩y盒,根据题意,列出方程,即可求解;(2)根据题意可得3286040m m-=,从而得到m=12,即可求解.(1)解:设免费发放给该社区环卫工人的A型口罩x盒,B型口罩y盒,依题意得:100100809200x yx y+=⎧⎨+=⎩,解得:6040xy=⎧⎨=⎩.答:免费发放给该社区环卫工人的A型口罩60盒,B型口罩40盒.(2)解:依题意得:328 6040m m-=,解得:m=12,①m+3m−28=20.①该街道社区人口总数=200020×500=50000(人).答:该街道社区人口总数为50000人.【点睛】本题主要考查了一元一次方程的应用,二元一次方程组的应用,明确题意,准确得到等量关系是解题的关键.一元一次方程(提升测评)一、单选题1.(2022·湖北十堰·一模)《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问合伙人数,羊价各是多少?如果我们设合伙人数为x ,则可列方程( ) A .54573x x +=+ B .54573x x -=-C .45357x x +=+D .45357x x-=+【答案】A【分析】根据每人出5钱,还差45钱;若每人出7钱,还差3钱,可以列出相应的一元一次方程,本题得以解决.【详解】解:设合伙人数为x ,则可列方程为 54573x x +=+;故选:A【点睛】本题考查由实际问题抽象出一元一次方程,解答本题的关键是明确题意,列出相应的方程. 2.(2022·浙江温州·二模)若代数式()()2132x x +++的值为8,则代数式()()2231x x -+-的值为( ) A .0 B .11 C .7- D .15-【答案】C【分析】由()()2132x x +++的值为8,求得x =0,再将x =0代入计算可得. 【详解】解:①()()2132x x +++的值为8, ①2x +2+3x +6=8, ①x =0,当x =0时,()()2231x x -+-=2×(-2)+3×(-1)=-7. 故选:C .【点睛】本题考查了解一元一次方程,代数式的求值,掌握解一元一次方程的解法是解题的关键. 3.(2022·河北·石家庄市第四十一中学模拟预测)已知m n =,下列等式不成立的是( ) A .2m n m += B .0-=m n C .22m x n x -=- D .235m n n -=【答案】D【分析】根据等式的性质和合并同类项即可判断. 【详解】由m n =,得2m n m m m +=+=,故A 成立; 0m n m m -=-=,故B 成立;根据等式的性质,等式两边同加或减一个等式,左右两边仍相等,22m x n x -=-,故C 成立;2323m n n n n -=-=-,故D 不成立;故选D .【点睛】本题考查了等式的性质和合并同类项,熟记运算法则是解题的关键.4.(2022·河北保定·一模)已知分式:341()()32a a a a -+---■的某一项被污染,但化简的结果等于2a +,被污染的项应为( ) A .0 B .1 C .23a a -- D .32a a -- 【答案】B【分析】设被污染的部分为p ,然后根据等式的性质解关于p 的方程,求出p 的表达式即可. 【详解】解:设被污染的部分为p , 则341()()232a a p a a a -+-=+--, ①241()232a p a a a --=+--, ①()()()132222a p a a a a --=+⨯--+, ①3122a p a a -=+--, ①22a p a -=-, ①1p =. 故选:B .【点睛】本题主要考查了分式的混合运算和利用等式的性质解一元一次方程,解题的关键是根据等式的性质解方程和掌握分式混合运算顺序和运算法则. 5.(2022·重庆·三模)下列四种说法中正确的有( ) ①关于x 、y 的方程24107x y +=存在整数解.①若两个不等实数a 、b 满足()()244222a b a b +=+,则a 、b 互为相反数.①若2()4()()0a c a b b c ---=-,则2b a c =+. ①若222x yz y xz z xy ---==,则x y z ==. A .①① B .①① C .①①① D .①①①【答案】B【分析】将24x y +提公因式2得2(2)x y +,由x 、y 为整数,则2(3)x y +为偶数,因为107为奇数,即原等式不成立,即可判断①;将442222()()a b a b +=+,整理得222()0a b -=,即得出22a b =,由于实数a 、b 不相等,即得出a 、b 互为相反数,故可判断①;2()4()()0a c a b b c ---=-整理得2(2)0a c b +-=,即得20a c b +-=,即2a c b +=,故可判断①;由222x yz y xz z xy ---==,得出2222x xz y yz y xy z xz ⎧+=+⎨+=+⎩,即可变形为222211()()2211()()22x z y z y x z x ⎧+=+⎪⎪⎨⎪+=+⎪⎩,可以得出x y z ==或0x y z ++=,故可判断①. 【详解】解:①262(3)x y x y +=+, ①如果x 、y 为整数,那么2(3)x y +为偶数, ①107为奇数,①24107x y +=不存在整数解,故①错误; 442222()()a b a b +=+444422222a b a b a b +++=442220a b a b +-=222()0a b -=①22a b =,①实数a 、b 不相等,①a 、b 互为相反数,故①正确; 2()4()()0a c a b b c ---=-222244440a ac c ab ac b bc -+-++-=()()22440a c b a c b +-++=2(2)0a c b +-=①20a c b +-=,即2a c b +=,故①正确; ①222x yz y xz z xy ---==①2222x xz y yzy xy z xz ⎧+=+⎨+=+⎩, ①2222222211441144x xz z y yz z y xy x z xz x ⎧++=++⎪⎪⎨⎪++=++⎪⎩,即222211()()2211()()22x z y z y x z x ⎧+=+⎪⎪⎨⎪+=+⎪⎩,①11()2211()22x z y z y x z x ⎧+=±+⎪⎪⎨⎪+=±+⎪⎩,①x y z ==或0x y z ++=,故①不一定正确. 综上可知正确的有①①.故选B.【点睛】本题考查因式分解,整式的混合运算.熟练掌握完全平方公式是解题关键.二、填空题6.(2022·山东临沂·一模)如图,用一块长7.5cm、宽3cm的长方形纸板,和一块长6cm、宽1.5cm 的长方形纸板,与一块小正方形纸板以及另两块长方形纸板,恰好拼成一个大正方形,则小正方形的边长是______cm,拼成的大正方形的面积是______cm2.【答案】 4.581【分析】设小正方形的边长为x cm,然后表示出大正方形的边长,利用正方形的面积相等列出方程求得小正方形的边长,然后求得大正方形的边长即可求得面积.【详解】解:设小正方形的边长为x cm,则大正方形的边长为(6+7.5-x)cm或(x+3+1.5)cm,根据题意得:6+7.5-x=x+3+1.5,解得:x=4.5,则大正方形的边长为6+7.5-x=6+7.5-4.5=9(cm),大正方形的面积为92=81(cm2),故答案为:4.5;81.【点睛】此题主要考查了一元一次方程的应用,关键是正确理解题意,设出小正方形的边长并表示出大正方形的边长.7.(2022·上海静安·1=的解是________.【答案】x=1【分析】首先方程两边同时平方,把无理方程化为有理方程,再解方程即可求得【详解】解:方程两边同时平方,得3x-2=1,解得x=1,经检验,x=1是原方程的解,所以,原方程的解为x=1.故答案为:x=1.【点睛】本题考查了无理方程的解法,熟练掌握和运用无理方程的解法是解决本题的关键,注意要检验.三、解答题8.(2022·河北·育华中学三模)如图,数轴上a 、b 、c 三个数所对应的点分别为A 、B 、C ,已知b是最小的正整数,且a 、c 满足2(6)20c a -++=.(1)①直接写出数a 、c 的值 , ; ①求代数式222a c ac +-的值;(2)若将数轴折叠,使得点A 与点C 重合,求与点B 重合的点表示的数; (3)请在数轴上确定一点D ,使得AD =2BD ,则D 表示的数是 . 【答案】(1)①-2,6;①64 (2)3 (3)4或0【分析】(1)①根据平方和绝对值的非负性即可求出a 和c ,①把a 和c 的值代入222a c ac +-求值即可;(2)根据题意,求出b 的值,然后求出线段AC 的中点,即可求出结论;(3)设点D 表示的数为x ,然后根据点D 的位置分类讨论,分别根据2AD BD =列出方程即可分别求出结论. (1) 解:①①()2620c a -++=, ①20a +=,60c -=, 解得2a =-,6c =. 故答案为:-2,6.①把2a =-,6c =代入222a c ac +-,2224362464a c ac +-=++=;(2)解:①b 是最小的正整数,①1b =,①线段AC 的中点为()2622-+÷=,设与点B 重合的点表示的数为n ,则(1+n )÷2=2, 解得:n =3.①与点B 重合的点表示的数是3. 故答案为:3. (3)解:因为a =-2,b =1,c =6,设点D 表示的数为x ,若2AD BD =,分三种情况讨论: ①若点D 在点A 的左侧,则x <-2且()221x x --=-, 解得4x =(不符合题意,舍去);①若点D 在点A 、B 之间,则-2<x <1且()()221x x --=-, 解得0x =;①若点D 在点B 右侧,则x >1且x -(-2)=2(x -1), 解得:x =4.综上所述,点D 表示的数是0或4. 故答案为:0或4.【点睛】此题考查了非负性的应用、数轴上两点之间的距离、中点公式和一元一次方程的应用,解题的关键是掌握平方、绝对值的非负性、数轴上两点之间的距离公式、中点公式和等量关系.。
解一元一次方程
➢ 课前预习
1. 含有_______的_______叫做方程.
2. 等式的基本性质
性质1:
等式两边同时加上(或减去)_________,所得结果仍是等式.
性质2:
等式两边同时乘___________(或_____________________),所得结果仍是等式.
3. 已知a ,b ,x ,y 都是未知数,给出下列式子:
①21x +;②325+=;③231x +≠;④321a +=;
⑤531a b +=;⑥23x y =;⑦2
51x x =+.
其中是方程的有_________________.(填序号)
4. 解下列方程:
(1)192x -=; (2)36248a +=.
➢ 知识点睛
1. 一元一次方程的定义:只含有__________ ,______________,等号两边都是
_______的方程叫做一元一次方程.
2. 使方程中等号左右两边________的___________叫做方程的解.
3. 等式的基本性质:①等式两边加(或减)同一个__________结果仍___________;
②等式两边乘同一个数,或除以同一个_________的数,结果仍___________.
4. 解方程的五个步骤:①______________;②______________;③_____________;
④______________;⑤_______________.
➢ 精讲精练
1. 下列各式中,是一元一次方程的为_________(填序号).
①210x +=;②3x -5y =1;③21x x +=;④3+7=10.
2. 若(1)6a
a x -=-是关于x 的一元一次方程,则a =______.
3. 如果x =2是方程5ax =的解,那么a =__________.
4. 解下列方程:
(1)1036x x +=-;
解:移项,得
合并同类项,得
系数化为1,得
(2)3653x x x --=+;
(3)2(10)52(1)x x x x -+=+-;
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
(4)37(1)32(3)x x x --=-+;
(5)15
2
33 442
x x
+=-;
解:去分母,得
移项,得
合并同类项,得
系数化为1,得
(6)111 3312
x x
+=-;
(7)11051 2442
x x
x x
+-
-=+;
解:去分母,得
去括号,得
移项,得
合并同类项,得
系数化为1,得
(8)
151
1 36
x x
+-
-=;
(9)1337y y --
=;
(10)
14
126110312--=+--x x x ;
(11)
4 1.
5 1.250830.50.12
x x x ----=+; 解:原方程可化为 去分母,得
去括号,得
移项,得
合并同类项,得
系数化为1,得
(12)0.89 1.33511.20.20.3
x x x --+-=.
5. m 为何值时,代数式3152--m m 的值与代数式2
7m -的值的和等于5?
【参考答案】
➢ 课前预习
1. 未知数 等式
2. 同一个数 同一个数 除以同一个不为0的数
3. ④⑤⑥⑦
4. (1)21x = (2)6a =
➢ 知识点睛
1. 一个未知数 未知数的次数都是1 整式
2. 相等 未知数的值
3. 数(或式子),相等
不为0,相等
4. 去分母 去括号 移项 合并同类项 系数化为1 ➢ 精讲精练
1. ①
2. -1
3. 2.5
4. (1)8x =;(2)3x =-; (3)43
x =-; (4)5x =; (5)8x =;(6)58x =; (7)43
x =-; (8)1x =-; (9)47y =;(10)12
x =; (11)2x =-;(12)1x =-. 5. 7m =-。