七年级(初一)下册一元一次方程复习讲义

第三章 一元一次方程(韩老师)本章知识网络结构图3.1一元一次方程的概念和性质【本讲主要内容】1. 等式与方程表示相等关系的式子叫做等式。

含有未知数的等式叫做方程。

可见方程必须具备两个条件：一是必须含有未知数，二是必须是一个等式。

2. 等式的性质等式的性质1：等式两边加（减）同一个数（式子）。

结果仍相等。

等式的性质2：等式两边乘同一个数，或除以同一个不为0的数，结果仍相等。

应用等式的性质对等式进行变形时，必须注意“同”字。

要对等式进行变形，就要保证等式两边始终相等，也就是说，运用等式的性质时，等式两边必须同时进行变形。

3. 一元一次方程的概念我们把含有一个未知数，并且未知数的指数都是1的方程叫做一元一次方程。

一元一次方程的最简形式是b ax =（≠a 0）。

方程中的未知数叫做“元”，一个方程中有几个未知数，就称这个方程为几元方程。

方程中含未知数的项的最高次数叫做方程的次数，这一点和多项式的次数有类似的地方。

例如27x 3-=-是一元一次方程，4y 4y 2y 2-=+是一元二次方程，0y x 3=-是二元一次方程，6y 4x 32-=+是二元二次方程。

4. 方程的解与解方程方程是一个有待研究的等式，即研究这个等式中的未知数取什么值时等式才成立。

解方程就是确定使方程中等号左右两边相等的未知数的值，我们把这样的未知数的值叫做方程的解。

这样的值可能有一个或多个，也可能没有，所以方程可能有一个解、多个解，也可能无解。

如方程3x-5=4x+3只有一个解x=-8。

方程2x-7=5x-（3x+7）有无数个解，而方程2x-3=2x+2无解。

求方程的解或判定方程无解的过程叫做解方程。

利用等式的性质，对方程进行一系列的变形，就可以求出方程的解。

5. 思想方法（本单元常用到的数学思想方法小结）⑴建模思想：通过对实际问题中的数量关系的分析，抽象成数学模型，建立一元一次方程的思想.⑵方程思想：用方程解决实际问题的思想就是方程思想.⑶化归思想：解一元一次方程的过程，实质上就是利用去分母、去括号、移项、合并同类项、未知数的系数化为1等各种同解变形，不断地用新的更简单的方程来代替原来的方程，最后逐步把方程转化为x=a 的形式. 体现了化“未知”为“已知”的化归思想.⑷数形结合思想：在列方程解决问题时，借助于线段示意图和图表等来分析数量关系，使问题中的数量关系很直观地展示出来，体现了数形结合的优越性.⑸分类思想：在解含字母系数的方程和含绝对值符号的方程过程中往往需要分类讨论，在解有关方案设计的实际问题的过程中往往也要注意分类思想在过程中的运用.【典型例题】例1. 已知方程2x m －3+3x=5是一元一次方程，则m= .解析：由一元一次方程的定义可知m －3=1，解得m=4.或m －3=0，解得m=3所以m=4或m=3警示：很多同学做到这种题型时就想到指数是1，从而写成m=1，这里一定要注意x 的指数是（m －3）.例2. 已知2x =-是方程ax 2－（2a －3）x+5=0的解，求a 的值.解析：∵x=－2是方程ax 2－（2a －3）x+5=0的解∴将x=－2代入方程，得 a·（－2）2－（2a －3）·（－2）+5=0化简，得 4a+4a －6+5=0∴ a=81 点拨：要想解决这道题目，应该从方程的解的定义入手，方程的解就是使方程左右两边值相等的未知数的值，这样把x=－2代入方程，然后再解关于a 的一元一次方程就可以例3.已知a 、b 为定值，无论k 为何值，关于x 的一元一次方程26bk x 3a kx 3=--+的解总是1，试求a 、b 的值。

第三章一元一次方程复习讲义知识点1．等式：用“=”号连接而成的式子叫等式.2．等式的性质：等式性质1：等式两边都加上(或减去)同一个数或同一个整式，所得结果仍是等式；等式性质2：等式两边都乘以(或除以)同一个不为零的数，所得结果仍是等式.例1(1)怎样从等式x-5=y-5得到等式x=y?(2)怎样从等式3+x=1得到等式x=-2?(3)怎样从等式4x=12得到等式x=3?例2利用等式的性质解下列方程：(1)x+7=26(2)-5x=203．方程：只含有一个未知数，未知数的次数是1，等号两边都是整式，这样的方程叫做一元一次方程.4．方程的解：使等式左右两边相等的未知数的值叫方程的解；注意：“方程的解就能代入”！5．移项：改变符号后，把方程的项从一边移到另一边叫移项.移项的依据是等式性质1. 6．一元一次方程：只含有一个未知数，并且未知数的次数是1，并且含未知数项的系数不是零的整式方程是一元一次方程.7.一元一次方程的标准形式：ax+b=0(x是未知数，a、匕是已知数，且aW0).8．一元一次方程解法的一般步骤：化简方程分数基本性质去分母同乘(不漏乘)最简公分母去括号先去小括号,再去中括号,最后去大括号.依据是去括号法则和乘法分配律，注意符号变化移项把含有未知数的项移到一边,常数项移到另一边.“过桥变号”，依据是等式性质一合并同类项将未知数的系数相加，常数项相加.依据是乘法分配律合并后注意符号系数化为1在方程的两边除以未知数的系数.依据是等式性质二.例1解下列方程[1]用合并同类项的方法解一元一次方程(1)2x-£%=6-8;(2)7x—2.5x+3x-1.5x=-15x4—6x3.[2]用移项的方法解一元一次方程(1)7-2x=3-4x(2)4x+10=6x[3]利用去括号解一元一次方程去括号法则：去掉“+()”，括号内各项的符号不变.去掉“-()”，括号内各项的符号改变.用三个字母a、b、c表示去括号前后的变化规律：a+(b+c)=a+b+ca-(b+c)=a—b—c(1)2x-(x+10)=5x+2(x—1)(2)3x—7(x—1)=3—2(x+3)[4]利用去分母解一元一次方程(总结：像上面这样的方程中有些系数是分数，如果能化去分母，把系数化为整数，则可以使解方程中的计算更方便些.)2x+2x+7x+x=33(2)3x+x-1=3-2x-1(1)^要点归纳1.去分母时，应在方程的左右两边乘以分母的最小公倍数；2.去分母的依据是等式性质2，去分母时不能漏乘没有分母的项；3.去分母与去括号这两步分开写，不要跳步，防止忘记变号.10．列一元一次方程解应用题：(1)读题分析法:多用于“和，差，倍，分问题”仔细读题，找出表示相等关系的关键字，例如：“大，小，多，少，是，共，合，为，完成，增加，减少，配套”，利用这些关键字列出文字等式，并且据题意设出 未知数，最后利用题目中的量与量的关系填入代数式，得到方程.（2）画图分析法:…………多用于“行程问题”利用图形分析数学问题是数形结合思想在数学中的体现，仔细读题，依照题意画出有关图形，使图形各部分具有特定的含义，通过图形找相等关系是解决问题的关键，从而取得列方程的依据，最后利用量与量之间的关系（可把未知数看做已知量），填入有关的代数式是获得方程的基础.11.列方程（组）的应用题的一般步骤：审：审清题意，分清题中的已知量、未知量．设：设未知数，设其中某个未知量为x.列：根据题意寻找等量关系列方程．解：解方程．验：检验方程的解是否符合题意．答：写出答案（包括单位）．［注意］审题是基础，找等量关系是关键.11．解实际应用题：知识点1:市场经，^、打折销售问题（1）商品利润=商品售价一商品成本价（3）商品销售额=商品销售价X 商品销售量（4）商品的销售利润=（销售价一成本价）X 销售量例1一商店在某一时间以每件60元的价格卖出两件衣服，其中一件盈利25%，另一件亏损25%，卖这两件衣服总的是盈利还是亏损，或是不盈不亏?变式1.某琴行同时卖出两台钢琴，每台售价为960元.其中一台盈利20%，另一台亏损20%.这次琴行是盈利还是亏损，或是不盈不亏？例2一件服装先将进价提高25%出售，后进行促销活动，又按标价的8折出售,此时售价为60元.请问商家是盈是亏，还是不盈不亏？例3.某商品的进价是1000元，售价是1500元，由于销售情况不好，商店决定降价出 售，但又要保证利润率不低于5%,那么商店最多可打几折出售此商品？（2） 商品利润率= 商品利润 商品成本价X 100%例4.某商场国庆节搞促销活动，购物不超过200元不给优惠，超过200元但不超过500元的优惠10%，超过500元，其中500元按9折优惠，超过的部分按8折优惠。

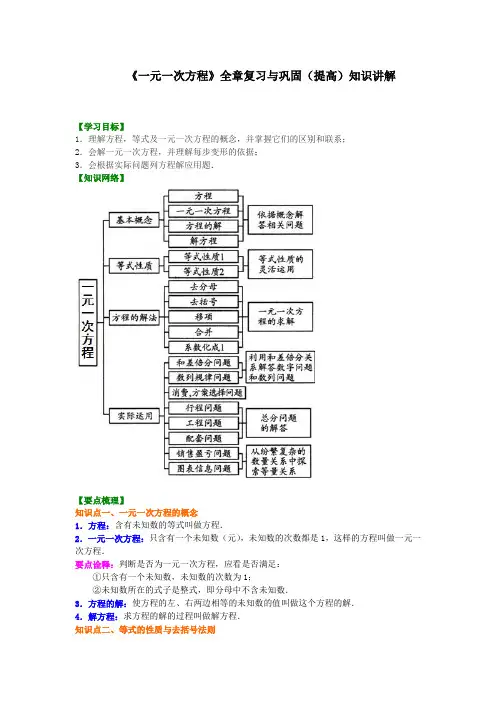
《一元一次方程》全章复习与巩固（提高）知识讲解【学习目标】1．理解方程，等式及一元一次方程的概念，并掌握它们的区别和联系；2．会解一元一次方程，并理解每步变形的依据；3．会根据实际问题列方程解应用题．【知识网络】【要点梳理】知识点一、一元一次方程的概念1．方程：含有未知数的等式叫做方程．2．一元一次方程：只含有一个未知数（元），未知数的次数都是1，这样的方程叫做一元一次方程．要点诠释：判断是否为一元一次方程，应看是否满足：①只含有一个未知数，未知数的次数为1；②未知数所在的式子是整式，即分母中不含未知数．3．方程的解：使方程的左、右两边相等的未知数的值叫做这个方程的解．4．解方程：求方程的解的过程叫做解方程．知识点二、等式的性质与去括号法则1．等式的性质：等式的性质1：等式两边加(或减)同一个数(或式子)，结果仍相等．等式的性质2：等式两边乘同一个数，或除以同一个不为0的数，结果仍相等．2．合并法则：合并时，把系数相加(减)作为结果的系数，字母和字母的指数保持不变．3．去括号法则：（1）括号外的因数是正数，去括号后各项的符号与原括号内相应各项的符号相同．（2）括号外的因数是负数，去括号后各项的符号与原括号内相应各项的符号相反． 知识点三、一元一次方程的解法解一元一次方程的一般步骤：(1)去分母：在方程两边同乘以各分母的最小公倍数．(2)去括号：依据乘法分配律和去括号法则，先去小括号，再去中括号，最后去大括号．(3)移项：把含有未知数的项移到方程一边，常数项移到方程另一边．(4)合并：逆用乘法分配律，分别合并含有未知数的项及常数项，把方程化为ax ＝b(a ≠0)的形式．(5)系数化为1：方程两边同除以未知数的系数得到方程的解b x a=(a ≠0)． (6)检验：把方程的解代入原方程，若方程左右两边的值相等，则是方程的解；若方程左右两边的值不相等，则不是方程的解．知识点四、用一元一次方程解决实际问题的常见类型1.行程问题：路程＝速度×时间2.和差倍分问题：增长量＝原有量×增长率3.利润问题：商品利润＝商品售价－商品进价4.工程问题：工作量＝工作效率×工作时间，各部分劳动量之和＝总量5.银行存贷款问题：本息和＝本金+利息，利息＝本金×利率×期数6.数字问题：多位数的表示方法：例如：32101010abcd a b c d =⨯+⨯+⨯+.【典型例题】类型一、一元一次方程的相关概念1．已知方程(3m-4)x 2-(5-3m)x-4m ＝-2m 是关于x 的一元一次方程，求m 和x 的值．【思路点拨】若一个整式方程经过化简变形后，只含有一个未知数，并且未知数的次数都是1，系数不为0，则这个方程是一元一次方程．【答案与解析】解：因为方程(3m-4)x 2-(5-3m)x-4m ＝-2m 是关于x 的一元一次方程，所以3m-4＝0且5-3m ≠0．由3m-4＝0解得43m =，又43m =能使5-3m ≠0，所以m 的值是43． 将43m =代入原方程，则原方程变为485333x ⎛⎫--⨯= ⎪⎝⎭，解得83x =-． 所以43m =，83x =-． 【总结升华】解答这类问题，一定要严格按照一元一次方程的定义．方程(3m-4)x 2-(5-3m)x-4m ＝-2m 2是关于x 的一元一次方程，就是说x 的二次项系数3m-4＝0，而x的一次项系数5-3m≠0，m的值必须同时符合这两个条件．举一反三：【高清课堂：一元一次方程复习393349 等式和方程例3】【变式】下面方程变形中，错在哪里：(1)方程2x=2y两边都减去x+y，得2x-(x+y)=2y-(x+y), 即x-y=-(x-y).方程 x-y=-(x-y)两边都除以x-y, 得1=-1.（2）3721223x xx-+=+，去分母，得3(3-7x)=2(2x+1)+2x，去括号得：9-21x=4x+2+2x.【答案】（1）答：错在第二步，方程两边都除以x-y.（2）答：错在第一步，去分母时2x项没乘以公分母6.2.如果5(x+2)＝2a+3与(31)(53)35a x a x+-=的解相同，那么a的值是________．【答案】7 11【解析】由5(x+2)＝2a+3，解得275ax-=．由(31)(53)35a x a x+-=，解得95x a=-．所以27955aa-=-，解得711a=．【总结升华】因为两方程的解相同，可把a看做已知数，分别求出它们的解，令其相等，转化为求关于a的一元一次方程．举一反三：【变式】（2015•温州模拟）已知3x=4y，则= ．【答案】．解：根据等式性质2，等式3x=4y两边同时除以3y，得：=．类型二、一元一次方程的解法3．（2016春•淅川县期中）解方程﹣=．【思路点拨】方程整理后，去分母，去括号，移项合并，把x系数化为1，即可求出解．【答案与解析】解：原方程可化为6x﹣=，两边同乘以6得36x﹣21x=5x﹣7，解得：x=﹣0.7．【总结升华】此题考查了解一元一次方程，注意第一步用到的是分数的基本性质：分子和分母扩大相同的倍数，分数的值不变.举一反三：【变式1】解方程26752254436z z z z z +---++=- 【答案】解：把方程两边含有分母的项化整为零，得 267522544443366z z z z z +++-=--+． 移项，合并同类项得：1122z =，系数化为1得：z ＝1． 【高清课堂：一元一次方程复习 393349 解方程例1（2）】 【变式2】解方程：0.10.050.20.05500.20.54x x +--+=. 【答案】 解：把方程可化为：0.520.550254x x +--+=， 再去分母得：232x =-解得：16x =-4．解方程3{2x-1-[3(2x-1)+3]}＝5．【答案与解析】解：把2x-1看做一个整体．去括号，得：3(2x-1)-9(2x-1)-9＝5．合并同类项，得-6(2x-1)＝14． 系数化为1得：7213x -=-，解得23x =-． 【总结升华】把题目中的2x-1看作一个整体，从而简化了计算过程．本题也可以考虑换元法：设2x-1＝a ，则原方程化为3[a-(3a+3)]＝5．类型三、特殊的一元一次方程的解法1．解含字母系数的方程5.解关于x 的方程：11()(2)34m x n x m -=+ 【思路点拨】这个方程化为标准形式后，未知数x 的系数和常数都是以字母形式出现的，所以方程的解的情况与x 的系数和常数的取值都有关系．【答案与解析】解：原方程可化为：(43)462(23)m x mn m m n -=+=+ 当34m ≠时，原方程有唯一解：4643mn m x m +=-； 当33,42m n ==-时，原方程无数个解； 当33,42m n =≠-时，原方程无解；【总结升华】解含字母系数的方程时，一般化为最简形式ax b =，再分类讨论进行求解，注意最后的解不能合并，只能分情况说明．2．解含绝对值的方程6. 解方程|x-2|＝3．【答案与解析】解：当x-2≥0时，原方程可化为x-2＝3，得x ＝5．当x-2＜0时，原方程可化为-(x-2)＝3，得 x ＝-1．所以x ＝5和x ＝-1都是方程|x-2|＝3的解．【总结升华】如图所示，可以看出点-1与5到点2的距离均为3，所以|x-2|＝3的意义为在数轴上到点2的距离等于3的点对应的数，即方程|x-2|＝3的解为x ＝-1和x ＝5．举一反三：【变式1】若关于x 的方程230x m -+=无解，340x n -+=只有一个解，450x k -+=有两个解，则,,m n k 的大小关系为： ( )A. m n k >>B.n k m >>C.k m n >>D.m k n >>【答案】A【变式2】若9x =是方程123x m -=的解，则__m =；又若当1n =时，则方程123x n -=的解是 ．【答案】1； 9或3． 类型四、一元一次方程的应用7．李伟从家里骑摩托车到火车站，如果每小时行30千米，那么比火车开车时间早到15分钟；若每小时行18千米，则比火车开车时间迟到15分钟，现在李伟打算在火车开车前10分钟到达火车站，求李伟此时骑摩托车的速度应是多少?【思路点拨】本题中的两个不变量为：火车开出的时间和李伟从家到火车站的路程不变．【答案与解析】解：设李伟从家到火车站的路程为y 千米，则有：151530601860y y +=-，解得：452y = 由此得到李伟从家出发到火车站正点开车的时间为4515213060+=(小时)． 李伟打算在火车开车前10分钟到达火车站时，设李伟骑摩托车的速度为x 千米/时, 则有：452271010116060y x ===--(千米/时) 答：李伟此时骑摩托车的速度应是27千米/时．【总结升华】在解决问题时，当发现某种方法不能解决问题时，应该及时变换思维角度，如本题直接设未知数较难时，应迅速变换思维的角度，合理地设置间接未知数以寻求新的解决问题的途径和方法．8.（2015春•万州区校级月考）一项工程，甲单独做要10天完成，乙单独做要15天完成，两人合做4天后，剩下的部分由乙单独做，还需要几天完成？【答案与解析】解：设乙还需x 天完成，由题意得 4×（+）+=1，解得x=5．答：乙还需5天完成．【总结升华】本题考查了一元一次方程的应用，解决问题的关键是找到所求的量的等量关系．当题中没有一些必须的量时，为了简便，可设其为1．举一反三：【变式】某商品进价2000元，标价4000元，商店要求以利润率不低于20%的售价打折出售，售货员最低可以打几折出售此商品？【答案】解：设售货员可以打x 折出售此商品，得：40000.12000(120%),x ⨯=+解得： 6.x =答：售货员最低可以打六折出售此商品．。

《一元一次方程》讲义一、什么是一元一次方程在数学的世界里，方程就像是一座神秘的桥梁，连接着已知和未知。

而一元一次方程，则是这座桥梁中较为基础和常见的一种。

一元一次方程，简单来说，就是指含有一个未知数，并且未知数的最高次数是 1 的整式方程。

我们可以用一个通用的形式来表示一元一次方程：ax ＋ b ＝ 0 （其中a ≠ 0 ）。

这里的“x”就是我们要寻找的未知数，“a”是未知数的系数，“b”则是常数项。

比如说，3x ＋ 5 ＝ 14 就是一个一元一次方程。

在这个方程中，未知数是 x ，系数是 3 ，常数项是 5 和 14 。

二、一元一次方程的求解接下来，让我们一起来探索如何求解一元一次方程。

求解一元一次方程的基本思路就是通过一系列的运算，将方程变形，最终求出未知数的值。

以方程 2x ＋ 7 ＝ 15 为例，我们的目标是让 x 单独在等号的一边。

首先，我们要把常数项 7 移到等号的右边，这时候要注意，移项时要变号，所以得到 2x ＝ 15 7 ，即 2x ＝ 8 。

然后，将方程两边同时除以系数 2 ，得到 x ＝ 4 。

再来看一个稍微复杂一点的方程，比如 5(x 3) ＋ 2 ＝ 17 。

第一步，先把括号展开，得到 5x 15 ＋ 2 ＝ 17 。

接着，合并同类项，5x 13 ＝ 17 。

然后，把－13 移到等号右边，5x ＝ 17 ＋ 13 ，即 5x ＝ 30 。

最后，两边同时除以 5 ，解得 x ＝ 6 。

三、一元一次方程的应用一元一次方程在我们的日常生活中有着广泛的应用。

比如，购物时计算折扣和价格。

假设一件商品原价为 x 元，打 8 折后的价格是 160 元，那么可以列出方程 08x ＝ 160 ，解得 x ＝ 200 ，就知道这件商品的原价是 200 元。

再比如，行程问题。

如果一辆汽车以每小时 60 千米的速度行驶，行驶了 x 小时后，总共行驶了 300 千米，那么可以列出方程 60x ＝300 ，解得 x ＝ 5 ，也就是这辆汽车行驶了 5 小时。